Assessment of Green Innovation Efficiency in Chinese Industrial Enterprises Based on an Improved Relational Two-Stage DEA Approach: Regional Disparities and Convergence Analysis

Abstract

Industrial enterprises are characterized by significant energy consumption and high emissions. Therefore, the implementation of green innovation by these enterprises is beneficial for promoting sustainable economic development and safeguarding the ecological environment. In this study, a relational two-stage DEA model containing shared inputs and undesired outputs is constructed to evaluate and decompose the green innovation efficiency (GIE) of Chinese industrial enterprises across 30 provinces from 2012 to 2021. Since the objective function of this model is nonlinear, a heuristic search method is employed for its resolution. On the basis of efficiency evaluation, the Gini coefficient, kernel density estimation, and convergence analysis are further employed to investigate the regional disparities and convergence properties in the two-stage efficiency of green innovation. Our findings are as follows: (1) The average GIE of Chinese industrial enterprises demonstrates a fluctuating upward trajectory, with significant regional disparities observed between provinces. (2) Regional disparities in R&D efficiency (RDE) and achievement conversion efficiency (ACE) have diminished in all regions. Super-variable density and interregional differences serve as the primary sources of regional disparities in RDE and ACE, respectively. (3) The presence of absolute and conditional convergence in RDE and ACE is observed across all regions. To improve the GIE of Chinese industrial enterprises, it is imperative to emphasize the heterogeneous impact of economic levels, industrial structure, and the degree of openness across various regions and stages of green innovation.

1. Introduction

The rapid development of industrial enterprises has provided robust support for China’s steady economic growth, contributing to nearly 40% of GDP growth and playing a pivotal role in the national economy. However, constrained by historical development stages and the levels of science and technology, the traditional extensive development mode of industrial enterprises persists, resulting in significant resource consumption and ecological degradation [1]. According to the 2022 Environmental Performance Index (EPI) report, China’s EPI score ranks 160th out of 180 countries, indicating a significant constraint on the green and sustainable development of China’s economy. In response to the new era, China has actively pursued the path of green transformation and entered a new stage of high-quality development. The traditional approach of driving industrial economic growth through extensive input of production factors such as capital, labor, and material resources and leveraging scale effects is no longer aligned with the requirements of the new era. Consequently, China has proposed to “vigorously develop the green economy”, with a focus on promoting the establishment of a market-oriented green technology innovation system and implementing pivotal actions in such innovation. Green innovation possesses a unique attribute, which is the organic integration of the two major development concepts of “green” and “innovation”; this not only emphasizes that green development must be achieved through innovative impetus but also underscores that innovative development must be grounded in the enhancement of the ecological environment. Consequently, green innovation has emerged as the driving force and assurance for high-quality development in the new era. As the primary market participants in advancing the achievement of energy conservation and emission reduction targets, the green innovation of industrial enterprises is intricately associated with the transformation and upgrading of the industrial structure, as well as the high-quality development of the economy and society; thus, its significance is progressively gaining prominence.

In this context, it is of significant practical importance to scientifically and accurately assess the green innovation efficiency (GIE) of Chinese industrial enterprises. Moreover, due to objective disparities such as resource endowment and infrastructure levels, substantial variations exist in economic status, industrial structure, degree of openness, and environmental regulatory intensity between different regions in China, which may exert a heterogeneous impact on the development of GIE in industrial enterprises. Therefore, following the evaluation of GIE in Chinese industrial enterprises, it is imperative to further investigate whether regional disparities in GIE exist and whether they are converging toward the same level. This endeavor will contribute to enhancing the GIE of Chinese industrial enterprises and fostering the coordinated development of green innovation across diverse regions.

The main contributions of this study are as follows:

Firstly, this study considers the negative externalities associated with green innovation. The direction of green innovation is constrained, viewing energy consumption as an additional intermediate input and environmental pollution as an undesirable output. Moreover, certain elements in the process of green innovation do not follow a simple linear flow; instead, they may be concurrently utilized as shared resources across different stages. Therefore, this study also accounts for the joint impact of shared inputs on the two stages of green innovation.

Secondly, most of the innovation efficiency evaluation models used in previous studies can be converted into linear models for solving. However, the improved relational two-stage DEA model presented in this paper, with shared inputs and undesired outputs, is difficult to transform into a linear model for solving under the assumption of VRS because of the product of unknown variables in its objective function. To this end, this study uses a heuristic search method to transform it into a linear programming equation with parameters for resolution.

Finally, this study employs the widely utilized Gini coefficient, kernel density estimation, and convergence analysis methods to examine, for the first time, the regional disparities and convergence trends in the two-stage efficiency of green innovation in Chinese industrial enterprises from the perspective of the innovation value chain. In contrast to previous studies focusing on overall innovation efficiency, this paper provides a more detailed exploration of the spatiotemporal characteristics of GIE at different stages.

The remainder of this paper is structured as follows: Section 2 introduces the literature on GIE. Section 3 presents the methods and data, and Section 4 analyzes the main results. Section 5 summarizes the research conclusions and provides policy recommendations.

2. Literature Review

Green innovation is a crucial avenue for promoting sustainable development, offering multiple economic, environmental, and social benefits to enterprises and society. Consequently, the evaluation of GIE has emerged as a significant area of research. From various research perspectives, regional-level studies are primarily focused on national [2,3] and provincial regions [4,5], while industrial-level research is concentrated in the high-tech [6,7] and manufacturing industries [8]. At the enterprise level, the focus is mainly on industrial enterprises [9,10] and new energy enterprises [11,12]. From the perspective of innovation efficiency evaluation methods, Stochastic Frontier Analysis (SFA) and Data Envelopment Analysis (DEA) have gradually emerged as the mainstream methods for evaluating efficiency.

SFA is a parameter analysis method proposed by Aigner et al. [13] that takes into account the impact of random errors on the results and evaluates efficiency through the stochastic frontier production function. This method has been widely utilized across various fields [14,15]. While SFA considers the impact of random factors on outputs, it is not suitable for evaluating the efficiency of decision-making units (DMUs) with multiple outputs [6]. In contrast, DEA, proposed by Charnes et al. [16], is a nonparametric efficiency evaluation method that does not require fixed production functions and predetermined parameter weights; it also does not necessitate dimensional consistency of input and output indices, making it suitable for evaluating the relative efficiency between homogeneous DMUs with multiple inputs and outputs. DEA has gained popularity as an efficiency evaluation method in various fields [17,18]. When evaluating the GIE in industrial enterprises, several challenges arise. Firstly, the innovation process involves multiple inputs and outputs, making it difficult to determine the specific form of the production function. Secondly, there is a significant difference in the dimensionality of the input and output indicators, which is challenging to estimate using parameter methods. Therefore, it is more appropriate to apply DEA to evaluate the GIE of industrial enterprises.

Currently, the application of DEA to evaluate innovation efficiency can be categorized into two approaches: one treats the innovation process as a “black box” [19,20,21], while the other divides the innovation process into different interrelated stages [22,23,24] and examines the overall and stage efficiency of innovation. As innovation is a long-term process that involves steps [25] such as exploration, selection, implementation, and value acquisition, it is more reasonable to divide the green innovation process into different stages for efficiency assessment.

To open the “black box” for efficiency evaluation, Paradi et al. [26] and Zhang et al. [27] utilize the classical DEA model to calculate the efficiency of the two stages, but they approach the two-stage production system as independent stages, disregarding the coherence of the intermediate outputs as the outputs of the first stage and the inputs of the second stage. Wang et al. [28] developed an additive two-stage DEA model with the objective function weighted by sub-stage efficiency, which is applicable to the assumptions of constant returns to scale (CRS) and variable returns to scale (VRS). However, the weighted average of the efficiency scores for both stages is only applicable under specific weight choices. Kao and Hwang [29] constructed a relational two-stage DEA model with an objective function based on the product of sub-stage efficiency, which is considered to be more reasonable but is only applicable to the assumption of CRS. In the assumption of VRS, the model cannot be transformed into a linear model for solving due to the product of unknown variables in its objective function. The CRS hypothesis is valid only when all DMUs are operating at the optimal production scale, while the VRS hypothesis is more in line with the actual situation of large differences in the production scale of industrial enterprises. Additionally, the utilization of relational models for evaluating the efficiency of complex network production systems with nonlinear flow characteristics of innovative resources has been limited. This constraint also arises from the inclusion of the product of unknown variables in the objective function, resulting in an intractable programming equation. Therefore, our study aims to improve the relational model proposed by Kao, adapting it to complex network production structures and extending it from CRS to VRS. This adaptation is intended to better align with the actual circumstances of green innovation within industrial enterprises.

Furthermore, scholars have yet to reach a consensus on the selection of input and output indicators for green innovation. Nevertheless, the prevailing tendency is to consider input indicators from the perspectives of labor and capital while emphasizing the output indicators on the basis of scientific and technological achievements, overlooking the energy consumption and environmental pollution inherent in the green innovation process. Given that green innovation integrates the concepts of “innovation” and “green” development, it is imperative to incorporate considerations of energy consumption and environmental pollution into the indicator system. Additionally, within the innovation systems constructed by these scholars, resources often exhibit one-way, linear flows, with minimal regard for the sharing of resources in complex network structures. Resource inputs, such as fixed assets, can contribute throughout all stages of the innovation process, and recognizing them as shared resources can provide a more accurate reflection of the real situation with respect to innovation.

Therefore, this study considers the shared input of fixed assets, the intermediate input of energy consumption, and the undesired output of environmental pollution and constructs an improved relational two-stage DEA model to evaluate the GIE of Chinese industrial enterprises. Then, the heuristic search method is used for solving the model.

Gini coefficient decomposition and kernel density estimation are commonly employed to analyze regional disparities. Gini coefficient decomposition allows for visual observation of indicators and facilitates comparison of differences while also addressing the crossover issues between sample data [30]. On the other hand, kernel density estimation provides an intuitive way to observe dynamic evolutionary trends and to identify spatial patterns of evolution [31]. Convergence analysis is also frequently utilized to explore regional disparities, encompassing σ convergence, absolute β convergence, and conditional β convergence [32]. The utilization of these methodologies has led scholars to derive fruitful results in the investigation of regional differences and convergence trends in innovation efficiency. However, the current research on regional disparities [31,33] and convergence properties [34,35] mainly focuses on overall innovation efficiency, with few studies investigating the regional disparities and convergence of efficiency at different stages from the perspective of the innovation value chain. Therefore, based on the calculation of stage efficiency, this study further analyzes the regional disparities and convergence characteristics of GIE at different stages.

3. Methodology and Data

3.1. Measurement of Green Innovation Efficiency

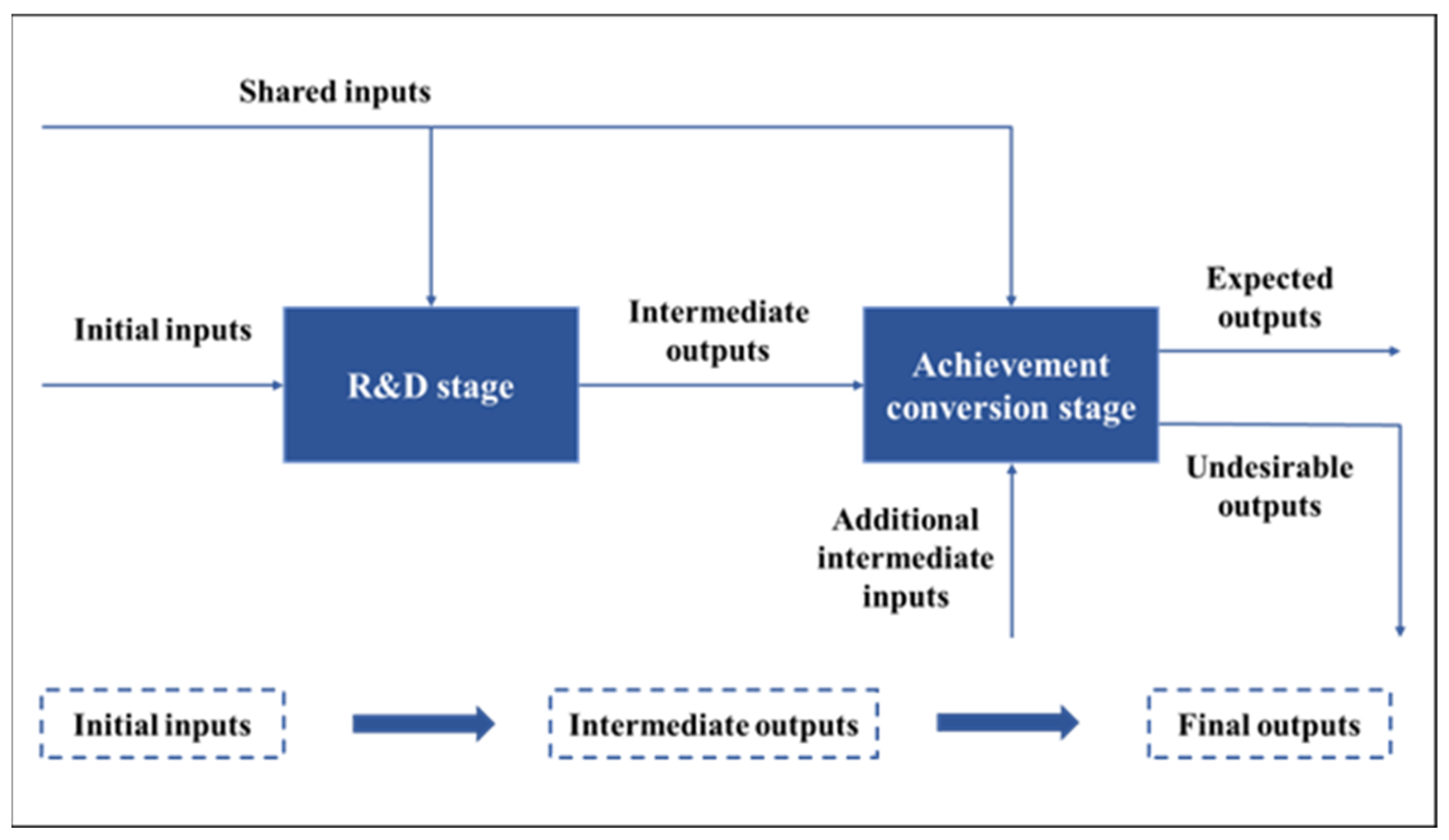
3.1.1. Green Innovation Process of Industrial Enterprises

The green innovation within industrial enterprises is a complex, dynamic, and multi-stage endeavor. In contrast to the early holistic theory of innovation, which overlooked the internal structure of technological innovation and led to the “black box” deconstruction dilemma of the innovation process, the study of green innovation now places greater emphasis on its internal operating mechanisms. This necessitates the deconstruction and analysis of the various stages of the innovation process. For instance, Hall and Sharmistha [36] proposed that the innovation process of enterprises comprises stages of basic research, applied research, and commercial value realization. Similarly, Chen et al. [37] delineated the innovation process of the Chinese high-tech industry into the research and development (R&D) stage and the commercialization stage. These studies share common characteristics, as they all partition the innovation process into interrelated and synergistic stages. At each stage of innovation, specific innovative products or services are generated based on the input of production factors.

From the perspective of the value chain [38,39], the green innovation activities of enterprises constitute a dynamic process that initially involves the transformation of various innovation resources into innovation achievements. Subsequently, these innovation achievements are integrated with a diverse range of production factors to collectively impact the production and operational processes of enterprises, ultimately leading to the realization of economic benefits and environmental effects. Therefore, unlike the innovation activities of scientific research institutions [40], which aim at scientific discovery or pure technological progress, the green innovation of industrial enterprises represents a process that is both discrete and unified in terms of “technology”, “economy”, and “environment”. Based on the “innovation value chain” theory of Hansen and Birkinshaw [41] and the innovation chain structure proposed by Furman et al. [42], and further integrating the development characteristics of industrial enterprises, the green innovation process of industrial enterprises can be divided into two stages: R&D, and achievement conversion, as illustrated in Figure 1. During the R&D stage, the enterprise invests labor, material resources, and capital with the aim of transforming them into technology, patents, and other forms of innovation achievements with practical value. Subsequently, the enterprise progresses to the achievement conversion stage, where the primary focus is on integrating the innovation outcomes obtained in the R&D stage with a series of specific production inputs. Through the production and operation processes, the enterprise endeavors to convert these innovation outcomes into economic benefits for the enterprise. Given the high energy consumption and emissions characteristic of industrial enterprises, this stage is often accompanied by significant energy consumption and environmental pollutants. It is noteworthy that throughout the entire process of green innovation, certain resources, such as the fixed assets of enterprises, not only play a role in the R&D stage but also significantly influence the output of the achievement conversion phase. These resources are thus considered to be shared inputs [37,40,43] and are allocated and utilized proportionally between the two phases.

3.1.2. Design of Green Innovation Efficiency Evaluation Index

(1)

Inputs and outputs in the R&D stage

In previous studies, R&D personnel and R&D expenses [4,37,40,44,45] have frequently been utilized to quantify innovation inputs during the R&D stage. In line with these studies, we selected the full-time equivalent of R&D personnel and intramural expenditure on R&D as key innovation inputs. It is important to note that, due to the cumulative effect of R&D expenditure, we employ the perpetual inventory method [46] to calculate the stock of intramural expenditure on R&D, as demonstrated in Equation (1):

$$K_t=\left(1-\delta \right)\times K_{t-1}+R_{t-1}$$

(1)

where $K_t$ and $K_{t-1}$ represent the stock of R&D investment in phases t and t − 1, respectively. The symbol $\delta$ denotes the depreciation rate, set at 15% [47], while $R_{t-1}$ represents the actual intramural expenditure on R&D in phase t − 1. In order to eliminate the influence of price fluctuations, the R&D price index was constructed in a base period of 2012 to deflate the intramural expenditure on R&D.

It is evident that fixed assets play a significant role in both stages (R&D and achievement conversion); thus, they are commonly regarded as shared inputs in the green innovation process. Consistent with the study of Chen et al. [37], we selected the fixed assets of industrial enterprises as shared inputs.

The output of the R&D stage primarily consists of scientific and technological achievements, among which patents are considered to be one of the indicators that most closely reflect the outcomes of technological innovation [6,48,49,50,51]. However, as noted by Griliches [52], not all innovations are patented. Therefore, this study also includes the count of new product items as another output of R&D.

(2)

Inputs and outputs in the achievement conversion stage

The inputs in the achievement conversion stage can be categorized into three components: the first being the outputs from the R&D stage, the second being the shared inputs utilized by both stages, and the third being the non-R&D additional intermediate inputs aimed at facilitating the transformation of technological achievements. These additional intermediate inputs encompass labor and capital inputs [37], quantified in terms of employed personnel and expenditures on the acquisition and renovation of technology, respectively. Furthermore, taking into account the energy-intensive nature of industrial enterprises, energy consumption [4,5] is incorporated into the input index (

Table 1. Input and output indicators in green innovation process.

Green Innovation Process	Variable	Unit	Source
Initial inputs	Full-time equivalent of R&D personnel	Man-year	China Science and Technology Statistical Yearbook
	Intramural expenditure on R&D	CNY 10,000	China Science and Technology Statistical Yearbook
Shared inputs	Fixed assets	CNY 100 million	China Industrial Statistical Yearbook
Intermediate outputs	Number of patent applications	Piece	China Science and Technology Statistical Yearbook
	Number of new product items	Piece	China Science and Technology Statistical Yearbook
Additional intermediate inputs	Employed personnel	10,000 person	China Industrial Statistical Yearbook
	Expenditures on the acquisition and renovation of technology	CNY 10,000	China Science and Technology Statistical Yearbook
	Energy consumption	10,000 tons of standard coal	China Statistical Yearbook
Expected outputs	Sales revenue of new products	CNY 10,000	China Science and Technology Statistical Yearbook
Undesirable outputs	Environmental pollution index	/	China Environmental Statistical Yearbook

).

The outputs of this stage primarily encompass two aspects: the expected economic benefits and the undesirable environmental effects. In terms of economic benefits, sales revenue of new products was chosen as the measurement metric. Regarding environmental impact, an environmental pollution index was developed to gauge the environmental externalities [51] in the green innovation process, utilizing pollution indicators such as industrial wastewater, waste gas, and solid waste.

3.1.3. An Improved Relational Two-Stage DEA Model

The traditional DEA model treats the green innovation process as a black box, leading to certain limitations, as it overlooks the internal structure of green innovation and fails to account for resource allocation across different stages. As an improvement to the traditional DEA, network DEA takes into account the internal structure of the innovation process, reconstructs the production frontier of the DMU, and can utilize the input and output data from each stage in the evaluation process, which is effectively consistent with green innovation from the perspective of the value chain. Therefore, based on the green innovation processes of industrial enterprises, this study establishes an improved two-stage network DEA model to measure the overall efficiency and stage efficiency of green innovation in industrial enterprises.

Suppose that there are $n$ DMUs, denoted as ${DMU}_j(j=1,\dots ,n)$. During the R&D stage, each DMU consumes $m$ regular inputs $X_{ij}(i=1,\dots ,m)$ and $P$ shared inputs $H_{pj}(p=1,\dots ,P)$ to produce $D$ intermediate outputs $Z_{dj}(d=\mathrm{1,2},\dots ,D)$. During the achievement conversion stage, each DMU generates $s$ expected outputs $Y_{rj}(r=1,\dots ,s)$ and $B$ undesirable outputs $Q_{bj}(b=1,\dots ,B)$ by utilizing the $P$ shared inputs $H_{pj}(p=1,\dots ,P)$, $D$ intermediate outputs $Z_{dj}(d=1,\dots ,D)$, and $K$ additional intermediate inputs $R_{kj}(k=1,\dots ,K)$. Note that $H_{pj}$ is the shared input for the two stages and $Z_{dj}$ is the intermediate output connecting the two stages. We assume that the allocative factor ${\omega }_p(0\le {\omega }_p\le 1)$ represents the proportion of shared inputs used in the R&D stage. Thus, ${\omega }_p{H}_{pj}$ and $\left(1-{\omega }_p\right) H_{pj}$ correspond to the shared inputs flowing into the first and second stages, respectively.

Since environmental pollution (an undesirable output) is a byproduct brought about by industrial enterprises in the achievement conversion stage, it is hoped that the less environmental pollution, the better when evaluating the GIE. Therefore, to address this issue, this study adopts the transformation method proposed by Seiford and Zhu [53] to handle undesirable outputs. This method is implemented as follows: Each undesirable output is first multiplied by −1, and then a suitable conversion vector $V_b$ is added to make the undesirable output positive; that is, ${\overline{Q}}_{bj}=-Q_{bj}+V_b(b=1,\dots ,B)$, $V_b={max}_j\left\{Q_{bj}\right\}+1,b\in B$. After the conversion, the larger the $Q_{bj}$, the smaller the ${\overline{Q}}_{bj}$. In the situation of VRS, this method provides the same efficient frontier.

In this study, the GIE is decomposed into R&D efficiency (RDE) and achievement conversion efficiency (RDE). Following the general practice, it is assumed that the DMU to be evaluated is denoted as ${DMU}_0$, and the RDE and ACE are denoted as $e_{10}$ and $e_{20}$, respectively. Under the assumption of VRS, the expression of stage efficiency can be obtained via Equations (2) and (3):

$$e_{10}={\displaystyle \frac{{\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\mu }^1}{{\Sigma }_{i=1}^m{v}_i{X}_{i0}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{p0}}}$$

(2)

$$e_{20}={\displaystyle \frac{{\Sigma }_{r=1}^s{u}_r{Y}_{r0}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{b0}+{\mu }^2}{{\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\Sigma }_{p=1}^P{\tau }_p\left(1-{\omega }_p\right)H_{p0}+{\Sigma }_{k=1}^K{\eta }_k{R}_{k0}}}$$

(3)

where $v_i$, ${\pi }_d$, ${\tau }_p$, ${\eta }_k, u_r,$ and ${\xi }_b$ are the nonnegative multipliers related to $X_{ij}$, $Z_{dj}$, $H_{pj}$, $R_{kj}, Y_{rj}$, and ${\overline{Q}}_{bj}$, respectively, while ${\mu }^1$ and ${\mu }^2$ are free variables associated with $Z_{dj}$ and $Y_{rj}$ ${\overline{Q}}_{bj}$, respectively.

According to Kao and Hwang [29], the overall efficiency of green innovation, $e_0$, is defined as the product of the efficiencies of two stages.

$$e_0=e_{10}\times e_{20}$$

(4)

Then, the GIE of the evaluated ${DMU}_0$ can be obtained via the following model:

$$\begin{gathered} {maxe}_0={max(e}_{10}\times e_{20})= \\ max\left({\displaystyle \frac{{\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\mu }^1}{{\Sigma }_{i=1}^m{v}_i{X}_{i0}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{p0}}}\ast {\displaystyle \frac{{\Sigma }_{r=1}^s{u}_r{Y}_{r0}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{b0}+{\mu }^2}{{\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\Sigma }_{p=1}^P{\tau }_p\left(1-{\omega }_p\right)H_{p0}+{\Sigma }_{k=1}^K{\eta }_k{R}_{k0}}}\right) \\ s.t. {\displaystyle \frac{{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\mu }^1}{{\Sigma }_{i=1}^m{v}_i{X}_{ij}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{pj}}}\le 1, \forall j \\ {\displaystyle \frac{{\Sigma }_{r=1}^s{u}_r{Y}_{rj}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{bj}+{\mu }^2}{{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\Sigma }_{p=1}^P{\tau }_p\left(1-{\omega }_p\right)H_{pj}+{\Sigma }_{k=1}^K{\eta }_k{R}_{kj}}}\le 1, \forall j \\ {L}_p\le {\omega }_p\le U_p, \forall p \\ {v}_i,{\pi }_d,{\tau }_p,{\eta }_k,u_r,{\xi }_b\ge 0, \forall i,d,p,k,r,b \\ {\mu }^1,{\mu }^2 free \end{gathered}$$

(5)

The objective function of Model (5) represents the GIE of an industrial enterprise as the product of RDE and ACE, with the first two constraints ensuring that the efficiency value of the sub-stage does not exceed 1, while the third constraint avoids the extreme situation where the proportion of shared inputs consumed in the two stages reaches 0 or 1. According to the research of Kao et al. [29] and Liang et al. [54], the weight of the intermediate output is the same regardless of whether it is the output in the first stage or the input in the second stage. This is because the intermediate output connects two sub-stages and represents a serial relationship [55] between the two sub-stages.

Model (5) is a fractional programming problem, which is challenging to transform into a linear model due to the presence of free variables, shared inputs, and additional intermediate inputs. To address this issue, the heuristic search method proposed by Li et al. [56] can be employed. The following steps can be considered:

$$\begin{gathered} \mathit{max}{e}_{10}=max{\displaystyle \frac{{\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\mu }^1}{{\Sigma }_{i=1}^m{v}_i{X}_{i0}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{p0}}} \\ s.t. {\displaystyle \frac{{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\mu }^1}{{\Sigma }_{i=1}^m{v}_i{X}_{ij}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{pj}}}\le 1, \forall j \\ {\displaystyle \frac{{\Sigma }_{r=1}^s{u}_r{Y}_{rj}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{bj}+{\mu }^2}{{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\Sigma }_{p=1}^P{\tau }_p\left(1-{\omega }_p\right)H_{pj}+{\Sigma }_{k=1}^K{\eta }_k{R}_{kj}}}\le 1, \forall j \\ {L}_p\le {\omega }_p\le U_p, \forall p \\ {v}_i,{\pi }_d,{\tau }_p,{\eta }_k,u_r,{\xi }_b\ge 0, \forall i,d,p,k,r,b \\ {\mu }^1,{\mu }^2 free \end{gathered}$$

(6)

The optimal objective function value of Model (6) is denoted as $e_{10}^{\mathrm{*}}$. Then, the maximum possible value of RDE is $e_{10}^{\mathrm{*}}$. Therefore, the value range of RDE is (0, $e_{10}^{\mathrm{*}}$]. Model (6) is also a fractional programming problem but can be converted to a linear model by means of the Charnes–Cooper (C-C) transformation. Model (6) is equivalent to the following linear programming model:

$$\begin{gathered} \mathit{max}{e}_{10}=max({\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\mu }^1) \\ s.t. {\Sigma }_{i=1}^m{v}_i{X}_{i0}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{p0}=1 \\ {\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\mu }^1-{\Sigma }_{i=1}^m{v}_i{X}_{ij}-{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{pj}\le 0, \forall j \\ {\Sigma }_{r=1}^s{u}_r{Y}_{rj}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{bj}+{\mu }^2-{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}-{\Sigma }_{p=1}^P{\tau }_p{H}_{pj}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{pj}-{\Sigma }_{k=1}^K{\eta }_k{R}_{kj}\le 0, \forall j \\ {L}_P{\tau }_p-{\tau }_p{\omega }_p\le 0, \forall p \\ {\tau }_p{\omega }_p-U_p{\tau }_p\le 0, \forall p \\ {v}_i,{\pi }_d,{\tau }_p,{\eta }_k,u_r,{\xi }_b\ge 0, \forall i,d,p,k,r,b \\ {\mu }^1,{\mu }^2 free \end{gathered}$$

(7)

Model (7) is a standard linear programming equation, so it can be solved directly. The $e_{10}^{\mathrm{*}}$ obtained by solving Model (7) is equivalent to that of Model (6). Since $e_{10}$∈ (0, $e_{10}^{\mathrm{*}}$], $e_{10}$ can be viewed as a known variable within a range of values when measuring the overall GIE. Therefore, the original Model (5) can be expressed as follows:

$$\begin{gathered} {maxe}_0=max(e_{10}\times e_{20})= \\ max\left(e_{10}\ast {\displaystyle \frac{{\Sigma }_{r=1}^s{u}_r{Y}_{r0}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{b0}+{\mu }^2}{{\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\Sigma }_{p=1}^P{\tau }_p\left(1-{\omega }_p\right)H_{p0}+{\Sigma }_{k=1}^K{\eta }_k{R}_{k0}}}\right) \\ s.t. {\displaystyle \frac{{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\mu }^1}{{\Sigma }_{i=1}^m{v}_i{X}_{ij}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{pj}}}\le 1, \forall j \\ {\displaystyle \frac{{\Sigma }_{r=1}^s{u}_r{Y}_{rj}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{bj}+{\mu }^2}{{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\Sigma }_{p=1}^P{\tau }_p\left(1-{\omega }_p\right)H_{pj}+{\Sigma }_{k=1}^K{\eta }_k{R}_{kj}}}\le 1, \forall j \\ {L}_p\le {\omega }_p\le U_p, \forall p \\ {e}_{10}\in [0,e_{10}^{*}] \\ {v}_i,{\pi }_d,{\tau }_p,{\eta }_k,u_r,{\xi }_b\ge 0, \forall i,d,p,k,r,b \\ {\mu }^1,{\mu }^2 free \end{gathered}$$

(8)

Model (8) is also a fractional program, which can be transformed into the following model via C-C transformation:

$$\begin{gathered} {maxe}_0=max[e_{10}\ast \left({\Sigma }_{r=1}^s{u}_r{Y}_{r0}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{b0}+{\mu }^2\right)] \\ s.t. {\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\Sigma }_{p=1}^P{\tau }_p{H}_{p0}-{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{p0}+{\Sigma }_{k=1}^K{\eta }_k{R}_{k0}=1 \\ { \Sigma }_{d=1}^D{\pi }_d{Z}_{dj}+{\mu }^1-{\Sigma }_{i=1}^m{v}_i{X}_{ij}-{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{pj}\le 0,\forall j \\ {\Sigma }_{r=1}^s{u}_r{Y}_{rj}+{\Sigma }_{b=1}^B{\xi }_b{\overline{Q}}_{bj}+{\mu }^2-{\Sigma }_{d=1}^D{\pi }_d{Z}_{dj}-{\Sigma }_{p=1}^P{\tau }_p{H}_{pj}+{\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{pj}-{\Sigma }_{k=1}^K{\eta }_k{R}_{kj}\le 0,\forall j \\ {L}_p{\tau }_p-{\tau }_p{\omega }_p\le 0,\forall p \\ {\tau }_p{\omega }_p-U_p{\tau }_p\le 0,\forall p \\ {\Sigma }_{d=1}^D{\pi }_d{Z}_{d0}+{\mu }^1-e_{10}\ast {\Sigma }_{i=1}^m{v}_i{X}_{i0}-e_{10}\ast {\Sigma }_{p=1}^P{\tau }_p{\omega }_p{H}_{p0}=0 \\ {e}_{10}\in [0,e_{10}^{*}] \\ {v}_i,{\pi }_d,{\tau }_p,{\eta }_k,u_r,{\xi }_b\ge 0, \forall i,d,p,k,r,b \\ {\mu }^1,{\mu }^2 free \end{gathered}$$

(9)

In order to compute the optimal solution for Model (9), we set $e_{10}=e_{10}^{\mathrm{*}}-t\ast \epsilon$. Here, $\epsilon$ represents the step size of the heuristic search method, and the smaller the value of $\epsilon$, the more accurate the result; $t=0,\dots ,\left[t_{max}\right]$, where $\left[t_{max}\right]$ is the largest integer that $e_{10}^{\mathrm{*}}/\epsilon$ can attain. When solving Model (9), $t$ is gradually increased from the initial value 0 to $\left[t_{max}\right]$ as the step size increases. For each value of $t$, a specific $e_{10}\left(t\right)$ can be obtained. At this stage, Model (9) no longer includes the product of unknown parameters, and it can be solved as a linear programming problem. The optimal objective function value of Model (9) for each $t$ is represented as $e_0^{\mathrm{*}}\left(t\right)$. Subsequently, the global optimal solution for the overall GIE can be determined as $e_0^{\mathrm{*}}=\underset{t}{\mathrm{m}\mathrm{a}\mathrm{x}{e}_0^{\mathrm{*}}\left(t\right)}$. When ${DMU}_0$ achieves the optimal overall efficiency value of green innovation, denoted as $e_0^{\mathrm{*}}$, the RDE value is $e_{10}\left(t^{\mathrm{*}}\right)=e_{10}^{\mathrm{*}}-t^{\mathrm{*}}\ast \epsilon$. At this time, the value of $t^{\mathrm{*}}$ makes the corresponding $e_0^{\mathrm{*}}\left(t^{\mathrm{*}}\right)$ equal to the optimal overall efficiency value of green innovation $e_0^{\mathrm{*}}$. Therefore, the corresponding ACE value is $e_{20}\left(t^{\mathrm{*}}\right)={\displaystyle \frac{e_0^{\mathrm{*}}}{e_{10}\left(t^{\mathrm{*}}\right)}}=e_0^{\mathrm{*}}/{(e}_{10}^{\mathrm{*}}-t^{\mathrm{*}}\ast \epsilon )$.

3.2. Research Methods on Regional Disparities of Green Innovation Efficiency

3.2.1. Dagum Gini Coefficient and Its Decomposition

In this study, the Dagum Gini coefficient and its decomposition method were employed to investigate regional disparities and the sources of green innovation efficiency among China’s industrial enterprises. The calculation method is outlined as follows:

$$G=\sum _{j=1}^k\sum _{h=1}^k\sum _{i=1}^{n_j}\sum _{r=1}^{n_h}\left|E_{ji}-E_{hr}\right|/2n^2\overline{E}$$

(10)

where $G$ represents the overall Gini coefficient, $n$ denotes the number of provinces, $k$ signifies the number of subgroups, $E_{ji}$ ($E_{hr}$) denotes the RDE or ACE of industrial enterprises in province $i$ ($r$) in region $j$ ($h$), and $\overline{E}$ represents the average RDE or ACE of industrial enterprises across all provinces.

Then, the overall regional disparities $G$ can be further decomposed into the within-region difference contribution ($G_w$), between-region difference ($G_{nb}$), and transvariation intensity ($G_t$).

$${ G}_w=\sum _{j=1}^k{G}_{jj}{p}_j{s}_j$$

(11)

$${ G}_{nb}=\sum _{j=2}^k\sum _{h=1}^{j-1}{G}_{jh}{D}_{jh}(p_j{s}_h+p_h{s}_j)$$

(12)

$$G_t=\sum _{j=2}^k\sum _{h=1}^{j-1}{G}_{jh}{(1-D}_{jh}\left)\right(p_j{s}_h+p_h{s}_j)$$

(13)

3.2.2. Kernel Density Estimation

Kernel density estimation is a crucial nonparametric estimation method that has been widely utilized in the analysis of spatially disparate distributions. Suppose that the probability density function $f\left(x\right)$ of a random variable $X$ [57] is as follows:

$$f(x)={\displaystyle \frac{1}{Nh}}\sum _{i=1}^{N}K\left({\displaystyle \frac{X_i-\overline{X}}{h}}\right)$$

(14)

where $K(·)$ represents the kernel function and $h$ is the bandwidth. In this study, the Gaussian kernel is employed to estimate the distribution dynamics of RDE and ACE.

3.3. Methodology for Assessing the Convergence of Green Innovation Efficiency

(1)

σ Convergence

The σ convergence can indicate whether the disparity in GIE among industrial enterprises in different regions decreases over time. As the coefficient of variation allows for the comparison of data indicators across different dimensions, this study employed the unweighted coefficient of variation to assess the RDE and ACE of industrial enterprises:

$${\mathsf{\sigma }}_j={\displaystyle \frac{\sqrt{\sum _i^{N_j}{(y_{ij}-\overline{y_{ij}})}^2/N_j}}{\overline{y_{ij}}}}$$

(15)

where $j$ represents the region, $i$ represents the province, $y$ represents RDE or ACE, and $\overline{y}$ represents the mean of RDE or ACE.

(2)

β Convergence

Absolute β convergence refers to the convergence in the GIE of industrial enterprises in each region to the same level over time without taking into account regional heterogeneity factors. Conditional β convergence is where the GIE of industrial enterprises in different regions shows a converging trend under the influence of regional heterogeneity. The model settings are presented below.

$$\ln \left({\displaystyle \frac{y_{i,t+1}}{y_{i,t}}}\right)=\alpha +\beta ln{y}_{i,t}+\gamma {lncontrol}_{i,t+1}+{\mu }_i+{\eta }_t+{\epsilon }_{it}$$

(16)

Here, $\beta$ represents the convergence coefficient. If $\beta$ is less than 0 and passes the significance test, this indicates that the GIE of Chinese industrial enterprises exhibits β convergence; otherwise, it diverges. Meanwhile, $\gamma$ is the parameter to be estimated for the control variables. When there is no control variable in the model, it is the absolute β convergence test; otherwise, it is the conditional β convergence test.

By examining the positive and negative properties, as well as the significance of $\beta$ and $\gamma$, we can assess whether the GIE converges in each region to its own steady state and identify the primary factors influencing its convergence. Furthermore, the estimated $\beta$ coefficient of convergence can be used to calculate the convergence rate ($s$) and the half-life period ($\tau$), as demonstrated in Formula (17):

$$s=-{\displaystyle \frac{\mathit{ln}\left(1+\beta \right)}{T}}, \tau ={\displaystyle \frac{ln\left(2\right)}{s}}$$

(17)

Based on relevant studies, we selected the following control variables for this study:

Level of economic development ($PGDP$): GDP serves as a crucial indicator of regional economic strength, and real per capita GDP [4] was chosen as an indicator.

Degree of openness ($OPEN$): Regions with a high degree of openness can acquire advanced technology and management expertise. Hence, we utilize the ratio of total imports and exports of goods to GDP [58,59] as an expression of this openness.

Industrial structure ($INDU$): With the transformation and upgrading of the industrial structure, the demand for environmental protection and sustainable development is increasing. This trend provides greater impetus and opportunities for industrial enterprises to engage in green innovation. Therefore, we chose the ratio of value added in the tertiary industry to the secondary industry [60] as a representation.

Environmental regulation ($ER$): Due to the environmental externalities of green innovation, it necessitates government intervention through environmental regulation [61]. Therefore, we selected the ratio of industrial pollution control investment to industrial added value as an indicator.

Government R&D subsidies ($GOV$): The spillover effect of knowledge results in positive externalities in green innovation. Government subsidies for R&D can alleviate these positive externalities [62] in green innovation, thereby fostering enterprises’ enthusiasm for green innovation. Consequently, we assess it by examining the proportion of government funding within R&D investments.

Human capital ($HC$): Human capital serves as a significant driving force for enterprise technological innovation [63], directly influencing the selection of the initial technological path of enterprises. Therefore, this study employs the proportion of college students to the total population to reflect the level of human capital.

3.4. Sample Selection and Data Sources

This study selected industrial enterprises above the designated size in 30 regions (including provinces, autonomous regions, and municipalities directly under the Central Government) in China as samples. Industrial enterprises above the designated size are defined as enterprises with an annual main business income of CNY 20 million or more, encompassing a variety of sectors such as light and heavy industries, mining, processing, and manufacturing. It is important to note that Tibet, Hong Kong, Macau, and Taiwan were excluded from this study due to data unavailability. Furthermore, given that the output results of green innovation processes often exhibit a high level of real-time performance, especially the undesired output (environmental pollutants) is generated in real time along with the production of industrial enterprises, the potential influence of lag time on the output results is not considered in this study.

Influenced by historical and regional characteristics, China’s regional industrial innovation system exhibits significant differences. To further explore these regional disparities and convergence trends, this study aims to assess and analyze the green innovation efficiency of China’s regional industrial enterprises from four perspectives: eastern, central, western, and overall. The division of regions into east, central, and west is predicated on varying levels of economic development from high to low rather than conforming to administrative or geographical boundaries. Currently, the eastern region comprises 11 provincial-level administrative regions, the central region encompasses 8 provincial-level administrative regions, and the western region includes 12 provincial-level administrative regions (including Tibet). However, due to data unavailability in Tibet, the eastern, central, and western regions discussed in this paper consist of 11, 8, and 11 provincial-level administrative regions, respectively.

The primary data sources for this study consist of the China Statistical Yearbook (2013–2022), China Industrial Statistical Yearbook (2013–2022), China Science and Technology Statistical Yearbook (2013–2022), China Environmental Statistical Yearbook (2013–2022), and the provincial Statistical Yearbooks (2013–2022). The study period spans from 2012 to 2021. Specifically, the total energy consumption is determined by multiplying the actual consumption quantities of various types of energy by the corresponding coal equivalent coefficient and then aggregating the results. And the environmental pollution index is calculated by using the entropy method for industrial wastewater, exhaust gases, and solid waste.

4. Results

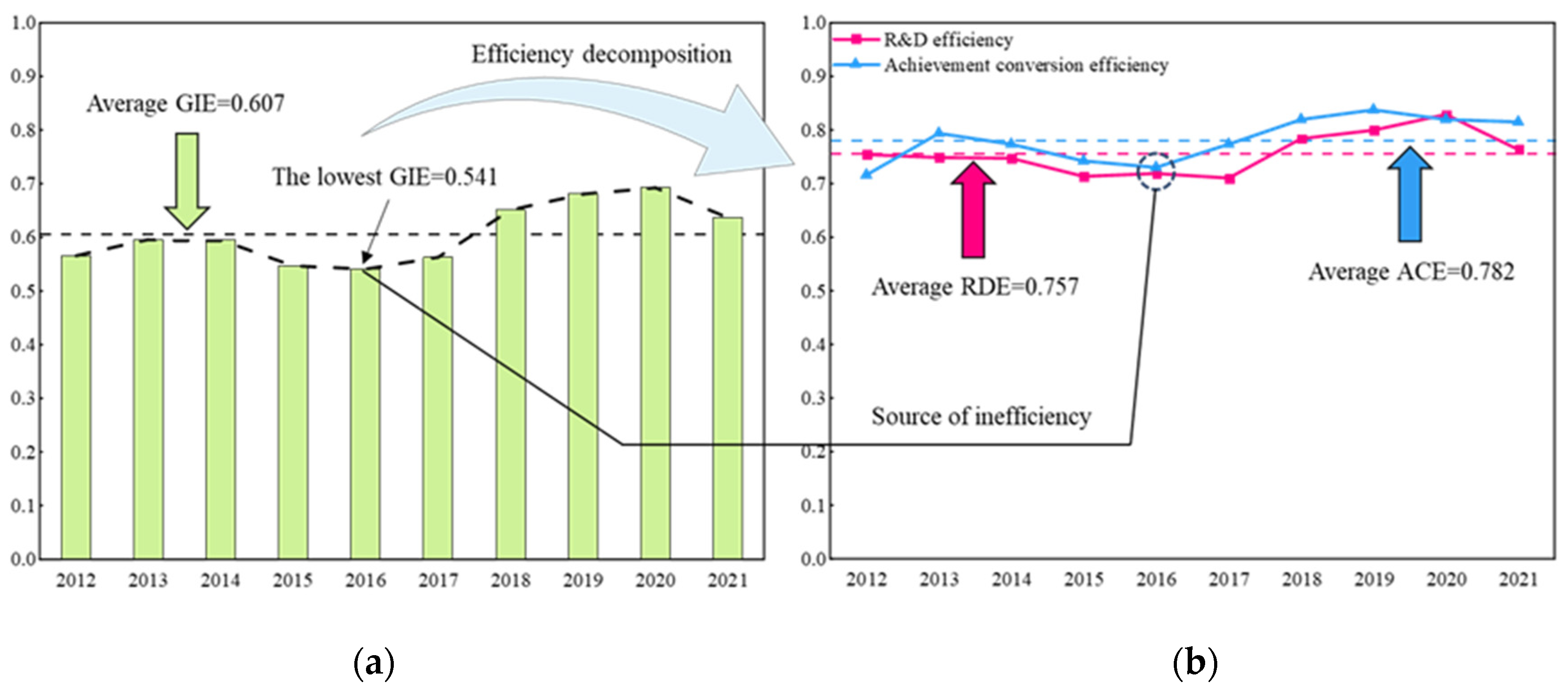
4.1. Results of Green Innovation Efficiency Measurement

Following the methodology outlined above, the GIE, RDE, and ACE of industrial enterprises in 30 provinces of China from 2012 to 2021 were calculated using MATLAB (R2018a). Due to space limitations, only the data for the year 2021 are presented in

Table 2. Average GIE of industrial enterprises by province from 2012 to 2021.

Region	Province	GIE	Rank	RDE	Rank	ACE	Rank
Eastern	Beijing	1.000	1	1.000	1	1.000	1
	Tianjin	0.845	8	0.931	7	0.908	15
	Hebei	0.686	14	0.828	11	0.828	17
	Liaoning	0.426	22	0.588	25	0.725	21
	Shanghai	0.847	7	0.847	9	1.000	1
	Jiangsu	0.692	13	0.692	19	1.000	1
	Zhejiang	1.000	1	1.000	1	1.000	1
	Fujian	0.331	28	0.566	26	0.585	26
	Shandong	0.709	12	0.720	17	0.984	11
	Guangdong	1.000	1	1.000	1	1.000	1
	Hainan	1.000	1	1.000	1	1.000	1
Western	Inner Mongolia	0.540	18	0.718	18	0.752	20
	Guangxi	0.626	17	0.804	14	0.779	19
	Chongqing	0.643	16	0.669	20	0.961	14
	Sichuan	0.393	26	0.812	12	0.484	27
	Guizhou	0.274	29	0.602	24	0.456	29
	Yunnan	0.233	30	0.550	27	0.424	30
	Shaanxi	0.419	23	0.534	28	0.785	18
	Gansu	0.396	25	0.662	23	0.598	24
	Qinghai	1.000	1	1.000	1	1.000	1
	Ningxia	0.397	24	0.664	21	0.597	25
	Xinjiang	0.447	20	0.946	6	0.473	28
Central	Shanxi	0.445	21	0.533	29	0.836	16
	Jilin	0.879	6	0.879	8	1.000	1
	Heilongjiang	0.507	19	0.761	15	0.666	22
	Anhui	0.786	10	0.809	13	0.971	13
	Jiangxi	0.822	9	0.841	10	0.977	12
	Henan	0.353	27	0.531	30	0.665	23
	Hubei	0.661	15	0.664	22	0.997	10
	Hunan	0.747	11	0.747	16	1.000	1
Average	Overall	0.637		0.763		0.815
	Eastern	0.776		0.834		0.912
	Western	0.488		0.724		0.664
	Central	0.650		0.721		0.889

.

4.1.1. National-Level Analysis

Overall, the GIE of Chinese industrial enterprises still holds significant potential for improvement. As depicted in Figure 1, the average GIE of Chinese industrial enterprises from 2012 to 2021 stands at only 0.607, indicating that it has not yet reached a state of high efficiency. When considering stage efficiency, the average RDE of Chinese industrial enterprises is 0.757, while the average ACE is 0.782. This suggests that the low efficiency at the R&D and achievement conversion stages is a common factor limiting the improvement of GIE in Chinese industrial enterprises. It is worth noting that the efficiency of the R&D stage is slightly lower than that of the achievement conversion stage, which is consistent with the conclusions of Zhu et al. [40]. This phenomenon underscores the necessity for industrial enterprises to prioritize the improvement of RDE in the green innovation process; it also emphasizes the need for enterprises to strengthen R&D management, allocate R&D funds rationally, and avoid wasting resources. The primary reason for this phenomenon is that the majority of Chinese industrial enterprises tend to follow an innovation model that places a strong emphasis on technology importation while neglecting efforts in digesting and absorbing these technologies. This lack of original research outcomes and reinvention of imported technologies leads to inadequate breakthroughs in cutting-edge technologies. Furthermore, the rapid growth of the emerging information technology field has resulted in a significant exodus of R&D talents from these industrial enterprises, causing a shortage in replenishing R&D personnel and a deficiency in core elements necessary to support R&D activities.

From a change trend perspective (Figure 2), the average GIE increased from 0.565 in 2012 to 0.637 in 2021. In terms of stage efficiency, the average RDE rose from 0.754 in 2012 to a peak of 0.823 in 2020 before declining to 0.763 in 2021. The average ACE exhibited relatively significant changes, ascending from 0.716 (below the RDE) in 2012 to 0.815 in 2021 and exceeding the RDE for most of the subsequent periods. GIE, RDE, and ACE have all undergone fluctuations, experiencing periods of decline, followed by resurgence and then decline. However, the overall trend indicates fluctuation with an upward trajectory. This is because China regards ecological protection and green development as an important direction of industrial efforts and has provided strong support for green innovation in terms of fiscal expenditure. The data from the National Bureau of Statistics indicate that China’s fiscal expenditure on environmental protection escalated from CNY 296.3 billion in 2012 to CNY 821 billion in 2021, registering a compound annual growth rate of 12%. These financial investments have effectively steered and mobilized a substantial amount of social capital to engage in the green innovation process of industrial enterprises across the country and promoted the improvement of green innovation efficiency. However, the enhancement of quality and efficiency of green innovation in industrial enterprises is still in a transitional phase, and the incentive mechanisms for technological research, development, and application are not perfect. Consequently, the efficiency of green innovation cannot rise steadily and continuously. Moreover, following the year 2020, the COVID-19 pandemic has significantly disrupted the supply and circulation of green innovation elements, leading to a discernible decline in GIE, RDE, and ACE.

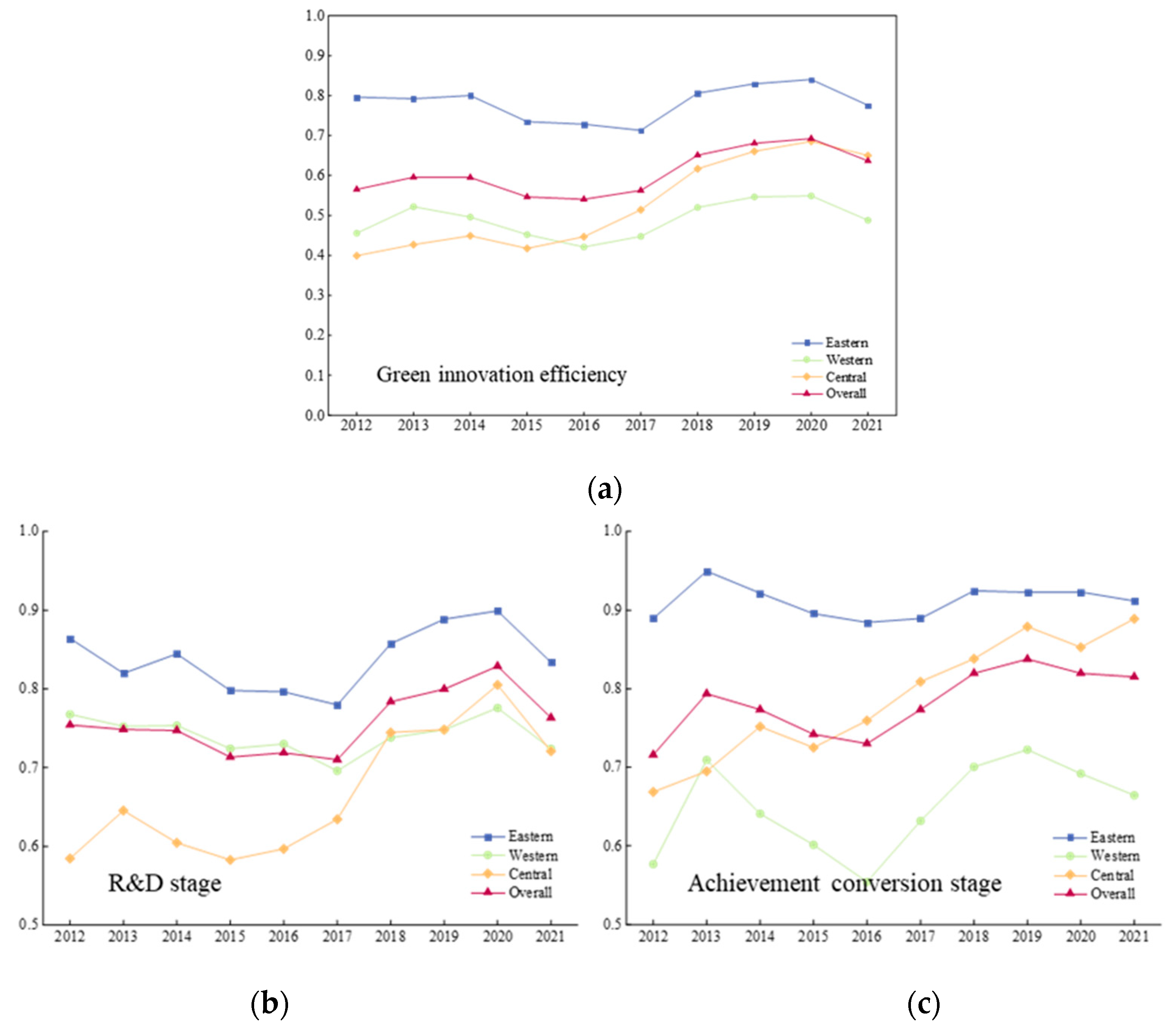
4.1.2. Regional-Level Analysis

The changing trend of the GIE of industrial enterprises in different regions is illustrated in Figure 3a. GIE has shown improvement across various regions, with the average GIE in the eastern region always surpassing that of the whole country and the other regions, aligning with the conclusions drawn by Zhou and Wang [64]. The expenditure on environmental protection, science, and technology in the eastern region significantly surpasses other regions, setting the stage for the leading advancement of green technology within its industrial enterprises. Environmental protection expenditure drives green development, while science and technology investment propel innovative development, both playing a crucial role in promoting green innovation. The average GIE level in the central region has undergone the most significant change, progressing from being initially below the level of the western region to exceeding it and ultimately catching up with or even surpassing the national level after 2020. This is because, on the one hand, various provinces in the central region have been proactive in implementing policies. For instance, Anhui Province was the first to propose an implementation plan for establishing a market-oriented green innovation system. On the other hand, the central region has generally maintained a leading position in the growth rate of funds. In particular, since 2017, R&D investment in the central region has continued to strengthen, laying a solid foundation for the rapid development of green innovation. As depicted in Figure 3b, the eastern region has consistently maintained a significant lead in RDE development. This can be attributed to the region’s developed economy and high level of education, which have enabled industrial enterprises to possess more advanced technology and a higher-quality labor force [65]. In contrast, RDE development in the central region has been relatively lagging, but after years of catching up, it has gradually approached the national average. As depicted in Figure 3c, the ACE of the eastern region has consistently maintained its leading position, while the central region has been steadily catching up and gradually narrowing the gap. Meanwhile, ACE in the western region shows continuous fluctuations, consistently remaining at a low level. One significant contributing factor is that China’s western regions are relatively remote, with a lower level of economic development and less advanced infrastructure, which hinders the effective translation of innovation achievements into economic benefits.

In order to more intuitively observe the trend in the GIE changes of industrial enterprises in different provinces, we drew a visual GIE distribution map. As depicted in Figure 4, the initial spatial distribution of GIE ranked as follows: eastern region > western region > central region, southern region > northern region. There were significant disparities in GIE among provinces, with high GIE predominantly concentrated in eastern areas. Due to the presence of the resource curse, some mineral-rich provinces, such as Shanxi, Shaanxi, and Inner Mongolia, exhibited relatively low GIE. Despite being rich in mineral resources, these provinces continue to be dominated by extractive and raw material industries during their economic development, leading to a singular industrial structure and a lack of new developmental momentum. Over time, GIE has shown improvement in most provinces, with notable enhancements in the northern and central regions, leading to a gradual narrowing of the differences between regions. The final GIE distribution pattern is as follows: eastern region > central region > western region, southern region > northern region. Throughout the study period, only Beijing, Shanghai, Zhejiang, Guangdong, Hainan, and Qinghai maintained high levels of GIE. Most of these provinces are located in the eastern region, indicating that the development of green innovation in the eastern region is significantly advanced. Taking 2021 as an example, the number of patents in the eastern region accounted for 71% of the country, and the industrial added value represented 56% of the country. Qinghai stands out as an exception among these provinces, being located in the western region. The reason for Qinghai’s sustained high GIE is rooted in its status as a major province for hydropower and energy, as well as its strong sense of green innovation. In recent years, Qinghai has actively pursued the development of clean energy and promoted technological innovation and the transformation of achievements in the field of clean energy.

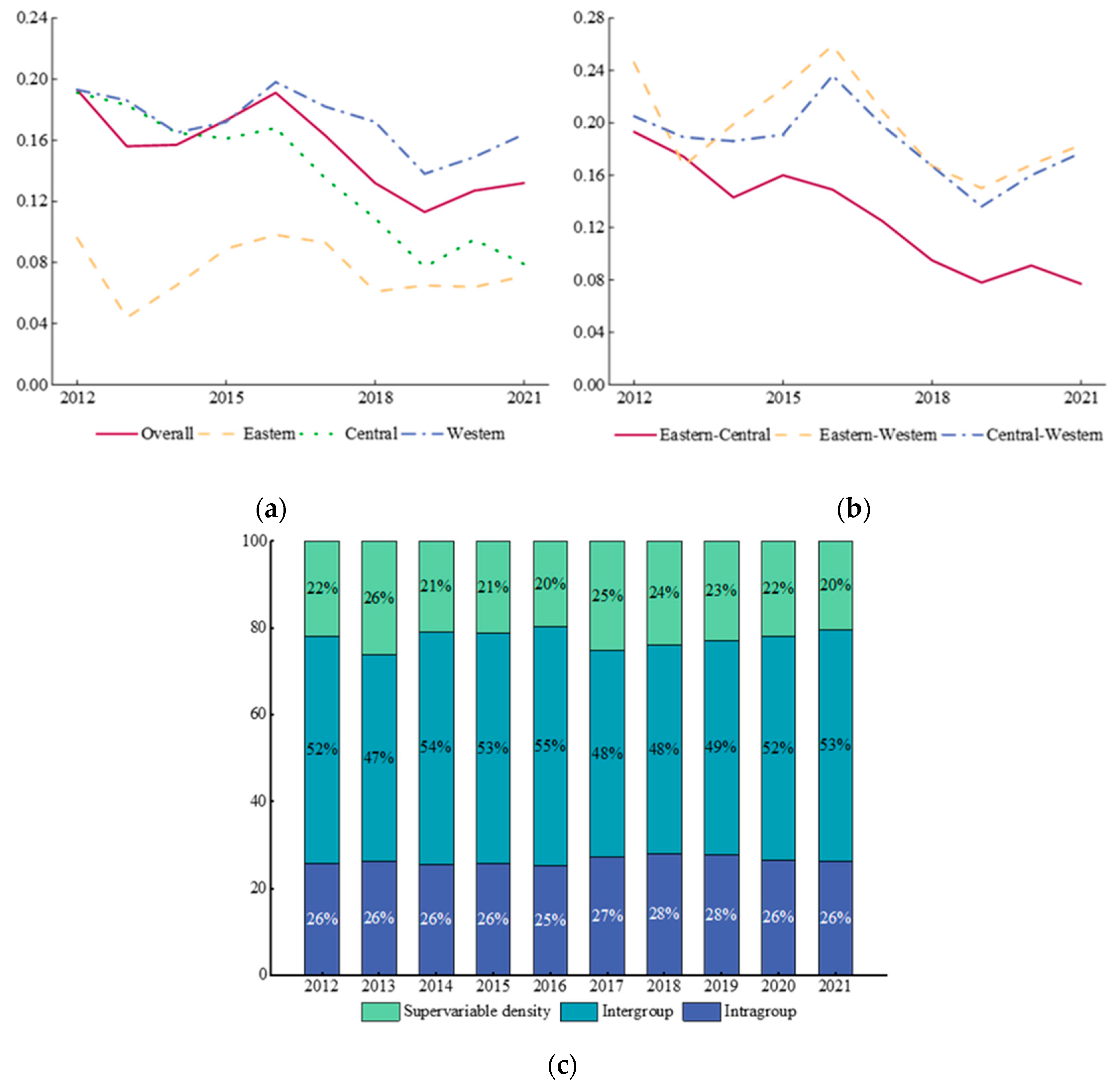
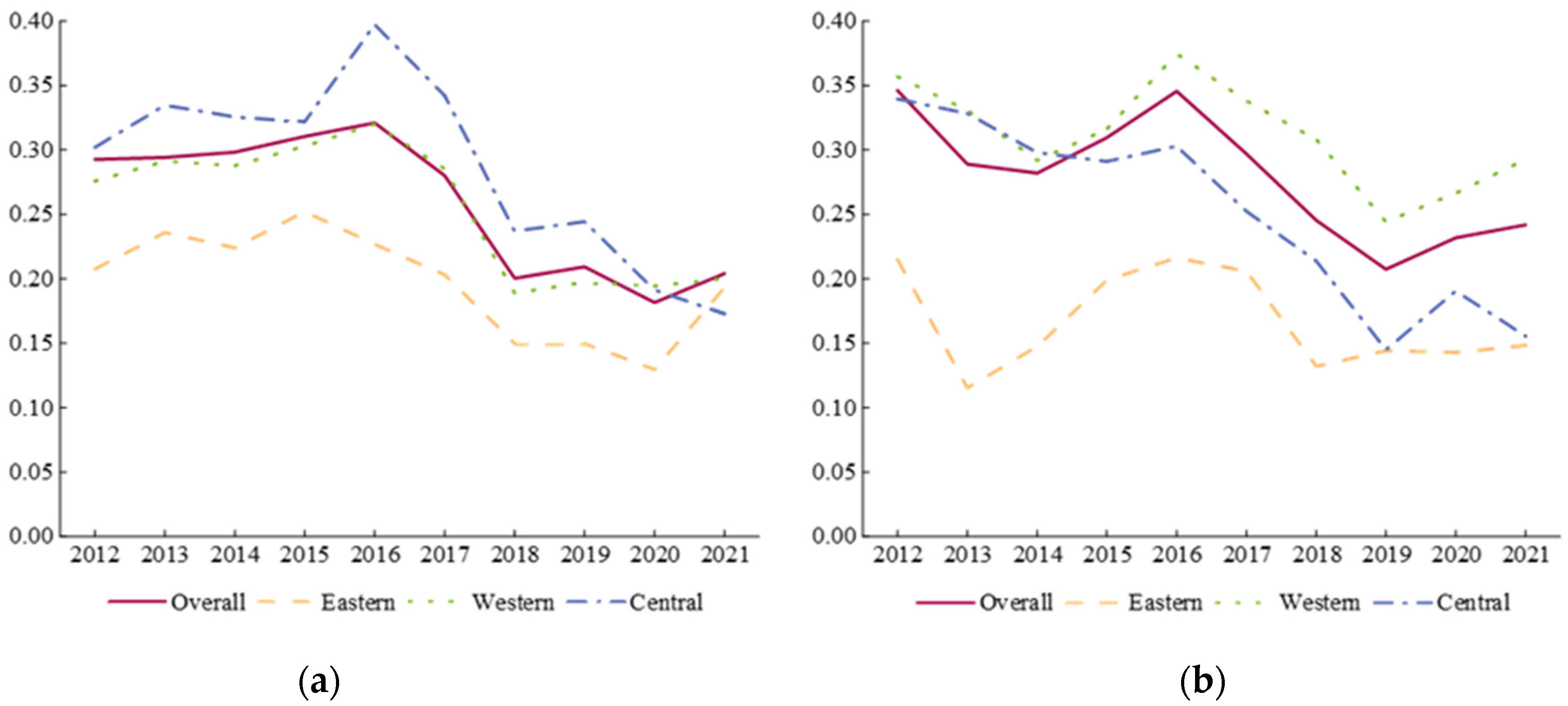
4.2. Regional Disparities in Green Innovation Efficiency and Its Decomposition

In order to investigate the regional disparities in GIE among Chinese industrial enterprises, this study employed the Dagum Gini coefficient and its decomposition method to measure and decompose the regional differences in the two-stage efficiency of green innovation. The measured results of the RDE and ACE Gini coefficients, along with the contribution rates for the whole nation and the three major regions from 2012 to 2021, are shown in Figure 5 and Figure 6.

4.2.1. Regional Disparities in R&D Efficiency and Its Decomposition

As depicted in Figure 5, the overall Gini coefficient of RDE decreased from 0.164 in 2012 to 0.117 in 2021, indicating a fluctuating downward trend and suggesting a narrowing of differences in RDE over time. In terms of intraregional differences, the central region exhibits the largest disparity, while the eastern region shows the smallest difference, with the RDE Gini coefficients of all three regions displaying a downward trend. Regarding interregional differences, the variance between the eastern and western regions is the smallest, while the difference between the eastern and central regions is the largest, albeit also demonstrating a downward trend. In comparison to the slow decline of the intraregional Gini coefficient, the decline of the interregional Gini coefficient is more obvious. This is because China has put forth a regional coordinated development strategy, which includes providing support to the central and western regions in areas such as (1) strengthening the guarantee of attracting talent and intelligence, (2) increasing investment in innovation, and (3) deepening the reform of the science and technology system. These policies serve to not only remove various barriers that impede the cross-regional flow of innovative elements, thus facilitating the full and orderly movement of talents, funds, and technologies, but also ameliorate the current situation in the central and western regions where the low levels of their own R&D and the scarcity of innovative elements hinder their ability to achieve innovation at the technological, product, or market levels. Consequently, these policies are helpful in greatly enhancing the efficiency of resource allocation and significantly reducing the disparity in R&D efficiency among regions.

Figure 5c illustrates the sources of the differences in RDE. Among these, the intraregional contribution rate remained relatively stable, at approximately 30%, while the interregional contribution rate exhibited a decreasing trend. Conversely, the contribution rate of super-variable density showed an increasing trend. The average contribution rates of intraregional differences, interregional differences, and super-variable density were 29.95%, 34.13%, and 35.92%, respectively. Prior to 2015, the primary factor contributing to regional disparities in RDE was interregional disparities. However, post-2015, the main factor leading to regional disparities in RDE shifted to super-variable density. This change in the primary source of the contribution rate, from interregional differences to super-variable density, also reflects that the coordinated development of R&D among regional industrial enterprises in China has yielded certain results.

4.2.2. Regional Disparities in Achievement Conversion Efficiency and Its Decomposition

As depicted in Figure 6, the overall Gini coefficient of ACE decreased from 0.193 in 2012 to 0.132 in 2021, indicating a narrowing difference in ACE over time. The ACE Gini coefficient in all three regions exhibits an overall downward trend, with the most significant drop observed in the central region, decreasing from 0.191 in 2012 to 0.079 in 2021. In terms of intraregional differences, the western region exhibits the largest disparity, while the eastern region displays the smallest difference, which can be attributed to its superior geographical position and relatively balanced economic development. Conversely, the western region faces economic challenges and inadequate infrastructure, leading most provinces to prioritize the development of provincial capital cities. Consequently, industrial enterprises concentrate their main resources on production in the major cities of the western region, neglecting coordinated development within the region. From the perspective of interregional differences, the disparity between the eastern and central regions is the smallest, while the difference between the eastern and western regions is the largest, which corresponds to the smaller gap in economic and infrastructure conditions between the eastern and central regions.

The contribution rates from different sources of ACE, including intraregional differences, interregional differences, and super-variable density, have remained stable. The average contribution rates for intraregional differences, interregional differences, and super-variable density were 26.44%, 51.12%, and 22.44%, respectively. The primary factor affecting the overall difference in ACE among Chinese industrial enterprises is the disparity between regions, particularly the unbalanced development of ACE between the eastern and western regions. The western region should fully leverage its natural conditions and resource endowment advantages, accelerate the conversion of scientific and technological achievements into economic benefits, and improve its own ACE.

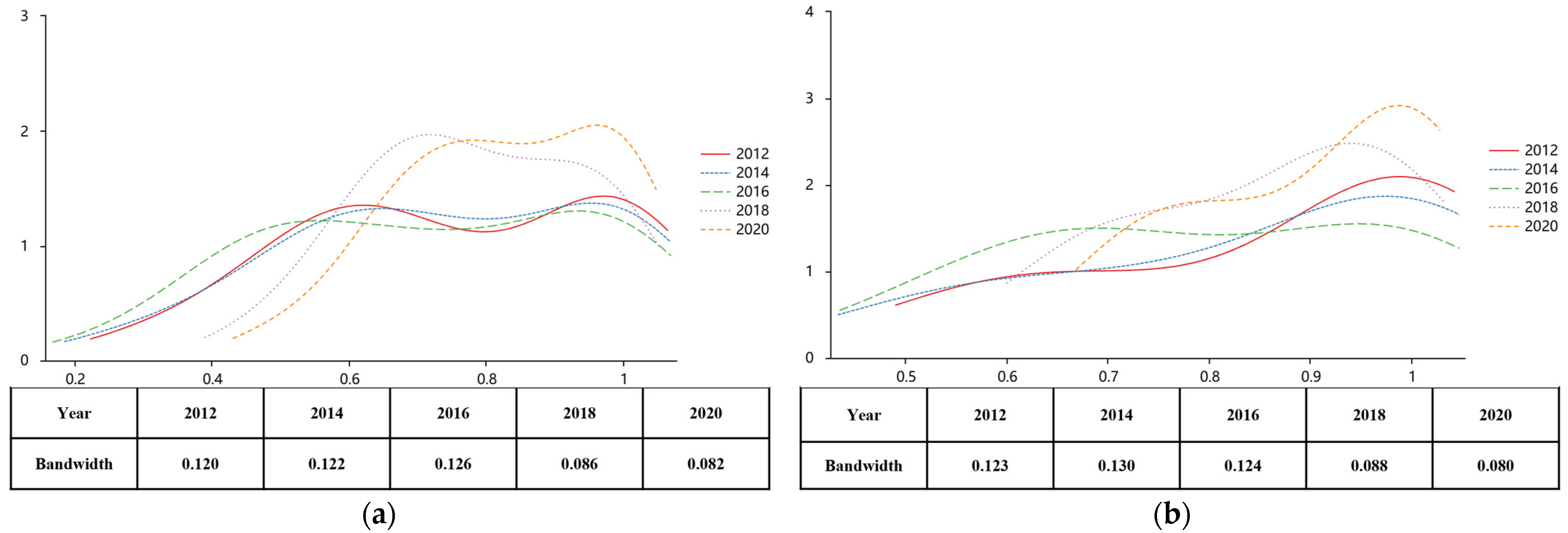
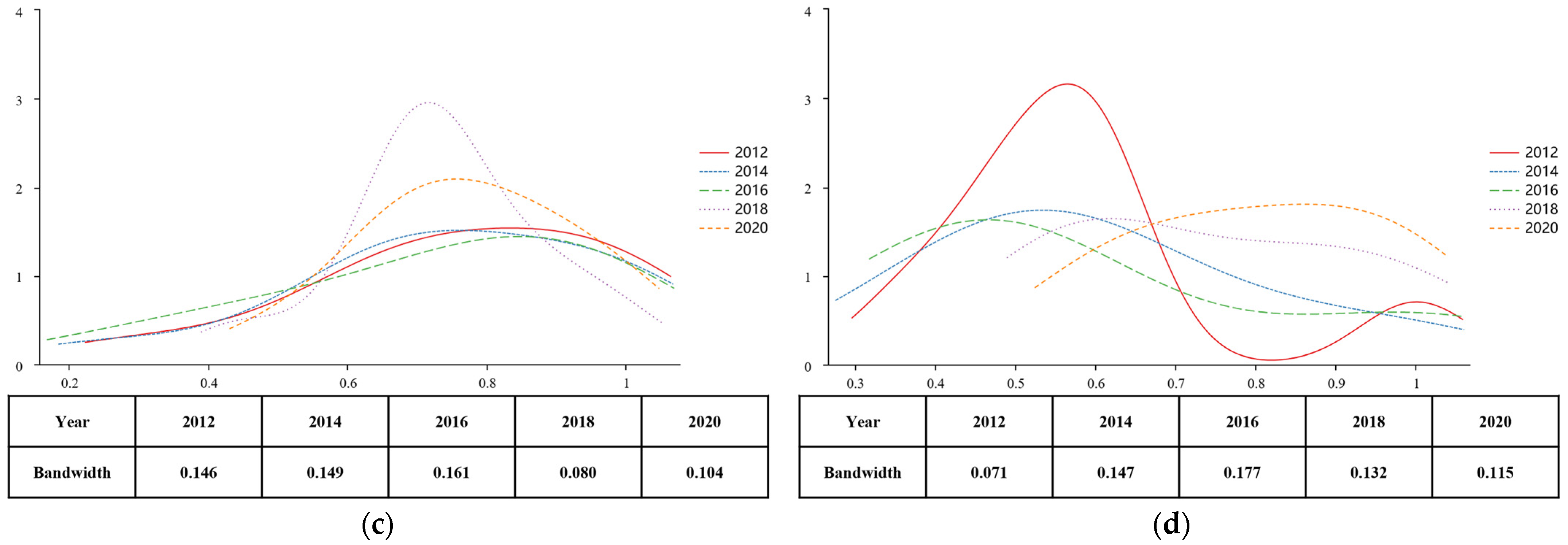
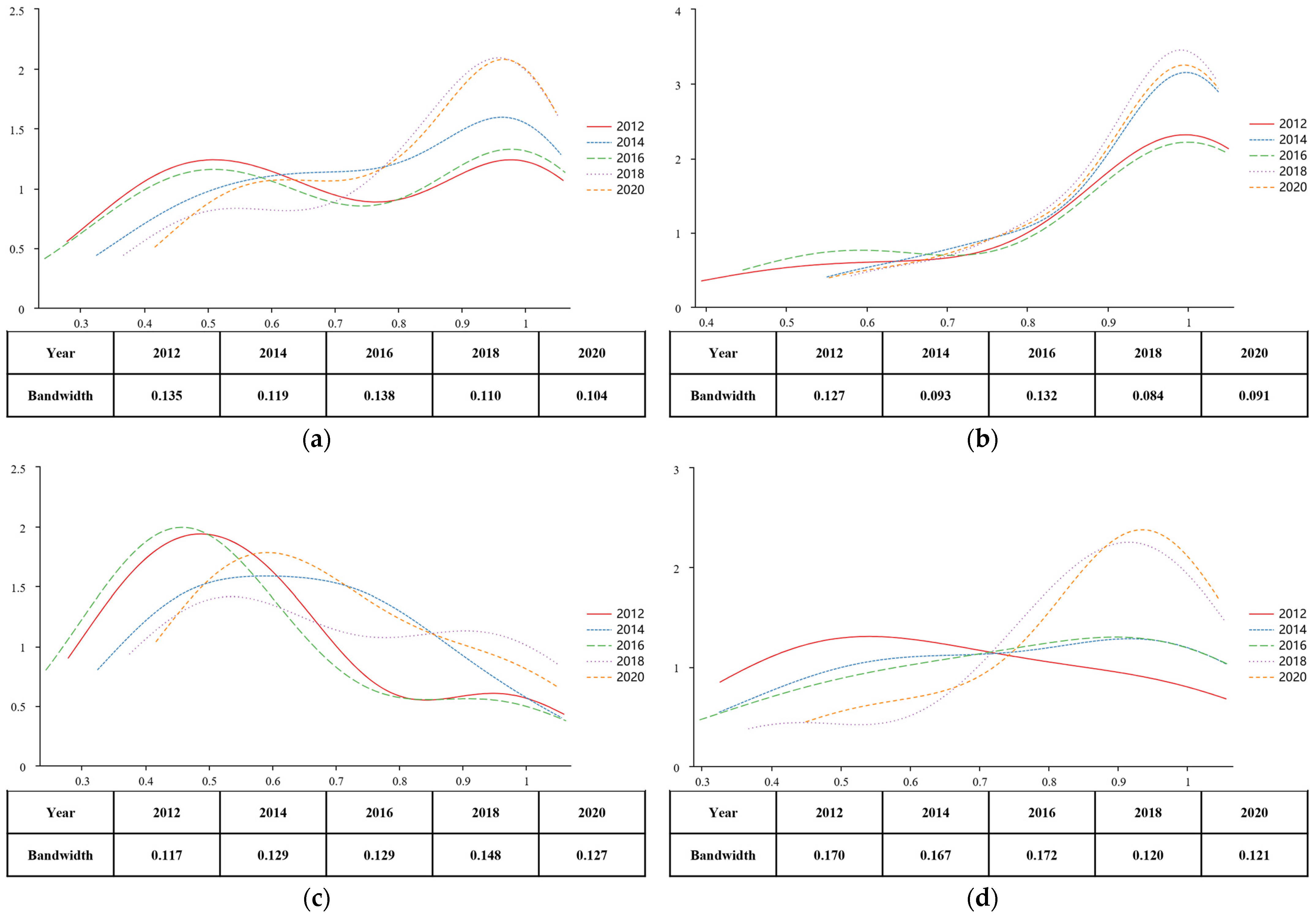
4.3. Dynamic Evolution of Green Innovation Efficiency

The Gini coefficient has been utilized to analyze regional disparities and their sources in terms of relative differences. Additionally, kernel density estimation can visually and dynamically illustrate the overall morphological and temporal changes in GIE. Therefore, this study further employed kernel density estimation to analyze the dynamic distribution characteristics of the two-stage efficiency of green innovation in Chinese industrial enterprises, aiming to investigate regional absolute differences. The distribution dynamics of RDE and ACE in the entire country and the three regions are depicted in Figure 7 and Figure 8.

4.3.1. Dynamic Evolution of R&D Efficiency

Figure 7a illustrates the overall dynamic evolution of RDE in China. In terms of the distribution position, the curve shows a trend of shifting to the right, indicating a gradual increase in the RDE of industrial enterprises. Regarding the main peak morphology, the height of the main peak increases while the bandwidth of the main peak narrows, indicating that the distribution of RDE is more concentrated and the absolute difference decreases. In relation to distribution ductility, the curve exhibits a left-trailing feature, which has improved over time, indicating a narrowing gap between high-RDE and low-RDE provinces. From the perspective of the polarization trend, the distribution curve still presents a bimodal state, indicating a two-level differentiation in RDE among Chinese regional industrial enterprises.

In Figure 7b–d, the distribution curves of the eastern and central regions exhibit a rightward shift, while the western region shows a leftward shift, indicating an improvement in the RDE of the eastern and central regions but a decrease in the RDE of the western region. Among them, the distribution curve in the central region transitions from an initial left-slanted shape to a right-slanted shape, indicating that the initial RDE in the central region was generally low and has significantly improved over time. In the eastern and western regions, the peak height increases, and the bandwidth narrows, suggesting a decrease in the absolute difference in RDE. In the central region, the height of the main peak initially decreases and then rises, and the bandwidth first increases and then decreases, indicating an initial increase and subsequent decrease in the difference in RDE in the central region. The trailing of the distribution curve in all three regions has improved, indicating that the gap between the provinces with high RDE and those with low RDE has decreased.

4.3.2. Dynamic Evolution of Achievement Conversion Efficiency

The overall dynamic evolution of ACE in China is depicted in Figure 8a. In terms of the distribution position, the central point of the overall distribution curve gradually shifts to the right, indicating a gradual increase in the ACE of industrial enterprises. Regarding the main peak morphology, the height of the main peak increases, and its bandwidth narrows, suggesting a decrease in the absolute differences in ACE. In relation to distribution ductility, the curve exhibits a left-trailing feature, which has been improved, indicating a reduction in the gap between provinces with high ACE and those with low ACE. Furthermore, the polarization trend shows that the curve has changed from bimodal to unimodal, indicating that the ACE in some provinces has progressed from a low level to a high level and that the polarization phenomenon has been mitigated.

As observed in Figure 8b–d, the distribution curves in the central and western regions have undergone a significant rightward shift, indicating an increase in ACE in both regions. Specifically, the distribution curve in the central region has transitioned from a left-slanted shape to a right-slanted shape, signifying a significant increase in ACE. In the eastern and central regions, the peak height has increased, and the bandwidth has narrowed, suggesting a decrease in the absolute difference in ACE. In the western region, the height of the main peak first decreased and then increased, and the bandwidth first increased and then decreased, indicating that the difference in ACE in the western region initially increased and then decreased. The trailing of the distribution curves in all three regions has improved, indicating a narrowing gap between the provinces with high ACE and those with low ACE.

4.4. Convergence Analysis of Green Innovation Efficiency

The investigation of the convergence trend of GIE among Chinese industrial enterprises holds significant importance for advancing the coordinated development of regional industries and reducing regional disparities. Therefore, the convergence characteristics of the two-stage efficiency of green innovation were further explored based on the analysis of the absolute and relative differences in GIE among regional industrial enterprises.

4.4.1. Convergence Analysis of R&D Efficiency

(1)

σ Convergence

Figure 9a illustrates the dynamic change trend of the RDE variation coefficient of industrial enterprises in the whole country and the three regions over the study period. The coefficient of variation at the national level exhibits a significant downward trend over time, decreasing from 0.293 in 2012 to 0.204 in 2021. At the regional level, the coefficient of variation also demonstrates a declining trend, with the most pronounced decrease observed in the central region, dropping from 0.302 in 2012 to 0.173 in 2021, reflecting a reduction of 42.8%. This indicates that the evolution of RDE exhibits characteristics of σ convergence at both the national and regional levels, with the central region showing the fastest convergence and a “catch-up” phenomenon.

(2)

β Convergence

Table 3. Test results of absolute and conditional β convergence of RDE.

Variables	Overall		Eastern		Western		Central
β	−0.425 *** (−7.15)	−0.542 *** (−8.79)	−0.452 *** (−4.25)	−0.611 *** (−5.90)	−0.243 ** (−2.50)	−0.471 *** (−4.45)	−0.688 *** (−5.36)	−0.881 *** (−5.97)
α	−0.151 *** (−4.94)	4.336 *** (3.94)	−0.137 *** (−4.01)	0.374 (0.22)	−0.107 ** (−2.13)	9.666 *** (3.94)	−0.309 *** (−3.37)	6.354 ** (2.45)
$lnOPEN$		0.095 ** (2.59)		0.066 (0.55)		0.084 * (1.86)		0.098 (0.70)
$lnINDU$		0.024 (0.25)		0.494 ** (2.63)		−0.282 * (−1.67)		−0.079 (−0.40)
$lnPGDP$		−0.408 *** (−4.04)		−0.105 (−0.65)		−0.860 *** (−3.72)		−0.631 *** (−2.78)
$lnER$		0.014 (0.33)		0.066 (1.17)		−0.053 (−0.68)		−0.079 (−0.78)
$lnGOV$		0.022 (0.10)		0.232 (0.75)		−0.291 (−0.71)		0.069 (0.13)
$lnHC$		−0.072 (−0.54)		0.091 (0.36)		−0.102 (−0.46)		−0.188 (−0.34)
Province FE	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Year FE	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
s	0.055	0.078	0.060	0.094	0.028	0.064	0.116	0.213
τ	12.526	8.876	11.524	7.341	24.898	10.885	5.951	3.256
R2	0.302	0.391	0.398	0.536	0.187	0.386	0.484	0.5667
N	270	270	99	99	99	99	72	72

Note: * p < 0.1, ** p < 0.05, *** p < 0.01; values in parentheses are t statistics.

reports the test results of absolute and conditional β convergence of the RDE of industrial enterprises in the whole country and the three regions. To ensure unbiased and robust estimation results, all regressions were controlled for province-fixed effects and time-fixed effects. It is evident that the β coefficients of all regions were significantly negative without the inclusion of control variables, indicating an absolute β convergence in the RDE of industrial enterprises across all regions. The convergence rates for the overall, eastern, western, and central regions were 0.055, 0.060, 0.028, and 0.116, respectively. Notably, the central region exhibited the fastest convergence rate, corresponding to the shortest half-life cycle of 5.951.

It is important to note that the absolute β convergence test only considers the initial state of each region and does not take into account the influence of regional heterogeneity factors. Ignoring these factors may lead to bias in the estimation results. Therefore, it is necessary to further test the conditional β convergence feature to ensure the robustness of the conclusions. After incorporating control variables, the β coefficients of RDE for industrial enterprises in all regions remained significantly negative at the 1% level, indicating the presence of conditional β convergence. In essence, this suggests that even after accounting for regional heterogeneity factors, RDE in different regions can still converge to the same steady-state level. The convergence rates for the overall and the eastern, western, and central regions were 0.078, 0.094, 0.064, and 0.213, respectively, revealing a spatial distribution pattern of “central > eastern > western”. This observation implies that the inclusion of relevant heterogeneity factors has led to an improvement in the convergence rate, thereby effectively promoting the convergence of RDE.

The coefficients for the degree of openness in the overall and western regions are significantly positive, which is not conducive to reducing regional disparities. In contrast, the significantly negative coefficients for the economic level in the overall, western, and central regions indicate their potential to alleviate spatial disparities within the regions. The industrial structure exerts a heterogeneous impact on the RDE in different regions, contributing to the narrowing of regional disparities in the western region but exacerbating them in the eastern region. The coefficient on the environmental regulation, government R&D subsidies, and human capital are not significant. There may be a complex nonlinear relationship between them and RDE, and further analysis is needed to elucidate such intricate connections.

4.4.2. Convergence Analysis of Achievement Conversion Efficiency

(1)

σ Convergence

Figure 9b presents the trend of the variation coefficient of ACE for industrial enterprises across the whole country and the three regions. Both the national and regional levels exhibited a declining trend in the coefficient of variation. The overall coefficient of variation decreased from 0.346 in 2012 to 0.242 in 2021, with the central region demonstrating the most notable decrease, at 54.2%. The results show that the change in ACE demonstrates σ convergence at both the national and regional levels, with the convergence rate in the central region being the fastest, ultimately approaching the variation coefficient of the eastern region.

(2)

β Convergence

Table 4. Test results of absolute and conditional β convergence of ACE.

Variables	Overall		Eastern		Western		Central
β	−0.736 *** (−12.42)	−0.814 *** (−12.86)	−0.793 *** (−9.76)	−0.816 *** (−9.59)	−0.694 *** (−6.94)	−0.799 *** (−7.05)	−0.758 *** (−6.38)	−0.938 *** (−7.04)
α	−0.203 *** (−10.13)	−2.128 ** (−2.30)	−0.084 *** (−7.02)	−1.115 (−1.25)	−0.321 *** (−6.22)	−4.391 ** (−2.03)	−0.191 *** (−4.47)	−3.233 (−1.40)
$lnOPEN$		0.104 ** (2.41)		0.052 (0.66)		0.105 * (1.70)		−0.143 (−0.85)
$lnINDU$		0.037 (0.54)		−0.162 ** (−2.21)		0.106 (0.83)		−0.022 (−0.12)
$lnPGDP$		0.170 ** (2.06)		0.119 (1.45)		0.374 * (1.76)		0.176 (0.86)
$lnER$		0.008 (0.18)		0.001 (0.01)		−0.077 (−0.85)		0.068 (0.55)
$lnGOV$		0.103 (0.38)		−0.149 (−0.60)		0.197 (0.36)		0.162 (0.25)
$lnHC$		−0.028 (−0.21)		0.205 (1.22)		−0.368 (−1.36)		0.486 (1.07)
Province FE	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Year FE	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
s	0.133	0.168	0.158	0.169	0.118	0.160	0.142	0.278
τ	5.205	4.121	4.401	4.095	5.853	4.320	4.885	2.493
R2	0.392	0.427	0.523	0.563	0.356	0.415	0.393	0.472
N	270	270	99	99	99	99	72	72

Note: * p < 0.1, ** p < 0.05, *** p < 0.01; values in parentheses are t statistics.

presents the results of the absolute and conditional β convergence tests for the ACE of industrial enterprises in the whole country and the three regions, with all regressions controlling for individual and time-fixed effects.

When no control variables are included, the β coefficients in all regions are significantly negative, indicating absolute β convergence in the ACE of industrial enterprises. The convergence rates were 0.133, 0.158, 0.118, and 0.142 in the overall, eastern, western, and central regions, respectively. Among these, the convergence speed was the fastest in the eastern region, with a corresponding half-life cycle of 4.401.

After the introduction of control variables, the β coefficient of the ACE of industrial enterprises in each region remained significantly negative at the 1% level, indicating the presence of conditional β convergence. The convergence rates were 0.168, 0.169, 0.160, and 0.278, respectively, revealing a spatial distribution pattern of “central > eastern > western”. It is noteworthy that, following the introduction of control variables, the region with the highest convergence rate shifted from the eastern region to the central region, suggesting that these control variables have a more pronounced impact on the convergence of ACE in the central region.

The coefficients for the degree of openness in the overall and western regions are significantly positive, which is not conducive to narrowing the gap in regional ACE. Similarly, the coefficients related to the economic level in both the overall and western regions also exhibit a significantly positive relationship, hindering efforts to mitigate regional gaps. Conversely, the influence coefficient of industrial structure in the eastern region is negative, indicating a favorable impact on reducing regional disparities. It can be observed that these control variables have a heterogeneous impact on the GIE convergence across different regions and stages.

5. Discussion

This study divides the green innovation process of industrial enterprises into the R&D stage and the achievement conversion stage. A two-stage DEA model incorporating shared inputs, additional inputs, and undesired outputs is constructed to evaluate the overall efficiency and stage efficiency of green innovation. Different from the majority of existing studies that use additive two-stage DEA models [37,40,43,44] for efficiency evaluation, where the overall efficiency in their models is typically the weighted sum of stage efficiencies and can be transformed into linear models for solving through C-C transformation, this study proposes a model where the overall efficiency is the product of stage efficiencies. In the case of VRS and the presence of shared inputs or additional intermediate input variables, our model is difficult to transform into a linear model for solving. Therefore, a heuristic search method is required to convert our model into a linear programming problem with parameters for resolution. In the model of Du et al. [66], the overall efficiency is also defined as the product of stage efficiencies; however, they compute the overall efficiency by multiplying the two optimal efficiency values obtained from separately solving the two-stage efficiency models. Their approach results in inconsistent optimal weights for the two-stage efficiency models, which do not reflect real-world scenarios, potentially leading to an inflated overall efficiency value. In contrast, our study establishes a unified model to first determine the optimal overall efficiency and then calculate the efficiencies of each stage based on the optimal weights obtained.

The results reveal that the GIE of Chinese industrial enterprises exhibited a fluctuating upward trend from 2012 to 2021, which is closely similar to the findings of Zhao et al. [4], albeit their utilization of a “black-box” evaluation model. This indicates that Chinese industrial enterprises are entering a crucial period of green transformation, requiring them to actively take on social responsibilities and promote the high-quality development of the Chinese economy and society. In terms of stage efficiency performance, we observed that the RDE was slightly lower than the ACE, a finding consistent with those of Zhu et al. [40] and Du et al. [66] but diverging from the conclusions drawn by Chen et al. [37] and Wang et al. [43]. This variance may be attributed to the fact that, on the one hand, their research samples belong to high-tech industries characterized by technological intensity, emphasizing input and output in R&D innovation; on the other hand, their studies did not account for environmental pollution as an undesired output, leading to deviations in the results. Moreover, existing studies have primarily focused on analyzing regional disparities and convergence trends in the overall efficiency of green innovation, while this study takes a viewpoint based on the innovation value chain to separately analyze the two-stage efficiencies of green innovation. In terms of regional disparity research, the study conducted by Zhao et al. [4] revealed that the Gini coefficient of GIE at the national and regional levels exhibited a decreasing trend. Prior to 2010, the primary factor influencing the disparity in GIE was interregional differences; however, after 2010, it shifted to super-variable density. This finding aligns with the discovery by Yao et al. [67], who identified interregional differences and super-variable density as the main sources of spatial disparities in GIE. Our research results differ slightly from theirs. We found that the primary source of the overall disparity in RDE has shifted from interregional differences to super-variable density, while the primary contributor to the overall disparity in ACE is still interregional differences, with the largest differences between the eastern and western regions. In terms of convergence trend research, our results demonstrate absolute and conditional β convergence in the GIE of industrial enterprises in all regions. This indicates the presence of spillover effects from green technologies, where regions with higher GIE levels will radiate to adjacent areas and eventually reach the same level. Moreover, the inclusion of control variables significantly enhances the convergence rate. Our findings are consistent with those of Zhao et al. [4], but differ from those of Xu et al. [68]. The study by Xu et al. revealed that the GIE in different regions of the Yangtze River Economic Belt exhibits heterogeneous convergence characteristics. In addition, similar to the findings of Zhao et al. [69], we observed that the impact of different control variables on efficiency varies heterogeneously across different regions and innovation stages.

This study presents a thorough analysis of the green innovation efficiency within industrial enterprises in China, aiming to facilitate policymakers in obtaining accurate insights into the current status of green innovation in the industrial sector. The outcomes of this study can serve as valuable references for the implementation of relevant policies.

6. Conclusions and Policy Recommendations

6.1. Conclusions

As China’s economy continues to grow at a rapid pace, it is also confronted with significant environmental pollution and ecological degradation. As major contributors to pollution and energy consumption, industrial enterprises are under pressure to pursue sustainable development. Green innovation is paramount in achieving sustainable development [70], and its significance to industrial enterprises is self-evident.

In this study, the green innovation process of industrial enterprises was segmented into the R&D stage and the achievement conversion stage, considering fixed assets as a shared input, energy consumption as an intermediate input, and pollution emissions as undesirable outputs. An improved relational two-stage DEA model was developed to measure and decompose the GIE of industrial enterprises across 30 provinces in China from 2012 to 2021. Based upon this, the Dagum Gini coefficient, kernel density estimation, and convergence analysis methods were further employed to investigate the regional disparities and convergence trends in the two-stage efficiency of green innovation from the perspective of the innovation value chain. The primary conclusions are as follows:

(1)

The average GIE of industrial enterprises in China as a whole demonstrates a fluctuating upward trend, and there is potential for further improvement. The low RDE and ACE have become common factors constraining the improvement of GIE in industrial enterprises. Particular attention should be directed toward improving RDE, given that it consistently lags behind ACE across most periods. The eastern region consistently exhibits the highest two-stage efficiency, positioning it as the frontrunner in green innovation. In contrast, the central and western regions are catching up, with the central region demonstrating the fastest rate of improvement in two-stage efficiency.

(2)

From the perspective of relative differences, the GIE of Chinese industrial enterprises exhibits characteristics of spatial disequilibrium. The primary source of the overall disparity in RDE has shifted from interregional differences to super-variable density, while the primary contributor to the overall disparity in ACE is still interregional differences, with the largest differences between the eastern and western regions. The Gini coefficients of RDE and ACE for the whole country and the three regions demonstrate a downward trend during the study period, indicating mitigation of regional disparities.

(3)

From the perspective of σ convergence, the coefficients of variation of RDE and ACE in the whole country and the three regions show a decreasing trend. Among them, the convergence rate in the central region is the fastest. Considering β convergence, significant absolute and conditional β convergence can be observed in the whole country and the three regions. Their conditional β convergence rate is greater than the absolute β convergence rate, corresponding to a shorter half-life cycle. When considering control variables, the degree of openness, economic level, and industrial structure were found to significantly impact the convergence of the two-stage efficiency of green innovation in industrial enterprises. The coefficients and significance of these variables are heterogeneous across different regions and stages of green innovation.

6.2. Policy Recommendations

(1)

Enhance the awareness of green innovation and foster an environment conducive to green innovation. The government should enhance the market mechanism and bolster enterprises’ enthusiasm for independent innovation; support the research, development, and application of green technology; and encourage enterprises to increase investment in green innovation. Efforts should be made to improve the efficiency of R&D, address the deficiencies in green innovation, and ensure the effective transformation of R&D results into productive forces. Simultaneously, stringent environmental protection standards should be established to compel industrial enterprises to reduce their pollution emissions and improve the efficiency of green innovation on the whole.

(2)

Reinforce regional connectivity and enhance its leading and driving roles. There are significant regional disparities in green innovation efficiency among industrial enterprises in China. To achieve high efficiency of green innovation in both stages, it is essential to overcome technological and resource flow barriers between regions and take the development path of high driving low. The eastern region has been at the forefront of green innovation, yielding remarkable results and accumulating advanced experience in ecological governance, innovation-driven development, and industrial transformation and upgrading. This experience can serve as a reference and complement for other regions. The green innovation highland can be built by strengthening the radiation-driven role of Beijing, Shanghai, Zhejiang, Guangdong, and other key provinces and cities, and the development of green innovation integration can be gradually promoted.

(3)

Combined with the resources and policy advantages, green innovation efficiency should be enhanced with differentiated development. The resource endowment and fundamental conditions for the development of green innovation in industrial enterprises vary across different regions, leading to objective spatial imbalances in green innovation efficiency. Achieving regional coordinated development depends not only on reducing these spatial imbalances but also on understanding the characteristics of industrial green innovation in each region and leveraging their respective advantages to forge distinct paths of green innovation. The government should align regional resource endowments, enhance interregional complementary cooperation, and formulate strategies for differentiated and coordinated development. All regions should fully leverage their local advantages, cultivate competitive industries, and pursue a path of harmonious yet diverse development.