Mobile Energy-Storage Technology in Power Grid: A Review of Models and Applications
Abstract
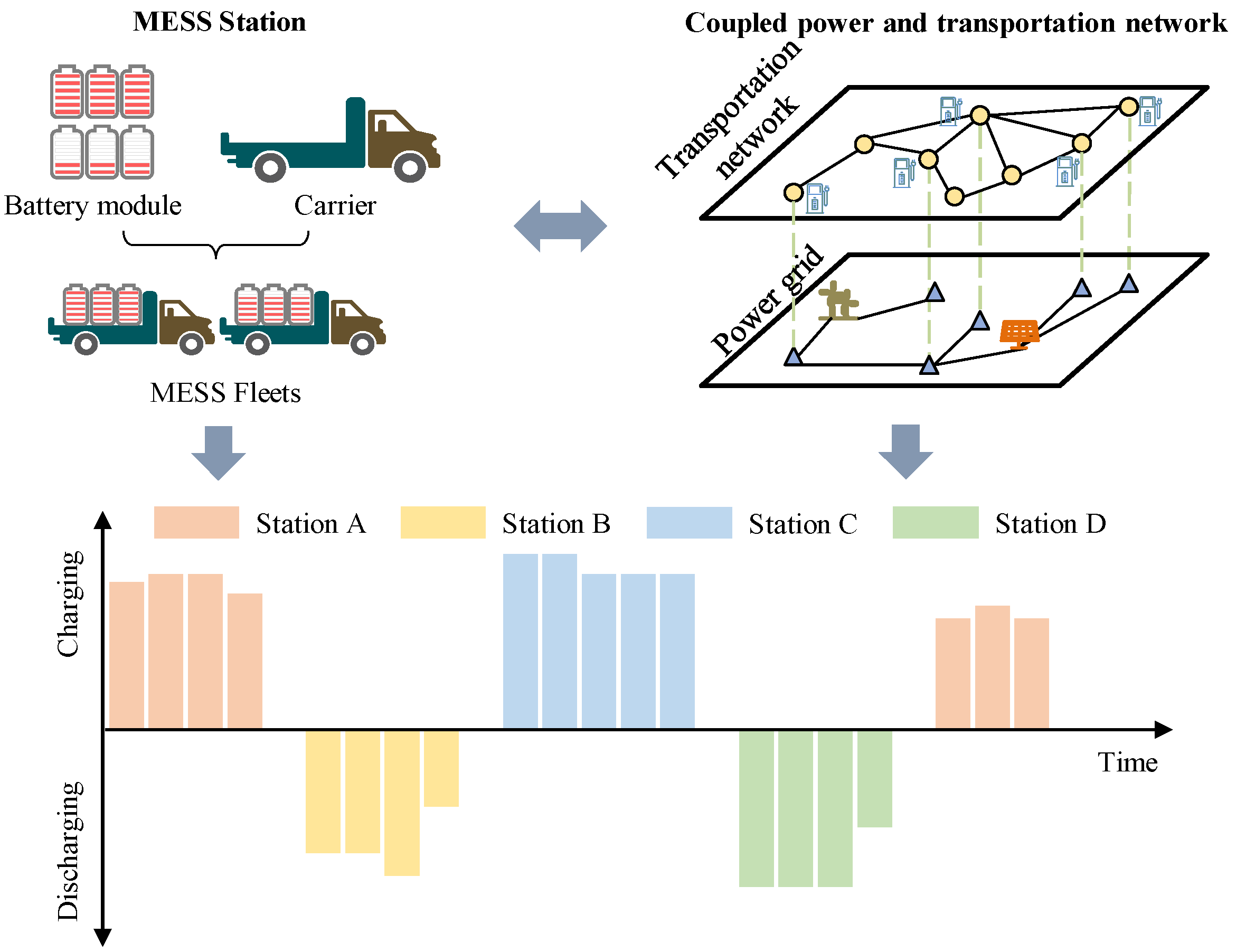
1. Introduction
2. MESS Modeling
2.1. Mobility Model
- (1)
- Sliding time window-based model
- (2)
- Time–space network model
- (3)
- Virtual switch model
| Model | Characteristic | Decisions | Travel Time | Number of Binary Variables | Number of Constraints |
|---|---|---|---|---|---|
| (1)–(2) | Sliding window-based model [25] | Traveling and parking state | Modeled by transition delay constraints | M(D + 1)(N + 1) | M[(2D + 1) Tik − T2 ik + 4D + 4]/2 |
| (3)–(13) | Linear-constrained travel behavior [27] | Traveling and parking state | Modeled by traveling state transition constraints | M(D + 1)(2N + 1) | MD(5N + 6) + 7M |
| (14)–(17) | Time–space network [29] | Mobility arc | Modeled by arcs | DM(N2 + 2Nv), where Nv = Σk>iTik − N(N − 1)/2 | DM(N2 + 3Nv + 1) − M(N2 − N + 2Nv) |
| (18)–(24) | Virtual switch model [30] | Switch state | Modeled by switching time | M(D + 1)(N2 + 3N) | M[(D + 1)(N + 5) + 2DN + Σi∈NΣj∈N\{i} (D + 1 − Tij,D + 1)] |
2.2. Battery Energy Model
3. Grid Application of MESS
3.1. MESS Planning
- (1)
- Independent investment
- (2)
- Sharing investment
3.2. MESS Operation
- (1)
- Optimal operation models and solution methods
| Ref. | Purpose | Mobility Model | Uncertainty | Optimization Model | Solution Method |
|---|---|---|---|---|---|
| [55] | Resilience improvement | (1) | - | MIQCP | commercial solver |
| [52,54] | Resilience improvement | (1) | Power grid | MINLP | reformulation |
| [53] | Resilience improvement | (1) | Power grid | MILP | heuristic method |
| [50] | Resilience improvement | (1) | Power grid | MISOCP | decomposition |
| [62] | Resilience improvement | (3) | Power grid | - | deep learning |
| [63] | Resilience improvement | (1) | Power grid | - | deep learning |
| [58] | Resilience improvement | (3) | transportation network and power grid | MILP | commercial solver |
| [48] | Renewable consumption | (3) | - | MILP | commercial solver |
| [59] | Renewable consumption | (3) | transportation network and power grid | MINLP | reformulation |
| [57] | Renewable consumption | (4) | transportation network and power grid | MINLP | decomposition |
| [61] | Renewable consumption | (3) | transportation network and power grid | - | deep learning |
| [49] | Security operation | (1) | Power grid | MISOCP | commercial solver |
- (2)
- Demonstration projects
3.3. Business Model
- (1)
- Electricity arbitrage
- (2)
- Energy-storage service sharing and pricing
4. Research and Application Prospect
4.1. Modeling and Solution of MESS Operation Problem
4.2. Comprehensive Application of MESS in Power Grids
4.3. Business Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Xiong, X.; He, Y.; Hu, J.; Chen, H. Scheduling of separable mobile energy storage systems with mobile generators and fuel tankers to boost distribution system resilience. IEEE Trans. Smart Grid 2021, 13, 443–457. [Google Scholar] [CrossRef]
- Saboori, H.; Jadid, S. Capturing curtailed renewable energy in electric power distribution networks via mobile battery storage fleet. J. Energy Storage 2022, 46, 103883. [Google Scholar] [CrossRef]
- Qu, Z.; Chen, J.; Peng, K.; Zhao, Y.; Rong, Z.; Zhang, M. Enhancing stochastic multi-microgrid operational flexibility with mobile energy storage system and power transaction. Sustain. Cities Soc. 2021, 71, 102962. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Balaskas, G.A.; Bakirtzis, A.G. An investigation of plug-in electric vehicle charging impact on power systems scheduling and energy costs. IEEE Trans. Power Syst. 2016, 32, 1902–1912. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Badri, A.; Parvania, M. A survey on mobile energy storage systems (MESS): Applications, challenges and solutions. Renew. Sustain. Energy Rev. 2014, 40, 161–170. [Google Scholar] [CrossRef]
- Wu, C.; Han, H.; Gao, S.; Liu, Y. Coordinated Scheduling for Multi-Microgrid Systems Considering Mobile Energy Storage Characteristics of Electric Vehicles. IEEE Trans. Transp. Electrif. 2022, 9, 1775–1783. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, R.; Xie, S.; Zhang, Y.; Yau, D.K.Y. On stability and robustness of demand response in V2G mobile energy networks. IEEE Trans. Smart Grid 2016, 9, 3203–3212. [Google Scholar] [CrossRef]
- Xu, W.; Tang, Q.; Li, T.; Lei, Y.; Liu, F.; Jia, Z.; Xiang, Y.; Liu, J.; Jawad, S. Optimal Investment of Mobile Energy Storage Based on Life Cycle Cost-benefit Analysis. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 508–513. [Google Scholar]
- Sulaiman, M.A.; Hasan, H. Development of Lithium-Ion Battery as Energy Storage for Mobile Power Sources Applications. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2009; Volume 1169, pp. 38–47. [Google Scholar]
- Curtis, T.L.; Smith, L.; Buchanan, H.; Heath, G. A Circular Economy for Lithium-Ion Batteries Used in Mobile and Stationary Energy Storage: Drivers, Barriers, Enablers, and US Policy Considerations; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2021. [Google Scholar]
- Huang, Y.; Cheng, Y.; Zhang, J. A review of high density solid hydrogen storage materials by pyrolysis for promising mobile applications. Ind. Eng. Chem. Res. 2021, 60, 2737–2771. [Google Scholar] [CrossRef]
- Ban, M.; Bai, W.; Song, W.; Zhu, L.; Xia, S.; Zhu, Z.; Wu, T. Optimal Scheduling for Integrated Energy-Mobility Systems Based on Renewable-to-Hydrogen Stations and Tank Truck Fleets. IEEE Trans. Ind. Appl. 2021, 58, 2666–2676. [Google Scholar] [CrossRef]
- Hassan, I.; Ramadan, H.S.; Saleh, M.A.; Hissel, D. Hydrogen storage technologies for stationary and mobile applications: Review, analysis and perspectives. Renew. Sustain. Energy Rev. 2021, 149, 111311. [Google Scholar] [CrossRef]
- Sun, Y.; Zhong, J.; Li, Z.; Tian, W.; Shahidehpour, M. Stochastic scheduling of battery-based energy storage transportation system with the penetration of wind power. IEEE Trans. Sustain. Energy 2016, 8, 135–144. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, D.; Lin, X.; Sui, Q.; Wei, F.; Li, Z. A novel energy cooperation framework for multi-island microgrids based on marine mobile energy storage systems. Energy 2022, 252, 124060. [Google Scholar] [CrossRef]
- Saboori, H.; Jadid, S. Optimal scheduling of mobile utility-scale battery energy storage systems in electric power distribution networks. J. Energy Storage 2020, 31, 101615. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Y.; Mei, S.; Huang, S.; Xu, Y. Resilience-oriented pre-hurricane resource allocation in distribution systems considering electric buses. Proc. IEEE 2017, 105, 1214–1233. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Z.; Huang, S.; Meng, K.; Luo, F.; Huang, J.; Hill, D. Optimal integration of mobile battery energy storage in distribution system with renewables. J. Mod. Power Syst. Clean Energy 2015, 3, 589–596. [Google Scholar] [CrossRef]
- Dong, C.; Gao, Q.; Xiao, Q.; Chu, R.; Jia, H. Spectrum-domain stability assessment and intrinsic oscillation for aggregated mobile energy storage in grid frequency regulation. Appl. Energy 2020, 276, 115434. [Google Scholar] [CrossRef]
- He, G.; Zhang, D.; Pi, X.; Chen, Q.; Kar, S.; Whitacre, J. Spatiotemporal arbitrage of large-scale portable energy storage for grid congestion relief. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Liu, X.; Soh, C.B.; Zhao, T.; Wang, P. Stochastic scheduling of mobile energy storage in coupled distribution and transportation networks for conversion capacity enhancement. IEEE Trans. Smart Grid 2020, 12, 117–130. [Google Scholar] [CrossRef]
- Huang, D.; Chen, B.; Huang, T.; Fang, X.; Zhang, H.; Cao, J. Open capacity enhancement model of medium voltage distribution network with mobile energy storage system. IEEE Access 2020, 8, 205061–205070. [Google Scholar] [CrossRef]
- Sun, C.; Wang, X.; Tong, W.; Chen, L. Establishment and analysis of traffic assignment model under the user equilibrium and system optimization principle. China Sci. 2013, 8, 1073–1077. [Google Scholar]
- Lotfi, M.; Venkatasubramanian, B.V.; Papadopoulos, I.; Panteli, M. Incorporating Mobile Energy Resources in Optimal Power Flow Models Considering Geographical and Road Network Data. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Lei, S.; Chen, C.; Zhou, H.; Hou, Y. Routing and scheduling of mobile power sources for distribution system resilience enhancement. IEEE Trans. Smart Grid 2018, 10, 5650–5662. [Google Scholar] [CrossRef]
- Kim, J.; Dvorkin, Y. Enhancing distribution system resilience with mobile energy storage and microgrids. IEEE Trans. Smart Grid 2018, 10, 4996–5006. [Google Scholar] [CrossRef]
- Wang, W.; Xiong, X.; Xiao, C.; Wei, B. A novel mobility model to support the routing of mobile energy resources. IEEE Trans. Smart Grid 2022, 13, 2675–2678. [Google Scholar] [CrossRef]
- Xing, Q.; Chen, Z.; Leng, Z.; Lu, Y.; Liu, Y. Route Planning and Charging Navigation Strategy for Electric Vehicles Based on Real-time Traffic Information. Proc. Chin. Soc. Electr. Eng. 2020, 40, 534–549. [Google Scholar]
- Yao, S.; Wang, P.; Zhao, T. Transportable energy storage for more resilient distribution systems with multiple microgrids. IEEE Trans. Smart Grid 2018, 10, 3331–3341. [Google Scholar] [CrossRef]
- Sun, W.; Qiao, Y.; Liu, W. Economic scheduling of mobile energy storage in distribution networks based on equivalent reconfiguration method. Sustain. Energy Grids Netw. 2022, 32, 100879. [Google Scholar] [CrossRef]
- Wang, W.; Xiong, X.; Xiao, C.; Wei, B. Appendix of the Paper “A Novel Mobility Model to Support the Routing of Mobile Energy Resources”. Available online: https://drive.google.com/file/d/1jDeaAE3ONsgvme2jp0v8zrJ-fX7mqbeQ/view?usp=sharing (accessed on 16 March 2022).
- Rahmani-Andebili, M. Vehicle-for-grid (VfG): A mobile energy storage in smart grid. IET Gener. Transm. Distrib. 2019, 13, 1358–1368. [Google Scholar] [CrossRef]
- Lombardi, P.; Schwabe, F. Sharing economy as a new business model for energy storage systems. Appl. Energy 2017, 188, 485–496. [Google Scholar] [CrossRef]
- Moraski, J.W.; Popovich, N.D.; Phadke, A.A. Leveraging rail-based mobile energy storage to increase grid reliability in the face of climate uncertainty. Nat Energy 2023, 8, 736–746. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, J.; Zhang, W.; Wu, Q.; Zhang, Y.; Liu, J. Two-step optimal allocation of stationary and mobile energy storage systems in resilient distribution networks. J. Mod. Power Syst. Clean Energy 2021, 9, 788–799. [Google Scholar] [CrossRef]
- Abdeltawab, H.; Mohamed, Y.A.R.I. Mobile energy storage sizing and allocation for multi-services in power distribution systems. IEEE Access 2019, 7, 176613–176623. [Google Scholar] [CrossRef]
- Yang, Z.; Ghadamyari, M.; Khorramdel, H.; Alizadeh, S.M.; Pirouzi, S.; Milani, M.; Banihashemi, F.; Ghadimi, N. Robust multi-objective optimal design of islanded hybrid system with renewable and diesel sources/stationary and mobile energy storage systems. Renew. Sustain. Energy Rev. 2021, 148, 111295. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Y.; Wang, R.; Ming, M. Multi-objective configuration optimization for isolated microgrid with shiftable loads and mobile energy storage. IEEE Access 2019, 7, 95248–95263. [Google Scholar] [CrossRef]
- Ahmed, H.M.A.; Sindi, H.F.; Azzouz, M.A.; Awad, A.S.A. Optimal Sizing and Scheduling of Mobile Energy Storage Toward High Penetration Levels of Renewable Energy and Fast Charging Stations. IEEE Trans. Energy Convers. 2021, 37, 1075–1086. [Google Scholar] [CrossRef]
- Wang, Y.; Rousis, A.O.; Strbac, G. Resilience-driven optimal sizing and pre-positioning of mobile energy storage systems in decentralized networked microgrids. Appl. Energy 2022, 305, 117921. [Google Scholar] [CrossRef]
- Srivastava, A.; Kuppannagari, S.R.; Kannan, R.; Prasanna, V.K. Minimizing cost of smart grid operations by scheduling mobile energy storage systems. IEEE Lett. Comput. Soc. 2019, 2, 20–23. [Google Scholar] [CrossRef]
- Liu, F.; Chen, J.; Zhao, Y.; Xiao, C. Resilience Enhancement for Distribution System Based on Mobile Energy Storage Sharing in Peer-to-peer Transaction Mode. Autom. Electr. Power Syst. 2022, 46, 151–159. [Google Scholar]
- Pulazza, G.; Zhang, N.; Kang, C.; Nucci, C.A. Transmission planning with battery-based energy storage transportation for power systems with high penetration of renewable energy. IEEE Trans. Power Syst. 2021, 36, 4928–4940. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, W.; Zeng, B.; Hui, H.; Li, F. Enhancing distribution system resilience against extreme weather events: Concept review, algorithm summary, and future vision. Int. J. Electr. Power Energy Syst. 2022, 138, 107860. [Google Scholar] [CrossRef]
- Siddique, M.B.; Thakur, J. Assessment of curtailed wind energy potential for off-grid applications through mobile battery storage. Energy 2020, 201, 117601. [Google Scholar] [CrossRef]
- Ghasemi, S.; Moshtagh, J. Distribution system restoration after extreme events considering distributed generators and static energy storage systems with mobile energy storage systems dispatch in transportation systems. Appl. Energy 2022, 310, 118507. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.R.I. Mobile energy storage scheduling and operation in active distribution systems. IEEE Trans. Ind. Electron. 2017, 64, 6828–6840. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Shahidehpour, M.; Ai, B. Battery-based energy storage transportation for enhancing power system economics and security. IEEE Trans. Smart Grid 2015, 6, 2395–2402. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J.; Yi, Y.; Tao, Y. Cost-effective coordinated voltage control in active distribution networks with photovoltaics and mobile energy storage systems. IEEE Trans. Sustain. Energy 2021, 13, 501–513. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, W.; Yao, Q.; Wan, H.; He, J.; Xiong, X. Pre-layout and Dynamic Scheduling Strategy of Mobile Energy Storage for Resilience Enhancement of Distribution Network. Autom. Electr. Power Syst. 2022, 46, 37–45. [Google Scholar]
- Tong, L.; Zhao, S.; Jiang, H.; Zhou, J.; Xu, B. Multi-scenario and multi-objective collaborative optimization of distribution network considering electric vehicles and mobile energy storage systems. IEEE Access 2021, 9, 55690–55697. [Google Scholar] [CrossRef]
- Wu, H.; Xie, Y.; Xu, Y.; Wu, Q.; Yu, C.; Sun, J. Resilient scheduling of MESSs and RCs for distribution system restoration considering the forced cut-off of wind power. Energy 2022, 244, 123081. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Nematbakhsh, E.; Ahmarinejad, A.; Jordehi, A.R.; Javadi, M.S.; Marzband, M. A hierarchical scheduling framework for resilience enhancement of decentralized renewable-based microgrids considering proactive actions and mobile units. Renew. Sustain. Energy Rev. 2022, 168, 112854. [Google Scholar] [CrossRef]
- Nazemi, M.; Dehghanian, P.; Lu, X.; Chen, C. Uncertainty-aware deployment of mobile energy storage systems for distribution grid resilience. IEEE Trans. Smart Grid 2021, 12, 3200–3214. [Google Scholar] [CrossRef]
- Erenoğlu, A.K.; Erdinç, O. Post-Event restoration strategy for coupled distribution-transportation system utilizing spatiotemporal flexibility of mobile emergency generator and mobile energy storage system. Electr. Power Syst. Res. 2021, 199, 107432. [Google Scholar] [CrossRef]
- Jeon, S.; Choi, D.H. Joint optimization of Volt/VAR control and mobile energy storage system scheduling in active power distribution networks under PV prediction uncertainty. Appl. Energy 2022, 310, 118488. [Google Scholar] [CrossRef]
- Sun, W.; Liu, W.; Zhang, J.; Tian, K. Bi-level Optimal Operation Model of Mobile Energy Storage System in Coupled Transportation-power Networks. J. Mod. Power Syst. Clean Energy 2022, 10, 1725–1737. [Google Scholar] [CrossRef]
- Yao, S.; Wang, P.; Liu, X.; Zhang, H.; Zhao, T. Rolling optimization of mobile energy storage fleets for resilient service restoration. IEEE Trans. Smart Grid 2019, 11, 1030–1043. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, X.; Yan, Z.; Shahidehpour, M. Multistage Robust Optimization of Routing and Scheduling of Mobile Energy Storage in Coupled Transportation and Power Distribution Networks. IEEE Trans. Transp. Electrif. 2021, 8, 2583–2594. [Google Scholar] [CrossRef]
- Xu, R.; Xu, X.; Wang, H.; Yan, Z. Coordinated Dispatching of Electric Bus, Charging Station and Distribution Network Considering Bus Travelling Characteristics. Autom. Electr. Power Syst. 2022, 46, 36–44. [Google Scholar]
- Chen, T.; Xu, X.; Wang, H.; Yan, Z. Routing and Scheduling of Mobile Energy Storage System for Electricity Arbitrage Based on Two-layer Deep Reinforcement Learning. IEEE Trans. Transp. Electrif. 2022, 9, 1087–1102. [Google Scholar] [CrossRef]
- Yao, S.; Gu, J.; Zhang, H.; Wang, P.; Liu, X.; Zhao, T. Resilient load restoration in microgrids considering mobile energy storage fleets: A deep reinforcement learning approach. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Wang, Y.; Qiu, D.; Strbac, G. Multi-agent deep reinforcement learning for resilience-driven routing and scheduling of mobile energy storage systems. Appl. Energy 2022, 310, 118575. [Google Scholar] [CrossRef]
- Prabawa, P.; Choi, D.H. Multi-agent framework for service restoration in distribution systems with distributed generators and static/mobile energy storage systems. IEEE Access 2020, 8, 51736–51752. [Google Scholar] [CrossRef]
- Wagenitz, R.; Heiß, B.; Meißner, T.; Schuster, H. Mobile energy with E. DIS (Moew. e) pilot project within IElectrix. In Proceedings of the CIRED 2020 Berlin Workshop (CIRED 2020), Berlin, Germany, 22–23 September 2020; IET: London, UK, 2020; Volume 2020, pp. 448–450. [Google Scholar]
- Li, J.; Zhang, Z.; Li, Y.; Zhou, Y.; Yue, Y. Research on key technologies of mobile energy storage system under the target of carbon neutrality. Energy Storage Sci. Technol. 2022, 11, 1523–1536. [Google Scholar]
- Chen, N.; Li, M.; Wang, M.; Su, Z.; Li, J.; Shen, X.S. A dynamic pricing based scheduling scheme for electric vehicles as mobile energy storages. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Qin, J.; Poolla, K.; Varaiya, P. Mobile storage for demand charge reduction. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7952–7962. [Google Scholar] [CrossRef]
- Moura, P.; Sriram, U.; Mohammadi, J. Sharing mobile and stationary energy storage resources in transactive energy communities. In 2021 IEEE Madrid PowerTech; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Agwan, U.; Qin, J.; Poolla, K.; Varaiya, P. Electric vehicle battery sharing game for mobile energy storage provision in power networks. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 6364–6370. [Google Scholar]
- Mirzaei, M.A.; Hemmati, M.; Zare, K.; Mohammadi-Ivatloo, B.; Abapour, M.; Marzband, M.; Farzamnia, A. Two-stage robust-stochastic electricity market clearing considering mobile energy storage in rail transportation. IEEE Access 2020, 8, 121780–121794. [Google Scholar] [CrossRef]
- Fang, X.; Hodge, B.M.; Du, E.; Kang, C.; Li, F. Introducing uncertainty components in locational marginal prices for pricing wind power and load uncertainties. IEEE Trans. Power Syst. 2019, 34, 2013–2024. [Google Scholar] [CrossRef]
- Ye, H.; Ge, Y.; Shahidehpour, M.; Li, Z. Uncertainty marginal price, transmission reserve, and day-ahead market clearing with robust unit commitment. IEEE Trans. Power Syst. 2016, 32, 1782–1795. [Google Scholar] [CrossRef]
- Qin, Z.; Mo, Y.; Liu, H.; Zhang, Y. Operational flexibility enhancements using mobile energy storage in day-ahead electricity market by game-theoretic approach. Energy 2021, 232, 121008. [Google Scholar] [CrossRef]
- He, G.; Michalek, J.; Kar, S.; Chen, Q.; Zhang, D.; Whitacre, J.F. Utility-scale portable energy storage systems. Joule 2021, 5, 379–392. [Google Scholar] [CrossRef]
- Ding, Y.; Qu, G.; Chen, X.; Wang, J.; Song, J.; He, G. Deep Reinforcement Learning-Based Spatiotemporal Decision of Utility-Scale Highway Portable Energy Storage Systems. IEEE Trans. Ind. Appl. 2023, 60, 966–975. [Google Scholar] [CrossRef]
- Meng, H.; Jia, H.; Xu, T.; Wei, W.; Wu, Y.; Liang, L.; Cai, S.; Liu, Z.; Wang, R.; Li, M. Optimal configuration of cooperative stationary and mobile energy storage considering ambient temperature: A case for Winter Olympic Game. Appl. Energy 2022, 325, 119889. [Google Scholar] [CrossRef]
- Chuangpishit, S.; Katiraei, F.; Chalamala, B.; Novosel, D. Mobile Energy Storage Systems: A Grid-Edge Technology to Enhance Reliability and Resilience. IEEE Power Energy Mag. 2023, 21, 97–105. [Google Scholar] [CrossRef]
- Liu, D.; Wang, L.; Liu, M.; Jia, H.; Li, H.; Wang, W. Optimal energy storage allocation strategy by coordinating electric vehicles participating in auxiliary service market. IEEE Access 2021, 9, 95597–95607. [Google Scholar] [CrossRef]
- Xiao, D.; Sun, H.; Nikovski, D.; Kitamura, S.; Mori, K.; Hashimoto, H. CVaR-constrained stochastic bidding strategy for a virtual power plant with mobile energy storages. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Delft, The Netherlands, 26–28 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1171–1175. [Google Scholar]
- Kalathil, D.; Wu, C.; Poolla, K.; Varaiya, P. The sharing economy for the electricity storage. IEEE Trans. Smart Grid 2017, 10, 556–567. [Google Scholar] [CrossRef]
- Crespo-Vazquez, J.L.; AlSkaif, T.; González-Rueda, Á.M.; Gibescu, M. A community-based energy market design using decentralized decision-making under uncertainty. IEEE Trans. Smart Grid 2020, 12, 1782–1793. [Google Scholar] [CrossRef]
- Guerrero, J.; Chapman, A.C.; Verbič, G. Decentralized P2P energy trading under network constraints in a low-voltage network. IEEE Trans. Smart Grid 2018, 10, 5163–5173. [Google Scholar] [CrossRef]
- Guerrero, J.; Chapman, A.C.; Verbič, G. Local energy markets in LV networks: Community based and decentralized P2P approaches. In Proceedings of the 2019 IEEE Milan Powertech, Milan, Italy, 23–27 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Chang, W.; Dong, W.; Yang, Q. Day-ahead bidding strategy of cloud energy storage serving multiple heterogeneous microgrids in the electricity market. Appl. Energy 2023, 336, 120827. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, J.; Yang, Z.; Wang, X.; Pu, T.; Liu, J. Mobile Energy Storage Peer-to-Peer Transaction Control Method for Multi-Use Electricity Entities. Electrical Measurement & Instrumentation. 2022. Available online: https://kns.cnki.net/kcms/detail/23.1202.TH.20220711.1412.002.html (accessed on 12 July 2022).
- Guo, Z.; Liu, J.; Yang, Z.; Pu, T.; Wang, X.; Liu, J. Peer-to-Peer Transaction Mode between Mobile Energy Storage and Microgrid Customers and Mobile Energy Storage Scheduling Strategy under Power Shortage. Power Syst. Technol. 2022, 46, 4873–4884. [Google Scholar]
- Wang, Y.; Yan, Z.; Sang, L.; Hong, L.; Hu, Q.; Shahidehpour, M.; Xu, Q. Acceleration Framework and Solution Algorithm for Distribution System Restoration based on End-to-End Optimization Strategy. IEEE Trans. Power Syst. 2023, 39, 429–441. [Google Scholar] [CrossRef]
- Kotary, J.; Fioretto, F.; Van Hentenryck, P.; Wilder, B. End-to-end constrained optimization learning: A survey. arXiv 2021, arXiv:2103.16378. [Google Scholar]
- van Leeuwen, G.; AlSkaif, T.; Gibescu, M.; van Sark, W. An integrated blockchain-based energy management platform with bilateral trading for microgrid communities. Appl. Energy 2020, 263, 114613. [Google Scholar] [CrossRef]
- Xie, Y.-S.; Lee, Y.; Chang, X.-Q.; Yin, X.; Zheng, H. Research on the transaction mode and mechanism of grid-side shared energy storage market based on blockchain. Energy Rep. 2022, 8, 224–229. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Gärttner, J.; Rock, K.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing microgrid energy markets: A case study: The Brooklyn Microgrid. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]


| Flexibility | Controllability | Scale | Typical Functions | |
|---|---|---|---|---|
| EV | Spatiotemporal | Stochastic |
|
|
| MESS | Spatiotemporal | Fully controllable |
|
|
| Stationary ESS | Temporal | Fully controllable |
|
|
| Mobility | Power State | Energy State |
|---|---|---|
| Traveling | Discharging for travel | SOC decrease |
| Parking | Charging in the station | SOC increase |
| Discharging in the station | SOC decrease | |
| Idle | - |
| Year | Country | MESS Size | Application | ||
|---|---|---|---|---|---|
| Resilience Improvement | Economic Operation | Security Operation | |||
| 2016 | USA | 500 kW/800 kWh | √ | √ | |
| 2016 | China | megawatt scale | √ | ||
| 2019 | China | 1 MW/2 MWh | √ | ||
| 2020 | Germany | 500 kW/1000 kWh | √ | ||
| 2020 | China | 34 MWh | √ | √ | √ |
| 2022 | China | 10 MW/9 MWh | √ | ||
| 2022 | The Netherlands | 20 MWh | √ | ||
| 2023 | China | 6 MW/7.2 MWh | √ | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Xu, X.; Yan, Z.; Han, D.; Xia, S. Mobile Energy-Storage Technology in Power Grid: A Review of Models and Applications. Sustainability 2024, 16, 6857. https://doi.org/10.3390/su16166857
Lu Z, Xu X, Yan Z, Han D, Xia S. Mobile Energy-Storage Technology in Power Grid: A Review of Models and Applications. Sustainability. 2024; 16(16):6857. https://doi.org/10.3390/su16166857
Chicago/Turabian StyleLu, Zhuoxin, Xiaoyuan Xu, Zheng Yan, Dong Han, and Shiwei Xia. 2024. "Mobile Energy-Storage Technology in Power Grid: A Review of Models and Applications" Sustainability 16, no. 16: 6857. https://doi.org/10.3390/su16166857
APA StyleLu, Z., Xu, X., Yan, Z., Han, D., & Xia, S. (2024). Mobile Energy-Storage Technology in Power Grid: A Review of Models and Applications. Sustainability, 16(16), 6857. https://doi.org/10.3390/su16166857







