Applications of Novel Combined Controllers for Optimizing Grid-Connected Hybrid Renewable Energy Systems
Abstract
1. Introduction
2. Design of the Proposed System
2.1. Mathematical Modeling of the Proposed System
2.1.1. PV System
2.1.2. Wind System
2.1.3. Battery Storage System
2.1.4. Boost Converter DC/DC
3. Control and Improvement Power of HRES
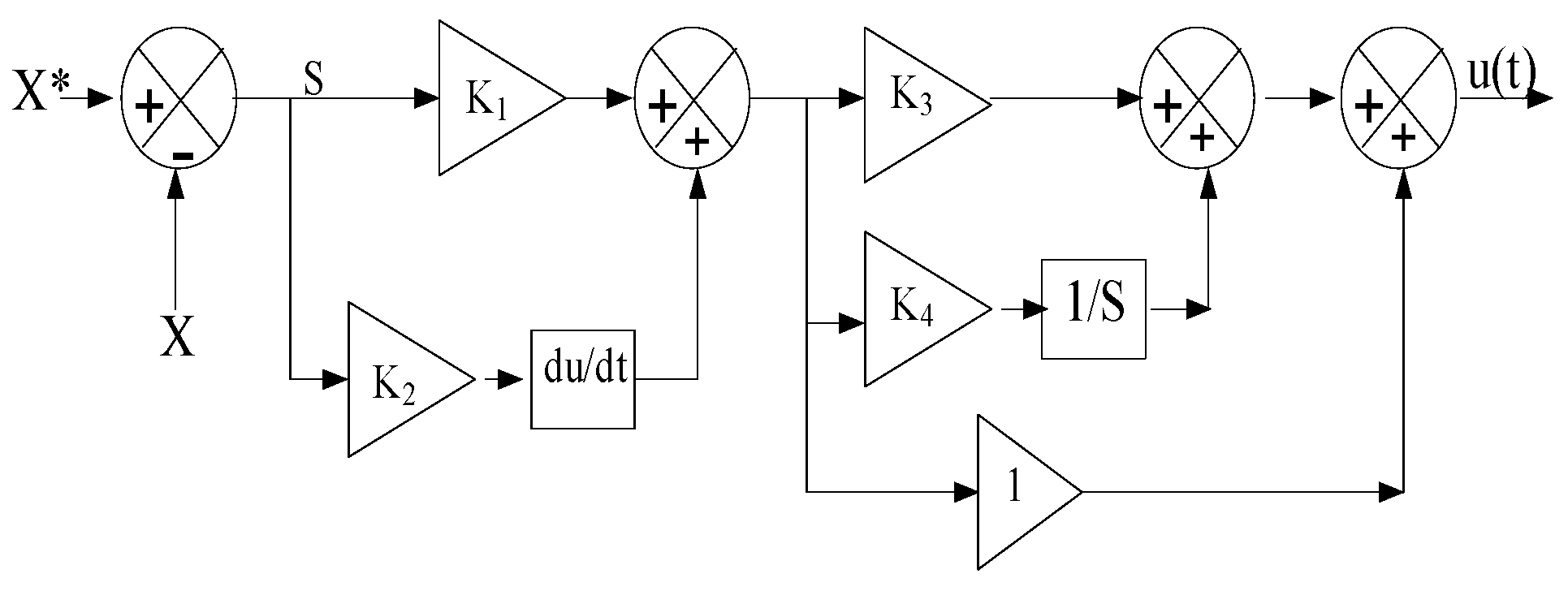
3.1. PD(1+PI) Controller
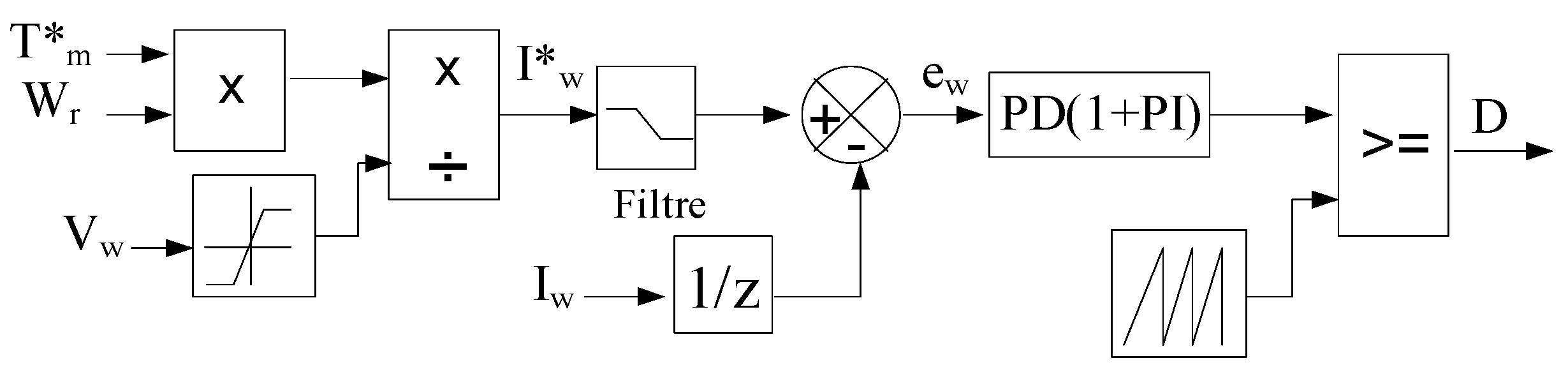
3.1.1. The Proposed MPPT-PD (1+PI) for PV Generator
3.1.2. The Proposed MPPT-PD (1+PI) for Wind Generator
3.1.3. Buck/Boost Converter Control Using PD(1+PI) for Battery System
3.2. Grid Control Side
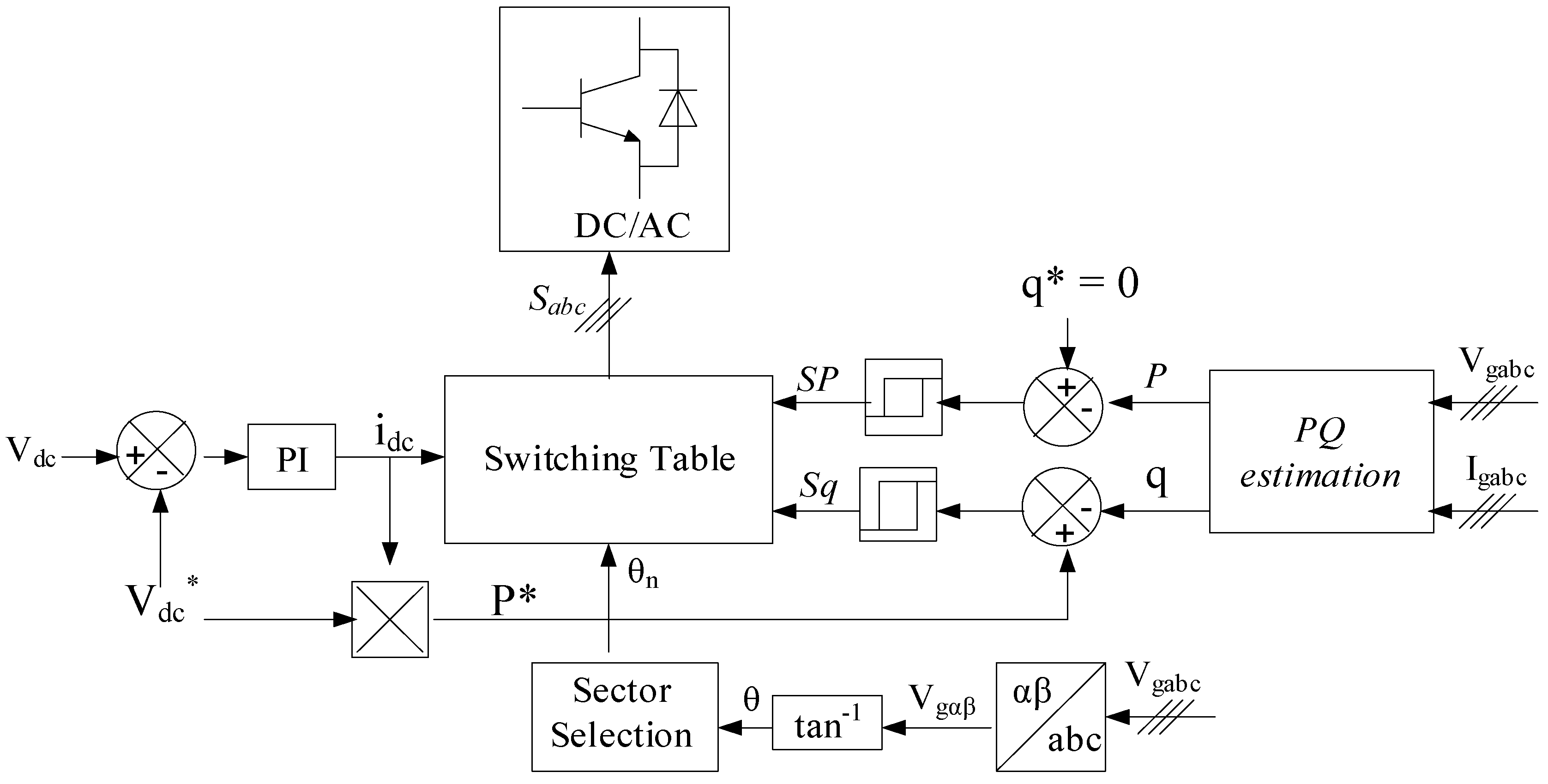
3.2.1. Classical Direct Power Control Strategy (PI-DPC)
3.2.2. Proposed PD(1+PI)-P-DPC Strategy
4. Simulation Results
- (a)
- RES analysis
- (b)
- Grid analysis
- (c)
- Total harmonic distortion analysis
- Transient Time and Settling Time: The PD (1+PI) technique generally exhibits shorter settling times compared with the PI technique. For example, in the time interval of 0–0.5 s, the settling time for the PD (1+PI) technique is 0.2 s, whereas it is slightly longer at 0.22 s for the PI technique. This indicates that the PD (1+PI) technique achieves stability faster in response to transient changes in the system.
- Ripple: The PD (1+PI) technique shows lower ripple values for the DC bus voltage compared with the PI technique. For instance, in the time interval of 0–0.5 s, the ripple for the PD (1+PI) technique is 0.07 volts, while it is slightly higher at 0.08 volts for the PI technique. This suggests that the PD (1+PI) technique produces a smoother and more consistent output voltage, which is desirable for stable operation.
- Overshoot/Undershoot: Both techniques exhibit some level of overshoot/undershoot in the DC bus voltage. In most cases, the PD (1+PI) technique shows lower overshoot/undershoot percentages compared with the PI technique. For example, in the time interval of 0–0.5 s, the overshoot/undershoot percentage for the PD (1+PI) technique is 1.6%, while it is higher at 2.43% for the PI technique. However, the absolute values of overshoot/undershoot (in volts) are higher for the PD (1+PI) technique in some cases.
- (d)
- Comparative study with recent studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PV System | |
| Iph, I0 | Photo-current and saturation current (A) |
| ID | Diode current (A) |
| Ish | Shunt resistor current |
| q | Electron charge (1.6 × 10−23 C) |
| k | Boltzmann’s constant (1.38 × 10−19 J/K) |
| n | Ideality constant of the diode |
| Rs | Equivalent series resistance of the PV module (Ω) |
| Rp | Equivalent parallel resistance of the PV module (Ω) |
| T | Module operating temperature (K) |
| Ns | Number of PV modules in series. |
| Np | Number of PV modules in parallel |
| Lboost | Boost converter inductance (mH) |
| Cdc | Boost link capacitor (µF) |
| Rotor current (A) | |
| Inductor flux (Wb) | |
| Tr | Pump electromagnetic torque (Nm) |
| ωr | Rotor electrical speed (rad/s) |
| DC-DC Converter | |
| Vin | Input voltage (PV or wind voltage) |
| Vout | Output voltage |
| D | Duty cycle |
| il | Inductor current |
| iload | Load current. |
| WT system | |
| λ | Tip speed ratio of the rotor blades |
| β | Blade pitch angle |
| ρ | Air density (Kg.m−3) |
| S | Swept area of turbine |
| Vwind | Wind speed (m/s) |
| Cp | Turbine power coefficient |
| R | Wind turbine rotor radius (m) |
| ωr | Wind turbine rotor speed |
| Tm | Mechanical torque (Nm) |
| Battery system | |
| ibat | Current in battery |
| Q | Capacity of the battery |
| Vbat: | Voltage of the battery |
| Vdc | DC bus voltage |
References
- Shan, Y.; Hu, J.; Chan, K.W.; Fu, Q.; Guerrero, J.M. Model predictive control of bidirectional DC-DC converters and AC/DC interlinking converters-A new control method for PV-wind-battery microgrids. IEEE Trans. Sustain. Energy 2018, 10, 1823–1833. [Google Scholar] [CrossRef]
- Akbulut, O.; Cavus, M.; Cengiz, M.; Allahham, A.; Giaouris, D.; Forshaw, M. Hybrid Intelligent Control System for Adaptive Microgrid Optimization: Integration of Rule-Based Control and Deep Learning Techniques. Energies 2024, 17, 2260. [Google Scholar] [CrossRef]
- Ascanio Villabona, J.; Romero, B.E.T.; Duran, M.A.; Lengerke, O.; Betancur, L. Evaluation of the thermal performance of housing envelopes as passive cooling systems. Sustain. Eng. Innov. 2023, 5, 177–188. [Google Scholar] [CrossRef]
- Durakovic, B.; Halilovic, M. Thermal performance analysis of PCM solar wall under variable natural conditions: An experimental study. Energy Sustain. Dev. 2023, 76, 101274. [Google Scholar] [CrossRef]
- Abdellatif, W.S.E.; Elborlsy, M.S.; Barakat, S.; Brisha, A. A Fuzzy Logic Controller Based MPPT Technique for Photovoltaic Generation System. Int. J. Electr. Electron. Eng. Instrum. IJEEI 2021, 13, 394–417. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, X.; Guo, L. Comprehensive Review of Hybrid Renewable Energy Systems for Electricity Generation: Opportunities and Challenges. Renew. Sustain. Energy Rev. 2020, 124, 109759. [Google Scholar]
- Gadouche, Z.; Belfedal, C.; Allaoui, T.; Denai, M.; Bey, M. Hybrid Renewable Energy System Controlled with Intelligent Direct Power Control. J. Energy Syst. Autom. 2022, 55, 467–475. [Google Scholar] [CrossRef]
- Oskouei, M.Z.; Şeker, A.A.; Tunçel, S.; Demirbaş, E.; Gözel, T.; Hocaoğlu, M.H.; Abapour, M.; Mohammadi-Ivatloo, B. A Critical Review on the Impacts of Energy Storage Systems and Demand-Side Management Strategies in the Economic Operation of Renewable-Based Distribution Network. Sustainability 2022, 14, 2110. [Google Scholar] [CrossRef]
- Yuan, W.; Yuan, X.; Xu, L.; Zhang, C.; Ma, X. Harmonic Loss Analysis of Low-Voltage Distribution Network Integrated with Distributed Photovoltaic. Sustainability 2023, 15, 4334. [Google Scholar] [CrossRef]
- Alramlawi, M.; Gabash, A.; Mohagheghi, E.; Li, P. Optimal operation of hybrid PV-battery system considering grid scheduled blackouts and battery lifetime. Sol. Energy 2018, 161, 125–137. [Google Scholar] [CrossRef]
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. An Efficient Fuzzy-Logic Based Variable-Step Incremental Conductance MPPT Method for Grid-Connected PV Systems. IEEE Access 2021, 9, 26420–26430. [Google Scholar] [CrossRef]
- Zebraoui, O.; Bouzi, M. Improved MPPT controls for a standalone PV/wind/battery hybrid energy system. Int. J. Power Electron. Drive Syst. IJPEDS 2020, 11, 988–1001. [Google Scholar] [CrossRef]
- Debdouche, N.; Deffaf, B.; Benbouhenni, H.; Laid, Z.; Mosaad, M.I. Direct Power Control for Three-Level Multifunctional Voltage Source Inverter of PV Systems Using a Simplified Super-Twisting Algorithm. Energies 2023, 16, 4103. [Google Scholar] [CrossRef]
- Jain, R.; Bakare, Y.B.; Pattanaik, B.; Alaric, J.S.; Balam, S.K.; Ayele, T.B.; Nalagandla, R. Optimization of energy consumption in smart homes using firefly algorithm and deep neural networks. Sustain. Eng. Innov. 2023, 5, 161–176. [Google Scholar] [CrossRef]
- Semeskandeh, S.; Hojjat, M.; Abardeh, M.H. Techno–economic–environmental feasibility study of a photovoltaic system in northern part of Iran including a two-stage multi-string inverter with DC–DC ZETA converter and a modified P&O algorithm. Clean Energy 2022, 6, 127–140. [Google Scholar] [CrossRef]
- Kassem, A.; Abdallah, I.; Zaiou, A.; Miloud, M.; Ali, L. Novel Algorithm-Based Optimization Approach for Sizing Standalone Hybrid Energy Systems. Mathematics 2023, 11, 1734. [Google Scholar]
- Thaveedu, A.S.R.; Ramaswamy, S.K.; Thirumurugan, S. PV-Wind-Battery Based Bidirectional DC-DC Converter for Grid-Connected Systems. IOP Conf. Ser. Mater. Sci. Eng. 2020, 955, 012070. [Google Scholar] [CrossRef]
- Ammar, A.; Belaroussi, O.; Fedorovich, K.V. Improved Adaptive Neuro-Fuzzy Based Maximum Power Point Tracking Approaches in Photovoltaic Pumping Systems. In Proceedings of the 2023 International Conference on Renewable Energy and Smart Technologies (ICRSEtoSET), Djelfa, Algeria, 6–8 May 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Zebraoui, O.; Hassan First University; Bouzi, M. Robust Sliding Mode Control based MPPT for a PV/Wind Hybrid Energy System. Int. J. Intell. Eng. Syst. 2018, 11, 290–300. [Google Scholar] [CrossRef]
- Mishra, D.P.; Rout, K.; Mishra, S.; Salkuti, S.R. Power Quality Enhancement of Grid-Connected PV System. Indones. J. Electr. Eng. Comput. Sci. 2023, 14, 369–377. [Google Scholar] [CrossRef]
- Ahmed, M.; Harbi, I.; Kennel, R.; Rodríguez, J.; Abdelrahem, M. Evaluation of the Main Control Strategies for Grid-Connected PV Systems. Sustainability 2022, 14, 11142. [Google Scholar] [CrossRef]
- Mohammadi, J.; Vaez-Zadeh, S.; Afsharnia, S.; Daryabeigi, E. A Combined Vector and Direct Power Control for DFIG-Based Wind Turbines. IEEE Trans. Sustain. Energy 2014, 5, 767–775. [Google Scholar] [CrossRef]
- Choudhary, P.K.; Shivkumar, S.A. Performance Analysis on PMSG Based Wind Generation System Interfaced Multilevel Converter with Artificial Intelligence Technique. Int. J. Trend Res. Dev. 2023, 8. [Google Scholar] [CrossRef]
- Zhou, Z.; Fang, Y. Research on Photovoltaic MPPT Control Strategy Based on Improved Manta Ray Foraging Optimization Algorithm. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Behabtu, H.A.; Vafaeipour, M.; Kebede, A.A.; Berecibar, M.; Van Mierlo, J.; Fante, K.A.; Messagie, M.; Coosemans, T. Smoothing Intermittent Output Power in Grid-Connected Doubly Fed Induction Generator Wind Turbines with Li-Ion Batteries. Energies 2023, 16, 7637. [Google Scholar] [CrossRef]
- Rouholamini, M.; Wang, C.; Nehrir, H.; Hu, X.; Hu, Z.; Aki, H.; Zhao, B.; Miao, Z.; Strunz, K. A Review of Modeling, Management, and Applications of Grid-Connected Li-Ion Battery Storage Systems. IEEE Trans. Smart Grid 2022, 13, 4505–4524. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E.P. A comprehensive review on wind turbine power curve modeling techniques. Renew. Sustain. Energy Rev. 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Li, X.; Yang, Z.; Zhang, H.; Chen, L. Development of a Robust Speed Controller for Permanent Magnet Synchronous Generator-Based Wind Systems Using Advanced Metaheuristic Optimization and Wind Speed Prediction. Renew. Energy 2023, 215, 658–674. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.; Zhao, S.; Zhang, T. Performance Evaluation of Wind-Driven PMSG Systems Under Extreme Operating Conditions Using Advanced Optimization Algorithms. Energy Rep. 2023, 9, 1800–1814. [Google Scholar] [CrossRef]
- Benavides, D.; Arévalo, P.; Tostado-Véliz, M.; Vera, D.; Escamez, A.; Aguado, J.A.; Jurado, F. An Experimental Study of Power Smoothing Methods to Reduce Renewable Sources Fluctuations Using Supercapacitors and Lithium-Ion Batteries. Batteries 2022, 8, 228. [Google Scholar] [CrossRef]
- Larrinaga, S.A.; Vidal, M.A.R.; Oyarbide, E.; Apraiz, J.R.T. Predictive Control Strategy for DC/AC Converters Based on Direct Power Control. IEEE Trans. Ind. Electron. 2007, 54, 1261–1271. [Google Scholar] [CrossRef]
- Yimen, N.; Tchotang, T.; Kanmogne, A.; Idriss, I.A.; Musa, B.; Aliyu, A.; Okonkwo, E.C.; Abba, S.I.; Tata, D.; Meva’a, L.; et al. Optimal Sizing and Techno-Economic Analysis of Hybrid Renewable Energy Systems—A Case Study of a Photovoltaic/Wind/Battery/Diesel System in Fanisau, Northern Nigeria. Processes 2020, 8, 1381. [Google Scholar] [CrossRef]
- Elnozahy, A.; Yousef, A.M.; Abo-Elyousr, F.K.; Mohamed, M.; Abdelwahab, S.A.M. Performance improvement of hybrid renewable energy sources connected to the grid using artificial neural network and sliding mode control. J. Power Electron. 2021, 21, 1–14. [Google Scholar] [CrossRef]
- Mousazadeh, H.; Li, L.; Wong, M.; Sadeghi, A. Advanced Multiport Converter Design for Integration of Photovoltaic, Wind, and Fuel Cell Systems with Energy Storage: Optimization and Performance Analysis. J. Renew. Sustain. Energy 2023, 15, 072301. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Wang, S.; Li, J.; Chen, G. Optimization of DC-DC Converter Controllers for Enhanced Stability in Wind-Powered PMSG Systems with Variable Input Voltages. Renew. Energy 2024, 210, 1207–1220. [Google Scholar]
- Benbouhenni, H.; Bounadja, E.; Gasmi, H.; Bizon, N.; Colak, I. A new PD(1+PI) direct power controller for the variable-speed multi-rotor wind power system driven doubly-fed asynchronous generator. Energy Rep. 2022, 8, 15584–15594. [Google Scholar] [CrossRef]
- Ghanem, S.; Al-Harbi, M.; El Hajj, M.; Batarseh, I. Enhancement Techniques for Fault Ride-Through Capability in Grid-Connected Permanent Magnet Synchronous Wind Generators: A Comparative Study. Electr. Power Syst. Res. 2023, 216, 108932. [Google Scholar]
- Wang, W.; Cao, Y.; Jiang, L.; Chen, C.; Li, Y. A Perturbation Observer-Based Fast Frequency Support Control for Low-Inertia Power Grids Through VSC-HVDC Systems. IEEE Trans. Power Syst. 2023, 39, 2461–2474. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Zhang, N.; Walker, P.D.; Gao, J. A voltage sensorless finite control set-model predictive control for three-phase voltage source PWM rectifiers. Chin. J. Electr. Eng. 2016, 2, 52–59. [Google Scholar] [CrossRef]
- Rahab, A.; Benalla, H.; Senani, F. Improved virtual flux direct power control of three phase PWM rectifier using SOGI-FLL estimator under disturbed voltage conditions. Int. J. Appl. Power Eng. IJAPE 2019, 8, 34–42. [Google Scholar] [CrossRef]
- Hossain, J.; Kadir, A.F.A.; Shareef, H.; Manojkumar, R.; Saeed, N.; Hanafi, A.N. A Grid-Connected Optimal Hybrid PV-BES System Sizing for Malaysian Commercial Buildings. Sustainability 2023, 15, 10564. [Google Scholar] [CrossRef]
- Laggoun, Z.E.Z.; Nebti, K.; Benalla, H. A Comparative Study Between DPC-SVM and PDPC-SVM. In Proceedings of the 2019 International Conference on Advances in Electrical Engineering (ICAEE) 2019, Algiers, Algeria, 19–21 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Skarvelis-Kazakos, S.; Rikos, E.; Rigas, E.L.; Karapidakis, N.C.; Hatziargyriou, N.D. Frequency control in autonomous smart grids using demand side management. IEEE Trans. Smart Grid 2012, 3, 30–38. [Google Scholar]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Design and implementation of predictive current control of three-phase PWM rectifier using space-vector modulation (SVM). Energy Convers. Manag. 2010, 51, 2473–2481. [Google Scholar] [CrossRef]
- Bouafia, A.; Krim, F.; Gaubert, J.-P. Fuzzy-Logic-Based Switching State Selection for Direct Power Control of Three-Phase PWM Rectifier. IEEE Trans. Ind. Electron. 2009, 56, 1984–1992. [Google Scholar] [CrossRef]
- Boudechiche, G.; Sarra, M.; Aissa, O.; Gaubert, J.-P. An investigation of solar active power filter based on direct power control for voltage quality and energy transfer in grid-tied photovoltaic system under unbalanced and distorted conditions. J. Eng. Res. 2021, 9, 13899. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. DC-Link Capacitor Voltage Regulation for Three-Phase Three-Level Inverter-Based Shunt Active Power Filter with Inverted Error Deviation Control. Energies 2016, 9, 533. [Google Scholar] [CrossRef]
- Bu, W.; Xu, L. Direct Power Control Strategy of PWM Rectifier Based on Improved Virtual Flux-Linkage Observer. J. Control. Sci. Eng. 2017, 2017, 9376735. [Google Scholar] [CrossRef]





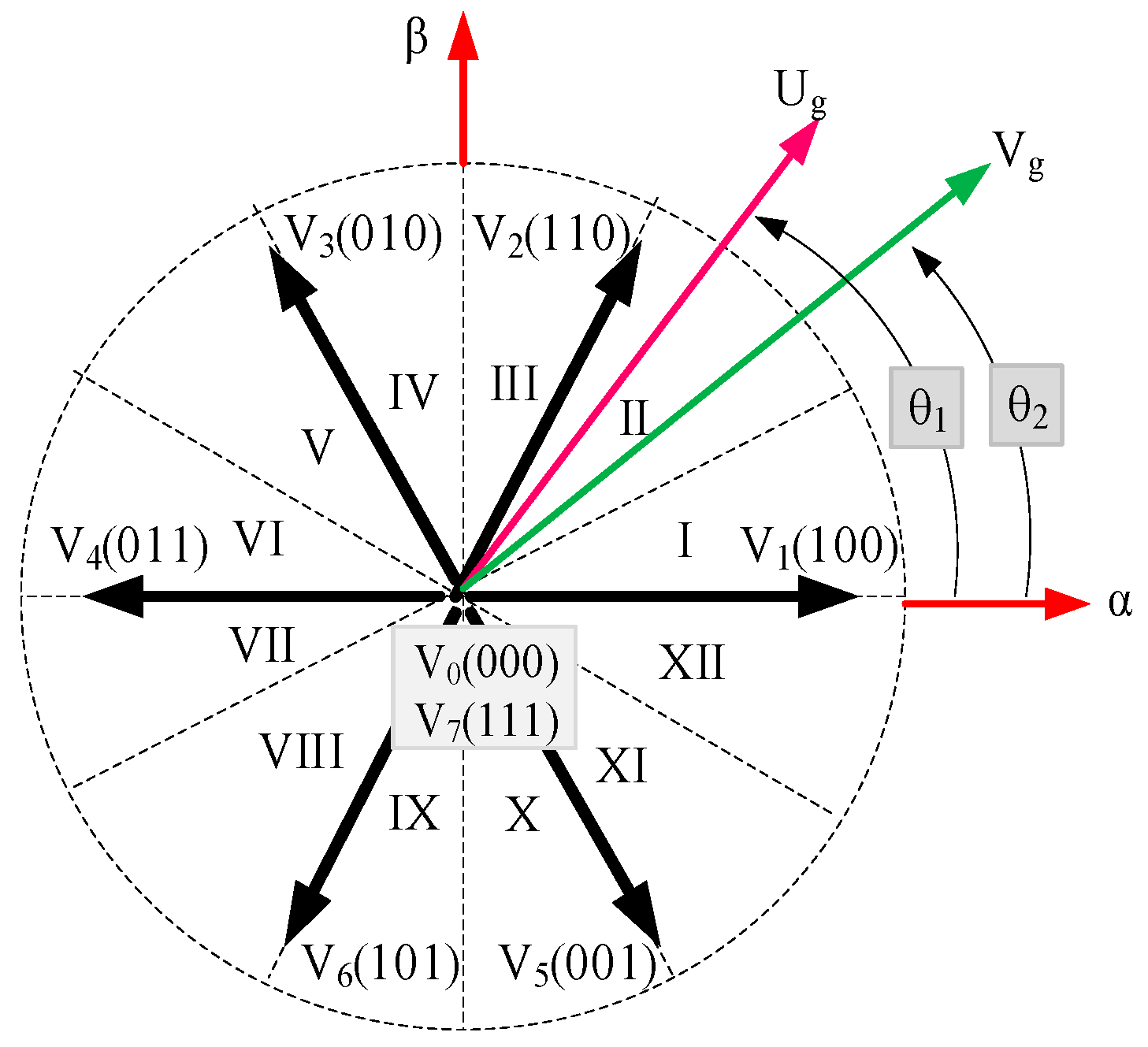











| Sp | Sq | θ 1 | θ 2 | θ 3 | θ 4 | θ 5 | θ 6 | θ 7 | θ 8 | θ 9 | θ 10 | θ 11 | θ 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | V5 | V6 | V6 | V1 | V1 | V2 | V2 | V3 | V3 | V4 | V4 | V5 |
| 1 | V3 | V4 | V4 | V5 | V5 | V6 | V6 | V1 | V1 | V2 | V2 | V3 | |
| 0 | 0 | V6 | V6 | V6 | V6 | V6 | V6 | V6 | V6 | V6 | V6 | V6 | V6 |
| 1 | V1 | V2 | V2 | V3 | V3 | V4 | V4 | V5 | V5 | V6 | V6 | V1 |
| THD (%) | |||||||
|---|---|---|---|---|---|---|---|
| PD (1+PI) | PI | ||||||
| PV SYSTEM | Ppv | 0.46 | 0.57 | 0.26 | 0.87 | 1.02 | 0.35 |
| Ipv | 0.05 | 0.06 | 0.02 | 0.09 | 0.09 | 0.05 | |
| Vpv | 0.77 | 2.64 | 1.27 | 0.95 | 2.93 | 1.75 | |
| WIND SYSTEM | Pw | 3.93 | 2.30 | 0.75 | 4.95 | 2.37 | 0.95 |
| Iw | 4.84 | 4.74 | 0.01 | 4.94 | 4.77 | 0.02 | |
| Vw | 0.07 | 0.02 | 0.04 | 0.1 | 0.04 | 0.08 | |
| DC Link | 1 s | 0.4 | 0.89 | ||||
| 1.5 s | 0.72 | 0.92 | |||||
| 2.5 s | 1.43 | 1.86 | |||||
| Transient Time (s) | Ripple (V) | Overshoot/Undershoot (%) | Settling Time (s) | |||
|---|---|---|---|---|---|---|
| PD(1+PI) | PI | PD (1+PI) | PI | PD (1+PI) | PI | |
| 0–0.5 | 0.07 | 0.08 | 1.6 | 2.43 | 0.2 | 0.22 |
| 0.5–1 | 0.03 | 0.03 | 0.4 | 0.89 | 0.035 | 0.04 |
| 1–1.5 | 0.01 | 0.02 | 0.72 | 0.92 | 0.05 | 0.056 |
| 1.5–2.5 | 0.09 | 0.1 | 1.43 | 1.86 | 0.1 | 0.18 |
| 2.5–3 | 0.03 | 0.035 | 0 | 0 | 0.01 | 0.016 |
| Study | Control Strategy | Efficiency (%) | THD (%) | Voltage Regulation (%) | Energy Savings (%) |
|---|---|---|---|---|---|
| Our Study | PD (1+PI) Control | 92 | 2.5 | 98.5 | 15 |
| Study A (2022) [1] | Traditional DPC | 88 | 3.0 | 95 | 12 |
| Study B (2023) [2] | Advanced PI Control | 90 | 2.8 | 97 | 13 |
| Study C (2023) [3] | Hybrid Control | 91 | 2.6 | 98 | 14 |
| PV system | Electrical characteristics | Battery Storage paramaters | ||
| Maximum Power Pmax (Wc) | 305 | Rated Capacity | 6.5 Ah | |
| Short-circuit Current Icc (A) | 5.96 | Nominal Voltage | 200 V | |
| Open-circuit Voltage Voc (V) | 64.2 | Maximum Capacity | 3.2308 Ah | |
| Optimum Voltage Vop (V) | 54.7 | Nominal Discharge Current | 0.6 A | |
| Mechanical characteristics | Exponential Voltage | 216.94 V | ||
| Cell Type | Monocrystalline | Internal Resistance | 0.6666 Ω | |
| Number of Cells | 96 | Fully Charged Voltage | 235.59 V | |
| Dimensions (mm/inches) | 156 × 156 (6+) | Capacity Nominal Voltage | 2.8846 Ah | |
| Weight | 24 Kg | Capacity Nominal Voltage | 0.6 Ah | |
| Wind system parameters | ||||
| Rated Capacity | V (m/s) | 12 | ||
| Nominal Voltage | w (rad/s) | 153 | ||
| Maximum Capacity | Pm (Kw) | 6 | ||
| Nominal Discharge Current | P | 5 | ||
| Exponential Voltage | Rs (Ω) | 0.425 | ||
| Internal Resistance | Ls (mH) | 8.35 | ||
| Fully Charged Voltage | J (kg.m2) | 0.01197 | ||
| Capacity Nominal Voltage | V (m/s) | 12 | ||
| Exponential Capacity | w (rad/s) | 153 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menzri, F.; Boutabba, T.; Benlaloui, I.; Chrifi-Alaoui, L.; Alkuhayli, A.; Khaled, U.; Mahmoud, M.M. Applications of Novel Combined Controllers for Optimizing Grid-Connected Hybrid Renewable Energy Systems. Sustainability 2024, 16, 6825. https://doi.org/10.3390/su16166825
Menzri F, Boutabba T, Benlaloui I, Chrifi-Alaoui L, Alkuhayli A, Khaled U, Mahmoud MM. Applications of Novel Combined Controllers for Optimizing Grid-Connected Hybrid Renewable Energy Systems. Sustainability. 2024; 16(16):6825. https://doi.org/10.3390/su16166825
Chicago/Turabian StyleMenzri, Fatima, Tarek Boutabba, Idriss Benlaloui, Larbi Chrifi-Alaoui, Abdulaziz Alkuhayli, Usama Khaled, and Mohamed Metwally Mahmoud. 2024. "Applications of Novel Combined Controllers for Optimizing Grid-Connected Hybrid Renewable Energy Systems" Sustainability 16, no. 16: 6825. https://doi.org/10.3390/su16166825
APA StyleMenzri, F., Boutabba, T., Benlaloui, I., Chrifi-Alaoui, L., Alkuhayli, A., Khaled, U., & Mahmoud, M. M. (2024). Applications of Novel Combined Controllers for Optimizing Grid-Connected Hybrid Renewable Energy Systems. Sustainability, 16(16), 6825. https://doi.org/10.3390/su16166825








