Analysis of the Convergence of Environmental Sustainability and Its Main Determinants: The Case of the Americas (1990–2022)
Abstract
1. Introduction
2. Materials and Methods
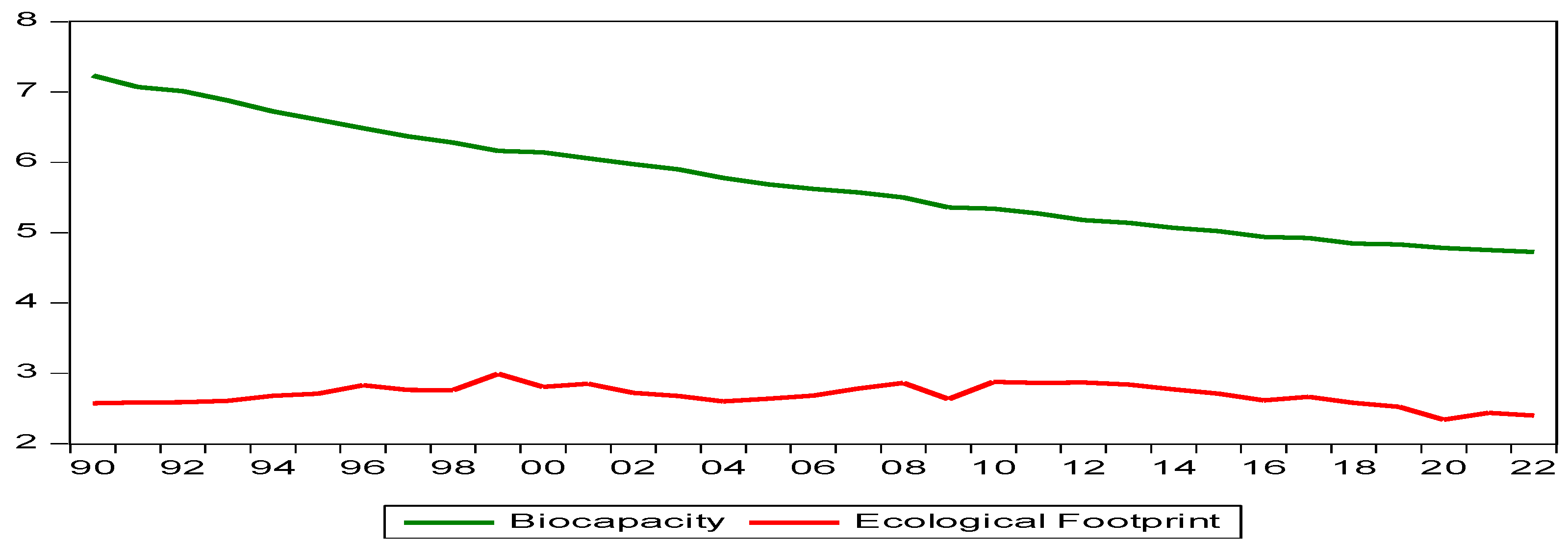
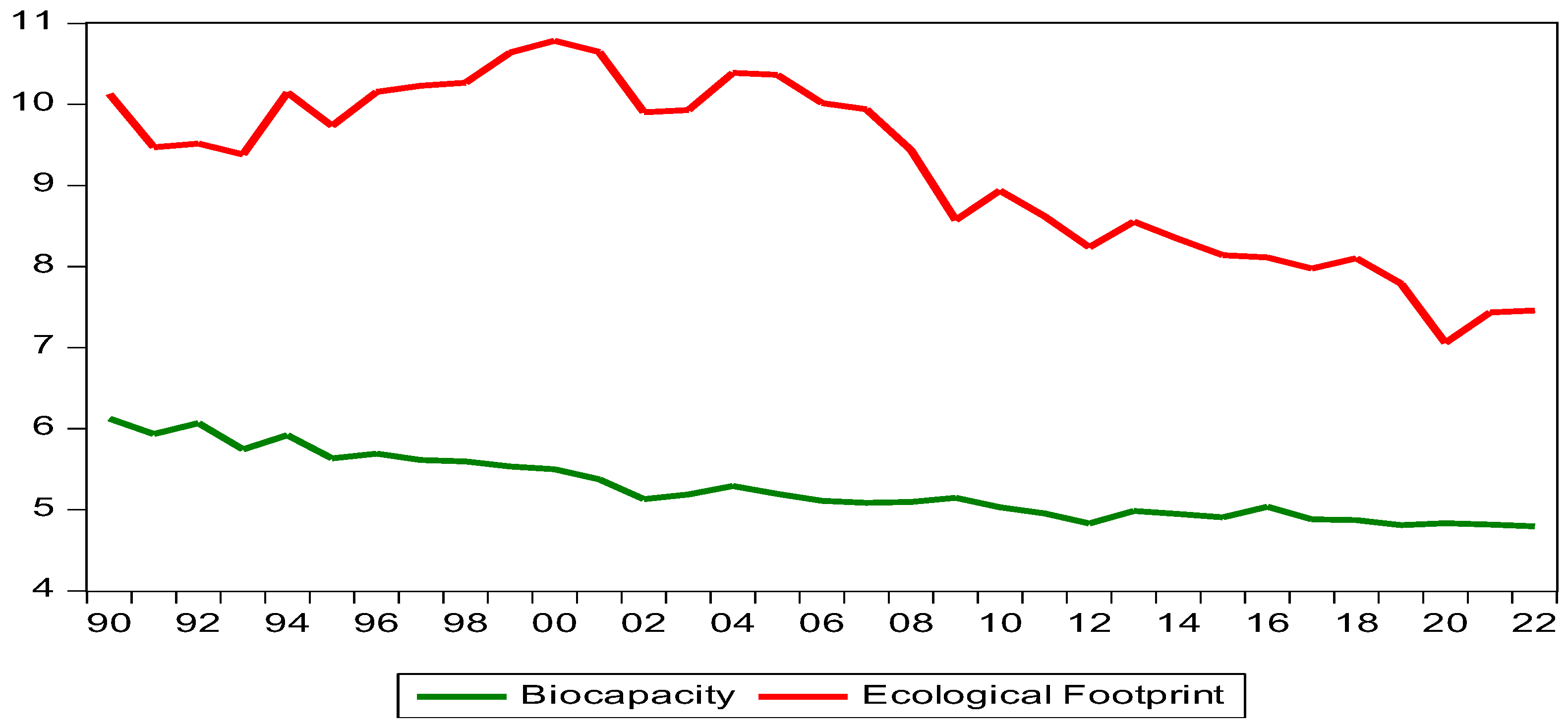
3. Results and Discussion
4. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- UNFCCC. The Paris Agreement, United Nations. 2015. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 5 July 2023).
- Guo, Q.; Ahmad, W.; Sofuoğlu, E.; Abbas, S. Testing the equity-pollution dilemma from a global perspective: Does reducing consumption inequality impose environmental burdens? Gondwana Res. 2023, 122, 125–137. [Google Scholar] [CrossRef]
- Panayotou, T. Technology and Employment Program. In Empirical Tests and Policy Analysis of Environmental Degradation at Different Stages of Economic Development; Working Paper WP238; International Labour Office: Geneva, Switzerland, 1993; pp. 1–42. [Google Scholar]
- Altıntaş, H.; Kassouri, Y. Is the environmental Kuznets Curve in Europe related to the per-capita ecological footprint or CO2 emissions? Ecol. Indic. 2020, 113, 106187. [Google Scholar] [CrossRef]
- Awad, A. Is there any impact from ICT on environmental quality in Africa? Evidence from second-generation panel techniques. Environ. Chall. 2020, 7, 100520. [Google Scholar] [CrossRef]
- Aydin, M.; Degirmenci, T.; Gurdal, T.; Yavuz, H. The role of green innovation in achieving environmental sustainability in European Union countries: Testing the environmental Kuznets curve hypothesis. Gondwana Res. 2023, 118, 105–116. [Google Scholar] [CrossRef]
- Kalim, R.; Ul-Durar, S.; Iqbal, M.; Arshed, N.; Shahbaz, M. Role of knowledge economy in managing demand-based Environmental Kuznets Curve. Geosci. Front. 2023, 15, 101594. [Google Scholar] [CrossRef]
- Karimi, M.; Khezri, M.; Khan, Y.A.; Somayeh, R. Exploring the influence of economic freedom index on fishing grounds footprint in environmental Kuznets curve framework through spatial econometrics technique: Evidence from Asia-Pacific countries. Environ. Sci. Pollut. Res. 2022, 29, 6251–6266. [Google Scholar] [CrossRef] [PubMed]
- Nizamani, R.A.; Shaikh, F.; Nizamani, A.G.; Mirjat, N.H.; Kumar, L.; Assad, M.E.H. The impacts of conventional energies on environmental degradation: Does Pakistan’s economic and environmental model follow the Kuznets curve? Environ. Sci. Pollut. Res. 2023, 30, 7173–7185. [Google Scholar] [CrossRef]
- Sesma-Martín, D.; Puente-Ajovín, M. The Environmental Kuznets Curve at the thermoelectricity-water nexus: Empirical evidence from Spain. Water Resour. Econ. 2022, 39, 100202. [Google Scholar] [CrossRef]
- Taghvaee, V.M.; Nodehi, M.; Saboori, B. Economic complexity and CO2 emissions in OECD countries: Sector-wise Environmental Kuznets Curve hypothesis. Environ. Sci. Pollut. Res. 2022, 29, 80860–80870. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, T.; Li, R. Does income inequality reshape the environmental Kuznets curve (EKC) hypothesis? A nonlinear panel data analysis. Environ. Res. 2023, 216, 114575. [Google Scholar] [CrossRef]
- Dogan, E.; Ulucak, R.; Kocak, E.; Isik, C. The use of ecological footprint in estimating the Environmental Kuznets Curve hypothesis for BRICST by considering cross-section dependence and heterogeneity. Sci. Total Environ. 2020, 723, 138063. [Google Scholar] [CrossRef] [PubMed]
- Wackernagel, M.; Monfreda, C.; Erb, K.H.; Haberl, H.; Schulz, N.B. Ecological footprint time series of Austria, the Philippines, and South Korea for 1961–1999: Comparing the conventional approach to an ‘actual land area’ approach. Land Use Policy 2004, 21, 261–269. [Google Scholar] [CrossRef]
- Galli, A. On the rationale and policy usefulness of Ecological Footprint Accounting: The case of Morocco. Environ. Sci. Policy 2004, 48, 210–224. [Google Scholar] [CrossRef]
- Pata, U.K.; Isik, C. Determinants of the load capacity factor in China: A novel dynamic ARDL approach for ecological footprint accounting. Resour. Policy 2021, 74, 102313. [Google Scholar] [CrossRef]
- Global Footprint Network. Available online: https://www.footprintnetwork.org/our-work/ (accessed on 1 October 2023).
- Siche, R.; Pereira, L.; Agostinho, F.; Ortega, E. Convergence of ecological footprint and emergy analysis as a sustainability indicator of countries: Peru as case study. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 3182–3192. [Google Scholar] [CrossRef]
- Caglar, A.E.; Pata, U.K.; Ulug, M.; Zafar, M.W. Examining the impact of clean environmental regulations on load capacity factor to achieve sustainability: Evidence from APEC economies. J. Clean. Prod. 2023, 429, 139563. [Google Scholar] [CrossRef]
- Djedaiet, A.; Ayad, H.; Ben-Salha, O. Oil prices and the load capacity factor in African oil-producing OPEC members: Modeling the symmetric and asymmetric effects. Resour. Policy 2024, 89, 104598. [Google Scholar] [CrossRef]
- Dogan, A.; Pata, U.K. The role of ICT, R&D spending and renewable energy consumption on environmental quality: Testing the LCC hypothesis for G7 countries. J. Clean. Prod. 2022, 380, 135038. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, T.; Yang, C. Nexus among natural resources, environmental sustainability, and political risk: Testing the load capacity factor curve hypothesis. Resour. Policy 2024, 90, 104791. [Google Scholar] [CrossRef]
- Cheng, C.; Ren, X.; Wang, Z. The impact of renewable energy and innovation on carbon emission: An empirical analysis for OECD countries. Energy Procedia 2019, 158, 1506–1512. [Google Scholar] [CrossRef]
- Alvarado, R.; Ponce, P.; Alvarado, R.; Ponce, K.; Huachizaca, V.; Toledo, E. Sustainable and non-sustainable energy and output in Latin America: A cointegration and causality approach with panel data. Energy Strat. Rev. 2019, 26, 100369. [Google Scholar] [CrossRef]
- Wolde-Rufael, Y.; Mulat-Weldemeskel, E. The moderating role of environmental tax and renewable energy in CO2 emissions in Latin America and Caribbean countries: Evidence from method of moments quantile regression. Environ. Chall. 2022, 6, 100412. [Google Scholar] [CrossRef]
- Vural, G. Analyzing the impacts of economic growth, pollution, technological innovation and trade on renewable energy production in selected Latin American countries. Renew. Energy 2021, 171, 210–216. [Google Scholar] [CrossRef]
- Moreno, L.A. Prefacio. In La Crisis de la Desigualdad: América Latina y el Caribe en la Encrucijada; Busso, M., Messina, J., Eds.; Banco Interamericano de Desarrollo: Washington, DC, USA, 2020. [Google Scholar]
- Boyce, J.K. Is Inequality Bad for the Environment? Res. Soc. Probl. 2008, 15, 267–288. [Google Scholar]
- Ridzuan, S. Inequality and the environmental Kuznets curve. J. Clean. Prod. 2019, 228, 1472–1481. [Google Scholar] [CrossRef]
- Stiglitz, J.E. Inequality and environmental policy. In Green Planet Blues: Critical Perspectives on Global Environmental Politics, 6th ed.; Dabelko, G.D., Ed.; Routledge: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Ehigiamusoe, K.U.; Majeed, M.T.; Dogan, E. The nexus between poverty, inequality and environmental pollution: Evidence across different income groups of countries. J. Clean. Prod. 2022, 341, 130863. [Google Scholar] [CrossRef]
- Khan, S.; Yahong, W.; Zeeshan, A. Impact of poverty and income inequality on the ecological footprint in Asian developing economies: Assessment of Sustainable Development Goals. Energy Rep. 2022, 8, 670–679. [Google Scholar] [CrossRef]
- Hailemariam, A.; Dzhumashev, R.; Shahbaz, M. Carbon emissions, income inequality, and economic development. Empir. Econ. 2020, 59, 1139–1159. [Google Scholar] [CrossRef]
- Ockwell, D.G.; Haum, R.; Mallett, A.; Watson, J. Intellectual property rights and low carbon technology transfer: Conflicting discourses of diffusion and development. Glob. Environ. Change 2010, 20, 729–738. [Google Scholar] [CrossRef]
- Töbelmann, D.; Wendler, T. The impact of environmental innovation on carbon dioxide emissions. J. Clean. Prod. 2020, 244, 118787. [Google Scholar] [CrossRef]
- Baumol, W.J. Productivity Growth, Convergence, and Welfare: What the Long-Run Data Show. Am. Econ. Rev. 1986, 76, 1072–1085. Available online: http://www.jstor.org/stable/1816469 (accessed on 8 June 2024).
- Barro, R.J.; Sala-i-Martin, X. Economic Growth and Convergence across the United States. NBER Work. Pap. 1990, 3419, 1–39. [Google Scholar]
- Carlino, G.; Mills, L. Testing neoclassical convergence in regional incomes. Reg. Sci. Urban Econ 1996, 26, 565–590. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Sul, D. Transition Modeling and Econometric Convergence Tests. J. Econom. Soc. 2007, 75, 1771–1855. Available online: https://www.jstor.org/stable/4502048 (accessed on 8 June 2024). [CrossRef]
- Phillips, P.C.B.; Sul, D. Economic transition and growth. J. Appl. Econom. 2009, 24, 1153–1185. [Google Scholar] [CrossRef]
- Mishra, V.; Smyth, R. Convergence in energy consumption per capita among ASEAN countries. Energy Policy 2014, 73, 180–185. [Google Scholar] [CrossRef]
- Haider, S.; Akram, V. Club convergence analysis of ecological and carbon footprint: Evidence from a cross-country analysis. Carbon Manag. 2019, 10, 451–463. [Google Scholar] [CrossRef]
- Meng, M.; Payne, J.E.; Lee, J. Convergence in per capita energy use among OECD countries. Energy Econ. 2013, 36, 536–545. [Google Scholar] [CrossRef]
- Karakaya, E.; Alataş, S.; Yılmaz, B. Replication of Strazicich and List (2003): Are CO2 emission levels converging among industrial countries? Energy Econ. 2019, 82, 135–138. [Google Scholar] [CrossRef]
- Romero-Ávila, D.; Tolga, O. Convergence of per capita energy consumption around the world: New evidence from nonlinear panel unit root tests. Energy Econ. 2022, 111, 106062. [Google Scholar] [CrossRef]
- Kazemzadeh, E.; Fuinhas, J.A.; Koengkan, M.; Shadmehri, M.T.A. Relationship between the share of renewable electricity consumption, economic complexity, financial development, and oil prices: A two-step club convergence and PVAR model approach. Int. Econ. 2023, 173, 260–275. [Google Scholar] [CrossRef]
- Vo, D.H.; Vo, L.H.; Ho, C.M. Regional convergence of nonrenewable energy consumption in Vietnam. Energy Policy 2022, 169, 113194. [Google Scholar] [CrossRef]
- Simionescu, M. Stochastic convergence in per capita energy use in the EU-15 countries. The role of economic growth. Appl. Energy 2022, 322, 119489. [Google Scholar] [CrossRef]
- He, W.; Chen, H. Will China’s provincial per capita energy consumption converge to a common level over 1990–2017? Evidence from a club convergence approach. Energy 2022, 249, 123624. [Google Scholar] [CrossRef]
- Salman, M.; Zha, D.; Wang, G. Assessment of energy poverty convergence: A global analysis. Energy 2022, 255, 124579. [Google Scholar] [CrossRef]
- Saba, C.S.; Ngepah, N. Convergence in renewable energy sources and the dynamics of their determinants: An insight from a club clustering algorithm. Energy Rep. 2022, 8, 3483–3506. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, W.; Xu, M. Total factor efficiency and convergence analysis of renewable energy in Latin American countries. Renew. Energy 2021, 170, 785–795. [Google Scholar] [CrossRef]
- Belloc, I.; Molina, J.A. Are greenhouse gas emissions converging in Latin America? Implications for environmental policies. Econ. Anal. Policy 2023, 77, 337–356. [Google Scholar] [CrossRef]
- Tillaguango, B.; Alvarado, R.; Dagar, V.; Murshed, M.; Pinzón, Y.; Méndez, P. Convergence of the ecological footprint in Latin America: The role of the productive structure. Environ. Sci. Pollut. Res. 2021, 28, 59771–59783. [Google Scholar] [CrossRef]
- Alvarado, R.; Tillaguango, B.; Cuesta, L.; Pinzon, S.; Alvarado-Lopez, M.R.; Işık, C.; Dagar, V. Biocapacity convergence clubs in Latin America: An analysis of their determining factors using quantile regressions. Environ. Sci. Pollut. Res. 2022, 29, 66605–66621. [Google Scholar] [CrossRef]
- Martins, M.A.; Heshmati, A. Convergence of carbon dioxide emissions in the Americas and its determinants. Lat. Am. Econ. Rev. 2022, 31, 1–33. [Google Scholar] [CrossRef]
- Gregory, A.W.; Hansen, B.E. Residual-based tests for cointegration in models with regime shifts. J. Econom. 1996, 70, 99–126. [Google Scholar] [CrossRef]
- Karavias, Y.; Tzavalis, E. Testing for unit roots in short panels allowing for a structural break. Comput. Stat. Data Anal. 2014, 76, 391–407. [Google Scholar] [CrossRef]
- Lee, J.; Strazicich, M.C. Minimum Lagrange Multiplier Unit Root Test with Two Structural Breaks. Rev. Econ. Stat. 2003, 85, 1082–1089. [Google Scholar] [CrossRef]
- Perron, P. Further Evidence on Breaking Trend Functions in Macroeconomic Variables. J. Econom. 1997, 80, 355–385. [Google Scholar] [CrossRef]
- Chen, P.; Karavias, Y.; Tzavalis, E. Panel Unit Root Tests with Structural Breaks; Discussion Papers 21-12; Department of Economics, University of Birmingham: Birmingham, UK, 2021. [Google Scholar]
- Juodis, A.; Karavias, Y.; Sarafidis, V. A homogeneous approach to testing for Granger non-causality in heterogeneous panels. Empir. Econ. 2021, 60, 93–112. [Google Scholar] [CrossRef]
- The Enerdata Yearbook. World Energy & Climate Statistics. Available online: https://www.enerdata.net (accessed on 25 July 2023).
- World Bank. World Development Indicators. Available online: http://data.worldbank.org/ (accessed on 5 July 2023).
- Solt, F. Measuring Income Inequality across Countries and Over Time: The Standardized World Income Inequality Database, SWIID Version 9.5. 2020. Available online: https://fsolt.org/swiid/ (accessed on 10 November 2023).
- Baltagi, B.H. Econometric Analysis of Panel Data, 1st ed.; John Wiley and Sons: New York, NY, USA, 1995. [Google Scholar]
- Ivanovski, K.; Churchill, S.A.; Smyth, R. A club convergence analysis of per capita energy consumption across Australian regions and sectors. Energy Econ. 2018, 76, 519–531. [Google Scholar] [CrossRef]
- Westerlund, J. Testing for error correction in panel data. Oxf. Bull. Econ. Stat. 2007, 69, 709–748. [Google Scholar] [CrossRef]
- Beck, N.; Katz, J.N. What to do (and not to do) with time series cross-section data. Am. Political Sci. Rev. 1995, 89, 634–647. [Google Scholar] [CrossRef]
- Parks, R. Efficient estimation of a regression equation system when disturbances are serially and contemporaneously correlated. J. Am. Stat. Assoc. 1967, 62, 500–509. [Google Scholar] [CrossRef]
- You, W.; Zhang, Y.; Lee, C.C. The dynamic impact of economic growth and economic complexity on CO2 emissions: An advanced panel data estimation. Econ. Anal. Policy 2022, 73, 112–128. [Google Scholar] [CrossRef]
- Xiao, J.; Karavias, Y.; Juodis, A.; Sarafidis, V.; Ditzen, J. Improved tests for Granger noncausality in panel data. Stata J. 2023, 23, 230–242. [Google Scholar] [CrossRef]
- Dumitrescu, E.I.; Hurlin, C. Testing for Granger non-causality in heterogeneous panels. Econ. Model. 2012, 29, 1450–1460. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, W.K. Further evidence on the great crash, the oil-price shock, and the unit root hypothesis. J. Bus. Econ. Stat. 1992, 10, 251–270. [Google Scholar] [CrossRef]
- Breusch, T.; Pagan, A. The Lagrange Multiplier Test and its Application to Model Specification in Econometrics. Rev. Econ. Stud. 1980, 47, 239–253. [Google Scholar] [CrossRef]
- Pesaran, M.H. General Diagnostic Tests for Cross Section Dependence in Panels; Cambridge Working Papers in Economics No. 0435; Faculty of Economics, University of Cambridge: Cambridge, UK, 2004. [Google Scholar]
- Baltagi, B.H.; Feng, Q.; Kao, C. A Lagrange Multiplier test for Cross-sectional Dependence in a Fixed Effects Panel Data Model. J. Econom. 2012, 170, 164–177. [Google Scholar] [CrossRef]
- Im, K.S.; Pesaran, M.H.; Shin, Y. Testing for unit roots in heterogeneous panels. J. Econom. 2003, 115, 53–74. [Google Scholar] [CrossRef]
- Pesaran, M.H. A simple panel unit root test in the presence of cross section dependence. J. Appl. Econom. 2007, 22, 265–312. [Google Scholar] [CrossRef]
- Strazicich, M.C.; List, J.A. Are CO2 Emission Levels Converging Among Industrial Countries? Environ. Resour. Econ. 2003, 24, 263–271. [Google Scholar] [CrossRef]
- Kao, C. Spurious Regression and Residual-Based Tests for Cointegration in Panel Data. J. Econom. 1999, 90, 1–44. [Google Scholar] [CrossRef]
- Allard, A.; Takman, J.; Uddin, G.S.; Ahmed, A. The N-shaped environmental Kuznets curve: An empirical evaluation using a panel quantile regression approach. Environ. Sci. Pollut. Res. 2017, 25, 5848–5861. [Google Scholar] [CrossRef] [PubMed]







| Enercon | DF or DFA Test C/CT | Zivot–Andrews Test One Break | Lee–Strazicich Test Two Breaks | ||
|---|---|---|---|---|---|
| Crash | Break | Crash | Break | ||
| Argentina | −1.527/−1.850 | −3.015 (2006) | −3.149 (2006) | −3.874 ** (2003, 2005) | −7.773 *** (2002, 2007) |
| Brazil | −0.323/−1.766 | −3.539 (2007) | −3.528 (2008) | −2.788 (2007, 2013) | −6.521 ** (2006, 2014) |
| Chile | −2.239/−1.973 | −2.998 (1996) | −2.999 (1996) | −4.112 *** (2013, 2017) | −5.773 (2001, 2013) |
| Canada | −1.733/−3.740 ** | −5.042 ** (2016) | −5.516 ** (2010) | −4.462 ***(2006, 2015) | −7.062 *** (2007, 2014) |
| Colombia | −1.123/−1.514 | −3.874 (2013) | −4.156 (1999) | −4.627 *** (2008, 2012) | −13.314 *** (2002, 2011) |
| Mexico | −1.601/−1.729 | −3.061 (2001) | −3.111 (2001) | −4.124 *** (2010, 2019) | −5.258 (2001, 2013) |
| USA | −0.720/−1.789 | −2.801 (2011) | −3.288 (2011) | −2.546 (2002, 2018) | −5.196 (2001, 2010) |
| CO2 | DF or DFA Test C/CT | Zivot–Andrews Test One Break | Lee–Strazicich Test Two Breaks | ||
|---|---|---|---|---|---|
| Crash | Break | Crash | Break | ||
| Argentina | −1.060/−2.111 | −3.627 (2006) | −3.293 (2006) | −4.749 *** (2003, 2010) | −5.624 (2002, 2017) |
| Brazil | −1.081/−1.739 | −3.005 (2010) | −3.547 (2012) | −3.379 ** (2001, 2016) | −6.677 ** (2003, 2018) |
| Chile | −1.136/−1.852 | −4.224 (2011) | −4.147 (2011) | −5.104 *** (2003, 2010) | −6.733 ** (2005, 2013) |
| Canada | −3.233 **/−3.222 ** | −4.275 (2000) | −4.142 (2000) | −4.489 *** (2006, 2011) | −5.785 (2005, 2010) |
| Colombia | −0.930/−1.209 | −3.485 (1999) | −4.257 (2009) | −4.093 *** (2007, 2010) | −4.414 (2004, 2018) |
| Mexico | −2.564/−2.596 | −3.652 (2002) | −3.841 (2009) | −3.612 ** (2003, 2006) | −5.998 * (2009, 2018) |
| USA | −0.462/−2.924 | −4.976 (2011) ** | −2.842 (2000) | −3.097 (2011, 2016) | −7.525 *** (2004, 2009) |
| Ecologf | DF or DFA Test C/CT | Zivot–Andrews Test One Break | Lee–Strazicich Test Two Breaks | ||
|---|---|---|---|---|---|
| Crash | Break | Crash | Break | ||
| Argentina | −3.087 **/−3.417 * | −4.499 (1997) | −5.178 ** (2006) | −3.968 ** (2008, 2015) | −8.003 *** (2003, 2008) |
| Brazil | −1.782/−1.928 | −3.870 (2008) | −3.999 (2008) | −3.412 * (2007, 2011) | −8.266 *** (2003, 2009) |
| Chile | −1.630/−2.593 | −4.927 ** (1997) | −4.353 (1997) | −5.203 *** (2001, 2010) | −4.342 (2000, 2010) |
| Canada | −3.520 **/−4.054 ** | −5.409 *** (1999) | −5.449 ** (2007) | −3.812 ** (2000, 2012) | −5.630 (2000, 2013) |
| Colombia | −1.830/−1.895 | −4.046 (1999) | −4.487 (1999) | −4.332 *** (2001, 2011) | −4.758 (2003, 2008) |
| Mexico | −3.548 **/−3.537 ** | −3.125 (1997) | −3.422 (2009) | −3.464 * (2003, 2012) | −10.291 *** (2002, 2010) |
| USA | −1.107/−2.160 | −4.556 (2010) | −4.325 (2010) | −3.286 (2009, 2013) | −5.023 (2005, 2008) |
| Energyint | DF or DFA Test C/CT | Zivot–Andrews Test One Break | Lee–Strazicich Test Two Breaks | ||
|---|---|---|---|---|---|
| Crash | Break | Crash | Break | ||
| Argentina | −0.634/−2.730 | −3.793 (2002) | −3.811 (2002) | −4.856 *** (2005, 2011) | −9.674 *** (2000, 2008) |
| Brazil | −0.458/−3.500 * | −4.211 (2010) | −5.247 ** (2014) | −4.954 *** (2009, 2015) | −6.448 *** (2006, 2012) |
| Chile | −2.756 */−6.048 *** | −4.776 * (1997) | −4.562 (2003) | −5.850 *** (2006, 2009) | −6.372 ** (2009, 2015) |
| Canada | −0.682/−1.974 | −5.013 ** (2016) | −4.694 (2016) | −3.434 * (2006, 2009) | −4.468 (2005, 2013) |
| Colombia | −2.458/−2.483 | −7.270 *** (2013) | −6.450 (2013) | −4.175 *** (2010, 2012) | −11.809 *** (2003, 2011) |
| Mexico | −1.258/−3.110 | −4.416 (2014) | −5.212 ** (2008) | −5.175 *** (2000, 2002) | −6.888 *** (2005, 2013) |
| USA | 0.619/−2.672 | −4.667 * (2007) | −5.320 ** (2007) | −3.336 * (2011, 2018) | −5.305 (2005, 2017) |
| Locf | DF or DFA Test C/CT | Zivot–Andrews Test One Break | Lee–Strazicich Test Two Breaks | ||
|---|---|---|---|---|---|
| Crash | Break | Crash | Break | ||
| Argentina | −2.616/−2.717 | −4.218 (1997) | −4.996 * (1999) | −3.642 ** (2008, 2012) | −4.665 (2010, 2017) |
| Brazil | −1.636/−3.330 * | −4.298 (2011) | −4.685 (2011) | −4.550 ** (2008, 2015) | −7.818 ** (2003, 2007) |
| Chile | −2.741 */−3.896 ** | −4.661 * (1999) | −4.739 (2004) | −4.155 *** (2008, 2014) | −5.925 * (2000, 2013) |
| Canada | −2.554/−2.610 | −4.824 * (1999) | −5.331 ** (2007) | −4.727 *** (2000, 2009) | −6.583 *** (2001, 2009) |
| Colombia | −2.344/−2.693 | −3.889 (2016) | −4.511 (2012) | −4.553 *** (2013, 2019) | −5.590 *(2000, 2008) |
| Mexico | −3.282 **/−3.306 * | −3.583 (1997) | −4.552 * (1999) | −3.900 ** (2010, 2012) | −13.829 * (2006, 2012) |
| USA | −0.205/−1.867 | −5.925 *** (2008) | −4.009 (2008) | −3.683 ** (2003, 2019) | −5.711 (2002, 2010) |
| Tests | Enercon | CO2 | Ecologf | Energyint | Locf |
|---|---|---|---|---|---|
| Breusch–Pagan LM | 250.725 *** | 219.456 *** | 134.365 *** | 280.055 *** | 121.463 *** |
| Pesaran scaled LM | 34.365 *** | 29.542 *** | 16.412 *** | 38.892 *** | 14.421 *** |
| Bias-corrected scaled LM | 34.257 *** | 29.433 *** | 16.303 *** | 38.783 *** | 14.312 *** |
| Pesaran CD | −3.044 *** | 0.480 | −2.654 *** | −4.053 *** | −4.076 *** |
| Variable | IPS | CIPS | CADF | KT (1 Break) | KT (2 Breaks) |
|---|---|---|---|---|---|
| Enercon | 0.600 | −2.082 | −2.126 | −0.768 | −1.101 |
| CO2 | 0.088 | −2.514 | −2.115 | −0.629 | −1.909 *** |
| Ecologf | −2.486 *** | −3.532 *** | −2.907 ** | −6.062 *** | −6.185 *** |
| Energyint | 0.824 | −2.128 | −1.713 | −1.505 *** | −1.798 *** |
| Locf | −2.023 ** | −2.158 ** | −1.985 | −5.595 *** | −6.094 *** |
| Variable | Coefficients | Standard Error | Statistic T | R |
|---|---|---|---|---|
| Enercon | −0.990 | 0.005 | −179.355 * | 0.3 |
| CO2 | −1.110 | 0.008 | −134.508 * | 0.3 |
| Ecologf | −1.050 | 0.016 | −62.546 * | 0.3 |
| Energyint | −1.159 | 0.006 | −167.114 * | 0.3 |
| Locf | −0.879 | 0.004 | −187.596 * | 0.3 |
| Variable | Countries | Coefficient | T-Stat |
|---|---|---|---|
| Club 1 | Canada, Chile, United States | 0.005 | 13.076 |
| Club 2 | Argentina, Brazil, Mexico | 0.229 | 3.300 |
| Group (divergent) | Colombia | - | - |
| Variable | Coefficients | Standard Error | T-Stat |
|---|---|---|---|
| Club 1 + Club 2 | −1.3042 | 0.0221 | −58.933 * |
| Club 2 + Club 3 | −0.411 | 0.0674 | −6.109 * |
| Variable | Countries | Coefficients | T-Stat |
|---|---|---|---|
| Club 1 | Argentina, Canada, Chile, Mexico, United States | 0.206 | 11.616 * |
| Group (divergent) | Brazil, Colombia | −1.233 | −11.974 |
| Variable | Countries | Coefficients | T-Stat |
|---|---|---|---|
| Club 1 | Argentina, Brazil, Canada, Chile, United States | 2.240 | 23.990 |
| Club 2 | Colombia, Mexico | 1.463 | 6.026 |
| Variable | Coefficients | Standard Error | T-Stat |
|---|---|---|---|
| Club 1 + Club 2 | −1.050 | 0.0168 | −62.546 |
| Variable | Countries | Coefficients | T-Stat |
|---|---|---|---|
| Club 1 | Brazil, Canada, United State | 0.206 | 11.616 |
| Group (divergent) | Argentina, Chile, Colombia, Mexico | −1.233 | −11.974 * |
| Variable | Countries | Coefficient | T-Stat |
|---|---|---|---|
| Club 1 | Brazil and Canada | 0.076 | 0.984 |
| Club 2 | Chile, Mexico, and USA | 0.194 | 3.760 |
| Group (divergent) | Argentina and Colombia | −0.479 | −11.788 |
| Variable | Coefficients | Standard Error | T-Stat |
|---|---|---|---|
| Club 1 + Club 2 | −0.947 | 0.017 | −54.700 * |
| Club 2 + Group 3 | −0.429 | 0.027 | −15.377 * |
| Club 1 | Club 2 | |||
|---|---|---|---|---|
| Variable | Odds Ratio | Marginal Effects dy/dx | Odds Ratio | Marginal Effects dy/dx |
| GDP | 0.131 *** | −0.465 ** | 1.782 ** | 0.137 ** |
| Patent | 14.007 *** | 0.633 *** | 0.461 *** | −0.183 *** |
| Renergy | 2.505 *** | 0.210 *** | 0.443 *** | −0.193 *** |
| Tradeopen | 280.788 *** | 1.294 *** | 0.095 *** | −0.559 *** |
| Wald chi2 = 100.39 Prob (0.000) | Wald chi2 = 74.91 Prob (0.000) | |||
| Club 1 | ||
|---|---|---|
| Variable | Odds Ratio | Marginal Effects dy/dx |
| GDP | 5.589 *** | 0.123 ** |
| Patent | 0.456 *** | −0.056 ** |
| Gini | 4.42 × 10−7 *** | −1.050 * |
| Tradeopen | 93.268 *** | 0.325 *** |
| Wald chi2 = 119.67 Prob (0.000) | ||
| Club 1 | Club 2 | |||
|---|---|---|---|---|
| Variable | Odds Ratio | Marginal Effects dy/dx | Odds Ratio | Marginal Effects dy/dx |
| GDP | 0.336 *** | −0.046 ** | 2.795 *** | 0.046 ** |
| Gini | 41.384 ** | 0.159 * | 0.024 ** | −0.159 * |
| Patent | 12.049 *** | 0.106 ** | 0.082 *** | −0.106 ** |
| Renergy | 5.153 *** | 0.070 *** | 0.194 *** | −0.070 *** |
| Tradeopen | 0.215 ** | −0.066 *** | 4.647 ** | 0.066 *** |
| Wald chi2 = 41.43 Prob (0.000) | Wald chi2 = 29.35 Prob (0.000) | |||
| Club 1 | ||
|---|---|---|
| Variable | Odds Ratio | Marginal Effects dy/dx |
| GDP | 12.974 *** | 0.555 *** |
| Gini | 5.45 × 10−7 *** | −3.126 *** |
| Tradeopen | 0.009 *** | −1.003 *** |
| Wald chi2 = 73.70 Prob (0.000) | ||
| Club 1 | Club 2 | |||
|---|---|---|---|---|
| Variable | Odds Ratio | Marginal Effects dy/dx | Odds Ratio | Marginal Effects dy/dx |
| GDP | 0.917 ** | −0.015 ** | 0.717 *** | −0.076 *** |
| Renergy | 5.240 *** | 0.304 *** | 0.046 *** | −0.708 *** |
| Tradeopen | 0.376 *** | −0.179 *** | 11.713 *** | 0.565 *** |
| Gini | -- | -- | 9.475 *** | 0.517 *** |
| Wald chi2 = 54.61 Prob (0.000) | Wald chi2 = 41.54 Prob (0.000) | |||
| Tests | GDP | Gini | Locf | Patents | Renergy | Tradeopen |
|---|---|---|---|---|---|---|
| Breusch–Pagan LM | 610.317 *** | 283.064 *** | 276.780 *** | 358.044 *** | 94.849 *** | 160.935 *** |
| Pesaran scaled LM | 89.853 *** | 39.357 *** | 38.387 *** | 50.926 *** | 10.315 *** | 20.512 *** |
| Bias-corrected scaled LM | 89.736 *** | 39.240 *** | 38.271 *** | 50.810 *** | 10.198 *** | 20.395 *** |
| Pesaran CD | 24.698 *** | 5.623 *** | 12.978 *** | 16.044 *** | 1.996 ** | 11.221 *** |
| Variables | CIPS (Levels) | CIPS (First Difference) |
|---|---|---|
| GDP | −1.610 | −3.621 *** |
| Gini | −1.544 | −3.002 *** |
| Locf | −1.954 | −5.134 *** |
| Patents | −2.531 | −5.638 *** |
| Renergy | −2.126 | −5.002 *** |
| Tradeopen | −2.149 | −4.293 *** |
| Cointegration test Kao [82] | Cointegration test Westerlund [68] | |
| Statistic−4.420 *** | Statistic−1.816 ** |
| Variables | FGLS Coefficients | PCSE Coefficients |
|---|---|---|
| GDP | −0.116 *** | −0.099 ** |
| Gini | −2.224 *** | −2.701 *** |
| Patents | −0.074 *** | −0.106 *** |
| Renergy | 0.824 *** | 0.873 *** |
| Tradeopen | −0.838 *** | −0.992 *** |
| Variables | GDP | Gini | Locf | Patents | Renergy | Tradeopen |
|---|---|---|---|---|---|---|
| GDP | - | −0.740 | −0.410 | −2.480 ** | −1.310 | 6.910 *** |
| Gini | −2.090 *** | - | −3.760 *** | 0.700 | 1.590 | −4.020 *** |
| Locf | −3.980 *** | 0.350 | - | 1.190 | 2.97 *** | −7.700 *** |
| Patents | 2.240 ** | 5.920 *** | 0.630 | - | −1.60 | 1.260 |
| Renergy | −0.110 | −0.880 | 2.510 ** | 4.440 *** | - | −2.060 ** |
| Tradeopen | 2.100 ** | 0.990 | −0.370 | −1.680 ** | −0.270 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, M.; Rodríguez, J.C. Analysis of the Convergence of Environmental Sustainability and Its Main Determinants: The Case of the Americas (1990–2022). Sustainability 2024, 16, 6819. https://doi.org/10.3390/su16166819
Gómez M, Rodríguez JC. Analysis of the Convergence of Environmental Sustainability and Its Main Determinants: The Case of the Americas (1990–2022). Sustainability. 2024; 16(16):6819. https://doi.org/10.3390/su16166819
Chicago/Turabian StyleGómez, Mario, and José Carlos Rodríguez. 2024. "Analysis of the Convergence of Environmental Sustainability and Its Main Determinants: The Case of the Americas (1990–2022)" Sustainability 16, no. 16: 6819. https://doi.org/10.3390/su16166819
APA StyleGómez, M., & Rodríguez, J. C. (2024). Analysis of the Convergence of Environmental Sustainability and Its Main Determinants: The Case of the Americas (1990–2022). Sustainability, 16(16), 6819. https://doi.org/10.3390/su16166819






