Impact of Heterogeneous Soil Conditions on the Life Cycle Assessment of a Multi-Storey Reinforced Concrete Structure
Abstract
1. Introduction
2. Materials and Methods
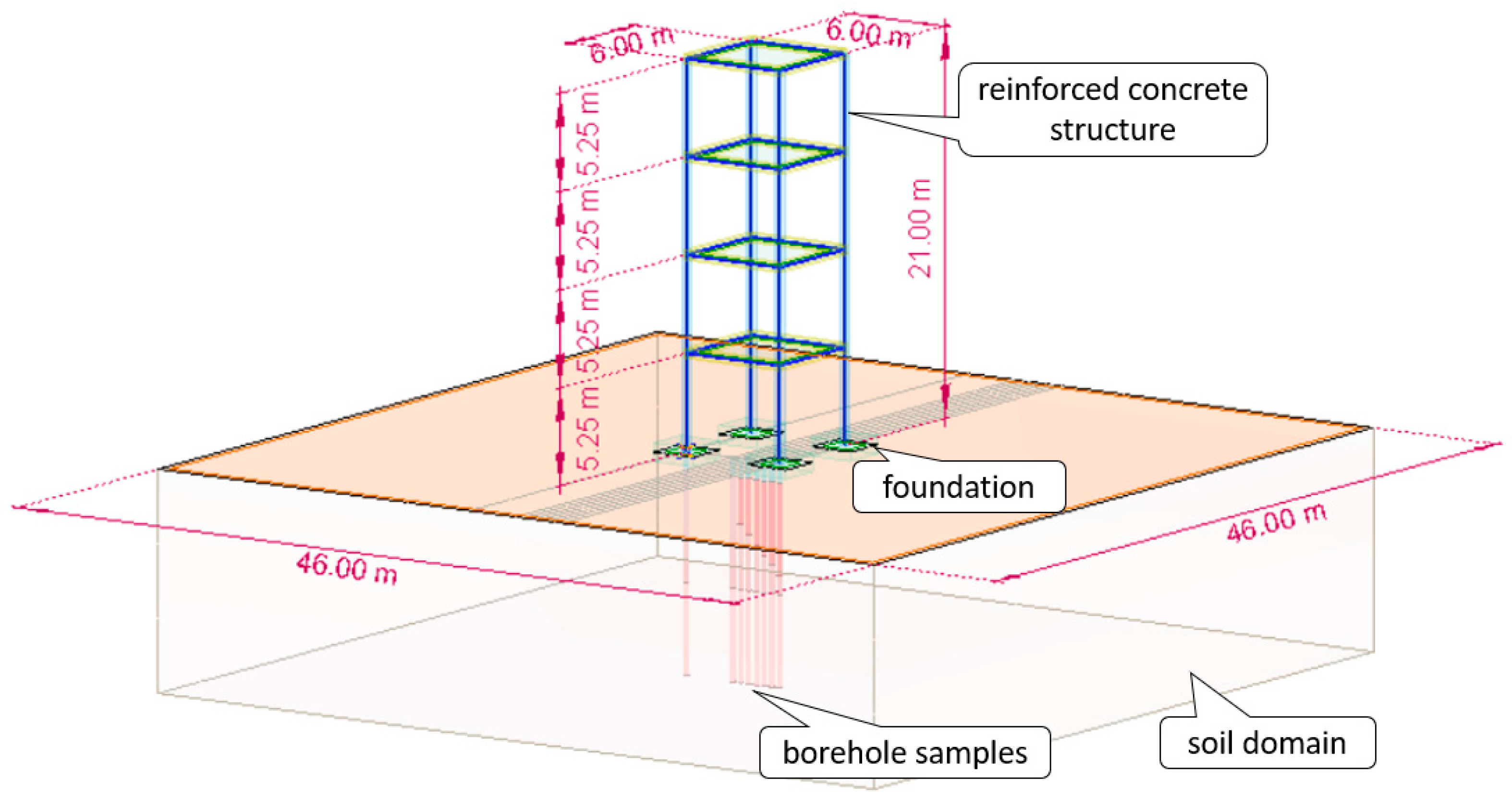
2.1. Task Parametrization
- the varying parameters of the soil interacting with the structure (parameter P1)
- the class of structural concrete used (parameter P2),
- the type of the foundations and their size (parameter P3)—set of four isolated footings (P3a) or foundation plate (P3b),
- the stiffness of the frame members (parameter P4),
2.1.1. Soil Type—Parameter P1
- S1 represents highly deformable, relatively uniform ground conditions under the whole of the analysed structure,
- S2 represents uneven ground conditions with a split: moderately deformable for the left part and highly deformable for the right part of the frame system,
- S3 represents uneven, more varied ground conditions with a split: low deformable for the left part of the system and highly deformable for the right side.
2.1.2. Reinforced Concrete Tower Parametrization
2.2. Numerical Model
3. Results and Discussions
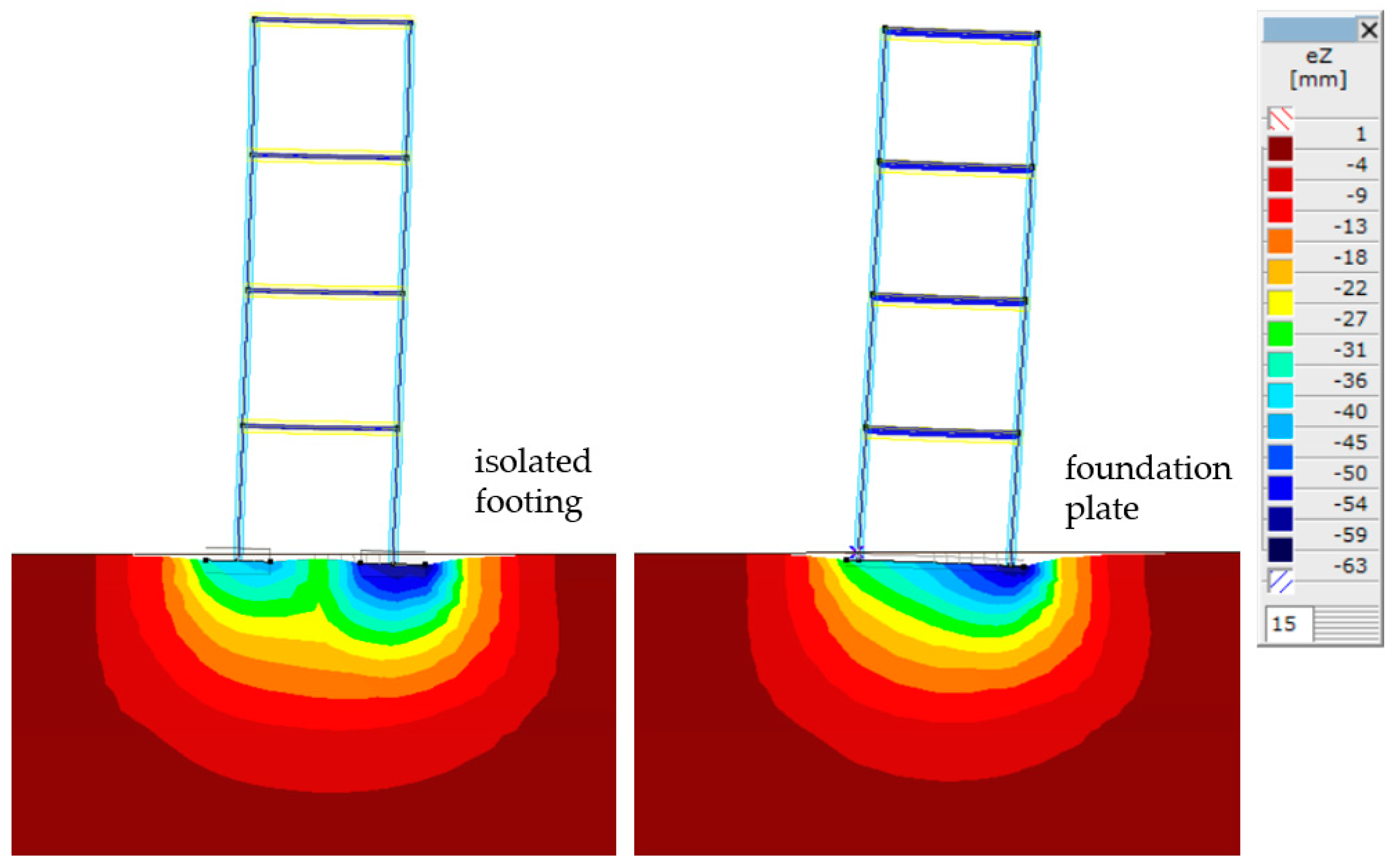
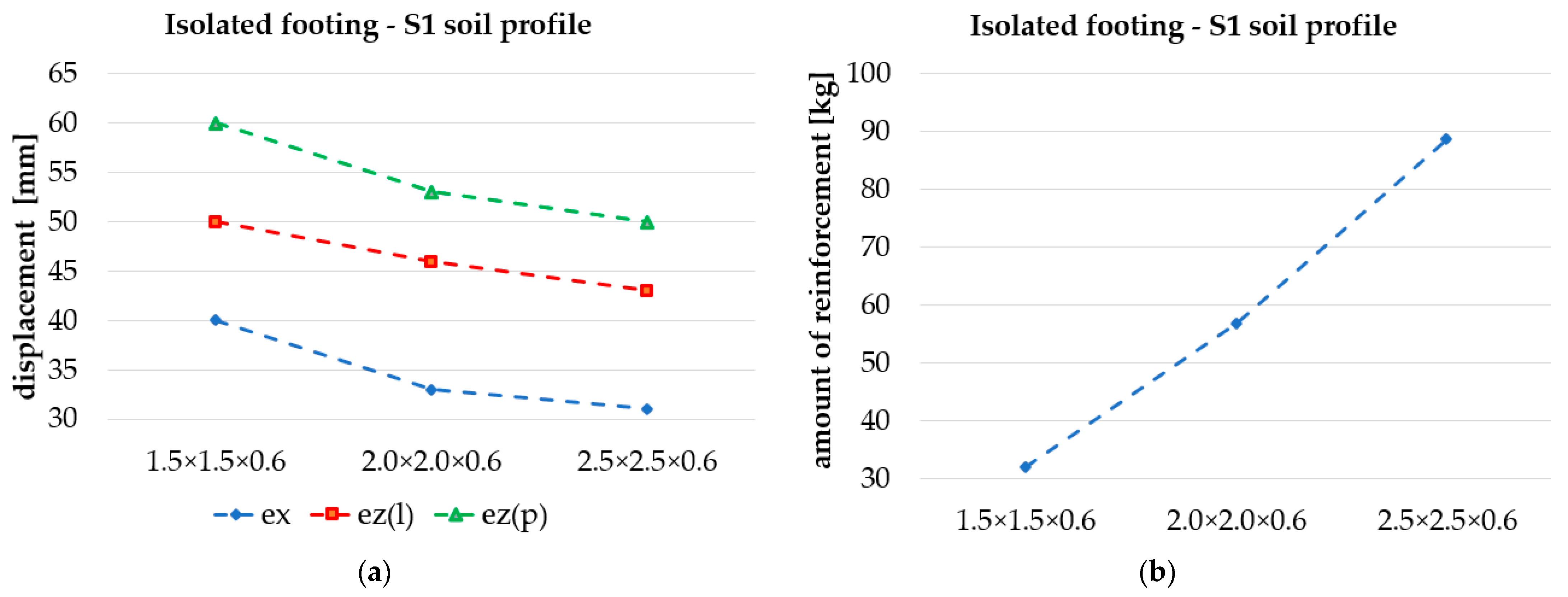
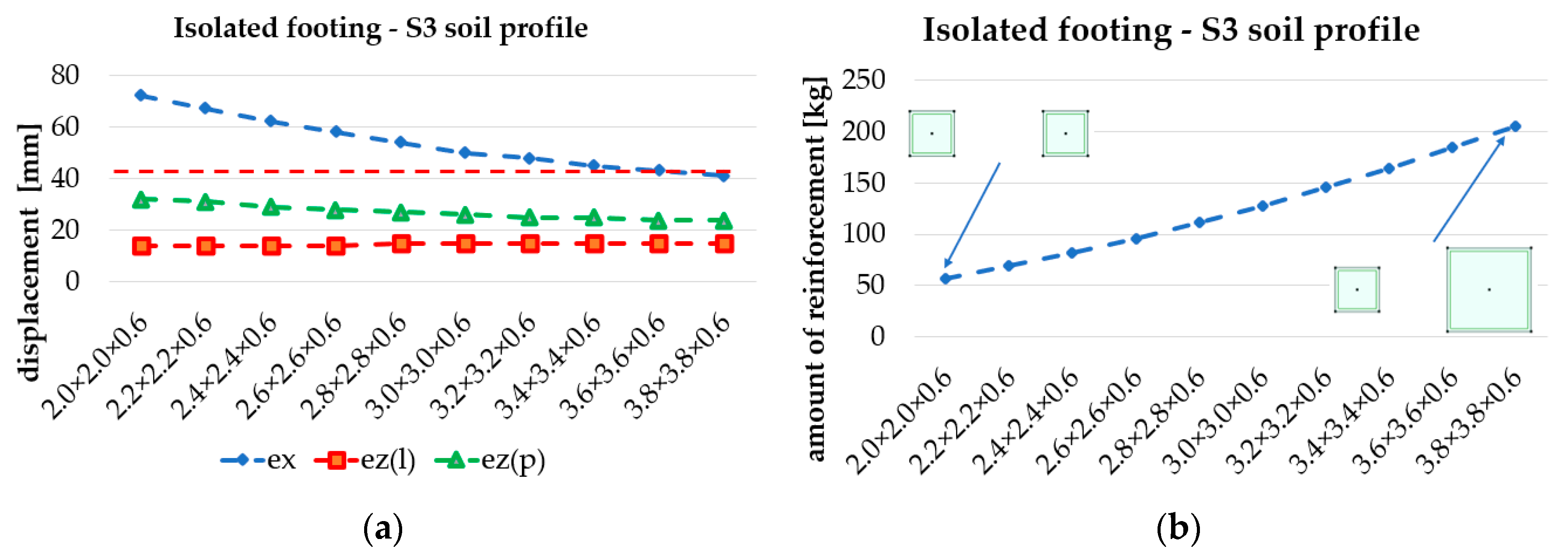
3.1. Structural Response for the Investigated Parameters
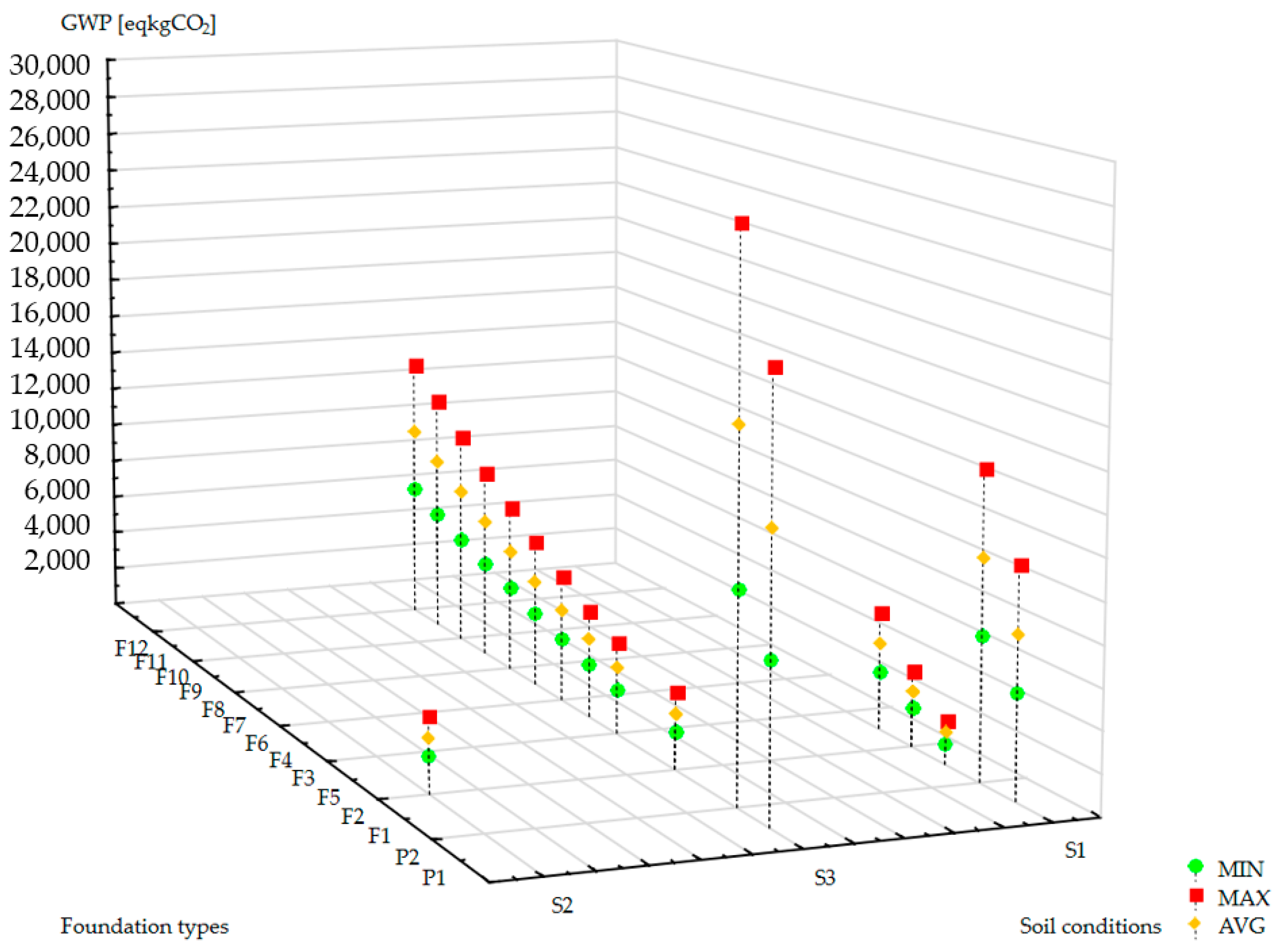
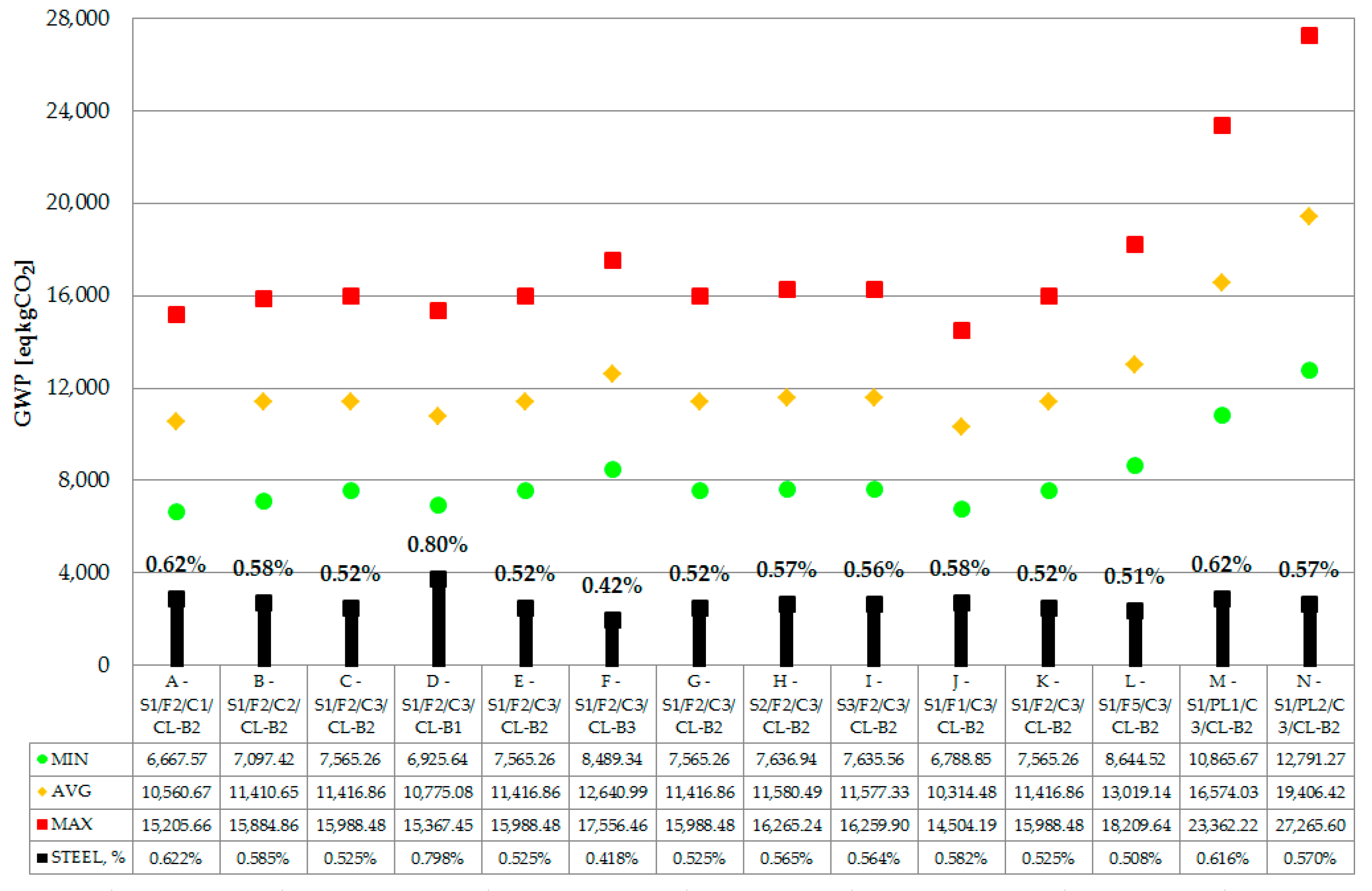
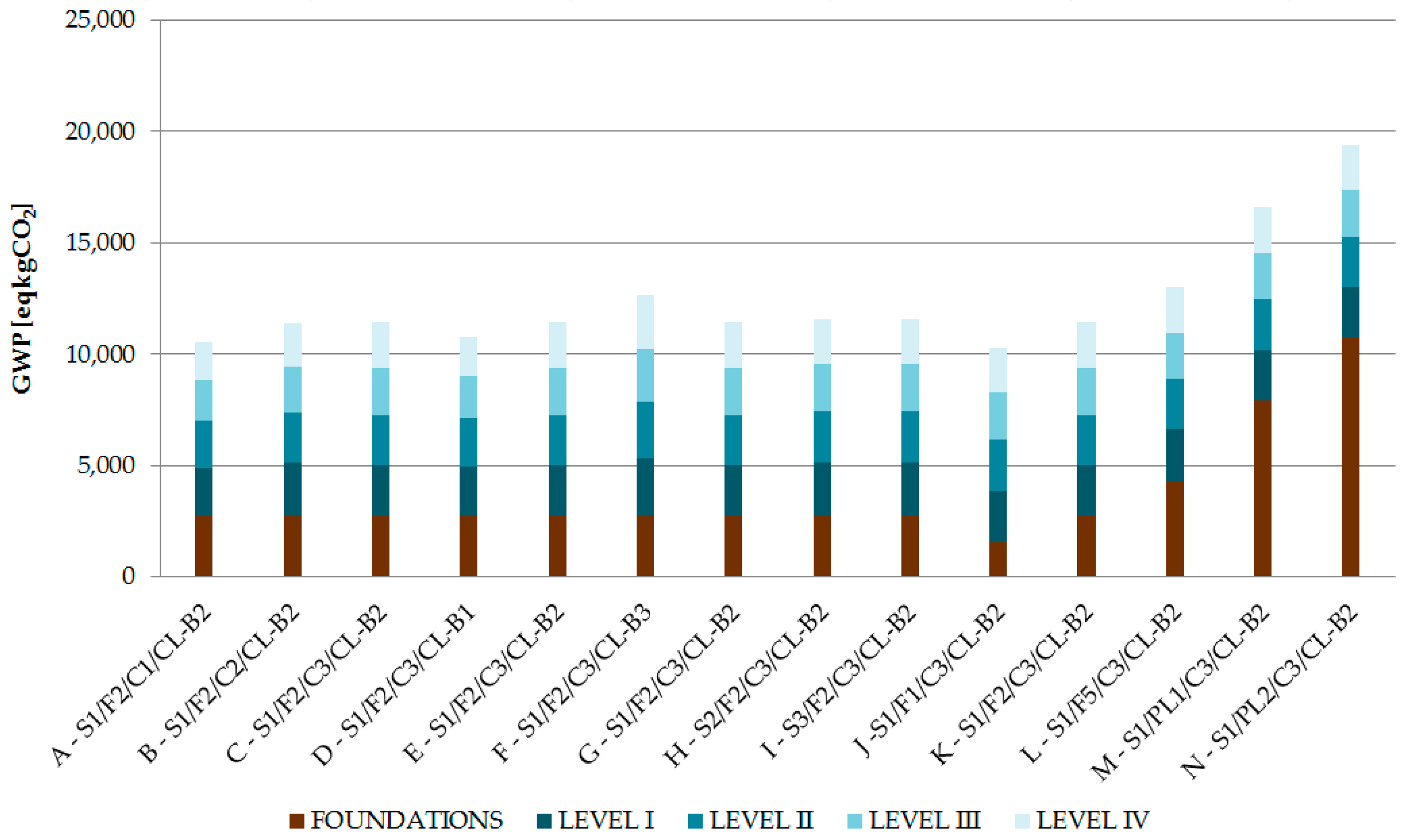
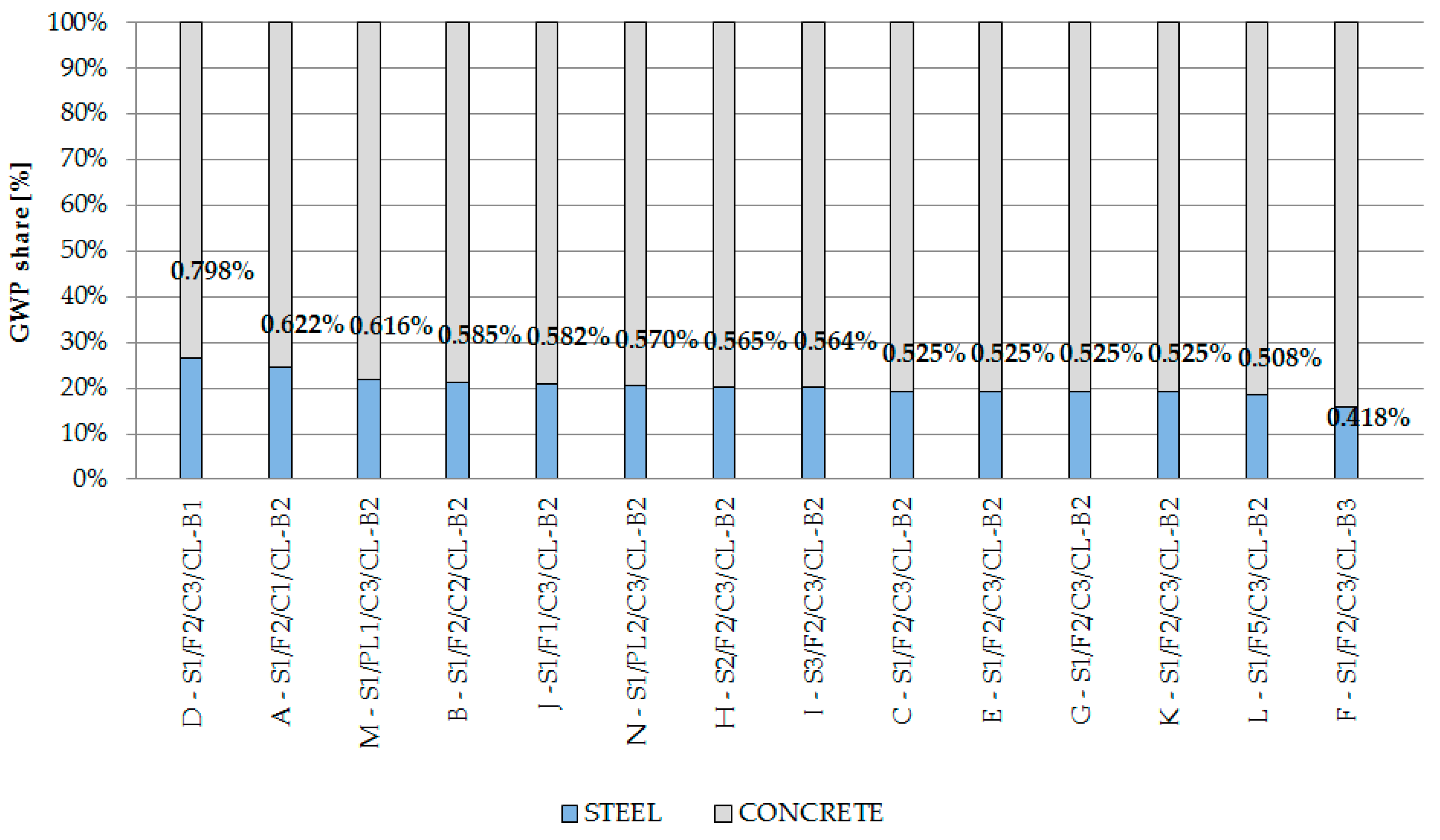
3.2. Life Cycle Assessment of Reinforced Concrete Tower
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lima, L.; Trindade, E.; Alencar, L.; Alencar, M.; Silva, L. Sustainability in the construction industry: A systematic review of the literature. J. Clean. Prod. 2021, 289, 125730. [Google Scholar] [CrossRef]
- Zavadskas, E.; Šaparauskas, J.; Antuchevičienė, J. Sustainability in Construction Engineering. Sustainability 2018, 10, 2236. [Google Scholar] [CrossRef]
- Adams, K.T.; Osmani, M.; Thorpe, T.; Thornback, J. Circular economy in construction: Current awareness, challenges and enablers. Proc. Inst. Civ. Eng.—Waste Resour. Manag. 2017, 170, 15–24. [Google Scholar] [CrossRef]
- Ding, G.K.C. Life cycle assessment (LCA) of sustainable building materials: An overview. In Eco-Efficient Construction and Building Materials; Pacheco-Torgal, F., Cabeza, L.F., Labrincha, J., de Magalhães, A., Eds.; Woodhead Publishing: Sawston, Cambridge, UK, 2014; pp. 38–62. [Google Scholar] [CrossRef]
- Schneider, M.; Romer, M.; Tschudin, M.; Bolio, H. Sustainable cement production present and future. Cem. Concr. Res. 2011, 41, 642–650. [Google Scholar] [CrossRef]
- Ali, M.B.; Saidura, R.; Hossain, M.S. A review on emission analysis in cement industries. Renew. Sustain. Energy Rev. 2011, 15, 2252–2261. [Google Scholar] [CrossRef]
- Benhelal, E.; Shamsaei, E.; Rashid, M.I. Challenges against CO2 abatement strategies in cement industry: A review. J. Environ. Sci. 2021, 104, 84–101. [Google Scholar] [CrossRef]
- Griffiths, S.; Sovacool, B.K.; Furszyfer Del Rio, D.D.; Foley, A.M.; Bazilian, M.D.; Kim, J.; Uratani, J.M. Decarbonizing the cement and concrete industry: A systematic review of socio-technical systems, technological innovations, and policy options. Renew. Sustain. Energy Rev. 2023, 180, 113291. [Google Scholar] [CrossRef]
- Pavlovič, A.; Donchev, T.; Petkova, D.; Staletovič, N. Sustainability of alternative reinforcement for concrete structures: Life cycle assessment of basalt FRP bars. Constr. Build. Mater. 2022, 334, 127424. [Google Scholar] [CrossRef]
- Cadenazzi, T.; Dotelli, G.; Rossini, M.; Nanni, S.N.A. Cost and environmental analyses of reinforcement alternatives for a concrete bridge. Struct. Infrastruct. Eng. 2020, 16, 787–802. [Google Scholar] [CrossRef]
- Kromoser, B.; Butler, M.; Hunger, M.; Kimm, M.; Kopf, F.; Mechtcherine, V.; Pressmair, N.; Traverso, M. Article of RILEM TC 292-MCC: Life cycle assessment (LCA) of non-metallic reinforcement for reinforcing concrete: Manufacturing, durability, dismantling, recycling and reuse: A review. Mater. Struct. 2023, 56, 126. [Google Scholar] [CrossRef]
- Pešta, P.T.; Vlach, J.; Fortová, T. Environmental Impact of Concrete Slab Made of Recycled Aggregate Concrete Based on Limit States of Load-Bearing Capacity and Serviceability—LCA Case Study. Materials 2023, 16, 616. [Google Scholar] [CrossRef] [PubMed]
- Renne, N.; Kara De Maeijer, P.; Craeye, B.; Buyle, M.; Audenaert, A. Sustainable Assessment of Concrete Repairs through Life Cycle Assessment (LCA) and Life Cycle Cost Analysis (LCCA). Infrastructures 2022, 7, 128. [Google Scholar] [CrossRef]
- Huang, B.; Gao, X.; Xu, X.; Song, J.; Geng, Y.; Sarkis, J.; Fishman, T.; Kua, H.; Nakatani, J. A Life Cycle Thinking Framework to Mitigate the Environmental Impact of Building Materials. One Earth 2020, 3, 564–573. [Google Scholar] [CrossRef]
- Negrin, I.; Kripka, M.; Yepes, V. Metamodel-assisted meta-heuristic design optimization of reinforced concrete frame structures considering soil-structure interaction. Eng. Struct. 2023, 293, 116657. [Google Scholar] [CrossRef]
- Xu, X.; You, J.; Wang, Y.; Luo, Y. Analysis and assessment of life-cycle carbon emissions of space frame structures. J. Clean. Prod. 2023, 385, 135521. [Google Scholar] [CrossRef]
- Negrin, I.; Kripka, M.; Yepes, V. Multi-criteria optimization for sustainability-based design of reinforced concrete frame buildings. J. Clean. Prod. 2023, 425, 139115. [Google Scholar] [CrossRef]
- Peng, J.; Feng, Y.; Zhang, Q.; Liu, X. Multi-objective integrated optimization study of prefabricated building projects introducing sustainable levels. Sci. Rep. 2023, 13, 2821. [Google Scholar] [CrossRef] [PubMed]
- Ek, K.; Mathern, A.; Rempling, R.; Brinkho, P.; Karlsson, M.; Norin, M. Life Cycle Sustainability Performance Assessment Method for Comparison of Civil Engineering Works Design Concepts: Case Study of a Bridge. Int. J. Environ. Res. Public Health 2020, 17, 7909. [Google Scholar] [CrossRef] [PubMed]
- Mathern, A.; Penadés-Plà, V.; Barros, J.A.; Yepes, V. Practical metamodel-assisted multi-objective design optimization for improved sustainability and buildability of wind turbine foundations. Struct. Multidiscip. Optim. 2022, 65, 46. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T. Cost and CO2 emission optimization of precast–prestressed concreto U-beam road bridges by a hybrid glowworm swarm algorithm. Autom. Constr. 2015, 49, 123–134. [Google Scholar] [CrossRef]
- Angelin, A.F.; Bento, R.C.; Gavioli, L.M.; Rossignolo, J.A. Life cycle assessment application in the optimum design of reinforced concrete structures. Ambiente Construído Porto Alegre 2023, 23, 187–202. [Google Scholar] [CrossRef]
- Negrin, I.A.; Chagoy’en, E.L. Economic and environmental design optimisation of reinforced concrete frame buildings: A comparative study. Structures 2022, 38, 64–75. [Google Scholar] [CrossRef]
- Camp, C.V.; Huq, F. CO2 and cost optimization of reinforced concrete frames using a big bang-big crunch algorithm. Eng. Struct. 2013, 48, 363–372. [Google Scholar] [CrossRef]
- Ruiz-Vélez, A.; Alcalá, J.; Yepes, V. Optimal Design of Sustainable Reinforced Concrete Precast Hinged Frames. Materials 2023, 16, 204. [Google Scholar] [CrossRef]
- Tahwia, A.M.; El-Far, O.; Amin, M. Characteristics of sustainable high strength concrete incorporating eco-friendly materials. Innov. Infrastruct. Solut. 2022, 7, 8. [Google Scholar] [CrossRef]
- Albarbary, M.M.; Tahwia, A.M.; Elmasoudi, I. Integration between Sustainability and Value Engineering in the Production of Eco-Friendly Concrete. Sustainability 2023, 15, 3565. [Google Scholar] [CrossRef]
- Kilicer, S.; Ozgan, K.; Daloglu, A. Effects of soil structure interaction on behavior of reinforced concrete structures. J. Struct. Eng. Appl. Mech. 2018, 1, 28–33. [Google Scholar] [CrossRef]
- Pinheiro dos Santos, Y.R.; Marques da Cunha Vieira Bello, M.I.; Duarte Gusmão, A.; Dantas Patricio, J. Soil-structure interaction analysis in reinforced concrete structures on footing foundation. Soils Rocks 2021, 44, e2021058020. [Google Scholar] [CrossRef]
- Mitropoulou, C.C.; Kostopanagiotis, C.; Kopanos, M.; Ioakim, D.; Lagaros, N.D. Influence of soil–structure interaction on fragility assessment of building structures. Structures 2016, 6, 85–98. [Google Scholar] [CrossRef]
- Nakhaei, M.; Ghannad, M.A. The effect of soil–structure interaction on damage index of buildings. Eng. Struct. 2008, 30, 1491–1499. [Google Scholar] [CrossRef]
- Anand, V.; Kumar, S.R.S. Seismic Soil-structure Interaction: A State-of-the-Art Review. Structures 2018, 16, 317–326. [Google Scholar] [CrossRef]
- Gravett, D.Z.; Mourlas, C.; Taljaard, V.-L.; Bakas, N.; Markou, G.; Papadrakakis, M. New fundamental period formulae for soil-reinforced concrete structures interaction using machine learning algorithms and ANNs. Structures 2021, 144, 106656. [Google Scholar] [CrossRef]
- Tsimplokoukou, K.; Lamperti, M.; Negro, P. Building Design for Safety and Sustainability; European Commission, Joint Research Centre, Institute for the Protection and Security of the Citizen: Ispra, Italy, 2014. [Google Scholar]
- Samsudin, M.K.; Azman, N.Z. The Sustainable Aspect of Safety in Architectural Early Design: An Introduction to Prevention through Design (PtD) Concept. Int. J. Sustain. Constr. Eng. Technol. 2022, 13, 34–50. [Google Scholar] [CrossRef]
- User Handbook AxisVM X7. Available online: https://gammacad.pl/app/uploads/acf-uploads/axisvm_x7_podrecznik.pdf (accessed on 21 May 2024).
- User Handbook Dlubal RFEM 6/RSTAB 9—Concrete Design. Available online: https://www.dlubal.com/en/downloads-and-information/documents/online-manuals/rfem-6-concrete-design (accessed on 21 May 2024).
- User Handbook Scia Engineering. Available online: https://downloads.scia.net/support/sciaengineer/manuals/TUT%20[Eng]%20SCIA21.1%20-%20Tutorial%20Concrete.pdf (accessed on 21 May 2024).
- Ding, G.K.C. Sustainable construction—The role of environmental assessment tools. J. Environ. Manag. 2008, 86, 451–464. [Google Scholar] [CrossRef] [PubMed]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardisation: Brussels, Belgium, 2004.
- EN 1997-1-1; Eurocode 7: Geotechnical Design—Part 1: General Rules. European Committee for Standardisation: Brussels, Belgium, 2004.
- EN-1990; Eurocode—Basis of Structural Design. European Committee for Standardisation: Brussels, Belgium, 2005.
- EN 1991-1-4; Eurocode 1: Actions on Structures—Part 1-4: General Actions—Wind Actions. European Committee for Standardisation: Brussels, Belgium, 2010.
- EN 1991-1-3; Eurocode 1: Actions on Structures—Part 1-3: General Actions—Snow Loads. European Committee for Standardisation: Brussels, Belgium, 2003.
- Ścigałło, J.; Studziński, R. Types of global analysis of bar reinforced concrete structures. Mater. Bud. Sci. 2024, 3, 1–5. [Google Scholar] [CrossRef]
- Bresler, B. Design Criteria for Reinforced Columns under Axial Load and Biaxial Bending. ACI J. Proc. 1960, 57, 481–490, discussion 1621–1638. [Google Scholar]
- Ramamurthy, L.N. Investigation of the Ultimate Strength of Square and Rectangular Columns under Biaxially Eccentric Loads. In Symposium on Reinforced Concrete Columns; American Concrete Institute: Detroit, MI, USA, 1966; pp. 263–298. [Google Scholar]
- Bouchaboub, M.; Samai, M.L. Nonlinear analysis of slender high-strength R/C columns under combined biaxial bending and axial compression. Eng. Struct. 2013, 48, 37–42. [Google Scholar] [CrossRef]
- Pannell, F.N. The Design of Biaxially Loaded Columns by Ultimate Load Methods. Mag. Concr. Res. 1960, 12, 99–108. [Google Scholar] [CrossRef]
- Araújo, J.M. Comparative study of the simplified methods of Eurocode 2 for second order analysis of slender reinforced concrete columns. J. Build. Eng. 2017, 14, 55–60. [Google Scholar] [CrossRef]
- The Sustainability Platform for Construction & Manufacturing. Available online: https://oneclicklca.com (accessed on 15 May 2024).
- Yeoa, D.; Gabbaib, R.D. Sustainable design of reinforced concrete structures through embodied Energy optimization. Energy Build. 2011, 43, 2028–2033. [Google Scholar] [CrossRef]


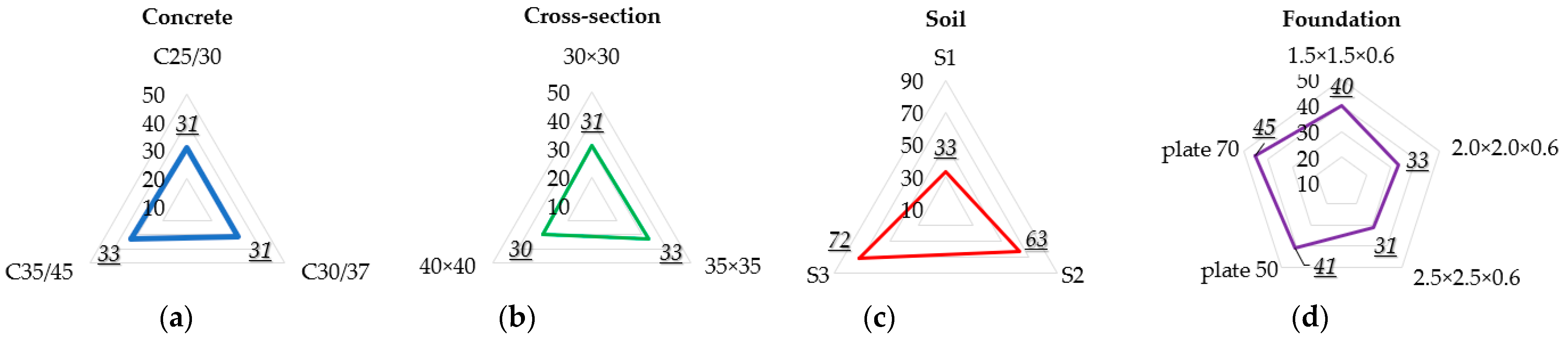
| Soil Layer Name (Acronym) | Description | Standard USCS | μ [–] | ρ [kg/m3] | φ [°] | φcv [°] | ν [–] | Es [N/mm2] | c [kN/m2] |
|---|---|---|---|---|---|---|---|---|---|
| Mixed silty sand (DNL) | Loose, humid, silty sand | SM | – | 1800 | 26 | 22 | 0.2 | 70 | – |
| Very fine sand (FNL) | Loose, humid, very fine sand | SP | – | 1700 | 22 | 26 | 0.25 | 10 | – |
| Homogenous coarse and medium sand (CNL) | Loose, humid sand | SW | – | 1800 | 32 | 32 | 0.2 | 20 | – |
| Homogenous coarse and medium sand (CNT) | Solid, humid sand | SW | – | 2100 | 35 | 32 | 0.2 | 70 | – |
| Lean clay (JS7) | Firm, lean clay | CH | 0.7 | 2000 | 16 | 15 | 0.31 | 6 | 85 |
| Lean clay (JK7) | Stiff, lean clay | CL | 0.7 | 1800 | 19 | 17 | 0.17 | 10 | 185 |
| Lean clay (JK10) | Stiff, lean clay | CL | 1.0 | 1600 | 17 | 17 | 0.17 | 10 | 185 |
| Fat clay (LS7) | Firm, fat clay | CH | 0.7 | 2100 | 7 | 13 | 0.35 | 5 | 100 |
| Silt (IP7) | Soft silt | MH | 0.7 | 2100 | 16 | 16 | 0.33 | 4 | 75 |
| Silt (IK7) | Stiff silt | ML | 0.7 | 1700 | 23 | 21 | 0.15 | 12 | 150 |
| Concrete Class | E [N/mm2] | ν [–] | fck [N/mm2] | ftk [N/mm2] |
|---|---|---|---|---|
| C25/30 | 31,500 | 0.2 | 25 | 2.56 |
| C30/37 | 32,800 | 0.2 | 30 | 2.90 |
| C35/45 | 34,100 | 0.2 | 37 | 3.21 |
| Parameter | P1 (Soil) | P2 (Concrete) | P3a (Isolated Footing) | P3b (Foundation Plate) | P4 (Column Cross-Sections) | P4 (Beam Cross-Sections) |
|---|---|---|---|---|---|---|
| P1 | S1 | |||||
| S2 | C35/45 | 2.0 × 2.0 × 0.6 | – | 0.35 × 0.35 | 0.35 × 0.50 | |
| S3 | ||||||
| P2 | C20/25 | |||||
| S1 | C30/37 | 2.0 × 2.0 × 0.6 | – | 0.35 × 0.35 | 0.35 × 0.50 | |
| C35/45 | ||||||
| P3a | 1.5 × 1.5 × 0.6 | |||||
| S1 | C35/45 | 2.0 × 2.0 × 0.6 | – | 0.35 × 0.35 | 0.35 × 0.50 | |
| 2.5 × 2.5 × 0.6 | ||||||
| P3b | S1 | C35/45 | – | 7.0 × 7.0 × 0.5 | 0.35 × 0.35 | 0.35 × 0.50 |
| 7.0 × 7.0 × 0.7 | ||||||
| P4 | 0.30 × 0.30 | 0.30 × 0.50 | ||||
| S1 | C35/45 | 2.0 × 2.0 × 0.6 | – | 0.35 × 0.35 | 0.35 × 0.50 | |
| 0.40 × 0.40 | 0.40 × 0.50 |
| Steel Reinforcement | Ready-Mix Concrete C25/30 | Ready-Mix Concrete C30/37 | Ready-Mix Concrete C35/45 | |
|---|---|---|---|---|
| Minimum value | 0.64 | 140.88 | 159.35 | 180.71 |
| Average value | 1.44 | 206.45 | 243.70 | 252.99 |
| Maximum value | 2.43 | 283.39 | 318.19 | 337.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Studziński, R.; Ścigałło, J.; Ratajczak, M.; Ciesielczyk, K. Impact of Heterogeneous Soil Conditions on the Life Cycle Assessment of a Multi-Storey Reinforced Concrete Structure. Sustainability 2024, 16, 6771. https://doi.org/10.3390/su16166771
Studziński R, Ścigałło J, Ratajczak M, Ciesielczyk K. Impact of Heterogeneous Soil Conditions on the Life Cycle Assessment of a Multi-Storey Reinforced Concrete Structure. Sustainability. 2024; 16(16):6771. https://doi.org/10.3390/su16166771
Chicago/Turabian StyleStudziński, Robert, Jacek Ścigałło, Maria Ratajczak, and Katarzyna Ciesielczyk. 2024. "Impact of Heterogeneous Soil Conditions on the Life Cycle Assessment of a Multi-Storey Reinforced Concrete Structure" Sustainability 16, no. 16: 6771. https://doi.org/10.3390/su16166771
APA StyleStudziński, R., Ścigałło, J., Ratajczak, M., & Ciesielczyk, K. (2024). Impact of Heterogeneous Soil Conditions on the Life Cycle Assessment of a Multi-Storey Reinforced Concrete Structure. Sustainability, 16(16), 6771. https://doi.org/10.3390/su16166771






