Study on the Partial Paste Backfill Mining Method in a Fully Mechanized Top-Coal Caving Face: Case Study from a Coal Mine, China
Abstract
1. Introduction
2. Partial-Filling Mining Method
2.1. Technical Principles
2.2. Mining and Filling Process
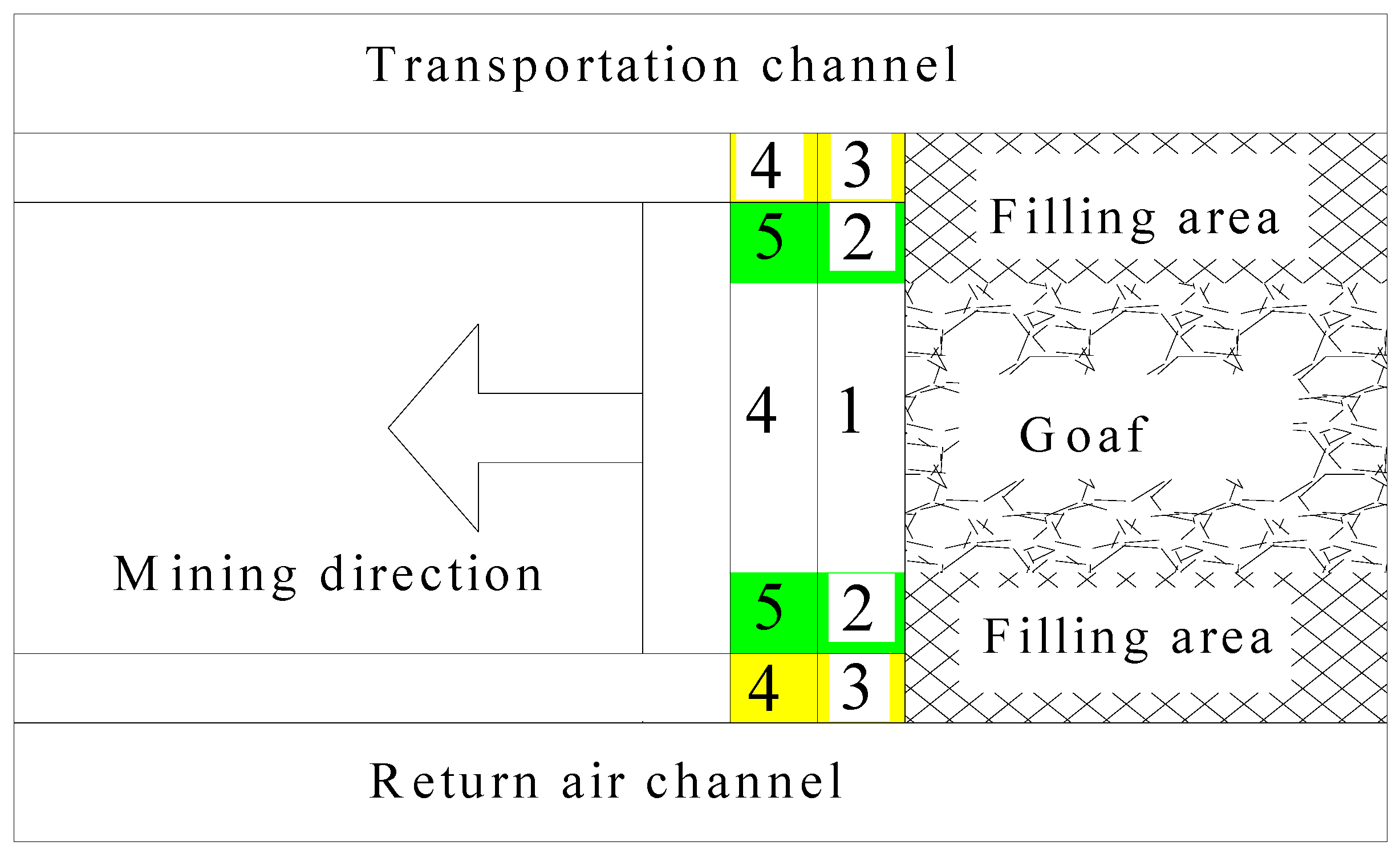
2.2.1. Pre-Mining Preparation
2.2.2. Filling Space Construction
2.2.3. Filling Process
3. Analysis of Filling Structure Factors Affecting the Filling Effect in End Partial Filling Mining
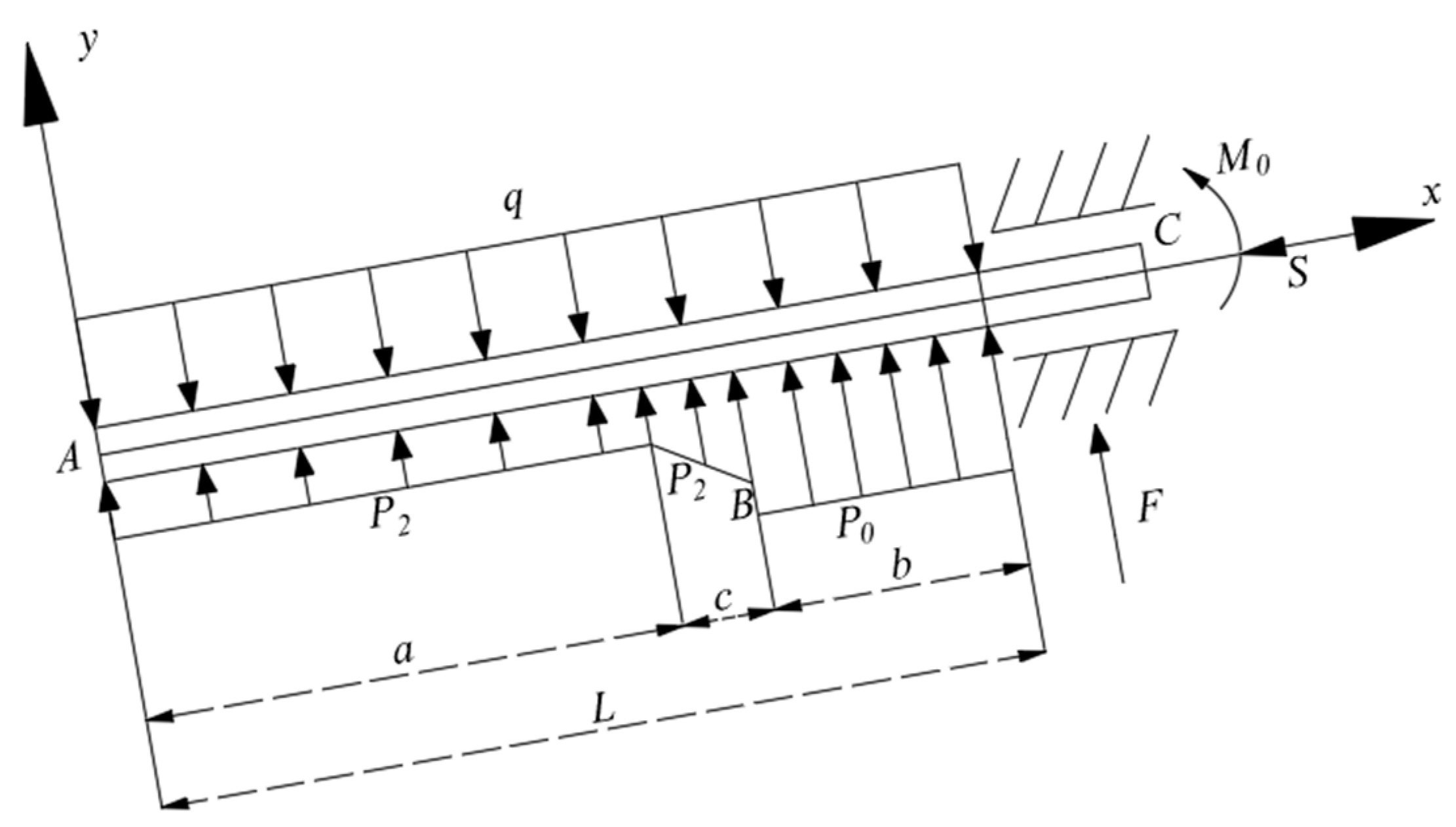
3.1. Establishment of the Mechanical Model of the Roof Beam
3.2. The Main Filling Structural Factors Affecting the Filling Effect
3.2.1. Filling Rate
3.2.2. Width of the Filling Body
3.2.3. Strength of the Filling Body
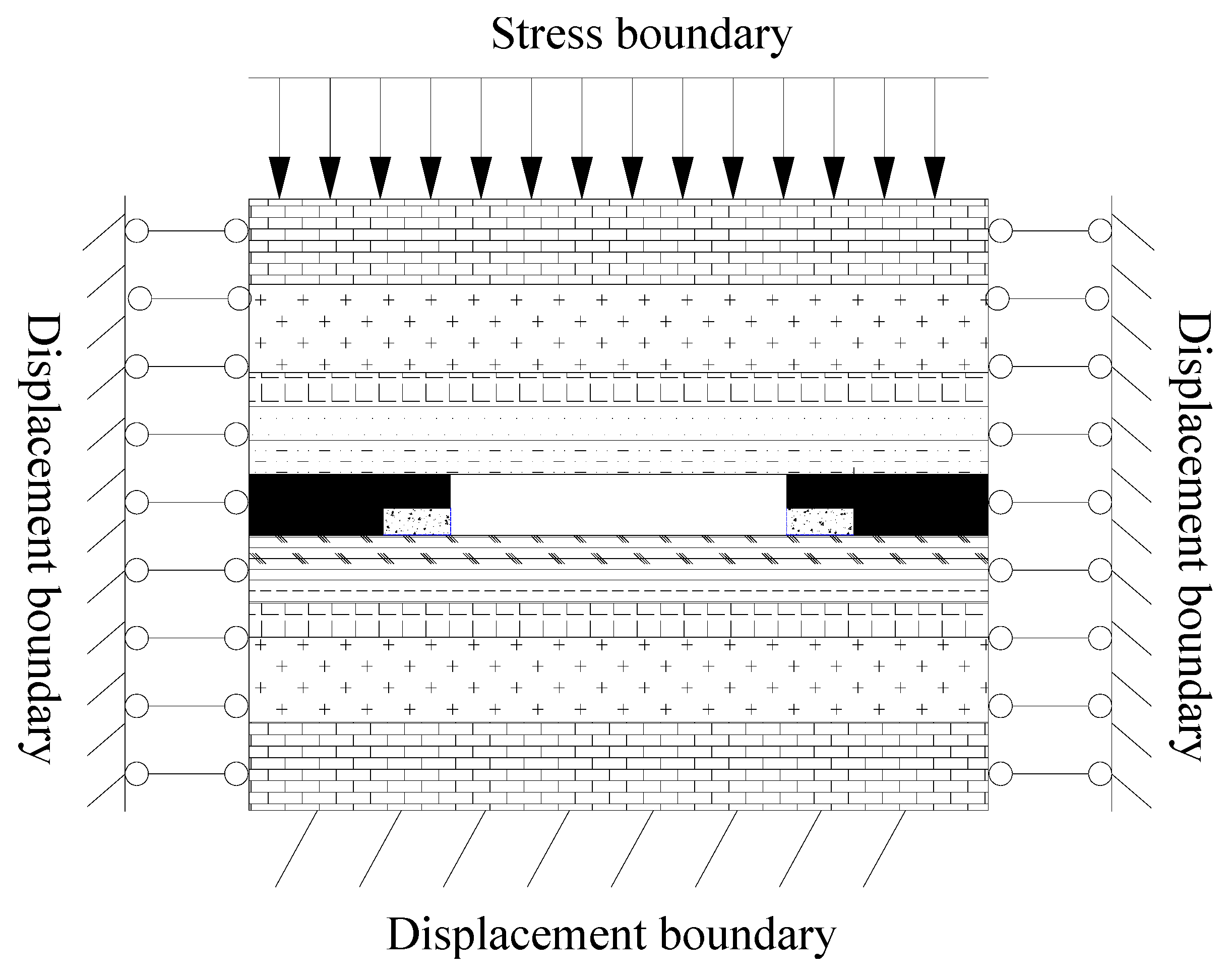
4. Establishment of Models in Numerical Simulation
5. Results and Discussion
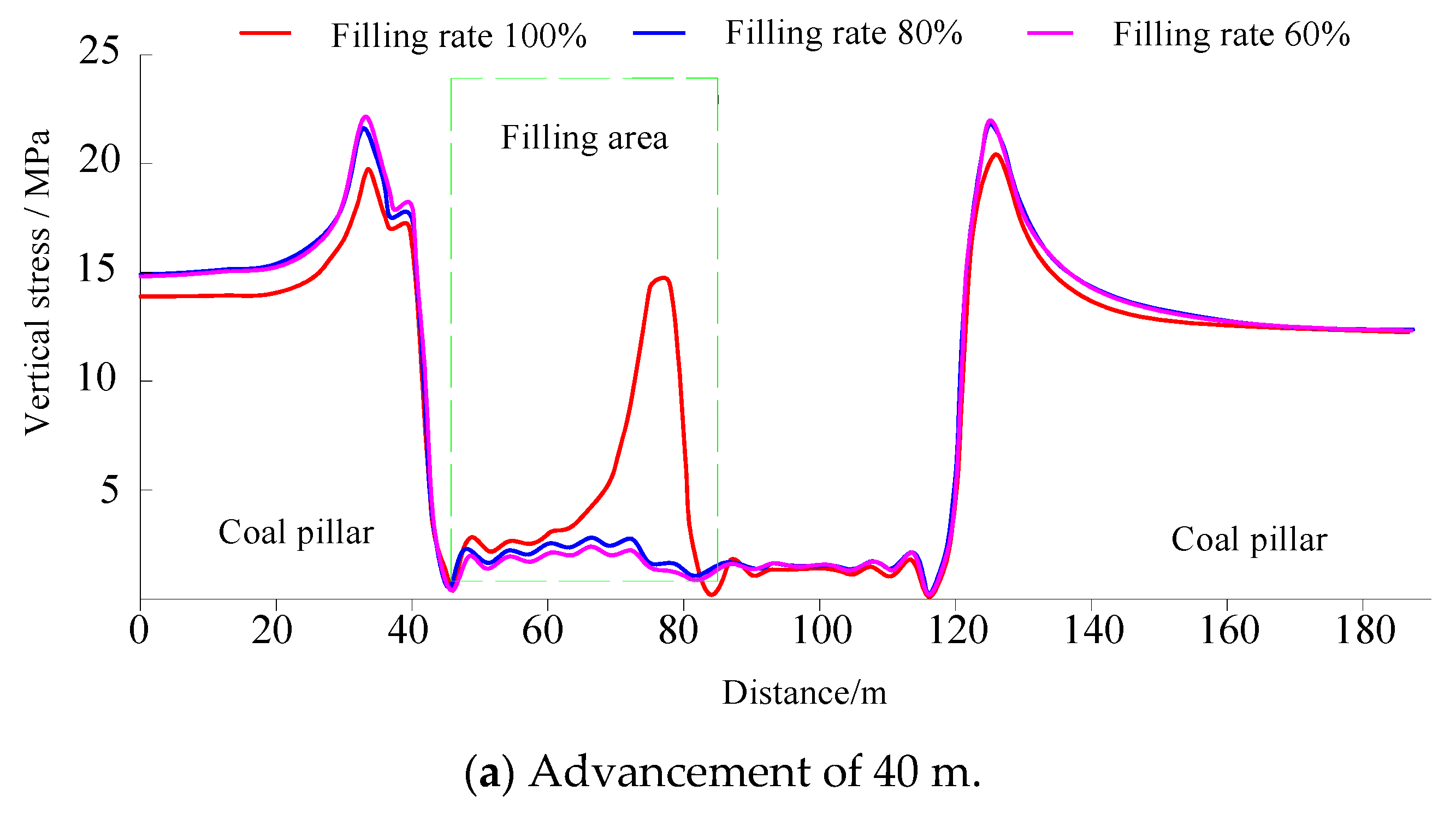
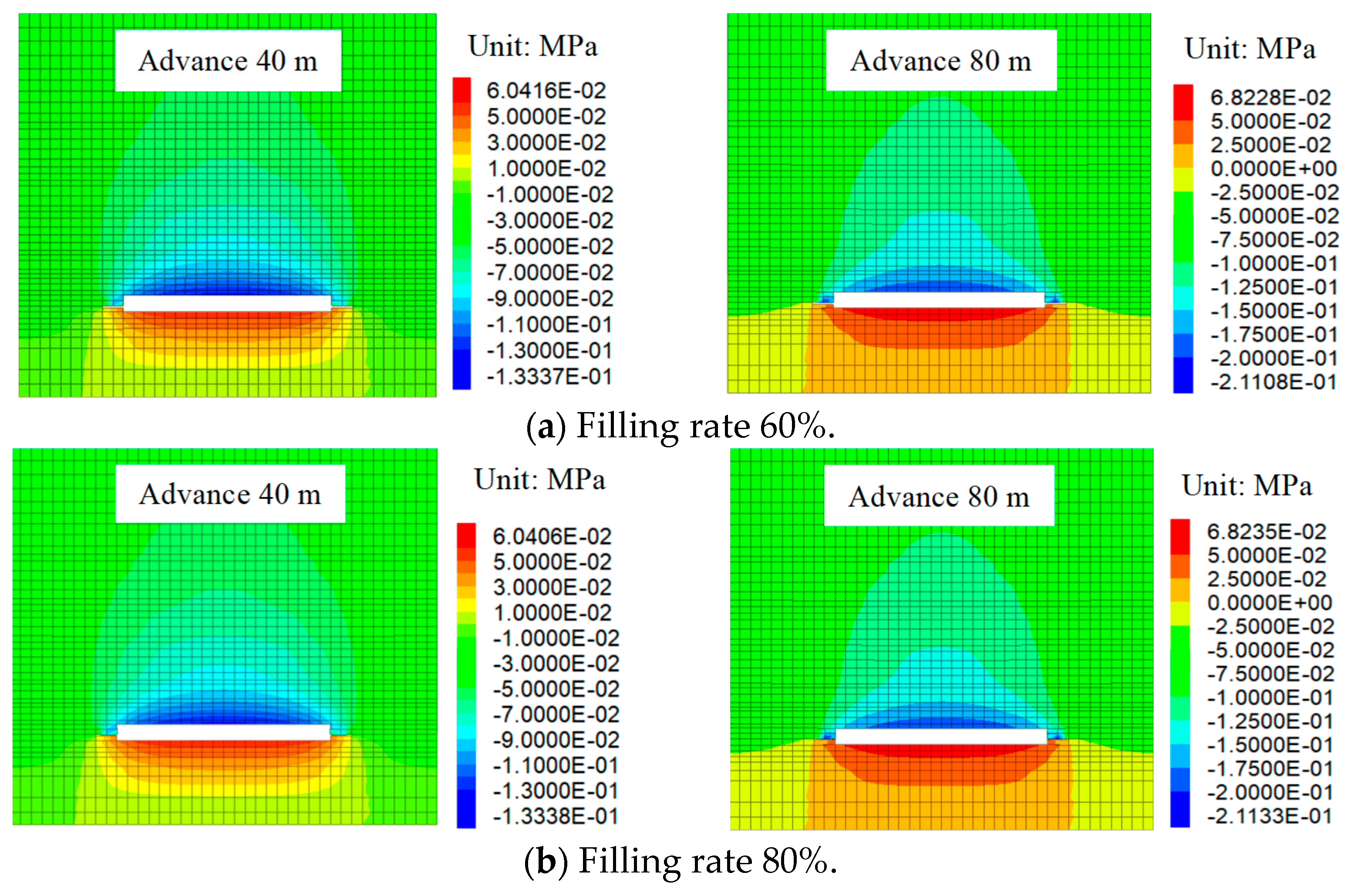
5.1. Study on the Law of Overburden Movement under Different Filling Rates
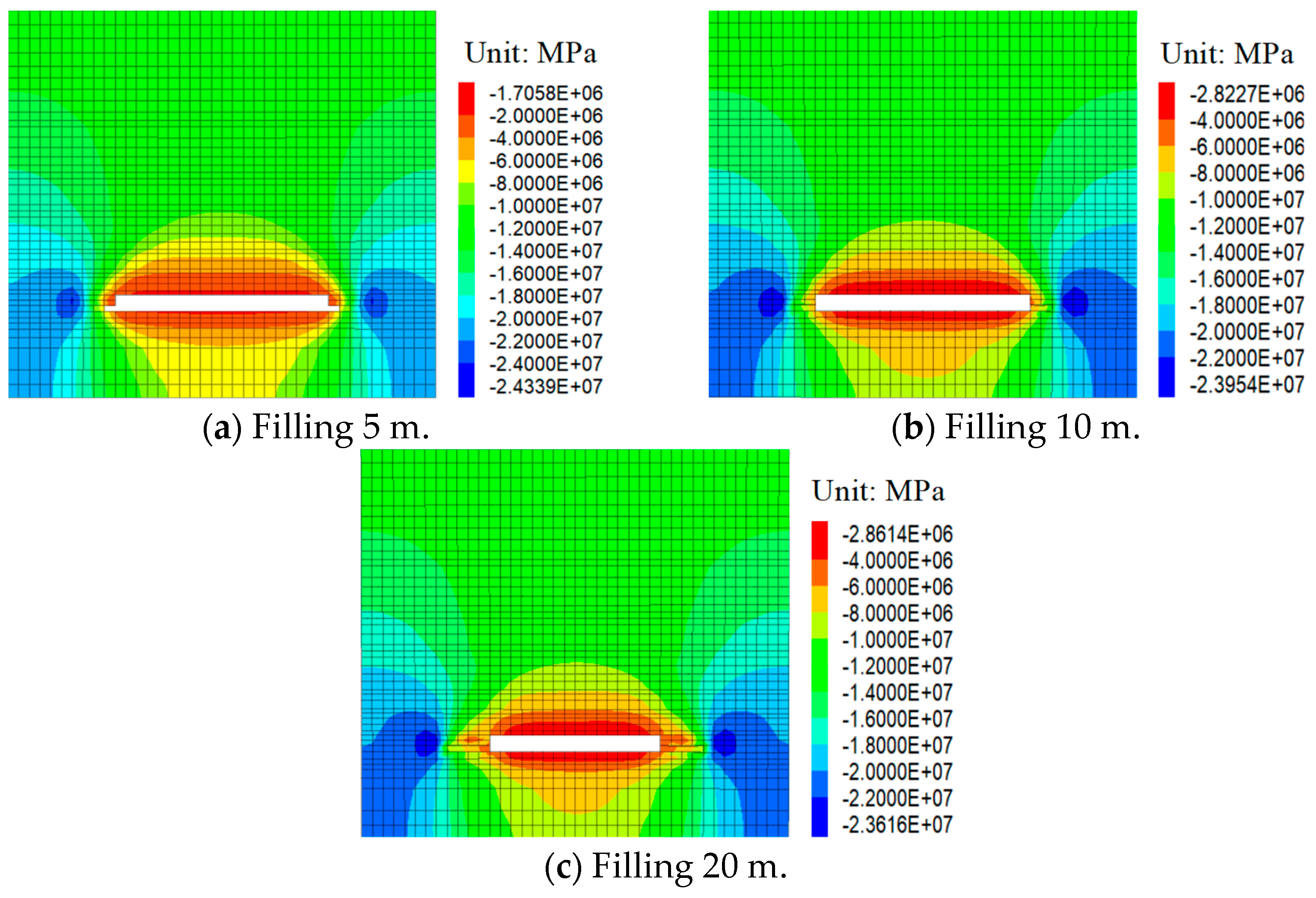
5.1.1. Stress Distribution Characteristics of Overburden under Different Filling Rates
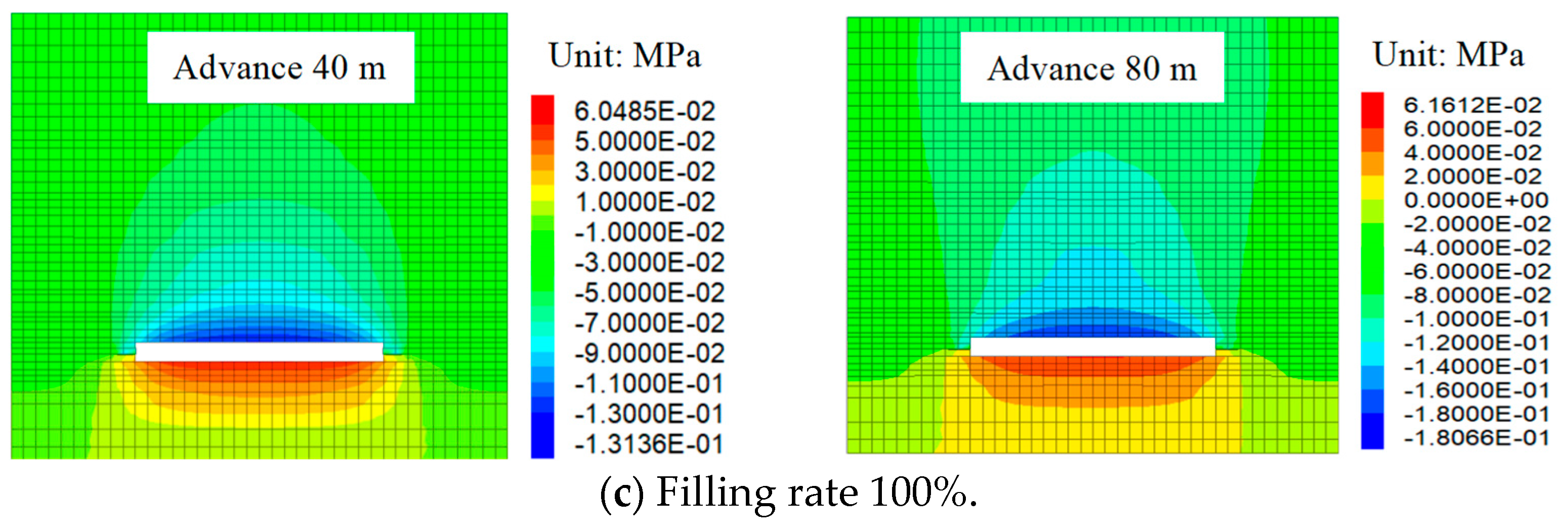
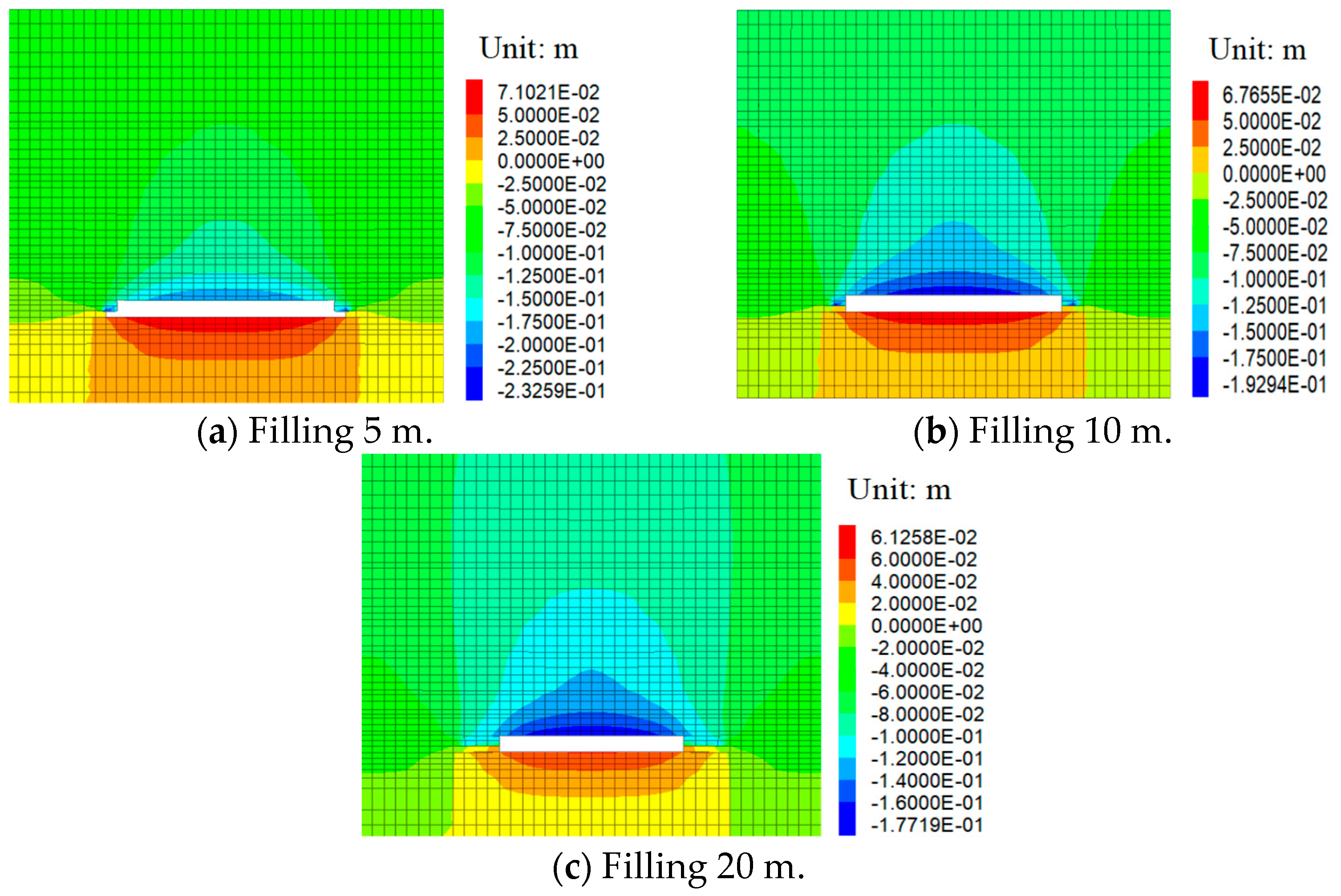
5.1.2. Distribution Characteristics of Overburden Displacement under Different Filling Rates
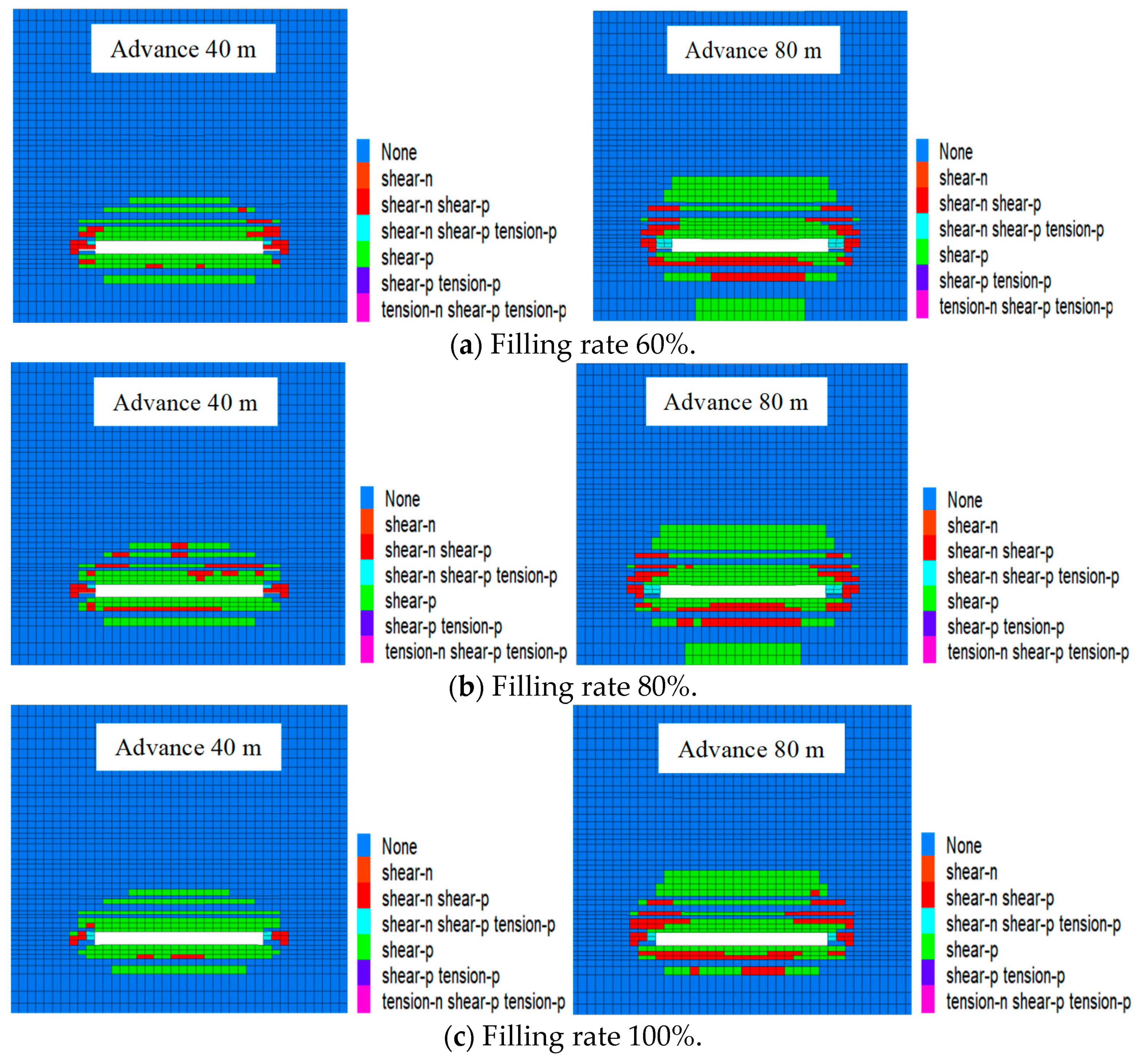
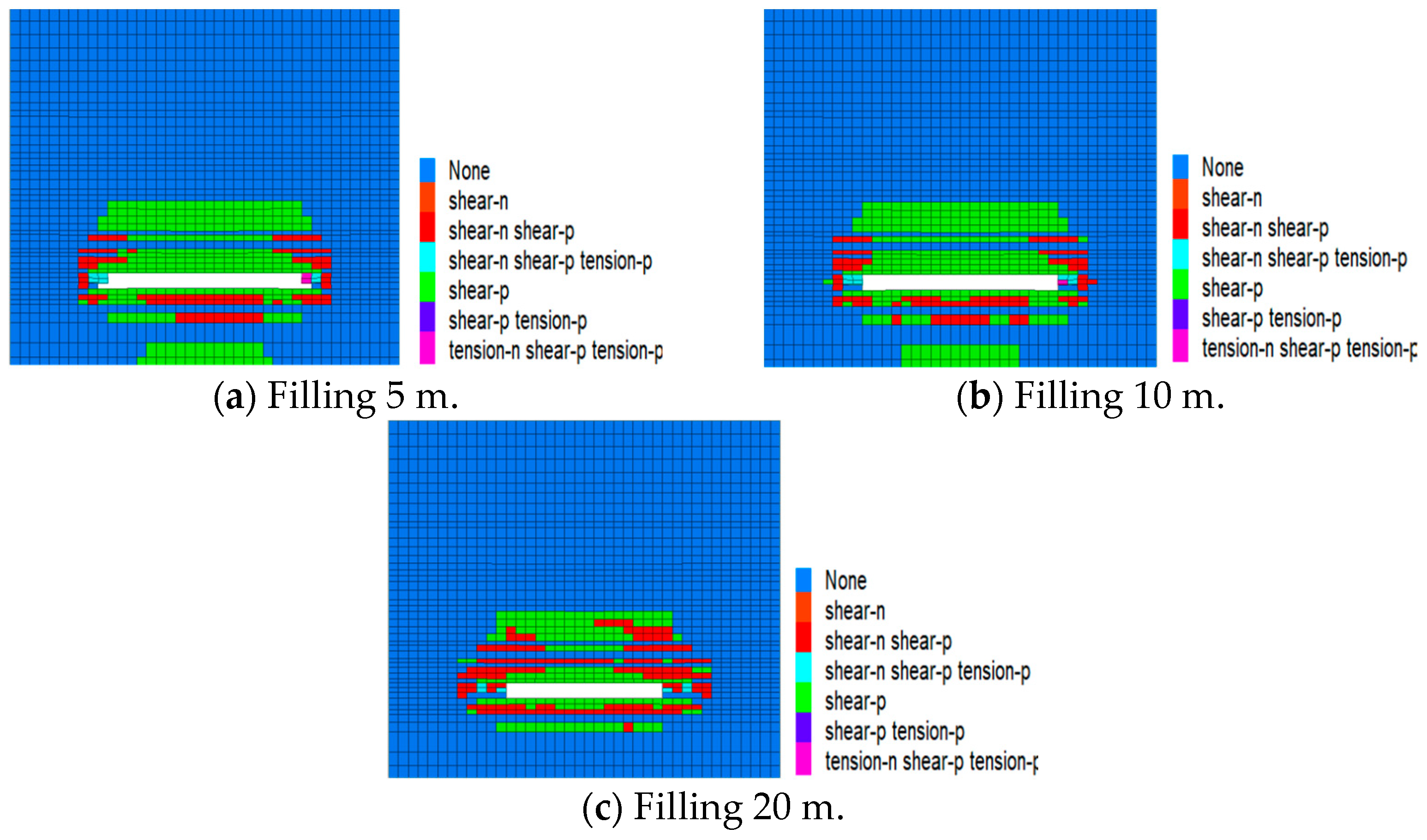
5.1.3. Plastic Failure Characteristics of Overburden under Different Filling Ratios
5.2. Study on the Evolution Law of Overburden under Different Filling Body Widths
5.2.1. Stress Distribution Characteristics of Overburden under Different Backfill Widths
5.2.2. Displacement Distribution Characteristics of Overburden under Different Filling Body Widths
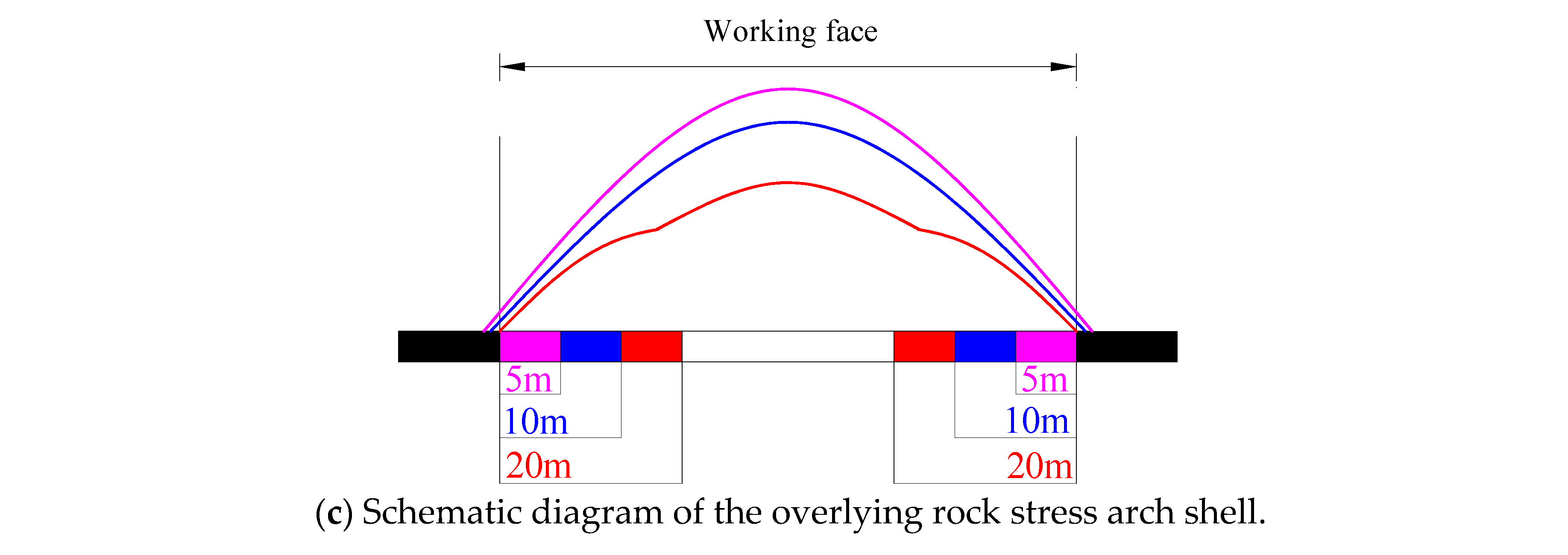
5.2.3. Failure Characteristics of the Overburden under Different Backfill Widths
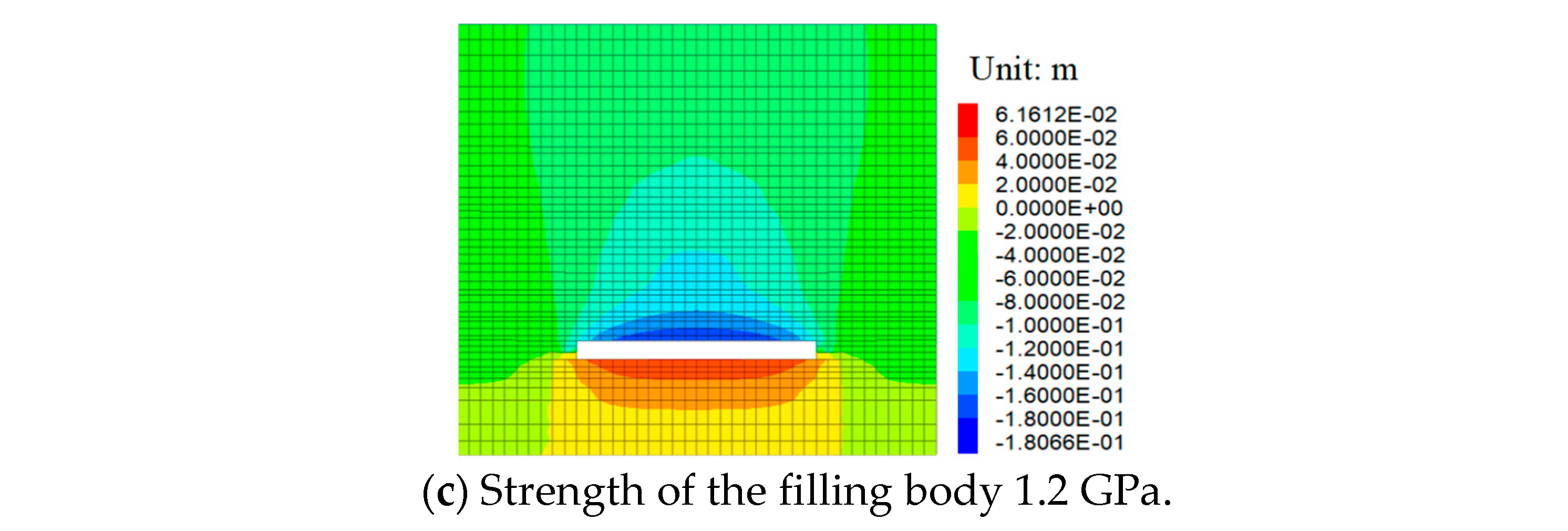
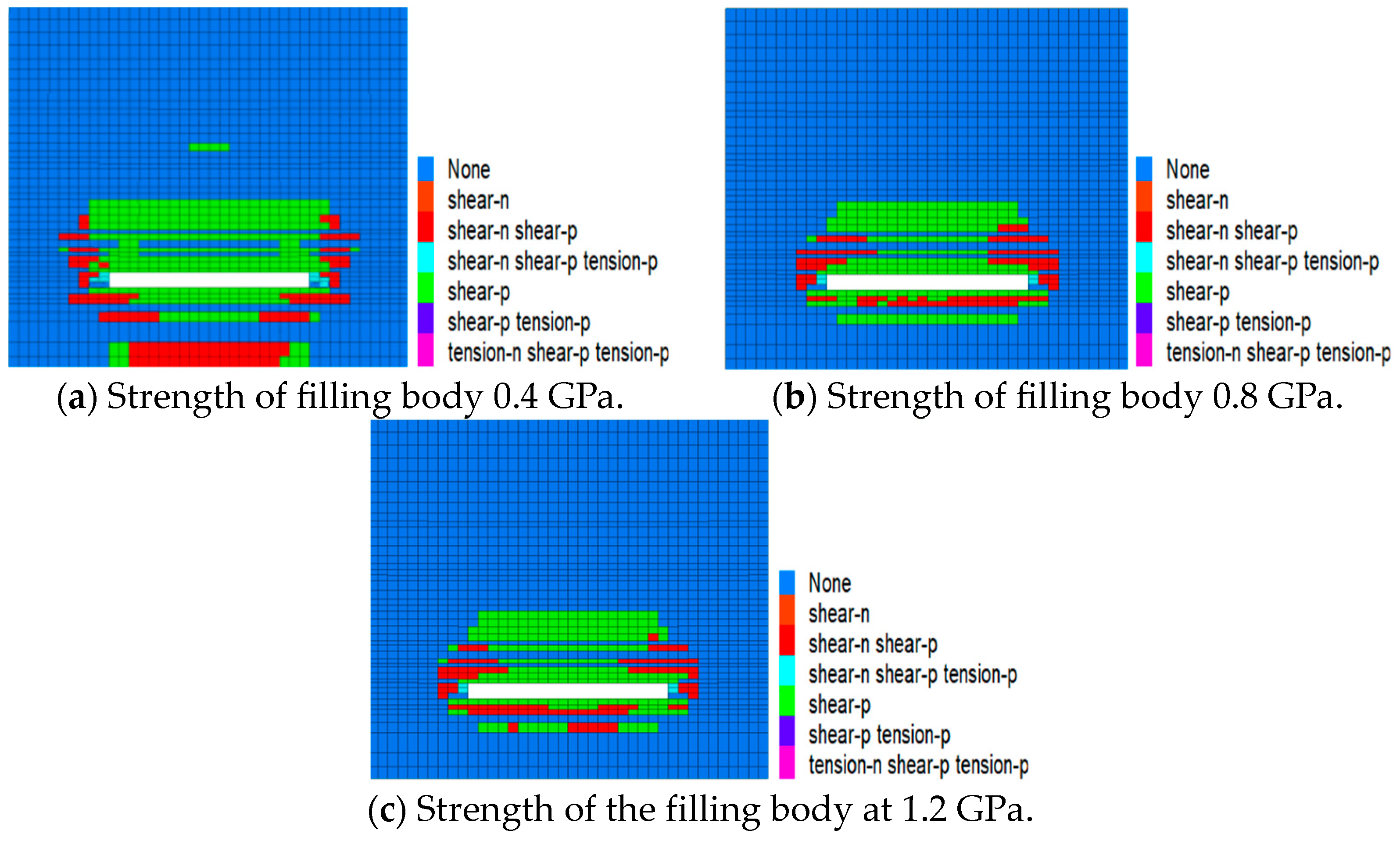
5.3. Study on the Migration Law of Overburden under Different Backfill Strengths
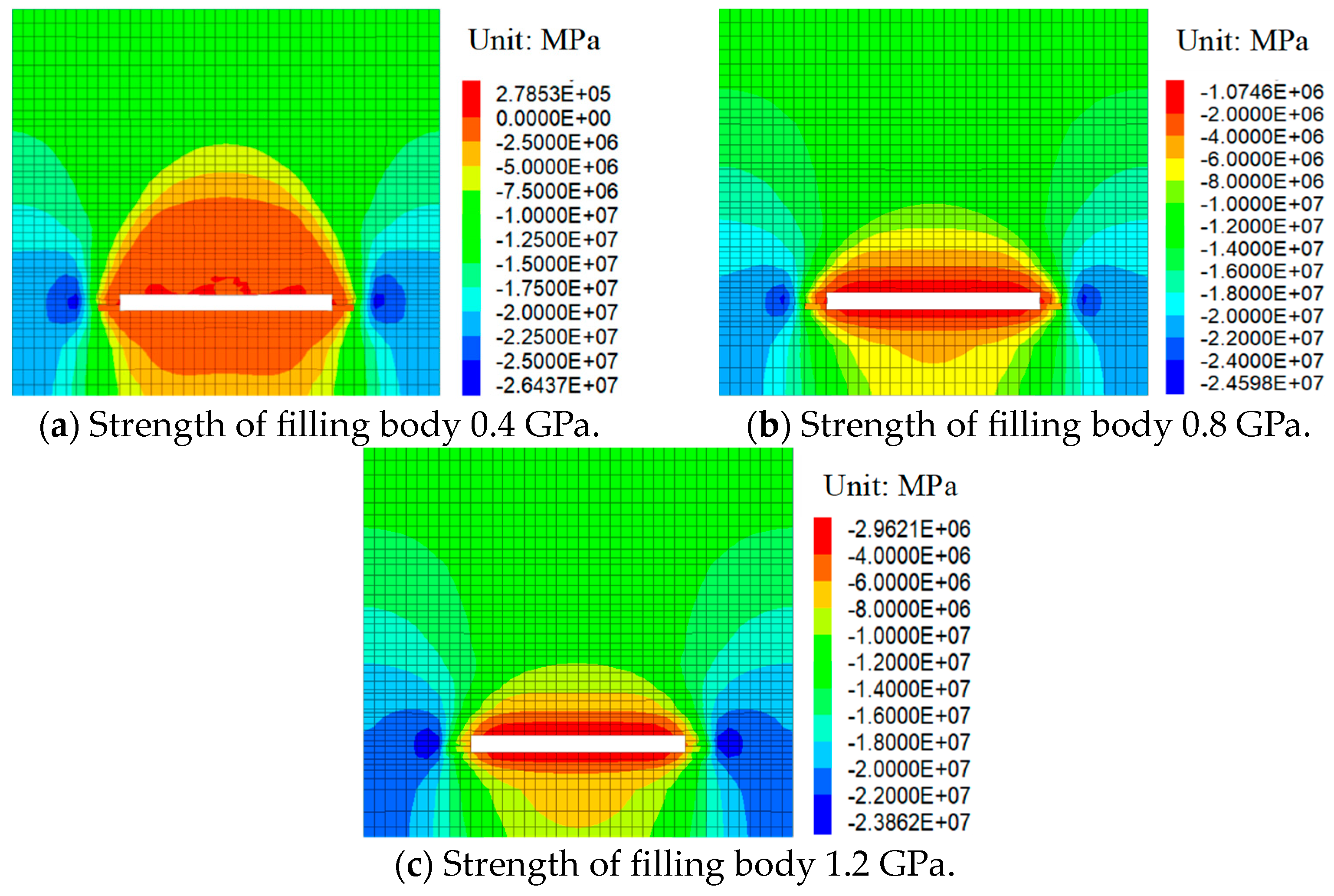
5.3.1. Stress Distribution Characteristics of Overburden under Different Backfill Strengths
5.3.2. Displacement Distribution Characteristics of Overburden under Different Backfill Strengths
5.3.3. Failure Characteristics of Overburden under Different Backfill Strengths
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Zuo, J.; Karakus, M.; Liu, L.; Zhou, H.; Yu, M. A new theoretical method to predict strata movement and surface subsidence due to inclined coal seam mining. Rock Mech. Rock Eng. 2021, 54, 2723–2740. [Google Scholar] [CrossRef]
- Chen, S.; Liu, J.; Wang, F.; Zhou, J.; Tang, P.; Gao, Z. Hydrochemical analysis of groundwater in coastal coal mining areas—A case study of the liangjia coal mine, north China. Mine Water Environ. 2022, 41, 415–427. [Google Scholar] [CrossRef]
- Bai, E.; Guo, W.; Zhang, H.; Tan, Y.; Ma, Z.; Wu, D.; Guo, M.; Wen, P. Coal mining method with near-zero impact on the ecological environment in a high-intensity mining area of Northwest China. Bull. Eng. Geol. Environ. 2022, 81, 80. [Google Scholar] [CrossRef]
- Deng, L.; Li, X.; Wu, Y.; Li, F.; Huang, Z.; Ji, Y.; Zou, C.; Liu, Z. Influence of cooling speed on the physical and mechanical properties of granite in geothermal-related engineering. Deep Undergr. Sci. Eng. 2022, 1, 40–57. [Google Scholar] [CrossRef]
- Huang, L.; Fang, Y.; Hou, Z.; Xie, Y.; Wu, L.; Lou, J.; Wang, Q.; Guo, Y.; Sun, W. A preliminary site selection system for underground hydrogen storage in salt caverns and its application in Pingdingshan, China. Deep Undergr. Sci. Eng. 2023, 3, 117–128. [Google Scholar] [CrossRef]
- Wang, X.; Guan, K.; Yang, T.; Liu, X. Instability mechanism of pillar burst in asymmetric mining based on cusp catastrophe model. Rock Mech. Rock Eng. 2021, 54, 1463–1479. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Guo, Y.; Pu, H.; Peng, Y. Influence of particle size distribution on fractal characteristics of waste rock backfill materials under compression. J. Mater. Res. Technol. 2022, 20, 2977–2989. [Google Scholar] [CrossRef]
- Yin, S.; Li, Z.; Wang, E.; Niu, Y.; Tian, H.; Li, X.; Li, H.; Yang, C. The infrared thermal effect of coal failure with different impact types and its relationship with bursting liability. Infrared Phys. Technol 2024, 134, 105263. [Google Scholar] [CrossRef]
- Wu, A.; Wang, Y.; Xiao, B.; Wang, J.; Wang, L. Key theory and technology of cemented paste backfill for green mining of metal mines. Green Smart Min. Eng. 2024, 1, 27–39. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, J.; Song, Z.; Fan, W.; Zhang, Y.; Dong, X.; Zhang, Y.; Kan, B.; Chen, Z.; Zhang, J.; et al. Review of the development status of rock burst disaster prevention system in China. J. Cent. South Univ. 2023, 30, 3763–3789. [Google Scholar] [CrossRef]
- Chen, F.; Liu, J.; Zhang, X.; Wang, J.; Jiao, H.; Yu, J. Review on the art of roof contacting in cemented waste backfill technology in a metal mine. Minerals 2022, 12, 721. [Google Scholar] [CrossRef]
- Xiao, Z.Q.; Zhang, W.C. Review of allanite: Properties, occurrence and mineral processing technologies. Green Smart Min Eng. 2024, 1, 40–52. [Google Scholar] [CrossRef]
- Skrzypkowski, K. 3D numerical modelling of the application of cemented paste backfill on displacements around strip excavations. Energies 2021, 14, 7750. [Google Scholar] [CrossRef]
- Xue, Z.; Gan, D.; Zhang, Y.; Liu, Z. Rheological behavior of ultrafine-tailings cemented paste backfill in high-temperature mining conditions. Constr. Build. Mater. 2020, 253, 119212. [Google Scholar] [CrossRef]
- Li, H.; Zhang, B.; Bai, H.; Wu, J.; Meng, Q.; Xiao, N.; Li, F.; Wu, G. Surface water resource protection in a mining process under varying strata thickness—A case study of buliangou coal mine, China. Sustainability 2019, 10, 4634. [Google Scholar] [CrossRef]
- Xue, Y.-C.; Xu, T.; Wasantha, P.L.P.; Yang, T.-H.; Fu, T.-F. Dynamic disaster control of backfill mining under thick magmatic rock in one side goaf: A case study. J. Cent. South Univ. 2020, 27, 3103–3117. [Google Scholar] [CrossRef]
- Li, X.; Chen, D.; Fu, J.; Liu, S.; Geng, X. Construction and application of fuzzy comprehensive evaluation model for rockburst based on microseismic monitoring. Appl. Sci. 2023, 13, 12013. [Google Scholar] [CrossRef]
- Xu, J.; Xuan, D.; Zhu, W.; Wang, X.; Wang, B.; Teng, H. Study and application of coal mining with partial backfilling. J. China Coal Soc. 2015, 40, 1303–1312. [Google Scholar] [CrossRef]
- Deng, X.J.; Zhang, J.X.; Zhou, N.; De Wit, B.; Wang, C.T. Upward slicing longwall-roadway cemented backfilling technology for mining an extra-thick coal seam located under aquifers: A case study. Environ. Earth Sci. 2017, 76, 789. [Google Scholar] [CrossRef]
- Cao, W.; Wang, X.; Li, P.; Zhang, D.; Sun, C.; Qin, D. Wide strip backfill mining for surface subsidence control and its application in critical mining conditions of a coal mine. Sustainability 2018, 10, 700. [Google Scholar] [CrossRef]
- Lu, B.; Zhang, X.; Li, F.; Zhang, B.; Pang, Z. Study and application of short-wall gangue cemented backfilling technology. J. China Coal Soc. 2017, 42, 7–15. [Google Scholar] [CrossRef]
- Liu, J.; Sui, W.; Zhao, Q. Environmentally sustainable mining: A case study of intermittent cut-and-fill mining un-der sand aquifers. Environ. Earth Sci. 2017, 76, 562. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Fu, J.; Zhu, N.; Chen, D.; Wang, Y.; Ding, S. Experimental study on compressive behavior and failure characteristics of imitation steel fiber concrete under uniaxial load imitation steel fiber concrete under uniaxial load. Constr. Build. Mater. 2023, 399, 132599. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Fu, J.; Gao, Z.; Chen, P.; Zhang, Z. Research on acoustic emission multi-parameter characteristics in the failure process of imitation steel fiber reinforced concrete. Phys. Fluids 2023, 35, 107109. [Google Scholar] [CrossRef]
- Fu, J.; Chen, D.; Li, X.; Li, X.; Li, H.; Liu, S.; Li, C.; Zhang, J. Research on the technology of gob-side entry retaining by pouring support beside the roadway in three soft coal seam A case study. Phys. Fluids 2024, 36, 017123. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Yu, Z.; Tan, Y.; Ding, Y.; Chen, D.; Wang, T. Influence of hole diameter on mechanical properties and stability of granite rock surrounding tunnels. Phys. Fluids 2023, 35, 064121. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, P.; Guo, W.; Gong, X.; Wang, C.; Chen, Y. Controlling roof with potential rock burst risk through different pre-crack length: Mechanism and effect research. J. Cent. South Univ. 2022, 29, 3706–3719. [Google Scholar] [CrossRef]
- Zou, Q.; Chen, Z.; Zhan, J.; Chen, C.; Gao, S.; Kong, F.; Xia, X. Morphological evolution and flow conduction charac-teristics of fracture channels in fractured sandstone under cyclic loading and unloading. Int. J. Min. Sci. Technol. 2023, 33, 1527–1540. [Google Scholar] [CrossRef]
- Li, M.; Peng, Y.; Zhang, J.; Zhu, C.; Ma, D.; Huang, P. Effects of compressive deformation of backfill materials on strata movement and stress evolution in deep gangue backfill mining. Bull. Eng. Geol. Environ. 2022, 81, 361. [Google Scholar] [CrossRef]
- Du, Z.; Sheng, S.; Guo, J. Effect of composite activators on mechanical properties, hydration activity and microstructure of red mud-based geopolymer. J. Mater. Res. Technol. 2023, 24, 8077–8085. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Song, T.; Kong, G.; Li, M. Analysis on filling ratio and shield supporting pressure for overburden movement control in coal mining with compacted backfilling. Energies 2017, 10, 31. [Google Scholar] [CrossRef]
- Zhou, N.; Jiang, H.Q.; Zhang, J.X. Application of solid backfill mining techniques for coal mine under embankment dam. Min. Technol. 2013, 122, 228–234. [Google Scholar] [CrossRef]
- Ma, C.; Li, H.; Zhang, P. Subsidence prediction method of solid backfilling mining with different filling ratios under thick unconsolidated layers. Arab. J. Geosci. 2017, 10, 511. [Google Scholar] [CrossRef]
- Sun, W.B.; Wang, Y.; Qiu, H.F.; Ding, Z.W. Numerical simulation study of strip filling for water-preserved coal mining. Environ. Sci. Pollut. Res. 2020, 27, 12899–12907. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Du, Z.; Zhang, Z.; Zhang, H.; Xia, Z.; Feng, F. Effects of chloride on the early mechanical properties and microstructure of gangue-cemented paste backfill. Constr. Build. Mater. 2020, 235, 117504. [Google Scholar] [CrossRef]
- Chen, S.; Du, Z.; Zhang, Z.; Yin, D.; Feng, F.; Ma, J. Effects of red mud additions on gangue-cemented paste backfill properties. Powder Technol. 2020, 367, 833–840. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, Y.; Wang, C.; Cui, B.; Guo, H.; Li, H.; Guo, Y. Effect of sulfate mine water on the durability of filling paste. Int. J. Green Energy 2018, 15, 864–873. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Li, F.; Wang, C. Force chains in top coal caving mining. Int. J. Rock Mech. Min. Sci. 2020, 12, 104218. [Google Scholar] [CrossRef]
- Cheng, Z.; Yang, S.; Li, L.; Zhang, L. Support working resistance determined on top-coal caving face based on coal-rock combined body. Geomech. Eng. 2019, 19, 255–268. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Y.; Li, X.; Wang, Z. Overlying strata movement and abutment pressure evolution process of fully mechanized top coal caving mining in extra thick coal seam. Geofluids 2021, 2021, 7839888. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, Z.; Ji, C.; Guo, Z.; Li, H. Research on the influence of the key stratum position on the support working resistance during large mining height top-coal caving mining. Adv. Civ. Eng. 2021, 2021, 6690280. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, H.; Nemcik, J.; Lan, T.; Han, J.; Chen, Y. Overburden movement characteristics of top-coal caving mining in multi-seam areas. Q. J. Eng. Geol. Hydrogeol. 2018, 51, 276–286. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, X. Study of the evolution of water-conducting fracture zones in overlying rock of a fully mechanized caving face in gently inclined extra-thick coal seams. Appl. Sci. 2022, 12, 9057. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Z.; Guo, G.; Wei, W.; Wang, F.; Zhong, L.; Gong, Y. Study on regional strata movement during deep mining of erdos coal field and its control. Int. J. Environ. Res. Public Health 2022, 19, 14902. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, C.; Liu, Y.; Xu, J.; Wang, T.; Li, Y.; Liu, Q. Exploration and improvement of fuzzy evaluation model for rockburst. Min. Metall. Explor. 2024, 41, 559–587. [Google Scholar] [CrossRef]
- Fan, D.; Liu, X.; Tan, Y.; Li, X.; Lkhamsuren, P. Instability energy mechanism of super-large section crossing chambers in deep coal mines. Int. J. Min. Sci. Technol. 2022, 32, 1075–1086. [Google Scholar] [CrossRef]
- Xue, Y. Study on the movement and deformation law of overlying strata in filling working face under different filling rates. Eng. Adv. 2023, 3, 52–55. [Google Scholar] [CrossRef]
- Xu, B.; Yang, R.; Li, Y.; Lu, B.; Luo, H.; Li, C. Three measurement relalionship and conlrol principle of overburden movement in cemenled filling. J. China Coal Soc. 2022, 47, 49–60. [Google Scholar] [CrossRef]





| No. | Name | Unit Weight (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | Cohesive Force (MPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|---|
| 1 | Coarse sandstone | 2500 | 25 | 0.27 | 2.4 | 3.2 | 29.5 |
| 2 | Fine sandstone | 2680 | 7.5 | 0.33 | 1.7 | 1.9 | 24 |
| 3 | Siltstone | 2550 | 11 | 0.34 | 2.1 | 1.2 | 26 |
| 4 | Medium-grained sandstone | 2160 | 15 | 0.31 | 2.4 | 2.1 | 28 |
| 5 | Coal | 1350 | 1.1 | 0.32 | 1 | 1.5 | 23 |
| 6 | Carbonaceous mudstone | 2580 | 8 | 0.38 | 1.5 | 1.2 | 25.5 |
| 7 | Mudstone | 2461 | 9 | 0.26 | 1.2 | 1,3 | 30 |
| 8 | Siltstone | 2550 | 11 | 0.34 | 2.1 | 1.2 | 26 |
| 9 | Coarse sandstone | 2500 | 25 | 0.27 | 2.4 | 3.2 | 29.5 |
| 10 | Backfill | 2450 | 1.2 | 0.32 | 1.8 | 3.3 | 23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Z.; Chen, D.; Li, X.; Jian, Y.; Zhang, W.; Zhang, D.; Tian, Y. Study on the Partial Paste Backfill Mining Method in a Fully Mechanized Top-Coal Caving Face: Case Study from a Coal Mine, China. Sustainability 2024, 16, 4393. https://doi.org/10.3390/su16114393
Du Z, Chen D, Li X, Jian Y, Zhang W, Zhang D, Tian Y. Study on the Partial Paste Backfill Mining Method in a Fully Mechanized Top-Coal Caving Face: Case Study from a Coal Mine, China. Sustainability. 2024; 16(11):4393. https://doi.org/10.3390/su16114393
Chicago/Turabian StyleDu, Zhaowen, Deyou Chen, Xuelong Li, Yong Jian, Weizhao Zhang, Dingding Zhang, and Yongfeng Tian. 2024. "Study on the Partial Paste Backfill Mining Method in a Fully Mechanized Top-Coal Caving Face: Case Study from a Coal Mine, China" Sustainability 16, no. 11: 4393. https://doi.org/10.3390/su16114393
APA StyleDu, Z., Chen, D., Li, X., Jian, Y., Zhang, W., Zhang, D., & Tian, Y. (2024). Study on the Partial Paste Backfill Mining Method in a Fully Mechanized Top-Coal Caving Face: Case Study from a Coal Mine, China. Sustainability, 16(11), 4393. https://doi.org/10.3390/su16114393







