The Development of Modeling Shared Spaces to Support Sustainable Transport Systems: Introduction to the Integrated Pedestrian–Vehicle Model (IPVM)
Abstract
1. Introduction
2. Literature Review
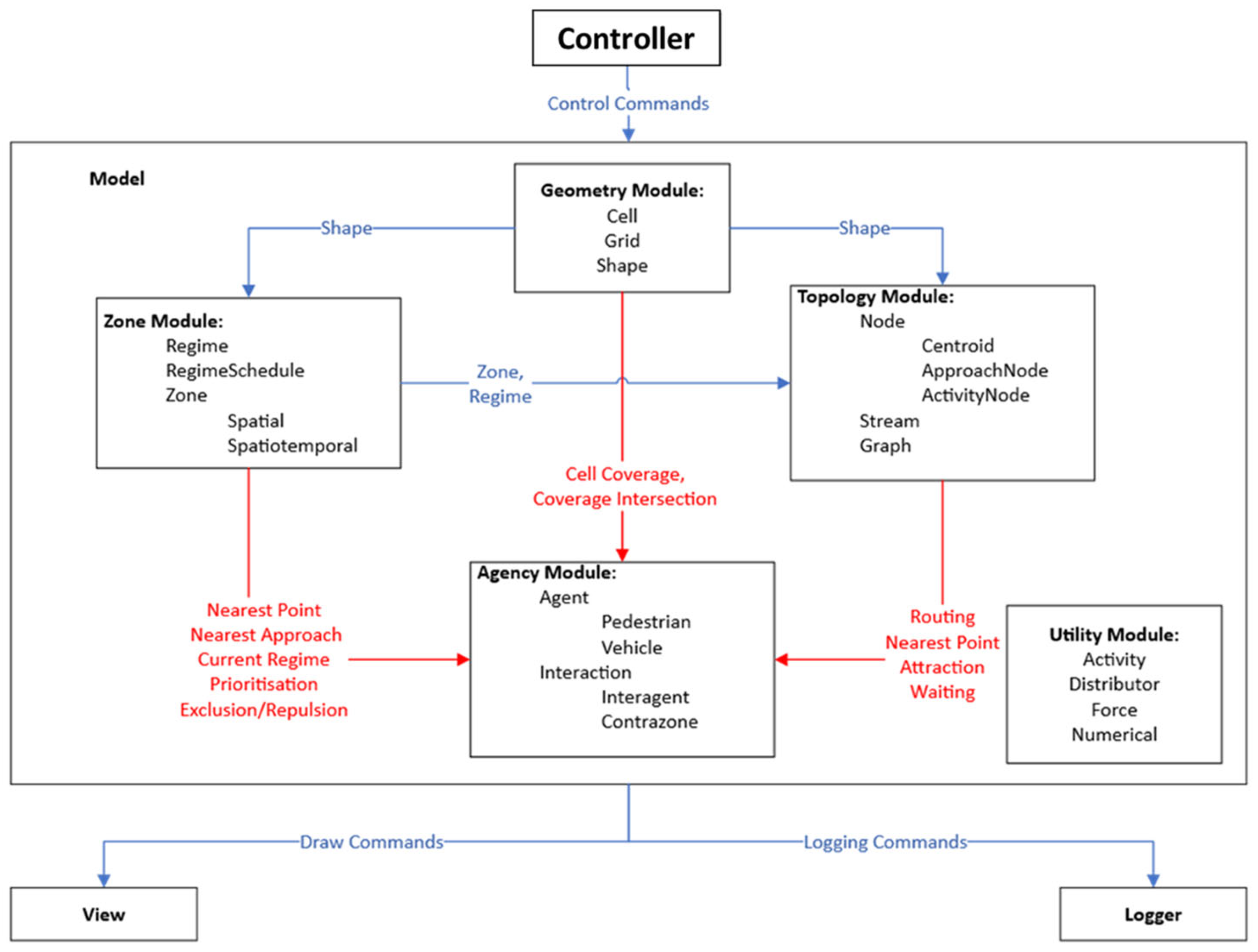
3. Novel Shared Space Modelling Framework: The IPVM
3.1. Integration of Models
- A pedestrian SFM;
- Waiting models such as those published in [50];
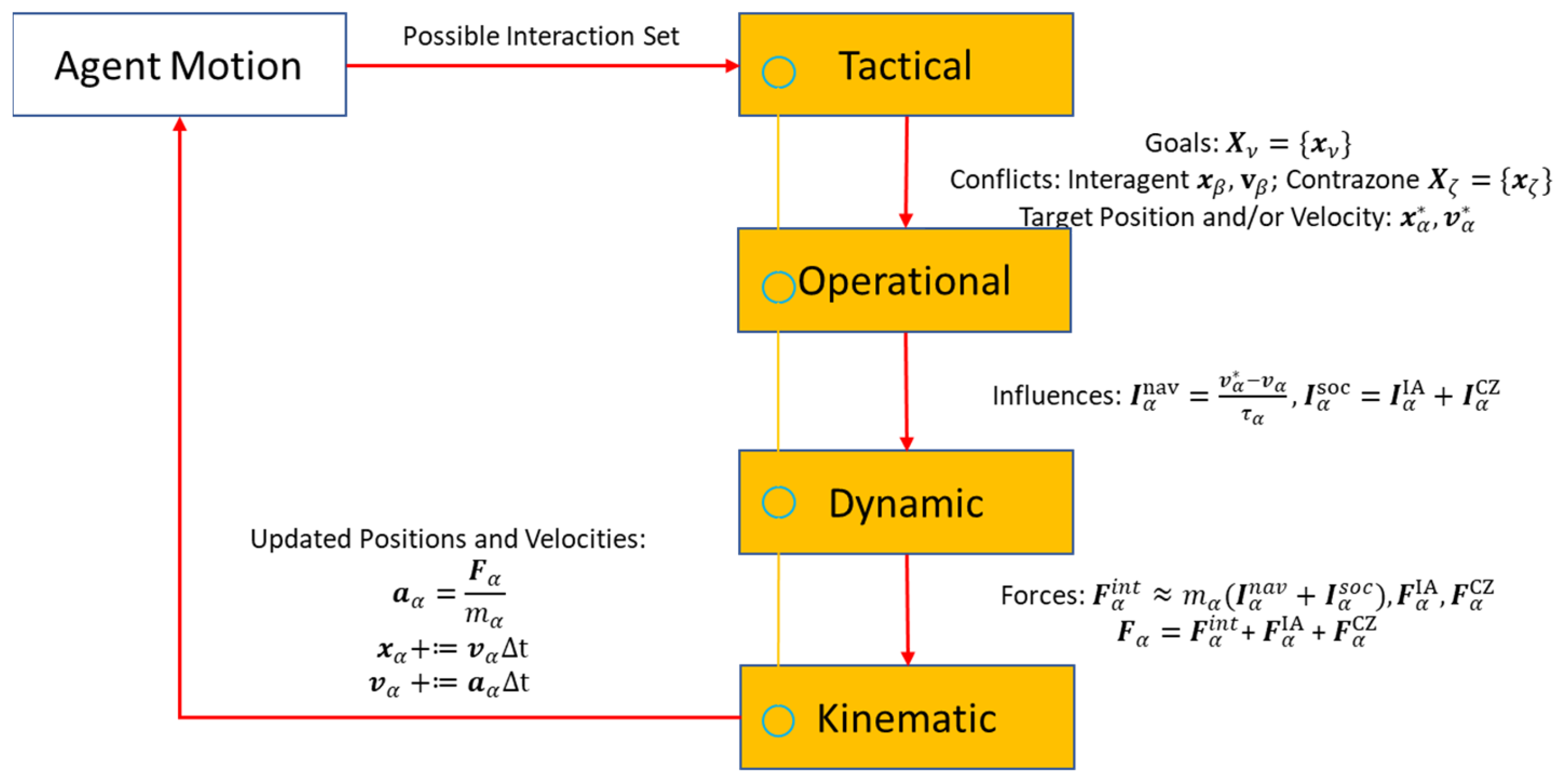
3.2. Agent Interactions and Conflicts
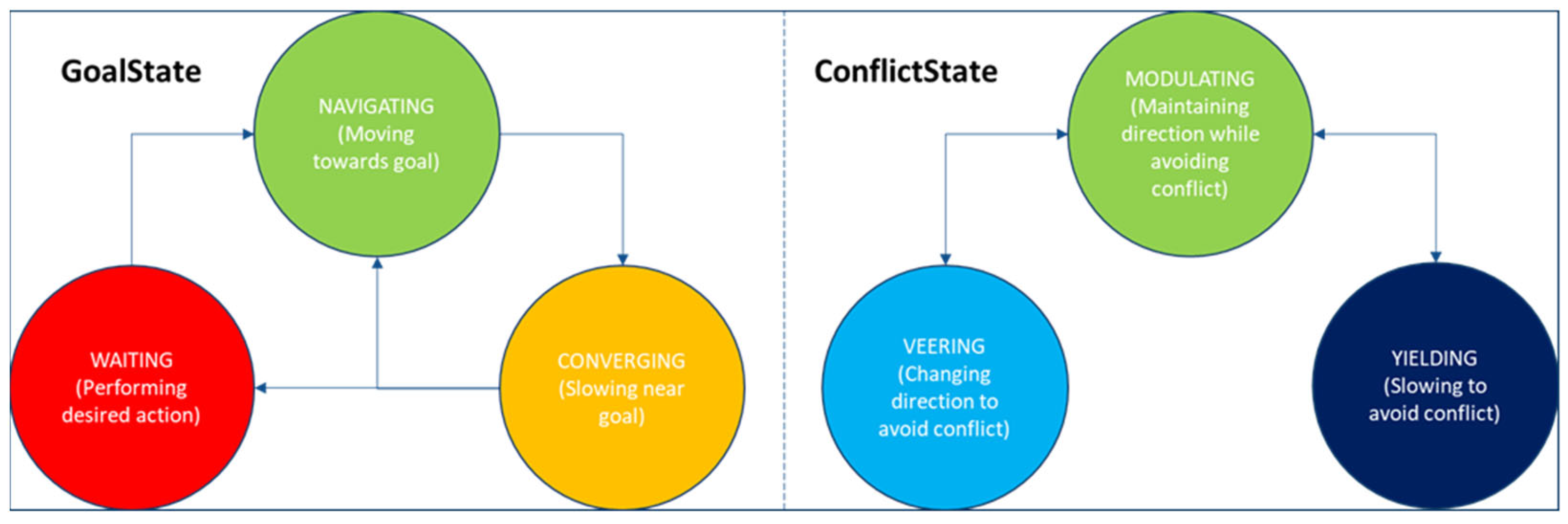
3.3. Agent States and Policies
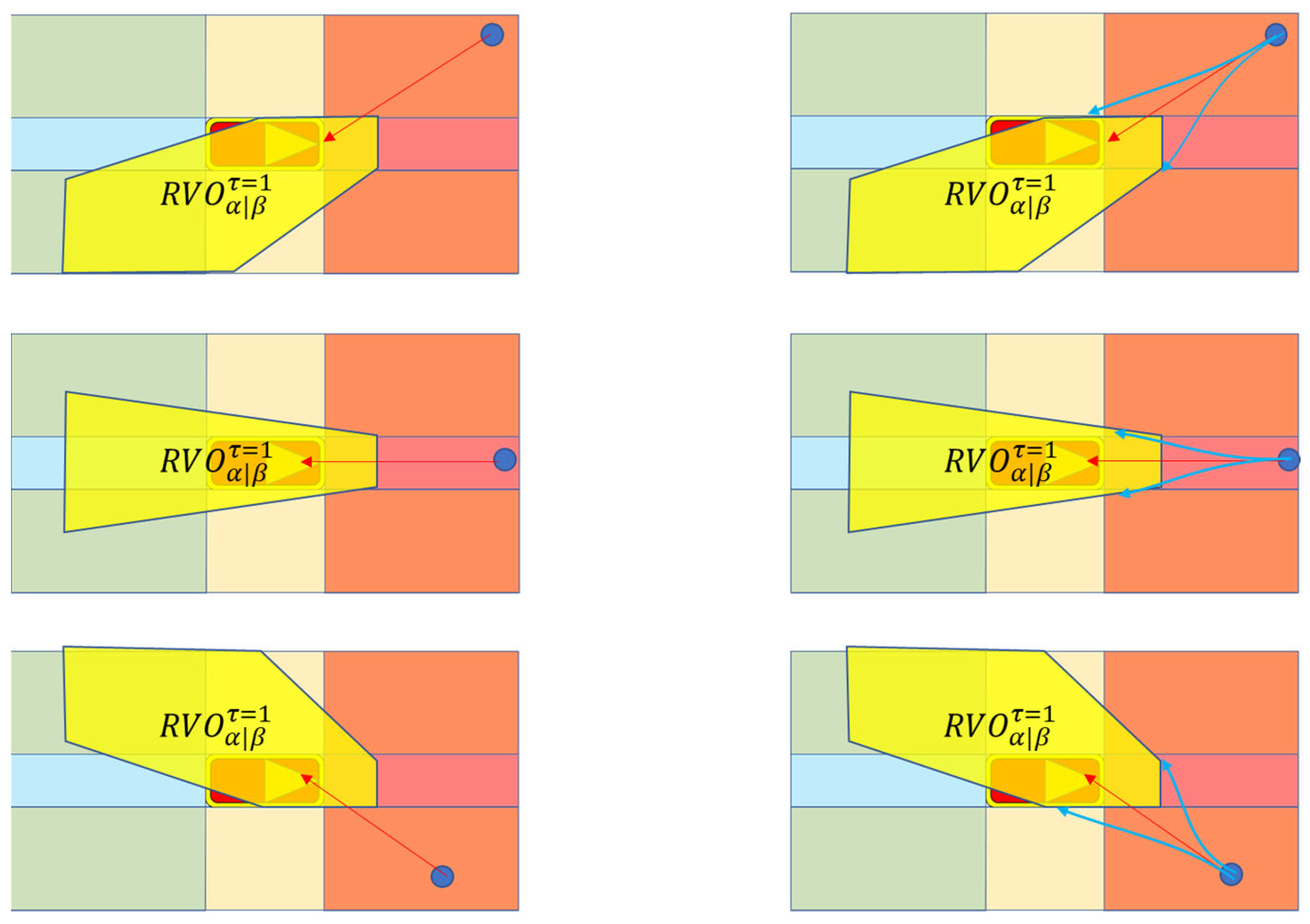
3.4. Positional Conflict Avoidance
3.5. Motion Curves
- Choosing a limited number of target positions and velocities depending on the agents’ positions and velocities;
- Constructing cubic splines which are close to elasticas using criteria derived from Brander et al. [61];
- Estimating the arc length and (curvature) energy of these splines using the algorithm of Gravesen [62];
- Estimating the time required to follow the splines from the estimated arc length, estimated energy, agent velocity, and agent maximum angular velocity;
- Rejecting any spline trajectory which cannot be completed within the time available until impact.
3.6. Veloci-Centric Conflict Avoidance
3.7. Kinematic Constraints
3.8. Model Functionality
4. Discussion
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
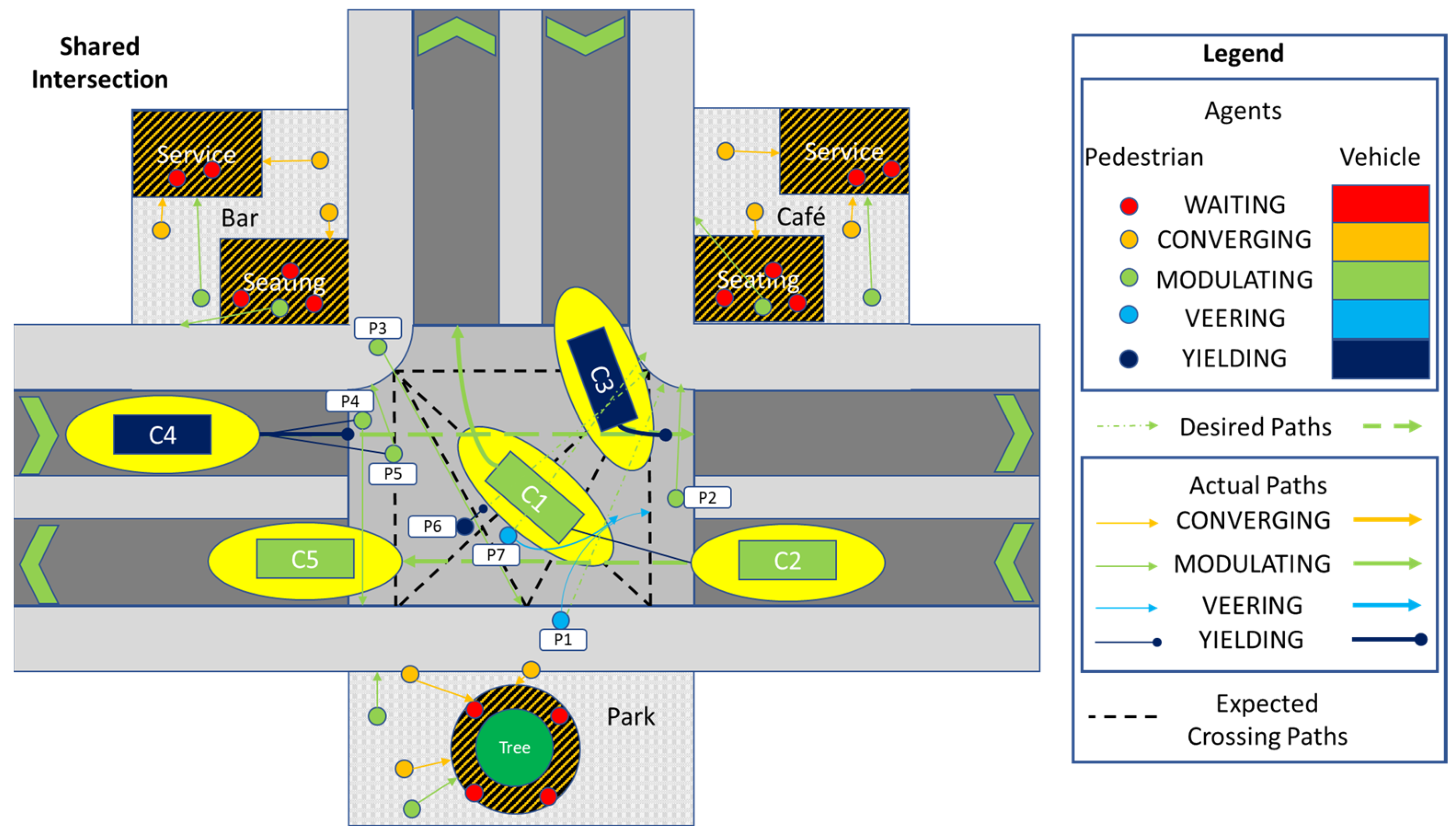
Appendix A. Explanation of Figure 1
| Reference Code | Authorship | Title | Numbered Citation |
|---|---|---|---|
| ABAO 14 | Anvari, Bell, Angeloudis, Ochieng (2014) | Long-range Collision Avoidance for Shared Space Simulation based on Social Forces | [59] |
| ABSO 15 | Anvari, Bell, Sivakumar, Ochieng (2015) | Modelling shared space users via rule-based social force model | [21] |
| ADK+ 13 | Anvari, Daamen, Knoop, Hoogendoorn, Bell (2012) | Shared Space Modeling Based on Social Forces and Distance Potential Field | [67] |
| AGDO 23 | Alligier, Gianazza, Durand, Olive (2023) | Dual-Horizon Reciprocal Collision Avoidance for Aircraft and Unmanned Aerial Systems | [38] |
| BB 13 | Bareiss and van den Berg (2013) | Reciprocal collision avoidance for robots with linear dynamics using LQR-Obstacles | [68] |
| BB 15 | Bareiss and van den Berg (2015) | Generalized reciprocal collision avoidance | [33] |
| BA 98 | Blue and Adler (1998) | Emergent Fundamental Pedestrian Flows from Cellular Automata Microsimulation | [69] |
| BA 99 | Blue and Adler (1999) | Cellular Automata Microsimulation of Bidirectional Pedestrian Flows | [70] |
| BLM 08 | van den Berg, Lin, Manocha (2008) | Reciprocal Velocity Obstacles for real-time multi-agent navigation | [13] |
| BGLM 09 | van den Berg, Guy, Lin, Manocha (2009) | Reciprocal n-Body Collision Avoidance | [31] |
| BSGM 11 | van den Berg, Snape, Guy, Manocha. (2011) | Reciprocal collision avoidance with acceleration-velocity obstacles | [14] |
| BP 11 | Baglietto and Parisi (2011) | Continuous-space automaton model for pedestrian dynamics | [71] |
| CHD 07 | Campanella, Hoogendoorn, Daamen (2007) | Microsimulation model of hybrid time-based and event driven management of pedestrians | [72] |
| CHD 14 | Campanella, Hoogendoorn, Daamen (2014) | The nomad model: Theory, developments and applications | [73] |
| CSS 10 | Chraibi, Seyfried, Schadschneider (2010) | Generalized centrifugal-force model for pedestrian dynamics | [74] |
| CZGM 13 | Curtis, Zafar, Gutub, Manocha (2013) | Right of way | [46] |
| D 18 | Durand (2018) | Constant speed optimal reciprocal collision avoidance | [36] |
| DCN+ 13 | Dutra, Cavalcante-Neto, Vidal, Musse (2013) | A Multipotential Field Model for Crowds with Scalable Behaviors | [41] |
| GNCL 13 | Golas, Narain, Curtis, Lin (2014) | Hybrid Long-Range Collision Avoidancefor Crowd Simulation | [42] |
| H 10 | Hartmann (2010) | - | [75] |
| HB 03 | Hoogendoorn and Bovy (2003) | Simulation of pedestrian flows by optimal control and differential games | [51] |
| HB 04 | Hoogendoorn and Bovy (2004ab) | Pedestrian route-choice and activity scheduling theory and models Dynamic user-optimal assignment in continuous time and space | [52,76] |
| HBJW 05 | Helbing, Buzna, Johansson, Werner (2005) | Self-Organized Pedestrian Crowd Dynamics: Experiments, Simulations, and Design Solutions | [18] |
| HFV 00 | Helbing, Farkas, Vicsek (2000) | Freezing by heating in a driven mesoscopic system | [17] |
| HKM 97 | Helbing, Keltsch, Molnár (1997) | Modelling the evolution of human trail systems | [77] |
| HJT 05 | Helbing, Jiang, Treiber (2005) | Analytical investigation of oscillations in intersecting flows of pedestrian and vehicle traffic | [48] |
| HM 95 | Helbing and Molnár (1995) | Social force model for pedestrian dynamics | [9] |
| HT 98 | Helbing and Tilch (1998) | Generalized force model of traffic dynamics | [19] |
| IN 07 | Ishaque and Noland (2007) | Behavioural Issues in Pedestrian Speed Choice and Street Crossing Behaviour: A Review | [78] |
| JHS 08 | Johansson, Helbing, Shukla (2008) | Specification of the social force pedestrian model by evolutionary adjustment to video tracking data | [79] |
| JM 18 | Johora and Müller (2018) | GSFM | [20] |
| JM 20 | Johora and Müller (2020) | Zone-Specific Interaction Modeling of Pedestrians and Cars in Shared Spaces | [28] |
| JPT 15 | Johansson, Peterson, Trapani (2015) | Waiting pedestrians in the social force model | [50] |
| KTH 07 | Kesting, Treiber, Helbing (2007) | General Lane-Changing Model MOBIL for Car-Following Models | [80] |
| KTH 10 | Kesting, Treiber, Helbing (2010) | Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity | [81] |
| KGL+ 14 | Kim, Guy, Liu, Wilkie, Lau, Lin, Manocha (2014) | BRVO: Predicting pedestrian trajectories using velocity-space reasoning | [43] |
| KGH+ 11 | Kretz, Große, Hengst, Kautzsch, Pohlmann, Vortisch (2011) | Quickest Paths in Simulations of Pedestrians | [82] |
| K 09 | Kretz (2009) | Pedestrian traffic: on the quickest path | [83] |
| KHB 13 | Kneidl, Hartmann, Borrmann (2013) | A hybrid multi-scale approach for simulation of pedestrian dynamics | [84] |
| KP 04 | Kluge and Prässler (2004) | Reflective navigation: individual behaviors and group behaviors | [85] |
| KP 06 | Kluge and Prässler (2006) | Recursive Probabilistic Velocity Obstacles for Reflective Navigation | [29] |
| KTG 13 | Köster, Treml, Gödel (2013) | Avoiding numerical pitfalls in social force models | [64] |
| LJXC+ 18 | Liu, Jiang, Xu, Cheng, Xie, Lin (2018) | Avoidance of High-Speed Obstacles Based on Velocity Obstacles | [86] |
| LKF 05 | Lakoba, Kaup, Finkelstein (2005) | Modifications of the Helbing-Molnár-Farkas-Vicsek Social Force Model for Pedestrian Evolution | [87] |
| MH+ 09 | Moussaïd, Helbing, Garnier, Johansson, Combe, Theraulaz (2009) | Experimental study of the behavioural mechanisms underlying self-organization in human crowds | [88] |
| MHT 11 | Moussaïd, Helbing, Theraulaz (2011) | How simple rules determine pedestrian behavior and crowd disasters | [53] |
| MPGHT 10 | Moussaïd, Perozo, Garnier, Helbing, Theraulaz (2010) | The walking behaviour of pedestrian social groups and its impact on crowd dynamics | [89] |
| MMW 18ab | Ma, Manocha, Wang (2018ab) | Efficient Reciprocal Collision Avoidance between Heterogeneous Agents Using CTMAT, AutoRVO: Local Navigation with Dynamic Constraints in Dense Heterogeneous Traffic | [44,45] |
| NMH 21 | Niu, Ma, Han (2021) | Directional optimal reciprocal collision avoidance | [37] |
| PRSFB 15 | Pascucci, Rinke, Schiermeyer, Friedrich, Berkhahn (2015) | Modeling of Shared Space with Multi-modal Traffic using a Multi-layer Social Force Approach | [23] |
| PRSBF 17 | Pascucci, Rinke, Schiermeyer, Berkhahn, Friedrich (2017) | A discrete choice model for solving conflict situations between pedestrians and vehicles in shared space | [24] |
| PRY 13 | Park Rojas, Yang (2013) | A collision avoidance behavior model for crowd simulation based on psychological findings | [65] |
| R 87 | Reynolds (1987) | Flocks, herds and schools: A distributed behavioral model | [30] |
| RAMS 13 | Rufli, Alonso-Mora, Siegwart (2013) | Reciprocal Collision Avoidance With Motion Continuity Constraints | [15] |
| RCB+ 17 | Ren, Charambolous, Bruneau, Peng, Pettré (2017) | Analysis of the influence of detouring obstacle avoidance behavior on unidirectional flow | [47] |
| RSF 13 | Rudloff, Schönauer, Fellendorf (2013) | Comparing Calibrated Shared Space Simulation Model with Real-Life Data | [26] |
| RSPBF 17 | Rinke, Schiermeyer, Pascucci, Berkhahn, Friedrich (2017) | A multi-layer social force approach to model interactions in shared spaces using collision prediction | [25] |
| SBGM 11 | Snape, van den Berg, Guy, Manocha (2011) | The Hybrid Reciprocal Velocity Obstacle | [35] |
| SM 10 | Snape and Manocha (2010) | Navigating multiple simple-airplanes in 3D workspace | [34] |
| SSH+ 12 | Schönauer, Stubenschrott, Huang, Rudloff, Fellendorf (2012) | Modeling Concepts for Mixed Traffic: Steps toward a Microscopic Simulation Tool for Shared Space Zones | [8] |
| SPRBF 17 | Schiermeyer, Pascucci, Rinke, Berkhahn, Friedrich (2017) | Modeling and Solving of Multiple Conflict Situations in Shared Spaces | [27] |
| THH 00 | Treiber Hennecke Helbing (2000) | Congested traffic states in empirical observations and microscopic simulations | [56] |
| WBM 09 | Wilkie, van den Berg, Manocha (2009) | Generalized velocity obstacles | [32] |
| YCP+ 08 | Yeh, Curtis, Patil, van den Berg, Manocha, Lin (2008) | Composite agents. in Symposium on Computer Animation | [39] |
| ZZGJ 23 | Zhang, Zhang, Guo, Jiang (2023) | Analysis of the influence of detouring obstacle avoidance behavior on unidirectional flow | [49] |
References
- Hamilton-Baillie, B. Shared Space: Reconciling People, Places and Traffic. Built Environ. 2008, 34, 161–181. [Google Scholar] [CrossRef]
- Zeibots, M.E. Space, Time, Economics and Asphalt: An Investigation of Induced Traffic Growth Caused by Urban Motorway Expansion and the Implications It Has for the Sustainability of Cities. Ph.D. Thesis, University of Technology Sydney, Ultimo, Australia, 2007. [Google Scholar]
- Auckland City Council. Shared Space Guidelines; Auckland City Council: Auckland, New Zealand, 2017. Available online: https://infocouncil.aucklandcouncil.govt.nz (accessed on 18 September 2023).
- Firth, K. Removing traffic engineering control—The awkward truth? Traffic Eng. Control. 2011, 52, 73–79. [Google Scholar]
- Imrie, R. Universalism, universal design and equitable access to the built environment. Disabil. Rehabil. 2012, 34, 873–882. [Google Scholar] [CrossRef]
- Imrie, R. Auto-disabilities: The case of shared space environments. Environ. Plan. A 2012, 44, 2260–2277. [Google Scholar] [CrossRef]
- Holmes, C. Accidents by Design: The Holmes Report on “Shared Space” in the UnitedKingdom; London, UK, 2015; Available online: https://chrisholmes.co.uk/wp-content/uploads/2020/12/Holmes-Report-on-Shared-Space-.pdf (accessed on 15 July 2023).
- Schönauer, R.; Stubenschrott, M.; Huang, W.; Rudloff, C.; Fellendorf, M. Modeling Concepts for Mixed Traffic: Steps toward a Microscopic Simulation Tool for Shared Space Zones. Transp. Res. Rec. 2012, 2316, 114–121. [Google Scholar] [CrossRef]
- Helbing, D.; Molnár, P. Social force model for pedestrian dynamics. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1995, 51, 4282–4286. [Google Scholar] [CrossRef]
- Anvari, B. A New Microscopic Model for the Simulation of Shared Space Schemes; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Slack-Smith, D.G.; Wijayaratna, K.; Zeibots, M.E. Enhancing the modelling of shared spaces: Evolution of the Social Force Model. In Proceedings of the Australasian Transport Research Forum, Perth, Australia, 29 November–1 December 2023; Available online: https://australasiantransportresearchforum.org.au/wp-content/uploads/2022/05/ATRF_2023_Paper_80.pdf (accessed on 20 December 2023).
- Fiorini, P.; Shiller, Z. Time optimal trajectory planning in dynamic environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 1552, pp. 1553–1558. [Google Scholar]
- van den Berg, J.; Lin, M.; Manocha, D. Reciprocal Velocity Obstacles for real-time multi-agent navigation. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 1928–1935. [Google Scholar]
- van den Berg, J.; Snape, J.; Guy, S.J.; Manocha, D. Reciprocal collision avoidance with acceleration-velocity obstacles. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3475–3482. [Google Scholar]
- Rufli, M.; Alonso-Mora, J.; Siegwart, R. Reciprocal Collision Avoidance with Motion Continuity Constraints. IEEE Trans. Robot. 2013, 29, 899–912. [Google Scholar] [CrossRef]
- Saberi, M.; Mahmassani, H.S. Exploring Areawide Dynamics of Pedestrian Crowds: Three-Dimensional Approach. Transp. Res. Rec. 2014, 2421, 31–40. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.J.; Vicsek, T. Freezing by heating in a driven mesoscopic system. Phys. Rev. Lett. 2000, 84, 1240–1243. [Google Scholar] [CrossRef]
- Helbing, D.; Buzna, L.; Johansson, A.; Werner, T. Self-Organized Pedestrian Crowd Dynamics: Experiments, Simulations, and Design Solutions. Transp. Sci. 2005, 39, 1–24. [Google Scholar] [CrossRef]
- Helbing, D.; Tilch, B. Generalized force model of traffic dynamics. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1998, 58, 133–138. [Google Scholar] [CrossRef]
- Johora, F.T.; Muller, J.P. Modeling Interactions of Multimodal Road Users in Shared Spaces. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 3568–3574. [Google Scholar]
- Anvari, B.; Bell, M.G.H.; Sivakumar, A.; Ochieng, W.Y. Modelling shared space users via rule-based social force model. Transp. Research. Part C Emerg. Technol. 2015, 51, 83–103. [Google Scholar] [CrossRef]
- Anvari, B.; Bell, M.G.H.; Angeloudis, P.; Ochieng, W.Y. Calibration and Validation of a Shared Space Model: Case Study. Transp. Res. Rec. 2016, 2588, 43–52. [Google Scholar] [CrossRef]
- Pascucci, F.; Rinke, N.; Schiermeyer, C.; Friedrich, B.; Berkhahn, V. Modeling of Shared Space with Multi-modal Traffic using a Multi-layer Social Force Approach. Transp. Res. Procedia 2015, 10, 316–326. [Google Scholar] [CrossRef]
- Pascucci, F.; Rinke, N.; Schiermeyer, C.; Berkhahn, V.; Friedrich, B. A discrete choice model for solving conflict situations between pedestrians and vehicles in shared space. arXiv 2017, arXiv:1709.09412. [Google Scholar]
- Rinke, N.; Schiermeyer, C.; Pascucci, F.; Berkhahn, V.; Friedrich, B. A multi-layer social force approach to model interactions in shared spaces using collision prediction. Transp. Res. Procedia 2017, 25, 1249–1267. [Google Scholar] [CrossRef]
- Rudloff, C.; Schönauer, R.; Fellendorf, M. Comparing Calibrated Shared Space Simulation Model with Real-Life Data. Transp. Res. Rec. 2013, 2390, 44–52. [Google Scholar] [CrossRef]
- Schiermeyer, C.; Pascucci, F.; Rinke, N.; Berkhahn, V.; Friedrich, B. Modeling and Solving of Multiple Conflict Situations in Shared Spaces; Springer International Publishing: Cham, Switzerland, 2019; pp. 451–458. [Google Scholar]
- Johora, F.T.; Müller, J.P. Zone-Specific Interaction Modeling of Pedestrians and Cars in Shared Spaces. Transp. Res. Procedia 2020, 47, 251–258. [Google Scholar] [CrossRef]
- Kluge, B.; Prassler, E. Recursive Probabilistic Velocity Obstacles for Reflective Navigation. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 71–79. [Google Scholar]
- Reynolds, C. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- van den Berg, J.; Guy, S.J.; Lin, M.; Manocha, D. Reciprocal n-Body Collision Avoidance. In Robotics Research. Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–19. [Google Scholar]
- Wilkie, D.; van den Berg, J.; Manocha, D. Generalized velocity obstacles. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 5573–5578. [Google Scholar]
- Bareiss, D.; van den Berg, J. Generalized reciprocal collision avoidance. Int. J. Robot. Res. 2015, 34, 1501–1514. [Google Scholar] [CrossRef]
- Snape, J.; Manocha, D. Navigating multiple simple-airplanes in 3D workspace. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3974–3980. [Google Scholar]
- Snape, J.; van den Berg, J.; Guy, S.J.; Manocha, D. The Hybrid Reciprocal Velocity Obstacle. IEEE Trans. Robot. 2011, 27, 696–706. [Google Scholar] [CrossRef]
- Durand, N. Constant speed optimal reciprocal collision avoidance. Transp. Research. Part C Emerg. Technol. 2018, 96, 366–379. [Google Scholar] [CrossRef]
- Niu, H.; Ma, C.; Han, P. Directional optimal reciprocal collision avoidance. Robot. Auton. Syst. 2021, 136, 103705. [Google Scholar] [CrossRef]
- Alligier, R.; Gianazza, D.; Durand, N.; Olive, X. Dual-Horizon Reciprocal Collision Avoidance for Aircraft and Unmanned Aerial Systems. J. Intell. Robot. Syst. 2023, 107, 3. [Google Scholar] [CrossRef]
- Yeh, H.; Curtis, S.; Patil, S.; van den Berg, J.; Manocha, D.; Lin, M. Composite agents. In Proceedings of the 2008 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Dublin, Ireland, 7–9 July 2008; pp. 39–47. [Google Scholar]
- Curtis, S. Pedestrian Velocity Obstacles: Pedestrian Simulation through Reasoning in Velocity Space; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Dutra, T.B.; Cavalcante-Neto, J.B.; Vidal, C.A.; Musse, S.R. A Multipotential Field Model for Crowds with Scalable Behaviors. In Proceedings of the 2013 XXVI Conference on Graphics, Patterns and Images, Arequipa, Peru, 5–8 August 2013; pp. 31–38. [Google Scholar]
- Golas, A.; Narain, R.; Curtis, S.; Lin, M.C. Hybrid Long-Range Collision Avoidancefor Crowd Simulation. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1022–1034. [Google Scholar] [CrossRef]
- Kim, S.; Guy, S.J.; Liu, W.; Wilkie, D.; Lau, R.W.H.; Lin, M.C.; Manocha, D. BRVO: Predicting pedestrian trajectories using velocity-space reasoning. Int. J. Robot. Res. 2015, 34, 201–217. [Google Scholar] [CrossRef]
- Ma, Y.; Manocha, D.; Wang, W. Efficient Reciprocal Collision Avoidance between Heterogeneous Agents Using CTMAT. arXiv 2018, arXiv:1804.02512. [Google Scholar]
- Ma, Y.; Manocha, D.; Wang, W. AutoRVO: Local Navigation with Dynamic Constraints in Dense Heterogeneous Traffic. arXiv 2018, arXiv:1804.02915. [Google Scholar]
- Curtis, S.; Zafar, B.; Gutub, A.; Manocha, D. Right of way. Vis. Comput. 2013, 29, 1277–1292. [Google Scholar] [CrossRef]
- Ren, Z.; Charalambous, P.; Bruneau, J.; Peng, Q.; Pettré, J. Group Modeling: A Unified Velocity-Based Approach. Comput. Graph. Forum 2017, 36, 45–56. [Google Scholar] [CrossRef]
- Helbing, D.; Jiang, R.; Treiber, M. Analytical investigation of oscillations in intersecting flows of pedestrian and vehicle traffic. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 046130. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, P.; Guo, Y.; Jiang, X. Analysis of the influence of detouring obstacle avoidance behavior on unidirectional flow. Physica A 2023, 624, 128896. [Google Scholar] [CrossRef]
- Johansson, F.; Peterson, A.; Tapani, A. Waiting pedestrians in the social force model. Physica A 2015, 419, 95–107. [Google Scholar] [CrossRef]
- Hoogendoorn, S.; Bovy, P.H.L. Simulation of pedestrian flows by optimal control and differential games. Optim. Control Appl. Methods 2003, 24, 153–172. [Google Scholar] [CrossRef]
- Hoogendoorn, S.P.; Bovy, P.H.L. Pedestrian route-choice and activity scheduling theory and models. Transp. Res. Part B Methodol. 2004, 38, 169–190. [Google Scholar] [CrossRef]
- Moussaïd, M.; Helbing, D.; Theraulaz, G. How simple rules determine pedestrian behavior and crowd disasters. Proc. Natl. Acad. Sci. USA 2011, 108, 6884–6888. [Google Scholar] [CrossRef]
- Köster, G.; Hartmann, D.; Klein, W. Microscopic Pedestrian Simulations: From Passenger Exchange Times to Regional Evacuation; Springer: Berlin/Heidelberg, Germany, 2011; pp. 571–576. [Google Scholar]
- Yuan, Y.; Goñi-Ros, B.; van Oijen, T.P.; Daamen, W.; Hoogendoorn, S.P. Social Force Model Describing Pedestrian and Cyclist Behaviour in Shared Spaces. In Traffic and Granular Flow’17; Springer: Cham, Switzerland, 2019; pp. 477–486. [Google Scholar]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 1805–1824. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Anvari, B.; Bell, M.G.H.; Angeloudis, P.; Ochieng, W.Y. Long-range Collision Avoidance for Shared Space Simulation based on Social Forces. Transp. Res. Procedia 2014, 2, 318–326. [Google Scholar] [CrossRef]
- Levien, R.L. From Spiral to Spline: Optimal Techniques in Interactive Curve Design; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Brander, D.; Bærentzen, J.A.; Fisker, A.-S.; Gravesen, J. Bézier curves that are close to elastica. Comput. Aided Des. 2018, 104, 36–44. [Google Scholar] [CrossRef]
- Gravesen, J. Adaptive subdivision and the length and energy of Bézier curves. Comput. Geom. Theory Appl. 1997, 8, 13–31. [Google Scholar] [CrossRef]
- Nicholl, T.M.; Lee, D.T.; Nicholl, R.A. An efficient new algorithm for 2-D line clipping: Its development and analysis. ACM SIGGRAPH Comput. Graph. 1987, 21, 253–262. [Google Scholar] [CrossRef]
- Köster, G.; Treml, F.; Gödel, M. Avoiding numerical pitfalls in social force models. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 063305. [Google Scholar] [CrossRef]
- Park, J.H.; Rojas, F.A.; Yang, H.S. A collision avoidance behavior model for crowd simulation based on psychological findings. Comput. Animat. Virtual Worlds 2013, 24, 173–183. [Google Scholar] [CrossRef]
- Carlsen, L.; Bruggemann, R. The 17 United Nations’ sustainable development goals: A status by 2020. Int. J. Sustain. Dev. World Ecol. 2022, 29, 219–229. [Google Scholar] [CrossRef]
- Anvari, B.; Daamen, W.; Knoop, V.L.; Hoogendoorn, S.P.; Bell, M.G.H. Shared Space Modeling Based on Social Forces and Distance Potential Field; Springer International Publishing: Cham, Switzerland, 2013; pp. 907–916. [Google Scholar]
- Bareiss, D.; van den Berg, J. Reciprocal collision avoidance for robots with linear dynamics using LQR-Obstacles. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3847–3853. [Google Scholar]
- Blue, V.J.; Adler, J.L. Emergent Fundamental Pedestrian Flows from Cellular Automata Microsimulation. Transp. Res. Rec. 1998, 1644, 29–36. [Google Scholar] [CrossRef]
- Blue, V.J.; Adler, J.L. Cellular Automata Microsimulation of Bidirectional Pedestrian Flows. Transp. Res. Rec. 1999, 1678, 135–141. [Google Scholar] [CrossRef]
- Baglietto, G.; Parisi, D.R. Continuous-space automaton model for pedestrian dynamics. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 83, 056117. [Google Scholar] [CrossRef]
- Campanella, M.; Hoogendoorn, S.; Daamen, W. A hybrid time-based and event-driven management of pedestrians in micro-simulation models. In Proceedings of the 10th International Conference on Computers in Urban Planning and Urban Management, Foz do Iguaçu, Paraná, Brasil, 11–13 July 2007. [Google Scholar]
- Campanella, M.; Hoogendoorn, S.; Daamen, W. The nomad model: Theory, developments and applications. Transp. Res. Procedia 2014, 2, 462–467. [Google Scholar] [CrossRef]
- Chraibi, M.; Seyfried, A.; Schadschneider, A. Generalized centrifugal-force model for pedestrian dynamics. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 82, 046111. [Google Scholar] [CrossRef]
- Hartmann, D. Adaptive pedestrian dynamics based on geodesics. New J. Phys. 2010, 12, 043032. [Google Scholar] [CrossRef]
- Hoogendoorn, S.P.; Bovy, P.H.L. Dynamic user-optimal assignment in continuous time and space. Transp. Res. Part B Methodol. 2004, 38, 571–592. [Google Scholar] [CrossRef]
- Helbing, D.; Keltsch, J.; Molnár, P. Modelling the evolution of human trail systems. Nature 1997, 388, 47–50. [Google Scholar] [CrossRef]
- Ishaque, M.M.; Noland, R.B. Behavioural Issues in Pedestrian Speed Choice and Street Crossing Behaviour: A Review. Transp. Rev. 2008, 28, 61–85. [Google Scholar] [CrossRef]
- Johansson, A.; Helbing, D.; Shukla, P. Specification of the social force pedestrian model by evolutionary adjustment to video tracking data. Adv. Complex Syst. 2007, 10, 271–288. [Google Scholar] [CrossRef]
- Kesting, A.; Treiber, M.; Helbing, D. General Lane-Changing Model MOBIL for Car-Following Models: Traffic Flow Theory 2007. Transp. Res. Rec. 2007, 1999, 86–94. [Google Scholar] [CrossRef]
- Kesting, A.; Treiber, M.; Helbing, D. Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2010, 368, 4585–4605. [Google Scholar] [CrossRef]
- Kretz, T.; GroßE, A.; Hengst, S.; Kautzsch, L.; Pohlmann, A.; Vortisch, P. Quickest Paths in Simulations of Pedestrians. Adv. Complex Syst. 2011, 14, 733–759. [Google Scholar] [CrossRef]
- Kretz, T. Pedestrian traffic: On the quickest path. J. Stat. Mech. 2009, 2009, P03012. [Google Scholar] [CrossRef]
- Kneidl, A.; Hartmann, D.; Borrmann, A. A hybrid multi-scale approach for simulation of pedestrian dynamics. Transp. Res. Part C Emerg. Technol. 2013, 37, 223–237. [Google Scholar] [CrossRef]
- Kluge, B.; Prassler, E. Reflective navigation: Individual behaviors and group behaviors. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA ’04, New Orleans, NJ, USA, 26 April–1 May 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 4174, pp. 4172–4177. [Google Scholar]
- Liu, Z.; Jiang, Z.; Xu, T.; Cheng, H.; Xie, Z.; Lin, L. Avoidance of High-Speed Obstacles Based on Velocity Obstacles. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 7624–7630. [Google Scholar]
- Lakoba, T.I.; Kaup, D.J.; Finkelstein, N.M. Modifications of the Helbing-Molnár-Farkas-Vicsek Social Force Model for Pedestrian Evolution. Simulation 2005, 81, 339–352. [Google Scholar] [CrossRef]
- Moussaïd, M.; Helbing, D.; Garnier, S.; Johansson, A.; Combe, M.; Theraulaz, G. Experimental study of the behavioural mechanisms underlying self-organization in human crowds. Proc. R. Soc. B Biol. Sci. 2009, 276, 2755–2762. [Google Scholar] [CrossRef] [PubMed]
- Moussaïd, M.; Perozo, N.; Garnier, S.; Helbing, D.; Theraulaz, G. The walking behaviour of pedestrian social groups and its impact on crowd dynamics. PLoS ONE 2010, 5, e10047. [Google Scholar] [CrossRef]







| Agent Properties | Description | Relationship Properties | Description |
|---|---|---|---|
| Agent | Counteragent | ||
| Mass | Zone | ||
| Relaxation time (duration) | Obstacle | ||
| Desired position | Node | ||
| Current position | Distance function | ||
| Preferred speed | Nearest point | ||
| Desired speed | Relative position | ||
| Desired direction | Relative distance | ||
| Desired velocity | Relative direction | ||
| Current velocity | Unit normal | ||
| Current direction | Unit tangent | ||
| Length and width | Relative velocity | ||
| Preferred netto (bumper-to-bumper) distance | Effective radius | ||
| Current netto distance | Sum of radii | ||
| Excess speed | Magnitude | ||
| Heaviside function | Characteristic distance | ||
| Expected (future) position |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slack-Smith, D.; Wijayaratna, K.P.; Zeibots, M. The Development of Modeling Shared Spaces to Support Sustainable Transport Systems: Introduction to the Integrated Pedestrian–Vehicle Model (IPVM). Sustainability 2024, 16, 4227. https://doi.org/10.3390/su16104227
Slack-Smith D, Wijayaratna KP, Zeibots M. The Development of Modeling Shared Spaces to Support Sustainable Transport Systems: Introduction to the Integrated Pedestrian–Vehicle Model (IPVM). Sustainability. 2024; 16(10):4227. https://doi.org/10.3390/su16104227
Chicago/Turabian StyleSlack-Smith, Delilah, Kasun P. Wijayaratna, and Michelle Zeibots. 2024. "The Development of Modeling Shared Spaces to Support Sustainable Transport Systems: Introduction to the Integrated Pedestrian–Vehicle Model (IPVM)" Sustainability 16, no. 10: 4227. https://doi.org/10.3390/su16104227
APA StyleSlack-Smith, D., Wijayaratna, K. P., & Zeibots, M. (2024). The Development of Modeling Shared Spaces to Support Sustainable Transport Systems: Introduction to the Integrated Pedestrian–Vehicle Model (IPVM). Sustainability, 16(10), 4227. https://doi.org/10.3390/su16104227









