Resilient Urban Flood Management: A Multi-Objective Assessment of Mitigation Strategies
Abstract
1. Introduction
1.1. Future Challenges of Urban Flooding
1.2. The Term Urban Flooding
1.3. Mitigation Strategies regarding Urban Flooding
1.4. Study Objective
2. Materials and Methods
2.1. Study Site: Feldbach
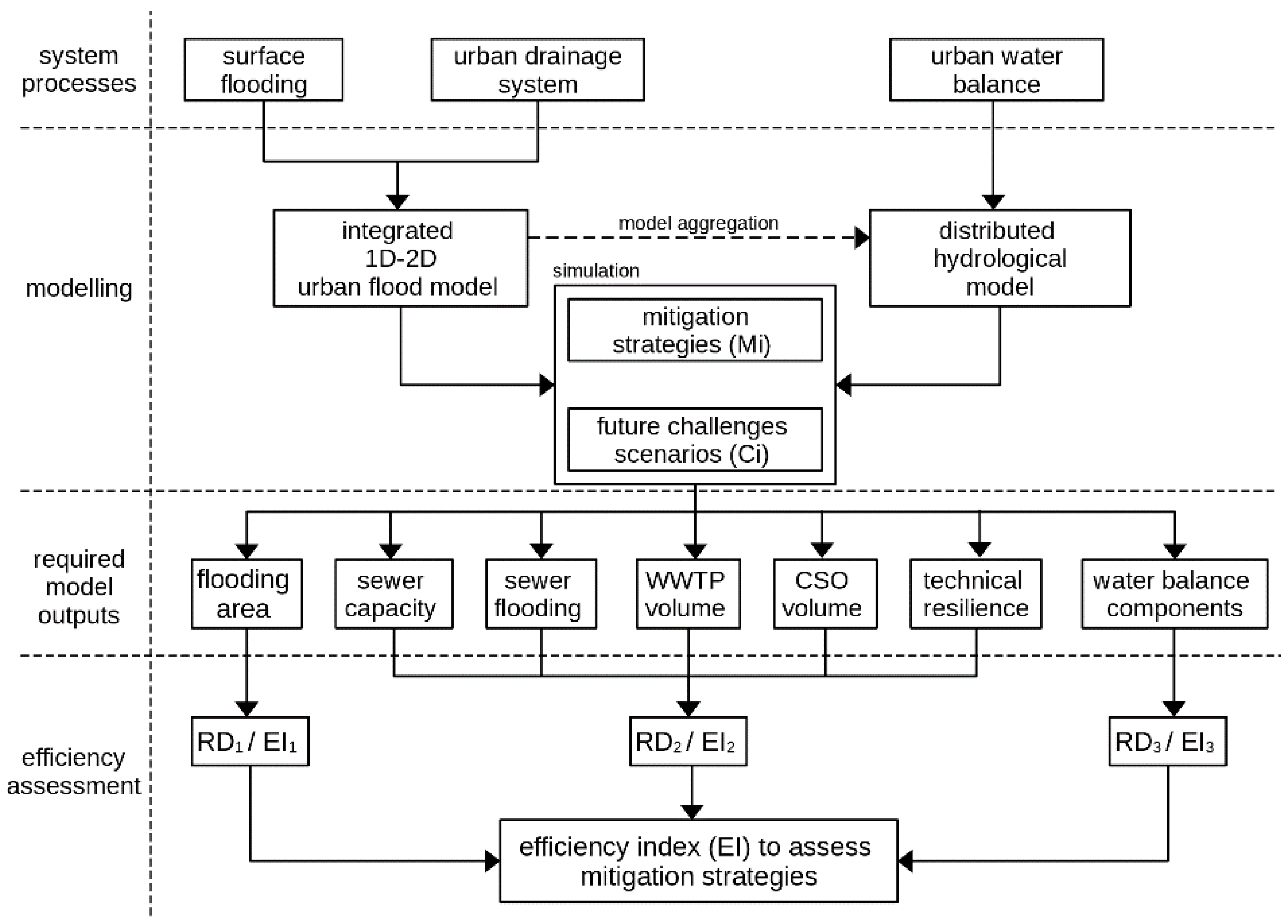
2.2. Assessment of Mitigation Strategies
2.2.1. Assessment regarding Surface Flooding
2.2.2. An Assessment of the Urban Drainage System
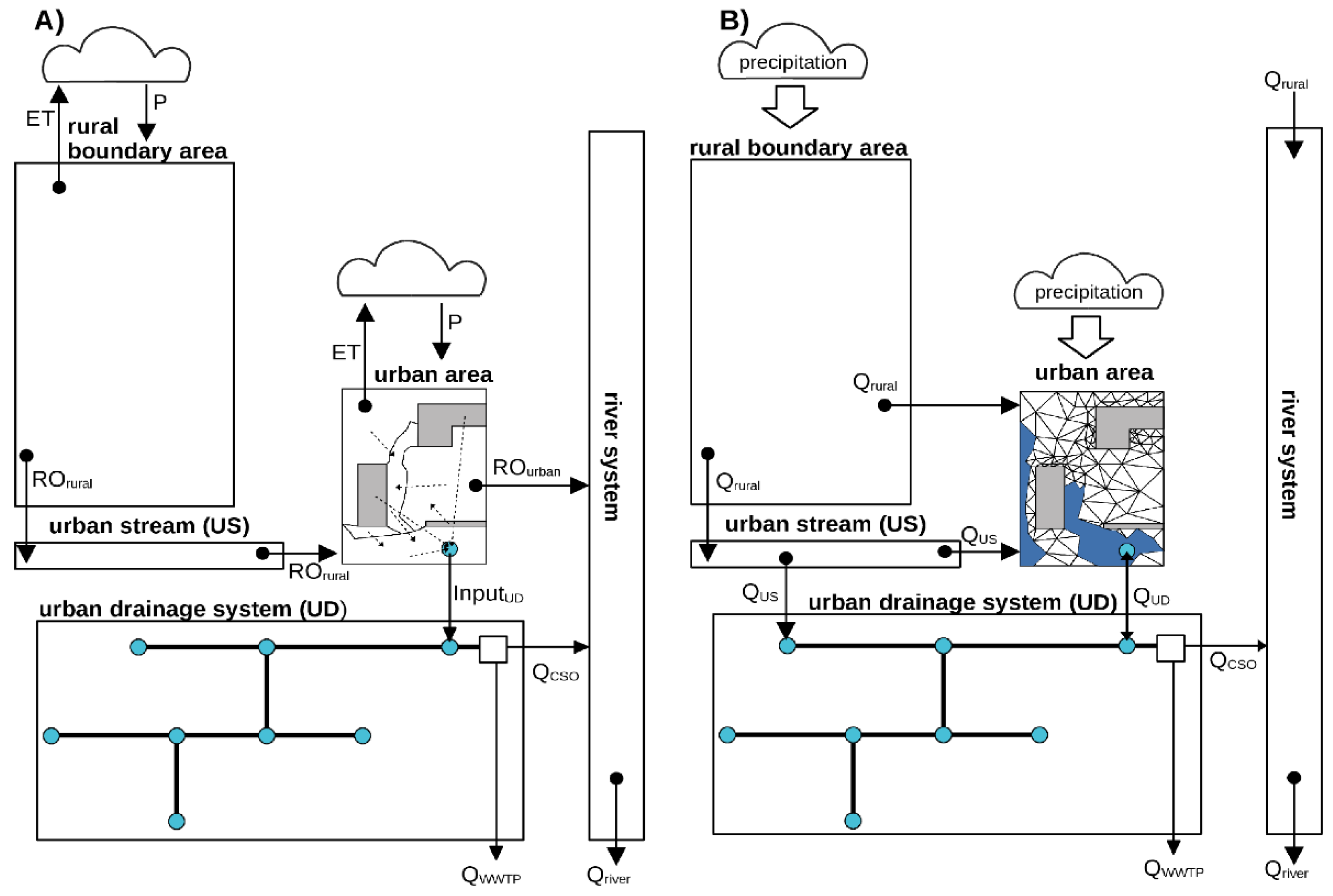
2.2.3. Hydrological Urban Water Balance to Assess the Sustainable Impact
2.2.4. A Combined Assessment of the Three Subparts of the Efficiency Index
2.3. Model Development
2.3.1. Integrated 1D–2D Urban Flood Model
2.3.2. Model Evaluation
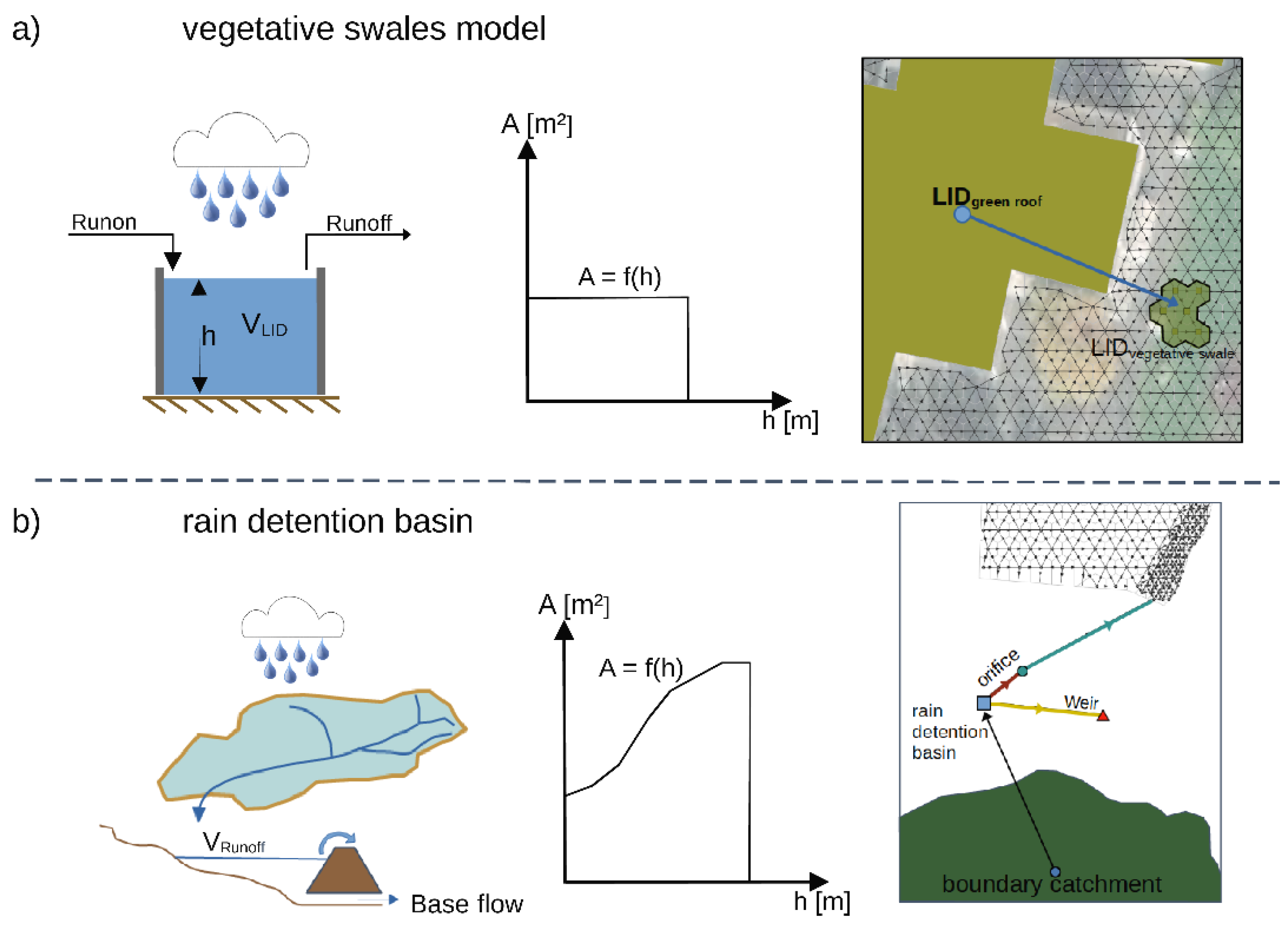
2.4. Mitigation Strategies
2.4.1. Modelling of Mitigation Strategies
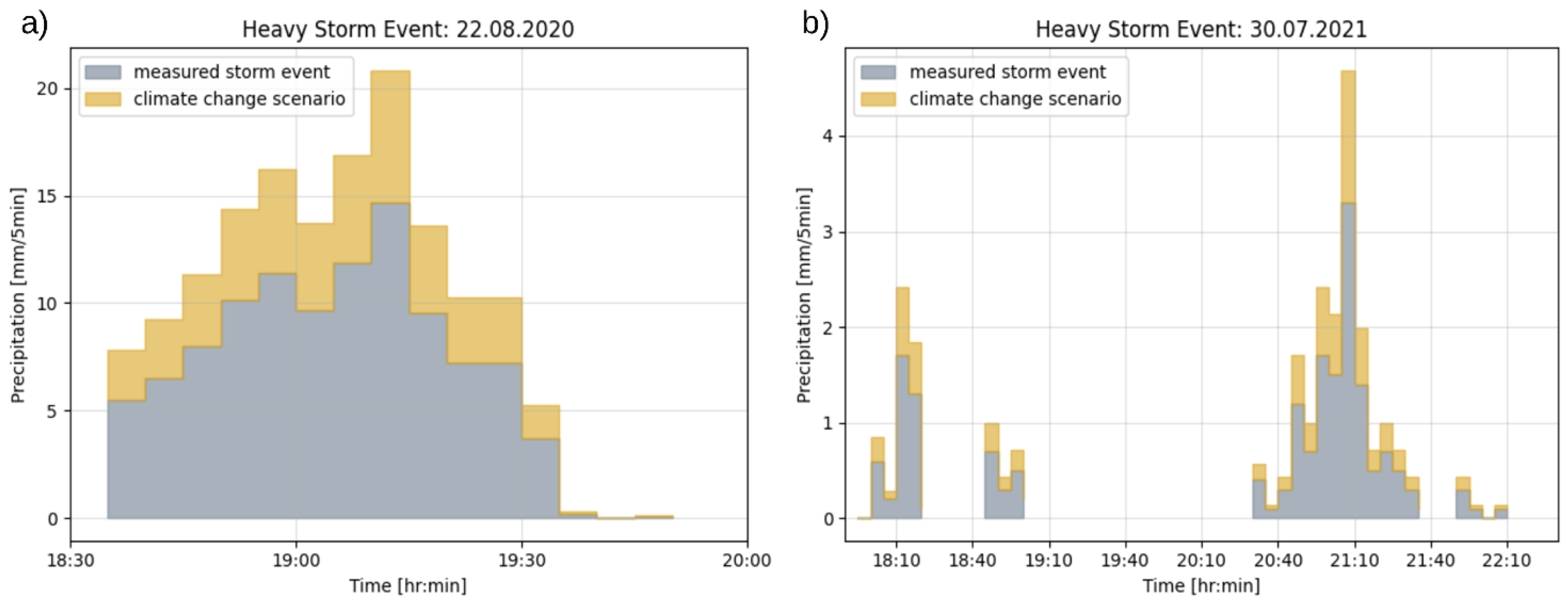
2.4.2. Future Challenge Scenarios
2.4.3. Hydrological Pre-Conditions
2.4.4. Simulation Scenarios
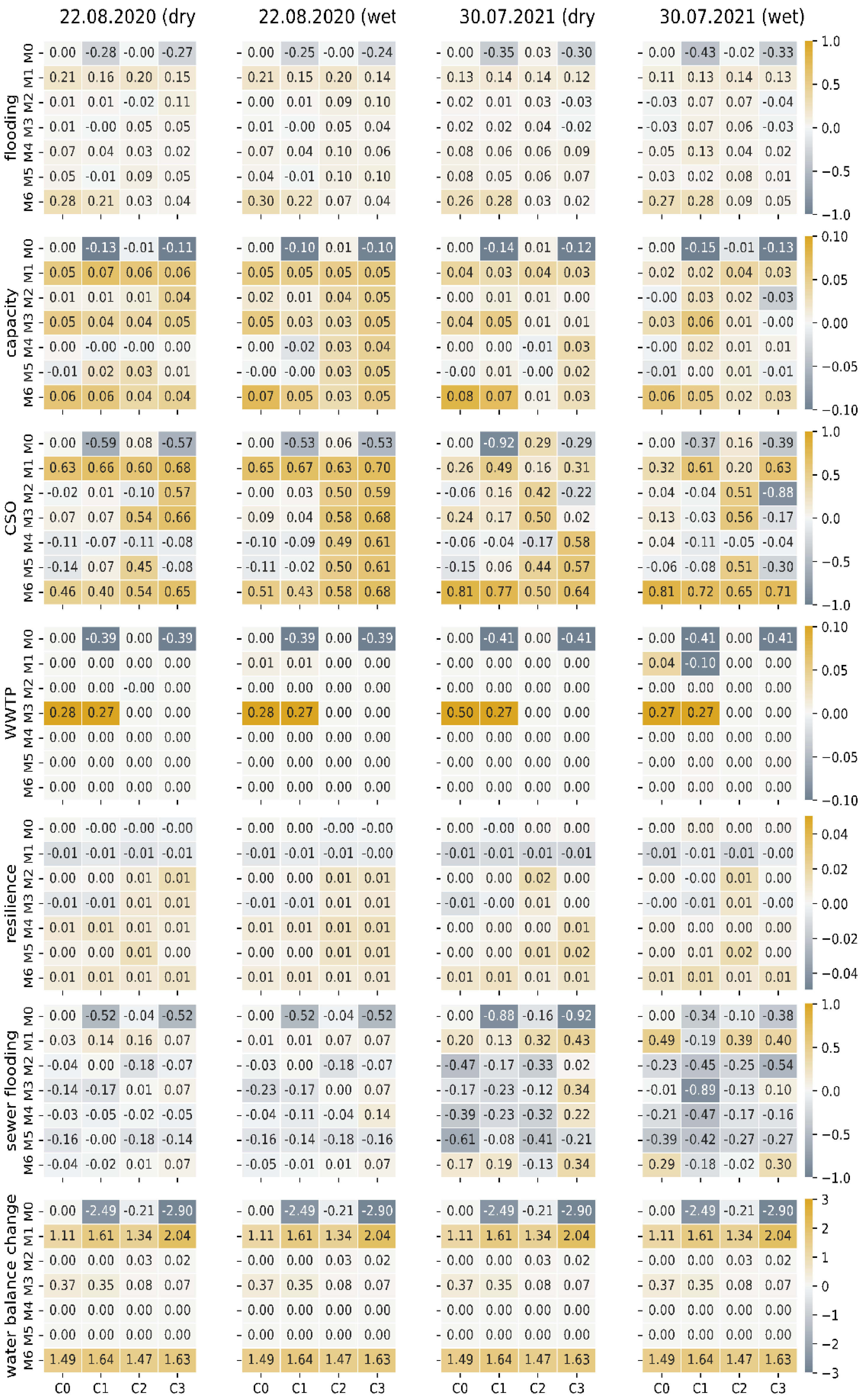
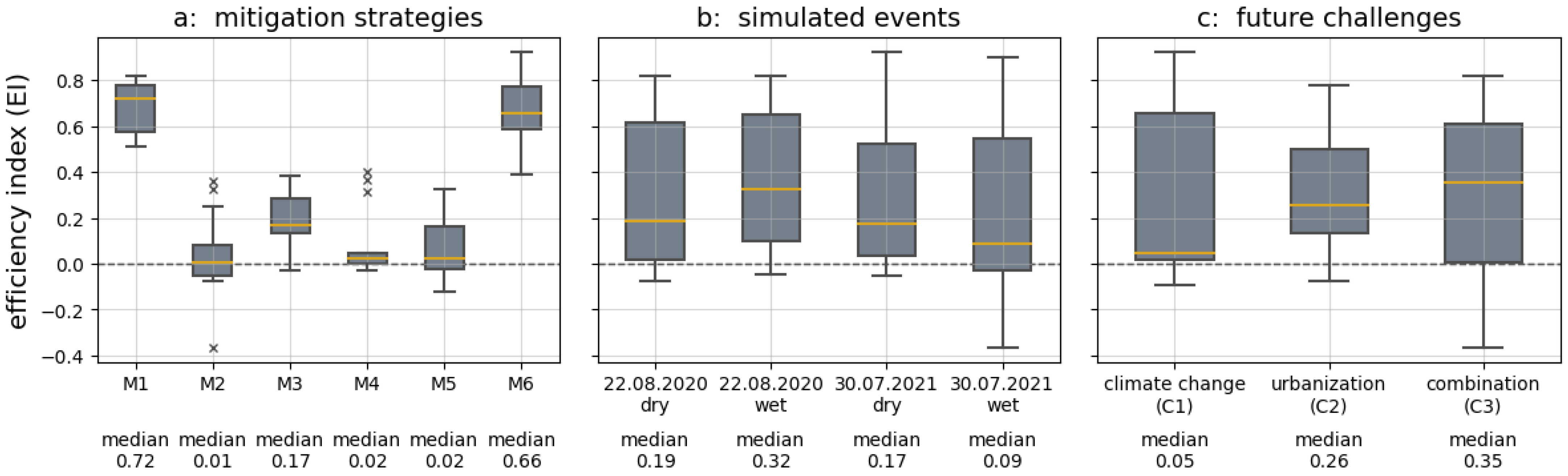
3. Results
4. Discussion
4.1. The Identification of the Most Effective Mitigation Strategy
4.2. Impact of Event Characteristic
4.3. Impact of Future Challenge Scenarios
4.4. Impact of Water Balance Change of Mitigation Strategies
4.5. Multi-Objective Assessment regarding Urban Flooding
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kundzewicz, Z.W.; Pińskwar, I.; Brakenridge, G.R. Changes in River Flood Hazard in Europe: A Review. Hydrol. Res. 2018, 49, 294–302. [Google Scholar] [CrossRef]
- Berndtsson, R.; Becker, P.; Persson, A.; Aspegren, H.; Haghighatafshar, S.; Jönsson, K.; Larsson, R.; Mobini, S.; Mottaghi, M.; Nilsson, J.; et al. Drivers of Changing Urban Flood Risk: A Framework for Action. J. Environ. Manag. 2019, 240, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Clarke, B.; Otto, F.; Stuart-Smith, R.; Harrington, L. Extreme Weather Impacts of Climate Change: An Attribution Perspective. Environ. Res. Clim. 2022, 1, 012001. [Google Scholar] [CrossRef]
- Bednar-Friedl, B.; Biesbroek, R.; Schmidt, D.N.; Alexander, P.; Børsheim, K.Y.; Carnicer, J.; Georgopoulou, E.; Haasnoot, M.; Cozannet, G.L.; Lionello, P.; et al. Europe. In Climate Change 2022: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; pp. 1817–1927. ISBN 978-1-00-932584-4. [Google Scholar]
- Berg, P.; Moseley, C.; Haerter, J. Strong Increase in Convective Precipitation in Response to Higher Temperature. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Rogers, R.R.; Rogers, R.R.; Yau, M.K.; Yau, M.K. A Short Course in Cloud Physics, 3rd ed.; International Series In Natural Philosophy, Reprint; Butterworth Heinemann: Woburn, MA, USA, 1996; ISBN 978-0-7506-3215-7. [Google Scholar]
- Maraun, D.; Knevels, R.; Mishra, A.; Truhetz, H.; Bevacqua, E.; Proske, H.; Zappa, G.; Brenning, A.; Petschko, H.; Schaffer, A.; et al. A Severe Landslide Event in the Alpine Foreland under Possible Future Climate and Land-Use Changes. Commun. Earth Environ. 2022, 3, 87. [Google Scholar] [CrossRef]
- Pfahl, S.; O’Gorman, P.A.; Fischer, E.M. Understanding the Regional Pattern of Projected Future Changes in Extreme Precipitation. Nat. Clim. Chang. 2017, 7, 423–427. [Google Scholar] [CrossRef]
- Hammond, M.J.; Chen, A.S.; Djordjević, S.; Butler, D.; Mark, O. Urban Flood Impact Assessment: A State-of-the-Art Review. Urban Water J. 2015, 12, 14–29. [Google Scholar] [CrossRef]
- UN. 68% of the World Population Projected to Live in Urban Areas by 2050, Says UN. Available online: https://www.un.org/development/desa/en/news/population/2018-revision-of-world-urbanization-prospects.html (accessed on 17 December 2020).
- Freddy, V.; El Mehdi Saidi, M.; Douvinet, D.; Fehri, N.; Nasrallah, W.; Menad, W.; Mellas, S. Urbanization and Land Use as a Driver of Flood Risk. In The Mediterranen Region under Climate Change; IRD Éditions/Institut de Recherche Pour le Développement Marseille: Marseille, France, 2016; pp. 563–575. ISBN 978-2-7099-2219-7. [Google Scholar]
- Mikovits, C.; Tscheikner-Gratl, F.; Jasper-Tönnies, A.; Einfalt, T.; Huttenlau, M.; Schöpf, M.; Kinzel, H.; Rauch, W.; Kleidorfer, M. Decision Support for Adaptation Planning of Urban Drainage Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017069. [Google Scholar] [CrossRef]
- Torelló-Sentelles, H.; Marra, F.; Peleg, N. Changing spatial patterns of convective rainfall across urban areas. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023. [Google Scholar] [CrossRef]
- Steensen, B.M.; Marelle, L.; Hodnebrog, Ø.; Myhre, G. Future Urban Heat Island Influence on Precipitation. Clim. Dyn. 2022, 58, 3393–3403. [Google Scholar] [CrossRef]
- O’Donnell, E.C.; Thorne, C.R. Drivers of Future Urban Flood Risk. Philos. Trans. R. Soc. A 2020, 378, 20190216. [Google Scholar] [CrossRef]
- Hosseinzadehtalaei, P.; Tabari, H.; Willems, P. Climate Change Impact on Short-Duration Extreme Precipitation and Intensity–Duration–Frequency Curves over Europe. J. Hydrol. 2020, 590, 125249. [Google Scholar] [CrossRef]
- Lee, E.H.; Lee, Y.S.; Joo, J.G.; Jung, D.; Kim, J.H. Flood Reduction in Urban Drainage Systems: Cooperative Operation of Centralized and Decentralized Reservoirs. Water 2016, 8, 469. [Google Scholar] [CrossRef]
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and Modeling of Flooding in Urban Drainage Systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.L.; et al. SUDS, LID, BMPs, WSUD and More—The Evolution and Application of Terminology Surrounding Urban Drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Zhou, L.; Guan, D.; Huang, X.; Yuan, X.; Zhang, M. Evaluation of the Cultural Ecosystem Services of Wetland Park. Ecol. Indic. 2020, 114, 106286. [Google Scholar] [CrossRef]
- Pinto, L.V.; Pereira, P.; Gazdic, M.; Ferreira, A.; Ferreira, C.S.S. Assessment of NBS Impact on Pluvial Flood Regulation Within Urban Areas: A Case Study in Coimbra, Portugal. In Nature-Based Solutions for Flood Mitigation: Environmental and Socio-Economic Aspects; Ferreira, C.S.S., Kalantari, Z., Hartmann, T., Pereira, P., Eds.; The Handbook of Environmental Chemistry; Springer International Publishing: Cham, Switzerland, 2022; pp. 289–312. ISBN 978-3-030-77505-6. [Google Scholar]
- Orta-Ortiz, M.; Geneletti, D. Reviewing the Performance of Nature-Based Solutions for Stormwater Management in Urban Areas. In Innovation in Urban and Regional Planning. INPUT 2021. Lecture Notes in Civil Engineering; La Rosa, D., Privitera, R., Eds.; Springer: Cham, Switzerland, 2021; Volume 146. [Google Scholar] [CrossRef]
- Apel, H.; Martínez Trepat, O.; Hung, N.N.; Chinh, D.T.; Merz, B.; Dung, N.V. Combined Fluvial and Pluvial Urban Flood Hazard Analysis: Concept Development and Application to Can Tho City, Mekong Delta, Vietnam. Nat. Hazards Earth Syst. Sci. 2016, 16, 941–961. [Google Scholar] [CrossRef]
- Qi, M.; Huang, H.; Liu, L.; Chen, X. An Integrated Approach for Urban Pluvial Flood Risk Assessment at Catchment Level. Water 2022, 14, 2000. [Google Scholar] [CrossRef]
- Qi, W.; Ma, C.; Xu, H.; Chen, Z.; Zhao, K.; Han, H. A Review on Applications of Urban Flood Models in Flood Mitigation Strategies. Nat. Hazards 2021, 108, 31–62. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Alamdari, N.; Tajrishy, M.; Ghanbari, S. Effectiveness of Retention Ponds for Sustainable Urban Flood Mitigation across Range of Storm Depths in Northern Tehran, Iran. J. Sustain. Water Built Environ. 2021, 7, 05021003. [Google Scholar] [CrossRef]
- Guido, B.I.; Popescu, I.; Samadi, V.; Bhattacharya, B. An Integrated Modeling Approach to Evaluate the Impacts of Nature-Based Solutions of Flood Mitigation across a Small Watershed in the Southeast United States. Nat. Hazards Earth Syst. Sci. 2023, 23, 2663–2681. [Google Scholar] [CrossRef]
- Ferreira, C.S.S.; Potočki, K.; Kapović-Solomun, M.; Kalantari, Z. Nature-Based Solutions for Flood Mitigation and Resilience in Urban Areas. In Nature-Based Solutions for Flood Mitigation: Environmental and Socio-Economic Aspects; Ferreira, C.S.S., Kalantari, Z., Hartmann, T., Pereira, P., Eds.; The Handbook of Environmental Chemistry; Springer International Publishing: Cham, Switzerland, 2022; pp. 59–78. ISBN 978-3-030-77505-6. [Google Scholar]
- Jacob, A.C.P.; Rezende, O.M.; de Sousa, M.M.; de França Ribeiro, L.B.; de Oliveira, A.K.B.; Arrais, C.M.; Miguez, M.G. Use of Detention Basin for Flood Mitigation and Urban Requalification in Mesquita, Brazil. Water Sci. Technol. 2019, 79, 2135–2144. [Google Scholar] [CrossRef]
- Liew, Y.S.; Mat Desa, S.; Md. Noh, M.N.; Tan, M.L.; Zakaria, N.A.; Chang, C.K. Assessing the Effectiveness of Mitigation Strategies for Flood Risk Reduction in the Segamat River Basin, Malaysia. Sustainability 2021, 13, 3286. [Google Scholar] [CrossRef]
- Abduljaleel, Y.; Salem, A.; ul Haq, F.; Awad, A.; Amiri, M. Improving Detention Ponds for Effective Stormwater Management and Water Quality Enhancement under Future Climate Change: A Simulation Study Using the PCSWMM Model. Sci. Rep. 2023, 13, 5555. [Google Scholar] [CrossRef]
- Nordbeck, R.; Steurer, R.; Löschner, L. The Future Orientation of Austria’s Flood Policies: From Flood Control to Anticipatory Flood Risk Management. J. Environ. Plan. Manag. 2019, 62, 1864–1885. [Google Scholar] [CrossRef]
- Kang, N.; Kim, S.; Kim, Y.; Noh, H.; Hong, S.J.; Kim, H.S. Urban Drainage System Improvement for Climate Change Adaptation. Water 2016, 8, 268. [Google Scholar] [CrossRef]
- Pour, S.H.; Wahab, A.K.A.; Shahid, S.; Asaduzzaman, M.; Dewan, A. Low Impact Development Techniques to Mitigate the Impacts of Climate-Change-Induced Urban Floods: Current Trends, Issues and Challenges. Sustain. Cities Soc. 2020, 62, 102373. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, L.; Hou, X.; Wei, G.; Zhang, X.; Shen, Z. Detailed Quantification of the Reduction Effect of Roof Runoff by Low Impact Development Practices. Water 2020, 12, 795. [Google Scholar] [CrossRef]
- Leimgruber, J. Model-Based Assessment of Cost-Effective Low Impact Development Strategies to Control Water Balance; Technischen Universität Graz: Graz, Austria, 2019. [Google Scholar]
- Keyvanfar, A.; Shafaghat, A.; Ismail, N.; Mohamad, S.; Ahmad, H. Multifunctional Retention Pond for Stormwater Management: A Decision-Support Model Using Analytical Network Process (ANP) and Global Sensitivity Analysis (GSA). Ecol. Indic. 2021, 124, 107317. [Google Scholar] [CrossRef]
- Liu, L.; Dobson, B.; Mijic, A. Optimisation of Urban-Rural Nature-Based Solutions for Integrated Catchment Water Management. J. Environ. Manag. 2023, 329, 117045. [Google Scholar] [CrossRef]
- Tamura, T. Improvement of the Flood-Reduction Function of Forests Based on Their Interception Evaporation and Surface Storage Capacities. In Green Infrastructure and Climate Change Adaptation: Function, Implementation and Governance; Nakamura, F., Ed.; Ecological Research Monographs; Springer Nature: Singapore, 2022; pp. 93–104. ISBN 9789811667916. [Google Scholar]
- Pudar, R.; Plavsic, J.; Todorovic, A. Evaluation of Green and Grey Flood Mitigation Measures in Rural Watersheds. Appl. Sci. 2020, 10, 6913. [Google Scholar] [CrossRef]
- Martínez Cano, C.; Sanchez Torres, A.; Toloh, B.; Vojinovic, Z. Multi-Objective Evaluation of Urban Drainage Networks Using a 1D/2D Flood Inundation Model. Water Resour. Manag. 2018, 32, 4329–4343. [Google Scholar] [CrossRef]
- Mugume, S.N.; Gomez, D.E.; Fu, G.; Farmani, R.; Butler, D. A Global Analysis Approach for Investigating Structural Resilience in Urban Drainage Systems. Water Res. 2015, 81, 15–26. [Google Scholar] [CrossRef]
- Li, J.; Strong, C.; Wang, J.; Burian, S. An Event-Based Resilience Index to Assess the Impacts of Land Imperviousness and Climate Changes on Flooding Risks in Urban Drainage Systems. Water 2023, 15, 2663. [Google Scholar] [CrossRef]
- Li, J.; Burian, S.J.; Johnson, R.C. Exploring Cost-Effective Implementation of Real-Time Control to Enhance Flooding Resilience against Future Rainfall and Land Cover Changes. Preprints 2023. [Google Scholar] [CrossRef]
- Rezende, O.M.; de Franco, A.B.R.; Oliveira, A.K.B.; Jacob, A.C.P.; Miguez, M.G. A Framework to Assess Urban Floods Resilience. In New Trends in Urban Drainage Modelling. UDM 2018; Mannina, G., Ed.; Springer: Cham, Switzerland, 2018; pp. 533–538. ISBN 978-3-319-99867-1. [Google Scholar]
- Martínez, C.; Vojinovic, Z.; Sanchez Torres, A. Multi-Objective Model-Based Assessment of Green-Grey Infrastructures for Urban Flood Mitigation. Hydrology 2021, 8, 110. [Google Scholar] [CrossRef]
- Reinstaller, S.; Funke, F.; Kleidorfer, M.; Muschalla, D. Maßnahmen zur urbanen Überflutungsprävention: Wirksamkeit von dezentraler Niederschlagswasserbewirtschaftung im Vergleich zu konventionellen Maßnahmen. Osterr. Wasser-Abfallwirtsch. 2023, 75, 626–633. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. Multi-Criteria Decision Making (MCDM) Methods and Concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Miguez, M.G.; Veról, A.P. A Catchment Scale Integrated Flood Resilience Index to Support Decision Making in Urban Flood Control Design. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 925–946. [Google Scholar] [CrossRef]
- Bertilsson, L.; Wiklund, K.; de Moura Tebaldi, I.; Rezende, O.M.; Veról, A.P.; Miguez, M.G. Urban Flood Resilience—A Multi-Criteria Index to Integrate Flood Resilience into Urban Planning. J. Hydrol. 2019, 573, 970–982. [Google Scholar] [CrossRef]
- Iradukunda, P.; Mwanaumo, E.M.; Kabika, J. A Review of Integrated Multicriteria Decision Support Analysis in the Climate Resilient Infrastructure Development. Environ. Sustain. Indic. 2023, 20, 100312. [Google Scholar] [CrossRef]
- Grahn, T.; Nyberg, L. Assessment of Pluvial Flood Exposure and Vulnerability of Residential Areas. Int. J. Disaster Risk Reduct. 2017, 21, 367–375. [Google Scholar] [CrossRef]
- Bundesanstalt Statistik Österreich Ein Blick Auf Die Gemeinde. Available online: https://www.statistik.at/blickgem/gemDetail.do?gemnr=62379 (accessed on 4 May 2023).
- DIN EN 752:2017-07; Entwässerungssysteme Außerhalb von Gebäuden Kanalmanagement. Deutsches Institut für Normung: Berlin, Germany, 2017. [CrossRef]
- Pistrika, A.; Tsakiris, G.; Nalbantis, I. Flood Depth-Damage Functions for Built Environment. Environ. Process. 2014, 1, 553–572. [Google Scholar] [CrossRef]
- Smith, G.P.; Davey, E.K.; Cox, R. Flood Hazard WRL Technical Report 2014/07; University of New South Wales: Sydney, Australia, 2014. [Google Scholar]
- Landesanstalt für Umwelt, Messungen und Naturschutz Baden-Württemberg (Ed.) Leitfaden Kommunales Starkregenrisikomanagement in Baden-Württemberg; Stand Dezember 2016; LUBW Landesanstalt für Umwelt, Messungen und Naturschutz: Karlsruhe, Germany, 2016; ISBN 978-3-88251-391-2. [Google Scholar]
- Reinstaller, S.; Muschalla, D. Qualitative Techniques to Evaluate Urban Flood Models. In Proceedings of the 12th International Conference of Urban Drainage Modelling, Costa Mesa, CA, USA, 10–12 January 2022. [Google Scholar]
- Brears, R.C. From Traditional Grey Infrastructure to Blue-Green Infrastructure. In Blue and Green Cities; Springer International Publishing: Cham, Switzerland, 2023; pp. 5–42. ISBN 978-3-031-41392-6. [Google Scholar]
- Hwang, H.; Lansey, K.; Quintanar, D.R. Resilience-Based Failure Mode Effects and Criticality Analysis for Regional Water Supply System. J. Hydroinform. 2014, 17, 193–210. [Google Scholar] [CrossRef]
- Sörensen, J.; Persson, A.S.; Olsson, J.A. A Data Management Framework for Strategic Urban Planning Using Blue-Green Infrastructure. J. Environ. Manag. 2021, 299, 113658. [Google Scholar] [CrossRef] [PubMed]
- James, R.; Finney, K.; Perera, N.; Peyron, N. SWMM5/PCSWMM Integrated 1D-2D Modeling. In Proceedings of the Engineering Conferences International ECI Digital Archives, Iceland, 23–27 July 2012. [Google Scholar]
- Rossman, L.A.; Simon, A.M. Storm Water Management Model User’s Manual Version 5.2; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2022. [Google Scholar]
- Reinstaller, S.; Krebs, G.; Pichler, M.; Muschalla, D. Identification of High-Impact Uncertainty Sources for Urban Flood Models in Hillside Peri-Urban Catchments. Water 2022, 14, 1973. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising Performance of Environmental Models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual Volume III—Water Quality; EPA—United States Environmental Protection Agency: Cincinnati, OH, USA, 2016. [Google Scholar]
- Schroeer, K.; Kirchengast, G.; Sungmin, O. Strong Dependence of Extreme Convective Precipitation Intensities on Gauge Network Density. Geophys. Res. Lett. 2018, 45, 8253–8263. [Google Scholar] [CrossRef]
- Wu, W.; Li, C.; Liu, M.; Hu, Y.; Xiu, C. Change of Impervious Surface Area and Its Impacts on Urban Landscape: An Example of Shenyang between 2010 and 2017. Ecosyst. Health Sustain. 2020, 6, 1767511. [Google Scholar] [CrossRef]
- Funke, F.; Kleidorfer, M. Sensitivity of Sustainable Urban Drainage Systems to Precipitation Events and Malfunctions. Blue-Green Syst. 2024, 6, 33–52. [Google Scholar] [CrossRef]
- Ngo, T.T.; Yoo, D.G.; Lee, Y.S.; Kim, J.H. Optimization of Upstream Detention Reservoir Facilities for Downstream Flood Mitigation in Urban Areas. Water 2016, 8, 290. [Google Scholar] [CrossRef]
- Mei, C.; Liu, J.; Wang, H.; Li, Z.; Yang, Z.; Shao, W.; Ding, X.; Weng, B.; Yu, Y.; Yan, D. Urban Flood Inundation and Damage Assessment Based on Numerical Simulations of Design Rainstorms with Different Characteristics. Sci. China Technol. Sci. 2020, 63, 2292–2304. [Google Scholar] [CrossRef]
- Qin, H.; Li, Z.; Fu, G. The Effects of Low Impact Development on Urban Flooding under Different Rainfall Characteristics. J. Environ. Manag. 2013, 129, 577–585. [Google Scholar] [CrossRef] [PubMed]
- Gülbaz, S.; Kazezyilmaz-Alhan, C.M. Experimental Investigation on Hydrologic Performance of LID with Rainfall-Watershed-Bioretention System. J. Hydrol. Eng. 2017, 22, D4016003. [Google Scholar] [CrossRef]
- Jackisch, N.; Weiler, M. The Hydrologic Outcome of a Low Impact Development (LID) Site Including Superposition with Streamflow Peaks. Urban Water J. 2017, 14, 143–159. [Google Scholar] [CrossRef]



| Number | Strategy Name | Modelling Approach | Model Description | Design Conditions |
|---|---|---|---|---|
| M0 | reference | hydrological–hydraulic | evaluated the 1D–2D urban flood model of the current state | |
| M1 | rain detention basin | hydraulic | hydraulic storage node modelled with an area/depth function | T = 100a |
| M2 | multifunctional retention basin | hydraulic | combination of depth-modified nodes in the 2D mesh for the waterways and storage nodes as multifunctional retention ponds | T = 30a |
| M3 | green infrastructure combination | hydrological–hydraulic | combination of the LID approach for green roofs and hydraulic storage nodes for vegetative swales | T = 5a |
| M4 | sewer system modification | hydraulic | modification of the conduit geometry of the 1D sewer model | T = 10–50a |
| M5 | mobile barriers | hydraulic | increasing the depth of the fictive nodes of the mesh where the mobile barriers are implemented | |
| M6 | agriculture and forestry measure | hydrological | modification of the loss parameters (depression storage and interception storage) and hydraulic conductivity in the hydrological model |
| Statistical Objective | Mitigation Strategies | Simulated Events | Future Challenges |
|---|---|---|---|
| F-value | 55.907 | 1.333 | 3.505759 |
| p-value | 1.3 × 10−29 | 2.7 × 10−1 | 1.8 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reinstaller, S.; Funke, F.; König, A.W.; Pichler, M.; Kleidorfer, M.; Muschalla, D. Resilient Urban Flood Management: A Multi-Objective Assessment of Mitigation Strategies. Sustainability 2024, 16, 4123. https://doi.org/10.3390/su16104123
Reinstaller S, Funke F, König AW, Pichler M, Kleidorfer M, Muschalla D. Resilient Urban Flood Management: A Multi-Objective Assessment of Mitigation Strategies. Sustainability. 2024; 16(10):4123. https://doi.org/10.3390/su16104123
Chicago/Turabian StyleReinstaller, Stefan, Fabian Funke, Albert Willhelm König, Markus Pichler, Manfred Kleidorfer, and Dirk Muschalla. 2024. "Resilient Urban Flood Management: A Multi-Objective Assessment of Mitigation Strategies" Sustainability 16, no. 10: 4123. https://doi.org/10.3390/su16104123
APA StyleReinstaller, S., Funke, F., König, A. W., Pichler, M., Kleidorfer, M., & Muschalla, D. (2024). Resilient Urban Flood Management: A Multi-Objective Assessment of Mitigation Strategies. Sustainability, 16(10), 4123. https://doi.org/10.3390/su16104123









