Competition between Green and Non-Green Travel Companies: The Role of Governmental Subsidies in Green Travel
Abstract
1. Introduction
2. Literature Review
2.1. Pricing and Effort Strategies for Green Travel
2.2. The Competition among Modes of Travel
2.3. Government Subsidies for Green Travel
3. Problem Description and Notations
4. Decisions without Governmental Subsidies
4.1. Centralized Decision-Making without Governmental Subsidies
4.2. Decentralized Decision-Making without Governmental Subsidies
4.3. Impact of Decision-Making Scenarios
5. Decisions with Governmental Subsidies
5.1. Centralized Decision-Making with Governmental Subsidies
5.2. Decentralized Decision-Making with Governmental Subsidies
5.3. Impact of Decision-Making Scenarios
6. Impact of Governmental Subsidies
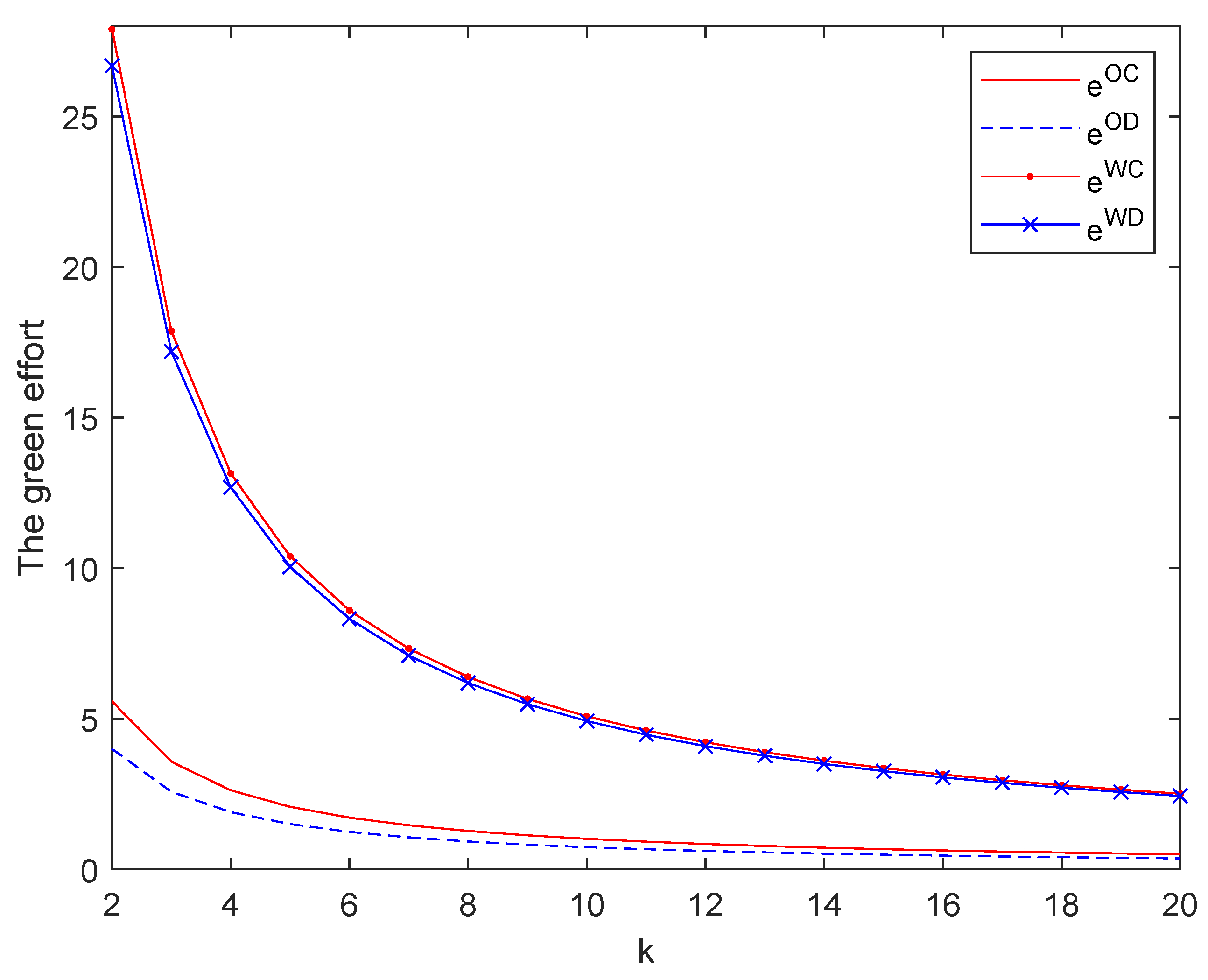
6.1. Impact on Green Effort
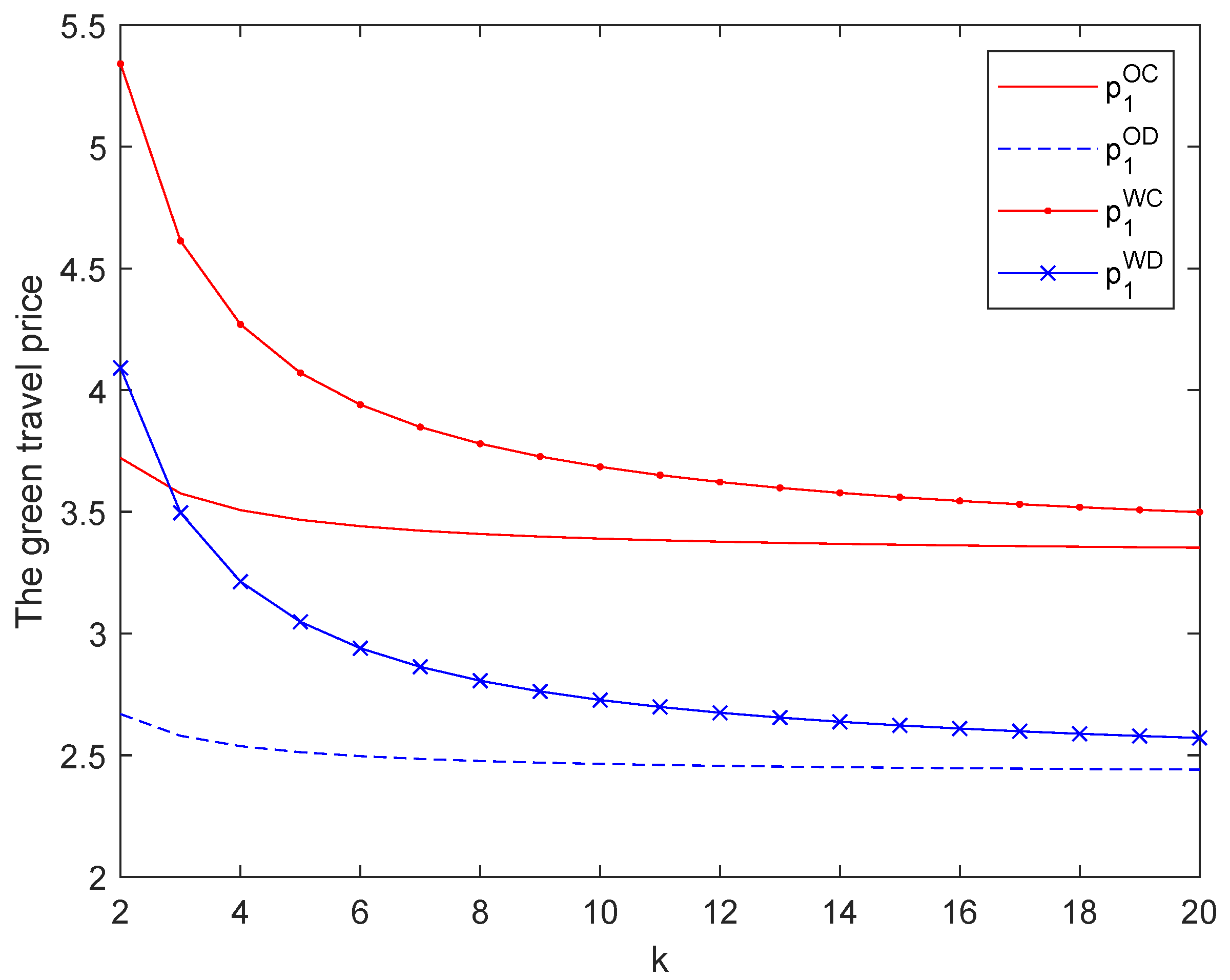
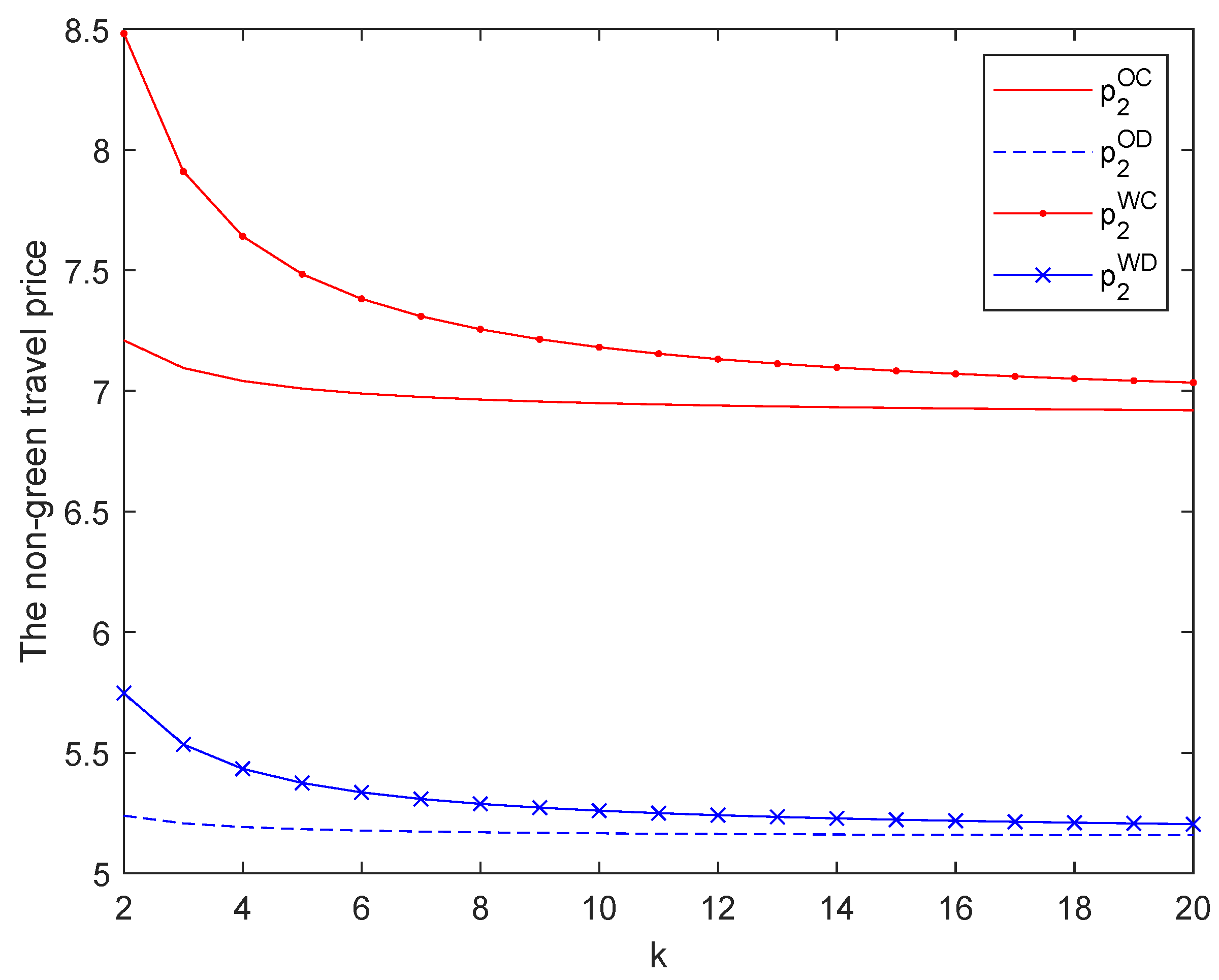
6.2. Impact on Travel Prices
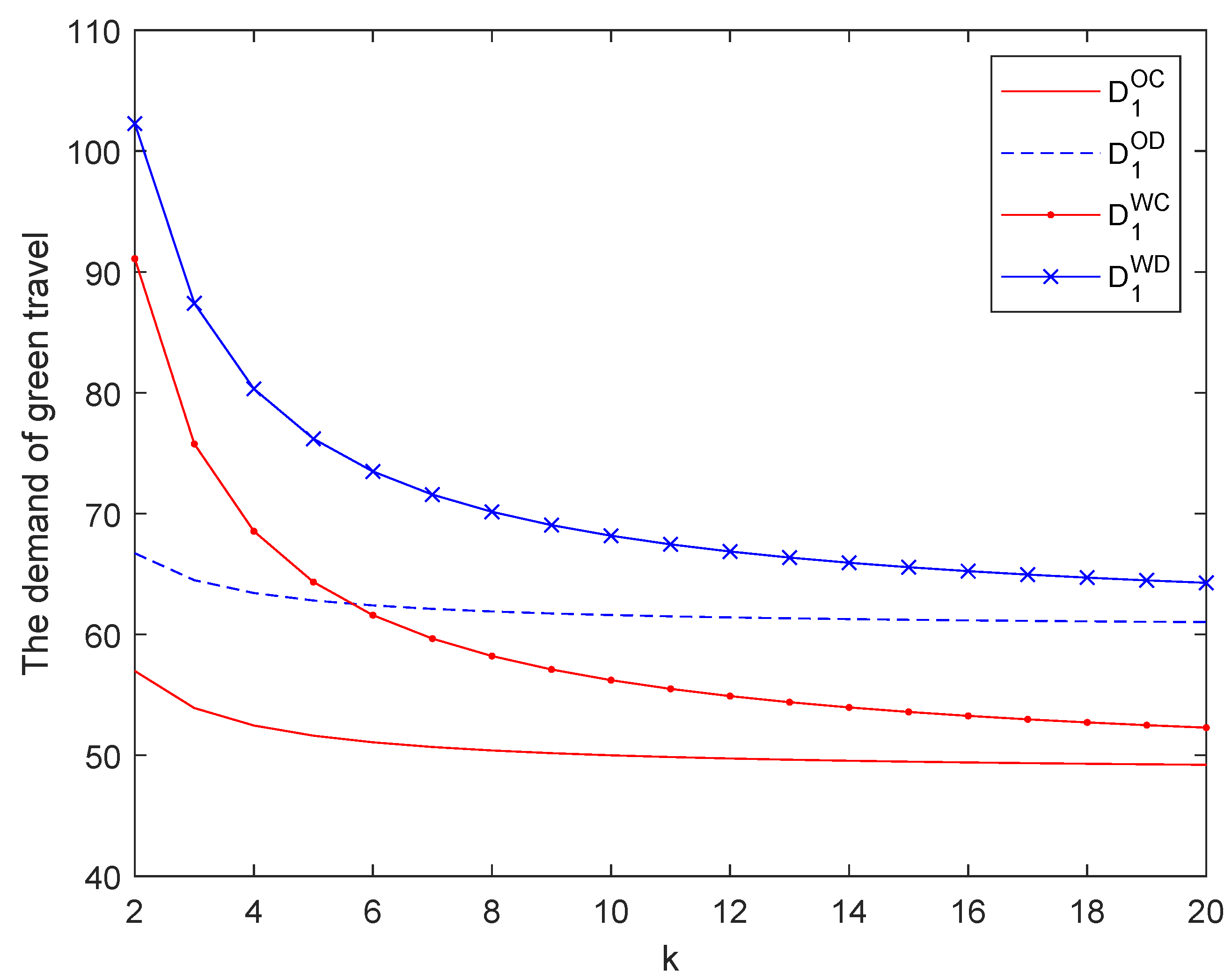
6.3. Impact on Travel Demand
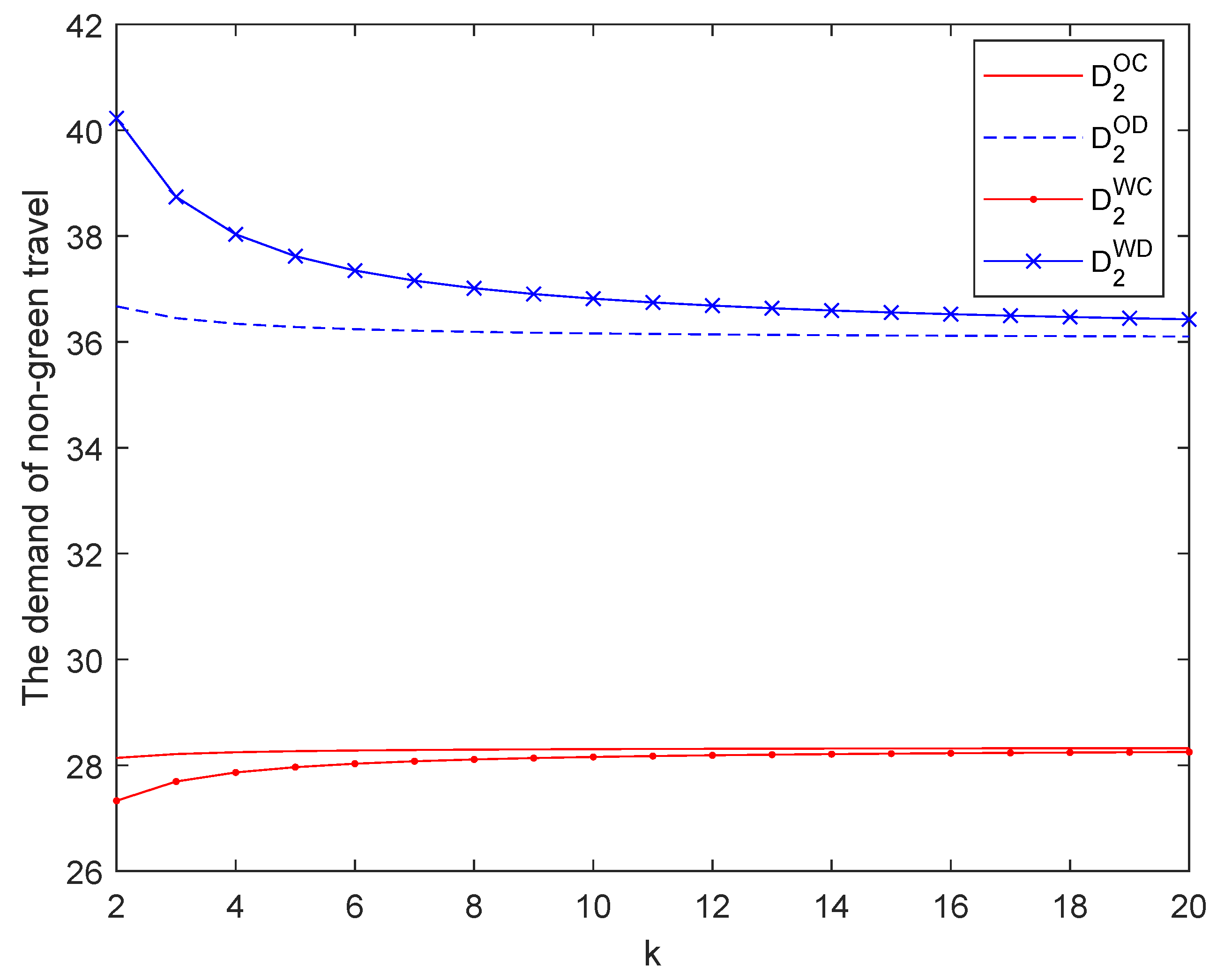
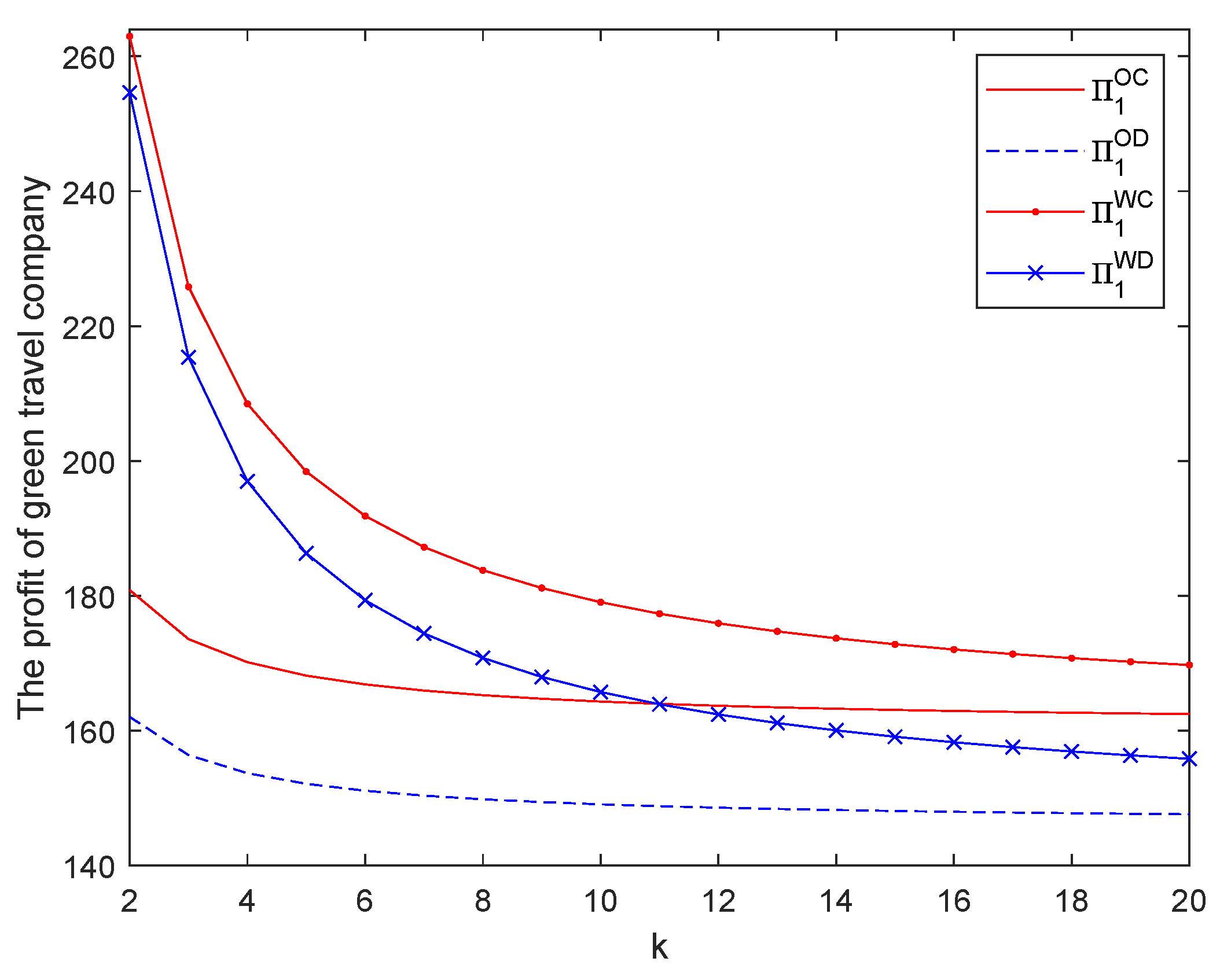
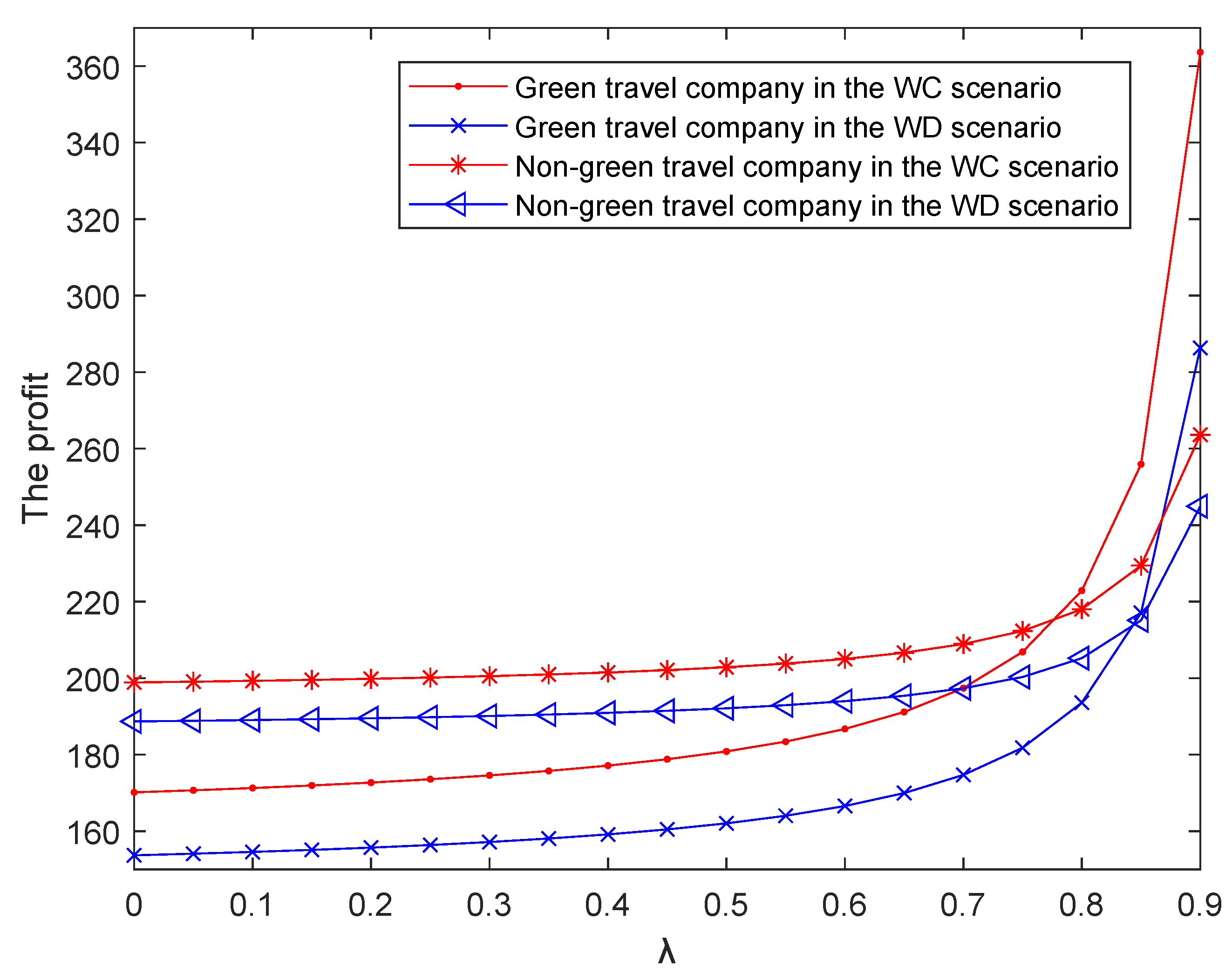
7. Numerical Experiments
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Huang, Y.; Zhu, H.; Zhang, Z. The heterogeneous effect of driving factors on carbon emission intensity in the Chinese transport sector: Evidence from dynamic panel quantile regression. Sci. Total Environ. 2020, 727, 138578. [Google Scholar] [CrossRef] [PubMed]
- Ding, N.; Pan, J.; Zhang, Z.; Yang, J. Life cycle assessment of car sharing models and the effect on GWP of urban transportation: A case study of Beijing. Sci. Total Environ. 2019, 688, 1137–1144. [Google Scholar] [CrossRef] [PubMed]
- Kitthamkesorn, S.; Chen, A. Alternate weibit-based model for assessing green transport systems with combined mode and route travel choices. Transp. Res. Part B Methodol. 2017, 103, 291–310. [Google Scholar] [CrossRef]
- Verplanken, B.; Aarts, H.; Van Knippenberg, A. Habit, information acquisition, and the process of making mode of travel choices. Eur. J. Soc. Psychol. 1997, 27, 539–560. [Google Scholar] [CrossRef]
- Sheu, J.B.; Li, F. Market Competition and Greening Transportation of Airlines Under the Emission Trading Scheme: A Case of Duopoly Market. Transp. Sci. 2014, 48, 684–694. [Google Scholar] [CrossRef]
- Hong, J.; Liu, X. The optimal pricing for green ride services in the ride-sharing economy. Transp. Res. Part D Transp. Environ. 2022, 104, 103205. [Google Scholar] [CrossRef]
- Yang, Y.; Long, R.; Bai, Y.; Li, L. The Influence of Household Heterogeneity Factors on the Green Travel Behavior of Urban Residents in the East China Region. Sustainability 2017, 9, 237. [Google Scholar] [CrossRef]
- Luo, P.; Guo, G.; Zhang, W. The role of social influence in green travel behavior in rural China. Transp. Res. Part D Transp. Environ. 2022, 107, 103284. [Google Scholar] [CrossRef]
- Geng, J.; Long, R.; Chen, H.; Li, W. Exploring the motivation-behavior gap in urban residents’ green travel behavior: A theoretical and empirical study. Resour. Conserv. Recycl. 2017, 125, 282–292. [Google Scholar] [CrossRef]
- Kłos-Adamkiewicz, Z.; Gutowski, P. The Outbreak of COVID-19 Pandemic in Relation to Sense of Safety and Mobility Changes in Public Transport Using the Example of Warsaw. Sustainability 2022, 14, 1780. [Google Scholar] [CrossRef]
- Fan, J.; Wang, J.; Zhang, X. An innovative subsidy model for promoting the sharing of Electric Vehicles in China: A pricing decisions analysis. Energy 2020, 201, 117557. [Google Scholar] [CrossRef]
- Mo, D.; Yu, J.; Chen, X. Modeling and managing heterogeneous ride-sourcing platforms with governmental subsidies on electric vehicles. Transp. Res. Part B Methodol. 2020, 139, 447–472. [Google Scholar] [CrossRef]
- Zhao, M.; Li, B.; Ren, J.; Hao, Z. Competition equilibrium of ride-sourcing platforms and optimal governmental subsidies considering customers’green preference under peak carbon dioxide emissions. Int. J. Prod. Econ. 2023, 255, 108679. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, D.; Chen, K.; Yong, Z.; Bi, G. Optimal pricing and availability strategy of a bike-sharing firm with time-sensitive customers. J. Clean. Prod. 2019, 228, 208–221. [Google Scholar] [CrossRef]
- Chen, Y.; Zha, Y.; Wang, D.; Li, H.; Bi, G. Optimal pricing strategy of a bike-sharing firm in the presence of customers with convenience perceptions. J. Clean. Prod. 2020, 253, 119905. [Google Scholar] [CrossRef]
- Chen, X.M.; Zheng, H.; Ke, J.; Yang, H. Dynamic optimization strategies for on-demand ride services platform: Surge pricing, commission rate, and incentives. Transp. Res. Part B Methodol. 2020, 138, 23–45. [Google Scholar] [CrossRef]
- Zhong, Y.; Yang, T.; Cao, B.; Chen, T.C.E. On-demand ride-hailing platforms in competition with the taxi industry: Pricing strategies and government supervision. Int. J. Prod. Econ. 2022, 243, 108301. [Google Scholar] [CrossRef]
- Jiang, Z.; Lei, C.; Ouyang, Y. Optimal investment and management of shared bikes in a competitive market. Transp. Res. Part B Methodol. 2020, 135, 143–155. [Google Scholar] [CrossRef]
- Cao, G.; Jin, G.; Weng, X.; Zhou, L.A. Market-expanding or Market-stealing? Competition with network effects in bike-sharing. Rand. J. Econ. 2021, 52, 778–814. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Zhang, S. Optimal pricing of customized bus services and ride-sharing based on a competitive game model. Omega 2021, 103, 102413. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, A.; He, Q.; Yang, H. Competition between the transportation network company and the government with subsidies to public transit riders. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102426. [Google Scholar] [CrossRef]
- Zhao, L.; Li, L.; Zhang, X. The greening of intercity travel: Environmental protection subsidy and HSR operation planning. Transp. Res. Part D Transp. Environ. 2021, 94, 102800. [Google Scholar] [CrossRef]
- Gómez-Lobo, A.; Tirachini, A.; Gutierrez, I. Optimal prices for ridesourcing in the presence of taxi, public transport and car competition. Transp. Res. Part C Emerg. Technol. 2022, 137, 103591–103608. [Google Scholar] [CrossRef]
- Zakharenko, A. Pricing shared vehicles. Econ. Transp. 2023, 33, 100296–100310. [Google Scholar] [CrossRef]
- Jiao, Z.; Ran, L.; Liu, X.; Zhang, Y.; Qiu, R.G. Integrating price-incentive and trip-selection policies to rebalance shared electric vehicles. Serv. Sci. 2020, 12, 148–173. [Google Scholar] [CrossRef]
- Jacob, J.; Roet-Green, R. Ride solo or pool: Designing price-service menus for a ride-sharing platform. Eur. J. Oper. Res. 2021, 295, 1008–1024. [Google Scholar] [CrossRef]
- Jiao, G.; Ramezani, M. Incentivizing shared rides in e-hailing markets: Dynamic discounting. Transp. Res. Part C Emerg. Technol. 2022, 144, 103879–103897. [Google Scholar] [CrossRef]
- Haider, Z.; Nikolaev, A.; Kang, J. Inventory rebalancing through pricing in public bike sharing systems. Eur. J. Oper. Res. 2018, 270, 103–117. [Google Scholar] [CrossRef]
- Miao, R.; Guo, P.; Huang, W.; Li, Q.; Zhang, B. Profit model for electric vehicle rental service: Sensitive analysis and differential pricing strategy. Energy 2022, 249, 123736–123748. [Google Scholar] [CrossRef]
- Lin, X.; Sun, C.; Cao, B.; Zhou, Y.; Chen, C. Should ride-sharing platforms cooperate with car-rental companies? Implications for consumer surplus and driver surplus. Omega 2021, 102, 102309. [Google Scholar] [CrossRef]
- Zhong, Y.; Yang, J.; Zhou, Y.W.; Cao, B. The role of surcharge policy on a ride-hailing service platform with long-distance drivers. Int. J. Prod. Res. 2023; accepted. [Google Scholar] [CrossRef]
- Turan, B.; Pedarsani, R.; Alizadeh, M. Dynamic pricing and fleet management for electric autonomous mobility on demand systems. Transp. Res. Part C Emerg. Technol. 2020, 12, 102829–102848. [Google Scholar] [CrossRef]
- Guo, D.; Fan, Z.P.; Liu, Y. The strategic analysis of service mode selection for a ride-hailing platform. Int. Trans. Oper. Res. 2023; accepted. [Google Scholar] [CrossRef]
- Zhang, J.; Meng, M.; David, Z.W. A dynamic pricing scheme with negative prices in dockless bike sharing systems. Transp. Res. Part B Methodol. 2019, 127, 201–224. [Google Scholar] [CrossRef]
- Li, M.; Jiang, G.; Lo, H.S. Pricing strategy of ride-sourcing services under travel time variability. Transp. Res. Part E Logist. Transp. Rev. 2022, 159, 102631. [Google Scholar] [CrossRef]
- Liu, J.; Ma, W.; Qian, S. Optimal curbside pricing for managing ride-hailing pick-ups and drop-offs. Transp. Res. Part C Emerg. Technol. 2023, 146, 103960–103987. [Google Scholar] [CrossRef]
- Ke, J.; Yang, H.; Li, X.; Wang, H.; Ye, J. Pricing and equilibrium in on-demand ride-pooling markets. Transp. Res. Part B Methodol. 2020, 139, 411–431. [Google Scholar] [CrossRef]
- Xu, K.; Saberi, M.; Liu, W. Dynamic pricing and penalty strategies in a coupled market with ridesourcing service and taxi considering time-dependent order cancellation behaviour. Transp. Res. Part C Emerg. Technol. 2022, 138, 103621–103643. [Google Scholar] [CrossRef]
- Afifah, F.; Guo, Z. Spatial pricing of ride-sourcing services in a congested transportation network. Transp. Res. Part C Emerg. Technol. 2022, 142, 103777–103798. [Google Scholar] [CrossRef]
- Li, S.; Yang, H.; Poolla, K.; Varaiya, P. Spatial pricing in ride-sourcing markets under a congestion charge. Transp. Res. Part B Methodol. 2021, 152, 18–45. [Google Scholar] [CrossRef]
- Ni, L.; Sun, B.; Wang, S.; Tsang, D.H. Dynamic pricing mechanism design for electric mobility-on-demand systems. IEEE Trans. Intell. Transp. 2021, 23, 11361–11375. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, F. Ride-pooling services with differentiated pooling sizes under endogenous congestion effect. Transp. Res. Part C Emerg. Technol. 2022, 144, 103883–103913. [Google Scholar] [CrossRef]
- Mo, B.; Cao, Z.; Zhang, H.; Shen, Y.; Zhao, J. Competition between shared autonomous vehicles and public transit: A case study in Singapore. Transp. Res. Part C Emerg. Technol. 2021, 127, 103058–103085. [Google Scholar] [CrossRef]
- Emami, M.; Haghshenas, H.; Talebian, A.; Kermanshahi, S. A game theoretic approach to study the impact of transportation policies on the competition between transit and private car in the urban context. Transp. Res. Part A Policy Pract. 2022, 163, 320–337. [Google Scholar] [CrossRef]
- Socorro, M.; Betancor, O. Air transport subsidies for resident passengers: The unexpected effects on competition. Res. Transp. Econ. 2020, 79, 100772. [Google Scholar] [CrossRef]
- Szaruga, E.; Załoga, E. Sustainable Development Programming of Airports by Identification of Non-Efficient Units. Energies 2022, 15, 932. [Google Scholar] [CrossRef]
- Hsu, C.; Lee, Y.; Liao, C. Competition between high-speed and conventional rail systems: A game theoretical approach. Expert Syst. Appl. 2010, 37, 3162–3170. [Google Scholar] [CrossRef]
- Yang, Y.; Han, X.; Jiang, R.; Jia, B.; Gao, Z.Y. Competition and coordination in public transport: A mode choice experiment. Transp. Res. Part C Emerg. Technol. 2022, 143, 103858–103880. [Google Scholar] [CrossRef]
- Rategh, Y.; Tamannaei, M.; Zarei, H. A game-theoretic approach to an oligopolistic transportation market: Coopetition between incumbent systems subject to the entrance threat of an HSR service. Transp. Res. Part A Policy Pract. 2022, 165, 144–171. [Google Scholar] [CrossRef]
- Zhang, K.; Nie, Y.M. To pool or not to pool: Equilibrium, pricing and regulation. Transp. Res. Part B Methodol. 2021, 151, 59–90. [Google Scholar] [CrossRef]
- Wei, K.; Vaze, V.; Jacquillat, A. Transit planning optimization under ride-hailing competition and traffic congestion. Transp. Sci. 2022, 56, 725–749. [Google Scholar] [CrossRef]
- Guo, H.; Chen, Y.; Liu, Y. Shared autonomous vehicle management considering competition with human-driven private vehicles. Transp. Res. Part C Emerg. Technol. 2022, 136, 103547–103569. [Google Scholar] [CrossRef]
- Yang, S.; Wu, J.; Sun, H.; Qu, Y.; Wang, D.Z. Integrated optimization of pricing and relocation in the competitive carsharing market: A multi-leader-follower game model. Transp. Res. Part C Emerg. Technol. 2022, 138, 103613–103630. [Google Scholar] [CrossRef]
- Jiang, Z.; Ouyang, Y. Pricing and resource allocation under competition in a docked bike-sharing market. Transp. Res. Part C Emerg. Technol. 2022, 143, 103833–103847. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, H.; Ke, J. Price of competition and fragmentation in ride-sourcing markets. Transp. Res. Part C Emerg. Technol. 2022, 143, 103851–103881. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, H.; Ke, J.; Wang, H.; Li, X. Competition and third-party platform-integration in ride-sourcing markets. Transp. Res. Part B Methodol. 2022, 159, 76–103. [Google Scholar] [CrossRef]
- Zhang, K.; Nie, Y.M. Inter-platform competition in a regulated ride-hail market with pooling. Transp. Res. Part E Logist. Transp. Rev. 2021, 151, 102327–102351. [Google Scholar] [CrossRef]
- Xie, Y.; Wu, D.; Zhu, S. Can new energy vehicles subsidy curb the urban air pollution? Empirical evidence from pilot cities in China. Sci. Total Environ. 2021, 754, 142232. [Google Scholar] [CrossRef]
- Srivastava, A.; Kumar, R.R.; Chakraborty, A.; Mateen, A.; Narayanamurthy, G. Design and selection of government policies for electric vehicles adoption: A global perspective. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102726–102749. [Google Scholar] [CrossRef]
- Zhu, W.; He, Y. Green product design in supply chains under competition. Eur. J. Oper. Res. 2017, 258, 165–180. [Google Scholar] [CrossRef]
- Nash, J.F. Noncooperative games. Ann. Math. 1951, 45, 286–295. [Google Scholar] [CrossRef]
- Simaan, M.; Cruz, J.B., Jr. On the Stackelberg strategy in nonzero-sum games. J. Optim. Theory App. 1973, 11, 533–555. [Google Scholar] [CrossRef]
- Bai, Q.; Chen, M.; Nikolaidis, Y.; Xu, J. Improving sustainability and social responsibility of a two-tier supply chain investing in emission reduction technology. Appl. Math. Model. 2021, 95, 688–714. [Google Scholar] [CrossRef]

| References | Green Effort | Travel Mode Competition | Government Subsidy |
|---|---|---|---|
| Fan et al. [11] | |||
| Chen et al. [14] | |||
| Mo et al. [12] | |||
| Zhao et al. [13] | |||
| Srivastava et al. [59] | |||
| Hong and Liu [6] | |||
| Rategh et al. [49] | |||
| Wei et al. [51] | |||
| Yang et al. [53] | |||
| Mo et al. [43] | |||
| Zhu et al. [21] | |||
| Zhong et al. [17] | |||
| Zhao et al. [22] | |||
| Present paper |
| Notation | Description |
|---|---|
| Parameters | |
| Demand of the ith mode of travel, where and denote the green and non-green modes of travel, respectively | |
| Market size of the demand of the ith mode of travel | |
| Marginal effect coefficient of the ith travel price on the demand of the ith mode of travel | |
| Marginal effect coefficient of the (3-i)th travel price on the demand of the ith mode of travel | |
| g | Marginal effect coefficient of the green effort on green travel demand |
| k | Cost coefficient of the green effort |
| Unit carbon emission cost of the ith mode of travel | |
| Decision variables | |
| Travel price of the ith mode of travel | |
| e | Green effort of the green travel company |
| Government’s sharing coefficient of the green effort cost | |
| Superscripts | |
| Centralized decision-making without governmental subsidies | |
| Decentralized decision-making without governmental subsidies | |
| Centralized decision-making with governmental subsidies | |
| Decentralized decision-making with governmental subsidies |
| Parameter | g | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | 90 | 60 | 25 | 7 | 6 | 5 | 3 | 20 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, J.; Du, J.; Huang, M. Competition between Green and Non-Green Travel Companies: The Role of Governmental Subsidies in Green Travel. Sustainability 2023, 15, 7712. https://doi.org/10.3390/su15097712
Tu J, Du J, Huang M. Competition between Green and Non-Green Travel Companies: The Role of Governmental Subsidies in Green Travel. Sustainability. 2023; 15(9):7712. https://doi.org/10.3390/su15097712
Chicago/Turabian StyleTu, Jun, Juan Du, and Min Huang. 2023. "Competition between Green and Non-Green Travel Companies: The Role of Governmental Subsidies in Green Travel" Sustainability 15, no. 9: 7712. https://doi.org/10.3390/su15097712
APA StyleTu, J., Du, J., & Huang, M. (2023). Competition between Green and Non-Green Travel Companies: The Role of Governmental Subsidies in Green Travel. Sustainability, 15(9), 7712. https://doi.org/10.3390/su15097712




