1. Introduction
A stable and smooth track is one of the essential conditions for high–speed, safe, and comfortable train operation. The subgrade is the foundation of the track. High–speed railways require a stable subgrade that is not easy to deform and has a high stiffness and uniform longitudinal distribution so as to achieve a stable and smooth track. The vacuum–surcharge preloading method is one of many methods for drainage consolidation of soft foundations. It is very effective for soft clay foundations with the characteristics of a high water content, high compressibility, low strength, low permeability, and deep burial depth [
1,
2,
3].
Many scholars have used the sand–drain consolidation theory, learned from methods of calculating the surcharge for the consolidation of soft foundations, and changed the load boundary conditions to derive the exact analytical solutions for consolidation that would be suitable for vacuum preloading and vacuum–surcharge preloading [
4,
5,
6,
7,
8,
9,
10]. However, because there are too many simplified assumptions, obscure and complicated derivation processes, large numbers of parameters, and high requirements for these methods, the calculation results differ greatly from the actual results, which is not convenient for practical applications and promotions.
In recent years, some scholars used various types of software to carry out research with numerical simulations with the goal of obtaining the approximate consolidated solutions for actual projects of vacuum preloading and vacuum–surcharge preloading [
10,
11,
12,
13,
14]. Currently, for the numerical simulation of strip subgrade consolidation, plane strain models are most commonly used; these equate a plastic drainage board foundation or a sand–drain foundation to a sand–wall foundation. However, whether it is vacuum preloading or surcharge preloading, the seepage and mechanical action of subgrade soil are in a three–dimensional state, which should be studied by using a three–dimensional model. Therefore, the accuracy of pore water pressure and settlement prediction results obtained with previous models for calculating subgrade soil consolidation has significant deviations. On the other hand, although the method of numerically simulating fluid–solid coupling is widely used in the field of geotechnical engineering [
15,
16,
17], there are few examples of its application to vacuum preloading and combined vacuum–surcharge preloading projects, and there are fewer comparisons of pore water pressure and settlement prediction results with measured values. In the process of theoretical exploration and practical application, the mechanical disturbance and fluid disturbance in vacuum preloading and vacuum–surcharge preloading are very significant. Therefore, it is very important to analyze the settlement and pore water pressure of soft foundations with this construction method by using the fluid–solid coupling method.
The authors intend to introduce an engineering example of using vacuum–surcharge preloading to strengthen the soft foundation of a high–speed railway, as well as to establish a calculation model for the consolidation of a single–sand drain foundation undergoing vacuum–surcharge preloading by using the FLAC3D finite difference method software. By simulating the on–site soil layer distribution, the soil consolidation process was calculated by using the parameters obtained from an experiment, and the calculated results were compared with the actual measured values. This is expected to provide a reference for design and construction when using this construction method.
2. Engineering Background
The soft foundation reinforcement test section of the Beijing–Shanghai high–speed railway is located in Kunshan, Jiangsu Province, and it is a Quaternary Holocene alluvial lacustrine deposit. From top to bottom, it is mainly composed of clay, muddy silty clay, silty clay, silty sand and other strata. The results of a field sampling test are summarized in
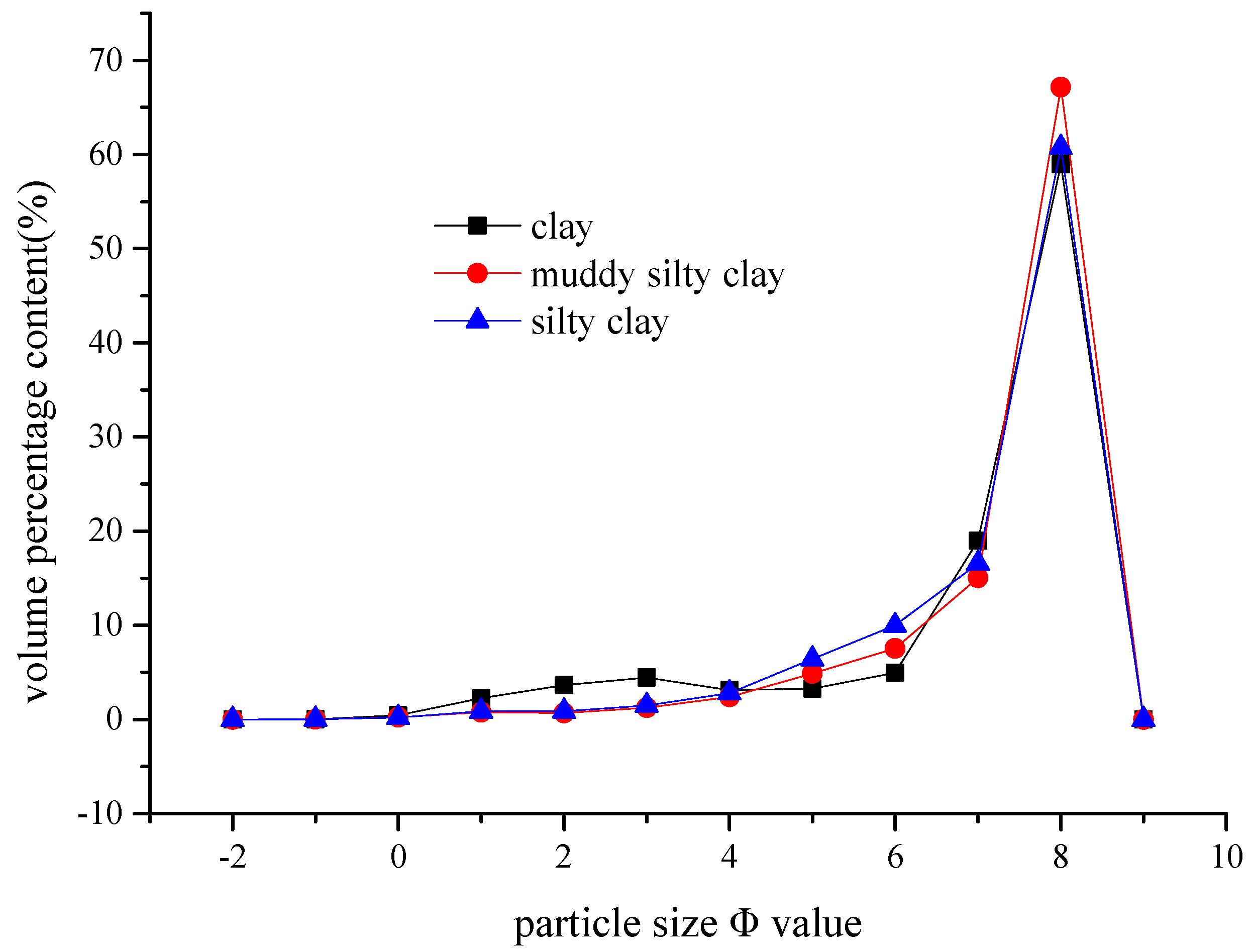
Table 1. A particle size distribution curve is shown in
Figure 1. The Provisional Regulations on the Design of High–Speed Railway stipulate that the annual settlement rate at the initial stage of completion should be less than or equal to 3 cm, that the post–construction settlement of an embankment should be less than or equal to 10 cm, and that the post–construction settlement of the subgrade at the bridge–road transition should be less than or equal to 5 cm. The requirements for the scheme and effect of soft foundation reinforcement are extremely high. After a comprehensive demonstration, the vacuum–surcharge preloading method was adopted for soft foundation reinforcement.
The route of the test section is a double track. The distance between the routes is 5.0 m. The width of the top surface of the roadbed is 13.8 m. Considering the settlement of the embankment and soft foundation after construction, the roadbed will be widened by 0.2 m on each side. The filling height of the embankment is 4.2–5.5 m, and the slope ratio of the embankment is 1:1.5. During the embankment filling process, a layer of geogrid is laid every 0.3 m within the 2.5 m width range of the slope. The k0 + 276.51~k0 + 515 section is reinforced by vacuum preloading, with an area of approximately 28.8 m × 238.5 m and a reinforcement depth of 14.5~18.5 m. The vertical drainage body is plastic drainage boards, with a depth of approximately 18 m. The plastic drainage boards are arranged in a plum blossom shape with a spacing of 1.2 m. A 0.6 m thick sand cushion layer is laid on the top surface of the plastic drainage board. A layer of geogrid is laid inside the sand cushion. The vacuum pressure under the membrane should not be less than 80 kPa. After vacuum loading, within 8 h, the vacuum degree under the membrane reached over 80 kPa.
The vacuum preloading method was used for 56 days, after which vacuum–surcharge preloading was used. The surcharge was loaded to the top of the subgrade, and the duration of the surcharge was 71 days. The settlement and pore water pressure were monitored with a sedimentation plate, sedimentation meter, pore water pressure meter, and other instruments and equipment [
18], and large amounts of measurement data were obtained.
According to a numerical analysis, the surface layer of the cross–section was a moderately compressible clay layer with a thickness of about 1 m; this was characterized as hard plastic. Below it was a layer that was about 17 m thick, consisting of muddy silty clay that was compressible at high pressures; this was characterized as flow plastic. The bottom layer consisted of a silty clay that had a moderately low compressibility and a thickness of about 5 m; this was characterized as hard plastic. The depth of the groundwater level was 0.5–1.5 m. The calculations are shown in
Figure 2.
3. Establishment of the 3D Fluid–Solid Coupling Model
The finite difference method software FLAC3D, which is based on the Lagrangian continuum method, can be used to study the mechanical seepage coupling of geotechnical materials because of its strong analytical abilities in complex engineering problems. This software was used to simulate the fluid–solid coupling of soft soil under the combined action of a vacuum and surcharge.
3.1. Constitutive and Seepage Models of Soil Mass
Of the many constitutive models of rock and soil, Mohr–Coulomb plastic constitutive model is the most general, and it is applicable to materials that yield under shear stress, such as loose or cemented granular soil. Therefore, a Mohr–Coulomb plastic constitutive model was used to simulate the stress–strain relationship of the soil, and an anisotropic seepage model was used to set a three–dimensional permeability coefficient for simulating the anisotropic seepage characteristics of the soil [
19,
20]. The parameters for the cases considered in the computation are summarized in
Table 1.
To use the Mohr–Coulomb plastic model, four parameters, namely, the bulk modulus
K, shear modulus
G, cohesion
c, and internal friction angle
φ, needed to be input into FLAC
3D. The bulk modulus
K and shear modulus could be calculated by using Equations (1) and (2).
In the formula, E is the elastic modulus (Young’s modulus) and ν is the Poisson’s ratio.
In engineering, the elastic modulus of soil refers to its deformation modulus. Because the time taken for elastic deformation of soil is very short, the deformation modulus and compression modulus are of the same order of magnitude. Therefore the elastic modulus
E can be calculated according to Equation (3) [
20].
Table 1 shows the compression modulus
ES, Poisson’s ratio
ν, cohesion
c, and internal friction angle
φ of each soil layer.
E can be calculated according to Equation (3), and then
K and
G can be calculated according to Equations (1) and (2).
It should be noted that Equation (3) is derived from the generalized Hooke law in elastic theory, but soil is not an ideal elastic body and does not fully comply with Hooke’s law, so Equation (3) is only an approximate formula.
3.2. Gridding
The whole model had the following dimensions: 2.8 m × 2.8 m × 23 m. The single–sand–drain foundation was axisymmetric, and 1/4 was used for the calculation. The width of the calculation model was 1.4 m, and the depth was 23 m. A described in [
21,
22,
23], the plastic drain board foundation of the actual project was converted into a sand–drain foundation. After considering the smear layer, a grid for the single sand–drain foundation consolidation model was established. The radius of the sand drain was 0.05 m, the radius of the smear layer was 0.15 m, and the radius of the affected area was 0.35 m. Single soil layers were placed in a group, the smear layers that belonged to different soil layers were placed in a group, and the sand drains were divided into an independent group. The foundation was divided into six groups, with 2128 units and 2772 nodes, as shown in
Figure 3.
3.3. Boundary and Initial Conditions
The top face of the model was considered a free boundary. Since the depth was very deep, the bottom of the model was considered as non–displaceable and was set as a fixed boundary. Due to the constraints of the surrounding soil, the four sides of the model were considered as having no horizontal displacement, but only vertical displacement. All six sides of the model were considered as permeable boundaries.
Assuming that the groundwater level was flush with the ground, the static pore water pressure at the node on the top surface of the model was 0, and it increased linearly along the depth according to a gradient of 10 kPa. The initial stress field was the gravity field. The acceleration of gravity was set, the density and self–weight stress distribution were assigned to each group, and the final initial stress field was calculated. After the soil mass reached equilibrium, the node deformation and rate of the whole model were adjusted to 0.
In the numerical analysis of fluid–solid coupling, the pore water pressure at the top node of the model was adjusted to −80 kPa during the 56 d of vacuum preloading because the vacuum degree under the membrane quickly reached above 80 kPa. The influence depth of the vacuum load was suggested to be at the bottom of the sand drain. There was no negative or excess pore pressure caused by the vacuum at this node, but only a static pore pressure, which was 0 kPa. The node pore pressure within the sand drain’s range was linearly distributed, increasing from −80 kPa at the top to 0 kPa at the bottom. A sub–cycle command flow was compiled to realize the application of the vacuum load. The unbalanced force ratio was set to 10−4. The master–slave programming method was used to solve the problem. The number of mechanical sub steps was subordinated to the number of seepage sub steps, and the seepage time was set to 4.8384 × 107 s.
The subgrade was filled with 5 m soil, so the surcharge was applied in five levels; each level was 20 kPa, and the total was 100 kPa. The construction interval of each level of the surcharge was 14.2 d. The surcharge was applied to the top surface of the model, and a uniformly distributed load was used to replace the surcharge. The setting of the application of the vacuum load in the stage of combined vacuum–surcharge preloading was the same as that with only vacuum preloading.
4. Analysis of the Calculation Results
4.1. Settlement Analysis
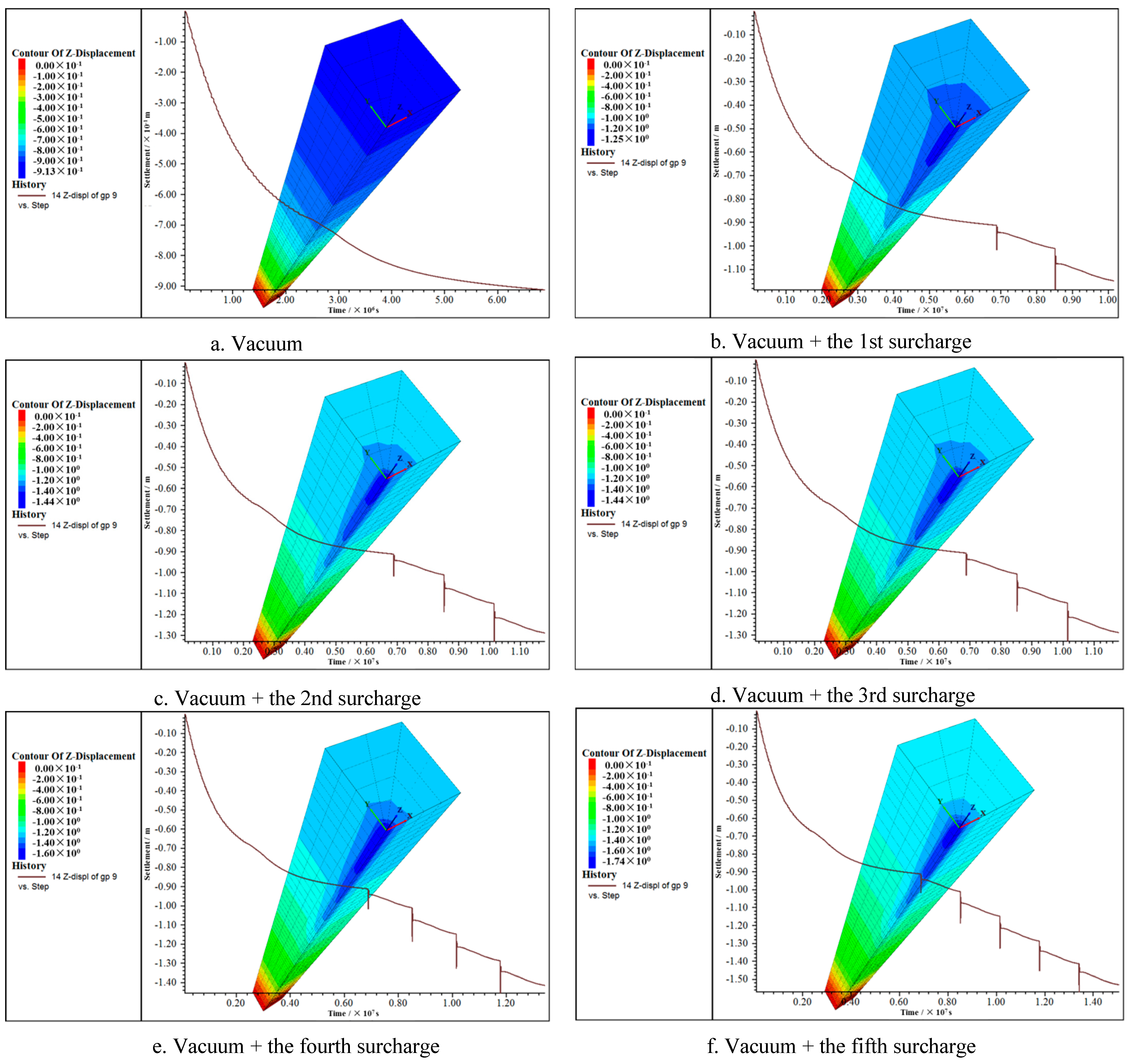
Figure 4 shows cloud diagrams of the deformation of the settlement of the soft foundation under a load at each stage.
In the vacuum preloading stage, the settlement on the same horizontal plane was very uniform, and the calculated surface settlement was finally stable at about 90 cm, with little difference in the sand drain, smear layer, and soil; the difference between the measured settlement values on the same horizontal plane was also small. In the stage of vacuum–surcharge preloading, the soil settlement increased instantaneously at the moment of application of each level of surcharge; then it instantaneously decreased to a certain extent, and the value of the instantaneous decrease was smaller than the value of the instantaneous increase; the range of fluctuation in the settlement caused by the first level of surcharge was small, and the ranges of fluctuation in the settlement caused by the second to fifth levels of surcharge were large and basically consistent. After the transient fluctuations, the settlement continued to develop with time. In the stage of vacuum–surcharge preloading, a difference in the settlement on the same horizontal plane appeared. The sand drain’s location had the largest settlement, and the settlement gradually decreased along the radius of the sand drain, showing a “pot–bottom” settlement, with the sand drain as the center of the “pot bottom”.
Each soil layer that was set in the calculation with the computer was completely horizontal, but the actual soil layer was not completely horizontal, and there was anisotropy in each soil layer due to the different thickness. Therefore, in the vacuum preloading stage, the results of the calculation of the settlement on the same horizontal plane under negative isotropic pressure were very uniform, and the actual difference in soil settlement was small, though it was present. In the stage of combined vacuum–surcharge preloading, the soil was subjected not only to negative isotropic pressure, but also to positive non–isotropic pressure due to the post–imposed surcharge. The soft foundation macroscopically showed a “pot–bottom” settlement due to the effect of the surcharge alone, and a difference in the settlement appeared. An instantaneous settlement of the actual soft foundation existed at the moment of applying the surcharge, which was generally considered to be caused by shear deformation of the soil. In the stage of combined vacuum–surcharge preloading, the instantaneous application of a graded load would cause the pore pressure in the soft foundation to instantaneously rise; the calculated settlement value of the soft foundation would also instantaneously increase, and the value of the increase would be large. However, due to the existence of a relatively stable negative pressure in the soft foundation, the settlement would instantaneously decrease, and the superposition effect of positive and negative pressure would be obvious. After that, the settlement would continue to develop over time.
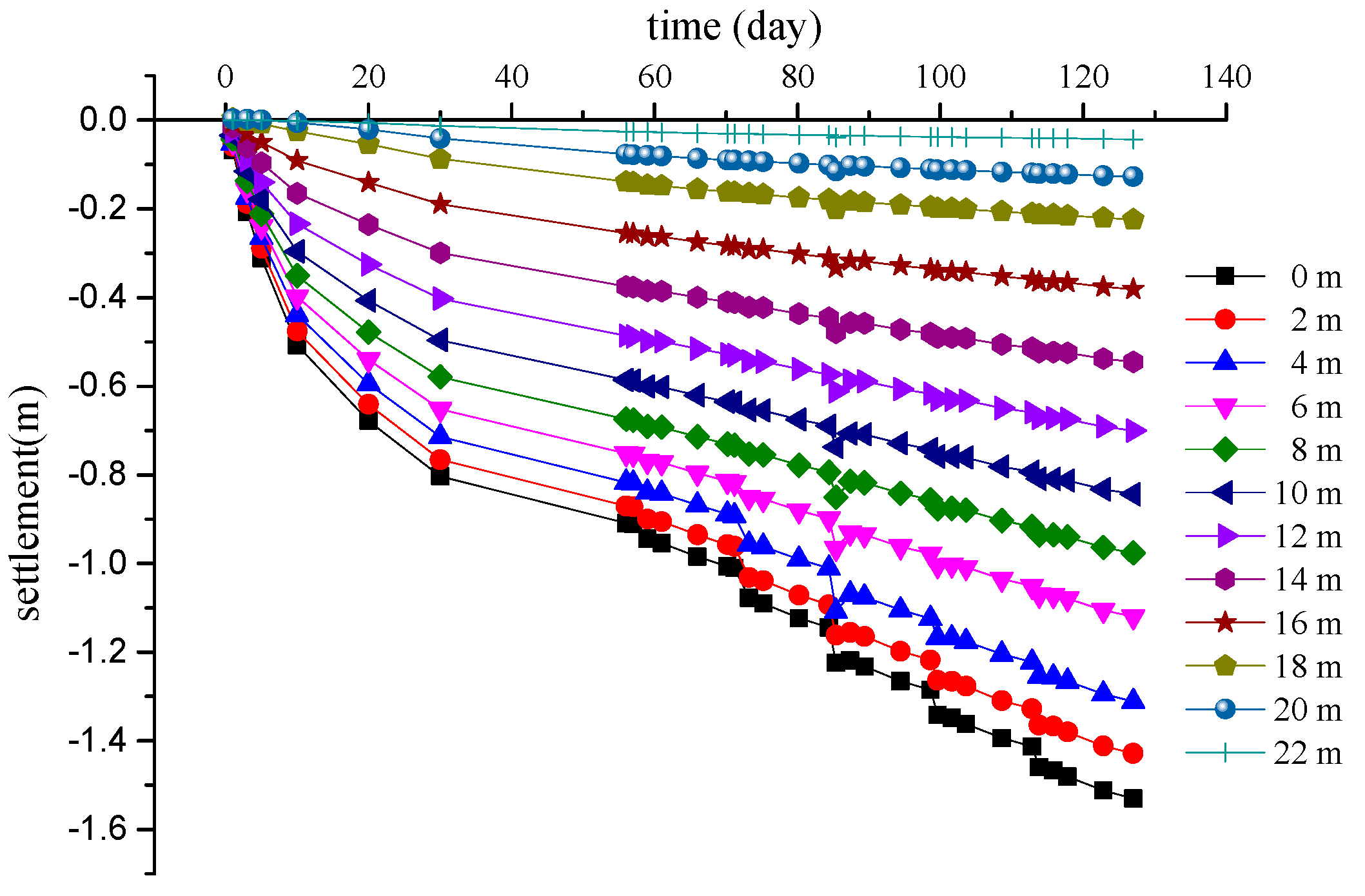
Since the actual construction filling rate was relatively uniform, the filling load could not be instantaneously applied by dividing it into five fixed levels as in the computer calculation, so the measured settlement curve would not be subjected to significant adjustments in fluctuation. The settlement data calculated by the computer were sorted out and the curve of the layered settlement versus time was constructed, as shown in
Figure 5. In the vacuum preloading stage (0–56 d), the settlement of the soft foundation developed very rapidly in days 0–30, slowed down after 30 d, and finally tended to be stable. The settlement of the surface soil mass was the largest. The settlement decreased with the increase in depth. The closer to the surface, the faster and more obviously the settlement changed, and the deeper, the slower and less obviously the settlement changed. In the stage of vacuum–surcharge preloading (57–127 d), the settlement gradually developed with the application of the graded surcharge.
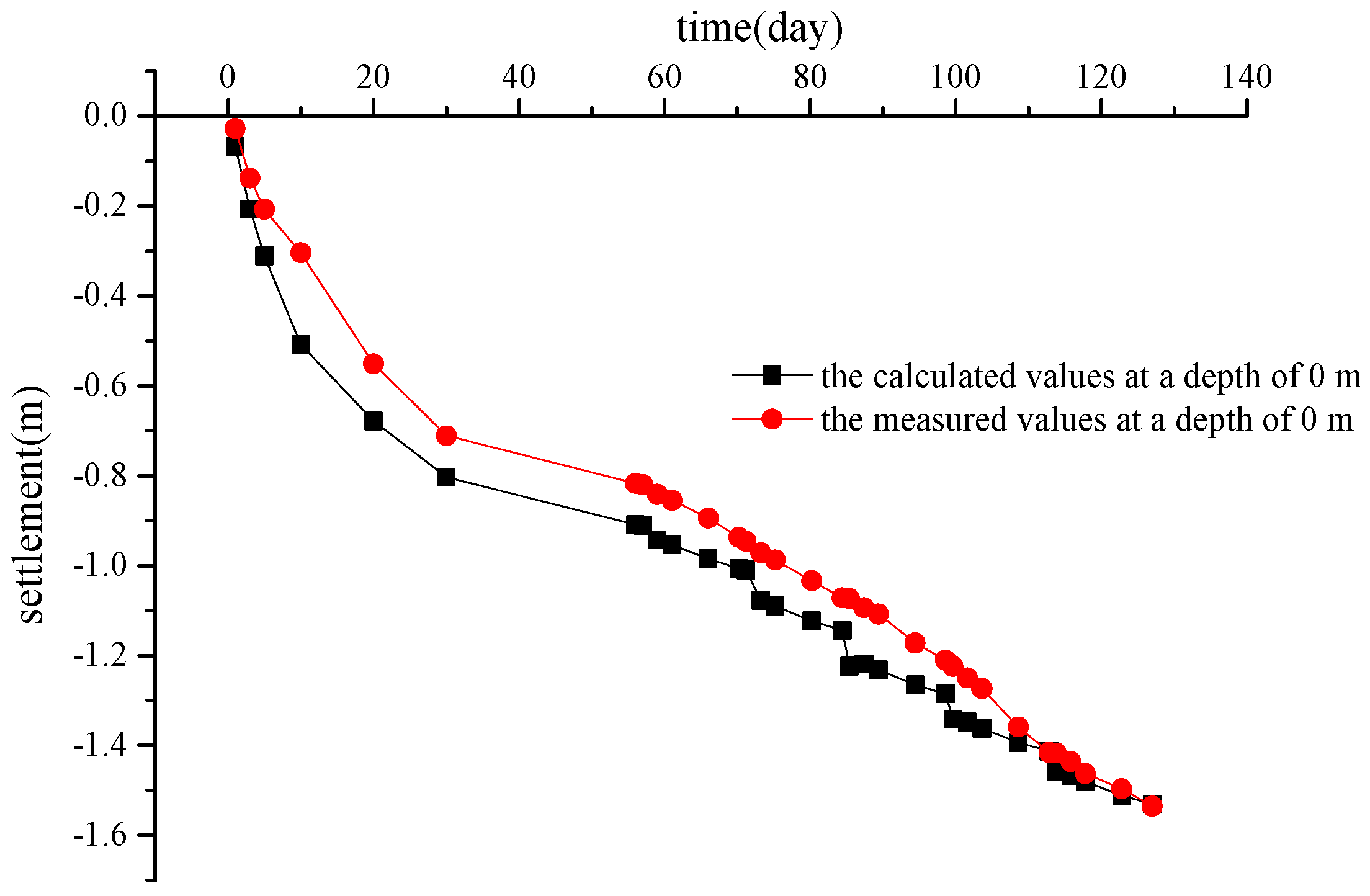
Figure 6 shows the curve of the surface settlement versus time and the curve of the measured values; the trend of the development of the calculated curve was consistent with the measured values. In the period of 0–5 d, the calculated curve was highly consistent with the curve of the measured values. From 5 to 60 d, there was a certain gap between the calculated curve and the measured values, which was about 10 cm. After 60 d, the difference between the calculated curve and the curve of the measured values gradually decreased. From 105 to 127 d, the trend of the changes in the two curves was highly consistent. The vacuum load caused a negative pore pressure in the soft foundation, the surcharge load caused a positive pore pressure in the soft foundation, and the uneven effect of the superposition of positive and negative pore pressures caused the consolidation of the soil. In the whole process of soft foundation reinforcement, the uneven pore pressure fluctuations caused the soil particles to constantly adjust and change, which was macroscopically reflected in that the settlement–time curve was not smooth, and the measured values and calculated values in each time period were different, but the final settlement results were basically consistent.
4.2. Pore water Pressure Analysis
Figure 7 shows the cloud diagrams of the changes in load pore pressure at each stage. In the vacuum preloading stage, the pore pressure fluctuated greatly and rapidly dropped to a constant negative value within 0–20 d. In the stage of combined vacuum–surcharge preloading, the pore pressure of the soft foundation instantaneously increased with a large value at the moment of applying each level of surcharge, then it instantaneously decreased to a level slightly higher than the pore pressure value under the previous level of load, and gradually decreased with time, finally stabilizing at the final value in the stage of vacuum preloading. On the same horizontal plane, the surface distribution of the pore water pressure also had a similar law to that of the surface settlement. In the stage of vacuum preloading, the pore pressure distribution was uniform. In the stage of combined vacuum–surcharge preloading, the pore pressure distribution presented a “pot–bottom” shape.
In the stage of vacuum–surcharge preloading, the surcharge caused the soft foundation to instantly generate a positive pore pressure, but there had already been a constant negative pore pressure caused by vacuum preloading in the soft foundation. The constant negative pore pressure caused the positive pore pressure to instantaneously decrease. This phenomenon can be called positive–negative pressure superposition. After superposition, the pore pressure was basically stabilized in the pore pressure range after the vacuum preloading stage was stabilized. This phenomenon occurred at each level of surcharge.
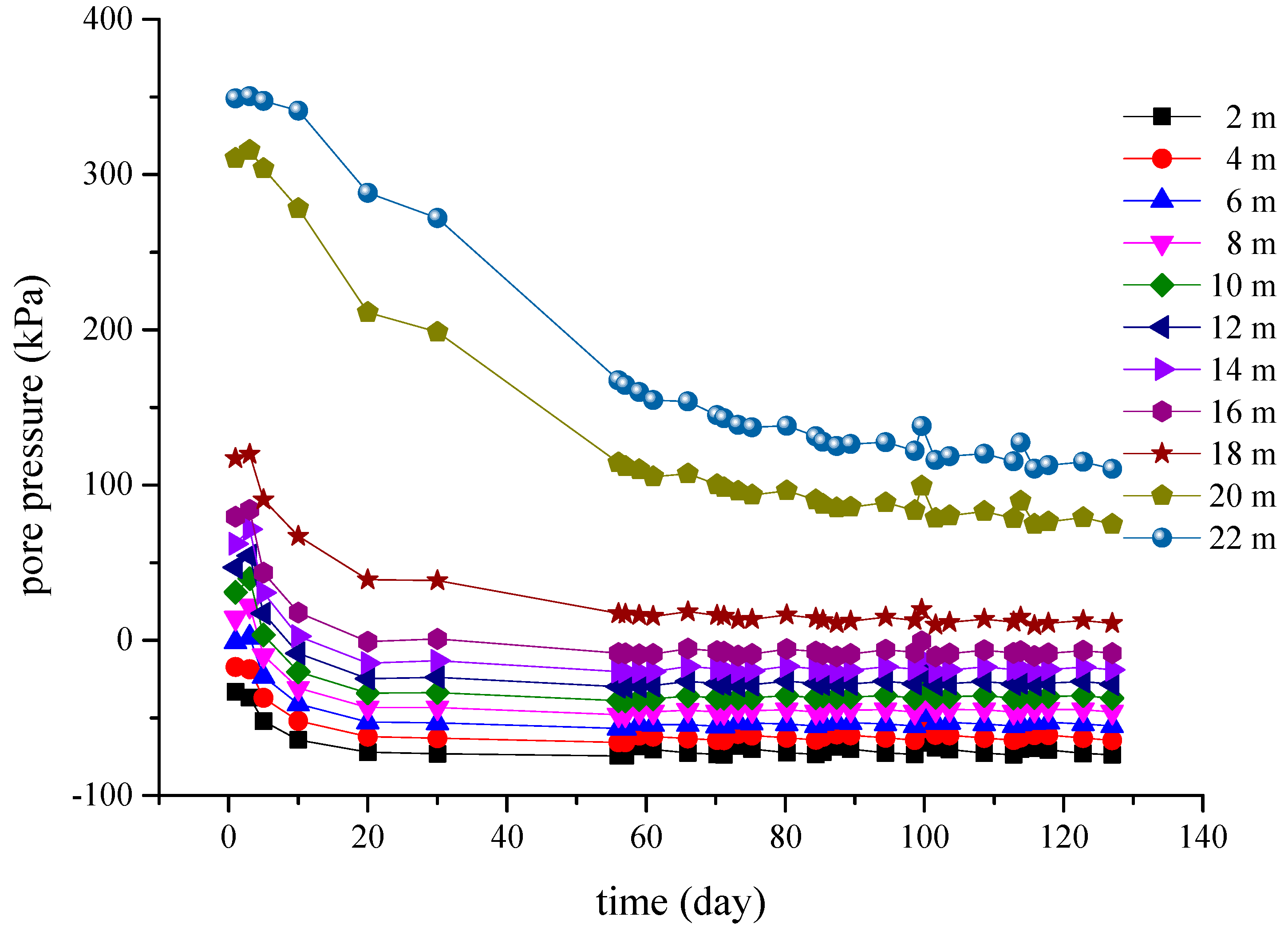
In actual construction, the filling load would not be applied at the moment in which it would be divided into fixed five levels, as in the computer calculation, so the measured pore pressure curve would not be subjected to significant adjustment s in fluctuation. The calculated pore water pressure data were sorted out, and the curve of the layered pore water pressure versus time was drawn, as shown in
Figure 8. The initial pore pressure at each point in the soft foundation was the static water pressure. After vacuum pumping, all points in the soil decreased to varying degrees. From 0 to 20 d, the pore water pressure at the depth of 18 m significantly decreased. From 20 to 30 d, the rate of pore water pressure significantly decreased and gradually became stable. After 30 d, the pore water pressure at each depth was basically unchanged and was maintained at a constant value. The pore water pressure at the depth of 16 m was finally stabilized at about 0 kPa. The pore water pressure of the soil layer above 16 m was negative, and the pore water pressure of the soil layer below 16 m was positive, indicating that the range of influence of vacuum pumping was about 16 m. The final value of the pore water pressure in the stage of vacuum preloading was basically consistent with that in the stage of combined vacuum–surcharge preloading, which indicated that the pore water pressure of the soil mass instantaneously fluctuated when each level of surcharge was applied, and the final pore water pressure field of the soft foundation under combined vacuum–surcharge preloading was determined by the vacuum load.
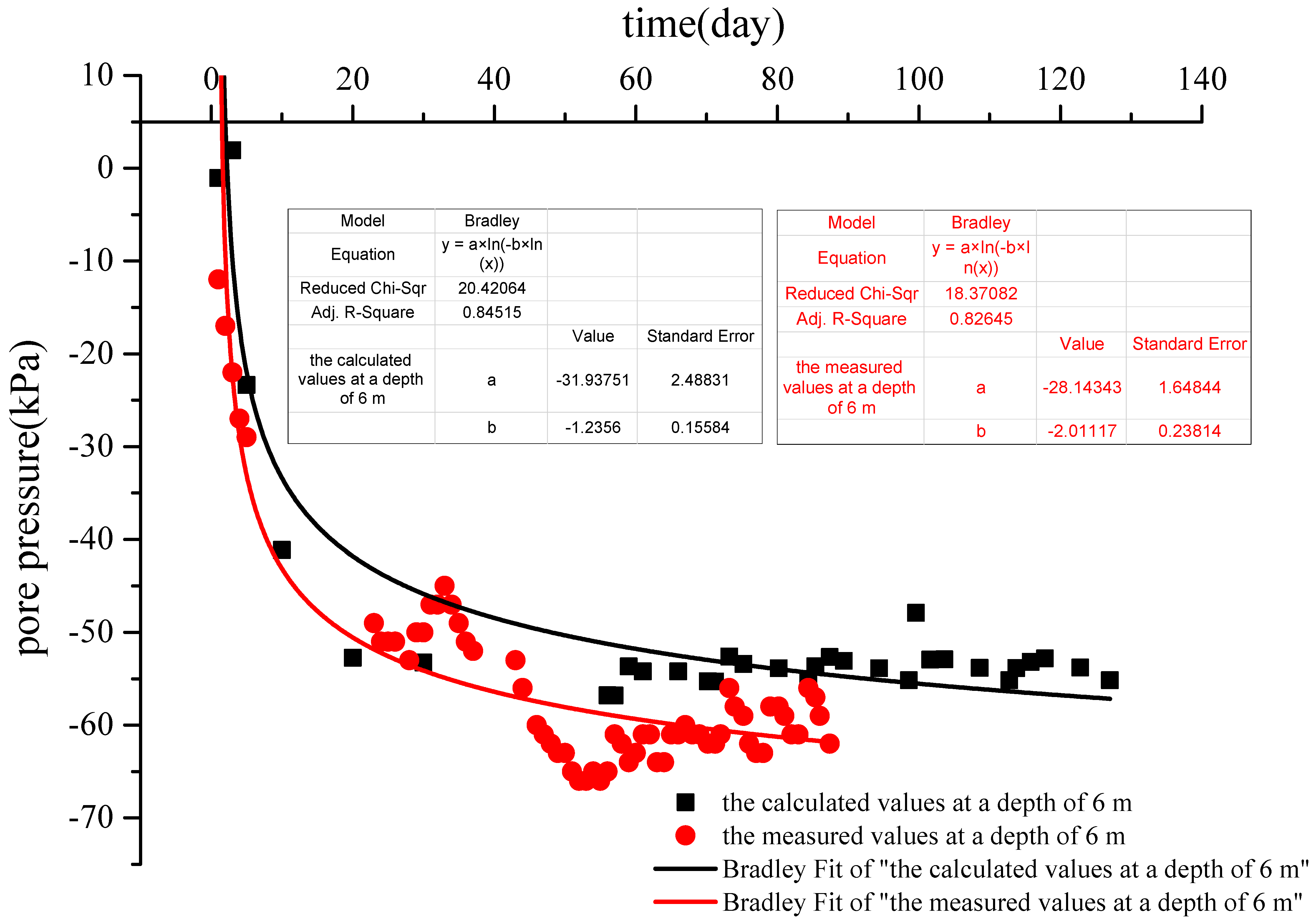
Figure 9 shows a scatter–plot and logarithmic fitting curve of the calculated and measured pore water pressures at a depth of 6 m as a function of time. The trend of variation in the scatter–plots of the calculated values and the measured values was basically consistent, and it fit well in the vacuum preloading stage (0–56 d); the gap was about 10 kPa in the combined vacuum–surcharge preloading stage. The measured pore pressure rose in about 30 days because the pump was stopped at the construction site. After continuing to apply the vacuum, the pore pressure dropped into the original trajectory of change. The measured values and the calculated values ultimately tended toward a final constant pore pressure in the vacuum preloading stage. The actual surcharge caused the pore pressure to rise, and the uniformly distributed load applied in the computer also caused the pore pressure to slightly rise, but the rise was not obvious.
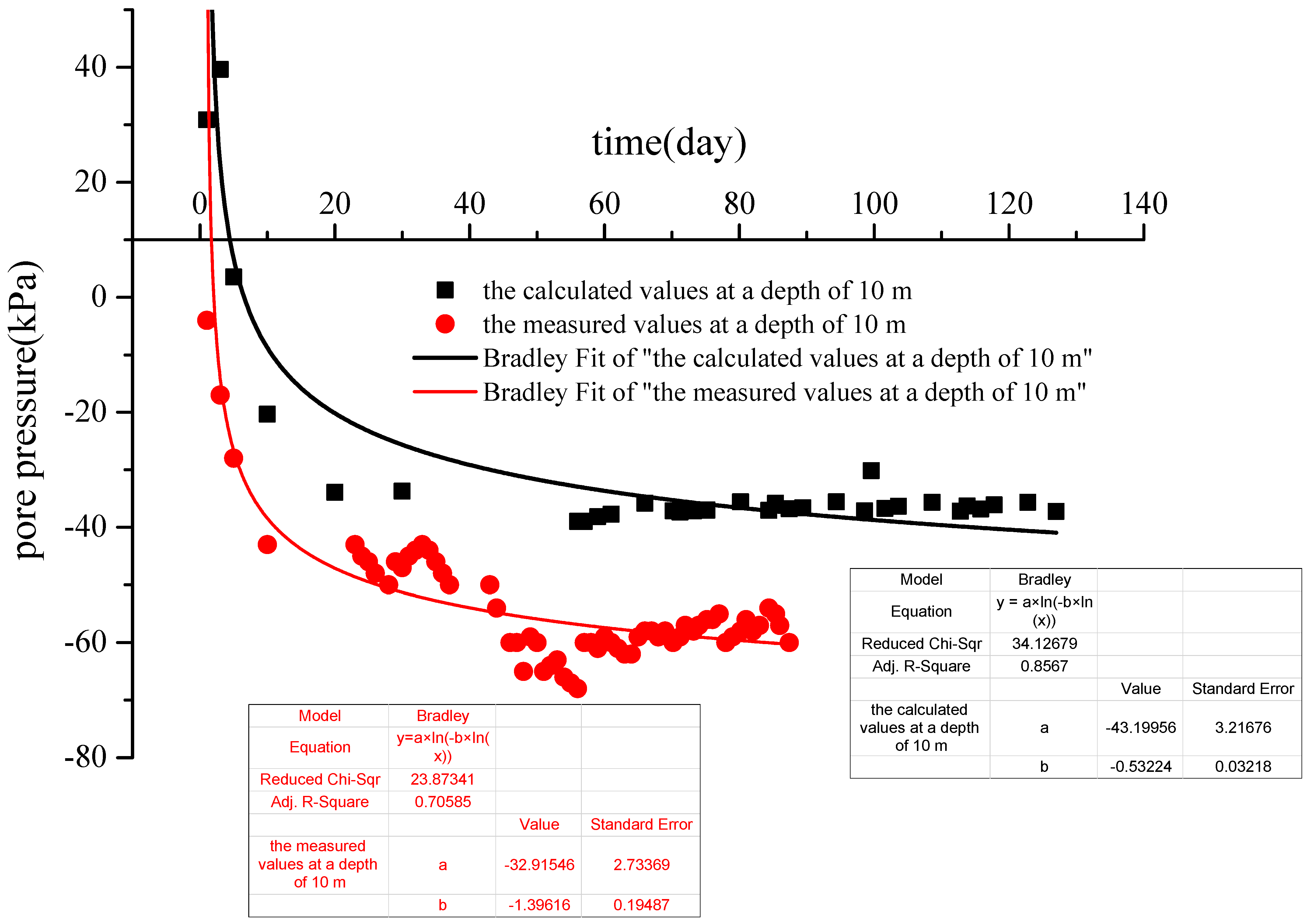
Figure 10 shows the scatter–plots and logarithmic fitting curves of the calculated and measured pore pressures at a depth of 10 m over time. The trend of variation in the calculated values was consistent with that of the measured values. The calculated pore pressure in the vacuum preloading stage (0–56 d) was more consistent with the measured values than in the combined vacuum–surcharge preloading stage (56–127 d). At about 30 days the measured pore pressure at a depth of 10 m rebounded and was the same as the pore pressure at a depth of 6 m. This was due to a pump shutdown at the site. After continuing to vacuum, the pore pressure dropped into the original trajectory of change. The calculated values of the pore water pressure were quite different from the measured values, which may have been caused by the deep calculation depth. The measured values and calculated values of the pore pressure ultimately tended to a final constant pore pressure value in the vacuum preloading stage. The actual surcharge caused the pore pressure to rise, and the uniformly distributed load applied during the calculation process also caused the pore pressure to slightly rise, but the rise was not significant.
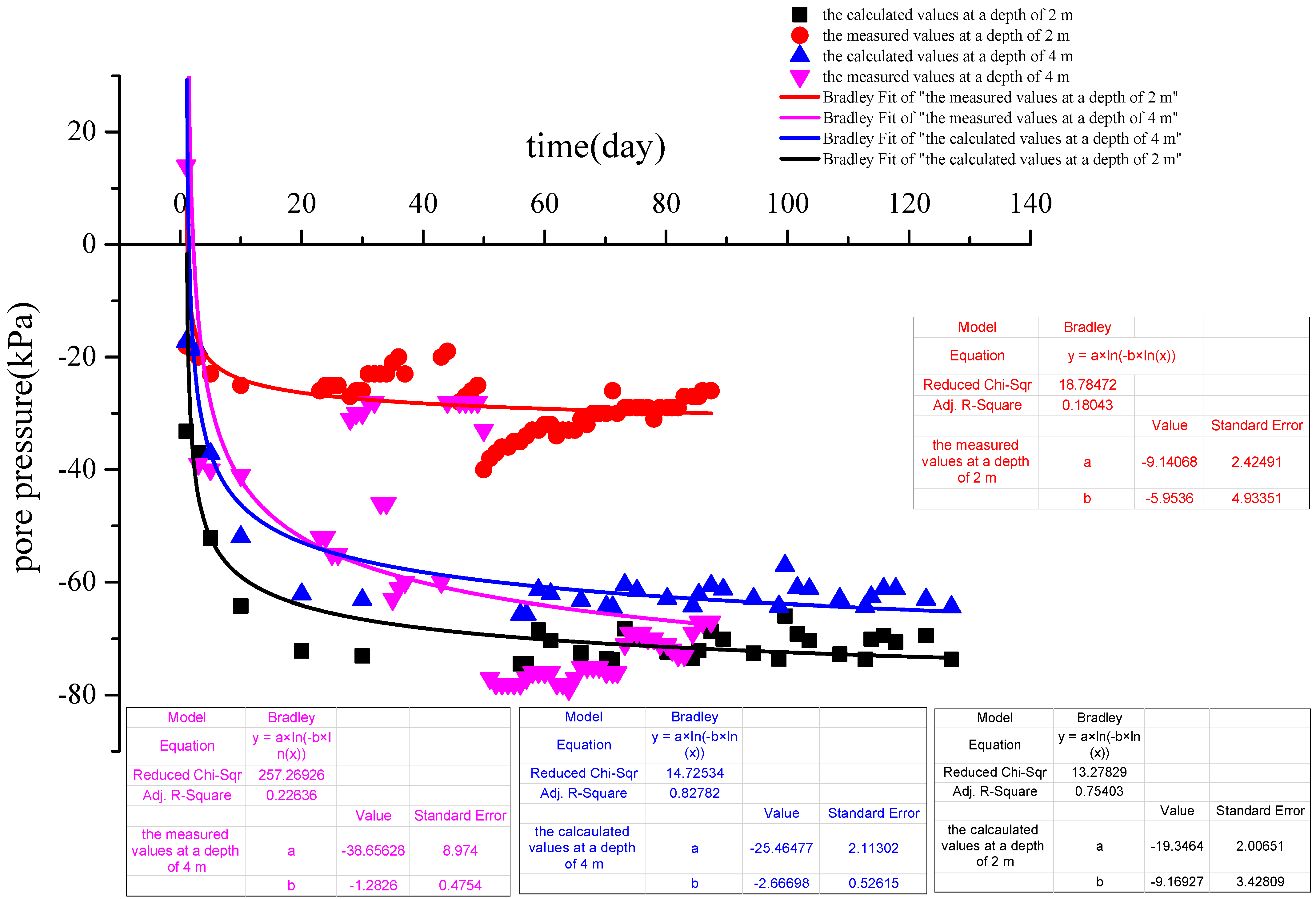
Figure 11 shows the scatter–plots and logarithmic fitting curves of the calculated and measured pore pressures at depths of 2 m and 4 m (shallow soil) over time. The trend of the variation in the calculated values at depths of 2 m and 4 m was consistent with that of the measured values in the scatter–plot. The calculated values at a depth of 4 m were in good agreement with the measured values. The calculated values at a depth of 2 m were highly discrete from the measured values, which may have been caused by problems with the pore pressure monitoring equipment.
It is not easy to accurately predict the changes in pore water pressure and settlement in soft foundations strengthened by vacuum-surcharge preloading. It is even more difficult to ensure that the simulation results of pore water pressure are consistent with the measured values, while also ensuring that the simulation results of settlement are consistent with the measured values. On the other hand, the measured values of pore water pressure are closely related to the burial of pore pressure gauges. If the pore pressure gauge malfunctions during construction, it is also difficult to accurately measure the pore water pressure. Therefore, when calculating pore water pressure, we mainly examine whether the trend of changes in pore water pressure is consistent with the trend of measured values.
5. Conclusions
A test project of vacuum–surcharge preloading for soft foundation reinforcement on the Beijing–Shanghai high–speed railway was introduced. A three–dimensional foundation consolidation model using fluid–solid coupling with a single sand drain of a large size in the depth direction was established, and the consolidation process of the soft foundation was calculated. The main conclusions were as follows.
(1) The three–dimensional fluid–solid coupling consolidation model can be used for the numerical analysis of vacuum–surcharge preloading. The actual sequence of load application should be considered. The influence of the initial stress cannot be ignored. Treatment with a vacuum load can be realized by adjusting the pore pressure at the top node of the model and the sand–drain node.
(2) In the stage of vacuum preloading alone, the settlement and pore pressure were evenly distributed on the horizontal plane, and the “pot–bottom” phenomenon was not obvious. In the stage of combined vacuum–surcharge preloading, the phenomenon of the “pot–bottom “ of the settlement and pore pressure on the horizontal surface gradually became obvious with the increase in the surcharge. This showed that the consolidation behaviors of soil under a vacuum and surcharge are different.
(3) In the numerical calculation, the pore pressure and settlement fluctuate greatly at the moment at which each level of surcharge was applied, while the actual construction has little fluctuation in the pore pressure and settlement due to the uniform filling and short interval. The changes in the settlement were basically consistent with the measured values after the adjustment of positive and negative pressure, and the variation trend of the pore pressure was consistent with the measured value.
(4) The final pore pressure at a depth of 16 m was stabilized at about 0 kPa, the final pore pressure of the soil layer above 16 m was negative, and the final pore pressure of the soil layer below 16 m is positive. This showed that the vacuum’s influence depth could reach at least 16m.
(5)The final value of pore pressure in the vacuum preloading stage was basically the same as that in the combined vacuum–surcharge preloading stage, indicating that the final pore pressure field of the soft foundation when subjected to combined vacuum–surcharge preloading was determined by the vacuum load.
(6) The actual application sequence of a vacuum load and surcharge load should be considered in the design and prediction of the settlement and pore pressure of a soft foundation that is strengthened by using vacuum–surcharge preloading. It is recommended to strengthen the soil with vacuum preloading alone for 2–4 months, and then to further strengthen it with graded surcharge loads until the surcharge height reaches the designed elevation of the fill.
This paper established a three–dimensional fluid–solid coupling model for a single sand-drain vacuum–surcharge preloading foundation, without considering the impacts of multiple sand-drains. If the influence of the group sand-drains is considered, three–dimensional modeling and calculation will be extremely difficult, but this could be used as a future research direction.
Author Contributions
M.L.: Writing—original draft. S.L.: Conceptualization. J.C.: Data curation. R.Z. and X.K.: Formal Analysis. J.J.: Software. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (42107166), Hunan Provincial Natural Science Foundation (Nos 22021JJ40632, 2021JJ30758 and 2022JJ40521), Key project of Teaching Reform Research in Hunan Province (HNJG-2021-0209) and Changsha Municipal Natural Science Foundation (Nos: kq2202065 and kq2202063).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data, models, and code generated or used during the study are available from the corresponding author by request.
Acknowledgments
We want to express our sincere thanks to the editor and four anonymous reviewers, who contributed their time, effort, and patience in reading the manuscript conscientiously and providing some insightful comments.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Lei, M.; Xu, H.; Kuang, X.; Xia, L. Analysis of consolidation mechanism and example of treating soft foundation in vacuum preloading. J. Railw. Sci. Eng. 2019, 16, 1433–1439. [Google Scholar]
- Liu, S.; Sun, H.; Geng, X.; Cai, Y.; Shi, L.; Deng, Y.; Cheng, K. Consolidation considering increasing soil column radius for dredged slurries improved by vacuum preloading method. Geotext. Geomembr. 2022, 50, 535–544. [Google Scholar] [CrossRef]
- Bergado, D.T.; Jamsawang, P.; Jongpradist, P.; Likitlersuang, S.; Pantaeng, C.; Kovittayanun, N.; Baez, F. Case study and numerical simulation of PVD improved soft Bangkok clay with surcharge and vacuum preloading using a modified air-water separation system. Geotext. Geomembr. 2022, 50, 137–153. [Google Scholar] [CrossRef]
- Dong, Z. Consolidation theory on heaped load & vacuum preloading of sand drain foundation. Port Waterw. Eng. 1992, 9, 1–7. [Google Scholar]
- Bao, S.; Zhou, Q.; Chen, P. Consolidation analysis for sand drains foundations with non-uniform distribution of negative pressure boundary condition. Port Waterw. Eng. 2015, 3, 12–20. [Google Scholar]
- Zhou, Q.; Zhang, G.; Wang, Y. Hansbo’s consolidation solution for sand-drained ground under vacuum preloading. Chin. J. Rock Mech. Eng. 2010, 29 (Suppl. 2), 3994–3998. [Google Scholar]
- Hu, Y. A Hansbo’s consolidation solution of sand-drained ground with impeded boundaries under vacuum and surcharge preloading. Chin. J. Eng. 2018, 40, 783–792. [Google Scholar]
- Guo, B.; Gong, X.; Lu, M. Analytical solution for consolidation of vertical drains by vacuum-surcharge preloading. Chin. J. Geotech. Eng. 2013, 35, 1045–1054. [Google Scholar]
- Lin, W.; Jiang, W.-H.; Zhang, L.-T. General analytical solution for consolidation of sand-drained foundation considering the vacuum loading process and the time-dependent surcharge loading. Rock Soil Mech. 2021, 42, 1829–1838. [Google Scholar]
- Nguyen, T.N.; Bergado, D.T.; Kikumoto, M.; Dang, P.H.; Chaiyaput, S.; Nguyen, P.C. A simple solution for prefabricated vertical drain with surcharge preloading combined with vacuum consolidation. Geotext. Geomembr. 2021, 49, 304–322. [Google Scholar] [CrossRef]
- Cheung, Y.K.; Lee, P.K.; Xie, K.H. Some remarks on two and three dimensional consolidation analysis of sand-drained ground. Comput. Geotech. 1991, 12, 73–87. [Google Scholar] [CrossRef]
- Hird, C.C.; Pyrah, I.C.; Russel, D. Modeling the effect of vertical drains in two–dimensional finite element analysis of embankments on soft ground. Can. Geotech. J. 2011, 32, 795–807. [Google Scholar] [CrossRef]
- Indraratna, B.; Redana, I.W. Numerical modeling of vertical drains with smear and well resistance installed in soft clay. Can. Geotech. J. 2000, 37, 132–145. [Google Scholar] [CrossRef]
- Chai, J.C.; Shen, S.L.; Miura, N. Simple method of modeling PVD-Improved subsoil. J. Geotech. Geoenvironmental Eng. 2001, 127, 965–972. [Google Scholar] [CrossRef]
- Sha, L.; Liu, H.; Wang, G. Finite element analysis on large deformations of dredger fill improved by combined vacuum and surcharge preloading. J. Zhejiang Univ. Technol. 2021, 49, 140–146. [Google Scholar]
- Wang, D.; Wei, D.; Lin, G.; Zheng, J.; Tang, Z.; Fan, L.; Yuan, B. Finite Element Analysis of Vertical and Horizontal Drainage Structures under Vacuum Combined Surcharge Preloading. Adv. Civ. Eng. 2021, 2021, 9448436. [Google Scholar] [CrossRef]
- Zhao, Y.; Luo, S.; Wang, Y.; Wang, W.; Zhang, L.; Wan, W. Numerical Analysis of Karst Water Inrush and a Criterion for Establishing the Width of Water-Resistant Rock Pillars. Mine Water Environ. 2017, 36, 508–519. [Google Scholar] [CrossRef]
- Zhu, C.; Long, S.; Zhang, J.; Wu, W.; Zhang, L. Time Series Multi–Sensors of Interferometry Synthetic Aperture Radar for Monitoring Ground Deformation. Front. Environ. Sci. 2022, 10, 929958. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, D. FLAC/FLAC3D Foundation and Engineering Example; China Water Power Press: Beijing, China, 2013. [Google Scholar]
- Qian, J. Soil Mechanics, 1st ed.; Hohai University Press: Nanjing, China, 1988; 77p. [Google Scholar]
- Gao, C.; Zhang, L.; Wang, Z.; Wei, R. Equivalent diameter of prefabricated drains. Hydro-Sci. Eng. 2002, 2002, 28–32. [Google Scholar]
- Holtz, R.; Jamiolkowski, M.; Lancellotta, R. Prefabricated Vertical Drains: Design and Performance, 1st ed.; Plymouth Company Ltd.: London, UK, 1991; pp. 9–56. [Google Scholar]
- Dai, G.; Gu, H. Soil Mechanics and Foundation Engineering, 1st ed.; Chongqing University Press: Chongqing, China, 2017; 408p. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).