Abstract
In shipbuilding gantry cranes in long-term service in the coastal humid salt-spray environment, the main beam is affected in many places by corrosion fatigue-formed corrosion pits, affecting the structural strength of the main beam. This paper focuses on the impact of corrosion-generated pits under the conditions of crack nucleation. Corrosion fatigue crack nucleation is a local damage evolution process and the stress intensity factor criterion is one of the critical conditions to discern whether a crack sprouts at the corrosion pit. This paper establishes a corrosion pit-crack model based on the overall finite element model of the portal crane, and uses ANSYS software to simulate the stress intensity factor under complex boundary conditions. The results show that the different sizes and depth-to-diameter ratio of the pits greatly affect the value of the stress intensity factor and the stress concentration phenomenon may be the main factor causing the emergence of cracks; the change in the size of the pits on the stress intensity factor is not obvious, but with the increase in the depth-to-diameter ratio of the pits, the stress intensity factor of the pit-crack model is significantly increased. According to the hypothesis of semi-ellipsoidal pitting, the relationship between the stress intensity factor and the stress concentration factor at the pit is proposed, and its calculation results are within 5% error compared with the finite element method, and it is found that the effect of the etch pit on the stress intensity factor is positively correlated with the stress concentration factor; with the increase in the etch pit depth–diameter ratio, the crack budding location changes with the change in the stress concentration location, and the crack is more likely to be generated from the shoulder of the etch pit when the depth–diameter ratio of etch pit exceeds 1.
1. Introduction
The gantry crane main girder is a box structure, consisting of side walls, a top plate and a lower cover plate, which has high strength and resistance to deformation and is usually used to carry heavier loads. The girder structure of the gantry crane is subjected to corrosion by salt and chloride ions in the open ocean environment for long periods of time and produces large corrosion pits, as shown in Figure 1. The extent to which these larger pits affect the gantry crane structure is the key to studying its remaining fatigue life. When the gantry crane is under load, the edges of the corrosion crater profile will produce severe stress concentration phenomena leading to the emergence of cracks, seriously jeopardising the strength and damage tolerance performance of the components, which eventually leads to fracture failure of the sheet metal.

Figure 1.
Portal crane and main beam etching pit diagram.
In order to understand the effect of pitting corrosion on crack initiation and expansion, a number of in-depth studies have been carried out by Pidaparti et al. [1], who systematically analysed the stress concentration at the edges of pitting corrosion; Kondon [2] first studied the transition from corrosion pits to corrosion fatigue cracks and proposed a theoretical model. Pyun et al. [3] carried out further research based on the model proposed by Kondon and found that early pitting evolution dominated during the coupled corrosion fatigue action and was subsequently replaced by fatigue crack extension. Rokhlin et al. [4] investigated the location of crack initiating at the corrosion pits; Huang Xiaoguang et al. [5] studied the energy principle of pitting evolution and corrosion fatigue crack nucleation, which determined the critical pitting size for crack nucleation based on the stress intensity factor criterion for the transformation of pitting to corrosion fatigue crack nucleation and predicted the corrosion fatigue crack nucleation life based on the energy principle. David Taylor and Pluvinage et al. [6,7] proposed a unified model of pitting and cracking based on the critical distance and the concept of pitting stress intensity factor through theoretical analysis and experimental validation. Heikki R et al. [8] proposed a simulation method of microscopic short cracks based on the fatigue mechanism of plastic irreversibility of the slip zone, and obtained the crack nucleation and the expansion law of microscopic short cracks. Tsunehiro T [9] et al. proposed the Tanaka–Mura model based on the nucleation mechanism of microscopic short cracks.
Many scholars have also used theories related to corrosion fatigue in engineering practice. Ziguang Chen [10] et al. used a near-field kinetic model to simulate the evolution of pitting damage; Alexander Hermann [11] et al. proposed a computational framework to predict the decrease in mechanical strength of metal models; Xu Shanhua et al. [12] studied the fatigue performance and fatigue fracture mechanism of rusted high-strength steel wires in bridges and provided an experimental basis for fatigue life evaluation of rusted high-strength steel wires based on the fracture mechanics theory; Song Deshuang and Yu Jianxing et al. [13,14] studied the pitting pit-crack stress intensity factor of pipes under the action of internal pressure; Yu Dazhao et al. [15] conducted fatigue tests on aerospace aluminum alloys and analysed the feasibility of equating corrosion pits to surface cracks.
When the metal components are subjected to corrosion and alternating loads at the same time, stress concentration is easy to occur at the initial defect, and corrosion fatigue damage also accumulates at this place. When the damage value reaches the critical state when the crack begins to sprout, many scholars in the metal specimens of pre-corrosion fatigue loading experiments found that cracks always initiate and expand from the corrosion pit [15,16,17,18]. In this paper, by analysing the stress values at the shoulder and bottom of the corrosion pits with different dimensional parameters and depth-to-diameter ratios, it was found that the maximum stress concentration gradually transitions from the bottom of the pit to the shoulder of the pit as the depth-to-diameter ratio increases, and the edges of the pit are also prone to cracking, as shown in Figure 2, which is different from the critical depth of crack initiation assumed by Kondon and the crack model prefabricated at the bottom of the pit used by other scholars [13,14,15]; therefore, it is still important to further study the stress concentration at the pit and analyse the effect of the pit as an initial defect on crack initiation and the critical size of crack nucleation at the pit. The semi-ellipsoidal pitting theory is applied to analyse the relationship between crack nucleation at the corrosion pit and the corrosion pit size depth-to-diameter ratio, and to calculate the critical characteristic stress value for crack nucleation at the pit and crack nucleation life prediction, the results of which can provide a reference for portal crane life safety assessment.

Figure 2.
Cracking at the edge of the corrosion pit.
2. Crane Finite Element Modelling and Sub-Modelling
According to the research object 900 t × 182 m shipbuilding portal crane structure, for the establishment of the finite element plate and beam cell model, as shown in Figure 3a, the total number of cells is 386,916 and the total number of nodes is 425,224, with boundary conditions according to the study conditions and 900 t load applied at the span of the main beam. As the overall structural finite element model of the portal crane is established by the plate and shell unit, it cannot directly simulate the tiny ellipsoidal erosion pits, and the size of the overall model mesh division is large, and the mesh needs to be refined when conducting local analysis, so the sub-model method of local structural analysis is used. The sub-model method, also known as the cut boundary displacement method or the specific boundary displacement method, is based on St. Venant’s principle and allows for refined analysis and the conversion of boundary conditions between different units using the sub-model method. This process is used to calculate the overall structural model, cut the locations to be analysed, extract the plate and shell unit boundary conditions for the difference calculation and apply them to the sub-model, and finally carry out the solution of the sub-model.
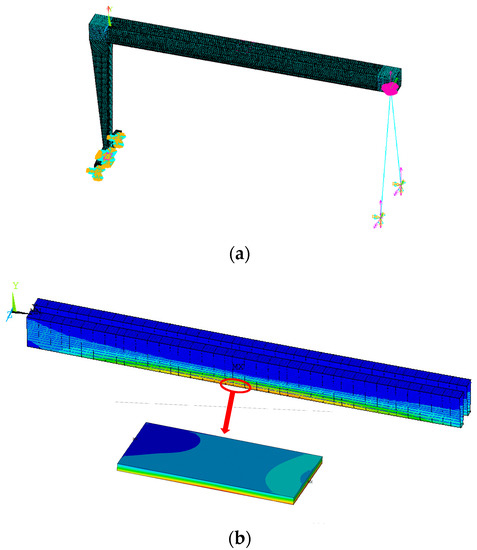
Figure 3.
Portal crane finite element models and sub-models. (a) Portal crane finite element model. (b) Portal crane finite element models and sub-models.
The sub-model is a flat plate with an ellipsoidal pit in the centre, with dimensions of 2000 × 1000 × 80 mm3, positioned at the lower cover at the span of the main beam of the portal crane plate and shell model, as shown in Figure 3b. The finite element crane integral model established for the plate and shell unit is extracted here to extract the boundary conditions and applied to the sub-model, where the effect of the stress intensity factor can be studied.
In the finite element method to calculate the stress intensity factor there is mainly the mutual integration method and the extended finite element method. In order to verify the accuracy of the mutual integration method and extended finite element method, two methods are used to simulate the crack in the sub-model, in the main beam lower cover plate smooth lower surface (no corrosion pits) perpendicular to the span direction of the main beam pre-set semi-circular crack, and the crack is a two-dimensional surface crack with zero thickness; the shape is shown in Figure 4a. The stress intensity factor is calculated when the crack is loaded in the portal crane span and the mutual integration method is used to calculate the type I, II and III stress intensity factor results as shown in Figure 4b–d.
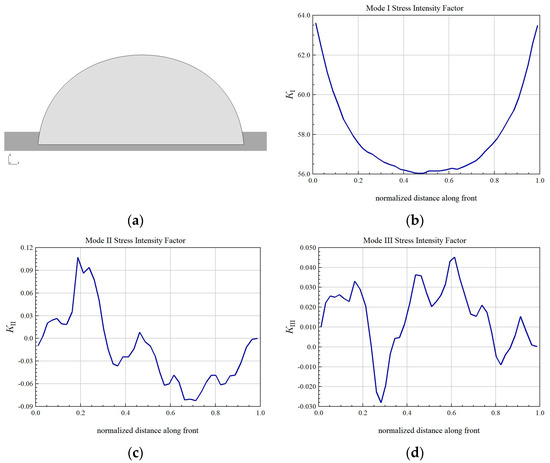
Figure 4.
Finite element calculations of stress intensity factors for cracks on the lower surface of the lower cover of the main beam in the absence of corrosion pits. (a) Semi-circular prefabricated cracks to a depth of 0.1 mm. (b) Type I stress intensity factor finite element calculation value. (c) Type II stress intensity factor finite element calculation values. (d) Type III stress intensity factor finite element calculation values.
Analysis of the main girder section of the portal crane can be seen, as shown in Figure 5a, when the load at the midspan of the main girder section box structure withstands the bending moment, as the main girder upper and lower cover plate are far away from the shape of the centre. Mechanical analysis can be considered as these are only subject to compressive and tensile stresses along the axis direction, and finite element calculation results also show that the span of the lower cover plate sub-model location of the first main stress along the section width direction of the stress gradient distribution is small in absolute value, as shown in Figure 5b. Thus, in the calculation of the stress intensity factor it is equivalent to the main girder lower cover plate which is subject to uniform tension in the axis direction, and theoretical calculations and finite element simulation results also show its reasonableness.
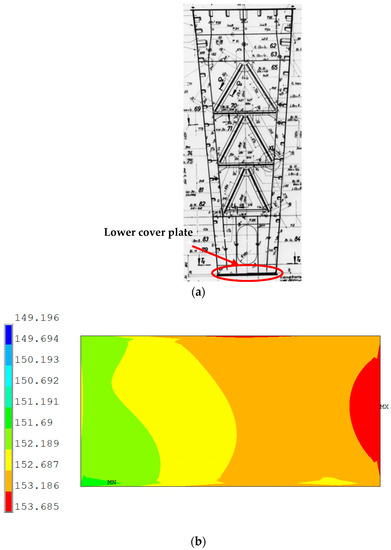
Figure 5.
Main girder cross-sectional structure of gantry crane with first principal stress cloud at mid-span position of the lower cover of the main girder. (a) Main beam section. (b) First principal stress cloud of the lower cover sub-model (elevation view).
The crack front strength factor for a surface crack with a semi-elliptical profile subjected to uniform tensile forces can be written as [19]
where the stress σ is given by the results of the sub-model under the calculated working conditions, taking a value of 152.36 MPa. The lower cover plate thickness h at the span of the portal crane is 80 mm; E(k) is the second type of fully elliptical integral; Mf is the surface shape correction factor, taking a fixed value of 1.03 according to the table; a is the crack radius; b is the crack depth; and the crack shape ratio b/a is 1.
The comparison of the results of the mutual integration method and the extended finite element method with the theoretical calculation Equation (1) is shown in Table 1. The mutual integration method has the same boundary conditions as the extended finite element method for calculating the model. It can be seen that the mutual integration method is more accurate, as its use of symmetric mesh can reduce the local discretization error, and the mutual integration is path-independent, which can bypass the crack tip singularity zone. The physical description of the crack tip by the XFEM method is still approximate, and although its solution is not grid-dependent, an accurate description of the stress-strain field at the crack tip still requires the use of the cells and nodes of the grid. When the crack tip is located inside the mesh, the crack tip profile will be cut into tiny line segments, which will not adequately describe the stress distribution at the crack tip, resulting in less accurate calculation results.

Table 1.
Type I crack stress intensity factor values for a smooth surface of the lower cover at mid-span of the main beam without corrosion pits.
Therefore, the stress intensity factor of the pit-crack model is calculated by the mutual integration method in all subsequent analyses in this paper, and the pitting pit and crack are taken as a whole model, to investigate the influence of pitting pit morphology and crack morphology on the crack stress intensity factor on the surface of the lower cover plate of the main beam under load in gantry cranes.
3. Corrosion Pit-Crack Model
As the pits are mostly found in the middle of the main beam cover where the water accumulates, away from the weld, the pit model is built at the base metal without considering the influence of the weld etc. The pit model is shown in Figure 6. The crater surface shape is a circle with radius r, the vertical profile is semi-elliptical, d is the crater depth, d varies along the depth direction when studying the crater model with different depth-to-diameter ratios, the cracks in the crater-crack model are simplified to semi-circular surface cracks, and the direction is perpendicular to the gantry crane main beam span direction, as shown in Figure 6b. The crack-sprouting process at the corrosion pit occurs under the combined influence of corrosion and fatigue loading. Tianliang Zhao et al. [20] found through corrosion fatigue tests that when the peak stress was close to or higher than the material yield stress, the crack sprouted from the corrosion pit into a nucleus, and then transformed into a crack at the bottom of the pit or at the stress concentration at the shoulder. The main reason for this process is the stress concentration caused by the etch pits, which causes the stress intensity factor at the crack nucleation to exceed the threshold stress intensity factor value ΔKth.
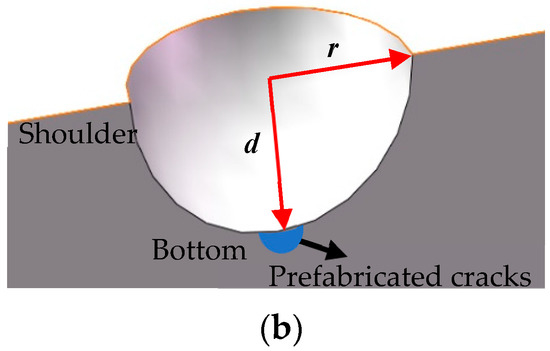
Figure 6.
3D model of an ellipsoidal corrosion pit. (a) Corrosion pit surface shape (top view). (b) Cutaway view of the pit-crack model.
As can be seen from Figure 7, for the same depth-to-diameter ratio of the corrosion pits, the expansion of the corrosion pits along the radius direction has a weak effect on the stress concentration, with an increase in the depth-to-diameter ratio of the stress concentration coefficient with the curve of the corrosion pit radius rise rate, but it is also limited and not obvious; the greater impact on the stress concentration is the change in the depth-to-diameter ratio, for the same radius of the corrosion pits, and the increase in the depth-to-diameter ratio greatly causes the stress concentration phenomenon. For different radii of the pit, the stress increase is more or less the same, with the maximum stress increase being around 50%; the stress concentration at the bottom of the pit is more obvious than at the shoulder of the pit when the depth-to-diameter ratio is low, and as the depth-to-diameter ratio increases, the maximum stress concentration area gradually transitions from the bottom of the pit to the shoulder of the pit, which means that cracks are more likely to emerge from the bottom of the pit when the pit is shallow, and surface cracks from the shoulder of the pit are more likely to occur when the pit is deeper.
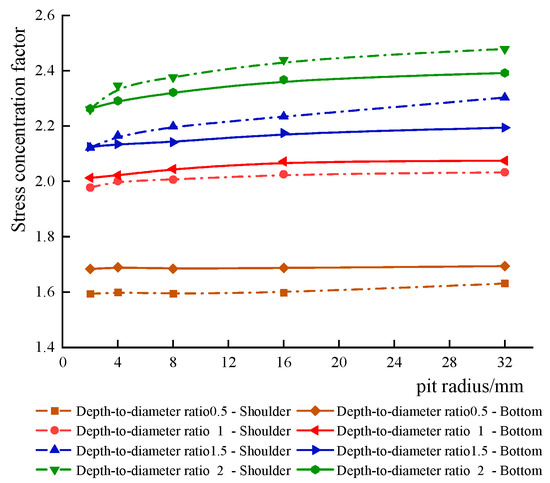
Figure 7.
Stress concentration coefficients at the shoulder and bottom of the corrosion pits at different sizes.
By studying the evolutionary distribution of pitting on metal surfaces, Harlow and Wei [21] concluded that pitting pit evolution is always a semi-long ellipsoid, and therefore ellipsoidal pits with different depth-to-diameter ratios (d/r) were used to simulate pitting in the solid modelling of pitting-cracking, as shown in Figure 8a. The cracks at the pitting corrosion need to be implanted with singular units at the crack tips due to the need to use the mutual integration method to ensure the accuracy of the stress intensity factor calculation, as shown in Figure 8b.
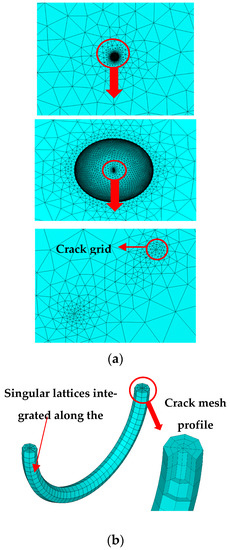
Figure 8.
Corrosion pit-crack finite element model and singular mesh at the crack front. (a) Pit-crack finite element model. (b) Cracked front odd grid.
4. Stress Intensity Factor Analysis of the Pit-Crack Model
The pit-crack model established in this paper is based on the “single dominant flaw approach” [22], i.e., although the actual sheet metal produces multiple corrosion pits at the same time (individually or in a series), only the deepest pits reaching a critical depth are considered for transformation into cracks. As the crane main beam lower cover plate is under the surface of the three-way stress to the tensile stress, for the possible emergence of the main beam cross-sectional direction of the most dangerous open type of crack, Figure 6 shows the stress intensity factor calculation, and it also shows that the type I stress intensity factor is dominant. The type II and III stress intensity factors are too small to be negligible, so this paper mainly analyses the most dangerous type I stress intensity factor and the relationship between the different corrosion pit sizes.
A corrosion pit-crack model with different depth-to-diameter ratios was developed and the effect of corrosion pits on the stress intensity factor of prefabricated cracks at different initial depths is shown in Figure 9. It can be seen clearly that the different sizes of the corrosion pits all greatly affect the stress intensity factor at the crack fronts, and the stress intensity factor increases when the depth-to-diameter ratio increases; with the increase in the depth of the precast crack, the growth trend of the stress intensity factor decreases continuously, which corresponds to the stress intensity factor in the expression of the stress intensity factor proportional to the 1/2 power of the crack radius. The increase in the stress intensity factor at different depths of cracks becomes progressively slower as the pit depth-to-diameter ratio increases, which may be due to an increase in the depth-to-diameter ratio of the pit resulting in a change in the location of the maximum stress concentration in the inner wall of the pit. The previous analysis of the stress concentration at the corrosion pits also showed that as the depth-to-diameter ratio increases, the maximum stress concentration area gradually transitions from the bottom of the corrosion pits to the shoulders of the corrosion pits, resulting in a weakening of the stress concentration at the bottom of the corrosion pits and a slowing of the increase in the stress intensity factor. Based on this pattern, the effect of different depth-to-diameter ratios on the stress intensity factor of surface cracks at the bottom of the pit and the stress intensity factor of cracks at the shoulder of the pit were investigated.
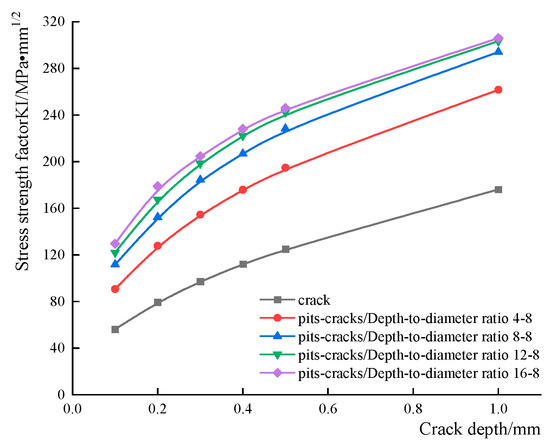
Figure 9.
Effect of pit size and precast crack depth on stress intensity factor.
This paper studies the critical conditions for the transition from pits to cracks. The size of the crack in the pit-crack model needs to be much smaller than the size of the pit, but it is generally considered that the crack expansion is slow when the microcrack size is too small, and the crack “starts to expand” only when the stress intensity factor reaches the expansion threshold. A semi-circular crack with a radius of 0.1 mm was selected as a prefabricated crack for subsequent analysis. Set different sizes and depth of the etch pits, the size parameters are shown in Table 2. The trend of the stress intensity factor for different sizes of pits is shown in Figure 10, and the stress cloud at the location of the crack at the pit is shown in Figure 11. It can be seen that the stress intensity factor is not sensitive to the change in pit radius, and the rising trend of all four curves in the figure is relatively flat when the pit radius has a large increase, while the stress intensity factor of different pit radii has a large increase when the depth-to-diameter ratio increases, and this phenomenon is the same as the change in stress values at the shoulder and the bottom of the pit with different size parameters, as in the previous paper. The crack nucleation process may not be directly associated with the expansion of the pit, but the pit acts as a medium in the process of being subjected to the coupling effect of corrosion and fatigue, and its macroscopic and microscopic morphological changes cause severe stress concentration phenomena.

Table 2.
Type I stress intensity factor values when the crack is at the bottom of the pit at different depth-to-diameter ratios.
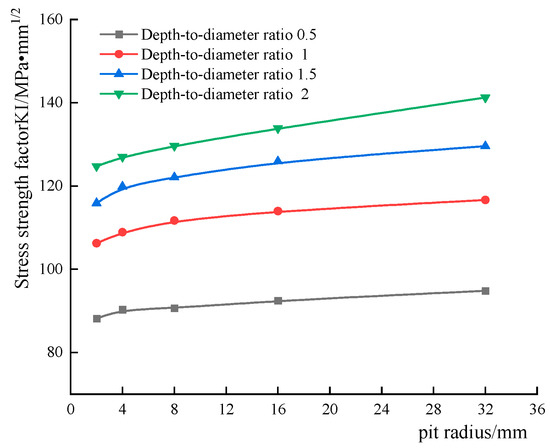
Figure 10.
Trend of type I stress intensity factor when cracks are at the bottom of the corrosion pit at different depth-to-diameter ratios.
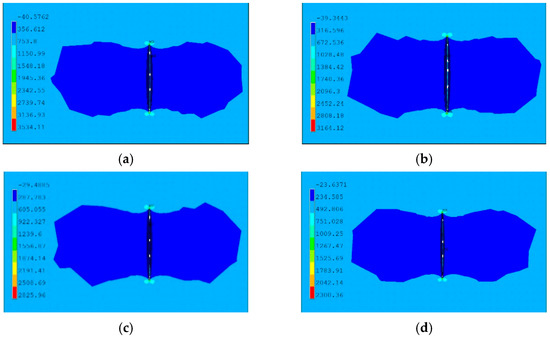
Figure 11.
First principal stress clouds of cracks at the bottom of corrosion pits with different depth-to-diameter ratios (deformation magnified by 30×). (a) r = 32 d = 64. (b) r = 32 d = 48. (c) r = 32 d = 32. (d) r = 32 d = 16.
By further analysing the correlation between the stress concentration phenomenon and the stress intensity factor, according to the semi-ellipsoidal pitting assumption, a semi-infinite body containing a hemispherical pit is equivalent to an infinite plane containing a two-dimensional semi-circular surface crack [23], so the stress intensity factor Kp at the pit can be written as an expression for the stress concentration factor, stress and crack size.
where Kt is the stress concentration factor, b is the crack depth, σ is the stress value and Mf is the shape correction factor; the above equation can be written further in the form of Equation (3).
where KI is the type Ⅰ stress intensity factor under smooth and defect-free material, and the analysis is replaced by the value calculated by the mutual integration method in Table 1, which is brought into Equation (3) and the theoretical assumption KIP is calculated, compared with the stress intensity factor calculated for the precast cracks at the corrosion pits, as shown in Figure 12. There is an interval effect of the pit depth-to-diameter ratio on the value of the shape correction factor, and the shape correction factor M under different depth–diameter ratios is shown in Table 3, which increases slowly with the increase in the depth–diameter ratio. It can be seen from Figure 12 that the assumed stress intensity factor curves at different depth–diameter ratios fit well with the finite element calculation curves, and the accuracy of the KIP calculation is higher when the depth–diameter ratio is smaller, and the overall error is within 5%, so it can be considered that Equation (3) can calculate the stress intensity factor value of the crack at the pit with good accuracy. This also indicates that crack nucleation may not be directly related to the corrosion depth of the pit, but due to the macroscopic and microscopic morphological changes caused by the corrosion of the pit, which are caused by the local stress concentration caused by the crack, and the location of the stress concentration from the above analysis is not always in the bottom of the pit.
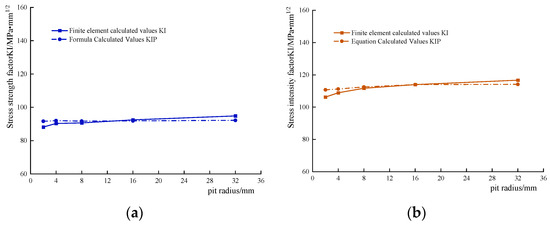
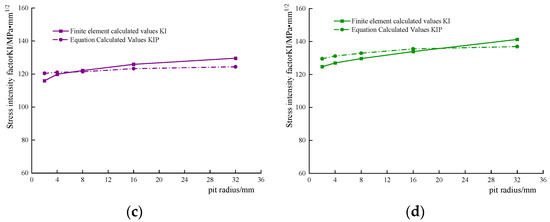
Figure 12.
Comparison between the finite element calculated value KI and the theoretical formula calculated value KIP. (a) Depth-to-diameter ratio 0.5. (b) Depth-to-diameter ratio 1. (c) Depth-to-diameter ratio 1.5. (d) Depth-to-diameter ratio 2.

Table 3.
Theoretical assumptions KIP calculated values.
To further investigate the etch pit-crack sprouting, the location of the maximum stress concentration for each etch pit with different size parameters was identified on the basis of the previously established etch pit model, and cracks were prefabricated at the maximum stress concentration and compared with the previously calculated stress intensity factor for the prefabricated cracks at the bottom of the etch pit as shown in Figure 13. It can be seen that when the depth-to-diameter ratio is small, although the location of the stress concentration does not coincide with the bottom of the corrosion pit, the stress intensity factor values of the two are relatively close to each other. As the depth-to-diameter ratio increases, the maximum stress moves closer to the shoulder of the corrosion pit and there is a significant increase in the stress intensity factor value of the crack preformation at the maximum stress, with cracks more likely to sprout close to the shoulder of the pit when the depth-to-diameter ratio exceeds 1.
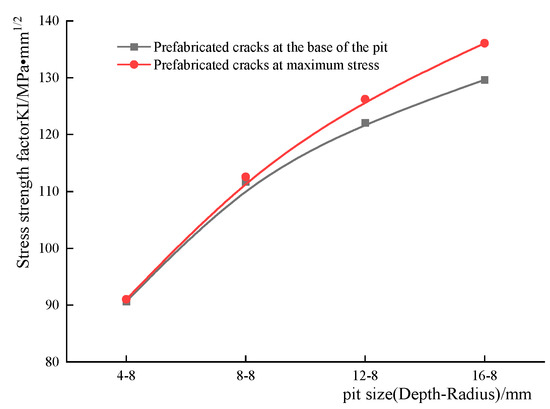
Figure 13.
Stress intensity factor values for crack preformation at different locations with different depth-to-diameter ratios.
5. Corrosion Fatigue Crack Nucleation Life Prediction
Even if a metal component is defect-free (ideally a smooth part without cracks) although the nominal stresses applied are less than the yield limit of the material, the material is not homogeneous at the microscopic level and local areas of the component surface can still slip. The process of repeated cyclic slip under external alternating loads produces a slip band of metal extrusion and squeezing, resulting in the formation of a nucleus of microcracks, and typically the process of corrosion fatigue crack nucleation takes up most of the overall corrosion fatigue life.
During the evolution of corrosion fatigue, the initial phase is dominated by pitting, which is then replaced by fatigue cracking extension. Kondon [2] proposed a criterion for the transformation of pitting to corrosion fatigue cracking based on the competing mechanisms between pitting evolution and corrosion fatigue crack extension, i.e., the development of pitting pits into corrosion fatigue, and cracks are subject to certain conditions:
This paper assumes that cracks leading to material damage only form “immediately” at the corrosion pit where a critical stress concentration is reached, but the time of crack initiation is actually the time between the growth of the pit and this stage, i.e., the transition from pit to crack when the fatigue crack growth rate exceeds the pit growth rate. Corrosion pit growth law can be expressed as:
where Cp is the coefficient, t is the time, N is the number of stress cycles, f is the frequency, and dp is the corrosion pit depth.
Mura and Nakasone [24] proposed a theory of Gibbs free energy change based on fatigue crack initiating, which assumes that the accumulated energy from the number of stress cycles reaches a critical value and causes crack initiating, but it does not consider the effect of cyclic loading and the interaction of the corrosive environment. The emergence and growth of pits is not only related to electrochemical corrosion but also influenced by fatigue stresses [25], and Ishihara [26] et al. found that the effect of stresses is expressed in the exponential form Cσ, and the relationship between pit depth and time can be further expressed as:
where M is the molecular weight of the corroding material, ρ is the density, n is the number of electrons released during corrosion, F is the Faraday constant, and Ip is the pitting current. Equation (2) in the critical stress intensity factor corresponds to the depth of the corrosion pit dPth, which is brought into the formula (6), and it can be obtained by:
It is important to note that although Equation (8) is expressed by dPth as the critical life depth of crack nucleation for pit growth, it is clear from the previous analysis that crack nucleation is not directly related to pit depth, but only when the actual stress concentration level at the pit reaches the critical threshold, causing the crack to initiate when the stress intensity factor exceeds ΔKth, at which point the time used for pit growth and the number of stress cycles can be approximated by Equations (7) and (8).
Through the above analysis, it can be seen that the crane main beam should be inspected with more attention to small and deep pits, which are more likely to produce more serious stress concentrations and thus cause cracks. The larger and gentler pits are smaller in diameter and should be inspected for small cracks at the bottom of the pits. Large pits that are prone to cracking can be polished to change their morphology and reduce the level of stress concentration to greatly extend the crack nucleation life.
6. Conclusions
- The stress values at the pit are not sensitive to the size of the pit, but are more strongly correlated with the depth-to-diameter ratio; as the depth-to-diameter ratio increases, the stress value at the maximum stress concentration rises and the stress concentration area gradually transitions from the bottom of the pit to the shoulder of the pit.
- The depth of the pit and the depth-to-diameter ratio together influence crack initiation, but their influence on crack nucleation is more likely to be reflected in the stress concentration caused by the shape of the pit, i.e., the stress concentration is the main factor that induces cracking, which is also likely to occur on the sidewalls and shoulders of the pit.
- The relationship between the stress intensity factor and the stress concentration factor at the erosion crater is proposed, and it is found that the effect of the erosion crater on the stress intensity factor is positively related to the stress concentration factor.
- When the established pit-crack model is an ideal model, the applied constraints and far-field stresses are also uniform. In this case the critical crack nucleation depth of the pit has a universal law; however, the actual construction machinery in the metal material which is subject to stress is complex and variable, and so a single critical depth determination loses meaning. As such, the critical stress concentration factor may be more representative of the criteria for determining the transformation of pits into cracks.
- The analysis of corrosion pits in large construction machinery carried out in this paper makes it possible to predict the nucleation life of corrosion fatigue cracks.
Author Contributions
Conceptualization and project administration, X.W. and F.Z.; methodology and software, F.Z.; validation, X.W., F.Z. and R.T.; investigation and resources, X.G., Y.W. and R.T.; data curation and writing—original draft preparation, F.Z. and X.W.; writing—review and editing, F.Z. and X.W.; supervision, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Liaoning Provincial University Innovation Team Project, grant number LT2014001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pidaparti, R.M.; Patel, R.R. Correlation between corrosionpits and stresses in Al alloys. Mater. Lett. 2008, 21, 57–62. [Google Scholar]
- Kondo, Y. Prediction of fatigue crack initiation life based on pit growth. Corrosion 1989, 45, 7–11. [Google Scholar] [CrossRef]
- Pyun, S.I.; Orr, S.J.; Nam, S.W. Corrosion fatigue crack initiation of Al-Zn-Mg-Mn alloy in 0.5 M Na2SO4 solution. Mater. Sci. Eng. A 1997, 241, 281–284. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Kim, J.Y.; Nagy, H.; Zoofan, B. Effect of pittingcorrosion on fatigue crack initiation and fatigue life. Eng. Fract. Mech. 1999, 62, 425–444. [Google Scholar] [CrossRef]
- Xiaoguang, H.; Jingquan, X. Energy principles of pitting evolution and corrosion fatigue crack nucleation. J. Solid Mech. 2013, 34, 7–12. [Google Scholar]
- Taylor, D. Geometrical effects in fatigue: A unifying theoretical model. Int. J. Fatigue 1999, 21, 413–420. [Google Scholar] [CrossRef]
- Pluvinage, G. Notch effects in high cycles fatigue. In Proceedings of the Nineth International Congress on Fracture (ICF9), Sydney, Australia, 1–5 April 1997; Pergamon: Oxford, UK, 1997; pp. 1239–1250. [Google Scholar]
- Heikki, R.; Petri, V.; Jani, R. Continuum approach to fatigue crack initiation and propagation in welded steel joints. Int. J. Fatigue 2012, 40, 16–26. [Google Scholar]
- Tsunehiro, T.; Tetsutaro, S. A dislocation model for fatigue crack initiation. Int. J. Appl. Mech. 1981, 48, 97–103. [Google Scholar]
- Shanhua, X.; Haijiang, Z.; Zhexun, Z.; Yaxin, W. Degradation mechanism and degradation law of fracture properties of rusted steel plates containing central cracks under static load. J. Southeast Univ. Nat. Sci. Ed. 2020, 50, 808–813. [Google Scholar]
- Chen, Z.; Bobaru, F. Peridynamic modeling of pitting corrosion damage. J. Mech. Phys. Solids 2015, 78, 352–381. [Google Scholar] [CrossRef]
- Hermann, A.; Shojaei, A.; Steglich, D.; Höche, D.; Zeller-Plumhoff, B.; Cyron, C.J. Combining peridynamic and finite element simulations to capture the corrosion of degradable bone implants and to predict their residual strength. Int. J. Mech. Sci. 2022, 220, 107143. [Google Scholar] [CrossRef]
- Deshuang, S.; Hu, Z.; Yun, Z.; Chao, W.; Kangkang, S. Study on pitting crater-crack stress strength factor of oil pipe under axial loading. Pet. Mach. 2021, 49, 116–122. [Google Scholar]
- Jianxing, Y.; Xiubo, L.; Yuna, T.; Chengxing, J.; Zhiqiang, F.; Xiangxi, H.; Fei, F. Stress intensity factor analysis of pipeline surface etch pits-cracks. J. Tianjin Univ. Nat. Sci. Eng. Technol. Ed. 2019, 52, 522–528. [Google Scholar]
- Dazhao, Y.; Yueliang, C.; Wenlin, L.; Yong, G.; Zhonghu, J. Analysis of the effectiveness of corrosion pits equivalent to surface cracks in service environment. J. Appl. Mech. 2011, 28, 79–84, 112. [Google Scholar]
- Youhong, Z. Corrosion Damage of Aircraft Structures and Its Effect on Life. Ph.D. Thesis, Northwestern Polytechnic University, Fremont, CA, USA, 2007. [Google Scholar]
- DuQuesnay, D.L.; Underhill, P.R.; Britt, H.J. Fatigue crack growth from corrosion damage in 7075-T6511 aluminum slloy under aircraft loading. Int. J. Fatigue 2003, 25, 371–377. [Google Scholar] [CrossRef]
- Dazhao, Y.; Yueliang, C. Effects of pitting corrosion on fatigue life of aluminum alloy LY12CZ based on initial discontinuity state. Trans. Monferrous Met. Soc. China 2006, 16, s1319–s1322. [Google Scholar]
- China Academy of Aeronautics. Handbook of Stress Strength Factors; Science Press: Beijing, China, 1981. [Google Scholar]
- Zhao, T.L.; Liu, Z.Y.; Du, C.W.; Dai, C.; Li, X.; Zhang, B. Corrosion fatigue crack initiation and initial propagation mechanism of E690 steel in simulated seawater. Mater. Sci. Eng. 2017, 708, 181–192. [Google Scholar] [CrossRef]
- Harlow, D.G.; Wei, R.P. A probability model for the growth of corrosion pits in aluminum alloys induced by constituent particles. Eng. Fract. Mech. 1998, 59, 305–325. [Google Scholar] [CrossRef]
- Sriraman, M.R.; Pidaparti, R.M. Crack initiation life of materials under combined pitting corrosion and cyclic loading. J. Mater. Eng. Perform. 2010, 19, 7–12. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Pidaparti, R.M.; Palakal, M.J. Comparative Study of Corrosion-Fatigue in Aircraft Materials. AIAA J. 2001, 39, 325–330. [Google Scholar] [CrossRef]
- Mura, T.; Nakasone, Y. A Theory of Fatigue Crack Initiation in Solids. J. Appl. Mech. 1990, 57, 1. [Google Scholar] [CrossRef]
- Chandrasekaran, V.; Yoon, Y.L.; Hoeppner, D.W. Analysis of Fretting Damage Using Confocal Microscope. In Fretting Fatigue: Current Technology and Practices; Hoeppner, D.W., Chandrasekaran, V., Elliott, C.B., Eds.; ASTM STP 1367; ASTM: West Conshohocken, PA, USA, 2000; pp. 337–351. [Google Scholar]
- Ishihara, S.; Saka, S.; Nan, Z.Y.; Goshima, T.; Sunada, S. Prediction of Corrosion-Fatigue Lives of Aluminum Alloy on the Basis of Corrosion Pit Growth Law, Fatigue Fract. Eng. Mater. Struct. 2006, 29, 472–480. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).