Solving Bi-Objective Vehicle Routing Problems with Driving Risk Consideration for Hazardous Materials Transportation
Abstract
1. Introduction
2. Driving Risk Evaluation
2.1. Driving Risk Impact Index
2.2. Weights of Criterion
3. Problem Formulation
3.1. Assumption
3.2. Symbols Definition
3.3. Risk and Cost
3.4. Mathematical Model
4. Solution Methodology
4.1. NSGA-II Algorithm
4.2. Encoding and Decoding
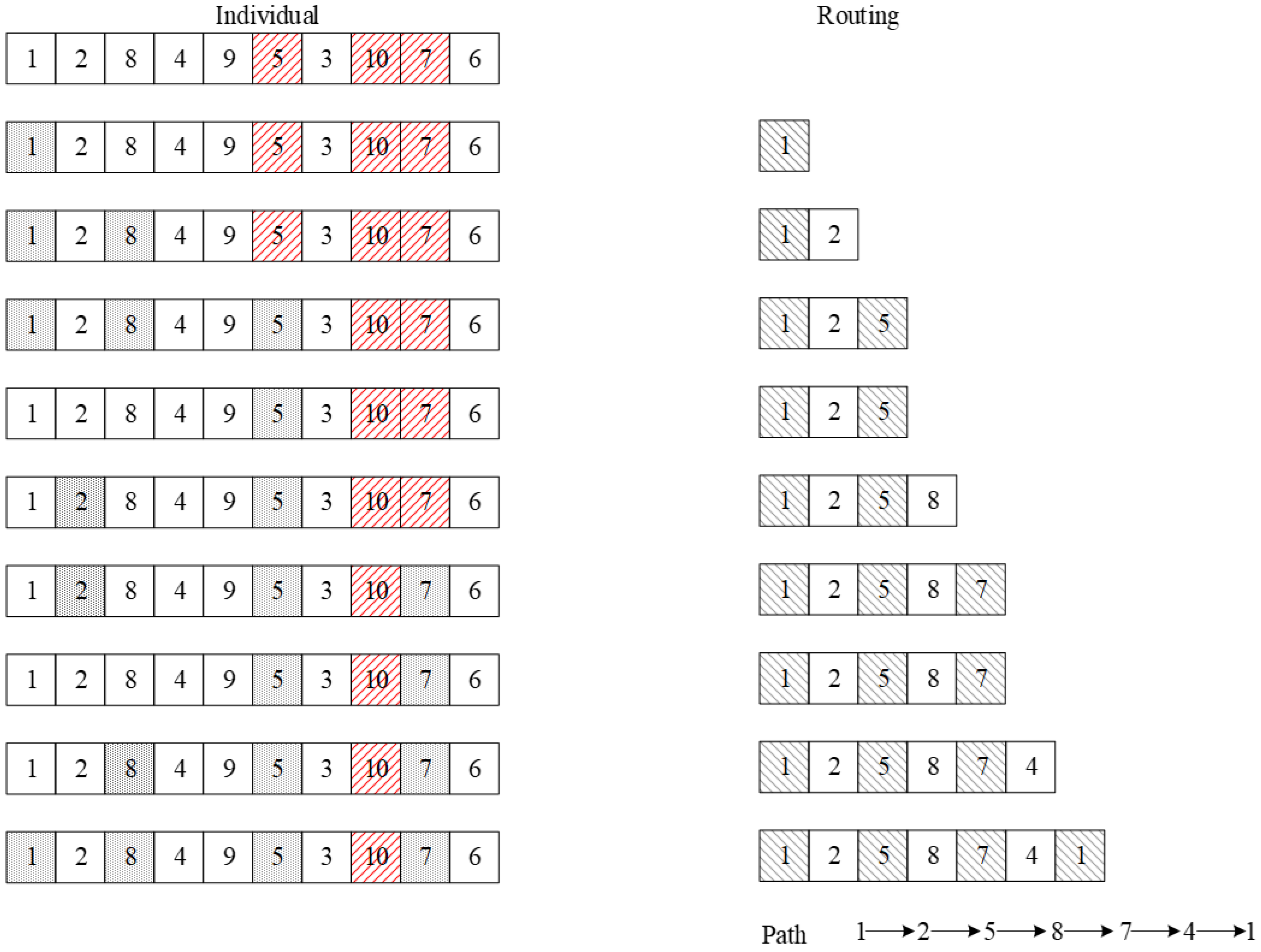
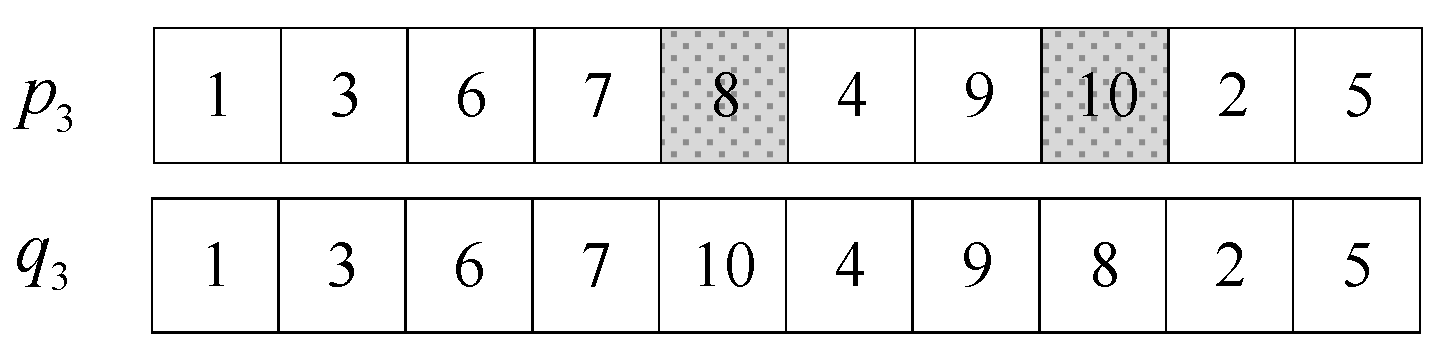
4.2.1. Encoding
4.2.2. Decoding
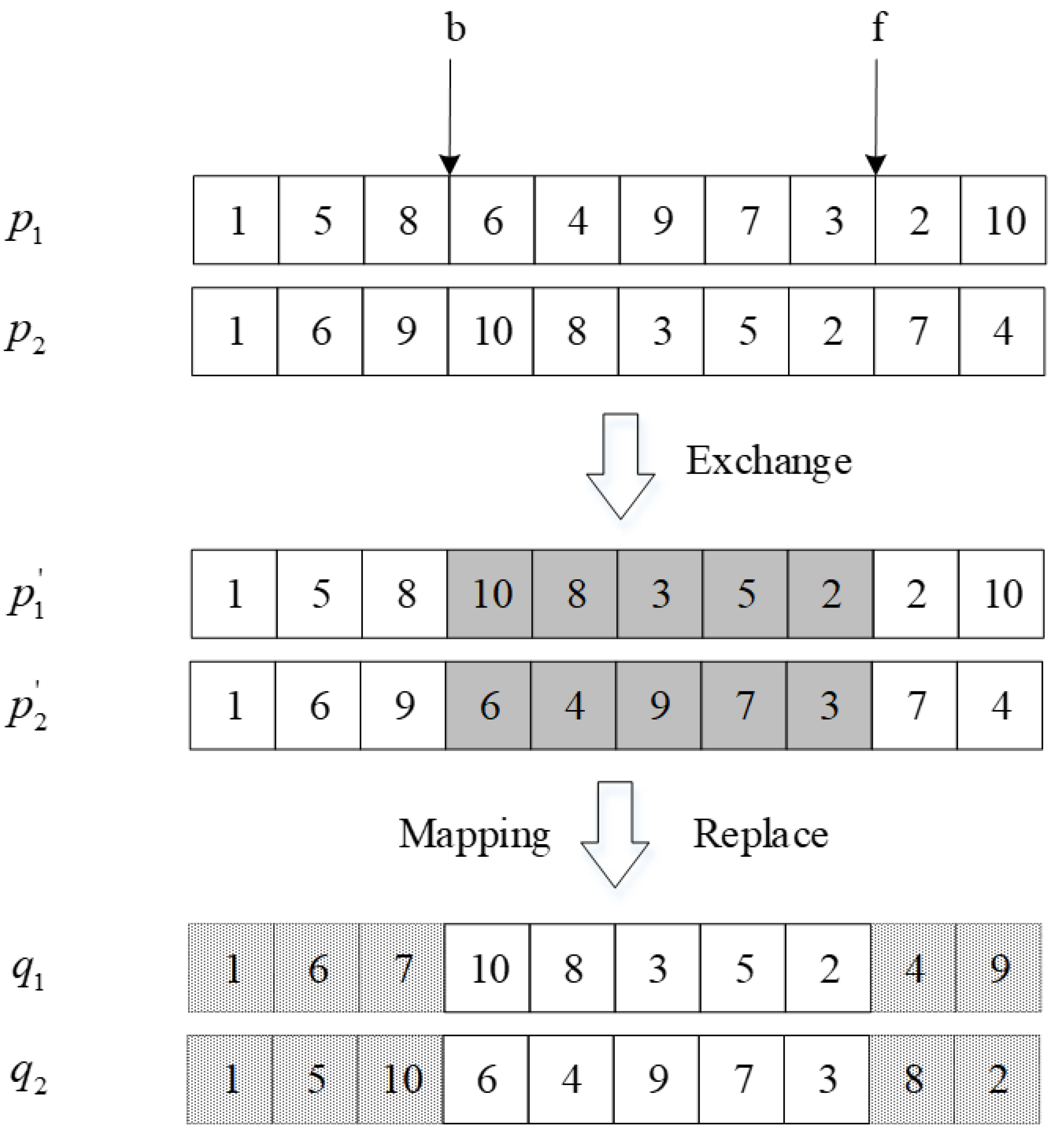
4.3. Crossover Operator
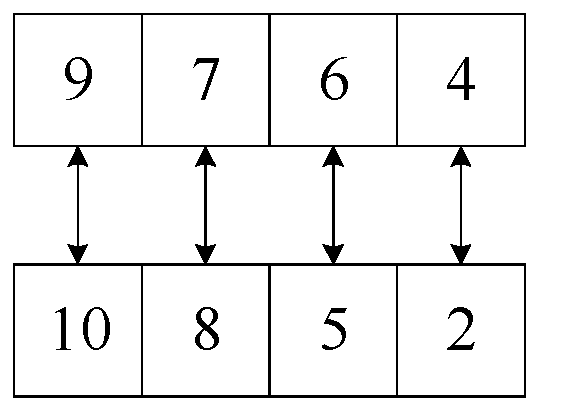
4.4. Mutation Operator
5. Numerical Experiments
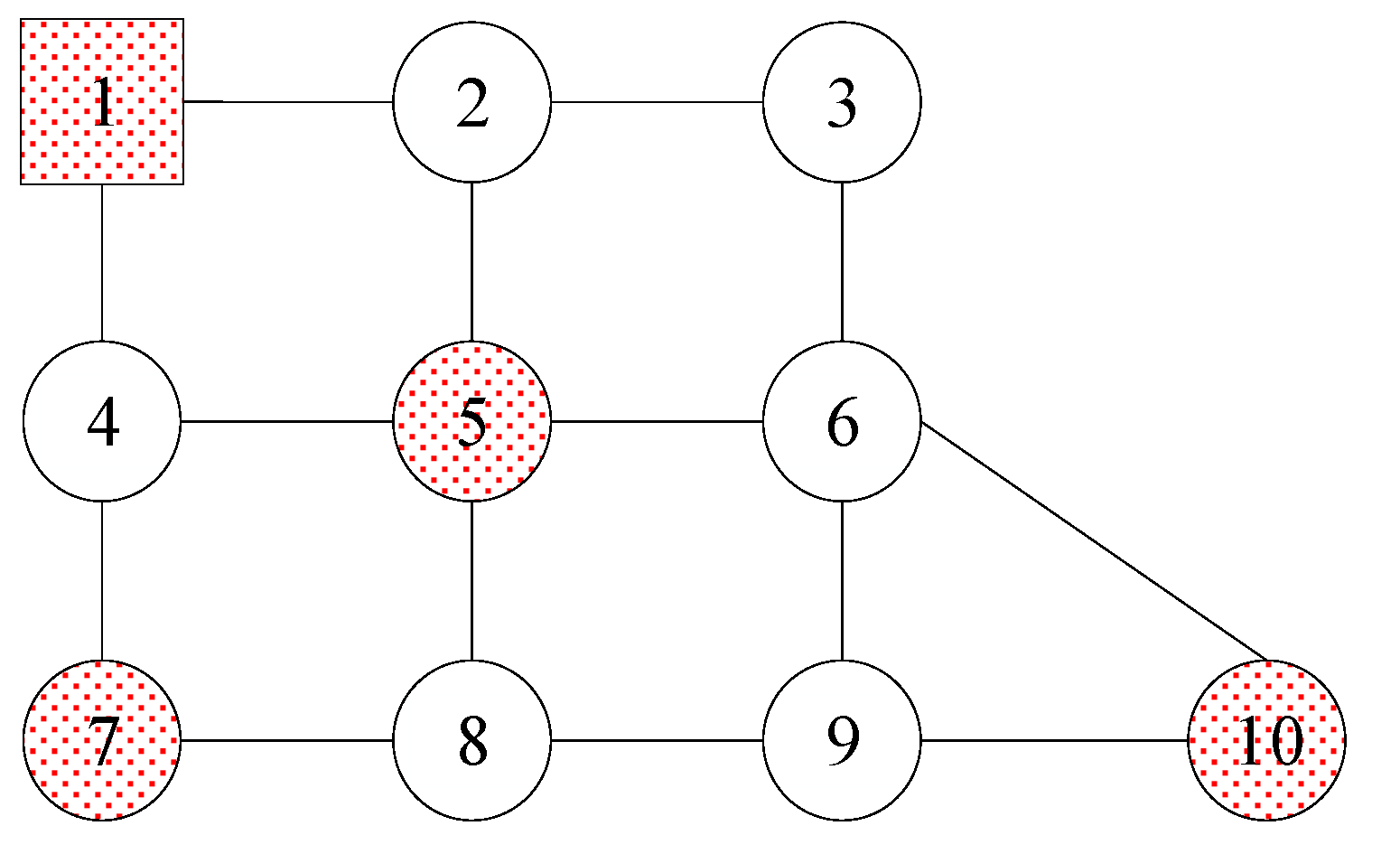
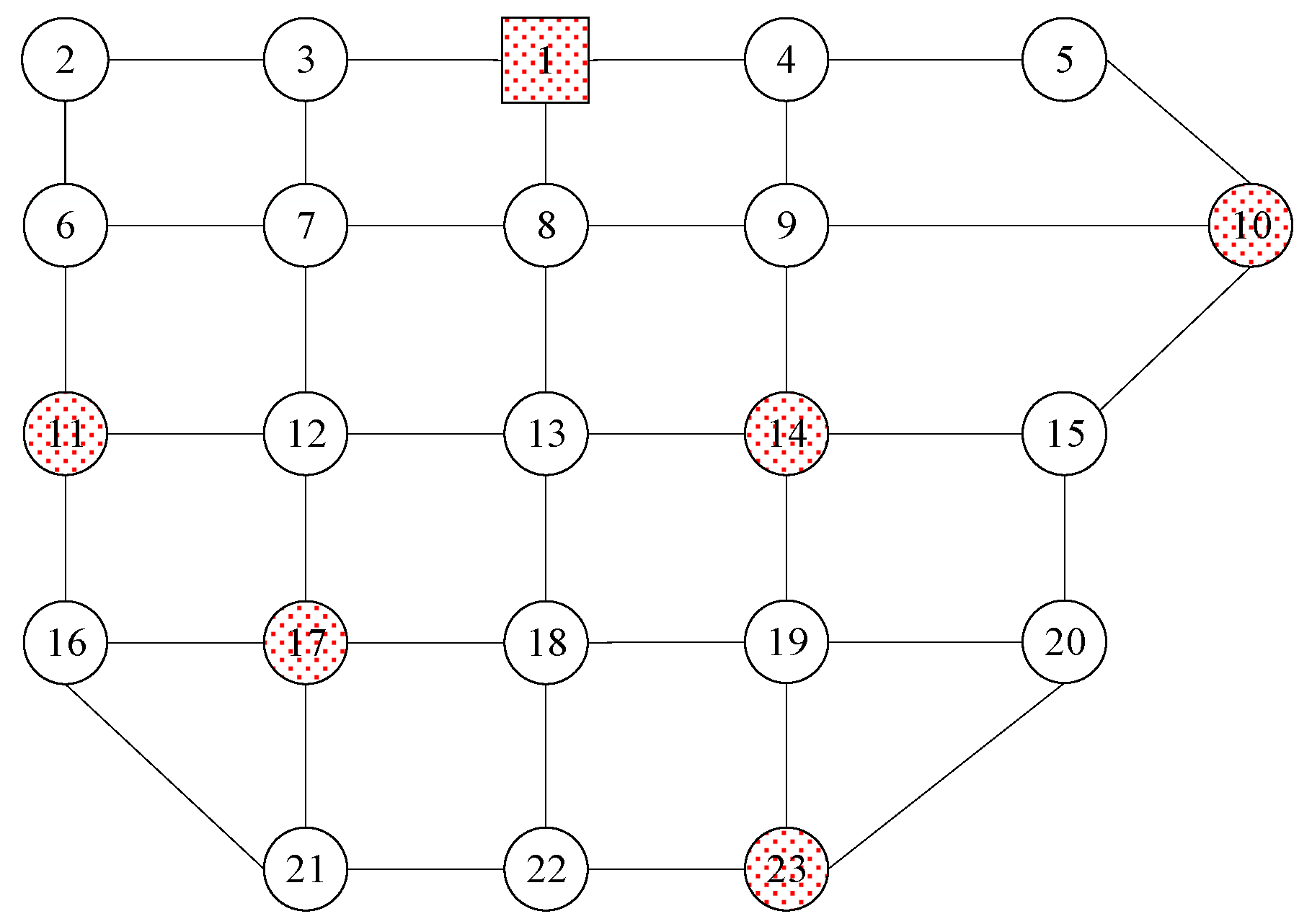
5.1. Road Network
5.2. Driving Risk and Cost
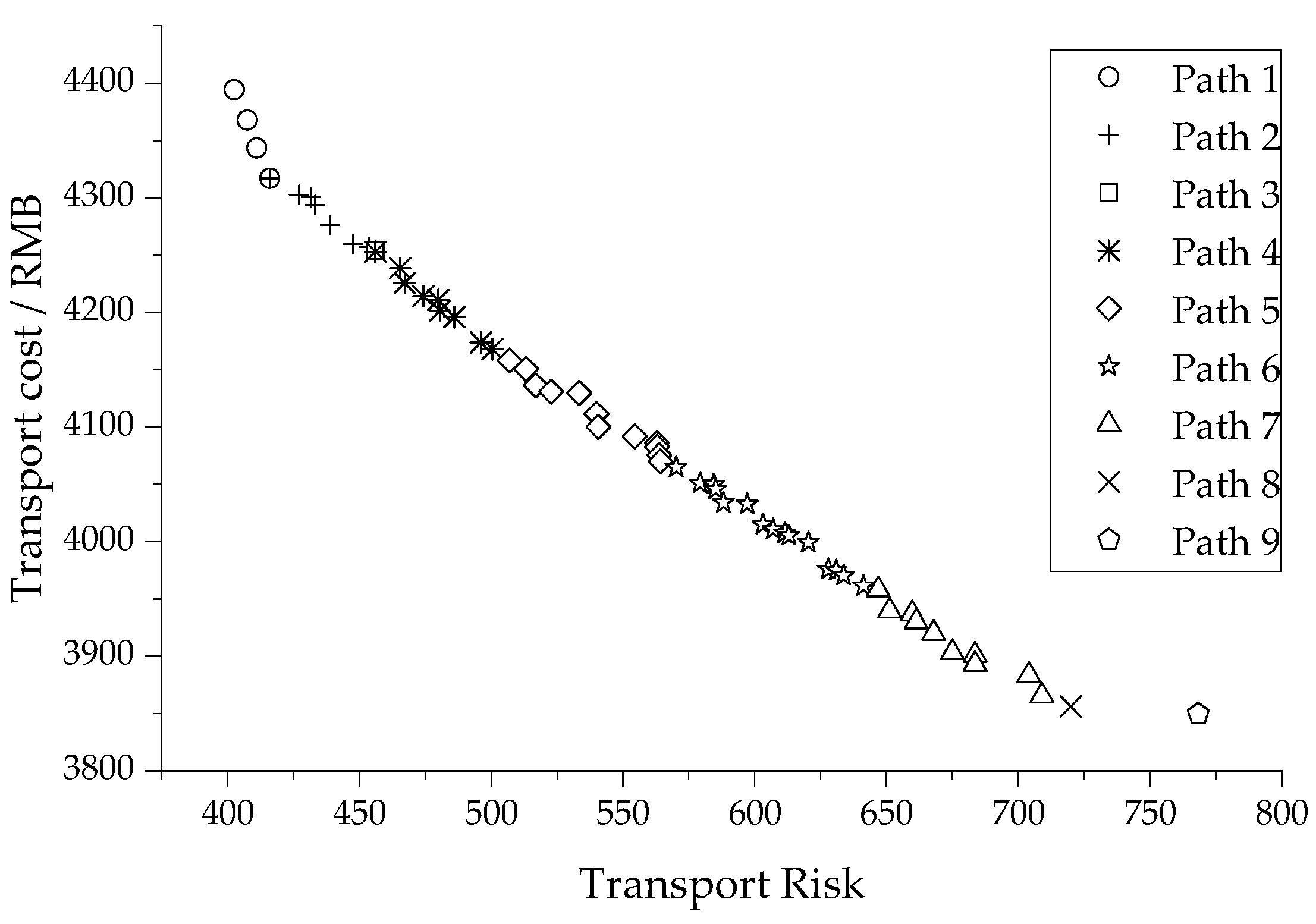
5.3. Solution by NSGA-II
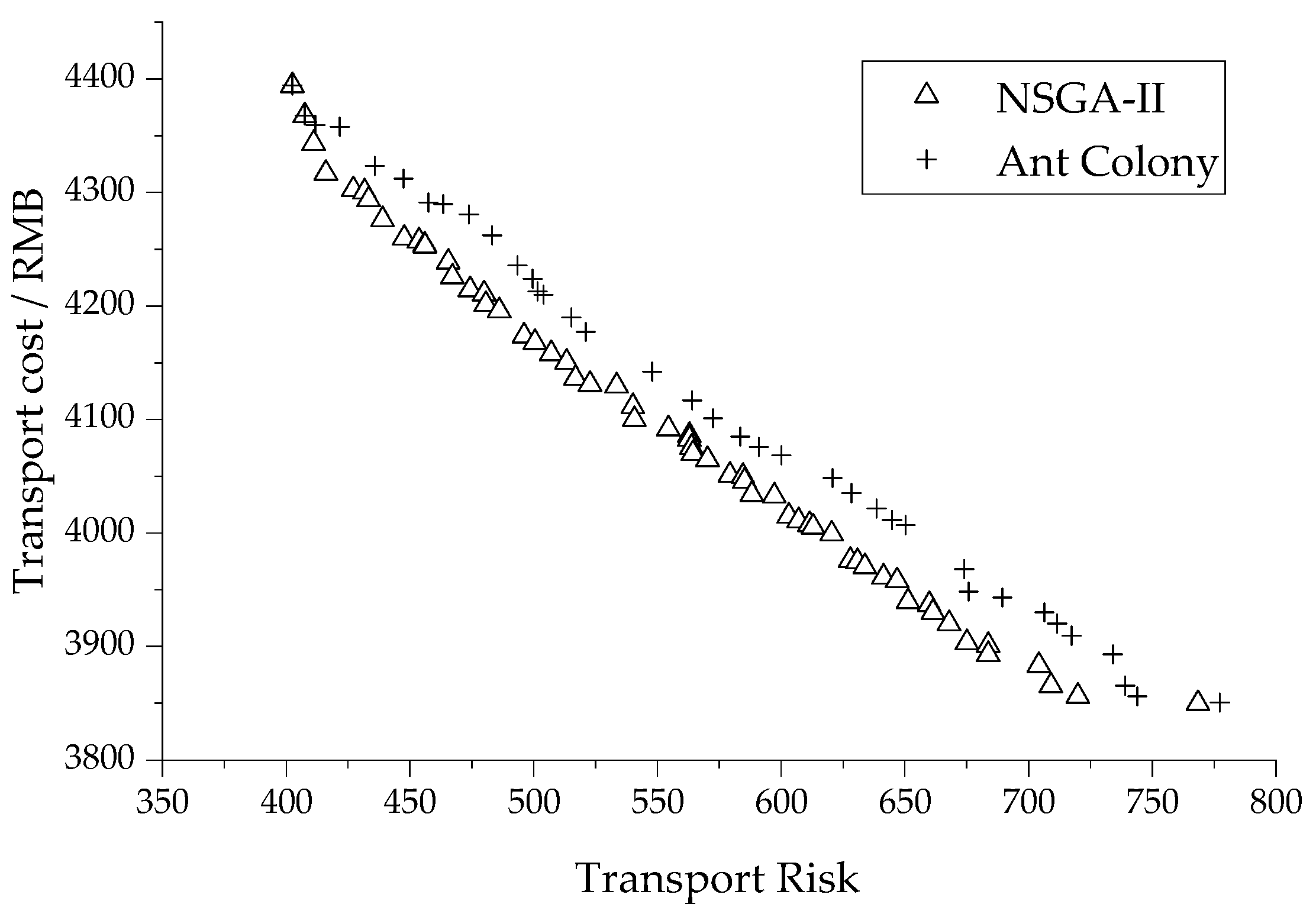
5.4. Results and Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Torretta, V.; Rada, E.C.; Schiavon, M.; Viotti, P. Decision Support Systems for Assessing Risks Involved in Transporting Hazardous Materials: A Review. Saf. Sci. 2017, 92, 1–9. [Google Scholar] [CrossRef]
- Yang, J.; Li, F.; Zhou, J.; Zhang, L.; Huang, L.; Bi, J. A Survey on Hazardous Materials Accidents during Road Transport in China from 2000 to 2008. J. Hazard. Mater. 2010, 184, 647–653. [Google Scholar] [CrossRef] [PubMed]
- Erkut, E.; Verter, V. Modeling of Transport Risk for Hazardous Materials. Oper. Res. 1998, 46, 625–642. [Google Scholar] [CrossRef]
- Frank, W.C.; Thill, J.; Batta, R. Spatial Decision Support System for Hazardous Material Truck Routing. Transp. Res. Part C Emerg. Technol. 2000, 8, 337–359. [Google Scholar] [CrossRef]
- List, G.F.; Zografos, K.G. Modeling and Analysis for Hazardous Materials Transportation: Risk Analysis, Routing/Scheduling and Facility Location. Transp. Sci. 1991, 25, 100–114. [Google Scholar] [CrossRef]
- Tarantilis, C.D.; Ioannou, G.; Kiranoudis, C.T.; Prastacos, G.P. Solving the Open Vehicle Routeing Problem via a Single Parameter Metaheuristic Algorithm. J. Oper. Res. Soc. 2005, 56, 588–596. [Google Scholar] [CrossRef]
- Zografos, K.G.; Androutsopoulos, K.N. A Decision Support System for Integrated Hazardous Materials Routing and Emergency Response Decisions. Transp. Res. Part C Emerg. Technol. 2008, 16, 684–703. [Google Scholar] [CrossRef]
- Androutsopoulos, K.N.; Zografos, K.G. A Bi-Objective Time-Dependent Vehicle Routing and Scheduling Problem for Hazardous Materials Distribution. Eur. J. Transp. Logist. 2012, 1, 157–183. [Google Scholar] [CrossRef]
- Pradhananga, R.; Taniguchi, E.; Yamada, T. Ant Colony System Based Routing and Scheduling for Hazardous Material Transportation. Procedia Soc. Behav. Sci. 2010, 2, 6097–6108. [Google Scholar] [CrossRef]
- Zheng, B. Multi-Objective Vehicle Routing Problem in Hazardous Material Transportation. In Proceedings of the International Conference of Logistics Engineering and Management (ICLEM), Chengdu, China, 8–10 October 2010; Volume 1, pp. 154–163. [Google Scholar] [CrossRef]
- Garrido, R.A.; Bronfman, A.C. Equity and Social Acceptability in Multiple Hazardous Materials Routing through Urban Areas. Transp. Res. Part A Policy Pract. 2017, 102, 244–260. [Google Scholar] [CrossRef]
- Chai, H.; He, R.; Ma, C.; Dai, C.; Zhou, K. Path Planning and Vehicle Scheduling Optimization for Logistic Distribution of Hazardous Materials in Full Container Load. Discret. Dyn. Nat. Soc. 2017, 2017, 13. [Google Scholar] [CrossRef]
- Cuneo, V.; Nigro, M.; Carrese, S.; Ardito, C.F.; Corman, F. Risk Based, Multi Objective Vehicle Routing Problem for Hazardous Materials: A Test Case in Downstream Fuel Logistics. Transp. Res. Procedia 2018, 30, 43–52. [Google Scholar] [CrossRef]
- Bula, G.A.; Murat Afsar, H.; González, F.A.; Prodhon, C.; Velasco, N. Bi-Objective Vehicle Routing Problem for Hazardous Materials Transportation. J. Clean Prod. 2019, 206, 976–986. [Google Scholar] [CrossRef]
- Bula, G.A.; Prodhon, C.; Gonzalez, F.A.; Afsar, H.M.; Velasco, N. Variable Neighborhood Search to Solve the Vehicle Routing Problem for Hazardous Materials Transportation. J. Hazard. Mater. 2017, 324, 472–480. [Google Scholar] [CrossRef] [PubMed]
- Men, J.; Jiang, P.; Xu, H.; Zheng, S.; Kong, Y.; Hou, P.; Wu, F. Robust Multi-Objective Vehicle Routing Problem with Time Windows for Hazardous Materials Transportation. IET Intell. Transp. Syst. 2020, 14, 154–163. [Google Scholar] [CrossRef]
- Kang, R.G.; Chai, H.; Zhang, Y.M.; Shi, L. Bi-objective Optimization of Vehicle Routing for Hazardous Materials Transportation Considering Driver’s Driving Risk. J. Wuhan Univ. Technol. 2021, 43, 43–52. (In Chinese) [Google Scholar]
- Holeczek, N. Analysis of Different Risk Models for the Hazardous Materials Vehicle Routing Problem in Urban Areas. Clean. Environ. Syst. 2021, 2, 100022. [Google Scholar] [CrossRef]
- Niu, S.; Ukkusuri, S.V. Risk Assessment of Commercial Dangerous -Goods Truck Drivers Using Geo-Location Data: A Case Study in China. Accid. Anal. Prev. 2020, 137, 105427. [Google Scholar] [CrossRef]
- Horrey, W.J.; Lesch, M.F.; Mitsopoulos-Rubens, E.; Lee, J.D. Calibration of Skill and Judgment in Driving: Development of a Conceptual Framework and the Implications for Road Safety. Accid. Anal. Prev. 2015, 76, 25–33. [Google Scholar] [CrossRef]
- Brown, T.G.; Ouimet, M.C.; Eldeb, M.; Tremblay, J.; Vingilis, E.; Nadeau, L.; Pruessner, J.; Bechara, A. The Effect of Age on the Personality and Cognitive Characteristics of Three Distinct Risky Driving Offender Groups. Pers. Individ. Differ. 2017, 113, 48–56. [Google Scholar] [CrossRef]
- Barr, G.C.; Kane, K.E.; Barraco, R.D.; Rayburg, T.; Demers, L.; Kraus, C.K.; Greenberg, M.R.; Rupp, V.A.; Hamilton, K.M.; Kane, B.G. Gender Differences in Perceptions and Self-Reported Driving Behaviors among Teenagers. J. Emerg. Med. 2015, 48, 366–370. [Google Scholar] [CrossRef] [PubMed]
- Arbabzadeh, N.; Jafari, M. A Data-Driven Approach for Driving Safety Risk Prediction Using Driver Behavior and Roadway Information Data. IEEE Trans. Intell. Transp. Syst. 2018, 19, 446–460. [Google Scholar] [CrossRef]
- Ayuso, M.; Guillén, M.; Pérez Marín, A.M. Using Gps Data to Analyse the Distance Travelled to the First Accident at Fault in Pay-as-You-Drive Insurance. Transp. Res. Part C Emerg. Technol. 2016, 68, 160–167. [Google Scholar] [CrossRef]
- Horberry, T.; Anderson, J.; Regan, M.A.; Triggs, T.J.; Brown, J. Driver Distraction: The Effects of Concurrent in-Vehicle Tasks, Road Environment Complexity and Age on Driving Performance. Accid. Anal. Prev. 2006, 38, 185–191. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, P.Y.; Grosch, J.W. Safety Climate: New Developments in Conceptualization, Theory, and Research. Accid. Anal. Prev. 2010, 42, 1421–1422. [Google Scholar] [CrossRef] [PubMed]
- Zohar, D. Thirty Years of Safety Climate Research: Reflections and Future Directions. Accid. Anal. Prev. 2010, 42, 1517–1522. [Google Scholar] [CrossRef]
- Bassani, M.; Catani, L.; Cirillo, C.; Mutani, G. Night-Time and Daytime Operating Speed Distribution in Urban Arterials. Transp. Res. Part F Traffic Psychol. Behav. 2016, 42, 56–69. [Google Scholar] [CrossRef]
- Lee, M.L.; Howard, M.E.; Horrey, W.J.; Liang, Y.; Anderson, C.; Shreeve, M.S.; O Brien, C.S.; Czeisler, C.A. High Risk of Near-Crash Driving Events Following Night-Shift Work. Proc. Natl. Acad. Sci. USA 2016, 113, 176–181. [Google Scholar] [CrossRef]
- Okasha, A.; Deb, K.; Lund, H. Bi-objective optimization of transcritical CO2 heat pump systems. Energy 2022, 247, 123469. [Google Scholar] [CrossRef]

| Criterion | Weight | Plan (Level 1) | Plan (Level 2) | ||
|---|---|---|---|---|---|
| Criterion | Weight | Criterion | Weight | ||
| Driver’s characteristics | 0.4425 | Age | 0.4039 | 25–30 | 0.1060 |
| 30–35 | 0.0665 | ||||
| 35–40 | 0.1646 | ||||
| 40–45 | 0.2698 | ||||
| ≥45 | 0.3931 | ||||
| Driving experience/years | 0.3404 | 3–7 | 0.4265 | ||
| 7–11 | 0.2537 | ||||
| 11–15 | 0.1507 | ||||
| 15–19 | 0.0867 | ||||
| ≥19 | 0.0824 | ||||
| Educational background | 0.1391 | Uneducated | 0.4743 | ||
| Primary | 0.2781 | ||||
| Junior school | 0.1184 | ||||
| High school | 0.0832 | ||||
| Higher education | 0.0460 | ||||
| Gender | 0.1166 | Male | 0.3333 | ||
| Female | 0.6667 | ||||
| Driving habits | 0.5575 | Driving Speed/km·h−1 (on urban roads) | 0.4182 | <45 | 0.0320 |
| 45–55 | 0.0583 | ||||
| 55–65 | 0.1031 | ||||
| 65–75 | 0.2976 | ||||
| ≥75 | 0.5089 | ||||
| Rapid acceleration/km·h−2 | 0.1906 | <5 | 0.0330 | ||
| 5–10 | 0.0627 | ||||
| 10–15 | 0.1401 | ||||
| 15–20 | 0.2626 | ||||
| ≥20 | 0.5016 | ||||
| Rapid deceleration/km·h−2 | 0.2707 | <5 | 0.0458 | ||
| 5–10 | 0.0907 | ||||
| 10–15 | 0.1343 | ||||
| 15–20 | 0.2515 | ||||
| ≥20 | 0.5326 | ||||
| Heavy vehicle mileage/km·d−1 | 0.1205 | 120–150 | 0.1248 | ||
| 150–180 | 0.0778 | ||||
| 180–210 | 0.3506 | ||||
| >210 | 0.4918 | ||||
| Vehicle | Customer Node | Service Order |
|---|---|---|
| 1 | 5, 7 | 1→5→7→1 |
| 2 | 10 | 1→10→1 |
| ID | Road Segment | Distance/km | Population Density/Person·km−2 | Accident Probability |
|---|---|---|---|---|
| 1 | 1-4 | 26.36 | 300 | 0.0042 |
| 2 | 1-8 | 25.80 | 400 | 0.0040 |
| 3 | 2-3 | 26.12 | 120 | 0.0031 |
| 4 | 2-6 | 28.40 | 75 | 0.0032 |
| 5 | 3-1 | 25.62 | 180 | 0.0034 |
| 6 | 3-7 | 21.29 | 360 | 0.0036 |
| 7 | 4-5 | 30.09 | 320 | 0.0062 |
| 8 | 4-9 | 25.09 | 290 | 0.0035 |
| 9 | 5-10 | 30.06 | 260 | 0.0065 |
| 10 | 6-11 | 30.89 | 200 | 0.0042 |
| 11 | 6-7 | 23.19 | 690 | 0.0040 |
| 12 | 7-12 | 24.14 | 660 | 0.0042 |
| 13 | 7-8 | 21.35 | 400 | 0.0044 |
| 14 | 8-9 | 25.12 | 480 | 0.0043 |
| 15 | 8-13 | 27.48 | 520 | 0.0047 |
| 16 | 9-10 | 40.20 | 400 | 0.0045 |
| 17 | 9-14 | 25.60 | 760 | 0.0049 |
| 18 | 10-15 | 32.50 | 430 | 0.0042 |
| 19 | 11-12 | 20.67 | 680 | 0.0054 |
| 20 | 11-16 | 35.60 | 300 | 0.0052 |
| 21 | 12-13 | 23.50 | 700 | 0.0045 |
| 22 | 12-17 | 30.20 | 620 | 0.0050 |
| 23 | 13-14 | 25.29 | 620 | 0.0050 |
| 24 | 13-18 | 35.55 | 710 | 0.0053 |
| 25 | 14-15 | 27.35 | 850 | 0.0049 |
| 26 | 14-19 | 36.78 | 720 | 0.0048 |
| 27 | 15-20 | 35.70 | 650 | 0.0055 |
| 28 | 16-17 | 21.10 | 550 | 0.0032 |
| 29 | 16-21 | 30.12 | 420 | 0.0060 |
| 30 | 17-18 | 28.50 | 640 | 0.0050 |
| 31 | 17-21 | 28.56 | 500 | 0.0040 |
| 32 | 18-19 | 28.30 | 630 | 0.0049 |
| 33 | 18-22 | 30.58 | 530 | 0.0052 |
| 34 | 19-20 | 27.08 | 640 | 0.0036 |
| 35 | 19-23 | 24.16 | 480 | 0.0042 |
| 36 | 20-23 | 29.46 | 160 | 0.0064 |
| 37 | 21-22 | 32.60 | 200 | 0.0058 |
| 38 | 22-23 | 30.60 | 240 | 0.0055 |
| Node | Demand/t | Service Duration/h | Time Window |
|---|---|---|---|
| 10 | 10 | 1 | 09:30–11:00 |
| 11 | 8 | 1 | 13:00–14:30 |
| 14 | 10 | 1 | 10:30–12:00 |
| 17 | 7 | 1 | 14:30–16:30 |
| 23 | 8 | 1 | 12:30–14:00 |
| Driver | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Driving risk () | 0.2129 | 0.1849 | 0.2417 | 0.1370 | 0.1622 | 0.2264 |
| 1.0965 | 0.9522 | 1.2447 | 0.7055 | 0.8352 | 1.1659 | |
| Driving cost/CNY·t−1·km−1 | 0.0881 | 0.0989 | 0.0770 | 0.1173 | 0.1076 | 0.0829 |
| Path No. | Vehicle | Path | Distance/km |
|---|---|---|---|
| 1 | 1 | 1→4→9→14→13→12→11→12→17→12→7→3→1 | 624.09 |
| 2 | 1→4→5→10→15→20→23→19→18→13→8→1 | ||
| 2 | 1 | 1→4→9→14→13→12→11→16→17→12→7→3→1 | 629.92 |
| 2 | 1→4→5→10→15→20→23→19→18→13→8→1 | ||
| 3 | 1 | 1→4→9→14→13→12→11→16→17→12→7→3→1 | 635.06 |
| 2 | 1→4→9→10→15→20→23→19→18→13→8→1 | ||
| 4 | 1 | 1→4→9→14→19→23→19→18→17→12→7→3→1 | 639.18 |
| 2 | 1→4→5→10→9→8→7→6→11→12→7→3→1 | ||
| 5 | 1 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 649.98 |
| 2 | 1→4→5→10→9→8→7→6→11→12→7→3→1 | ||
| 6 | 1 | 1→4→9→14→19→23→19→18→17→12→7→3→1 | 629.91 |
| 2 | 1→4→5→10→9→8→7→12→11→12→7→3→1 | ||
| 7 | 1 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 640.71 |
| 2 | 1→4→5→10→9→8→7→12→11→12→7→3→1 | ||
| 8 | 1 | 1→8→9→14→19→23→19→18→17→12→7→3→1 | 629.38 |
| 2 | 1→4→5→10→9→8→7→12→11→12→7→3→1 | ||
| 9 | 1 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 645.85 |
| 2 | 1→4→9→10→9→8→7→6→11→12→7→3→1 |
| Solution No. | Path | Driver | Risk | Cost /CNY |
|---|---|---|---|---|
| 1 | 1→8→9→14→19→23→19→18→17→12→7→3→1 | 4 | 402.5062 | 4394.09 |
| 1→4→5→10→9→8→7→12→11→12→7→3→1 | 5 | |||
| 59 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 3 | 768.3525 | 3849.75 |
| 1→4→9→10→9→8→7→6→11→12→7→3→1 | 6 |
| Solution No. | Path | Driver | Risk | Cost /CNY |
|---|---|---|---|---|
| 3 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 4 | 411.1256 | 4343.33 |
| 1→4→5→10→9→8→7→6→11→12→7→3→1 | 5 | |||
| 13 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 4 | 465.5105 | 4238.69 |
| 1→4→5→10→9→8→7→6→11→12→7→3→1 | 1 | |||
| 26 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 5 | 539.9801 | 4111.56 |
| 1→4→5→10→9→8→7→6→11→12→7→3→1 | 3 | |||
| 30 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 1 | 562.9320 | 4082.62 |
| 1→4→5→10→9→8→7→6→11→12→7→3→1 | 6 | |||
| 41 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 6 | 611.4671 | 4007.39 |
| 1→4→5→10→9→8→7→6→11→12→7→3→1 | 3 | |||
| 49 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 3 | 651.2104 | 3939.51 |
| 1→4→5→10→9→8→7→6→11→12→7→3→1 | 6 |
| Solution No. | Path | Driver | Risk | Cost /CNY |
|---|---|---|---|---|
| 2 | 1→4→9→14→13→12→11→16→17→12→7→3→1 | 4 | 407.4593 | 4367.60 |
| 1→4→9→10→15→20→23→19→18→13→8→1 | 5 | |||
| 4 | 1→4→9→14→13→12→11→16→17→12→7→3→1 | 4 | 416.0787 | 4316.85 |
| 1→4→5→10→15→20→23→19→18→13→8→1 | 5 | |||
| 7 | 1→4→9→14→13→12→11→12→17→12→7→3→1 | 4 | 433.2476 | 4293.67 |
| 1→4→5→10→15→20→23→19→18→13→8→1 | 5 |
| Solution No. | Path | Driver | Risk | Cost /CNY |
|---|---|---|---|---|
| 3 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 4 | 411.1256 | 4343.33 |
| 1→4→5→10→9→8→7→6→11→12→7→3→1 | 6 | |||
| 13 | 1→4→9→14→19→23→19→18→17→12→7→3→1 | 4 | 465.5105 | 4238.69 |
| 1→4→5→10→9→8→7→12→11→12→7→3→1 | 1 | |||
| 36 | 1→4→9→14→19→23→22→21→17→12→7→3→1 | 2 | 585.2382 | 4045.60 |
| 1→4→5→10→9→8→7→12→11→12→7→3→1 | 6 | |||
| 38 | 1→4→9→14→19→23→19→18→17→12→7→3→1 | 2 | 597.1895 | 4032.59 |
| 1→4→5→10→9→8→7→12→11→12→7→3→1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, H.; He, R.; Kang, R.; Jia, X.; Dai, C. Solving Bi-Objective Vehicle Routing Problems with Driving Risk Consideration for Hazardous Materials Transportation. Sustainability 2023, 15, 7619. https://doi.org/10.3390/su15097619
Chai H, He R, Kang R, Jia X, Dai C. Solving Bi-Objective Vehicle Routing Problems with Driving Risk Consideration for Hazardous Materials Transportation. Sustainability. 2023; 15(9):7619. https://doi.org/10.3390/su15097619
Chicago/Turabian StyleChai, Huo, Ruichun He, Ronggui Kang, Xiaoyan Jia, and Cunjie Dai. 2023. "Solving Bi-Objective Vehicle Routing Problems with Driving Risk Consideration for Hazardous Materials Transportation" Sustainability 15, no. 9: 7619. https://doi.org/10.3390/su15097619
APA StyleChai, H., He, R., Kang, R., Jia, X., & Dai, C. (2023). Solving Bi-Objective Vehicle Routing Problems with Driving Risk Consideration for Hazardous Materials Transportation. Sustainability, 15(9), 7619. https://doi.org/10.3390/su15097619






