All instances were solved using the Python version 3.9 with the SCIP solver version 7.0.2, and were run on a personal computer with the 12th Gen Intel(R) Core (TM) i5-12500H 2.50 GHz CPU and 16 GB RAM in order to achieve a near-optimal solution.
4.1.1. Transportation Model Simulation Results
The optimal schedule with values for all decision variables, including the amount of inventory at all PEs and IYs, the total number of each type of trucks and wagons that was used for delivery at every given time period, the grain quantity shipped from all PEs to all IYs and PCTs, and the grain quantity shipped from all IYs to all PCTs, are shown in
Table 3 and
Table 4. The optimal schedule minimizes the total cost of the supply chain, and the cost components’ values in the total cost of the supply chain are shown in
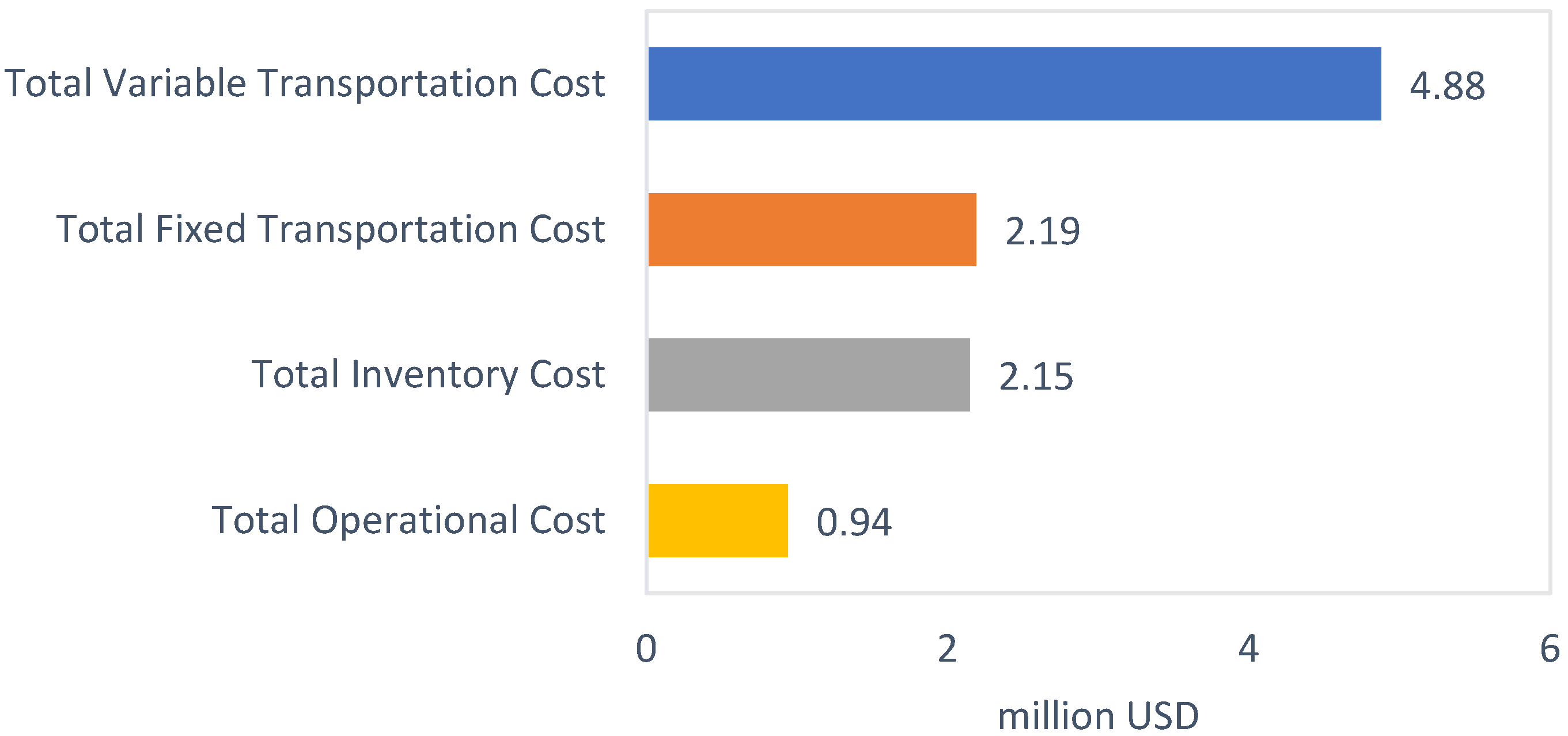
Figure 4. The dominant share, about 69.7% (USD 7,066,197) of the total supply chain cost, is the transportation cost, and the second contributor to the total cost of the supply chain is the inventory cost, which accounts for 21.1% (USD 2,145,448), followed by the operational cost, which accounts for 9.2% (USD 937,057). To better understand the correlation between the simulation parameters and the total supply chain cost, and to discuss the possibilities of further minimization of the total supply chain cost, three main parts of the total supply chain cost should be discussed separately.
The transportation cost: Total transportation cost consists of a fixed transportation cost and a variable transplantation cost, which are influenced by many simulation parameters and variables. For instance, the fixed transportation cost is influenced by the number and type of trucks and wagons that are used for transportation and the fixed transportation cost per truck or wagon of different types. The variable transportation cost is shaped by the number and type of trucks and wagons that are used for transportation, the quantity of grain shipped, the weight of an empty container, the unit shipment cost, and the distance between the nodes of the supply chain. The data on the fixed transportation cost, the weight of an empty container, the unit shipment cost, and the distance between the nodes of the supply chain in this simulation were based on real-life data in Ukraine and taken from reliable sources. This is why we do not consider the changes in these parameters as a tool for minimizing the total cost that is worthy of further investigation. The number of trucks and wagons that are used for delivery can be limited by the number of trucks and wagons that are available at a site in a given period of time, the capacity of the IY used, and the quantity of grains that is available at the PE used.
From the optimal schedule for this simulation, we can see that around 53.2% (72,372 tons) is transported by direct truck delivery from the PEs to PCTs, and only 46.8% (63,646 tons) is delivered through the IYs. This happens because direct delivery from the primary elevators that are located relatively close to the ports, such as , , and , is a nice alternative to multi-modal delivery. The economic feasibility of direct delivery can be further proven by the fact that for 52.3% of the quantity of grains shipped, it only represents 50.8% (USD 3,587,285) of total transportation cost. Multimodal transportation, on the other hand, provides better cost for middle-long distances. For a share of 47.7% of the quantity of grains shipped, multimodal transportation’s share in the total transportation cost is 49.2% (USD 3,478,912); in addition, multimodal transportation creates additional sources of operational cost (loading and unloading) at the IYs. However, it should be mentioned that the capacity of the IYs and the number of wagons available at the IYs set an additional restriction on the quantity of grains that can be shipped through them. It is also clear that the model gives a preference to the usage of trucks with higher capacity as being more economically feasible. Only 212 containers are transported by trucks with lower capacity . We can conclude that the number of trucks with higher capacity that are available at the PEs plays an important role in the transportation cost structure.
Based on the above results, we can conclude that the reasonable strategies to decrease the transportation cost of the supply chain are as follows:
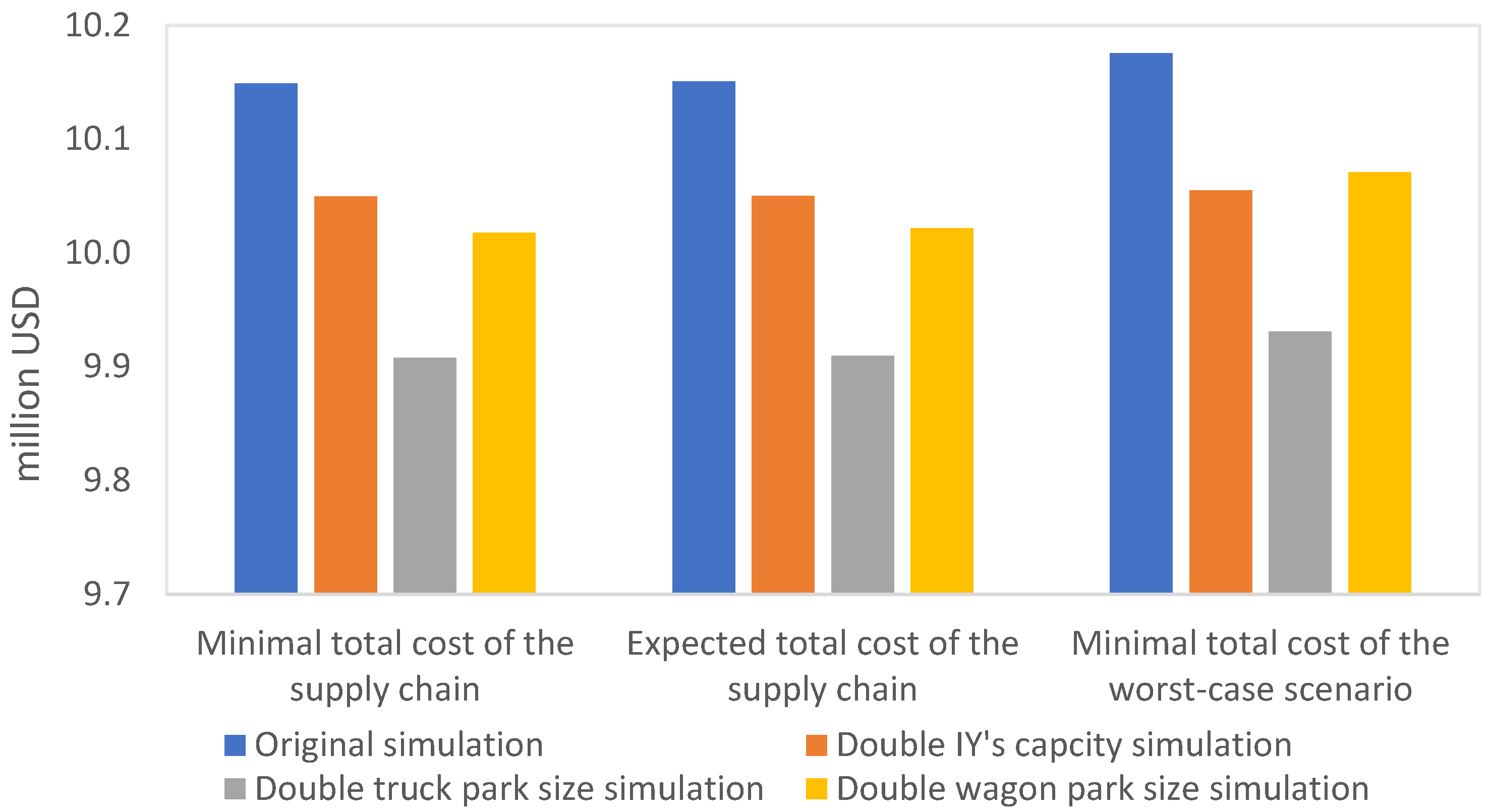
Increase the number of wagons that are available at the IYs to increase the outflow of the IYs.
Increase the capacity of the IYs to increase the inflow of the IYs.
Increase the number of trucks with high capacity that are available at the PEs, especially at those that are located relatively close to the PCTs.
The inventory holding cost: From the data that we used for the simulation, we can calculate the average inventory holding cost per container at the IYs and the average inventory holding cost of the bulk weight of a container with a full load of grains at the PEs. On average, it costs USD 134 to store a container at an IY for one quarter of the year, the same amount of grains as a full load of a container can be stored for one quarter of the year at a PE for USD 147. Even though inventory holding is cheaper, we need to take into account additional operational cost that comes with the use of multimodal transportation, which is the cost of unloading a container from a truck and loading it onto a wagon. This cost is applied to containers only once, regardless of the time that the containers spend in an IY. The average inventory holding cost and the cost of unloading and loading of a container at an IY is USD 137 for a container that has been stored for three months, which is 6.6% cheaper than the cost of storing the same amount of grains in bulk at the PE. However, the difference in cost will only increase with time duration since this additional operational cost occurs only once. On average, the storage of grains at an IY compared to the storage at a PE will be 7.7% cheaper for the duration of two quarters of the year, 8.1% for a storage period of three quarters, and 8.3% for a storage period of four quarters. This is the reason why the optimal schedule tries to deliver the scheduled quantity of grains as early as the capacitated number of vehicles at the PE and the capacity of the IY allow.
Based on the above results, we can conclude that the reasonable strategies to decrease the inventory holding cost of the supply chain are as follows:
Increase the capacity of the IYs to increase the number of containers that can be stored and shipped through the IYs.
Increase the number of trucks that are available at the PEs to make sure that grains are delivered to the IYs as early as possible.
The operational cost: The total operational cost has the smallest share in the total supply chain cost and affects the process of decision-making about the optimal schedule the least. In a primary elevator, a part of the operational cost occurs due to pricing, cleaning, weighting, sorting, blending, and quality control. This part of the operational cost occurs only once after grains are received by a PE from farms. Other sources of operational cost are the loading of bulk grains into containers and loading of containers onto trucks. The only sources of operational cost at the IYs and PCTs are the loading and unloading of containers to and from trucks and wagons. The only source of operational cost that varies depending on the schedule is the cost of loading and unloading of containers at the IYs. Therefore, it is hard to achieve significant changes in the operational cost simply by applying different schedules. In order to further minimize the operational cost without decreasing the quality and safety of products, processing facilities should be modernized, and staff training standards should be improved.
4.1.2. Disruption Management Model Simulation Results
The value of the minimal expected total cost is provided, as well as the probability and minimal total cost of the supply chain for each disruption scenario. The list of disruption scenarios that were simulated, the probability of each disruption scenario, the minimal total cost of each disruption scenario, and the expected total cost of the supply chain are shown in
Table 5 and
Table 6. The simulation considering disruptions that can occur at four IYs and at any point of four existing time periods leads to 50% loss in the capacity of the IYs in a given period of time. In case of a disruption in the previous time period, an IY will be able to recover its capacity in this time period since one time period, which is three-month long, provides an adequate amount of time to solve most of the possible disruption causes. All disruption cases can be described by 61 disruption scenarios. Each disruption scenario represents a unique subset of IYs that are currently disrupted and those that are working without disruption in a given period of time.
The expected total cost of the supply chain is USD 10,150,483, which is only 0.018% (USD 1781) greater than the minimal total cost of the supply chain that operates without disruption. Moreover, the minimal total cost of the worst-case scenario (scenario №60) with disruption at all IYs during the fourth time period is USD 10,175,507, which is only 0.26% (USD 26,805) more expensive than the minimal total cost of the supply chain that operates without disruption. The disruption scenario №60 provides us the highest total cost because all IYs are disrupted during a period of time with the highest demand out of the four time periods—41,000 tons—compared to the demand of time period three at 33,000 tons, time period two at 25,000 tons, and time period one at 36,000 tons. Because the IYs are only working at 50% of their actual capacity, the supply chain cannot fully exploit the benefits of the comparably cheaper railway delivery over long distances and the lower inventory cost of the IYs. However, the overall total cost is only raised by 0.26%, which is proof of the high sustainability of the proposed supply chain. The robustness of the supply chain is ensured by the possibility of direct truck delivery, the high quantity of grain suppliers (PEs) and IYs that are spread widely across the country, and the compatibility of the costs of short-distance truck delivery and multimodal delivery over long distances.