Impacts of Climate Change on Extreme Climate Indices in Türkiye Driven by High-Resolution Downscaled CMIP6 Climate Models
Abstract
1. Introduction
2. Materials and Methods
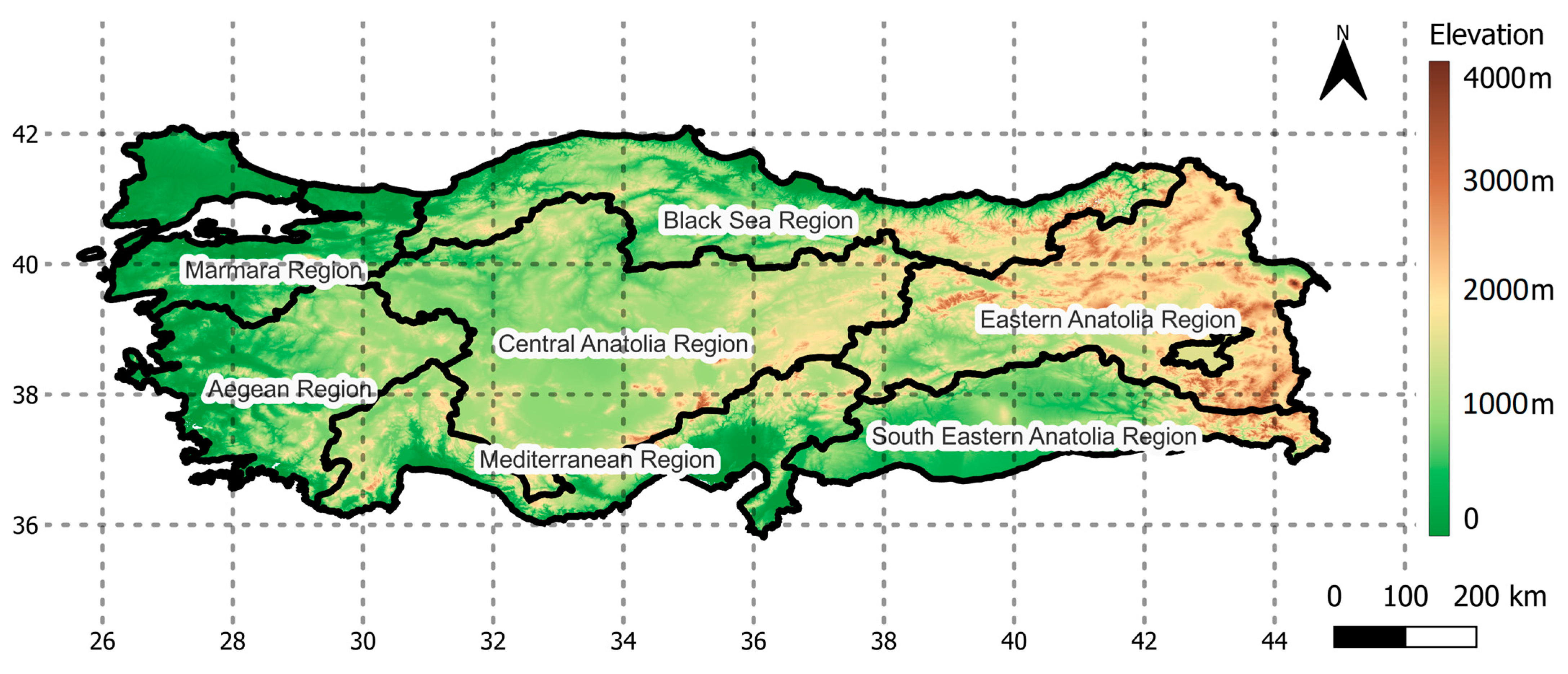
2.1. Study Area
2.2. Data
2.2.1. ERA5-Land
2.2.2. CMIP6 Global Climate Models
2.3. Methodology
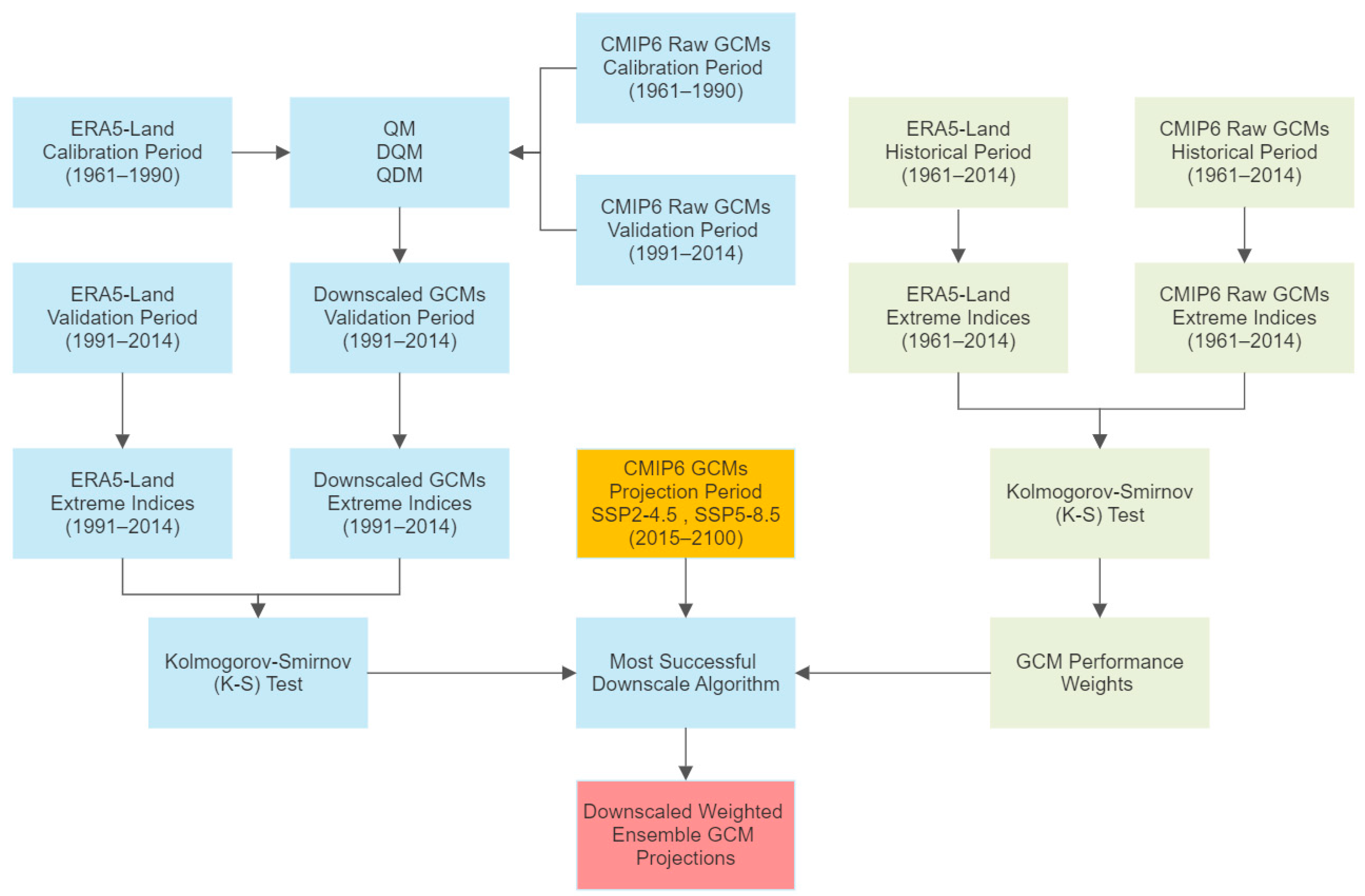
2.3.1. Bias Correction of Climate Variables
Quantile Mapping
Detrended Quantile Mapping
Quantile Delta Mapping
2.3.2. Performance Evaluation for Bias Corrected Data
Kolmogorov–Smirnov (K-S) Test
Multi-Model Ensemble Weighted Average
2.3.3. Expert Team on Sector-Specific Climate Indices (ET-SCI)
3. Results
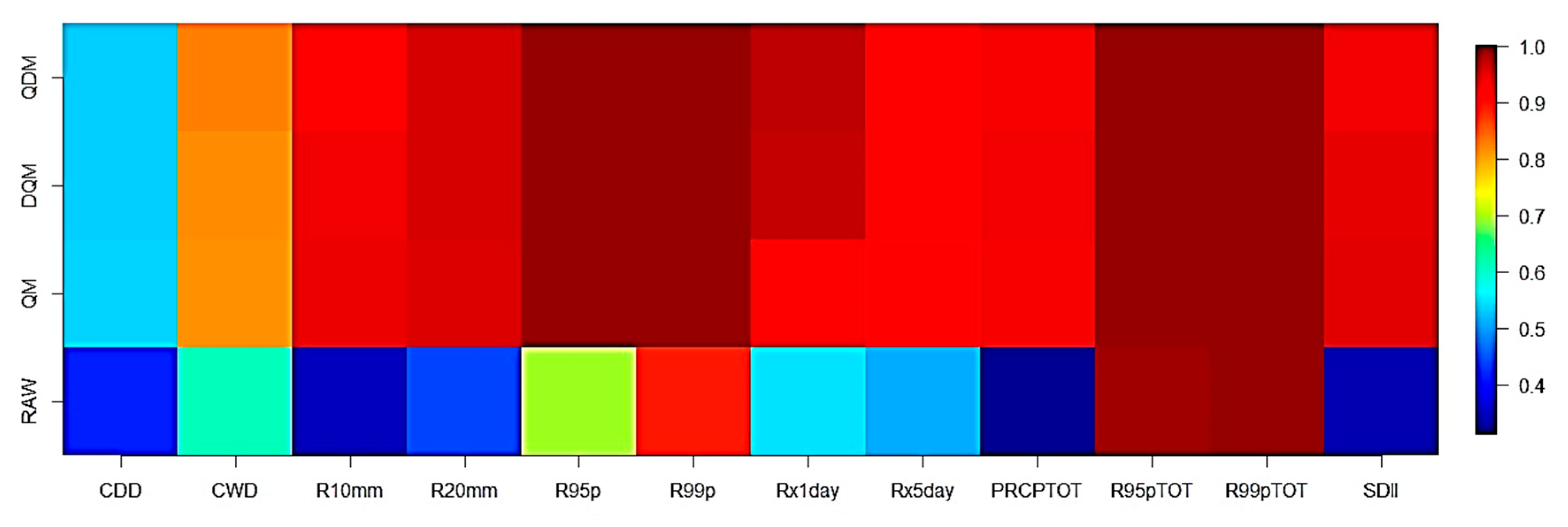
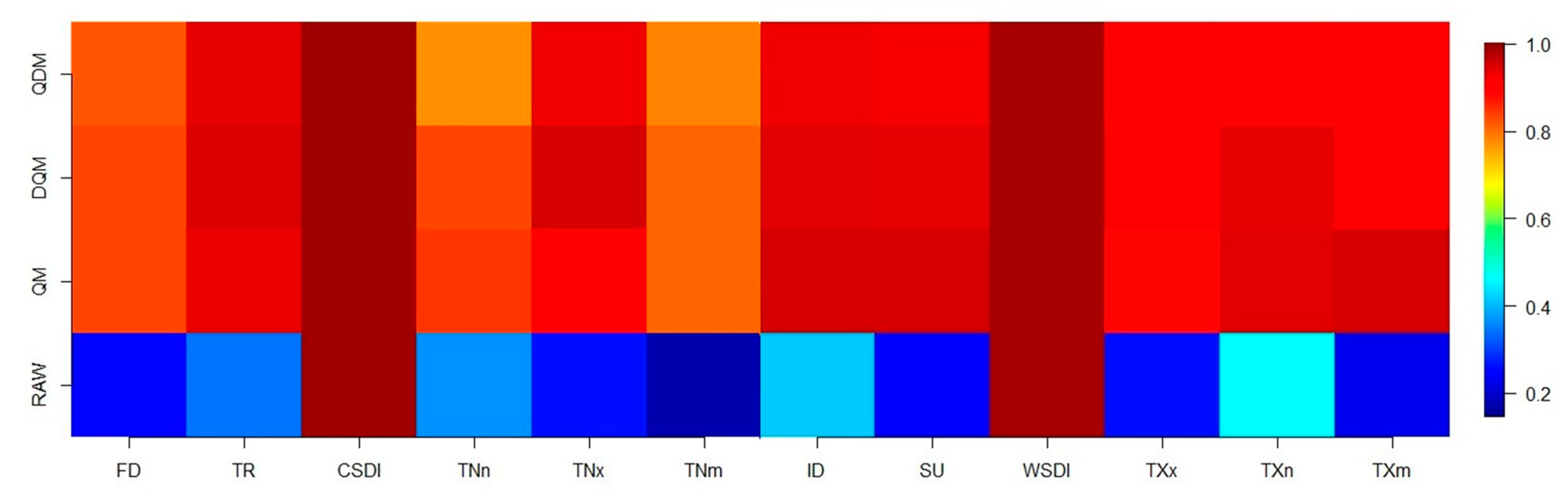
3.1. Performance and Validation of the Bias Correction Methods
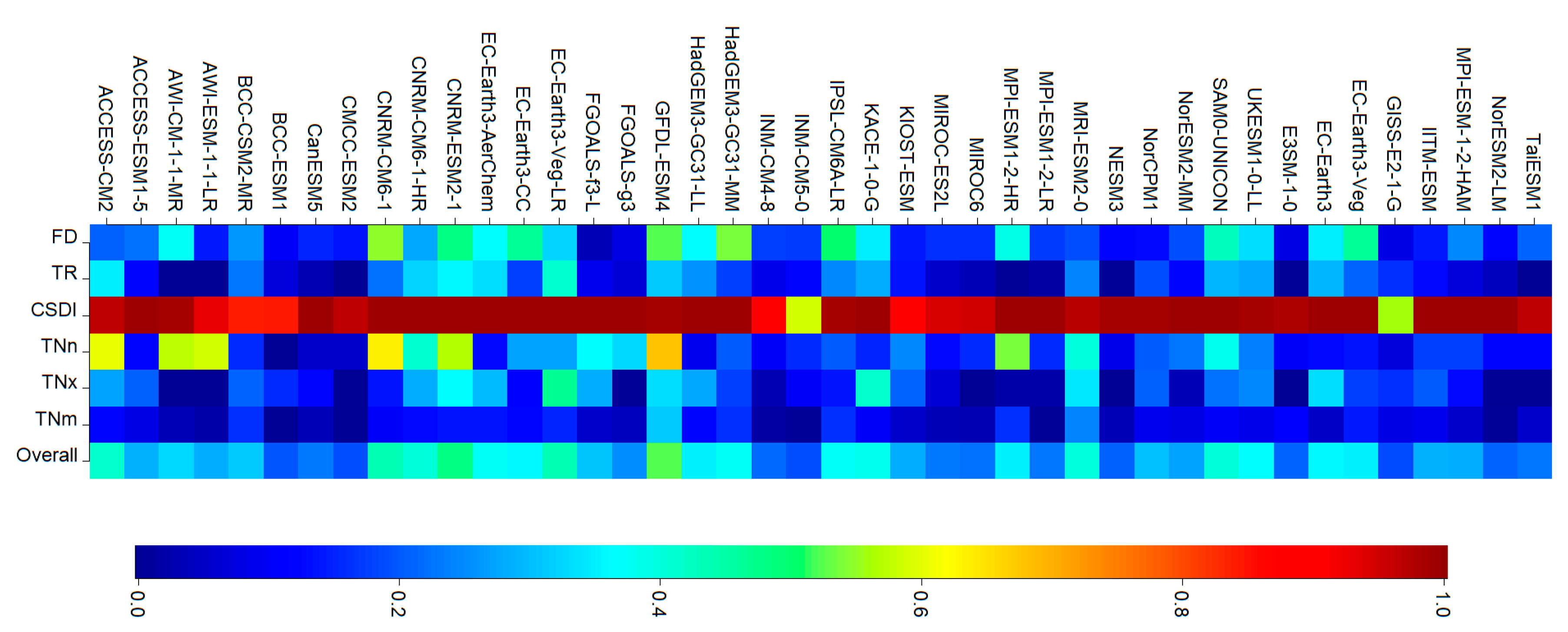
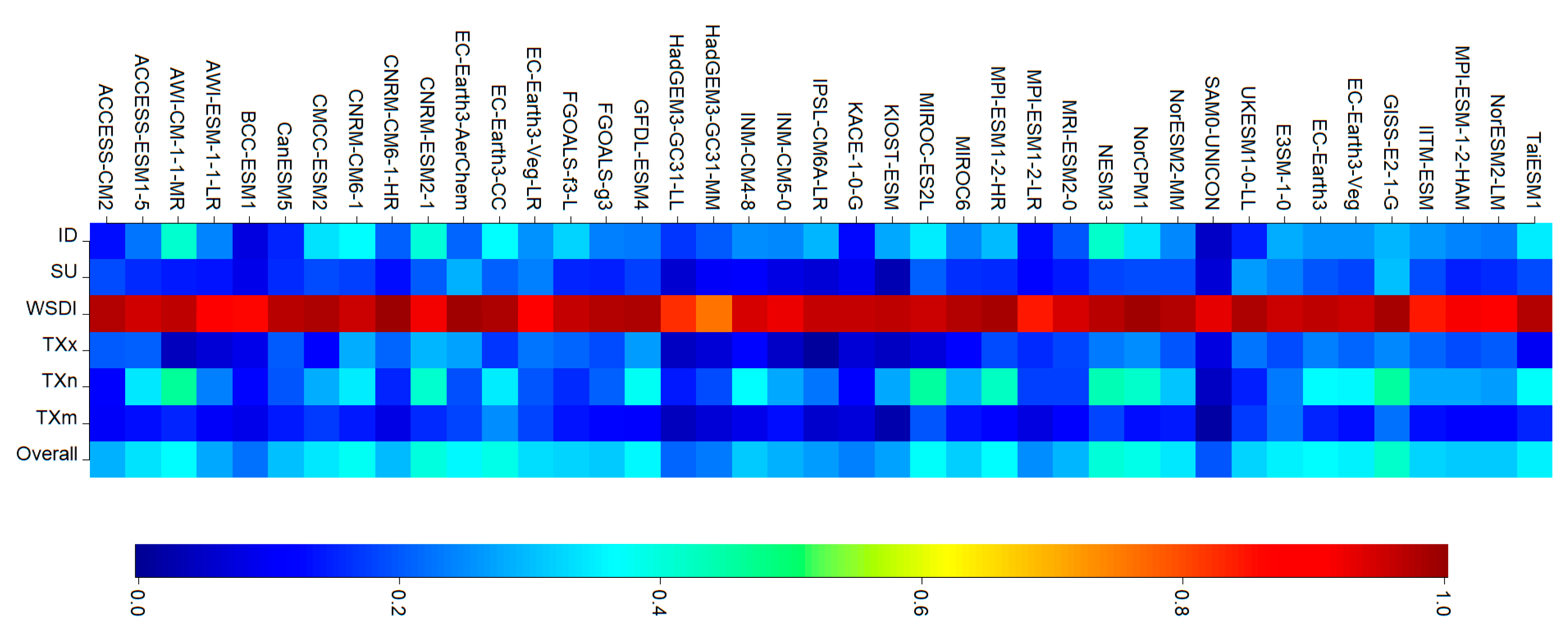
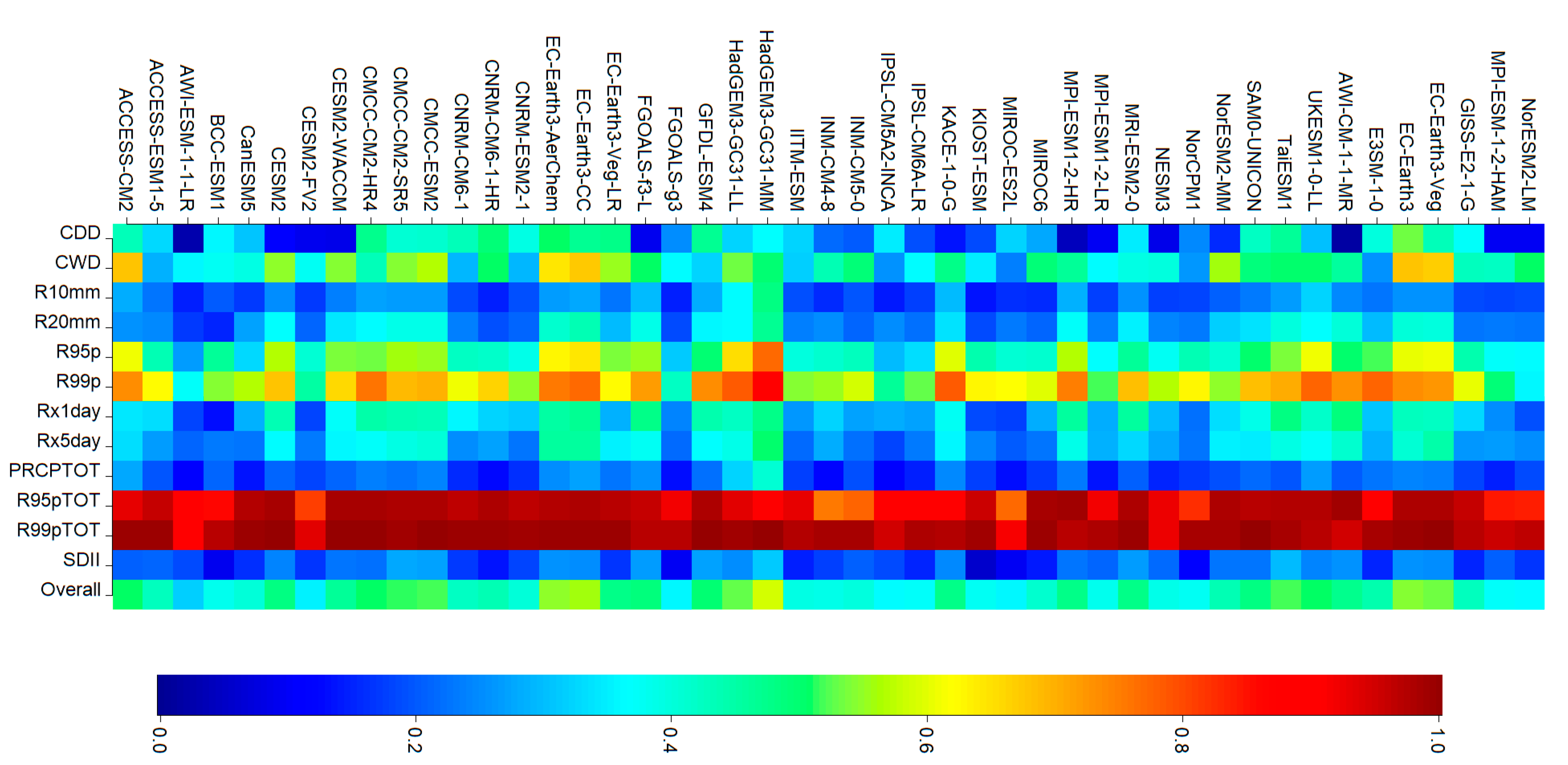
3.2. Performance of the GCM Models
3.3. Behavior of Indices
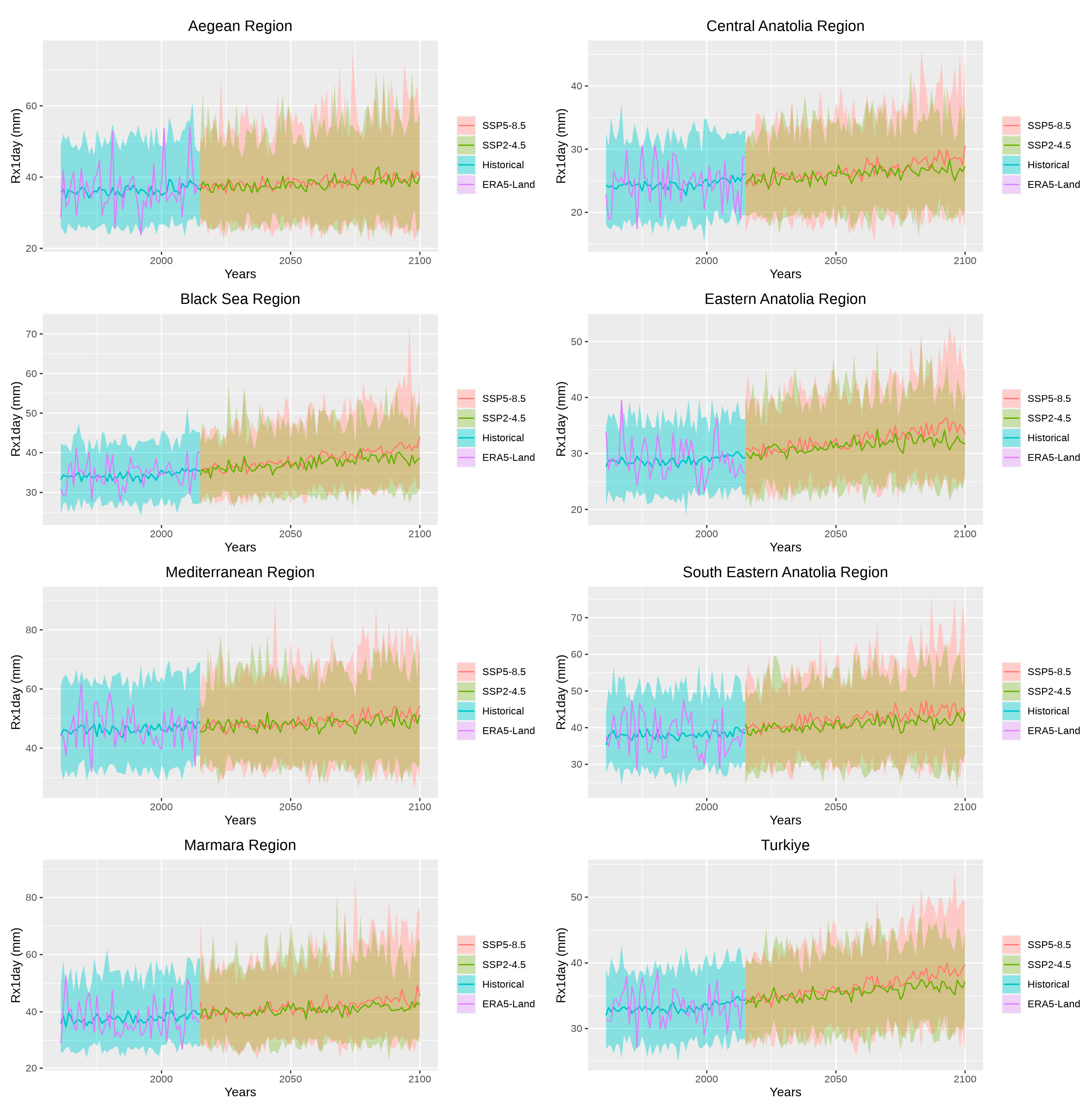
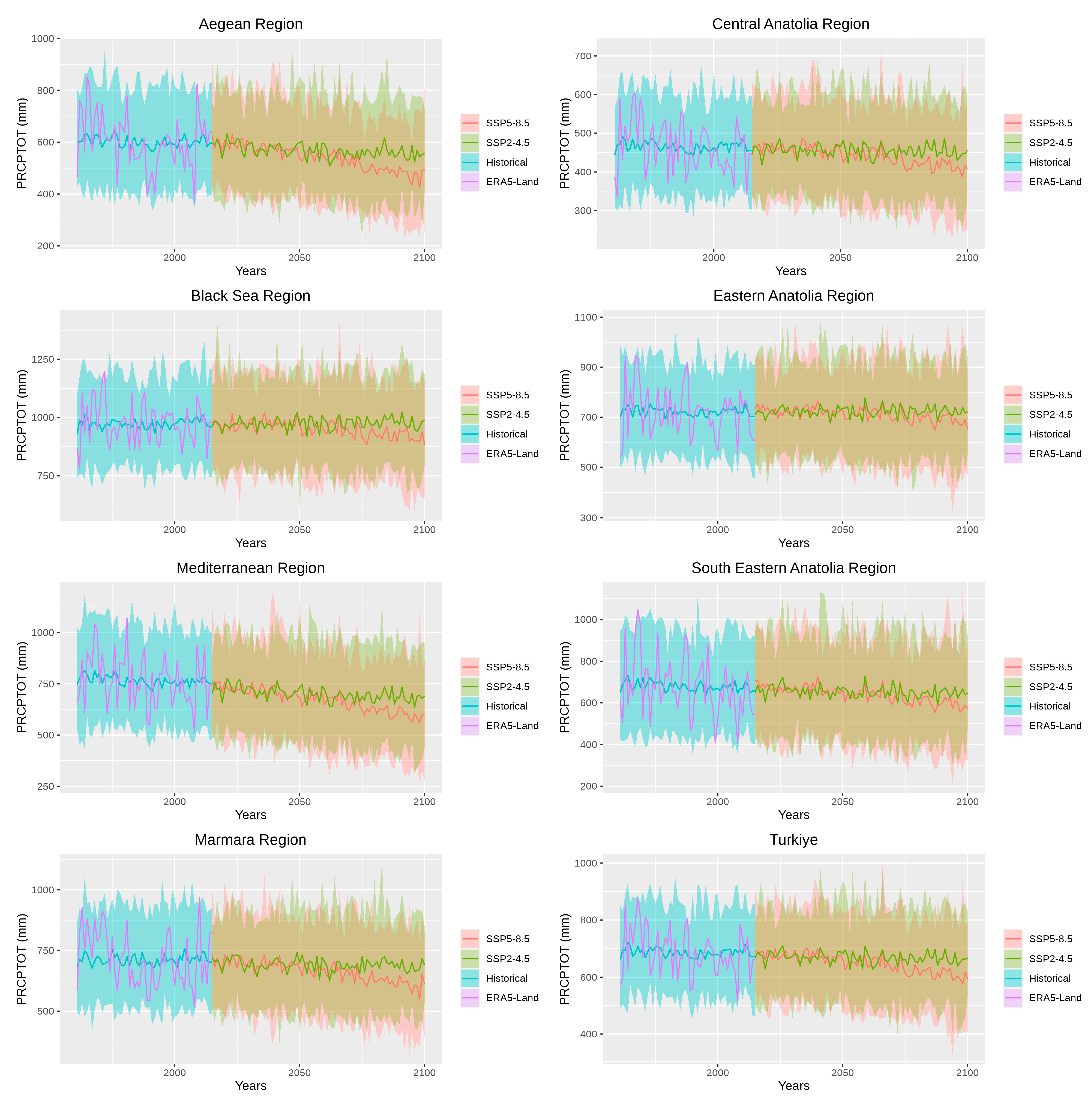
3.3.1. Extreme Precipitation Indices (EPI)
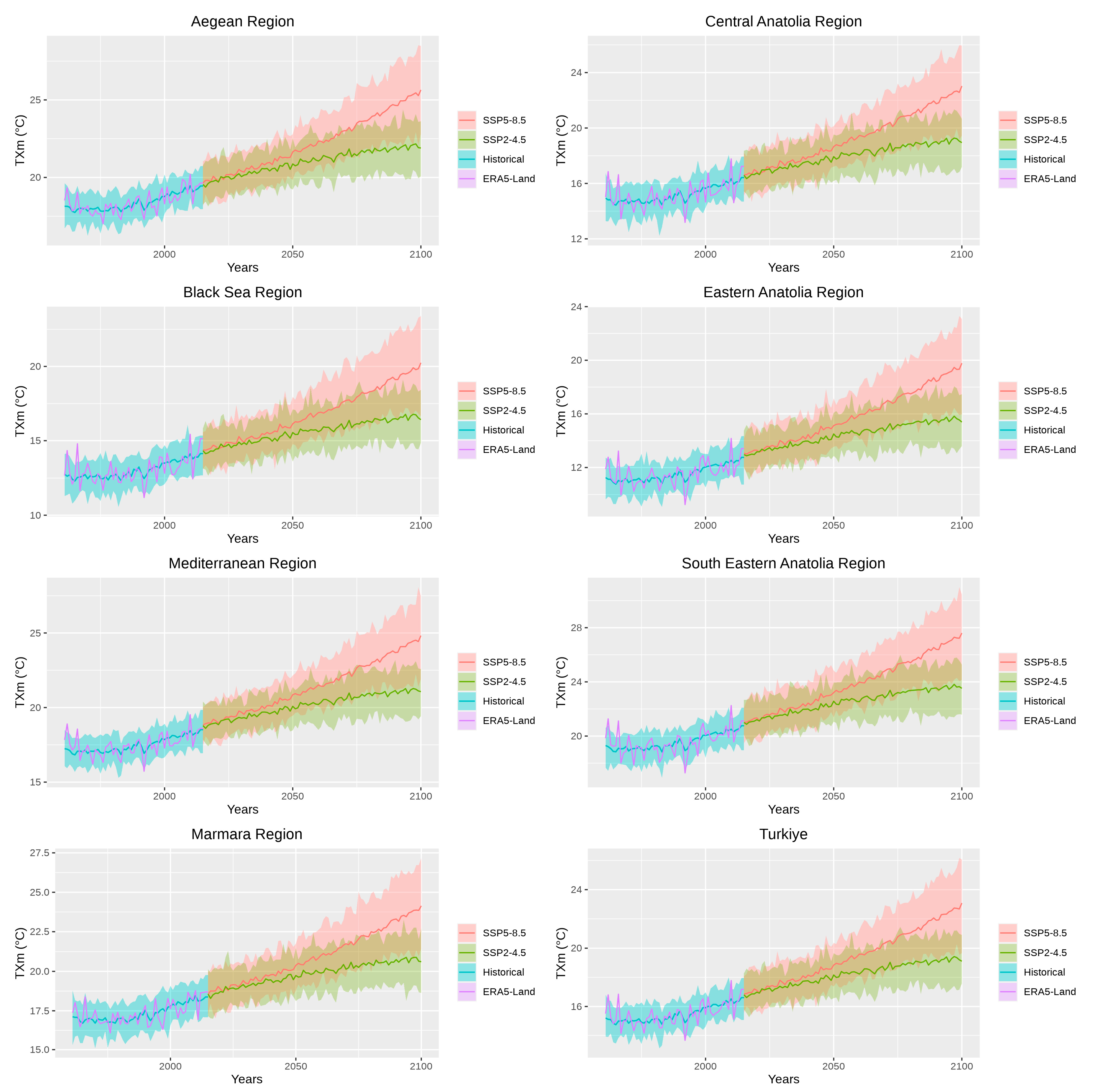
3.3.2. Extreme Temperature Indices (ETI)
Minimum Temperature Indices
Maximum Temperature Indices
4. Discussion
5. Conclusions and Remarks
- In general, all three bias correction algorithms are robust and capable of correcting large systematic biases that are present in the GCM representations of the ET-SCI indices over the historical simulation period.
- Intermodel agreement is better for temperature simulations compared to precipitation simulations.
- The temporal variations of the 12 EPIs and 12 ETIs from 2015 to 2100 consistently suggest drier conditions, yet more frequent and severe precipitation extremes and warming temperature extremes in Türkiye, under the two scenarios. The changes in the 12 EPIs and 12 ETIs were more significant for SSP5-8.5.
- Considering the dry day conditions, the Black Sea and Marmara regions emerge with greater dry periods compared to the Türkiye average, which means greater sensitivity to climate change than the other regions. In general, the SSP5-8.5 scenario indicates more severe water stress than the SSP2-4.5 scenario, especially in the future.
- Precipitation extremes indicate a decrease in the frequency of heavy rains but an increase in very heavy rains and an increasing contribution of very heavy rain days to the total precipitation. The increasing SDII and decreasing total precipitation also support these findings.
- Temperature extremes such as the coldest, warmest, and mean daily maximum temperature are expected to increase in all regions across Türkiye, indicating warming conditions. Additionally, the coldest daily maximums exhibit higher sensitivity to climate change in the Aegean, Southeastern Anatolia, Marmara, and Mediterranean regions of Türkiye, while the mean daily maximum temperature showed greater sensitivity in the Black Sea, Central Anatolia, and Eastern Anatolia regions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brás, T.A.; Seixas, J.; Carvalhais, N.; Jägermeyr, J. Severity of drought and heatwave crop losses tripled over the last five decades in Europe. Environ. Res. Lett. 2021, 16, 65012. [Google Scholar] [CrossRef]
- Carnicer, J.; Alegria, A.; Giannakopoulos, C.; Di Giuseppe, F.; Karali, A.; Koutsias, N.; Lionello, P.; Parrington, M.; Vitolo, C. Global warming is shifting the relationships between fire weather and realized fire-induced CO2 emissions in Europe. Sci. Rep. 2022, 12, 10365. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Roshani, A.; Parak, F.; Esmaili, H. Trend analysis of climate change compound indices in Iran. J. Water Clim. Chang. 2020, 12, 801–816. [Google Scholar] [CrossRef]
- Kim, Y.H.; Min, S.K.; Zhang, X.; Sillmann, J.; Sandstad, M. Evaluation of the CMIP6 multi-model ensemble for climate extreme indices. Weather. Clim. Extrem. 2020, 29, 100269. [Google Scholar] [CrossRef]
- Iyakaremye, V.; Zeng, G.; Zhang, G. Changes in extreme temperature events over Africa under 1.5 and 2.0 °C global warming scenarios. Int. J. Clim. 2021, 41, 1506–1524. [Google Scholar] [CrossRef]
- IPCC. IPCC Climate Change 2021: The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Chiang, F.; Mazdiyasni, O.; AghaKouchak, A. Evidence of anthropogenic impacts on global drought frequency, duration, and intensity. Nat. Commun. 2021, 12, 2754. [Google Scholar] [CrossRef] [PubMed]
- Baghel, T.; Babel, M.S.; Shrestha, S.; Salin, K.R.; Virdis, S.G.; Shinde, V. A generalized methodology for ranking climate models based on climate indices for sector-specific studies: An application to the Mekong sub-basin. Sci. Total Environ. 2022, 829, 154551. [Google Scholar] [CrossRef] [PubMed]
- Guan, J.; Yao, J.; Li, M.; Li, D.; Zheng, J. Historical changes and projected trends of extreme climate events in Xinjiang, China. Clim. Dyn. 2022, 59, 1753–1774. [Google Scholar] [CrossRef]
- CRED. Disasters in Numbers 2021; Centre for Research on the Epidemiology of Disasters (CRED): Brussels, Belgium, 2021. [Google Scholar]
- Myhre, G.; Alterskjær, K.; Stjern, C.W.; Hodnebrog, Ø.; Marelle, L.; Samset, B.H.; Stohl, A. Frequency of extreme precipitation increases extensively with event rareness under global warming. Sci. Rep. 2019, 9, 16063. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the worldâ €TM s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Montanari, A. Global and regional increase of precipitation extremes under global warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Donat, M.G.; Sillmann, J.; Wild, S.; Alexander, L.V.; Lippmann, T.; Zwiers, F.W. Consistency of Temperature and Precipitation Extremes across Various Global Gridded In Situ and Reanalysis Datasets. J. Clim. 2014, 27, 5019–5035. [Google Scholar] [CrossRef]
- Yao, J.; Chen, Y.; Chen, J.; Zhao, Y.; Tuoliewubieke, D.; Li, J.; Yang, L.; Mao, W. Intensification of extreme precipitation in arid Central Asia. J. Hydrol. 2020, 598, 125760. [Google Scholar] [CrossRef]
- Martinez-Villalobos, C.; Neelin, J.D. Regionally high risk increase for precipitation extreme events under global warming. Sci. Rep. 2023, 13, 5579. [Google Scholar] [CrossRef] [PubMed]
- Schleussner, C.F.; Lissner, T.K.; Fischer, E.M.; Wohland, J.; Perrette, M.; Golly, A.; Rogelj, J.; Childers, K.; Schewe, J.; Frieler, K.; et al. Differential climate impacts for policy-relevant limits to global warming: The case of 1.5 °C and 2 °C. Earth Syst. Dyn. 2016, 7, 327–351. [Google Scholar] [CrossRef]
- Kouman, K.D.; Kabo-bah, A.T.; Kouadio, B.H.; Akpoti, K. Spatio-Temporal Trends of Precipitation and Temperature Extremes across the North-East Region of Côte d’Ivoire over the Period 1981–2020. Climate 2022, 10, 74. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Mohammadi, B.; Shamshirband, S.; Chau, K. Coupling a firefly algorithm with support vector regression to predict evaporation in northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 584–597. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Li, M.; Li, L.; Liu, F.; Liu, D.L.; Pulatov, B. Projection of precipitation extremes in China’s mainland based on the statistical downscaled data from 27 GCMs in CMIP6. Atmos. Res. 2022, 280, 106462. [Google Scholar] [CrossRef]
- Wudineh, F.A.; Moges, S.; Kidanewold, B.B. Detecting Hydrological Variability in Precipitation Extremes: Application of Reanalysis Climate Product in Data-Scarce Wabi Shebele Basin of Ethiopia. J. Hydrol. Eng. 2022, 27, 5021035. [Google Scholar] [CrossRef]
- McGree, S.; Herold, N.; Alexander, L.; Schreider, S.; Kuleshov, Y.; Ene, E.; Finaulahi, S.; Inape, K.; Mackenzie, B.; Malala, H.; et al. Recent Changes in Mean and Extreme Temperature and Precipitation in the Western Pacific Islands. J. Clim. 2019, 32, 4919–4941. [Google Scholar] [CrossRef]
- Alexander, L.; Herold, N. ClimPACT2: Indices and Software. A Document Prepared on Behalf of the Commission for Climatology (CCl) Expert Team on Sector-Specific Climate Indices (ET-SCI); University of South New Wales: Sydney, Australia, 2016. [Google Scholar]
- Yosef, Y.; Aguilar, E.; Alpert, P. Changes in extreme temperature and precipitation indices: Using an innovative daily homogenized database in Israel. Int. J. Climatol. 2019, 39, 5022–5045. [Google Scholar] [CrossRef]
- Chapagain, D.; Dhaubanjar, S.; Bharati, L. Unpacking future climate extremes and their sectoral implications in western Nepal. Clim. Chang. 2021, 168, 8. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Srivastava, A.; Grotjahn, R.; Ullrich, P.A. Evaluation of historical CMIP6 model simulations of extreme precipitation over contiguous US regions. Weather. Clim. Extrem. 2020, 29, 100268. [Google Scholar] [CrossRef]
- Bağçaci, S.Ç.; Yucel, I.; Duzenli, E.; Yilmaz, M.T. Intercomparison of the expected change in the temperature and the precipitation retrieved from CMIP6 and CMIP5 climate projections: A Mediterranean hot spot case, Turkiye. Atmos. Res. 2021, 256, 105576. [Google Scholar] [CrossRef]
- Davy, R.; Outten, S. The Arctic Surface Climate in CMIP6: Status and Developments since CMIP5. J. Clim. 2020, 33, 8047–8068. [Google Scholar] [CrossRef]
- Bayar, A.S.; Yılmaz, M.T.; Yücel, İ.; Dirmeyer, P. CMIP6 Earth system models project greater acceleration of climate zone change due to stronger warming rates. Earth’s Future 2023, 11, e2022EF002972. [Google Scholar] [CrossRef]
- Otto-Bliesner, B.L.; Brady, E.C.; Zhao, A.; Brierley, C.M.; Axford, Y.; Capron, E.; Govin, A.; Hoffman, J.S.; Isaacs, E.; Kageyama, M.; et al. Large-scale features of Last Interglacial climate: Results from evaluating the lig127k simulations for the Coupled Model Intercomparison Project (CMIP6)–Paleoclimate Modeling Intercomparison Project (PMIP4). Clim. Past 2021, 17, 63–94. [Google Scholar] [CrossRef]
- Emanuel, K. Response of Global Tropical Cyclone Activity to Increasing CO2: Results from Downscaling CMIP6 Models. J. Clim. 2021, 34, 57–70. [Google Scholar] [CrossRef]
- Dosio, A.; Jury, M.W.; Almazroui, M.; Ashfaq, M.; Diallo, I.; Engelbrecht, F.A.; Klutse, N.A.B.; Lennard, C.; Pinto, I.; Sylla, M.B.; et al. Projected future daily characteristics of African precipitation based on global (CMIP5, CMIP6) and regional (CORDEX, CORDEX-CORE) climate models. Clim. Dyn. 2021, 57, 3135–3158. [Google Scholar] [CrossRef]
- Meresa, H.; Tischbein, B.; Mekonnen, T. Climate change impact on extreme precipitation and peak flood magnitude and frequency: Observations from CMIP6 and hydrological models. Nat. Hazards 2022, 111, 2649–2679. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, J.; Zhang, X.; Shen, M.; Chen, H.; Guo, S. A new two-stage multivariate quantile mapping method for bias correcting climate model outputs. Clim. Dyn. 2019, 53, 3603–3623. [Google Scholar] [CrossRef]
- Tong, Y.; Gao, X.; Han, Z.; Xu, Y.; Xu, Y.; Giorgi, F. Bias correction of temperature and precipitation over China for RCM simulations using the QM and QDM methods. Clim. Dyn. 2021, 57, 1425–1443. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Brogli, R.; Sørland, S.L.; Kröner, N.; Schär, C. Causes of future Mediterranean precipitation decline depend on the season. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. EGU2020-4638. [Google Scholar] [CrossRef]
- Tramblay, Y.; Koutroulis, A.G.; Samaniego, L.; Vicente-Serrano, S.M.; Volaire, F.; Boone, A.; Page, M.L.; Llasat, M.D.; Albergel, C.; Burak, S.; et al. Challenges for drought assessment in the Mediterranean region under future climate scenarios. Earth-Sci. Rev. 2020, 210, 103348. [Google Scholar] [CrossRef]
- Tuel, A.; Eltahir, E.A.B. Why Is the Mediterranean a Climate Change Hot Spot? J. Clim. 2020, 33, 5829–5843. [Google Scholar] [CrossRef]
- Driouech, F.; ElRhaz, K.; Moufouma-Okia, W.; Arjdal, K.; Balhane, S. Assessing Future Changes of Climate Extreme Events in the CORDEX-MENA Region Using Regional Climate Model ALADIN-Climate. Earth Syst. Environ. 2020, 4, 477–492. [Google Scholar] [CrossRef]
- Todaro, V.; D’Oria, M.; Secci, D.; Zanini, A.; Tanda, M.G. Climate Change over the Mediterranean Region: Local Temperature and Precipitation Variations at Five Pilot Sites. Water 2022, 14, 2499. [Google Scholar] [CrossRef]
- Aziz, R.; Yücel, İ. Assessing nonstationarity impacts for historical and projected extreme precipitation in Turkey. Theor. Appl. Climatol. 2021, 143, 1213–1226. [Google Scholar] [CrossRef]
- Türkeş, M.; Turp, M.T.; An, N.; Öztürk, T.; Kurnaz, M.L. Impacts of Climate Change on Precipitation Climatology and Variability in Turkey. Water Resour. Turk. 2020, 2, 467–491. [Google Scholar] [CrossRef]
- Uzuner, C.; Dengiz, O. Desertification risk assessment in Turkiye based on environmentally sensitive areas. Ecol. Indic. 2020, 114, 106295. [Google Scholar] [CrossRef]
- Öztürk, T. Projections of Future Change of Climatology and Extreme Events in the Mediterranean Basin, by the HIRHAM5. Int. J. Adv. Eng. Pure Sci. 2022, 34, 167–189. [Google Scholar] [CrossRef]
- Sen, O.L.; Unal, A.; Bozkurt, D.; Kindap, T. Temporal changes in the Euphrates and Tigris discharges and teleconnections. Environ. Res. Lett. 2011, 6, 24012. [Google Scholar] [CrossRef]
- Bozkurt, D.; Sen, O. Climate change impacts in the Euphrates-Tigris Basin based on different model and scenario simulations. J. Hydrol. 2013, 480, 149–161. [Google Scholar] [CrossRef]
- Yucel, I.; Güventürk, A.; Sen, O.L. Climate change impacts on snowmelt runoff for mountainous transboundary basins in eastern Turkiye. Int. J. Climatol. 2015, 35, 215–228. [Google Scholar] [CrossRef]
- Aziz, R.; Yucel, I.; Yozgatligil, C. Nonstationarity impacts on frequency analysis of yearly and seasonal extreme temperature in Turkiye. Atmos. Res. 2020, 238, 104875. [Google Scholar] [CrossRef]
- Sensoy, S.; Türkoğlu, N.; Akçakaya, A.; Ulupınar, Y.; Ekici, M.; Demircan, M.; Atay, H.; Tüvan, A.; Demirbaş, H. Trends in Turkey climate indices from 1960 to 2010. In Proceedings of the 6th Atmospheric Science Symposium, ITU, Istanbul, Turkey, 24–26 April 2013. [Google Scholar]
- Abbasnia, M.; Toros, H. Trend analysis of weather extremes across the coastal and non-coastal areas (case study: Turkey). J. Earth Syst. Sci. 2020, 129, 95. [Google Scholar] [CrossRef]
- Oruc, S. Performance of bias corrected monthly CMIP6 climate projections with different reference period data in Turkey. Acta Geophys. 2022, 70, 777–789. [Google Scholar] [CrossRef]
- Amjad, M.R.; Yilmaz, M.T.; Yucel, I.; Yilmaz, K.K. Performance evaluation of satellite- and model-based precipitation products over varying climate and complex topography. J. Hydrol. 2020, 584, 124707. [Google Scholar] [CrossRef]
- General Diroctorate of Meteorology (GDM). Offical Statistics/Parameter Analysis. 2023. Available online: https://www.mgm.gov.tr/FILES/iklim/yillikiklim/2022-iklim-raporu.pdf (accessed on 1 March 2023).
- Yilmaz, M. Accuracy assessment of temperature trends from ERA5 and ERA5-Land. Sci. Total Environ. 2023, 856, 159182. [Google Scholar] [CrossRef] [PubMed]
- Stouffer, R.J.; Eyring, V.; Meehl, G.A.; Bony, S.; Senior, C.A.; Stevens, B.; Taylor, K.E. CMIP5 Scientific Gaps and Recommendations for CMIP6. Bull. Am. Meteorol. Soc. 2017, 98, 95–105. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.; Zhao, T.; Han, L. Future changes of global potential evapotranspiration simulated from CMIP5 to CMIP6 models. Atmos. Ocean. Sci. Lett. 2020, 13, 568–575. [Google Scholar] [CrossRef]
- Wyser, K.; Kjellström, E.; Königk, T.; Martins, H.; Doescher, R. Warmer climate projections in EC-Earth3-Veg: The role of changes in the greenhouse gas concentrations from CMIP5 to CMIP6. Environ. Res. Lett. 2020, 15, 54020. [Google Scholar] [CrossRef]
- Afshar, M.H.; Yilmaz, M.T. The Added Utility of Nonlinear Methods Compared To Linear Methods In Rescaling Soil Moisture Products. Remote Sens. Environ. 2017, 196, 224–237. [Google Scholar] [CrossRef]
- Afshar, M.H.; Yilmaz, M.T.; Crow, W.T. Impact of rescaling approaches in simple fusion of soil moisture products. Water Resour. Res. 2019, 55, 7804–7825. [Google Scholar] [CrossRef]
- Heo, J.-H.; Ahn, H.; Shin, J.-Y.; Kjeldsen, T.R.; Jeong, C. Probability Distributions for a Quantile Mapping Technique for a Bias Correction of Precipitation Data: A Case Study to Precipitation Data Under Climate Change. Water 2019, 11, 1475. [Google Scholar] [CrossRef]
- Niranjan Kumar, K.; Thota, M.S.; Ashrit, R.; Mitra, A.K.; Rajeevan, M. Quantile mapping bias correction methods to IMDAA reanalysis for calibrating NCMRWF unified model operational forecasts. Hydrol. Sci. J. 2022, 67, 870–885. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Kim, S.; Joo, K.; Kim, H.; Shin, J.-Y.; Heo, J.-H. Regional quantile delta mapping method using regional frequency analysis for regional climate model precipitation. J. Hydrol. 2021, 596, 125685. [Google Scholar] [CrossRef]
- Wang, F.; Tian, D. On deep learning-based bias correction and downscaling of multiple climate models simulations. Clim. Dyn. 2022, 59, 3451–3468. [Google Scholar] [CrossRef]
- Bürger, G.; Murdock, T.Q.; Werner, A.T.; Sobie, S.R.; Cannon, A.J. Downscaling extremes—An intercomparison of multiple statistical methods for present climate. J. Clim. 2012, 25, 4366–4388. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, V.Y.; Fatichi, S. Climate change and uncertainty assessment over a hydroclimatic transect of Michigan. Stoch. Environ. Res. Risk Assess 2016, 30, 923–944. [Google Scholar] [CrossRef]
- Ahmed, K.; Sachindra, D.A.; Shahid, S.; Demirel, M.C.; Chung, E.S. Selection of multi-model ensemble of general circulation models for the simulation of precipitation and maximum and minimum temperature based on spatial assessment metrics. Hydrol. Earth Syst. Sci. 2019, 23, 4803–4824. [Google Scholar] [CrossRef]
- Grose, M.R.; Narsey, S.; Delage, F.; Dowdy, A.J.; Bador, M.; Boschat, G.; Chung, C.T.; Kajtar, J.B.; Rauniyar, S.P.; Freund, M.B.; et al. Insights from CMIP6 for Australia’s Future Climate. Earth’s Future 2020, 8, e2019EF001469. [Google Scholar] [CrossRef]
- Cooley, A.K.; Chang, H. Detecting change in precipitation indices using observed (1977–2016) and modeled future climate data in Portland, Oregon, USA. J. Water Clim. Chang. 2021, 12, 1135–1153. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate extreme indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Guan, T.; Liu, Y.; Sun, Z.; Zhang, J.; Chen, H.; Wang, G.; Jin, J.; Bao, Z.; Qi, W. A Framework to Identify the Uncertainty and Credibility of GCMs for Projected Future Precipitation: A Case Study in the Yellow River Basin, China. Front. Environ. Sci. 2022, 10, 863575. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Webb, M.J.; Annan, J.D.; Armour, K.C.; Forster, P.M.; Hargreaves, J.C.; Hegerl, G.; Klein, S.A.; Marvel, K.D.; Rohling, E.J.; et al. An Assessment of Earth’s Climate Sensitivity Using Multiple Lines of Evidence. Rev. Geophys. 2020, 58, e2019RG000678. [Google Scholar] [CrossRef] [PubMed]
- Bjordal, J.; Storelvmo, T.; Alterskjær, K.; Carlsen, T. Equilibrium climate sensitivity above 5 °C plausible due to state-dependent cloud feedback. Nat. Geosci. 2020, 13, 718–721. [Google Scholar] [CrossRef]
- Agel, L.; Barlow, M. How Well Do CMIP6 Historical Runs Match Observed Northeast, U.S. Precipitation and Extreme Precipitation–Related Circulation? J. Clim. 2020, 33, 9835–9848. [Google Scholar] [CrossRef]
- Enayati, M.; Bozorg-Haddad, O.; Bazrafshan, J.; Hejabi, S.; Chu, X. Bias correction capabilities of quantile mapping methods for rainfall and temperature variables. J. Water Clim. Chang. 2021, 12, 401–419. [Google Scholar] [CrossRef]
- Barcikowska, M.J.; Kapnick, S.B.; Krishnamurty, L.; Russo, S.; Cherchi, A.; Folland, C.K. Changes in the future summer Mediterranean climate: Contribution of teleconnections and local factors. Earth Syst. Dynam. 2020, 11, 161–181. [Google Scholar] [CrossRef]
- Ozturk, T.; Saygili-Araci, F.S.; Kurnaz, M.L. Projected Changes in Extreme Temperature and Precipitation Indices Over CORDEX-MENA Domain. Atmosphere 2021, 12, 622. [Google Scholar] [CrossRef]
- Mistry, M. A High-Resolution Global Gridded Historical Dataset of Climate Extreme Indices. Data 2019, 4, 41. [Google Scholar] [CrossRef]
- Alexander, L.V.; Fowler, H.J.; Bador, M.; Behrangi, A.; Donat, M.G.; Dunn, R.J.; Funk, C.; Goldie, J.; Lewis, E.; Rogé, M.; et al. On the use of indices to study extreme precipitation on sub-daily and daily timescales. Environ. Res. Lett. 2019, 14, 125008. [Google Scholar] [CrossRef]



| Model | Pr | Tasmax | Tasmin | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Hist | SSP | Hist | SSP | Hist | SSP | ||||
| 2-4.5 | 5-8.5 | 2-4.5 | 5-8.5 | 2-4.5 | 5-8.5 | ||||
| ACCESS-CM2 (Australia) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| ACCESS-ESM1-5 (Australia) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| AWI-CM-1-1-MR (Germany) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| AWI-ESM-1-1-LR (Germany) | 🗸 | 🗸 | 🗸 | ||||||
| BCC-CSM2-MR (China) | 🗸 | 🗸 | 🗸 | ||||||
| BCC-ESM1 (China) | 🗸 | 🗸 | 🗸 | ||||||
| CAMS-CSM1-0 (China) | |||||||||
| CanESM5 (Canada) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| CanESM5-CanOE (Canada) | |||||||||
| CESM2 (USA) | 🗸 | ||||||||
| CESM2-FV2 (USA) | 🗸 | ||||||||
| CESM2-WACCM (USA) | 🗸 | 🗸 | 🗸 | ||||||
| CESM2-WACCM-FV2 (USA) | |||||||||
| CIESM (China) | |||||||||
| CMCC-CM2-HR4 (Italy) | 🗸 | ||||||||
| CMCC-CM2-SR5 (Italy) | 🗸 | 🗸 | 🗸 | ||||||
| CMCC-ESM2 (Italy) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| CNRM-CM6-1 (France) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| CNRM-CM6-1-HR (France) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||
| CNRM-ESM2-1 (France) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| E3SM-1-0 (USA) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |||
| E3SM-1-1 (USA) | |||||||||
| E3SM-1-1-ECA (USA) | |||||||||
| EC-Earth3 (Europe) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| EC-Earth3-AerChem (Europe) | 🗸 | 🗸 | 🗸 | ||||||
| EC-Earth3-CC (Europe) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| EC-Earth3-Veg (Europe) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| EC-Earth3-Veg-LR (Europe) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| FGOALS-f3-L (China) | 🗸 | 🗸 | 🗸 | ||||||
| FGOALS-g3 (China) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| FIO-ESM-2-0 (China) | |||||||||
| GFDL-ESM4 (USA) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| GISS-E2-1-G (USA) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| GISS-E2-1-H (USA) | |||||||||
| HadGEM3-GC31-LL (UK) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| HadGEM3-GC31-MM (UK) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |||
| IITM-ESM (India) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||||
| INM-CM4-8 (Russia) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| INM-CM5-0 (Russia) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| IPSL-CM5A2-INCA (France) | 🗸 | ||||||||
| IPSL-CM6A-LR (France) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| KACE-1-0-G (Republic of Korea) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| KIOST-ESM (Republic of Korea) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| MCM-UA-1-0 (USA) | |||||||||
| MIROC6 (Japan) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| MIROC-ES2H (Japan) | |||||||||
| MIROC-ES2L (Japan) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| MPI-ESM-1-2-HAM (Switzerland) | 🗸 | 🗸 | 🗸 | ||||||
| MPI-ESM1-2-HR (Germany) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |
| MPI-ESM1-2-LR (Germany) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| MRI-ESM2-0 (Japan) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| NESM3 (China) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| NorCPM1 (Norway) | 🗸 | 🗸 | 🗸 | ||||||
| NorESM2-LM (Norway) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| NorESM2-MM (Norway) | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| SAM0-UNICON (Republic of Korea) | 🗸 | 🗸 | 🗸 | ||||||
| TaiESM1 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| UKESM1-0-LL | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| Temperature Indices | ||||
| Short Name | Long Name | Category | Definition | Units |
| FD | Frost days | Threshold | Number of days when TN < 0 °C | days |
| ID | Ice Days | Threshold | Number of days when TX < 0 °C | days |
| SU | Summer days | Threshold | Number of days when TX > 25 °C | days |
| TR | Tropical nights | Threshold | Number of days when TN > 20 °C | days |
| WSDI | Warm spell duration indicator | Duration | Annual number of days contributing to events where 6 or more consecutive days experience TX > 90th percentile | days |
| CSDI | Cold spell duration indicator | Duration | Annual number of days contributing to events where 6 or more consecutive days experience TN < 10th percentile | days |
| TXx | Max TX | Absolute | Warmest daily TX | °C |
| TNn | Min TN | Absolute | Coldest daily TN | °C |
| TNx | Max TN | Absolute | Warmest daily TN | °C |
| TXn | Min TX | Absolute | Coldest daily TX | °C |
| TXm | Mean TX | Absolute | Mean daily maximum temperature | °C |
| TNm | Mean TN | Absolute | Mean daily minimum temperature | °C |
| Precipitation Indices | ||||
| Short Name | Long Name | Category | Definition | Units |
| CDD | Consecutive Dry Days | Duration | Maximum number of consecutive dry days (when PR < 1.0 mm) | days |
| CWD | Consecutive Wet Days | Duration | Maximum annual number of consecutive wet days (when PR >= 1.0 mm) | days |
| R10 mm | Number of heavy rain days | Threshold | Number of days when PR >= 10 mm | days |
| R20 mm | Number of very heavy rain days | Threshold | Number of days when PR >= 20 mm | days |
| R95p | Total annual PR from heavy rain days | Percentile | Annual sum of daily PR > 95th percentile | mm |
| R99p | Total annual PR from very heavy rain days | Percentile | Annual sum of daily PR > 99th percentile | mm |
| Rx1day | Max 1-day PR | Absolute | Maximum 1-day PR total | mm |
| Rx5day | Max 5-day PR | Absolute | Maximum 5-day PR total | mm |
| PRCPTOT | Annual total wet-day PR | Other | Sum of daily PR >= 1.0 mm | mm |
| R95pTOT | Contribution from very wet days | Percentile | 100 × r95p/PRCPTOT | % |
| R99pTOT | Contribution from extremely wet days | Percentile | 100 × r99p/PRCPTOT | % |
| SDII | Daily PR intensity | Other | Annual total PR divided by the number of wet days (when total PR >= 1.0 mm) | mm/day |
| Index | Scenario&Period | Aeg. | Cen. Ana. | Blck. | East. Ana. | Med. | Se. Ana. | Mar. | Türkiye |
|---|---|---|---|---|---|---|---|---|---|
| CDD (days) | GCM BC Historical | 66.5 | 56.5 | 29.8 | 43.9 | 62.5 | 82.5 | 49.6 | 53.8 |
| GCM SSP2-4.5 14–40 | 68.9 | 58.0 | 32.7 | 45.1 | 64.6 | 84.7 | 54.4 | 56.1 | |
| GCM SSP2-4.5 41–70 | 71.9 | 61.0 | 35.4 | 47.3 | 67.1 | 87.5 | 58.6 | 58.9 | |
| GCM SSP2-4.5 71–100 | 75.9 | 64.8 | 38.2 | 49.0 | 70.3 | 89.6 | 62.3 | 62.0 | |
| GCM SSP5-8.5 14–40 | 68.1 | 58.3 | 33.3 | 46.2 | 65.1 | 85.4 | 54.5 | 56.5 | |
| GCM SSP5-8.5 41–70 | 75.7 | 65.4 | 39.2 | 49.4 | 70.9 | 89.5 | 63.2 | 62.4 | |
| GCM SSP5-8.5 71–100 | 85.4 | 73.4 | 47.1 | 55.9 | 77.4 | 96.3 | 74.4 | 70.4 | |
| CWD (days) | GCM BC Historical | 8.2 | 8.3 | 13.4 | 11.8 | 10.0 | 9.2 | 9.6 | 10.1 |
| GCM SSP2-4.5 14–40 | 7.9 | 8.0 | 12.7 | 11.5 | 9.2 | 8.7 | 9.1 | 9.7 | |
| GCM SSP2-4.5 41–70 | 7.8 | 8.0 | 12.7 | 11.3 | 9.0 | 8.5 | 9.1 | 9.6 | |
| GCM SSP2-4.5 71–100 | 7.7 | 7.9 | 12.7 | 11.3 | 8.8 | 8.4 | 9.0 | 9.5 | |
| GCM SSP5-8.5 14–40 | 8.0 | 8.1 | 12.6 | 11.4 | 9.3 | 8.7 | 9.2 | 9.7 | |
| GCM SSP5-8.5 41–70 | 7.6 | 7.9 | 12.4 | 11.1 | 8.8 | 8.3 | 8.8 | 9.4 | |
| GCM SSP5-8.5 71–100 | 6.9 | 7.3 | 11.7 | 10.4 | 8.0 | 7.8 | 8.2 | 8.7 | |
| R10mm (days) | GCM BC Historical | 18.2 | 10.8 | 28.9 | 19.4 | 23.7 | 22.9 | 21.7 | 19.7 |
| GCM SSP2-4.5 14–40 | 17.7 | 11.0 | 29.6 | 20.0 | 22.2 | 22.1 | 21.6 | 19.7 | |
| GCM SSP2-4.5 41–70 | 17.2 | 11.3 | 30.1 | 20.5 | 21.5 | 21.9 | 21.5 | 19.8 | |
| GCM SSP2-4.5 71–100 | 17.0 | 11.5 | 30.4 | 20.8 | 21.1 | 21.6 | 21.6 | 19.9 | |
| GCM SSP5-8.5 14–40 | 17.9 | 11.2 | 29.7 | 20.3 | 22.5 | 22.5 | 21.7 | 19.9 | |
| GCM SSP5-8.5 41–70 | 16.8 | 11.2 | 29.8 | 20.5 | 21.0 | 21.4 | 21.1 | 19.5 | |
| GCM SSP5-8.5 71–100 | 14.9 | 11.0 | 29.0 | 20.3 | 18.7 | 19.9 | 19.6 | 18.5 | |
| R20 mm (days) | GCM BC Historical | 5.4 | 1.5 | 6.4 | 3.7 | 8.1 | 7.0 | 5.4 | 4.8 |
| GCM SSP2-4.5 14–40 | 5.5 | 1.6 | 7.0 | 4.1 | 7.9 | 7.2 | 5.7 | 5.0 | |
| GCM SSP2-4.5 41–70 | 5.4 | 1.8 | 7.5 | 4.4 | 7.8 | 7.4 | 5.9 | 5.2 | |
| GCM SSP2-4.5 71–100 | 5.4 | 1.9 | 7.8 | 4.6 | 7.7 | 7.4 | 6.1 | 5.3 | |
| GCM SSP5-8.5 14–40 | 5.5 | 1.7 | 7.1 | 4.2 | 8.0 | 7.4 | 5.8 | 5.1 | |
| GCM SSP5-8.5 41–70 | 5.3 | 1.8 | 7.6 | 4.5 | 7.6 | 7.4 | 6.0 | 5.2 | |
| GCM SSP5-8.5 71–100 | 4.9 | 2.1 | 8.2 | 4.9 | 7.1 | 7.3 | 6.0 | 5.3 | |
| R95p (mm) | GCM BC Historical | 123.8 | 89.4 | 189.7 | 134.1 | 176.2 | 138.4 | 149.6 | 137.5 |
| GCM SSP2-4.5 14–40 | 130.3 | 95.2 | 211.4 | 152.6 | 178.5 | 151.4 | 163.2 | 154.1 | |
| GCM SSP2-4.5 41–70 | 130.5 | 102.8 | 228.8 | 164.8 | 179.4 | 159.5 | 170.3 | 162.8 | |
| GCM SSP2-4.5 71–100 | 135.0 | 107.1 | 243.6 | 172.8 | 181.6 | 163.5 | 180.5 | 170.3 | |
| GCM SSP5-8.5 14–40 | 130.6 | 97.7 | 214.6 | 157.4 | 180.3 | 159.0 | 165.7 | 157.2 | |
| GCM SSP5-8.5 41–70 | 130.8 | 103.8 | 235.5 | 170.6 | 176.1 | 164.9 | 175.7 | 166.1 | |
| GCM SSP5-8.5 71–100 | 130.1 | 111.7 | 258.7 | 188.3 | 178.3 | 173.6 | 181.8 | 177.0 | |
| R99p (mm) | GCM BC Historical | 35.3 | 25.9 | 54.5 | 37.3 | 52.7 | 38.4 | 44.0 | 39.5 |
| GCM SSP2-4.5 14–40 | 40.2 | 29.5 | 64.8 | 48.1 | 56.7 | 48.2 | 52.4 | 48.2 | |
| GCM SSP2-4.5 41–70 | 42.5 | 34.0 | 74.4 | 54.6 | 60.1 | 54.1 | 57.6 | 53.9 | |
| GCM SSP2-4.5 71–100 | 46.2 | 36.6 | 84.1 | 59.4 | 63.2 | 57.9 | 64.3 | 59.0 | |
| GCM SSP5-8.5 14–40 | 40.9 | 30.3 | 65.9 | 50.6 | 58.6 | 51.9 | 53.6 | 49.7 | |
| GCM SSP5-8.5 41–70 | 43.8 | 35.4 | 79.9 | 59.3 | 60.9 | 59.3 | 61.8 | 57.2 | |
| GCM SSP5-8.5 71–100 | 48.2 | 42.5 | 99.3 | 73.9 | 69.8 | 70.9 | 70.4 | 68.5 |
| Index | Scenario&Period | Aeg. | Cen. Ana. | Blck. | East. Ana. | Med | Se. Ana. | Mar. | Türkiye |
|---|---|---|---|---|---|---|---|---|---|
| Rx1day (mm) | GCM BC Historical | 36.3 | 24.5 | 34.3 | 28.8 | 46.4 | 38.1 | 37.7 | 33.2 |
| GCM SSP2-4.5 14–40 | 37.2 | 25.2 | 36.0 | 30.3 | 47.4 | 39.7 | 39.7 | 34.5 | |
| GCM SSP2-4.5 41–70 | 38.0 | 26.0 | 37.2 | 31.5 | 48.3 | 41.0 | 40.7 | 35.5 | |
| GCM SSP2-4.5 71–100 | 38.9 | 26.6 | 38.6 | 32.2 | 48.9 | 41.7 | 41.7 | 36.4 | |
| GCM SSP5-8.5 14–40 | 37.7 | 25.4 | 36.2 | 30.9 | 47.5 | 40.6 | 39.5 | 34.8 | |
| GCM SSP5-8.5 41–70 | 38.4 | 26.5 | 38.0 | 32.1 | 48.5 | 42.2 | 41.6 | 36.2 | |
| GCM SSP5-8.5 71–100 | 39.5 | 28.0 | 40.6 | 34.2 | 51.0 | 44.3 | 43.7 | 38.1 | |
| Rx5day (mm) | GCM BC Historical | 75.9 | 50.5 | 76.6 | 66.8 | 98.3 | 85.4 | 77.6 | 71.9 |
| GCM SSP2-4.5 14–40 | 77.2 | 51.3 | 79.7 | 70.0 | 98.6 | 87.7 | 80.5 | 73.8 | |
| GCM SSP2-4.5 41–70 | 77.4 | 52.4 | 81.9 | 70.9 | 98.4 | 88.8 | 81.7 | 74.9 | |
| GCM SSP2-4.5 71–100 | 77.8 | 53.3 | 83.9 | 72.3 | 98.6 | 89.8 | 83.4 | 76.0 | |
| GCM SSP5-8.5 14–40 | 77.8 | 51.7 | 79.7 | 70.7 | 98.6 | 89.1 | 80.0 | 74.2 | |
| GCM SSP5-8.5 41–70 | 76.6 | 52.9 | 82.9 | 71.9 | 97.7 | 90.0 | 82.5 | 75.3 | |
| GCM SSP5-8.5 71–100 | 75.9 | 53.9 | 86.4 | 74.9 | 97.7 | 92.1 | 84.1 | 77.0 | |
| PRCPTOT (mm) | GCM BC Historical | 601.4 | 465.5 | 973.8 | 722.3 | 766.3 | 679.8 | 712.1 | 686.1 |
| GCM SSP2-4.5 14–40 | 582.2 | 455.6 | 969.1 | 719.9 | 720.0 | 661.2 | 696.3 | 671.9 | |
| GCM SSP2-4.5 41–70 | 565.6 | 455.6 | 974.9 | 723.8 | 698.8 | 654.1 | 689.9 | 667.9 | |
| GCM SSP2-4.5 71–100 | 557.5 | 453.3 | 979.0 | 723.4 | 684.4 | 645.0 | 689.6 | 664.5 | |
| GCM SSP5-8.5 14–40 | 590.0 | 462.2 | 970.4 | 728.7 | 725.9 | 673.7 | 701.6 | 678.6 | |
| GCM SSP5-8.5 41–70 | 550.7 | 447.5 | 958.0 | 716.5 | 678.0 | 643.8 | 675.1 | 655.6 | |
| GCM SSP5-8.5 71–100 | 490.8 | 418.6 | 922.7 | 691.6 | 613.9 | 603.0 | 622.8 | 615.6 | |
| R95pTOT (%) | GCM BC Historical | 20.6 | 19.2 | 19.5 | 18.6 | 23.0 | 20.4 | 21.0 | 20.0 |
| GCM SSP2-4.5 14–40 | 22.4 | 20.9 | 21.8 | 21.2 | 24.8 | 22.9 | 23.4 | 22.9 | |
| GCM SSP2-4.5 41–70 | 23.1 | 22.6 | 23.5 | 22.8 | 25.7 | 24.4 | 24.7 | 24.4 | |
| GCM SSP2-4.5 71–100 | 24.2 | 23.6 | 24.9 | 23.9 | 26.5 | 25.3 | 26.2 | 25.6 | |
| GCM SSP5-8.5 14–40 | 22.1 | 21.1 | 22.1 | 21.6 | 24.8 | 23.6 | 23.6 | 23.2 | |
| GCM SSP5-8.5 41–70 | 23.7 | 23.2 | 24.6 | 23.8 | 26.0 | 25.6 | 26.0 | 25.3 | |
| GCM SSP5-8.5 71–100 | 26.5 | 26.7 | 28.0 | 27.2 | 29.1 | 28.8 | 29.2 | 28.8 | |
| R99pTOT (%) | GCM BC Historical | 5.9 | 5.6 | 5.6 | 5.2 | 6.9 | 5.6 | 6.2 | 5.8 |
| GCM SSP2-4.5 14–40 | 6.9 | 6.5 | 6.7 | 6.7 | 7.9 | 7.3 | 7.5 | 7.2 | |
| GCM SSP2-4.5 41–70 | 7.5 | 7.5 | 7.6 | 7.5 | 8.6 | 8.3 | 8.4 | 8.1 | |
| GCM SSP2-4.5 71–100 | 8.3 | 8.1 | 8.6 | 8.2 | 9.2 | 9.0 | 9.3 | 8.9 | |
| GCM SSP5-8.5 14–40 | 6.9 | 6.6 | 6.8 | 6.9 | 8.1 | 7.7 | 7.6 | 7.3 | |
| GCM SSP5-8.5 41–70 | 7.9 | 7.9 | 8.3 | 8.3 | 9.0 | 9.2 | 9.1 | 8.7 | |
| GCM SSP5-8.5 71–100 | 9.8 | 10.2 | 10.8 | 10.7 | 11.4 | 11.8 | 11.3 | 11.1 | |
| SDII (mm) | GCM BC Historical | 6.9 | 4.9 | 6.2 | 5.8 | 7.5 | 7.5 | 6.6 | 6.2 |
| GCM SSP2-4.5 14–40 | 7.1 | 5.0 | 6.4 | 6.0 | 7.7 | 7.7 | 6.9 | 6.4 | |
| GCM SSP2-4.5 41–70 | 7.2 | 5.1 | 6.6 | 6.1 | 7.7 | 7.9 | 7.0 | 6.5 | |
| GCM SSP2-4.5 71–100 | 7.3 | 5.2 | 6.7 | 6.2 | 7.8 | 8.0 | 7.1 | 6.6 | |
| GCM SSP5-8.5 14–40 | 7.1 | 5.0 | 6.5 | 6.0 | 7.7 | 7.8 | 6.9 | 6.4 | |
| GCM SSP5-8.5 41–70 | 7.2 | 5.2 | 6.7 | 6.2 | 7.8 | 8.0 | 7.1 | 6.6 | |
| GCM SSP5-8.5 71–100 | 7.4 | 5.4 | 6.9 | 6.5 | 8.0 | 8.3 | 7.4 | 6.8 |
| Index | Scenario&Period | Aeg. | Cen. Ana. | Blck. | East. Ana. | Med | Se. Ana. | Mar. | Türkiye |
|---|---|---|---|---|---|---|---|---|---|
| FD (days) | GCM BC Historical | 67.1 | 119.2 | 118.2 | 162.6 | 71.4 | 81.1 | 49.1 | 105.1 |
| GCM SSP2-4.5 14–40 | 50.8 | 100.4 | 99.4 | 141.1 | 56.5 | 59.2 | 34.1 | 86.6 | |
| GCM SSP2-4.5 41–70 | 44.0 | 90.4 | 88.9 | 130.7 | 49.1 | 51.3 | 27.8 | 77.6 | |
| GCM SSP2-4.5 71–100 | 38.1 | 80.9 | 79.4 | 121.4 | 42.6 | 44.5 | 22.8 | 69.6 | |
| GCM SSP5-8.5 14–40 | 47.9 | 96.7 | 97.2 | 134.5 | 54.5 | 56.0 | 32.4 | 83.1 | |
| GCM SSP5-8.5 41–70 | 37.2 | 79.4 | 79.5 | 116.1 | 42.4 | 42.6 | 22.4 | 68.0 | |
| GCM SSP5-8.5 71–100 | 24.3 | 58.0 | 57.4 | 91.4 | 28.3 | 28.2 | 12.4 | 49.4 | |
| TR (days) | GCM BC Historical | 18.4 | 2.1 | 1.2 | 3.2 | 22.4 | 42.5 | 15.5 | 11.7 |
| GCM SSP2-4.5 14–40 | 36.4 | 8.5 | 4.8 | 7.8 | 39.4 | 64.1 | 37.2 | 22.9 | |
| GCM SSP2-4.5 41–70 | 48.5 | 15.5 | 8.8 | 12.1 | 51.4 | 77.2 | 50.8 | 31.3 | |
| GCM SSP2-4.5 71–100 | 58.7 | 23.3 | 13.5 | 16.6 | 61.7 | 86.9 | 62.6 | 39.2 | |
| GCM SSP5-8.5 14–40 | 38.2 | 9.9 | 5.9 | 8.3 | 40.9 | 65.0 | 39.4 | 24.2 | |
| GCM SSP5-8.5 41–70 | 61.2 | 25.7 | 15.4 | 17.6 | 63.8 | 88.1 | 64.5 | 41.1 | |
| GCM SSP5-8.5 71–100 | 94.1 | 56.6 | 39.4 | 38.5 | 97.3 | 117.1 | 97.6 | 69.6 | |
| CSDI (days) | GCM BC Historical | 8.7 | 7.9 | 7.6 | 7.9 | 9.1 | 10.0 | 9.3 | 8.4 |
| GCM SSP2-4.5 14–40 | 2.3 | 2.6 | 2.6 | 2.1 | 2.4 | 2.5 | 2.3 | 2.4 | |
| GCM SSP2-4.5 41–70 | 1.1 | 1.3 | 1.2 | 0.9 | 1.1 | 1.1 | 1.2 | 1.1 | |
| GCM SSP2-4.5 71–100 | 0.6 | 0.8 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | |
| GCM SSP5-8.5 14–40 | 2.4 | 2.6 | 2.9 | 2.0 | 2.6 | 2.7 | 2.8 | 2.6 | |
| GCM SSP5-8.5 41–70 | 0.7 | 0.8 | 0.7 | 0.6 | 0.7 | 0.7 | 0.6 | 0.7 | |
| GCM SSP5-8.5 71–100 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| TNn (°C) | GCM BC Historical | −9.7 | −17.2 | −16.4 | −21.4 | −10.4 | −12.7 | −9.1 | −15.0 |
| GCM SSP2-4.5 14–40 | −7.7 | −14.6 | −14.3 | −19.1 | −8.2 | −10.0 | −7.1 | −12.7 | |
| GCM SSP2-4.5 41–70 | −6.5 | −13.1 | −13.1 | −17.8 | −7.1 | −8.8 | −5.8 | −11.4 | |
| GCM SSP2-4.5 71–100 | −5.7 | −12.0 | −11.9 | −16.8 | −6.3 | −7.6 | −4.8 | −10.4 | |
| GCM SSP5-8.5 14–40 | −7.4 | −14.2 | −14.0 | −18.7 | −7.8 | −9.9 | −6.8 | −12.3 | |
| GCM SSP5-8.5 41–70 | −5.7 | −11.9 | −11.9 | −16.6 | −6.2 | −7.5 | −4.8 | −10.3 | |
| GCM SSP5-8.5 71–100 | −3.5 | −8.7 | −8.9 | −13.4 | −3.9 | −4.5 | −2.3 | −7.4 | |
| TNx (°C) | GCM BC Historical | 21.2 | 18.8 | 17.6 | 17.0 | 21.1 | 23.9 | 21.5 | 19.6 |
| GCM SSP2-4.5 14–40 | 23.3 | 20.9 | 19.5 | 19.0 | 23.2 | 26.0 | 23.5 | 21.6 | |
| GCM SSP2-4.5 41–70 | 24.4 | 22.1 | 20.5 | 20.1 | 24.3 | 27.1 | 24.4 | 22.7 | |
| GCM SSP2-4.5 71–100 | 25.3 | 23.1 | 21.3 | 21.1 | 25.1 | 28.1 | 25.2 | 23.6 | |
| GCM SSP5-8.5 14–40 | 23.6 | 21.1 | 19.7 | 19.2 | 23.6 | 26.3 | 23.9 | 21.9 | |
| GCM SSP5-8.5 41–70 | 25.6 | 23.3 | 21.6 | 21.2 | 25.6 | 28.4 | 25.6 | 23.9 | |
| GCM SSP5-8.5 71–100 | 28.5 | 26.2 | 24.1 | 24.2 | 28.2 | 31.3 | 28.1 | 26.7 | |
| TNm (°C) | GCM BC Historical | 7.7 | 4.1 | 3.8 | 1.0 | 7.5 | 7.9 | 8.7 | 5.1 |
| GCM SSP2-4.5 14–40 | 9.2 | 5.7 | 5.3 | 2.8 | 9.1 | 9.6 | 10.1 | 6.7 | |
| GCM SSP2-4.5 41–70 | 10.0 | 6.6 | 6.2 | 3.8 | 10.0 | 10.6 | 10.9 | 7.6 | |
| GCM SSP2-4.5 71–100 | 10.7 | 7.4 | 7.0 | 4.6 | 10.7 | 11.4 | 11.7 | 8.4 | |
| GCM SSP5-8.5 14–40 | 9.2 | 5.8 | 5.4 | 3.0 | 9.2 | 9.7 | 10.2 | 6.8 | |
| GCM SSP5-8.5 41–70 | 10.8 | 7.4 | 7.0 | 4.8 | 10.8 | 11.5 | 11.7 | 8.5 | |
| GCM SSP5-8.5 71–100 | 13.0 | 9.7 | 9.1 | 7.2 | 13.0 | 14.0 | 13.8 | 10.7 |
| Index | Scenario&Period | Aeg. | Cen. Ana. | Blck. | East. Ana. | Med | Se. Ana. | Mar. | Türkiye |
|---|---|---|---|---|---|---|---|---|---|
| ID (days) | GCM BC Historical | 5.8 | 27.0 | 35.4 | 64.9 | 12.5 | 13.7 | 5.2 | 27.7 |
| GCM SSP2-4.5 14–40 | 3.7 | 19.5 | 26.5 | 48.7 | 8.2 | 8.1 | 2.6 | 20.1 | |
| GCM SSP2-4.5 41–70 | 2.7 | 15.5 | 22.0 | 40.5 | 6.2 | 6.1 | 1.8 | 16.3 | |
| GCM SSP2-4.5 71–100 | 2.0 | 12.1 | 17.9 | 32.6 | 4.6 | 4.6 | 1.2 | 13.0 | |
| GCM SSP5-8.5 14–40 | 3.6 | 19.5 | 26.4 | 47.7 | 8.1 | 7.8 | 2.6 | 19.8 | |
| GCM SSP5-8.5 41–70 | 2.1 | 12.6 | 18.5 | 33.6 | 4.9 | 4.7 | 1.2 | 13.4 | |
| GCM SSP5-8.5 71–100 | 0.9 | 6.5 | 10.6 | 18.6 | 2.2 | 2.1 | 0.4 | 7.2 | |
| SU (days) | GCM BC Historical | 102.6 | 73.9 | 31.6 | 46.8 | 96.7 | 131.8 | 81.7 | 74.9 |
| GCM SSP2-4.5 14–40 | 124.8 | 100.1 | 56.4 | 68.7 | 120.1 | 147.3 | 109.4 | 98.4 | |
| GCM SSP2-4.5 41–70 | 134.4 | 110.7 | 67.5 | 80.4 | 130.2 | 155.7 | 119.0 | 108.7 | |
| GCM SSP2-4.5 71–100 | 142.1 | 119.0 | 77.0 | 89.6 | 137.8 | 162.3 | 126.6 | 117.0 | |
| GCM SSP5-8.5 14–40 | 127.7 | 103.8 | 61.3 | 72.2 | 123.9 | 149.3 | 113.0 | 101.9 | |
| GCM SSP5-8.5 41–70 | 144.9 | 122.8 | 82.1 | 92.5 | 141.3 | 163.9 | 130.4 | 120.5 | |
| GCM SSP5-8.5 71–100 | 168.2 | 146.8 | 109.6 | 117.9 | 164.3 | 183.9 | 152.7 | 144.5 | |
| WSDI (days) | GCM BC Historical | 14.5 | 14.2 | 10.6 | 16.6 | 16.4 | 19.0 | 11.3 | 14.6 |
| GCM SSP2-4.5 14–40 | 52.1 | 48.9 | 37.3 | 59.1 | 62.2 | 67.5 | 41.1 | 51.0 | |
| GCM SSP2-4.5 41–70 | 84.5 | 76.8 | 58.3 | 90.1 | 98.3 | 106.0 | 67.4 | 80.4 | |
| GCM SSP2-4.5 71–100 | 115.3 | 104.1 | 81.5 | 121.2 | 131.4 | 140.3 | 94.2 | 109.2 | |
| GCM SSP5-8.5 14–40 | 59.7 | 56.9 | 45.4 | 66.9 | 72.1 | 75.6 | 49.5 | 59.3 | |
| GCM SSP5-8.5 41–70 | 120.9 | 111.3 | 89.5 | 127.5 | 137.8 | 144.5 | 101.2 | 115.8 | |
| GCM SSP5-8.5 71–100 | 203.4 | 189.6 | 163.1 | 210.5 | 221.3 | 227.9 | 179.4 | 195.5 | |
| TXx (°C) | GCM BC Historical | 35.6 | 33.5 | 30.4 | 30.5 | 34.0 | 38.8 | 33.9 | 33.4 |
| GCM SSP2-4.5 14–40 | 37.5 | 35.7 | 32.4 | 32.9 | 36.0 | 41.1 | 35.7 | 35.5 | |
| GCM SSP2-4.5 41–70 | 38.8 | 37.0 | 33.6 | 34.0 | 37.2 | 42.2 | 36.9 | 36.7 | |
| GCM SSP2-4.5 71–100 | 39.9 | 38.0 | 34.7 | 34.9 | 38.2 | 43.1 | 38.1 | 37.7 | |
| GCM SSP5-8.5 14–40 | 37.7 | 36.1 | 32.7 | 33.4 | 36.3 | 41.5 | 35.9 | 35.8 | |
| GCM SSP5-8.5 41–70 | 39.9 | 38.3 | 34.9 | 35.5 | 38.4 | 43.5 | 37.9 | 38.0 | |
| GCM SSP5-8.5 71–100 | 42.9 | 41.2 | 38.0 | 38.3 | 41.1 | 46.2 | 41.1 | 40.9 | |
| TXn (°C) | GCM BC Historical | −1.2 | −7.7 | −7.1 | −10.3 | −2.2 | −1.9 | −2.1 | −5.6 |
| GCM SSP2-4.5 14–40 | 0.4 | −5.9 | −5.5 | −8.4 | −0.5 | 0.2 | −0.4 | −3.8 | |
| GCM SSP2-4.5 41–70 | 1.2 | −5.0 | −4.8 | −7.8 | 0.4 | 1.0 | 0.5 | −3.0 | |
| GCM SSP2-4.5 71–100 | 1.9 | −4.1 | −4.0 | −6.9 | 1.2 | 1.9 | 1.3 | −2.2 | |
| GCM SSP5-8.5 14–40 | 0.7 | −5.6 | −5.3 | −8.3 | −0.2 | 0.5 | −0.2 | −3.6 | |
| GCM SSP5-8.5 41–70 | 1.9 | −4.1 | −3.9 | −6.8 | 1.2 | 1.9 | 1.3 | −2.2 | |
| GCM SSP5-8.5 71–100 | 3.8 | −1.7 | −2.0 | −4.5 | 3.3 | 4.2 | 3.2 | 0.0 | |
| TXm (°C) | GCM BC Historical | 18.4 | 15.2 | 13.0 | 11.5 | 17.5 | 19.6 | 17.3 | 15.5 |
| GCM SSP2-4.5 14–40 | 20.1 | 17.0 | 14.7 | 13.4 | 19.2 | 21.5 | 19.0 | 17.2 | |
| GCM SSP2-4.5 41–70 | 21.0 | 18.0 | 15.6 | 14.5 | 20.2 | 22.5 | 19.8 | 18.2 | |
| GCM SSP2-4.5 71–100 | 21.8 | 18.9 | 16.4 | 15.4 | 21.0 | 23.4 | 20.6 | 19.0 | |
| GCM SSP5-8.5 14–40 | 20.3 | 17.2 | 14.9 | 13.7 | 19.5 | 21.7 | 19.2 | 17.5 | |
| GCM SSP5-8.5 41–70 | 21.9 | 19.0 | 16.5 | 15.5 | 21.1 | 23.6 | 20.7 | 19.2 | |
| GCM SSP5-8.5 71–100 | 24.3 | 21.5 | 18.8 | 18.2 | 23.4 | 26.1 | 22.9 | 21.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gumus, B.; Oruc, S.; Yucel, I.; Yilmaz, M.T. Impacts of Climate Change on Extreme Climate Indices in Türkiye Driven by High-Resolution Downscaled CMIP6 Climate Models. Sustainability 2023, 15, 7202. https://doi.org/10.3390/su15097202
Gumus B, Oruc S, Yucel I, Yilmaz MT. Impacts of Climate Change on Extreme Climate Indices in Türkiye Driven by High-Resolution Downscaled CMIP6 Climate Models. Sustainability. 2023; 15(9):7202. https://doi.org/10.3390/su15097202
Chicago/Turabian StyleGumus, Berkin, Sertac Oruc, Ismail Yucel, and Mustafa Tugrul Yilmaz. 2023. "Impacts of Climate Change on Extreme Climate Indices in Türkiye Driven by High-Resolution Downscaled CMIP6 Climate Models" Sustainability 15, no. 9: 7202. https://doi.org/10.3390/su15097202
APA StyleGumus, B., Oruc, S., Yucel, I., & Yilmaz, M. T. (2023). Impacts of Climate Change on Extreme Climate Indices in Türkiye Driven by High-Resolution Downscaled CMIP6 Climate Models. Sustainability, 15(9), 7202. https://doi.org/10.3390/su15097202








