Optimal Planning of Electric Vehicle Fast-Charging Stations Considering Uncertain Charging Demands via Dantzig–Wolfe Decomposition
Abstract
1. Introduction
2. Literature Review
2.1. Fast-Charging Station Planning Problem
2.2. Dantzig–Wolfe Decomposition
2.3. Summary of Main Contributions
- (i)
- The data-driven chance constraints are introduced to address the uncertain charging demands, since it is difficult to extract the exact values and accurate probability distributions of the uncertain charging demands in practice. In this circumstance, date-driven chance constraints are viable alternatives to measure the service abilities of fast-charging stations.
- (ii)
- The original planning model is separated into multiple disjoint sub-components corresponding to the O-D pairs in the transportation network, which are facilitated to be implemented in a decentralized manner using parallel machines. Then, the Dantzig–Wolfe decomposition is utilized to solve the planning model, where the master problems and subproblems are one-to-one. Each possesses a moderate scale of decision variables, which makes it conducive to improve the computational performances.
- (iii)
- The computational performance is tested using the 25-node benchmark network, in which the proposed Dantzig–Wolfe decomposition is shown to be efficient for solving the planning problem over a large transportation network.
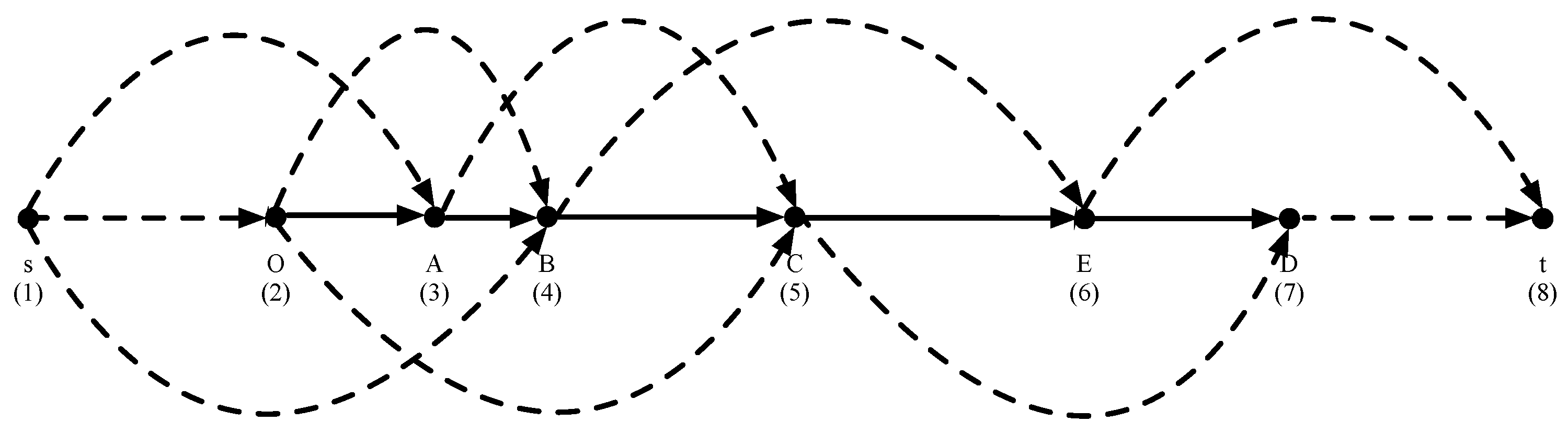
2.4. Expanded Network Generation
- (A1)
- More than half of the battery is full when travel starts at the original node.
- (A2)
- More than half of the battery is full when travel ends at the destination node.
- (A3)
- The driving ranges of electric vehicles are deterministic and fixed.
- Step 1
- Before the original node O, add a source node . After the destination node D, add a sink node . Note that is .
- Step 2
- Connect and O, D and . Note that .
- Step 3
- Ordering the nodes in sequentially. Let denote the ordering index of the nodes.
- Step 4
- Add arc to if is strictly less than ; add arc to if is strictly less than . Add arc to if and is strictly less than R.
2.5. Mathematical Model
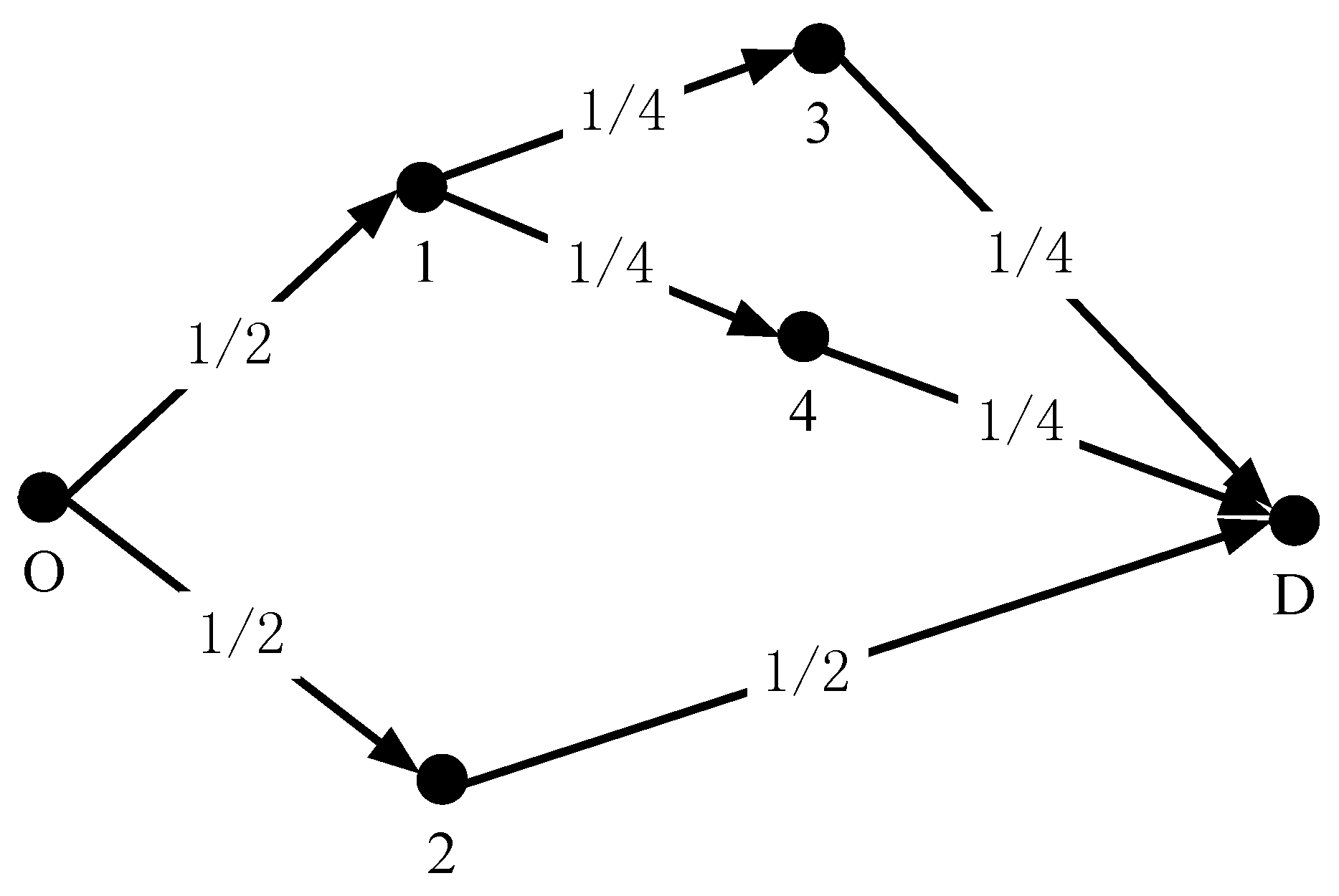
3. Scenario-Based Approach
3.1. Scenario-Based Reformulation
| Algorithm 1 Big-M Coefficients Generation algorithm. |
for do for do for do for do if q traverses node i then Compute . end if end for Sort all ’s as a descending order, . , , . while do . , . . end while . end for for all . end for end for |
3.2. Dantzig–Wolfe Decomposition for SRP
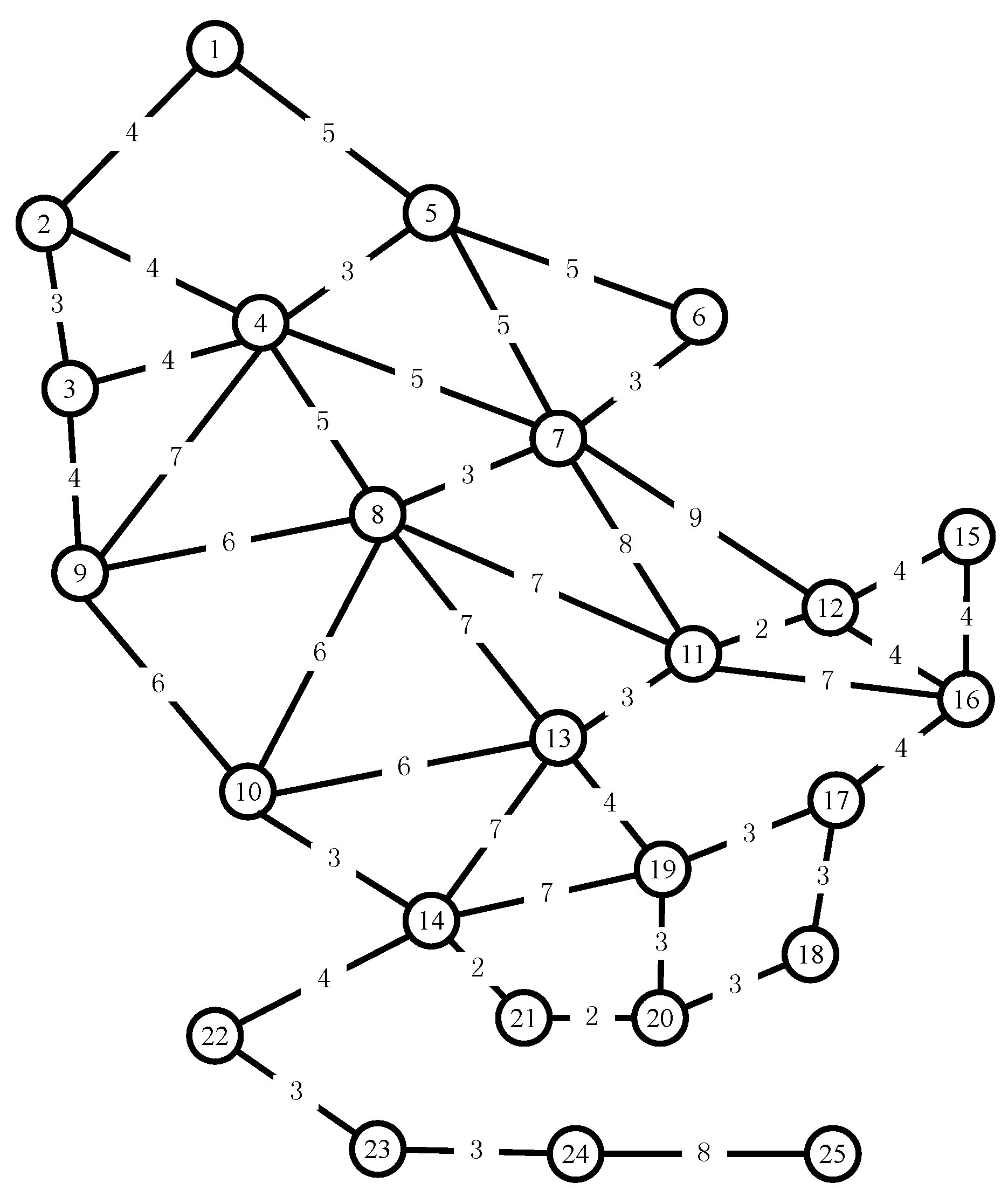
4. Numerical Experiments
- Driving ranges: .
- Service levels: .
- Sizing limits: .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Sets | Descriptions |
| Original network , where V and A are sets of nodes and arcs. | |
| Expanded network on O-D pair q, where and are sets of nodes and arcs. | |
| Q | Set of O-D pairs in original network, indexed by q. |
| , | Set of in-neighbors and out-neighbors of node i on expanded network. |
| Set of scenarios, indexed by . | |
| Set of nodes that traversed by the path between O-D pair q. | |
| Index set of extreme points of allocation variables on available arc | |
| between O-D pair q. |
| Parameters | Descriptions |
| Added source node of O-D pair q on expanded network. | |
| Added sink node of O-D pair q on expanded network. | |
| Uncertain charging demands on O-D pair q. | |
| Cost of building a fast-charging station at node . | |
| Cost of intalling a charging pile at node . | |
| Driving distance of arc . | |
| Sizing bound in fast-charging stations. | |
| Service level of the fast-charging stations. | |
| R | Driving ranges of electric vehicles. |
| Realizations of in scenario . | |
| Big-M coefficient at node i in scenario . | |
| Value of dual variables. | |
| Value of dual variables. | |
| Extreme points of allocation variables. | |
| Extreme points of planning cost on O-D pair q. | |
| The cardinality of set . | |
| Functions | Descriptions |
| Ceiling function, the lowest integer not less than a real number. | |
| Variables | Descriptions |
| Continuous variables, proportion of charging demands allocated on arc . | |
| Integer variables, the sizing of fast-charging stations at node . | |
| Continuous variables, relaxation of , the size of fast-charging stations at node . | |
| Binary variables, whether fast-charging station sites at node . | |
| Binary variable, whether fast-charging station sites at node i to accommodate | |
| the charging demands from O-D pair q. | |
| Continuous variable, the size of fast-charging stations at node i to accommodate | |
| the charging demands from O-D pair q. | |
| Continuous variable, combination weight of the extreme points for all , | |
| , . | |
| Binary variable, whether chance constraints is satisfied for all , . |
Appendix A. Experimental Results of the 25-Node Network
| Performance of SRP(q) | Performance of Dantzig–Wolfe Decomposition | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obj. | Runtime (in Sec.) | Obj. | Runtime of MP (in Sec.) | Runtime of SP (in Sec.) | Iter. (in Num.) | ||||||||||||||
| Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | ||||
| 8 | 800 | 54,180 | 7364.90 | 14.27 | 100.28 | 0.16 | 38,760 | 0.22 | 0.16 | 0.16 | 0.13 | 0.28 | 0.21 | 0.21 | 0.16 | 7 | 4 | 4 | 1 |
| 900 | 54,180 | 7383.03 | 22.66 | 97.67 | 0.21 | 38,760 | 0.29 | 0.13 | 0.13 | 0.08 | 0.65 | 0.24 | 0.24 | 0.14 | 9 | 5 | 6 | 1 | |
| 1000 | 54,180 | 7901.77 | 14.91 | 106.17 | 0.15 | 38,760 | 0.30 | 0.22 | 0.22 | 0.17 | 0.52 | 0.34 | 0.34 | 0.22 | 9 | 4 | 3 | 1 | |
| 1100 | 54,180 | 7880.42 | 17.23 | 117.96 | 0.14 | 38,760 | 0.32 | 0.16 | 0.19 | 0.13 | 0.45 | 0.22 | 0.25 | 0.16 | 7 | 3 | 2 | 1 | |
| 1200 | 54,180 | 7533.70 | 16.50 | 98.95 | 0.17 | 38,760 | 0.31 | 0.14 | 0.16 | 0.12 | 0.40 | 0.25 | 0.25 | 0.15 | 5 | 3 | 4 | 1 | |
| 1300 | 54,180 | 7750.69 | 23.94 | 123.61 | 0.24 | 38,760 | 0.36 | 0.17 | 0.18 | 0.14 | 0.42 | 0.21 | 0.24 | 0.13 | 8 | 6 | 6 | 1 | |
| 9 | 800 | 46,420 | 10,551.68 | 6.72 | 150.30 | 0.14 | 36,920 | 0.32 | 0.19 | 0.20 | 0.16 | 0.39 | 0.25 | 0.25 | 0.20 | 7 | 3 | 2 | 1 |
| 900 | 46,420 | 10,266.49 | 29.46 | 174.91 | 0.11 | 36,920 | 0.34 | 0.18 | 0.14 | 0.11 | 0.34 | 0.24 | 0.24 | 0.20 | 6 | 3 | 4 | 1 | |
| 1000 | 46,420 | 10,365.19 | 10.93 | 150.00 | 0.15 | 36,920 | 0.32 | 0.19 | 0.19 | 0.13 | 0.31 | 0.25 | 0.27 | 0.21 | 5 | 3 | 4 | 1 | |
| 1100 | 46,420 | 10,206.27 | 34.75 | 186.17 | 0.17 | 36,920 | 0.33 | 0.16 | 0.19 | 0.11 | 0.36 | 0.26 | 0.27 | 0.22 | 9 | 4 | 4 | 1 | |
| 1200 | 46,420 | 10,451.60 | 41.91 | 164.01 | 0.23 | 36,920 | 0.31 | 0.18 | 0.16 | 0.12 | 0.36 | 0.26 | 0.26 | 0.21 | 7 | 5 | 6 | 1 | |
| 1300 | 46,420 | 10,553.18 | 16.10 | 198.16 | 0.18 | 36,920 | 0.35 | 0.12 | 0.12 | 0.10 | 0.39 | 0.22 | 0.23 | 0.19 | 9 | 6 | 5 | 1 | |
| 10 | 800 | 37,380 | 13,421.00 | 4.45 | 214.82 | 0.16 | 35,220 | 0.36 | 0.24 | 0.25 | 0.21 | 0.46 | 0.30 | 0.30 | 0.24 | 7 | 2 | 3 | 1 |
| 900 | 37,380 | 13,137.68 | 4.54 | 222.84 | 0.06 | 35,220 | 0.35 | 0.26 | 0.23 | 0.20 | 0.42 | 0.31 | 0.32 | 0.23 | 5 | 2 | 2 | 1 | |
| 1000 | 37,380 | 13,108.08 | 13.84 | 273.30 | 0.10 | 35,220 | 0.34 | 0.29 | 0.29 | 0.22 | 0.47 | 0.33 | 0.34 | 0.27 | 9 | 2 | 3 | 1 | |
| 1100 | 37,380 | 13,633.3 | 22.03 | 220.92 | 0.14 | 35,220 | 0.37 | 0.25 | 0.25 | 0.21 | 0.44 | 0.34 | 0.36 | 0.26 | 9 | 3 | 4 | 1 | |
| 1200 | 37,380 | 13,863.36 | 25.54 | 275.85 | 0.08 | 35,220 | 0.38 | 0.26 | 0.26 | 0.23 | 0.47 | 0.33 | 0.35 | 0.25 | 8 | 2 | 3 | 1 | |
| 1300 | 37,380 | 13,654.73 | 16.97 | 220.27 | 0.17 | 35,220 | 0.32 | 0.28 | 0.25 | 0.20 | 0.46 | 0.32 | 0.34 | 0.27 | 5 | 3 | 3 | 1 | |
| 11 | 800 | — | 14,400 * | — | — | 0.11 | 33,540 | 0.46 | 0.28 | 0.29 | 0.26 | 0.49 | 0.34 | 0.34 | 0.28 | 9 | 2 | 1 | 1 |
| 900 | — | 14,400 * | — | — | 0.23 | 33,540 | 0.42 | 0.26 | 0.25 | 0.22 | 0.43 | 0.37 | 0.37 | 0.27 | 7 | 5 | 5 | 1 | |
| 1000 | — | 14,400 * | — | — | 0.12 | 33,540 | 0.45 | 0.29 | 0.28 | 0.24 | 0.47 | 0.38 | 0.37 | 0.26 | 5 | 3 | 4 | 1 | |
| 1100 | — | 14,400 * | — | — | 0.24 | 33,540 | 0.43 | 0.27 | 0.27 | 0.23 | 0.47 | 0.36 | 0.35 | 0.29 | 9 | 6 | 7 | 1 | |
| 1200 | — | 14,400 * | — | — | 0.20 | 33,540 | 0.42 | 0.26 | 0.26 | 0.22 | 0.49 | 0.34 | 0.34 | 0.26 | 7 | 5 | 4 | 1 | |
| 1300 | — | 14,400 * | — | — | 0.13 | 33,540 | 0.47 | 0.28 | 0.26 | 0.21 | 0.48 | 0.33 | 0.32 | 0.24 | 5 | 2 | 1 | 1 | |
| Performance of SRP(q) | Performance of Dantzig–Wolfe Decomposition | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obj. | Runtime (in Sec.) | Obj. | Runtime of MP (in Sec.) | Runtime of SP (in Sec.) | Iter. (in Num.) | ||||||||||||||
| Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | ||||
| 8 | 800 | 62,860 | 5308.90 | 10.34 | 32.17 | 0.15 | 44,720 | 0.47 | 0.35 | 0.35 | 0.30 | 0.74 | 0.41 | 0.41 | 0.34 | 5 | 2 | 2 | 1 |
| 900 | 62,160 | 5283.03 | 15.60 | 36.77 | 0.12 | 44,720 | 0.44 | 0.37 | 0.37 | 0.33 | 0.71 | 0.42 | 0.42 | 0.39 | 6 | 3 | 4 | 1 | |
| 1000 | 62,160 | 5101.77 | 10.62 | 34.79 | 0.17 | 44,720 | 0.41 | 0.35 | 0.34 | 0.30 | 0.75 | 0.43 | 0.43 | 0.34 | 8 | 2 | 1 | 1 | |
| 1100 | 62,160 | 5280.42 | 10.59 | 32.39 | 0.12 | 44,720 | 0.42 | 0.38 | 0.37 | 0.32 | 0.76 | 0.48 | 0.46 | 0.35 | 8 | 4 | 5 | 1 | |
| 1200 | 62,160 | 5233.70 | 11.59 | 32.39 | 0.12 | 44,720 | 0.49 | 0.32 | 0.34 | 0.31 | 0.78 | 0.45 | 0.45 | 0.32 | 5 | 2 | 3 | 1 | |
| 1300 | 62,160 | 5250.69 | 9.79 | 36.09 | 0.16 | 44,720 | 0.47 | 0.32 | 0.32 | 0.28 | 0.70 | 0.47 | 0.47 | 0.39 | 9 | 7 | 8 | 1 | |
| 9 | 800 | 52,950 | 5520.18 | 9.79 | 41.94 | 0.13 | 42,690 | 0.54 | 0.39 | 0.39 | 0.35 | 0.79 | 0.45 | 0.45 | 0.37 | 5 | 3 | 3 | 1 |
| 900 | 52,950 | 5533.75 | 13.38 | 42.05 | 0.15 | 42,690 | 0.57 | 0.33 | 0.33 | 0.30 | 0.74 | 0.44 | 0.44 | 0.37 | 9 | 6 | 6 | 1 | |
| 1000 | 52,950 | 5512.58 | 7.82 | 44.12 | 0.14 | 42,690 | 0.54 | 0.36 | 0.36 | 0.32 | 0.78 | 0.41 | 0.41 | 0.36 | 5 | 2 | 3 | 1 | |
| 1100 | 52,950 | 5490.68 | 12.29 | 38.28 | 0.17 | 42,690 | 0.52 | 0.39 | 0.38 | 0.31 | 0.72 | 0.40 | 0.40 | 0.38 | 6 | 3 | 3 | 1 | |
| 1200 | 52,950 | 5512.49 | 9.85 | 44.09 | 0.09 | 42,690 | 0.51 | 0.38 | 0.36 | 0.33 | 0.71 | 0.44 | 0.43 | 0.39 | 9 | 7 | 8 | 1 | |
| 1300 | 52,950 | 5510.95 | 8.77 | 46.17 | 0.09 | 42,690 | 0.56 | 0.35 | 0.35 | 0.30 | 0.70 | 0.45 | 0.44 | 0.34 | 6 | 2 | 3 | 1 | |
| 10 | 800 | 41,860 | 5639.59 | 9.74 | 56.85 | 0.10 | 40,690 | 0.60 | 0.42 | 0.42 | 0.38 | 0.74 | 0.47 | 0.48 | 0.42 | 6 | 2 | 3 | 1 |
| 900 | 41,860 | 5519.59 | 10.26 | 54.11 | 0.14 | 40,690 | 0.66 | 0.40 | 0.40 | 0.34 | 0.79 | 0.48 | 0.49 | 0.42 | 5 | 3 | 2 | 1 | |
| 1000 | 41,860 | 5561.04 | 7.44 | 57.17 | 0.15 | 40,690 | 0.68 | 0.42 | 0.42 | 0.32 | 0.75 | 0.46 | 0.47 | 0.42 | 7 | 3 | 4 | 1 | |
| 1100 | 41,860 | 5656.06 | 8.59 | 57.12 | 0.13 | 40,690 | 0.63 | 0.48 | 0.48 | 0.33 | 0.70 | 0.47 | 0.47 | 0.41 | 6 | 4 | 5 | 1 | |
| 1200 | 41,860 | 5513.64 | 10.41 | 53.25 | 0.11 | 40,690 | 0.64 | 0.47 | 0.47 | 0.32 | 0.72 | 0.41 | 0.41 | 0.36 | 8 | 2 | 3 | 1 | |
| 1300 | 41,860 | 5659.92 | 10.09 | 52.61 | 0.10 | 40,690 | 0.67 | 0.41 | 0.40 | 0.36 | 0.71 | 0.43 | 0.44 | 0.40 | 7 | 3 | 4 | 1 | |
| 11 | 800 | 36,680 | 5759.50 | 10.38 | 66.79 | 0.14 | 38,730 | 0.68 | 0.47 | 0.48 | 0.43 | 0.81 | 0.52 | 0.53 | 0.46 | 7 | 3 | 3 | 1 |
| 900 | 36,680 | 5644.64 | 6.46 | 65.52 | 0.12 | 38,730 | 0.69 | 0.48 | 0.49 | 0.43 | 0.89 | 0.57 | 0.57 | 0.44 | 7 | 2 | 3 | 1 | |
| 1000 | 36,680 | 5618.28 | 10.64 | 59.03 | 0.09 | 38,730 | 0.63 | 0.47 | 0.47 | 0.43 | 0.84 | 0.54 | 0.54 | 0.46 | 5 | 2 | 1 | 1 | |
| 1100 | 36,680 | 5638.48 | 16.09 | 66.79 | 0.09 | 38,730 | 0.66 | 0.49 | 0.49 | 0.42 | 0.88 | 0.50 | 0.51 | 0.44 | 5 | 3 | 3 | 1 | |
| 1200 | 36,680 | 5500.02 | 12.58 | 61.66 | 0.15 | 38,730 | 0.67 | 0.48 | 0.48 | 0.42 | 0.84 | 0.57 | 0.56 | 0.42 | 7 | 5 | 4 | 1 | |
| 1300 | 36,680 | 5632.61 | 13.33 | 67.85 | 0.11 | 38,730 | 0.65 | 0.48 | 0.48 | 0.43 | 0.85 | 0.56 | 0.56 | 0.45 | 8 | 5 | 6 | 1 | |
| Performance of SRP(q) | Performance of Dantzig–Wolfe Decomposition | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obj. | Runtime (in Sec.) | Obj. | Runtime of MP (in Sec.) | Runtime of SP (in Sec.) | Iter. (in Num.) | ||||||||||||||
| Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | ||||
| 8 | 800 | 71,640 | 137.77 | 8.85 | 15.12 | 0.08 | 50,880 | 0.76 | 0.51 | 0.52 | 0.46 | 0.75 | 0.56 | 0.57 | 0.50 | 9 | 3 | 4 | 1 |
| 900 | 71,640 | 129.82 | 7.15 | 13.84 | 0.08 | 50,880 | 0.70 | 0.59 | 0.59 | 0.49 | 0.78 | 0.52 | 0.52 | 0.48 | 5 | 2 | 3 | 1 | |
| 1000 | 71,640 | 139.59 | 8.93 | 12.73 | 0.13 | 50,880 | 0.71 | 0.51 | 0.58 | 0.45 | 0.77 | 0.54 | 0.54 | 0.51 | 9 | 7 | 6 | 1 | |
| 1100 | 71,640 | 103.66 | 5.22 | 14.23 | 0.12 | 50,880 | 0.79 | 0.52 | 0.50 | 0.42 | 0.79 | 0.57 | 0.57 | 0.53 | 8 | 3 | 2 | 1 | |
| 1200 | 71,640 | 119.82 | 6.53 | 15.35 | 0.13 | 50,880 | 0.75 | 0.58 | 0.57 | 0.41 | 0.70 | 0.52 | 0.52 | 0.51 | 8 | 2 | 3 | 1 | |
| 1300 | 71,640 | 127.83 | 5.90 | 12.55 | 0.09 | 50,880 | 0.77 | 0.50 | 0.50 | 0.44 | 0.75 | 0.54 | 0.54 | 0.50 | 7 | 4 | 4 | 1 | |
| 9 | 800 | 60,660 | 193.99 | 10.19 | 19.38 | 0.12 | 48,560 | 1.34 | 0.57 | 0.57 | 0.50 | 0.89 | 0.63 | 0.63 | 0.55 | 9 | 5 | 4 | 1 |
| 900 | 60,660 | 195.61 | 13.55 | 16.26 | 0.09 | 48,560 | 1.38 | 0.57 | 0.57 | 0.51 | 0.88 | 0.65 | 0.65 | 0.56 | 5 | 2 | 3 | 1 | |
| 1000 | 60,660 | 200.70 | 12.29 | 17.89 | 0.13 | 48,560 | 1.36 | 0.58 | 0.58 | 0.52 | 0.87 | 0.64 | 0.64 | 0.54 | 9 | 5 | 4 | 1 | |
| 1100 | 60,660 | 196.69 | 14.88 | 16.27 | 0.17 | 48,560 | 1.30 | 0.54 | 0.54 | 0.50 | 0.88 | 0.62 | 0.62 | 0.56 | 8 | 5 | 4 | 1 | |
| 1200 | 60,660 | 203.79 | 12.21 | 18.31 | 0.16 | 48,560 | 1.31 | 0.55 | 0.55 | 0.48 | 0.82 | 0.64 | 0.65 | 0.59 | 6 | 2 | 1 | 1 | |
| 1300 | 60,660 | 190.07 | 10.25 | 16.69 | 0.12 | 48,560 | 1.31 | 0.57 | 0.57 | 0.52 | 0.89 | 0.65 | 0.65 | 0.52 | 7 | 2 | 3 | 1 | |
| 10 | 800 | 48,950 | 279.19 | 14.98 | 20.68 | 0.13 | 46,160 | 0.55 | 0.06 | 0.06 | 0.04 | 0.44 | 0.12 | 0.13 | 0.07 | 5 | 2 | 2 | 1 |
| 900 | 48,950 | 276.79 | 14.18 | 22.73 | 0.13 | 46,160 | 0.59 | 0.11 | 0.12 | 0.07 | 0.46 | 0.14 | 0.14 | 0.10 | 8 | 4 | 4 | 1 | |
| 1000 | 48,950 | 268.56 | 13.86 | 21.07 | 0.13 | 46,160 | 0.52 | 0.09 | 0.09 | 0.06 | 0.40 | 0.18 | 0.17 | 0.12 | 8 | 3 | 3 | 1 | |
| 1100 | 48,950 | 263.13 | 13.22 | 21.56 | 0.11 | 46,160 | 0.50 | 0.12 | 0.11 | 0.05 | 0.46 | 0.12 | 0.12 | 0.07 | 6 | 2 | 1 | 1 | |
| 1200 | 48,950 | 262.90 | 19.42 | 22.64 | 0.14 | 46,160 | 0.51 | 0.08 | 0.07 | 0.03 | 0.47 | 0.13 | 0.14 | 0.06 | 7 | 2 | 2 | 1 | |
| 1300 | 48,950 | 267.42 | 14.83 | 21.02 | 0.10 | 46,160 | 0.58 | 0.07 | 0.07 | 0.04 | 0.42 | 0.17 | 0.16 | 0.09 | 6 | 3 | 2 | 1 | |
| 11 | 800 | 41,620 | 336.85 | 19.67 | 25.84 | 0.16 | 43,920 | 0.16 | 0.10 | 0.10 | 0.08 | 0.30 | 0.16 | 0.17 | 0.10 | 6 | 2 | 3 | 1 |
| 900 | 41,620 | 323.50 | 20.07 | 26.28 | 0.10 | 43,920 | 0.17 | 0.12 | 0.12 | 0.06 | 0.31 | 0.15 | 0.14 | 0.05 | 6 | 4 | 3 | 1 | |
| 1000 | 41,620 | 313.97 | 24.15 | 25.11 | 0.10 | 43,920 | 0.19 | 0.13 | 0.12 | 0.05 | 0.30 | 0.16 | 0.16 | 0.09 | 9 | 5 | 5 | 1 | |
| 1100 | 41,620 | 314.81 | 18.31 | 26.15 | 0.10 | 43,920 | 0.23 | 0.10 | 0.12 | 0.04 | 0.32 | 0.17 | 0.17 | 0.07 | 8 | 4 | 4 | 1 | |
| 1200 | 41,620 | 331.38 | 18.63 | 26.55 | 0.13 | 43,920 | 0.19 | 0.11 | 0.12 | 0.04 | 0.39 | 0.13 | 0.14 | 0.04 | 7 | 2 | 1 | 1 | |
| 1300 | 41,620 | 324.50 | 24.69 | 24.18 | 0.13 | 43,920 | 0.17 | 0.10 | 0.12 | 0.08 | 0.35 | 0.12 | 0.11 | 0.07 | 8 | 2 | 1 | 1 | |
| Performance of SRP(q) | Performance of Dantzig–Wolfe Decomposition | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obj. | Runtime (in Sec.) | Obj. | Runtime of MP (in Sec.) | Runtime of SP (in Sec.) | Iter. (in Num.) | ||||||||||||||
| Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | ||||
| 8 | 800 | 80,320 | 42.14 | 12.90 | 15.40 | 0.09 | 56,940 | 0.21 | 0.14 | 0.15 | 0.12 | 0.32 | 0.20 | 0.21 | 0.14 | 6 | 3 | 4 | 1 |
| 900 | 79,520 | 42.41 | 12.83 | 17.82 | 0.13 | 56,940 | 0.25 | 0.11 | 0.11 | 0.09 | 0.36 | 0.22 | 0.22 | 0.10 | 5 | 2 | 1 | 1 | |
| 1000 | 79,520 | 39.14 | 10.74 | 13.51 | 0.15 | 56,940 | 0.23 | 0.14 | 0.14 | 0.11 | 0.31 | 0.24 | 0.24 | 0.11 | 7 | 5 | 4 | 1 | |
| 1100 | 79,520 | 41.00 | 9.54 | 13.09 | 0.13 | 56,940 | 0.28 | 0.15 | 0.16 | 0.12 | 0.39 | 0.21 | 0.21 | 0.18 | 6 | 2 | 3 | 1 | |
| 1200 | 79,520 | 40.69 | 9.43 | 16.07 | 0.16 | 56,940 | 0.22 | 0.10 | 0.10 | 0.07 | 0.38 | 0.28 | 0.27 | 0.17 | 5 | 3 | 2 | 1 | |
| 1300 | 79,520 | 43.40 | 11.42 | 14.33 | 0.17 | 56,940 | 0.21 | 0.12 | 0.12 | 0.08 | 0.37 | 0.25 | 0.25 | 0.18 | 8 | 6 | 5 | 1 | |
| 9 | 800 | 67,080 | 48.81 | 10.72 | 14.36 | 0.11 | 54,230 | 0.29 | 0.19 | 0.19 | 0.16 | 0.33 | 0.25 | 0.25 | 0.18 | 7 | 2 | 2 | 1 |
| 900 | 66,980 | 47.68 | 10.74 | 17.49 | 0.18 | 54,230 | 0.24 | 0.14 | 0.14 | 0.11 | 0.39 | 0.25 | 0.24 | 0.17 | 6 | 4 | 3 | 1 | |
| 1000 | 66,980 | 48.39 | 12.38 | 13.19 | 0.09 | 54,230 | 0.27 | 0.18 | 0.18 | 0.14 | 0.30 | 0.22 | 0.21 | 0.13 | 6 | 2 | 3 | 1 | |
| 1100 | 66,980 | 49.41 | 9.88 | 14.66 | 0.15 | 54,230 | 0.28 | 0.17 | 0.17 | 0.12 | 0.35 | 0.21 | 0.22 | 0.14 | 8 | 6 | 5 | 1 | |
| 1200 | 66,980 | 47.39 | 9.57 | 17.78 | 0.13 | 54,230 | 0.23 | 0.19 | 0.18 | 0.13 | 0.43 | 0.26 | 0.25 | 0.15 | 8 | 3 | 3 | 1 | |
| 1300 | 66,980 | 48.06 | 9.69 | 17.96 | 0.15 | 54,230 | 0.28 | 0.15 | 0.15 | 0.10 | 0.31 | 0.25 | 0.25 | 0.11 | 6 | 4 | 5 | 1 | |
| 10 | 800 | 53,720 | 52.84 | 10.45 | 13.77 | 0.10 | 51,630 | 0.73 | 0.23 | 0.23 | 0.20 | 0.62 | 0.29 | 0.29 | 0.22 | 6 | 2 | 2 | 1 |
| 900 | 53,720 | 52.90 | 11.92 | 13.48 | 0.11 | 51,630 | 0.74 | 0.26 | 0.26 | 0.21 | 0.62 | 0.26 | 0.26 | 0.20 | 6 | 3 | 4 | 1 | |
| 1000 | 53,620 | 53.39 | 12.41 | 15.47 | 0.13 | 51,630 | 0.70 | 0.24 | 0.24 | 0.20 | 0.61 | 0.28 | 0.28 | 0.22 | 6 | 4 | 5 | 1 | |
| 1100 | 53,620 | 54.21 | 9.63 | 16.78 | 0.16 | 51,630 | 0.73 | 0.27 | 0.26 | 0.22 | 0.62 | 0.25 | 0.25 | 0.20 | 6 | 3 | 3 | 1 | |
| 1200 | 53,620 | 55.87 | 10.30 | 17.66 | 0.11 | 51,630 | 0.75 | 0.26 | 0.26 | 0.22 | 0.61 | 0.25 | 0.25 | 0.21 | 9 | 3 | 4 | 1 | |
| 1300 | 53,620 | 55.26 | 10.65 | 17.84 | 0.16 | 51,630 | 0.70 | 0.22 | 0.22 | 0.17 | 0.69 | 0.24 | 0.24 | 0.21 | 8 | 3 | 4 | 1 | |
| 11 | 800 | 46,760 | 57.13 | 9.07 | 10.92 | 0.14 | 49,110 | 0.37 | 0.27 | 0.27 | 0.24 | 0.47 | 0.33 | 0.34 | 0.27 | 6 | 2 | 3 | 1 |
| 900 | 46,760 | 56.04 | 10.48 | 9.44 | 0.09 | 49,110 | 0.34 | 0.24 | 0.24 | 0.20 | 0.40 | 0.30 | 0.31 | 0.22 | 8 | 3 | 2 | 1 | |
| 1000 | 46,760 | 58.50 | 10.24 | 15.01 | 0.08 | 49,110 | 0.35 | 0.21 | 0.21 | 0.17 | 0.45 | 0.38 | 0.38 | 0.31 | 9 | 7 | 7 | 1 | |
| 1100 | 46,760 | 55.52 | 10.69 | 10.10 | 0.16 | 49,110 | 0.35 | 0.22 | 0.22 | 0.16 | 0.42 | 0.32 | 0.32 | 0.25 | 9 | 6 | 6 | 1 | |
| 1200 | 46,760 | 58.39 | 10.13 | 17.79 | 0.15 | 49,110 | 0.39 | 0.23 | 0.23 | 0.14 | 0.48 | 0.35 | 0.35 | 0.27 | 9 | 3 | 2 | 1 | |
| 1300 | 46,760 | 59.84 | 9.72 | 13.27 | 0.10 | 49,110 | 0.32 | 0.22 | 0.22 | 0.18 | 0.41 | 0.32 | 0.32 | 0.21 | 5 | 2 | 1 | 1 | |
| Performance of SRP(q) | Performance of Dantzig–Wolfe Decomposition | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obj. | Runtime (in Sec.) | Obj. | Runtime of MP (in Sec.) | Runtime of SP (in Sec.) | Iter. (in Num.) | ||||||||||||||
| Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | Max. | Med. | Ave. | Min. | ||||
| 8 | 800 | 89,000 | 34.48 | 12.13 | 14.28 | 0.15 | 62,800 | 0.68 | 0.47 | 0.47 | 0.42 | 0.76 | 0.52 | 0.51 | 0.44 | 7 | 4 | 4 | 1 |
| 900 | 88,600 | 33.63 | 12.63 | 14.75 | 0.17 | 62,800 | 0.63 | 0.49 | 0.48 | 0.46 | 0.72 | 0.56 | 0.56 | 0.46 | 5 | 3 | 3 | 1 | |
| 1000 | 88,200 | 32.77 | 9.93 | 14.98 | 0.13 | 62,800 | 0.60 | 0.46 | 0.46 | 0.41 | 0.73 | 0.54 | 0.54 | 0.42 | 7 | 2 | 1 | 1 | |
| 1100 | 88,200 | 32.89 | 12.22 | 13.13 | 0.13 | 62,800 | 0.67 | 0.45 | 0.45 | 0.40 | 0.78 | 0.59 | 0.59 | 0.43 | 9 | 7 | 7 | 1 | |
| 1200 | 88,200 | 32.93 | 10.91 | 13.73 | 0.12 | 62,800 | 0.63 | 0.49 | 0.49 | 0.45 | 0.74 | 0.50 | 0.50 | 0.45 | 6 | 3 | 3 | 1 | |
| 1300 | 88,200 | 32.09 | 13.14 | 12.85 | 0.08 | 62,800 | 0.66 | 0.41 | 0.42 | 0.38 | 0.73 | 0.56 | 0.56 | 0.44 | 6 | 2 | 3 | 1 | |
| 9 | 800 | 75,430 | 35.65 | 13.38 | 15.16 | 0.11 | 60,000 | 0.51 | 0.07 | 0.07 | 0.04 | 0.59 | 0.13 | 0.13 | 0.07 | 5 | 2 | 1 | 1 |
| 900 | 75,430 | 34.83 | 12.05 | 14.40 | 0.1 | 60,000 | 0.55 | 0.08 | 0.08 | 0.04 | 0.59 | 0.14 | 0.14 | 0.07 | 5 | 2 | 2 | 1 | |
| 1000 | 75,430 | 32.98 | 11.76 | 13.46 | 0.12 | 60,000 | 0.53 | 0.09 | 0.09 | 0.03 | 0.51 | 0.10 | 0.11 | 0.05 | 8 | 4 | 4 | 1 | |
| 1100 | 75,430 | 32.32 | 10.49 | 9.00 | 0.17 | 60,000 | 0.55 | 0.08 | 0.08 | 0.05 | 0.55 | 0.15 | 0.14 | 0.07 | 5 | 3 | 3 | 1 | |
| 1200 | 75,430 | 32.20 | 7.52 | 11.27 | 0.16 | 60,000 | 0.53 | 0.07 | 0.07 | 0.03 | 0.52 | 0.13 | 0.13 | 0.05 | 5 | 2 | 1 | 1 | |
| 1300 | 75,430 | 32.99 | 7.73 | 12.17 | 0.17 | 60,000 | 0.50 | 0.09 | 0.09 | 0.06 | 0.50 | 0.19 | 0.19 | 0.08 | 6 | 2 | 1 | 1 | |
| 10 | 800 | 60,900 | 33.77 | 12.00 | 14.24 | 0.15 | 57,100 | 0.59 | 0.11 | 0.11 | 0.08 | 0.88 | 0.17 | 0.17 | 0.11 | 7 | 3 | 4 | 1 |
| 900 | 60,900 | 32.83 | 10.67 | 14.48 | 0.11 | 57,100 | 0.58 | 0.14 | 0.14 | 0.08 | 0.81 | 0.18 | 0.17 | 0.14 | 7 | 3 | 4 | 1 | |
| 1000 | 60,900 | 32.51 | 10.82 | 12.81 | 0.18 | 57,100 | 0.56 | 0.12 | 0.12 | 0.04 | 0.86 | 0.15 | 0.15 | 0.07 | 7 | 3 | 3 | 1 | |
| 1100 | 60,900 | 32.48 | 8.14 | 13.32 | 0.10 | 57,100 | 0.59 | 0.12 | 0.12 | 0.07 | 0.81 | 0.24 | 0.24 | 0.13 | 8 | 5 | 6 | 1 | |
| 1200 | 60,900 | 33.69 | 10.93 | 15.37 | 0.17 | 57,100 | 0.56 | 0.10 | 0.10 | 0.06 | 0.86 | 0.22 | 0.22 | 0.16 | 5 | 2 | 2 | 1 | |
| 1300 | 60,900 | 33.76 | 7.41 | 14.15 | 0.17 | 57,100 | 0.53 | 0.11 | 0.11 | 0.09 | 0.88 | 0.19 | 0.19 | 0.13 | 6 | 2 | 1 | 1 | |
| 11 | 800 | 51,500 | 37.42 | 7.36 | 7.79 | 0.09 | 54,300 | 0.53 | 0.06 | 0.07 | 0.04 | 5.26 | 0.14 | 0.17 | 0.09 | 6 | 3 | 4 | 1 |
| 900 | 51,500 | 37.87 | 7.19 | 13.46 | 0.14 | 54,300 | 0.53 | 0.15 | 0.15 | 0.11 | 4.39 | 0.24 | 0.24 | 0.14 | 5 | 3 | 4 | 1 | |
| 1000 | 51,500 | 36.11 | 9.27 | 14.33 | 0.10 | 54,300 | 0.59 | 0.19 | 0.19 | 0.15 | 4.59 | 0.21 | 0.21 | 0.14 | 6 | 2 | 3 | 1 | |
| 1100 | 51,500 | 38.28 | 11.28 | 14.57 | 0.08 | 54,300 | 0.54 | 0.13 | 0.13 | 0.10 | 4.45 | 0.24 | 0.24 | 0.11 | 7 | 5 | 5 | 1 | |
| 1200 | 51,500 | 35.54 | 13.16 | 15.16 | 0.12 | 54,300 | 0.53 | 0.12 | 0.13 | 0.09 | 4.37 | 0.23 | 0.24 | 0.19 | 6 | 3 | 2 | 1 | |
| 1300 | 51,500 | 38.68 | 11.91 | 12.36 | 0.18 | 54,300 | 0.26 | 0.18 | 0.18 | 0.15 | 4.41 | 0.25 | 0.24 | 0.19 | 5 | 2 | 2 | 1 | |
References
- Alshareef, S.M. Analyzing and mitigating the impacts of integrating fast-charging stations on the power quality in electric power distribution systems. Sustainability 2022, 14, 5595. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, Z.F.; Ren, Y.L. Research on factors that influence the fast charging behavior of private battery electric vehicles. Sustainability 2020, 12, 3439. [Google Scholar] [CrossRef]
- Chang, M.; Bae, S.; Cha, G.; Yoo, J. Aggregated electric vehicle fast-charging power demand analysis and forecast based on LSTM neural network. Sustainability 2021, 13, 13783. [Google Scholar] [CrossRef]
- Luedtke, J.; Ahmed, S. A sample approximation approach for optimization with probabilistic constraints. SIAM J. Optim. 2008, 19, 674–699. [Google Scholar] [CrossRef]
- Upchurch, C.; Kuby, M. Comparing the p-median and flow-refueling models for locating alternative-fuel stations. J. Transp. Geogr. 2010, 18, 750–758. [Google Scholar] [CrossRef]
- Abareshi, M.; Zaferanieh, M. A bi-level capacitated p-median facility location problem with the most likely allocation solution. Transp. Res. Part B Methodol. 2019, 123, 1–20. [Google Scholar] [CrossRef]
- An, Y.; Zeng, B.; Zhang, Y.; Zhao, L. Reliable p-median facility location problem: Two stage robust models and algorithms. Transp. Res. Part B Methodol. 2014, 64, 54–72. [Google Scholar] [CrossRef]
- Jackson, L.E.; Rouskas, G.N.; Stallmann, M.F.M. The directional p-median problem: Definition, complexity, and algorithms. Eur. J. Oper. Res. 2007, 179, 1097–1108. [Google Scholar] [CrossRef]
- Scutaru, M.L.; Vlase, S.; Marin, M.; Modrea, A. New analytical method based on dynamic response of planar mechanical elastic systems. Bound. Value Probl. 2020, 1, 104. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Hodgson, M.J. A flow-capturing location-allocation model. Geogr. Anal. 1990, 22, 270–279. [Google Scholar] [CrossRef]
- Kuby, M.; Lim, S. The flow-refueling location problem for alternative-fuel vehicles. Socio Econ. Plan. Sci. 2005, 39, 125–145. [Google Scholar] [CrossRef]
- Shen, Z.J.M.; Feng, B.; Mao, C.; Ran, L. Optimization models for electric vehicle service operations: A literature review. Transp. Res. Part B Methodol. 2019, 128, 462–477. [Google Scholar] [CrossRef]
- Mak, H.Y.; Rong, Y.; Shen, Z.J.M. Infrastructure planning for electric vehicles with battery swapping. Manag. Sci. 2013, 59, 423–443. [Google Scholar] [CrossRef]
- Zhang, H.C.; Moura, S.J.; Hu, Z.C.; Qi, W.; Song, Y.H. A second-order cone programming model for planning PEV fast-charging stations. IEEE Trans. Power Syst. 2019, 33, 2763–2777. [Google Scholar] [CrossRef]
- Zhang, H.C.; Moura, S.J.; Hu, Z.C.; Qi, W.; Song, Y.H. Joint PEV charging network and distributed PV generation planning based on accelerated generalized Benders decomposition. IEEE Trans. Transp. Electrif. 2018, 4, 789–803. [Google Scholar] [CrossRef]
- Ghelichi, Z.; Gentili, M.; Mirchandani, P.B. Drone logistics for uncertain demand of disaster-impacted populations. Transp. Res. Part C Emerg. Technol. 2022, 141, 103735. [Google Scholar] [CrossRef]
- Yang, D.T.; Sarma, N.J.S.; Hyland, M.F.; Jayakrishnan, R. Dynamic modeling and real-time management of a system of EV fast-charging stations. Transp. Res. Part C Emerg. Technol. 2021, 128, 103186. [Google Scholar] [CrossRef]
- Ye, B.J.; Ni, C.; Tian, Y.; Ochieng, W.Y. Data-driven distributionally robust generation of time-varying flow corridor networks under demand uncertainty. Transp. Res. Part C Emerg. Technol. 2022, 136, 103546. [Google Scholar] [CrossRef]
- Wu, F.; Soishansi, R. A stochastic flow-capturing model to optimize the location of fast-charging stations with uncertain electric vehicle flows. Transp. Res. Part D Transp. Environ. 2017, 53, 354–376. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, G.; Huang, T.W.; Song, Q.K.; Yuan, Y.F. Planning PEV fast-charging stations using data-driven distributionally robust optimization approach based on Φ-divergence. IEEE Trans. Transp. Electrif. 2020, 6, 170–180. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, G.; Song, Q.K.; Dong, Z.Y. Robust chance-constrained programming approach for the planning of fast-charging stations in electrified transportation networks. Appl. Energy 2020, 262, 114480. [Google Scholar] [CrossRef]
- Li, Y.; Kim, A.M. Allocating and scheduling resources for a mobile photo enforcement program. Transp. Res. Part C Emerg. Technol. 2019, 125, 103000. [Google Scholar] [CrossRef]
- Zhou, S.; Jamshidi, A.; Núñez, A.; Baldi, S.; Schutter, B.D. Integrated condition-based track maintenance planning and crew scheduling of railway networks. Transp. Res. Part C Emerg. Technol. 2019, 105, 359–384. [Google Scholar]
- Liu, J.T.; Mirchandani, P.; Zhou, X.S. Integrated vehicle assignment and routing for system-optimal shared mobility planning with endogenous road congestion. Transp. Res. Part C Emerg. Technol. 2020, 117, 102675. [Google Scholar] [CrossRef]
- Yıldız, B.; Arslan, O.; Karaşan, Q.E. A branch and price apporach for routing and refueling station location model. Eur. J. Oper. Res. 2016, 248, 815–826. [Google Scholar] [CrossRef]
- Xu, M.; Meng, Q. Optimal deployment of charging stations considering path deviation and nonlinear elastic demand. Transp. Res. Part B Methodol. 2020, 135, 120–142. [Google Scholar] [CrossRef]
- Lee, C.; Han, J. Benders-and-price approach for electric vehicle charging station location problem under probabilistic travel range. Transp. Res. Part B Methodol. 2017, 106, 130–152. [Google Scholar] [CrossRef]
- Appelgren, L.H. A column generation algorithm for a ship scheduling problem. Transp. Sci. 1969, 3, 53–68. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Wolfe, P. Decomposition principle for linear programs. Oper. Res. 1960, 8, 101–111. [Google Scholar] [CrossRef]
- Singh, K.J.; Philpott, A.B.; Wood, R.K. Dantzig-Wolfe decomposition for solving multistage stochastic capacity-planning problems. Oper. Res. 2009, 57, 1271–1286. [Google Scholar] [CrossRef]
- Kulkarnia, S.; Krishnamoorthyd, M.; Ranadef, A.; Ernstc, A.T.; Patilb, R. A new formulation and a column generation-based heuristic for the multiple depot vehicle scheduling problem. Transp. Res. Part B Methodol. 2018, 118, 457–487. [Google Scholar] [CrossRef]
- Wu, T.; Shi, Z.S.; Liang, Z.; Zhang, Z.N.; Zhang, C.R. Dantzig-Wolfe decomposition for the facility location and production planning problem. Comput. Oper. Res. 2020, 124, 105068. [Google Scholar] [CrossRef]
- Zhang, Z.; Dention, B.T.; Xie, X.L. Branch and price for chance-constrained bin packing. INFORM J. Comput. 2020, 32, 547–564. [Google Scholar] [CrossRef]
- Cruz, C.A.; Munari, P.; Morabito, R. A branch-and-price method for the vehicle allocation problem. Comput. Ind. Eng. 2020, 149, 106745. [Google Scholar] [CrossRef]
- MirHassani, S.A.; Ebrazi, R. A flexible reformulation of the refueling station location problem. Transp. Sci. 2013, 47, 617–628. [Google Scholar] [CrossRef]
- Wang, C.Z.; He, F.; Lin, X.; Shen, Z.-J.M.; Li, M. Designing locations and capacities for charging stations to support intercity travel of electric vehicles: An expanded network approach. Transp. Res. Part C Emerg. Technol. 2019, 102, 210–232. [Google Scholar] [CrossRef]
- Zhang, H.C.; Moura, S.J.; Hu, Z.C.; Song, Y.H. PEV fast-charging station siting and sizing on coupled transportation and power networks. IEEE Trans. Smart Grid 2018, 9, 2595–2605. [Google Scholar] [CrossRef]
- Xu, M.; Yang, H.; Wang, S.A. Mitigate the range anxiety: Siting battery charging stations for electric vehicle drivers. Transp. Res. Part C Emerg. Technol. 2020, 114, 164–188. [Google Scholar] [CrossRef]
- Deng, Y.; Shen, S.Q.; Denton, B. Chance-constrained surgery planning under conditions of limited and ambiguous data. INFORMS J. Comput. 2019, 31, 559–575. [Google Scholar] [CrossRef]
- Song, Y.; Luedtke, J.R.; Küçükyavuz, S. Chance-constrained binary packing problems. INFORMS J. Comput. 2014, 26, 735–747. [Google Scholar] [CrossRef]
- Liu, J.T.; Zhou, X.S. Observability quantification of public transportation systems with heterogeneous data sources: An information-space projection approach based on discretized space-time network flow models. Transp. Res. Part B Methodol. 2019, 128, 302–323. [Google Scholar] [CrossRef]
- Lamiri, M.; Xie, X.; Zhang, S. Column generation approach to operating theater planning with elective and emergency patients. IIE Trans. 2008, 40, 838–852. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the IEEE International Symposium on Computer Aided Control Systems Design, Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Simchi-Levi, D.; Berman, O. A heuristic algorithm for the traveling salesman location problem on networks. Oper. Res. 1988, 36, 478–484. [Google Scholar] [CrossRef]
- Trigg, T.; Telleen, P.; Boyd, R.; Cuenot, F.; D’Ambrosio, D.; Gaghen, R.; Gagné, J.; Hardcastle, A.; Houssin, D.; Jones, A. Global EV outlook: Understanding the electric vehicle landscape to 2020. Int. Energy Agency 2013, 1–40. Available online: https://iea.blob.core.windows.net/assets/af46e012-18c2-44d6-becd-bad21fa844fd/Global_EV_Outlook_2020.pdf (accessed on 1 March 2023).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhou, B. Optimal Planning of Electric Vehicle Fast-Charging Stations Considering Uncertain Charging Demands via Dantzig–Wolfe Decomposition. Sustainability 2023, 15, 6588. https://doi.org/10.3390/su15086588
Wang L, Zhou B. Optimal Planning of Electric Vehicle Fast-Charging Stations Considering Uncertain Charging Demands via Dantzig–Wolfe Decomposition. Sustainability. 2023; 15(8):6588. https://doi.org/10.3390/su15086588
Chicago/Turabian StyleWang, Luyun, and Bo Zhou. 2023. "Optimal Planning of Electric Vehicle Fast-Charging Stations Considering Uncertain Charging Demands via Dantzig–Wolfe Decomposition" Sustainability 15, no. 8: 6588. https://doi.org/10.3390/su15086588
APA StyleWang, L., & Zhou, B. (2023). Optimal Planning of Electric Vehicle Fast-Charging Stations Considering Uncertain Charging Demands via Dantzig–Wolfe Decomposition. Sustainability, 15(8), 6588. https://doi.org/10.3390/su15086588






