Flat Roofs Renovation Planning on Public Buildings Using Fuzzy Multi-Criteria Analysis

Abstract

Renovation of flat roofs typically involves repairing or replacing the existing roof to improve its performance and extend its lifespan. The renovation process may include a range of tasks depending on the condition of the roof, such as repairing leaks, replacing damaged or deteriorated materials, adding insulation, or upgrading drainage systems. This research aim was to establish the priority of renovation of flat roofs of the public building based on the principles of multi-criteria analysis and fuzzy set theory, using the multi-criteria method PROMETHEE II in fuzzy logic form (F-PROMETHEE II). The proposed approach is adequate due to its ability to transform the uncertain and vague information received from an expert into a fuzzy number. This way, the objective outcome can be obtained, the criteria conflict removed and the alternatives ranking and mutual comparison enabled. It was necessary to analyze the existing literature, the flat roofs of a public building in terms of their current condition, and define the main goals and criteria for the roof renovation project. Based on the defined goals and criteria, the roofs are evaluated and ranked according to the priority for renovation. The planning process of renovation of flat roofs was carried out specifically on the building of the Faculty of Civil Engineering, Architecture and Geodesy in Split.

1. Introduction

Roofs are one of the most important elements of any building, which are exposed to all weather conditions and difficulties. The condition of the roofs, whether they are old, dilapidated or renovated, tells us about the maintenance of the building and, thus, also about the users of that building. A proper and high-quality roof is of great importance for the building because it provides safety and comfort to users and protects against external climatic conditions and temperature differences. Along with the correct way of performing the roof, its maintenance is also important.

Flat roofs are subject to wear and gradual loss of protective properties and are particularly prone to this type of damage due to their geometry and use as coverings for some materials. The first minor defects may appear several years after the operation. Damage can be removed with timely roof repair. Simple measures to restore the roof will help to extend its life, and what is important, will not require higher costs.

The need for renovation of a flat roof depends on a variety of factors, such as the age of the roof, the materials used in its construction, the quality of the initial installation, the level of maintenance it has received, and the climate it is exposed to, among others. If a flat roof has been well-maintained, constructed with quality materials, and is relatively new, then it may not require renovation. However, if a flat roof has been poorly maintained, has suffered damage due to weather or other external factors, or is approaching the end of its lifespan, then renovation may be necessary. Renovation of a flat roof may involve repairing or replacing damaged areas, reinforcing the structure to improve its load-bearing capacity, and improving the waterproofing system to prevent leaks and water damage. It may also involve upgrading the insulation to improve energy efficiency and reduce heating and cooling costs. In general, it is important to regularly inspect and maintain flat roofs to detect any problems early on and prevent the need for costly renovations.

Flat roof renovation typically involves a series of phases to repair, restore or replace the roof system to improve its structural integrity and waterproofing properties. The specific steps involved in flat roof renovation will depend on the extent of the damage or deterioration and the type of flat roof system in place. Flat roof renovation can be a complex process that requires the expertise of experienced professionals. It is important to choose a reputable contractor who can provide a comprehensive renovation plan and deliver high-quality workmanship.

When renovating roofs, it is important to take care of finances. It may involve significant funds and project and technical documentation preparation. From all this, it can be seen that it is a complex problem that needs to be looked at from several angles. In addition to concluding that this assessment should be done using several methods of evaluation. So, it is a multi-criteria problem. The need to include important stakeholders in the renovation planning process also contributes to this, as they have different views on the planning process itself, i.e., the priorities and importance of the criteria, and thus the final ranking, may be different for them. When it comes to flat roof renovation decision-making, a multi-criteria approach can support and assist building owners or facility managers to make informed decisions based on a range of factors beyond just cost or aesthetics. This can lead to more informed decisions that take into account the full range of factors that can impact the performance, durability, and sustainability of a flat roof system.

This research analyzes the renovation of flat roofs of public buildings, i.e., priorities are established for the undertaking of flat roof renovation activities, specifically on the example of the building of the Faculty of Civil Engineering, Architecture and Geodesy in Split. In order to achieve the stated goal, an approach of multi-criteria analysis based on fuzzy set theory and using the PROMETHEE II method in the fuzzy logic form (F-PROMETHEE II) is carried out. The main advantage of the approach is that the uncertain and vogue information received from stakeholders or an expert can be transformed into fuzzy numbers and thus obtain an objective outcome. Using fuzzy multi-criteria analysis, the criteria conflict can be removed, enabling alternative ranking and mutual comparison. Defuzzification of net flows can easily be calculated using the centroid method. Preference usual and linear functions are used to define relationships between alternatives according to the selected criteria. Euclidian distance is proposed to use to determine the distance between alternatives.

The proposed approach is considered relevant and effective because it takes into account several aspects of the problem analysis. For the purposes of the mentioned method, it is necessary to establish a set of criteria, identify relevant stakeholders and determine the weights of the criteria that express the attitude of the involved stakeholders and their compromise attitude.

Various studies used multi-criteria analysis to solve problems with the repairs or renovations of buildings or their elements, among which are different types of roofs. Miniotaite [1] investigated thermal and technological methods of renovation alternatives of flat roofs using multi-criteria analysis, considering used materials, the structure of the roof and roofing technologies. Gagliano et al. [2], in their study, developed an analysis of comparison of three typologies of the roof, standard, cool and green roof. The roofs were numerically compared by their environmental and energy capabilities. Petrakova and Grznar [3] used multi-criteria decision-making to find an optimal solution for roof envelope repair. Goncalves et al. [4] investigated waterproofing options applied on the flat roofs. The life cycle of each option is compared regarding economic and environmental impact, using data from various European and generic databases. Aguacil et al. [5] presented a multi-criteria assessment of different scenarios of photovoltaic options in the renovation of buildings to achieve savings in energy costs and materials and reduce fossil fuels and greenhouse gas emissions. The renovations are also applied to the roofs of the buildings. Rosasco and Perini [6] developed a sustainability approach based on the multi-criteria analysis for the selection of green roof systems, considering the parameters that have an influence on the experts’ and decision makers’ decisions. Kuznecov and Šaparauskas [7] studied sloping-pitched roofs regarding renovation and reconstruction technologies and the efficiency and applicability of each technology. Firstly, the main characteristics of each roof are analyzed, as well as damaged and defective causes of roofs, and then suggestions and routines for roofs’ performance improvement are proposed. All mentioned was achieved by distinguishing three technologies of reconstruction. These technologies were mutually compared by multi-criteria methods, additive radio assessment and complex proportional assessment. Using a multi-criteria approach shows that polyurethane foam is the best selection for the reconstruction of a roof. Kalibatas and Kovalitis [8] used the multi-criteria method SAW and three game theory rules to select the most appropriate and effective membrane for the analyzed type of roof. Golić, Kosorić and Furundžić [9] proposed an approach for the renovation of the residential building by integrating solar water heating systems. The approach is applied through a few stages to extenuate problem-solving and to provide optimization of the different designs. Studying all the stages, the multi-criteria analysis is shown to be the most appropriate methodology to obtain a compromised ranking after the assessment of design alternatives and for selecting the best solar water heating system. Krstić Furundžić, Kosorić and Golić [10], in their other study, presented all the advantages of solar water heating systems regarding fuel oil-, gas- and electricity-based heating systems. Considering that solar thermal collectors were proposed and analyzed, and using a multi-criteria approach, collectors’ alternatives were evaluated and mutually compared to obtain their priority ranking. For the comparison process, various aspects are discussed, such are ecological, functional, economic, technical and esthetic aspects. Sangkakool et al. [11] defined and analyzed the main aspects that affect the adoption of green roofs by using the mixed method design. These aspects are the definition of qualitative analysis, structuring by internal and external factors, and numerical evaluation using the analytical hierarchy process under experts’ opinions. Turskis, Morkunaite and Kutut [12] developed a hybrid model to prioritize the ranking of heritage buildings according to the activity of renovation, considering the main elements of the buildings, such are facades and roofs. The model is based on two multi-criteria decision-making methods analytic hierarchy process and evaluation based on distance from average solution, identifying relevant criteria concerning the cultural heritage buildings renovation. Naing, Nitivattananon and Shipin [13] presented a methodology for green roof retrofitting on the campus of the Asian Institute of Technology. Using multi-criteria decision making, visual inspection, questionnaires survey literature review as inputs, evaluation of potential alternatives and their ranking were generated. Gonzales-Dominguez, Sanchez-Barroso and Garcia-Sanz-Calcedo [14], in their research, proposed an optimization process of the flat roofs maintenance periodicity. The process is applied in twelve hospitals in Spain to increase the usefulness, reliability and stability of the flat roofs. The Markov Chain approach is used, and three types of flat roofs were analyzed: elastomeric, bitumen and PVC. Wu et al. [15] developed a methodology of fusing fuzzy logic, multi-criteria analysis and multi-objective programming to select the best large-scale rooftop photovoltaic portfolio project. Furthermore, the criteria weights are defined using an analytic hierarchy process, and the PROMETHEE II method is applied to rank the large-scale rooftop photovoltaic portfolio alternatives.

The core problems addressed in the studies listed are related to flat roof renovation and the selection of the most appropriate renovation technologies, waterproofing membranes, and roof systems. Other core problems include the environmental and economic impact of roofing solutions, potential energy savings, CO₂ emissions reduction, and integration of solar water heating systems in building refurbishment. In addition, some papers address the prospect of green roofs in urban areas, multi-criteria decision-making in the choice of alternative solutions, and preventive maintenance optimization of accessible flat roofs in healthcare centers. Overall, the papers aim to provide innovative solutions to address the core problems in flat roof renovation, which include sustainability, cost-effectiveness, energy efficiency, and environmental impact. Examining these studies, the proposed approach has several differences and main contributions compared with previous studies. None of the studies considered the problem in a holistic manner, taking into account simultaneously technological, economic, environmental and sociological aspects of the problem to achieve the main goal. Moreover, the approach presents the multi-criteria analysis fused with fuzzy set theory, applied in the assessment process of the flat roofs renovation priority. To be precise, the fuzzy PROMETHEE II method, shown to be the most suitable methodology for problems with a high degree of uncertainty and complicatedness among the criteria, is used. The proposed methodology is applied to flat roof renovation planning to prove the applicability and efficiency of the participatory decision-making framework, which was not the case in other studies.

As for the fuzzy PROMETHEE II method, there were applications on various case studies and research such are: tourism environmental impact [16], supplier performance evaluation [17], selection of inland nuclear power plant [18], evaluation of solar power plant location [19], exploration of the landslide susceptibility mapping [20], evaluation and ranking of alternative energy exploitation schemes of a low temperature geothermal field [21], concepts assessment and ranking for a new product development process [22], machine tools selection for the company’s productivity and capabilities [23], quality of the passenger services in the railway [24], improvement of the emergency department and hospital resources [25], selection and ranking of the performance indicators for municipal solid waste management systems [26], evaluation of the power plants for the investment projects [27], evaluation of the irrigation methods for the two plains for cotton production in Turkey [28], assessment of the nuclear medicine imaging devices [29], evaluation of the outsourcing for the information systems field [30], risk ranking for the highway construction projects [31], evaluation of the solution for the cancer treatment [32] and selection of the facility location of new organization [33].

2. Materials and Methods

This section gives more about flat roofs, their main characteristics, types and renovation. Moreover, the fuzzy multi-criteria analysis is explained, as well as criteria for the evaluation of the flat roofs.

2.1. Flat Roofs

A flat roof is a structural element that consists of a load-bearing structure, a covering and a roof soffit. Roofs, especially flat roofs, are among the most critical parts of the building. The load-bearing part of the flat roof is, therefore, constructed as a mezzanine structure. The roof must protect the building from external influences such as precipitation, heat, cold and wind. With proper execution and the use of quality materials, a flat roof is an economical construction that provides significantly greater freedom in composing volume and space [34]. The external influences are water, snow, groats, sudden summer temperature changes (after storms), very high temperatures in summer, very low winter temperatures, sound penetration, moisture that occurs during construction, atmospheric water that arrives during construction, and during the process of binding and drying different materials, small cracks appear in the materials. The internal influences are desirable constant heat inside the rooms, large temperature differences inside/outside, increased indoor air humidity due to use, etc. [35]

The advantages of the flat roofs are lower price compared to a pitched roof, a flat roof has a smaller area, so the consumption of materials is lower. The installation and further maintenance are simplified, the arrangement of a flat construction is simpler than an inclined one, and it is easier to move along a horizontal plane than along an inclined one. There is a possibility of obtaining additional usable space; the surface of the flat roof can easily be used as a terrace, a walking platform, a garden with a lawn, etc. [35].

There are several types of roofs; they differ in layers, slope and purpose. Each one is specific in its own way, both in terms of appearance and functionality. Any type of flat roof must protect the structure from external influences. Every flat roof must be of high quality, mechanically resistant, waterproof, must have UV protection and protect the structure from condensation. Great importance is attached to the energy efficiency of the flat roof [34]. According to the slope, there are flat roofs with a small slope of 0.5–1%, with a normal slope of 1–2.5%, a higher slope of 4–15% and pitched roofs (15–40%). Types of flat roofs according to the arrangement of layers are classic (cold), reverse (warm) and ventilating, while according to purpose or accessibility, they are passable, impassable and green (intensive or extensive). Types of flat roofs according to the method of rainwater drainage are drainage of rainwater along the outer edges and drainage of stormwater using drains.

The function of the insulated roof structure primarily includes the protection of the structure and the space under the roof from climatic influences and the optimization of the energy efficiency of the space under the roof. The main factors when designing a roof are primarily physical construction. Then there are economic and environmental factors, of course, both in the function of the desired architectural solutions.

Among the most important construction physical influences on flat roofs, on which technical solutions depend, are considered [35]:

• Fire—in the event of a fire, the roof structure is the first structural system that is exposed to extremely high temperatures. The use of non-combustible materials prevents the spread of fire and the release of harmful gases or burning dripping particles, which are often the cause of numerous deaths.
• Temperature—temperatures on the surface of flat roofs, depending on the season and the geographical location of the building, can range from −25 °C to +75 °C. Often, in certain weather conditions, the temperature range in one day exceeds 80 °C, which directly affects the final layer or roof membrane. This certainly affects the layer of thermal insulation and the mode of passage of water vapor through the roof structure. By choosing an adequate thickness of flat roof thermal insulation, we reduce the building’s heat losses in the winter and prevent overheating of the premises in the summer. It is recommended that the thermal insulation does not change its dimensions with changes in temperature because, in this way, unwanted stretching is caused, which thereby burdens the roof membrane or causes unwanted thermal bridges at the contact of the insulation panels.
• Wind—wind loads at tall buildings are definitely significantly higher than at low ones. With the static calculation of the roof structure, we must also calculate the impact of wind load, which directly determines the method of attachment and the arrangement of dowels for attaching the thermal insulation and the final layer of the roof to the load-bearing structure. An important factor, in this case, is the weight of the thermal insulation layer itself, which is affected by the negative wind pressure. In this case, heavier materials, such as stone wool, have an advantage over light organic insulation.
• Mechanical load—static loads of a flat roof, such as the weight of its own structure and the weight of snow, affect the dimensioning of the load-bearing structure of the roof, while the dimensioning of the thermal insulation layer is affected by occasional mechanical loads of the roof during the installation phase or later maintenance of the roof surface. The key quality factor is not only the surface load-bearing capacity of the insulation layer but also the resistance to individual point loads. They occur at the places of mechanical fixing of the roof foil and also when walking on the roof. Occasional walking on the roof cannot be avoided because sometimes the roof needs to be maintained, and there may be subsequent works that require temporary use of that surface.
• Moisture and vapor pressure—rain, snow and ice directly load the roof membrane from the outside. In addition, moisture also stresses the roof structure from the inside. The mode of vapor passage through the building envelope must be such that moisture does not stop in the thermal insulation layer. Excessive ingress of moisture into the thermal insulation layer of a flat roof is prevented by installing a vapor barrier before the insulation layer on the inside.
• Noise—when designing buildings in an urban environment, we are often faced with the requirement of lowering the noise level from the surroundings to the interior of the building. Stone wool, with its interwoven structure of stone fibers, absorbs noise and vibrations from the environment much better than insulation materials of organic origin. Sound energy is broken down in the fibrous structure of stone wool and converted into other forms of energy.

2.2. Maintenance of Flat Roof

Maintaining a flat roof is an important segment of roof and building durability. The maintenance of the flat roof, and especially the maintenance of the waterproofing protection, should be approached immediately at the beginning of the exploitation of the flat roof and the building. The reason for this is to remove possible hidden defects that occurred during the execution of works and appeared during exploitation. Localized deformations and damages should be removed immediately after they appear.

In the process of maintaining a flat roof, the important elements that should be taken into account are as follows:

-

not to stress the roof surface, more specifically, the waterproofing protection with unforeseen subsequent loads;

-

not to damage and penetrate the waterproofing protection;

-

not to use the roof for purposes for which it was not intended (drying laundry, sunbathing in the summer);

-

to maintain and clean drains and bays (from leaves, paper, bags);

-

when cleaning heavy snow so as not to damage the waterproofing protection.

The above procedures and actions can and should be performed only with the knowledge and in the presence of an expert who knows how to evaluate and decide on actions that are planned, that is, that are undertaken on the roof. Flat roof maintenance also includes smaller repairs on the roof. Such repairs should be carried out immediately after they are noticed. If they are not removed as soon as possible, i.e., not immediately, they can cause new major deformations and damage. Then, their removal will be of greater scope, both physical and financial. Such minor procedures that should be carried out immediately are as follows:

-

repair of separate places of putty on the eaves sheets;

-

repair of possible wind damage on the eaves sheets;

-

repair of the drainage slits between the sheets;

-

if the wind has moved the layer of gravel, it should be evenly distributed again;

-

if the light protection on impenetrable roofs is washed or shed, repaint the surface with suitable paint for roofs.

In addition to those mentioned, other, smaller alterations should be carried out, which aim to extend the durability of the waterproofing protection and the flat roof. All these works should be performed by a professional contractor specializing in this type of work. A regular inspection should be performed on a flat roof twice a year. In this way, even for a long time, the occurrence of further harmful phenomena will be prevented.

2.3. Renovation of Flat Roof

The condition of roofs depends on the wear and tear of the cover, the type of cover, maintenance of the cover over time and other influences. Roofs must be properly maintained, which prolongs their life. Periodic inspections of the roofs are definitely recommended, and if it is necessary to clean the roofs of leaves and other impurities through annual plans and programs, depending on the needs of the building itself. Bigger problems on roofs are caused by accumulated dirt in drainage pipes or gutters.

Any reconstruction of a flat roof begins with identifying the problem. In most cases, the roof leaks, and it is precisely this circumstance that leads to the realization of the need for repair. The roof itself has three main functions: insulation, waterproofing and aesthetics.

• Aesthetics—in this case, classic general construction or repair work is carried out related to the replacement of the existing finish coating or the decoration of the parapet or the installation of equipment, etc. In the event of a violation of the thermal or waterproofing of a flat roof, the repair will be significantly more difficult both from an engineering point of view and with regard to the intensity of work and, as a rule, considering the price of work.
• Repair of thermal insulation—a roof leak is not always related to a breach of waterproofing. For example, the roof can simply “float” if the vapor barrier is not installed. A related but different case is insufficient roof insulation. In this case, the dew point is not located in the insulation, as it should be, but directly on the floor plate, thus causing abundant condensation. The recipe for “healing” this roof is quite effective—it needs to be re-insulated. If this is not feasible from above due to the already finished finish or for other reasons, it is possible to do it from the inside. To do this, it is necessary to attach an additional layer of insulation under the floorboard to the ceiling and install a vapor barrier. The simplest option is something made of self-adhesive tape. After that, the thickness of the insulation will be sufficient; the dew point will be in the insulation, a vapor barrier will be created and the roof will stop floating. Again, it is unprofitable to do it from the top because of the roof disassembly, but to do it from the bottom, under the floorboard, is quite simple and convenient.
• Repair of waterproofing—the most difficult case from the point of view of repairing a flat forge is a violation of waterproofing (its damage or leakage due to natural wear). If the roof waterproofing is open, that is, if the final layer is not laid on the roof, the repair is quite simple—first of all, you need to find holes and patch them. It is recommended to repair a flat roof using modern waterproofing materials. It is necessary to make waterproofing over the entire surface of the waterproofing because if it is a bitumen roof that has really lasted its term, then it has been destroyed in many places. If stone wool insulation was used and it got wet, in that case, the roof would have to be completely dismantled, the insulation replaced and a new waterproofing layer installed. In the event that the waterproofing is covered with gravel, tiles or some other finish, the repair will be a rather difficult task, as the search for damage may take a long time. In this case, the works are carried out with the complete removal of the roof, and depending on the condition of the waterproofing and insulation, either their replacement is performed or the waterproofing is repaired.
• Repair of local damage (cuts, punctures)—mechanical damage can occur as a result of snow removal in winter, city encroachment and human movement. Other potential reasons are base deformation and initial imperfections allowed during coating application. Local defects are removed by placing a patch on the damaged area. The patch should be made of the same material as the base cover. Its edges are usually rounded to reduce the probability of laying, and the size is made to cover the defect by 10–15 cm in all directions.

Therefore, repairing a flat roof is a complex and expensive task, usually associated with its disassembly completely or in separate sections. All linings and roof coverings are not eternal; even the most modern of them are subject to wear and gradual loss of protective properties. Under the influence of precipitation, temperature changes and mechanical factors, the roofing material collapses, cracks, bubbles, defects, etc., appear on it, and then leakage is just one step further.

2.4. Fuzzy Multi-Criteria Analysis

Multi-criteria analysis refers to structuring, planning and problem-solving. The analysis is approached only if it is determined with certainty that the problem is characterized by a number of alternative solutions. Therefore, if a multi-criteria analysis is used to solve the problem, it is necessary to define all possible solutions to the problem. The aim of the multi-criteria analysis is to support the decision maker when there is a wide choice of alternatives when solving a problem. When using multi-criteria decision-making, it is necessary to use the personal wishes of the decision-maker. A problem for solution may have the best of the alternatives offered, the best alternative or a small set of good alternatives.

The characteristics of multi-criteria analysis are a large number of criteria, inconsistencies between criteria, incomparable measurement units of criteria, the choice of the best solution and the ranking of alternatives.

Fuzzy multi-criteria analysis combines multi-criteria methods with fuzzy logic, in this case, is PROMETHEE II method. Some of the aspects of fuzzy set theory are given in the following:

Definition 1.

[36] Let $a$ be a triangular fuzzy number defined as $a=(a_L,a_M,a_U)$, where $0<a_L<a_M<a_U<1$, then the membership function can be written as

$$f_a\left(x\right)=\left\{\begin{array}{cc}\frac{x-a_L}{a_L-a_M}& a_L\le x{\le a}_M\\ \frac{a_U-x}{a_U-a_M}& a_M\le x\le a_U\\ 0& else\end{array}\right\}$$

(1)

2.5. The Approach for Flat Roofs Ranking Using F-PROMETHEE II Method

In this research, the PORMETHEE II method based on fuzzy set theory is used for ranking flat roofs for the activity of renovation. Fusing fuzzy theory with multi-criteria methods has proven to be more effective in numerous studies than traditional methods when dealing with uncertain and vague data and information. Compared to traditional decision-making methods, the F-PROMETHEE II approach presented here has several advantages and innovations, such as

• The fuzzy logic component of the method allows for the handling of imprecise and uncertain data. This is particularly useful when data are incomplete or subjective, as the fuzzy logic can provide a more nuanced evaluation of different options.
• The multi-criteria method allows for the evaluation of multiple criteria simultaneously, which can provide a more comprehensive evaluation of different options. The fuzzy logic component of the method allows the inclusion of subjective or qualitative criteria, which may not be easily quantifiable.
• The F-PROMETHEE II method provides a clear and easy-to-interpret ranking of different options. The use of decision matrices and preference functions can help stakeholders understand and compare the relative strengths and weaknesses of different options.
• The method is flexible and can be adapted to different decision-making contexts and criteria. This makes it useful in a wide range of applications, including flat roof renovation decision-making.

Overall, the biggest innovation and advantage of the F-PROMETHEE II method is its ability to handle imprecise and uncertain data while incorporating multiple criteria and providing a clear and robust outcome of different options. This can lead to more informed and transparent decision-making processes, particularly when dealing with incomplete or subjective data.

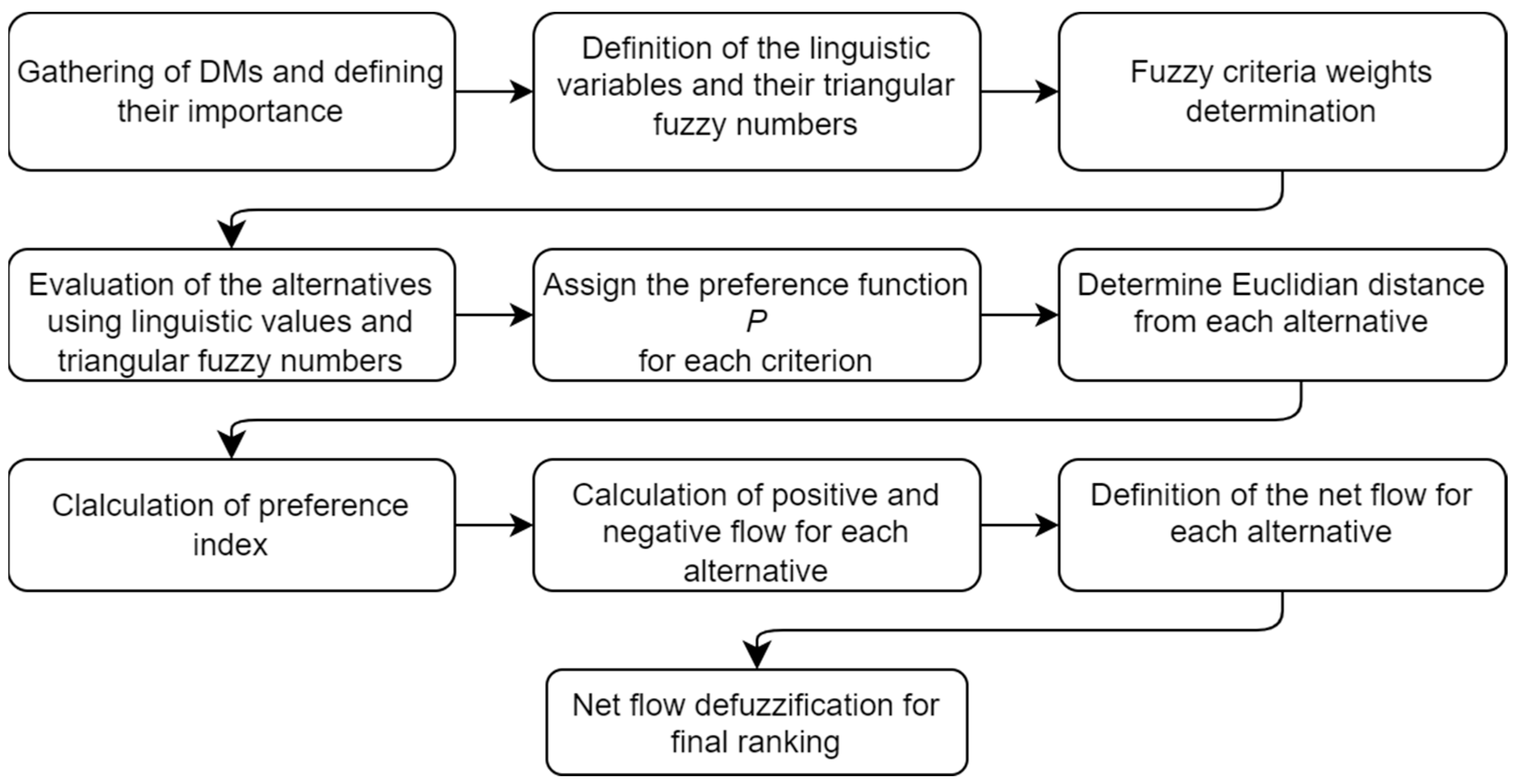
The F-PROMETHEE method is composed of three phases. In the first phase, stakeholders are selected and gathered together to discuss the problem and generate alternatives. In the second phase, adequate criteria are defined and their weights are assigned, while in the third phase, alternatives are evaluated according to criteria. The approach for flat roofs ranking using the F-PROMETHEE II method is presented in Figure 1 and in the following steps:

Step 1. Gathering of DMs and defining their importance.

Let $D$ be a set of decision-makers, where $D=\left\{{DM}_1,\dots ,{DM}_l\right\},$ then the weight of each DM $w_{DM}=${$w_{{DM}_1},\dots ,w_{{DM}_l}$}.

Step 2. Definition of the linguistic variables and their triangular fuzzy numbers.

Linguistic variables in the form of scale are defined with their triangular fuzzy numbers. These variables are used to define criteria weights and evaluations of the alternatives.

Step 3. Fuzzy criteria weights determination.

Each DM defined criteria weights using linguistic variables and their triangular fuzzy numbers. Aggregated weights are calculated as follows:

$$a_L=\frac{1}{n}\sum _{n=1}^n{a}_{L_n},a_M=\frac{1}{n}\sum _{n=1}^n{a}_{M_n},a_U=\frac{1}{n}\sum _{n=1}^n{a}_{U_n}$$

(2)

Step 4. Evaluation of the alternatives using linguistic values and triangular fuzzy numbers.

Alternatives are evaluated according to each criterion by each DM, then the aggregation of the alternatives evaluation is calculated. Finally, the normalized fuzzy decision matrix is determined as follows [37]:

For maximized criteria:

$$x_{ij}=\frac{a_{{L^{\_}}_j}}{a_{U_{ij}}},x_{ij}=\frac{a_{{L^{\_}}_j}}{a_{M_{ij}}},x_{ij}=\frac{a_{{L^{\_}}_j}}{a_{L_{ij}}}j\in E{a}_{{L^{\_}}_j}=\underset{i}{\min }{a}_{L_{ij}}$$

(3)

For minimized criteria:

$$x_{ij}=\frac{a_{L_{ij}}}{a_{{U^{+}}_j}},x_{ij}=\frac{a_{M_{ij}}}{a_{{U^{+}}_j}},x_{ij}=\frac{a_{U_{ij}}}{a_{{U^{+}}_j}}j\in F{a}_{{U^{+}}_j}\underset{i}{\max }{a}_{U_{ij}}$$

(4)

While normalized fuzzy decision matrix is

$$X={\left[x_{ij}\right]}_{m\times n}i=1,\dots ,mj=1,\dots ,n$$

(5)

where $x_{ij}=(t_{ij},v_{ij},y_{ij})$ is an evaluation by DMs based on jth criterion for ith alternative which. $u_{ij},v_{ij}$ and $y_{ij}$ denote the low boundary, medium boundary and up boundary of the triangular fuzzy number, respectively.

Step 5. Assign the preference function $P_j=(x_{ij},x_{kj})$ for each criterion.

According to [38], there are six types of preference functions. Hereby, the authors, together with stakeholders, decided to use the usual type and linear priority type, as they were the most appropriate way to describe the type of criteria.

Usual preference function:

$$P\left(d\right)=\left\{\begin{array}{cc}1,& d>0\\ 0,& d\le 0\end{array}\right.$$

(6)

Linear priority preference function:

$$P\left(d\right)=\left\{\begin{array}{cc}1,& d>p\\ \frac{d}{p},& d\le p\end{array}\right.$$

(7)

where $p$ is the threshold value between the indifferent and strict preference areas, and $d$ presents the Euclidean distance [37] between alternatives based on jth criterion. The value of $d$ is expressed for the maximized and minimized criteria as follows:

For maximized criteria:

$$d(x_{ij},x_{kj})=\left\{\begin{array}{c}\sqrt{\frac{{(t_{ij}-t_{kj})}^2+{(v_{ij}-v_{kj})}^2+{(y_{ij}-y_{kj})}^2}{2},}\\ 0,\end{array}\begin{array}{c}{x}_{ij}>x_{kj}\\ else\end{array}\right.$$

(8)

For minimized criteria:

$$d(x_{ij},x_{kj})=\left\{\begin{array}{c}\sqrt{\frac{{(t_{ij}-t_{kj})}^2+{(v_{ij}-v_{kj})}^2+{(y_{ij}-y_{kj})}^2}{2},}\\ 0,\end{array}\begin{array}{c}{x}_{ij}<x_{kj}\\ else\end{array}\right.$$

(9)

where $i\ne k$ and $i,k=\mathrm{1,2},\dots ,m.$

Step 6. Preference index calculation.

By using the preference index, it is proved that the degree of the ith alternative is higher than the jth alternative, which indicates the rank of the ith alternative. The index is expressed as follows:

$$\pi \left(x_i,x_k\right)={\sum }_{j=1}^n{w}_j\times P_j\left(x_{ij},x_{kj}\right)=\left(t_{ij}^{\pi },v_{ij}^{\pi },y_{ij}^{\pi }\right)i\ne k \mathrm{and} i,k=\mathrm{1,2},\dots ,m$$

(10)

Moreover, the criteria weight is denoted with $w_{ij}=\left\{w_1,\dots w_m\right\}$.

Step 7. Calculation of positive (leaving) and negative (entering) flow for each alternative.

The positive flow ${\Phi }^{+}\left(x_i\right)$ defines the strength of the ith alternative, while the entering flow ${\Phi }^{-}\left(x_i\right)$ measures its weakness. Following are the expressions of the positive and negative flows:

Positive flow:

$${\Phi }^{+}\left(x_i\right)={\sum }_{k=1}^m\pi \left(x_i,x_k\right)=\left(t_i^{{\Phi }^{+}},v_i^{{\Phi }^{+}},y_i^{{\Phi }^{+}}\right)i\ne k \mathrm{and} i,k=\mathrm{1,2},\dots ,m$$

(11)

Negative flow:

$${\Phi }^{-}\left(x_i\right)={\sum }_{k=1}^m\pi \left(x_i,x_k\right)=\left(t_i^{{\Phi }^{-}},v_i^{{\Phi }^{-}},y_i^{{\Phi }^{-}}\right)i\ne k \mathrm{and} i,k=\mathrm{1,2},\dots ,m$$

(12)

Step 8. Definition of the net flow for each alternative.

An alternative with a higher net flow will have a higher ranking. The net flow of ith alternative is expressed as

$$\Phi \left(x_i\right)={\Phi }^{+}\left(x_i\right)-{\Phi }^{-}\left(x_i\right)=(t_i^{\Phi },v_i^{\Phi },y_i^{\Phi })i=\mathrm{1,2},\dots ,m$$

(13)

Step 9. Net flow defuzzification for final ranking.

For the defuzzification of the alternatives evaluations defined with net flows, the centroid method is used as follows [39]:

$$\stackrel{-}{\Phi }\left(x_i\right)=\frac{t_i^{\Phi }+v_i^{\Phi }+y_i^{\Phi }}{3}i=\mathrm{1,2},\dots ,m$$

(14)

If $\stackrel{-}{\Phi }\left(x_1\right)>\stackrel{-}{\Phi }\left(x_2\right)$, it means that alternative 1 is higher ranked than alternative 2.

2.6. Criteria Definition

Multi-criteria decision-making includes four components: alternatives definition, criteria determination, criteria weights assignment and decision maker’s attitude. The decision-maker needs to rank the alternatives or choose between them, while criteria serve to evaluate and compare alternatives. In order to better carry out the assessment of the alternative, it is necessary to define measurement scales. By defining requirements for problem-solving, the goals of multi-criteria problems are established. In order for the goals to be defined as effectively as possible, the views of all stakeholders in the decision-making process must be taken into account. Furthermore, in

Table 1. Defined criteria, with preference functions, for renovation planning of flat roofs.

Label	Criteria Name	Description	Preference Function	Min/Max
C1	Condition of the roof	The current state of the roof is regarding mechanical stability and resistance.	Linear priority	min
C2	Selected material	Quality and durability of the material.	Linear priority	max
C3	The simplicity of renovation	It refers to the simplicity of roof renovation.	Linear	max
C4	Renovation cost	It refers to the price of materials for the roof construction and the costs of carrying out the work.	Linear priority	min
C5	Maintenance cost	Includes roof maintenance costs after renovation.	Linear priority	min
C6	Renovation duration	It includes the time required for the renovation of the roof structure and rainwater drainage.	Linear priority	min
C7	Thermal efficiency	Meeting the minimum requirements regarding the improvement of the thermal protection properties.	Usual	max
C8	Sound efficiency	Attenuation from noise and external sounds.	Usual	max
C9	Waterproofing	It includes protection against water penetration into the interior of the building.	Usual	max

, criteria are presented with a description, preference function and type regarding minimum or maximum. All criteria are defined by decision-makers, which were the project manager, construction engineer and user. Criteria C1, C2 and C3 are defined from the technical aspects of the problem, C4, C5 and C6 from the economical and C7, C8 and C9 from the ecological aspect. All stakeholders were gathered, and throughout the discussion, criteria were defined, considering the importance of all stakeholders equally. Criteria from C1 to C6 are defined with linear priority preference function, while criteria from C7 to C9 with usual. These functions were chosen as they were the most appropriate to describe each criterion preference.

3. Results

In this section, the effectiveness and applicability of the defined criteria and F-PROMETHEE II method are verified in the assessment of the flat roofs for the activity of renovation.

3.1. Case Study

The FCEAG’s building consists of three interconnected parts. Firstly, they were constructed separately, but today they represent a physical unit, sharing a common entrance, communication areas and other service areas. The building serves as a higher education institution. The analyzed flat roofs are located on three construction plots of the building, meaning building A at lot no. 6474/4, building B at lot no. 6474/8, and building C, at lot no. 6474/5. Building A consists of a basement, ground floor, three floors, roof and superstructure. Building B consists of a basement, ground floor, five floors, roof and superstructure. Building C consists of a basement, a ground floor, three floors and a roof. The roofs are presented in Figure 2.

Building A was completed in 1976, and building B in 1978. The first of the reconstructions was in 2005 when building C was completed. After the construction of building C, the outer envelope of building A and building B was reconstructed, including all the outer walls, i.e., facades, flat roofs and openings. The construction of the building consists of a system of load-bearing reinforced concrete beams and monolithic reinforced concrete slabs. The roof is solved as a flat structure, and the facades are in good condition. The roof of building A, located above the third floor, was renovated in 2021 when old layers were completely removed with new ones. The roof of building A above the first floor has not been renovated since the construction of the building in 1976, and considering that it has no thermal insulation at all, as determined from the existing project documentation, it does not meet the standards of thermal resistance of the building’s outer envelope. Based on field inspection, the roof is in an unmaintained state. Indentations on the roof slab, cracked concrete slabs and weeds are visible.

Building B consists of two flat roofs on the first and fifth floors, both of which were renovated in 2019. Moreover, in building B old layers were removed and new ones were constructed on the existing concrete. Gravel was placed on the roof above the first floor, while concrete slabs were placed on the roof above the fifth floor.

The roof of building C was built in 2005 and has not been renovated since then. Although it is visibly in satisfactory condition, it does not meet the thermal resistance standards of the building’s outer envelope and requires renovation [19].

Overall, seven roofs have been evaluated, which are as follows:

• building A: roof above the 1st flour (A1), roof A above the 4th flour (A2);
• building B: roof above the 1st flour (B1), roof B above the 5th flour (B2);
• roof above the corridor (H);
• building C: roof above the 1st flour (K1), and roof above the 4th flour (K2).

3.2. The Ranking of Flat Roofs

In this section, the ranking of seven flat roofs is obtained by the methodology presented in Section 2.4.

There are three decision makers (DM) with many years of experience in structural engineering. All three DMs are equally important, and for that reason, their weights are all defined with a crisp value of 1.

Furthermore, in

Table 2. The linguistic variables and corresponding fuzzy numbers.

Linguistic Variable	Fuzzy Numbers
Very Low/Poor (VL/VP)	(0.0, 0.0, 0.1)
Low/Poor (L/P)	(0.0, 0.1, 0.25)
Medium Low/Poor (ML/MP)	(0.1, 0.25, 0.4)
Fair (F)	(0.25, 0.4, 0.6)
Medium-High/Good (MH/MG)	(0.4, 0.6, 0.8)
High/Good (H/G)	(0.6, 0.8, 1.0)
Very High/Good (VH/VG)	(0.8, 1.0, 1.0)

, linguistic values with corresponding triangular fuzzy numbers are given. By using these values, DMs defined criteria weights and by Equation (2), aggregated fuzzy weight is calculated, as is presented in

Table 3. Criteria fuzzy weight and aggregated fuzzy weight.

Criteria	DM1	DM2	DM3	Aggregated Fuzzy Weight
C1	VH	VH	VH	(0.8, 9.97, 1.0)
C2	VH	H	H	(0.67, 0.87, 1.0)
C3	H	MH	H	(0.53, 0.73, 0.93)
C4	MH	F	MH	(0.35, 0.53, 0.73)
C5	MH	F	MH	(0.35, 0.53, 0.73)
C6	H	MH	H	(0.53, 0.73, 0.93)
C7	H	VH	H	(0.67, 0.87, 1.0)
C8	VH	H	VH	(0.73, 0.93, 1.0)
C9	VH	H	VH	(0.73, 0.93, 1.0)

.

Likewise, the evaluations of alternatives are given by DMs according to the values in Table 2, and aggregated fuzzy evaluations are calculated. The normalized fuzzy decision matrix is calculated using Equations (3) and (4), respectively.

Table 4. The evaluation of each alternative and aggregated fuzzy evaluation.

Criteria	Roof	DM1	DM2	DM3	Aggregated Fuzzy Evaluation	Normalized Fuzzy Decision Matrix
C1	A1	P	P	P	(0.1, 0.25, 0.4)	(0.25, 0.4, 1.0)
	A2	H	VH	H	(0.67, 0.87, 1.0)	(0.1, 0.12, 0.15)
	B1	H	VH	VH	(0.73, 0.93, 1.0)	(0.1, 0.11, 0.14)
	B2	H	VH	VH	(0.73, 0.93, 1.0)	(0.1, 0.11, 0.14)
	H	H	H	VH	(0.67, 0.87, 1.0)	(0.1, 0.12, 0.15)
	K1	F	H	MH	(0.42, 0.6, 0.8)	(0.13, 0.17, 0.24)
	K2	F	H	MH	(0.42, 0.6, 0.8)	(0.13, 0.17, 0.24)
C2	A1	H	H	H	(0.6, 0.8, 1.0)	(0.6, 0.8, 1.0)
	A2	MH	MH	MH	(0.4, 0.6, 0.8)	(0.4, 0.6, 0.8)
	B1	MH	MH	MH	(0.4, 0.6, 0.8)	(0.4, 0.6, 0.8)
	B2	MH	MH	MH	(0.4, 0.6, 0.8)	(0.4, 0.6, 0.8)
	H	MH	MH	F	(0.35, 0.53, 0.73)	(0.35, 0.53, 0.73)
	K1	MH	F	MH	(0.35, 0.53, 0.73)	(0.35, 0.53, 0.73)
	K2	MH	F	MH	(0.35, 0.53, 0.73)	(0.35, 0.53, 0.73)
C3	A1	P	MP	MP	(0.1, 0.25, 0.4)	(0.1, 0.25, 0.4)
	A2	MH	MH	MH	(0.4, 0.6, 0.8)	(0.4, 0.6, 0.8)
	B1	MH	MH	MH	(0.4, 0.6, 0.8)	(0.4, 0.6, 0.8)
	B2	MH	MH	MH	(0.4, 0.6, 0.8)	(0.4, 0.6, 0.8)
	H	MH	MH	MH	(0.4, 0.6, 0.8)	(0.4, 0.6, 0.8)
	K1	MH	MH	F	(0.35, 0.53, 0.73)	(0.35, 0.53, 0.73)
	K2	F	MH	F	(0.3, 0.47, 0.67)	(0.3, 0.47, 0.67)
C4	A1	H	H	H	(0.6, 0.8, 1.0)	(0.1, 0.13, 0.17)
	A2	MH	MH	MH	(0.4, 0.6, 0.8)	(0.13, 0.17, 0.25)
	B1	F	F	F	(0.25, 0.4, 0.6)	(0.17, 0.25, 0.4)
	B2	F	F	F	(0.25, 0.4, 0.6)	(0.17, 0.25, 0.4)
	H	MP	MP	MP	(0.1, 0.25, 0.4)	(0.25, 0.4, 1.0)
	K1	VH	VH	VH	(0.8, 1.0, 1.0)	(0.1, 0.1, 0.13)
	K2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.1, 0.1, 0.13)
C5	A1	H	H	H	(0.6, 0.8, 1.0)	(0.1, 0.13, 0.17)
	A2	F	F	F	(0.25, 0.4, 0.6)	(0.17, 0.25, 0.4)
	B1	MP	MP	MP	(0.1, 0.25, 0.4)	(0.25, 0.4, 1.0)
	B2	F	F	F	(0.25, 0.4, 0.6)	(0.17, 0.25, 0.4)
	H	MP	MP	MP	(0.1, 0.25, 0.4)	(0.25, 0.4, 1.0)
	K1	MH	MH	MH	(0.4, 0.6, 0.8)	(0.13, 0.17, 0.25)
	K2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.1, 0.1, 0.13)
C6	A1	VH	VH	VH	(0.67, 0.87, 0.93)	(0.11, 0.12, 0.15)
	A2	F	F	F	(0.25, 0.4, 0.6)	(0.17, 0.25, 0.4)
	B1	MP	MP	MP	(0.1, 0.25, 0.4)	(0.25, 0.4, 1.0)
	B2	MP	MP	MP	(0.1, 0.25, 0.4)	(0.25, 0.4, 1.0)
	H	MP	MP	MP	(0.1, 0.25, 0.4)	(0.25, 0.4, 1.0)
	K1	H	H	H	(0.6, 0.8, 1.0)	(0.1, 0.13, 0.17)
	K2	H	H	H	(0.6, 0.8, 1.0)	(0.1, 0.13, 0.17)
C7	A1	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
	A2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	B1	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	B2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	H	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	K1	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
	K2	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
C8	A1	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
	A2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	B1	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	B2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	H	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	K1	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
	K2	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
C9	A1	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
	A2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	B1	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	B2	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	H	VH	VH	VH	(0.8, 1.0, 1.0)	(0.8, 1.0, 1.0)
	K1	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)
	K2	VP	VP	VP	(0.0, 0.0, 0.1)	(0.0, 0.0, 0.1)

presents the evaluation of each alternative according to each criterion by each DM, their aggregated evaluations and the normalized decision matrix.

The preference intensity P is determined according to Equations (6) and (7), where $d$ is Euclidian distance calculated for the maximized and minimized criteria as defined in Equations (8) and (9), respectively. The P values are shown in

Table 5. The preference intensity of each alternative by each criterion.

	C1	C2	C3	C4	C5	C6	C7	C8	C9
P(A1,A2)	0.64	0.00	0.53	0.00	0.00	0.00	1.00	1.00	1.00
P(A1,B1)	0.65	0.00	0.53	0.00	0.00	0.00	1.00	1.00	1.00
P(A1,B2)	0.65	0.00	0.53	0.00	0.00	0.00	1.00	1.00	1.00
P(A1,H)	0.64	0.00	0.53	0.00	0.00	0.00	1.00	1.00	1.00
P(A1,K1)	0.57	0.00	0.46	0.00	0.00	0.01	0.00	0.00	0.00
P(A1,K2)	0.57	0.00	0.41	0.00	0.00	0.01	0.00	0.00	0.00
P(A2,A1)	0.00	0.24	0.00	0.11	0.19	0.21	0.00	0.00	0.00
P(A2,B1)	0.01	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P(A2,B2)	0.01	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P(A2,H)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P(A2,K1)	0.00	0.00	0.00	0.12	0.12	0.19	0.00	0.00	0.00
P(A2,K2)	0.00	0.00	0.00	0.12	0.23	0.19	0.00	0.00	0.00
P(B1,A1)	0.00	0.24	0.00	0.22	0.63	0.64	0.00	0.00	0.00
P(B1,A2)	0.00	0.00	0.00	0.20	0.44	0.44	0.00	0.00	0.00
P(B1,B2)	0.00	0.00	0.00	0.00	0.44	0.00	0.00	0.00	0.00
P(B1,H)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P(B1,K1)	0.00	0.00	0.00	0.59	0.56	0.63	0.00	0.00	0.00
P(B1,K2)	0.00	0.00	0.00	0.24	0.66	0.63	0.00	0.00	0.00
P(B2,A1)	0.00	0.24	0.00	0.22	0.19	0.64	0.00	0.00	0.00
P(B2,A2)	0.00	0.00	0.00	0.20	0.00	0.44	0.00	0.00	0.00
P(B2,B1)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P(B2,H)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P(B2,K1)	0.00	0.00	0.00	0.59	0.12	0.63	0.00	0.00	0.00
P(B2,K2)	0.00	0.00	0.00	0.24	0.23	0.63	0.00	0.00	0.00
P(H,A1)	0.00	0.32	0.00	0.66	0.63	0.64	0.00	0.00	0.00
P(H,A2)	0.00	0.08	0.00	0.62	0.44	0.44	0.00	0.00	0.00
P(H,B1)	0.01	0.08	0.00	0.57	0.00	0.00	0.00	0.00	0.00
P(H,B2)	0.01	0.08	0.00	0.57	0.44	0.00	0.00	0.00	0.00
P(H,K1)	0.00	0.00	0.00	0.68	0.56	0.63	0.00	0.00	0.00
P(H,K2)	0.00	0.00	0.00	0.68	0.66	0.63	0.00	0.00	0.00
P(K1,A1)	0.00	0.32	0.00	0.00	0.07	0.00	0.00	0.00	0.00
P(K1,A2)	0.08	0.08	0.35	0.00	0.00	0.00	0.00	0.00	0.00
P(K1,B1)	0.09	0.08	0.35	0.00	0.00	0.00	0.00	0.00	0.00
P(K1,B2)	0.09	0.08	0.35	0.00	0.00	0.00	0.00	0.00	0.00
P(K1,H)	0.08	0.00	0.35	0.00	0.00	0.00	0.00	0.00	0.00
P(K1,K2)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P(K2,A1)	0.00	0.32	0.35	0.00	0.00	0.00	0.00	0.00	0.00
P(K2,A2)	0.08	0.08	0.35	0.00	0.00	0.00	1.00	1.00	1.00
P(K2,B1)	0.09	0.08	0.35	0.00	0.00	0.00	1.00	1.00	1.00
P(K2,B2)	0.09	0.08	0.35	0.00	0.00	0.00	1.00	1.00	1.00
P(K2,H)	0.08	0.00	0.33	0.00	0.00	0.00	1.00	1.00	1.00
P(K2,K1)	0.00	0.00	0.34	0.00	0.00	0.00	0.00	0.00	0.00

. Consequently, shown in

Table 6. Preference index for each alternative.

Π	TFN	Π	TFN
Π(A1,A2)	(0.33, 0.42, 0.46)	Π(B2,H)	(0.0, 0.0, 0.0)
Π(A1,B1)	(0.33, 0.42, 0.46)	Π(B2,K1)	(0.07, 0.09, 0.12)
Π(A1,B2)	(0.33, 0.42, 0.46)	Π(B2,K2)	(0.06, 0.08, 0.1)
Π(A1,H)	(0.33, 0.42, 0.46)	Π(H,A1)	(0.11, 0.16, 0.21)
Π(A1,K1)	(0.08, 0.1, 0.11)	Π(H,A2)	(0.07, 0.11, 0.14)
Π(A1,K2)	(0.08, 0.1, 0.11)	Π(H,B1)	(0.03, 0.04, 0.06)
Π(A2,A1)	(0.04, 0.06, 0.07)	Π(H,B2)	(0.05, 0.07, 0.09)
Π(A2,B1)	(0.0, 0.0, 0.0)	Π(H,K1)	(0.9, 0.12, 0.17)
Π(A2,B2)	(0.0, 0.0, 0.0)	Π(H,K2)	(0.9, 0.13, 0.17)
Π(A2,H)	(0.0, 0.0, 0.0)	Π(K1,A1)	(0.03, 0.03, 0.04)
Π(A2,K1)	(0.02, 0.03, 0.04)	Π(K1,A2)	(0.03, 0.04, 0.05)
Π(A2,K2)	(0.02, 0.03, 0.04)	Π(K1,B1)	(0.03, 0.04, 0.05)
Π(B1,A1)	(0.09, 0.13, 0.16)	Π(K1,B2)	(0.03, 0.04, 0.05)
Π(B1,A2)	(0.05, 0.07, 0.1)	Π(K1,H)	(0.03, 0.04, 0.04)
Π(B1,B2)	(0.02, 0.03, 0.04)	Π(K1,K2)	(0, 0.01, 0.01)
Π(B1,H)	(0.0, 0.0, 0.0)	Π(K2,A1)	(0.04, 0.06, 0.07)
Π(B1,K1)	(0.08, 0.12, 0.16)	Π(K2,A2)	(0.27, 0.35, 0.39)
Π(B1,K2)	(0.07, 0.1, 0.14)	Π(K2,B1)	(0.27, 0.35, 0.39)
Π(B2,A1)	(0.07, 0.1, 0.13)	Π(K2,B2)	(0.27, 0.35, 0.39)
Π(B2,A2)	(0.03, 0.05, 0.06)	Π(K2,H)	(0.26, 0.34, 0.38)
Π(B2,B1)	(0.0, 0.0, 0.0)	Π(K2,K1)	(0.02, 0.03, 0.03)

, the preference index for each alternative is calculated by Equation (10).

Finally, in

Table 7. The positive and negative flows.

Roof	${\mathit{\Phi }}^{+}{\mathit{x}}_{\mathit{i}}$	${\mathit{\Phi }}^{-}{\mathit{x}}_{\mathit{i}}$	$\mathit{\Phi }\left({\mathit{x}}_{\mathit{i}}\right)$
A1	(1.46, 1.86, 2.06)	(0.39, 0.54, 0.68)	(1.07, 1.32, 1.38)
A2	(0.09, 0.13, 0.16)	(0.79, 1.03, 1.20)	(−0.7, −0.91, −1.03)
B1	(0.31, 0.45, 0.59)	(0.66, 0.85, 0.96)	(−0.35, −0.4, −0.36)
B2	(0.23, 0.32, 0.42)	(0.69, 0.91, 1.03)	(−0.47, −0.58, −0.61)
H	(0.43, 0.63, 0.84)	(0.62, 0.79, 0.88)	(−0.18, −0.16, −0.04)
K1	(0.16, 0.21, 0.25)	(0.35, 0.5, 0.64)	(−0.19, −0.29, −0.38)
K2	(1.14, 1.47, 1.64)	(0.32, 0.45, 0.58)	(0.82, 1.02, 1.06)

, the fuzzy positive and negative flows and fuzzy net flow are defined by Equations (11)–(13), while in

Table 8. The defuzzified net flows and rank of the flat roofs.

Roof	$\stackrel{-}{\mathit{\Phi }}\left({\mathit{x}}_{\mathit{i}}\right)$	Rank
A1	1.26	1
A2	−0.88	7
B1	−0.37	5
B2	−0.56	6
H	−0.13	3
K1	−0.29	4
K2	0.97	2

, defuzzified net flow, defined by centroid method (14), and ranking positions of flat roofs are presented. Centroid method values are also presented in Table 7, and the final ranking of alternatives is obtained.

4. Conclusions

This research presented theoretical features related to flat roofs, and a fuzzy multi-criteria analysis of the renovation problem of flat roofs on public buildings was carried out. The fuzzy multi-criteria approach is developed for the activity of renovation of flat roofs, using the F-PROMETHEE II method. Relevant stakeholders and their attitudes were identified, as well as their inclusion in the planning process of renovation activities was achieved. The approach is validated on the flat roofs of the Faculty of Civil Engineering, Architecture and Geodesy in Split. A total of seven roofs were analyzed, and an evaluation of each of them according to all defined criteria was carried out.

The final ranking is achieved when roof A1 is ranked first. This roof is ranked as the most priority for renovation, with a net flow value of $\stackrel{-}{\Phi }\left(x_i\right)=$ 1.26, and the least priority is roof A2, with $\stackrel{-}{\Phi }\left(x_i\right)=-0.88$.

Considering the obtained results, which were presented to the final decision makers and accepted by them, the following can be concluded about the proposed model:

• The proposed fuzzy multi-criteria approach is useful and effective for evaluating different flat roof renovation options, particularly in contexts where there is a high degree of uncertainty and imprecision.
• The use of a decision-making process where different stakeholders are involved in the evaluation and ranking of flat roofs ensures that all relevant factors are considered and that the final decision is widely accepted.
• The criteria are selected based on their relevance to the flat roof renovation context and are weighted appropriately based on their relative importance.
• The use of fuzzy set theory allowed the handling of imprecise and uncertain data, which is particularly important in the context of flat roof renovation where data are incomplete or unreliable.
• The F-PROMETHEE II method is a particularly effective method for flat roof renovation decision-making, as it provides a clear and easy-to-interpret ranking of different options based on the selected criteria.

While the proposed approach has shown to be useful and effective in the decision-making process for flat roof renovation, there may be several potential gaps in research and analysis that should be considered, including the identification of criteria. The selection of appropriate criteria for evaluating flat roofs for renovation can be challenging, particularly when considering the varying needs and preferences of different stakeholders. The proposed approach is designed to be used in a participatory decision-making process, where different stakeholders are involved in the evaluation and ranking of flat roofs for the activity of renovation. However, the involvement of stakeholders can be challenging, particularly when dealing with complex technical issues. Moreover, flat roof renovation decision-making often involves a high degree of uncertainty, particularly when considering the long-term performance and durability of different roofing materials and technologies. For this reason, it is important to handle a high uncertainty. Finally, for some non-experts, the proposed design might be complex and difficult to understand.

The future study will consider the wider application of the methodology on all public buildings in the town of Split, Croatia. Considering all the variants regarding green, standard and cool roofs, more research will be implemented to identify the most important criteria for different flat roof renovation contexts and to determine how to weigh and combine these criteria in the evaluation process. To handle missing or incomplete data, the most appropriate methods for collecting and analyzing data for flat roof renovation decision-making will be determined. Moreover, the methodology based on mixed integer programming will be used to obtain managers’ approaches regarding the financial cycle with defined required constraints. This way, the managing process of roof renovation will be more systematic, as each year, it will be known which roofs are going to be reconstructed. Moreover, an approach for predicting the future condition of roofs using fuzzy neural networks will be proposed to enable managers to maintain roofs for longer periods properly.