Impact of Urbanisation on the Spatial and Temporal Evolution of Carbon Emissions and the Potential for Emission Reduction in a Dual-Carbon Reduction Context
Abstract
:1. Introduction
1.1. Analysis of the Evolution Mechanism of Urbanisation and Carbon Emission and the Significance of Carbon Reduction Potential
1.2. The Impact of Urbanisation on the Spatio-Temporal Evolution Mechanism of Carbon Emissions and Their Reduction Potential
1.3. Analysis of the Spatial and Temporal Evolution Mechanisms and Dynamics of Carbon Emissions in the Context of Urbanisation
1.3.1. Model Construction for Measuring Carbon Emissions from Anthropogenic Sources
1.3.2. Analysis of Factors Influencing Carbon Emissions from Transport Sources and Construction of Regression Models
1.4. Analysis of the Spatial Change Mechanism of Carbon Emissions
1.4.1. Analysis of the Dynamics of Spatial Evolution
1.4.2. Analysis of Carbon Emission Projections and Reduction Potential
1.4.3. Analysis of Carbon Emission Regulation Mechanisms and Study of Strategies
1.5. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buck, H.J. Mining the air: Political ecologies of the circular carbon economy. Environ. Plan. E Nat. Space 2022, 5, 1086–1105. [Google Scholar] [CrossRef]
- Chen, S.; Mao, H.; Sun, J. Low-carbon city construction and corporate carbon reduction performance: Evidence from a quasi-natural experiment in China. J. Bus. Ethics 2022, 180, 125–143. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Li, Y. Research on the Impact of Multi-dimensional Urbanization on China’s Carbon Emissions under the Background of COP21. J. Environ. Manag. 2020, 273, 111123. [Google Scholar] [CrossRef]
- Udemba, E.N.; Philip, L.D.; Emir, F. Performance and sustainability of environment under entrepreneurial activities, urbanization and renewable energy policies: A dual study of Malaysian climate goal. Renew. Energy 2022, 189, 734–743. [Google Scholar] [CrossRef]
- Fan, J.; Wang, J.; Liu, M.; Sun, W.; Lan, Z. Scenario simulations of China’s natural gas consumption under the dual-carbon target. Energy 2022, 252, 124106. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, P. Industrialization, urbanization, and carbon emission efficiency of Yangtze River Economic Belt-empirical. Environ. Sci. Pollut. Res. 2021, 28, 66914–66929. [Google Scholar] [CrossRef]
- Hu, H.; Lv, T.; Zhang, X.; Fu, S.; Geng, C.; Li, Z. Spatiotemporal dynamics and decoupling mechanism of economic growth and carbon emissions in an urban agglomeration of China. Environ. Monit. Assess. 2022, 194, 616. [Google Scholar] [CrossRef]
- Sun, J.; Guo, X.; Wang, Y.; Shi, J.; Zhou, Y.; Shen, B. Nexus among energy consumption structure, energy intensity, population density, urbanization, and carbon intensity: A heterogeneous panel evidence considering differences in electrification rates. Environ. Sci. Pollut. Res. 2022, 29, 19224–19243. [Google Scholar] [CrossRef]
- Wang, W.; Chen, H.; Yang, R.; Wang, B.; Yang, Y. Spatial and Temporal Prediction of Carbon Peaking Goals and Zonal Governance Approaches to Achieve Carbon neutrality-A Case Study from Zhejiang Province, China. In Proceedings of the 2022 International Conference on Green Building, Civil Engineering and Smart City, Guilin, China, 8–10 April 2022; Springer: Singapore, 2022; Volume 211, pp. 151–165. [Google Scholar]
- Li, Y.; Li, Y.; Zhou, Y.; Shi, Y.; Zhu, X. Investigation of a “coupling model” of coordination between low-carbon development and urbanization in China. Energy Policy 2018, 121, 346–354. [Google Scholar]
- Tang, Y.; Zhu, H.; Yang, J. The asymmetric effects of economic growth, urbanization and deindustrialization on carbon emissions: Evidence from China. Energy Rep. 2022, 8, 513–521. [Google Scholar] [CrossRef]
- Qi, X.; Han, Y.; Kou, P. Population urbanization, trade openness and carbon emissions: An empirical analysis based on China. Air Qual. Atmos. Health 2020, 13, 519–528. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, H.; Yang, D.; Liu, H. Effects of urbanization on freight transport carbon emissions in China: Common characteristics and regional disparity. J. Clean. Prod. 2019, 211, 481–489. [Google Scholar] [CrossRef]
- Wang, Q.; Li, L. The effects of population aging, life expectancy, unemployment rate, population density, per capita GDP, urbanization on per capita carbon emissions. Sustain. Prod. Consum. 2021, 28, 760–774. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L. The nonlinear effects of population aging, industrial structure, and urbanization on carbon emissions: A panel threshold regression analysis of 137 countries. J. Clean. Prod. 2021, 287, 125381. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B. Investigating the differences in CO2 emissions in the transport sector across Chinese provinces: Evidence from a quantile regression model. J. Clean. Prod. 2018, 175, 109–122. [Google Scholar] [CrossRef]
- Qin, H.; Huang, Q.; Zhang, Z.; Lu, Y.; Li, M.; Xu, L.; Chen, Z. Carbon dioxide emission driving factors analysis and policy implications of Chinese cities: Combining geographically weighted regression with two-step cluster. Sci. Total Environ. 2019, 684, 413–424. [Google Scholar] [CrossRef]
- Xu, G.; Schwarz, P.; Yang, H. Determining China’s CO2 emissions peak with a dynamic nonlinear artificial neural network approach and scenario analysis. Energy Policy 2019, 128, 752–762. [Google Scholar] [CrossRef]
- Liu, B.; Tian, C.; Li, Y.; Song, H.; Ma, Z. Research on the effects of urbanization on carbon emissions efficiency of urban agglomerations in China. J. Clean. Prod. 2018, 197, 1374–1381. [Google Scholar] [CrossRef]
- Sun, Y.; Li, H.; Andlib, Z.; Genie, M.G. How do renewable energy and urbanization cause carbon emissions? Evidence from advanced panel estimation techniques. Renew. Energy 2022, 185, 996–1005. [Google Scholar] [CrossRef]
- Lai, S.; Lu, J.; Luo, X.; Ge, J. Carbon emission evaluation model and carbon reduction strategies for newly urbanized areas. Sustain. Prod. Consum. 2022, 31, 13–25. [Google Scholar] [CrossRef]
- An, Q.; Sheng, S.; Zhang, H.; Xiao, H.; Dong, J. Research on the construction of carbon emission evaluation system of low-carbon-oriented urban planning scheme: Taking the West New District of Jinan city as example. Geol. Ecol. Landsc. 2019, 3, 187–196. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, R. The sequential collaborative relationship between economic growth and carbon emissions in the rapid urbanization of the Pearl River Delta. Environ. Sci. Pollut. Res. 2019, 26, 30130–30144. [Google Scholar] [CrossRef] [PubMed]
- Majeed, M.T.; Tauqir, A. Effects of urbanization, industrialization, economic growth, energy consumption, financial development on carbon emissions: An extended STIRPAT model for heterogeneous income groups. Pak. J. Commer. Soc. Sci. (PJCSS) 2020, 14, 652–681. [Google Scholar]
- Abbasi, M.A.; Parveen, S.; Khan, S.; Kamal, M.A. Urbanization and energy consumption effects on carbon dioxide emissions: Evidence from Asian-8 countries using panel data analysis. Environ. Sci. Pollut. Res. 2020, 27, 18029–18043. [Google Scholar] [CrossRef]
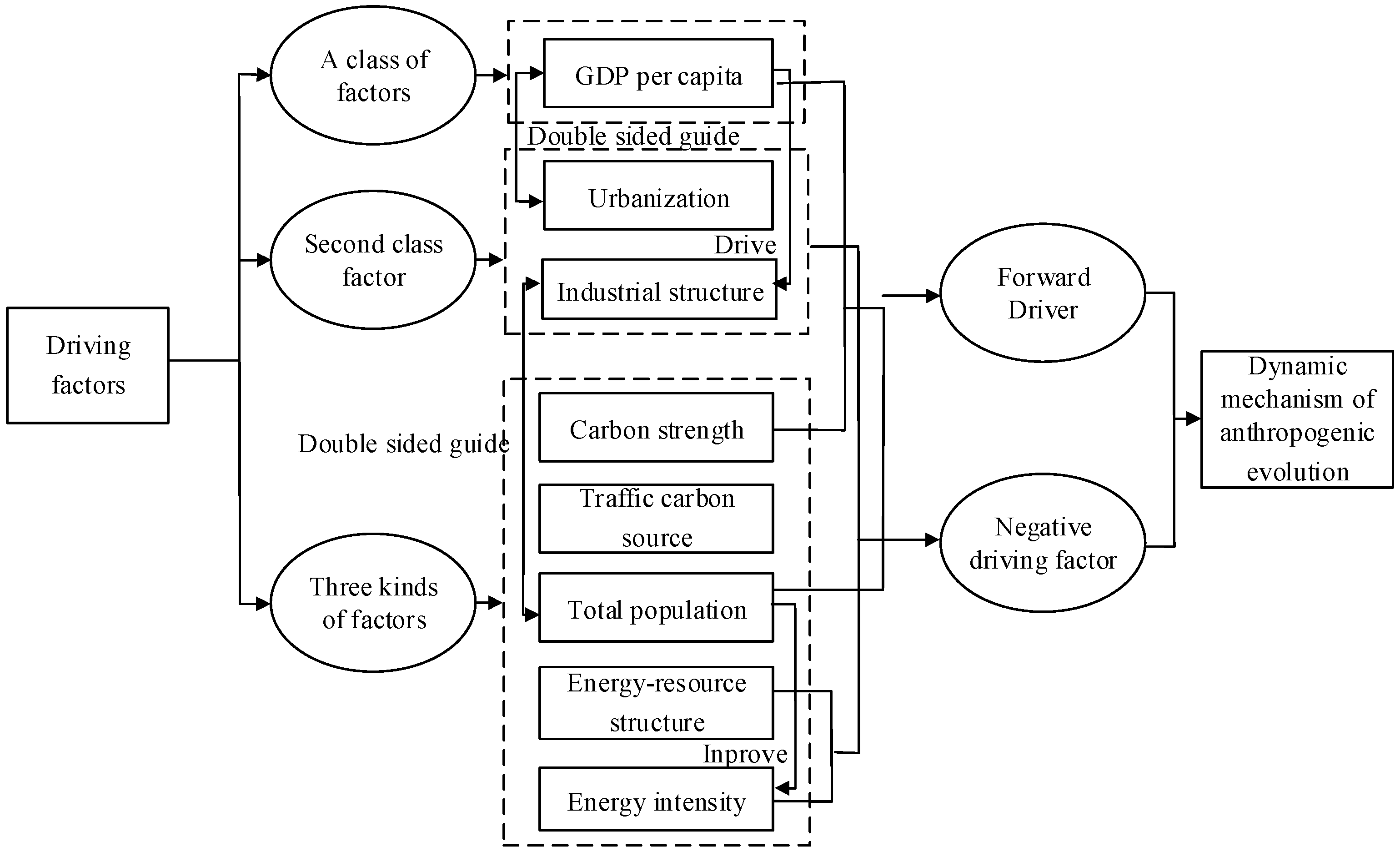
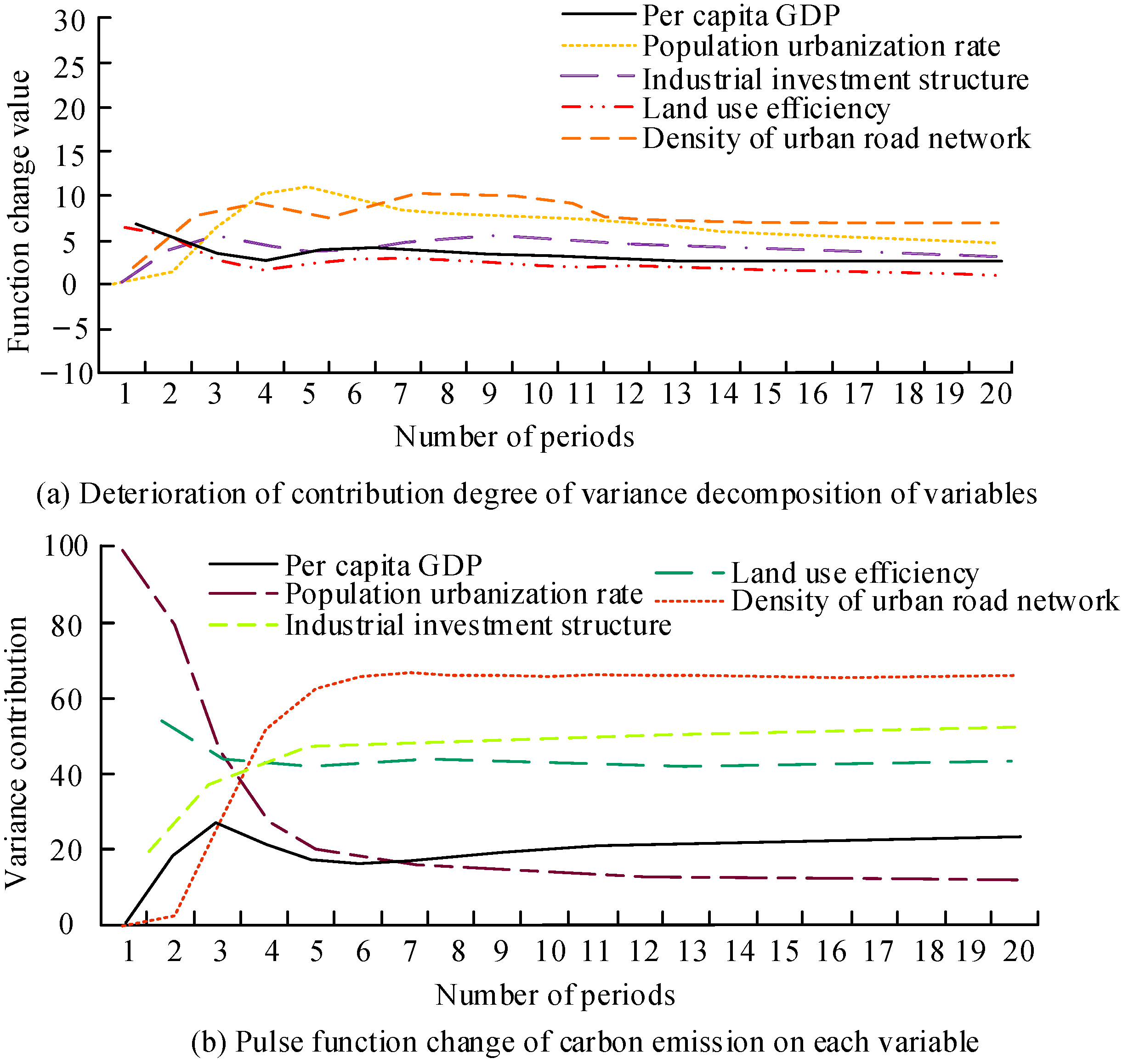
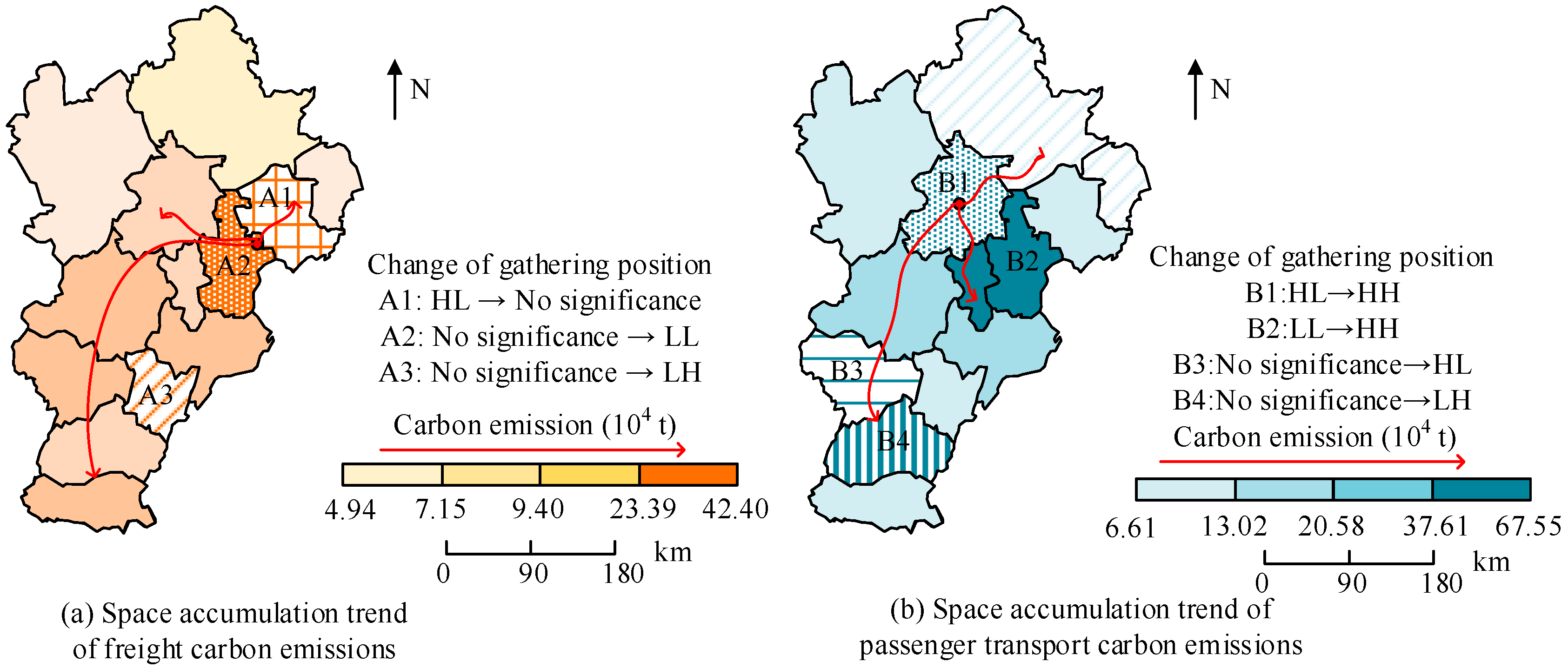
| Variable | Regression Model | Least Squares Model | ||
|---|---|---|---|---|
| Particular Year | Particular Year | |||
| 2008 | 2019 | 2008 | 2019 | |
| R2 | 0.71426 | 0.83613 | 0.5872 | 0.6753 |
| Correction value | 0.61328 | 0.82149 | 0.5741 | 0.6184 |
| AICc | 100.236 | 132.206 | 112.615 | 146.451 |
| Variable | ADF Test Value | Critical Value | Stability of Critical Value | ||
|---|---|---|---|---|---|
| 5% | 10% | 5% | 10% | ||
| Ln-GDP per capita | −5.8678 | −4.1919 | −3.5484 | Stable | Stable |
| Ln-Urbanisation rate | −3.4121 | −3.2975 | −2.6712 | Stable | Stable |
| Ln-Construction of traffic network | −3.6344 | −3.8696 | −3.4366 | Unstable | Stable |
| Ln-Industrial structure | −4.2687 | −4.2361 | −3.214 | Stable | Stable |
| Ln-Energy intensity | −7.8535 | −4.1941 | −3.1383 | Stable | Stable |
| Ln-Carbon emissions | −7.9128 | −4.254 | −3.1509 | Stable | Stable |
| Variable | ADF Test Value | Critical Value | Stability of Critical Value |
|---|---|---|---|
| 5% | 5% | ||
| R | −5.9264 | −4.1032 | Stable |
| Particular Year | Indicator Variable | Minimum | Average | Upper Quartile | Median | Lower Quartile |
|---|---|---|---|---|---|---|
| 2008 | GDP per capita | 5.966984 | 7.234974 | 6.383695 | 7.278717 | 7.965187 |
| Urbanisation rate | 0.343585 | 0.443742 | 0.401038 | 0.444257 | 0.476837 | |
| Construction of traffic network | −1.28616 | −1.06545 | −1.17016 | −1.09939 | −0.96977 | |
| Industrial structure | −2.089422 | −2.090591 | −2.090026 | −2.09048 | −2.0909 | |
| Energy intensity | 1.221207 | 1.222011 | 1.221458 | 1.221816 | 1.2224 | |
| 2012 | GDP per capita | 1.88838 | 1.894461 | 1.892081 | 1.89517 | 1.896353 |
| Urbanisation rate | 0.102161 | 0.54444 | 0.347625 | 0.566481 | 0.686907 | |
| Construction of traffic network | −3.025 | −3.02132 | −3.02274 | −3.02119 | −3.02004 | |
| Industrial structure | 0.773384 | 1.172486 | 1.028765 | 1.20872 | 1367383 | |
| Energy intensity | 1.453051 | 1.454019 | 1.453594 | 1.453968 | 1.454436 | |
| 2016 | GDP per capita | 2.605258 | 3.205114 | 2.743477 | 3.190831 | 3.58422 |
| Urbanisation rate | 0.014337 | 0.023335 | 0.016208 | 0.021658 | 0.030056 | |
| Construction of traffic network | 0.024088 | 0.029315 | 0.026246 | 0.029159 | 0.032167 | |
| Industrial structure | 0.511129 | 0.511835 | 0.511538 | 0.511894 | 0.512102 | |
| Energy intensity | 0.099268 | 0.107396 | 0.107185 | 0.117459 | 0.118547 | |
| 2020 | GDP per capita | 0.01351 | 0.018718 | 0.00488 | 0.017537 | 0.044421 |
| Urbanisation rate | 2.586638 | 3.204158 | 2.895692 | 3.236121 | 3.458852 | |
| Construction of traffic network | 1.076389 | 1.622078 | 1.186979 | 1.675626 | 2.012508 | |
| Industrial structure | 0.026762 | 0.032784 | 0.030445 | 0.032254 | 0.036196 | |
| Energy intensity | 0.0033 | 0.006264 | 0.002196 | 0.004966 | 0.010872 |
| Mode of Transportation | Particular Year | Moran Index | Variance | Z Value | p Value |
|---|---|---|---|---|---|
| Freight transport | 2008 | −0.365737 | 0.008912 | 3.808306 | 0.086382 |
| 2009 | −0.387147 | 0.008898 | 4.034794 | 0.086349 | |
| 2010 | −0.393646 | 0.008894 | 4.103740 | 0.086344 | |
| 2011 | −0.360375 | 0.008897 | 3.754949 | 0.086344 | |
| 2012 | −0.328091 | 0.008881 | 3.415216 | 0.086396 | |
| 2013 | −0.320648 | 0.008886 | 3.342334 | 0.086590 | |
| 2014 | −0.351584 | 0.008869 | 3.665287 | 0.086675 | |
| 2015 | −0.342744 | 0.008827 | 3.576313 | 0.086425 | |
| 2016 | −0.243632 | 0.008804 | 4.644982 | 0.086367 | |
| 2017 | −0.25416 | 0.008800 | 4.761851 | 0.086331 | |
| 2018 | −0.267069 | 0.008800 | 4.898989 | 0.086331 | |
| 2019 | −0.267069 | 0.008800 | 4.898989 | 0.086330 | |
| 2020 | −0.267071 | 0.008805 | 4.898985 | 0.086310 | |
| Passenger transport | 2008 | 0.270997 | 0.006923 | 2.808306 | 0.046347 |
| 2009 | 0.272891 | 0.006907 | 3.034794 | 0.046355 | |
| 2010 | 0.277996 | 0.006905 | 3.103737 | 0.046368 | |
| 2011 | 0.266091 | 0.006950 | 2.754949 | 0.046346 | |
| 2012 | 0.263701 | 0.006920 | 2.415216 | 0.046480 | |
| 2013 | 0.306428 | 0.006875 | 2.342334 | 0.046540 | |
| 2014 | 0.327364 | 0.006930 | 2.665287 | 0.046367 | |
| 2015 | 0.328524 | 0.006887 | 2.576313 | 0.046376 | |
| 2016 | 0.349042 | 0.006853 | 3.644982 | 0.046341 | |
| 2017 | 0.339905 | 0.006835 | 3.266723 | 0.046356 | |
| 2018 | 0.349998 | 0.006789 | 2.898337 | 0.046331 | |
| 2019 | 0.362062 | 0.006787 | 3.020208 | 0.046330 | |
| 2020 | 0.371654 | 0.006891 | 3.012609 | 0.046325 |
| Test Number | Actual Value | Analogue Value | Error (%) |
|---|---|---|---|
| 1 | 20,943.256 | 20,939.889 | 0.582 |
| 2 | 21,522.169 | 21,521.802 | 0.236 |
| 3 | 23,281.647 | 23,279.281 | 0.227 |
| 4 | 25,403.166 | 25,416.799 | 0.136 |
| 5 | 25,432.648 | 25,398.281 | 0.248 |
| 6 | 26,073.214 | 26,066.847 | 0.273 |
| 7 | 26,613.897 | 2641.531 | 0.384 |
| Particular Year | Baseline Scenario | High-Carbon Scenario | Low-Carbon Scenario |
|---|---|---|---|
| 2017 | 29,181.94 | 28,337.26 | 28,765.90 |
| 2018 | 30,632.25 | 28,701.26 | 29,020.62 |
| 2019 | 31,169.14 | 29,055.36 | 29,437.65 |
| 2020 | 32,133.91 | 29,399.46 | 29,777.43 |
| 2021 | 33,127.63 | 29,733.54 | 30,111.93 |
| 2022 | 33,809.98 | 30,057.58 | 30,490.52 |
| 2023 | 34,331.97 | 30,371.60 | 30,680.21 |
| 2024 | 34,685.18 | 30,675.64 | 30,777.23 |
| 2025 | 35,041.93 | 30,969.77 | 30,875.73 |
| 2026 | 35,222.08 | 31,254.07 | 30,975.74 |
| 2027 | 35,311.61 | 31,528.66 | 31,077.29 |
| 2028 | 35,346.94 | 31,793.67 | 31,180.42 |
| 2029 | 35,377.49 | 32,049.24 | 31,285.15 |
| 2030 | 35,403.91 | 32,295.52 | 31,391.52 |
| 2031 | 35,426.73 | 32,532.70 | 31,499.57 |
| 2032 | 35,690.01 | 32,760.96 | 31,325.38 |
| 2033 | 35,139.81 | 32,980.49 | 31,061.21 |
| 2034 | 34,590.86 | 33,191.50 | 30,900.50 |
| 2035 | 33,793.65 | 33,394.20 | 30,875.79 |
| 2036 | 33,663.71 | 33,588.80 | 30,851.24 |
| 2037 | 32,534.95 | 33,775.54 | 30,826.87 |
| 2038 | 32,407.34 | 33,954.61 | 30,778.60 |
| 2039 | 32,280.88 | 34,126.28 | 30,754.71 |
| 2040 | 32,031.34 | 34,290.75 | 30,730.99 |
| 2041 | 31,908.23 | 34,448.25 | 30,707.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, P.; Liu, J.; Liu, B.; Zhu, C. Impact of Urbanisation on the Spatial and Temporal Evolution of Carbon Emissions and the Potential for Emission Reduction in a Dual-Carbon Reduction Context. Sustainability 2023, 15, 4715. https://doi.org/10.3390/su15064715
Xue P, Liu J, Liu B, Zhu C. Impact of Urbanisation on the Spatial and Temporal Evolution of Carbon Emissions and the Potential for Emission Reduction in a Dual-Carbon Reduction Context. Sustainability. 2023; 15(6):4715. https://doi.org/10.3390/su15064715
Chicago/Turabian StyleXue, Pengcheng, Jiaxin Liu, Binbin Liu, and Chuang Zhu. 2023. "Impact of Urbanisation on the Spatial and Temporal Evolution of Carbon Emissions and the Potential for Emission Reduction in a Dual-Carbon Reduction Context" Sustainability 15, no. 6: 4715. https://doi.org/10.3390/su15064715
APA StyleXue, P., Liu, J., Liu, B., & Zhu, C. (2023). Impact of Urbanisation on the Spatial and Temporal Evolution of Carbon Emissions and the Potential for Emission Reduction in a Dual-Carbon Reduction Context. Sustainability, 15(6), 4715. https://doi.org/10.3390/su15064715







