An Analytical and Numerical Analysis for Hydraulic Fracture Propagation through Reservoir Interface in Coal-Measure Superimposed Reservoirs
Abstract
1. Introduction
2. Development of New Stress Intensity Factor at the Tip of a I/II Mixed Crack and Stress-Seepage-Damage Numerical Model
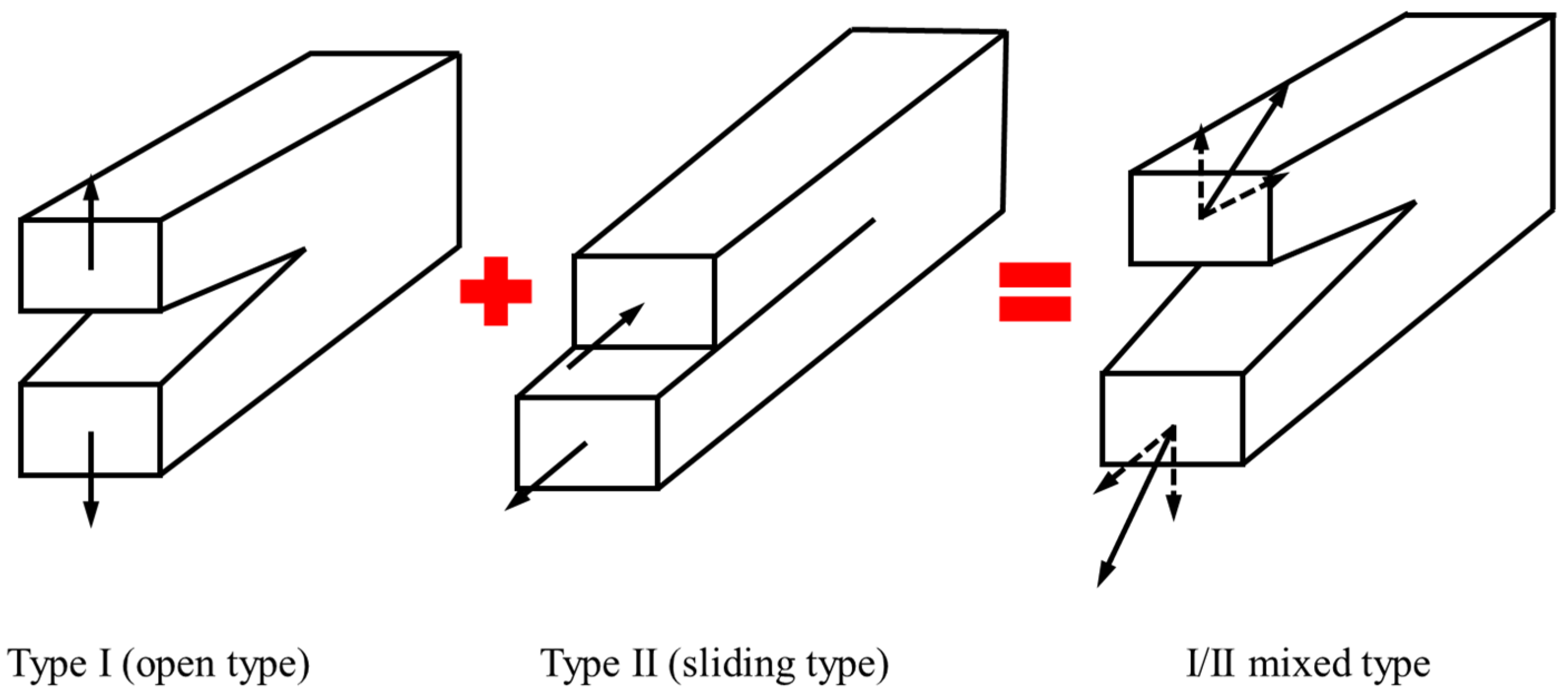
2.1. A New Stress Intensity Factor at the Tip of a I/II Mixed Crack
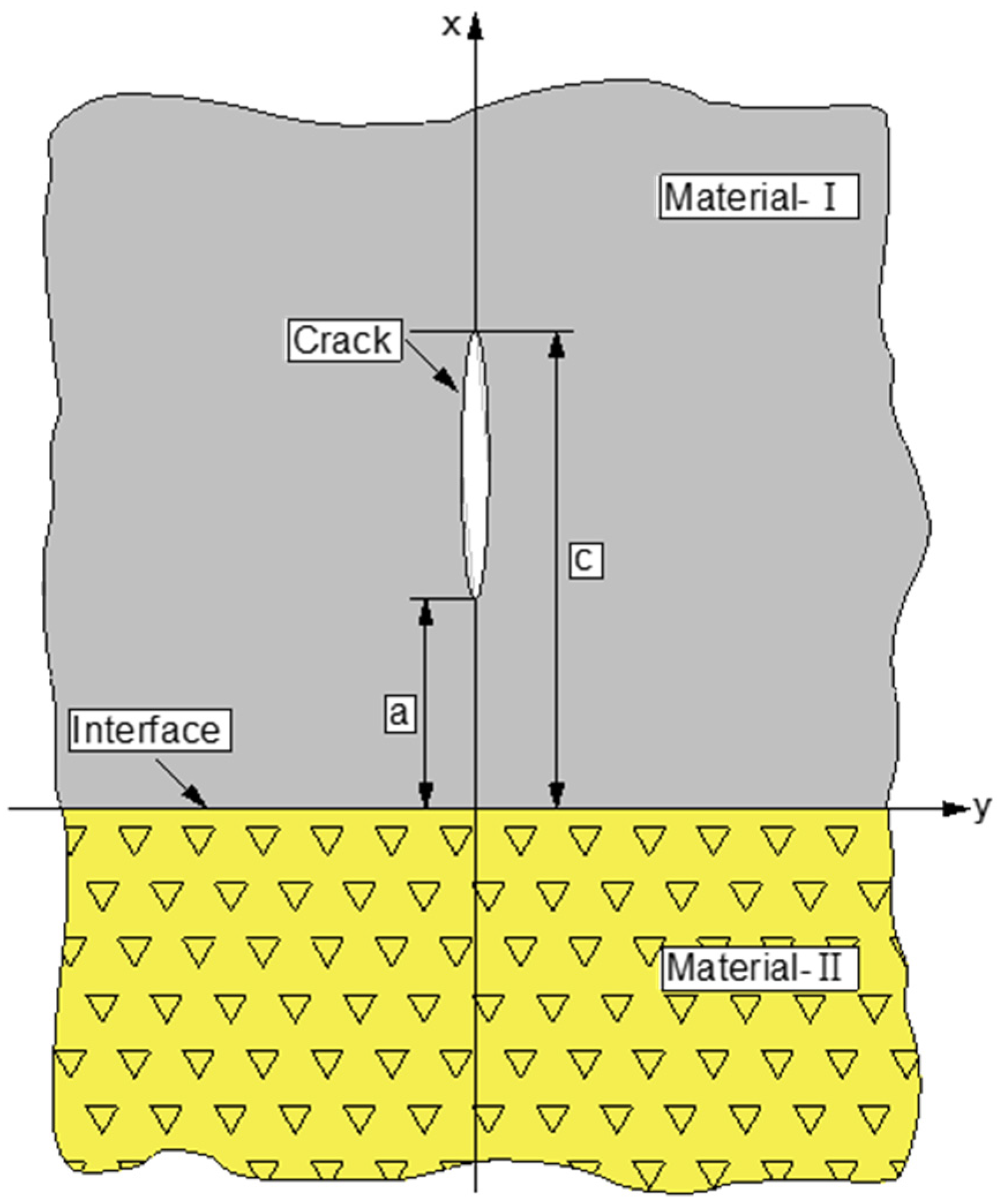
2.1.1. A stress Analytical Model at the Tipoff I/II Mixed Crack
2.1.2. Analytical Solutions of Stress Intensity Factor
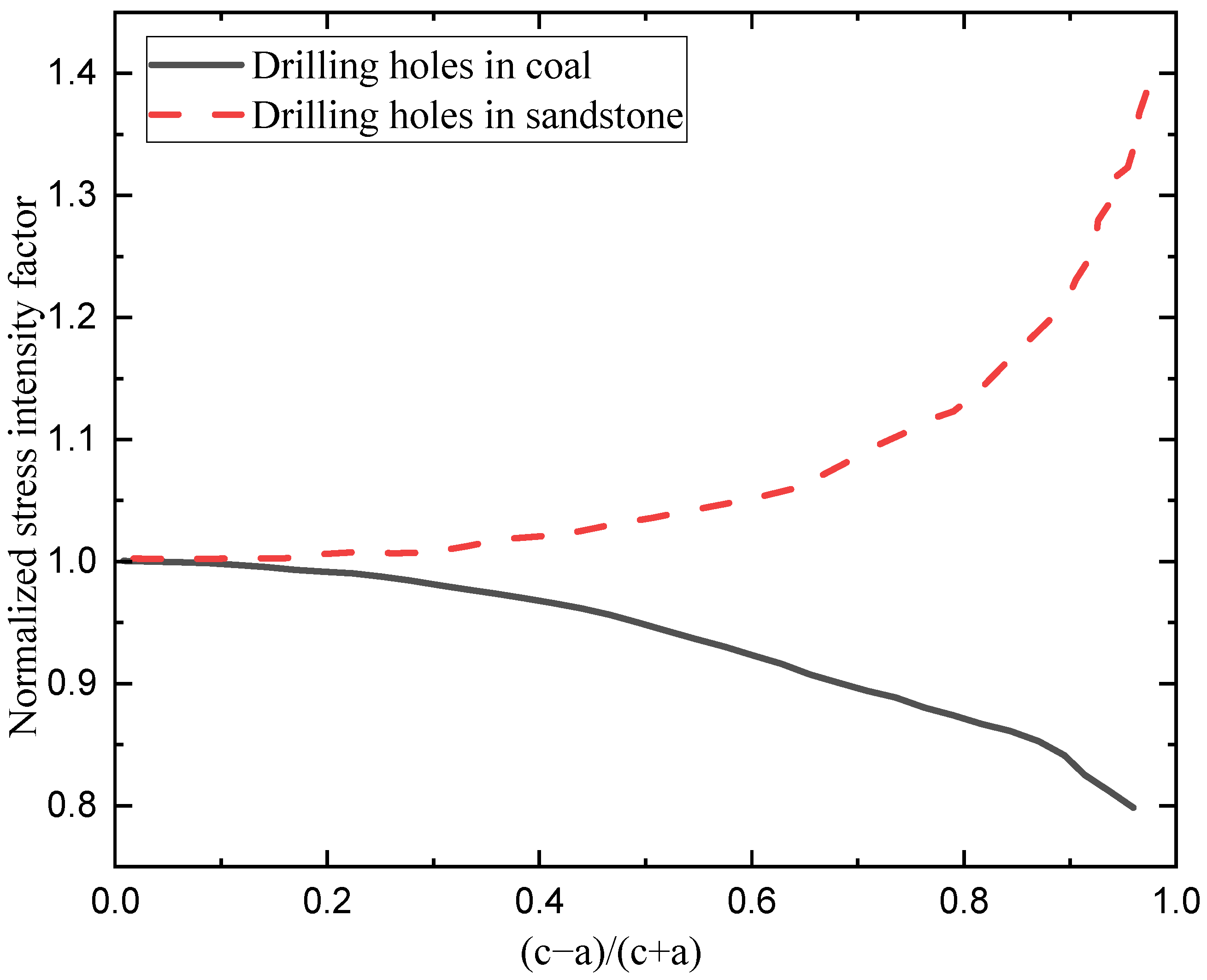
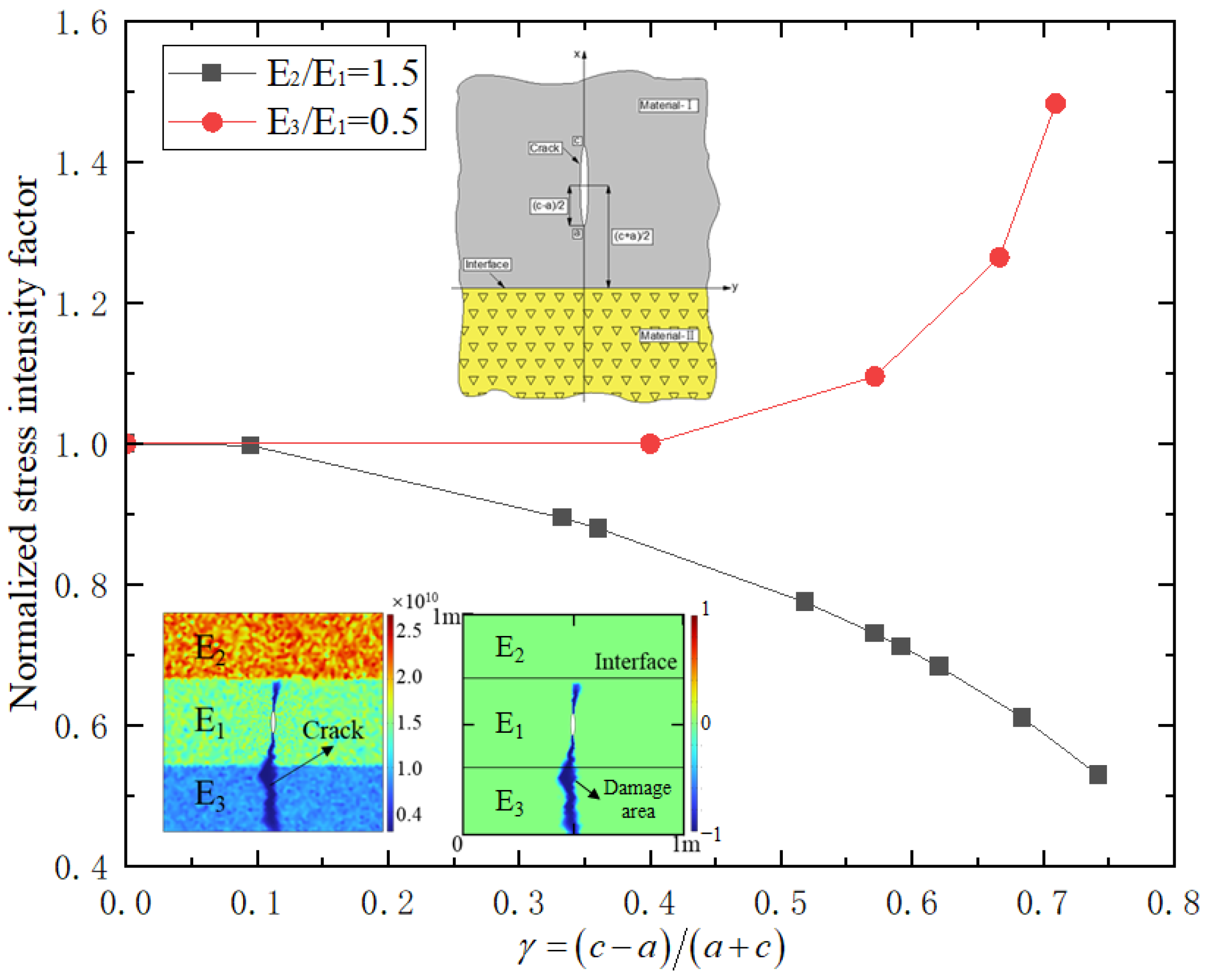
2.1.3. Analysis of Stress Intensity Factor of I/II Mixed Cracks at the Interface
2.2. Deevelopment of Seepage-Mechanical-Damage Numerical Model for Hydraulic Fracturing in a Coal–sandstone Superimposed Reservoir
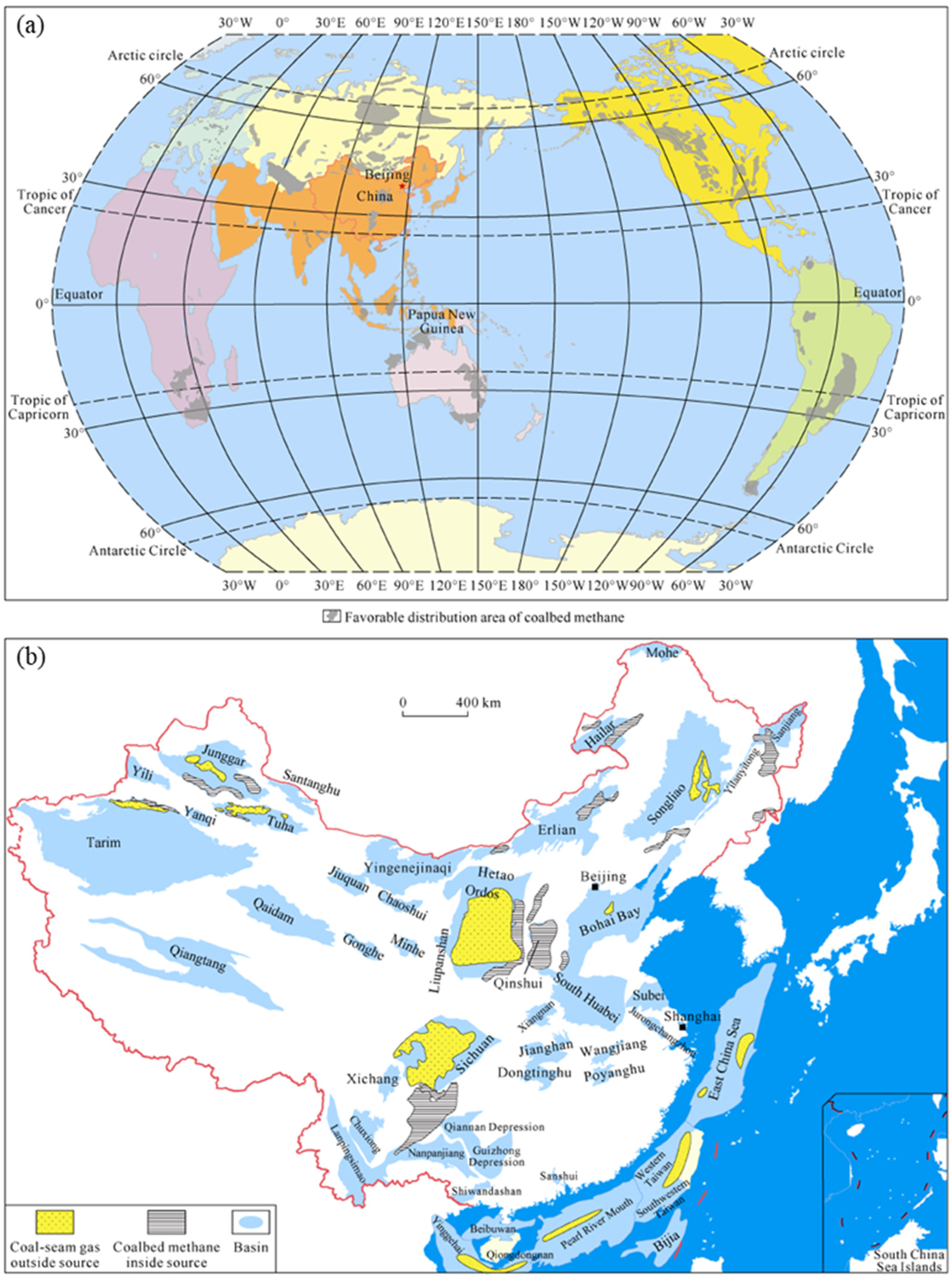
2.2.1. Geological Setting of Research Area
2.2.2. Numerical Model Establishment and Basic Assumptions
2.2.3. Governing Equations of Each Physical Process
2.2.4. Damage Constitutive Model
2.2.5. Effect of Rock Damage on Elastic Modulus and Permeability
2.2.6. Implementation of Seepage-Mechanical-Damage Numerical Model and Parameters
3. Verification of Numerical Simulation Model
3.1. Hydraulic Fracturing of Coal-Measure Shale in the Linxing Area
3.2. Hydraulic Fracturing of Sandstone in Southern Sichuan Basin
3.3. Simulation of Coal Pulse Hydraulic Fracturing
4. Numerical Simulation Results
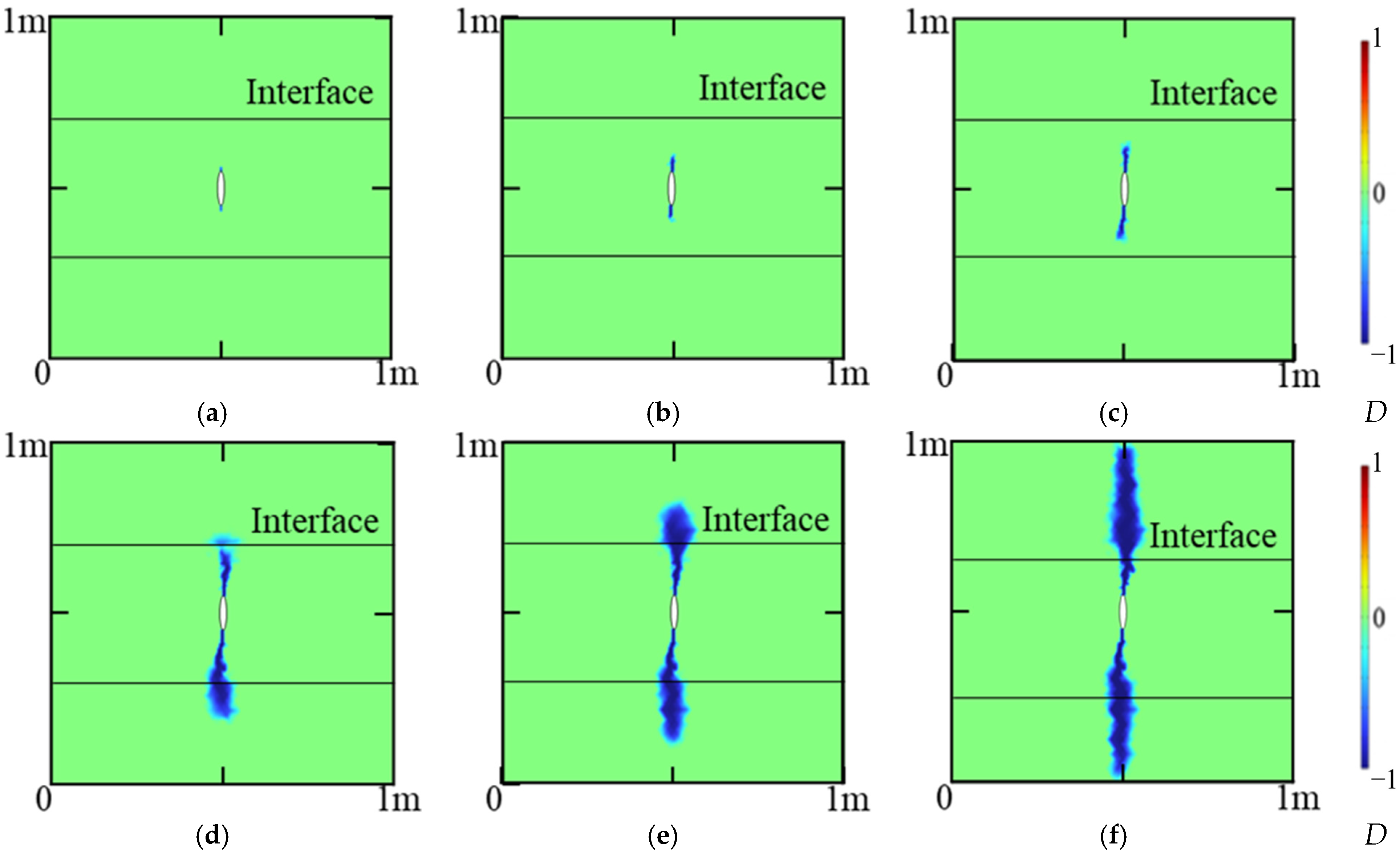
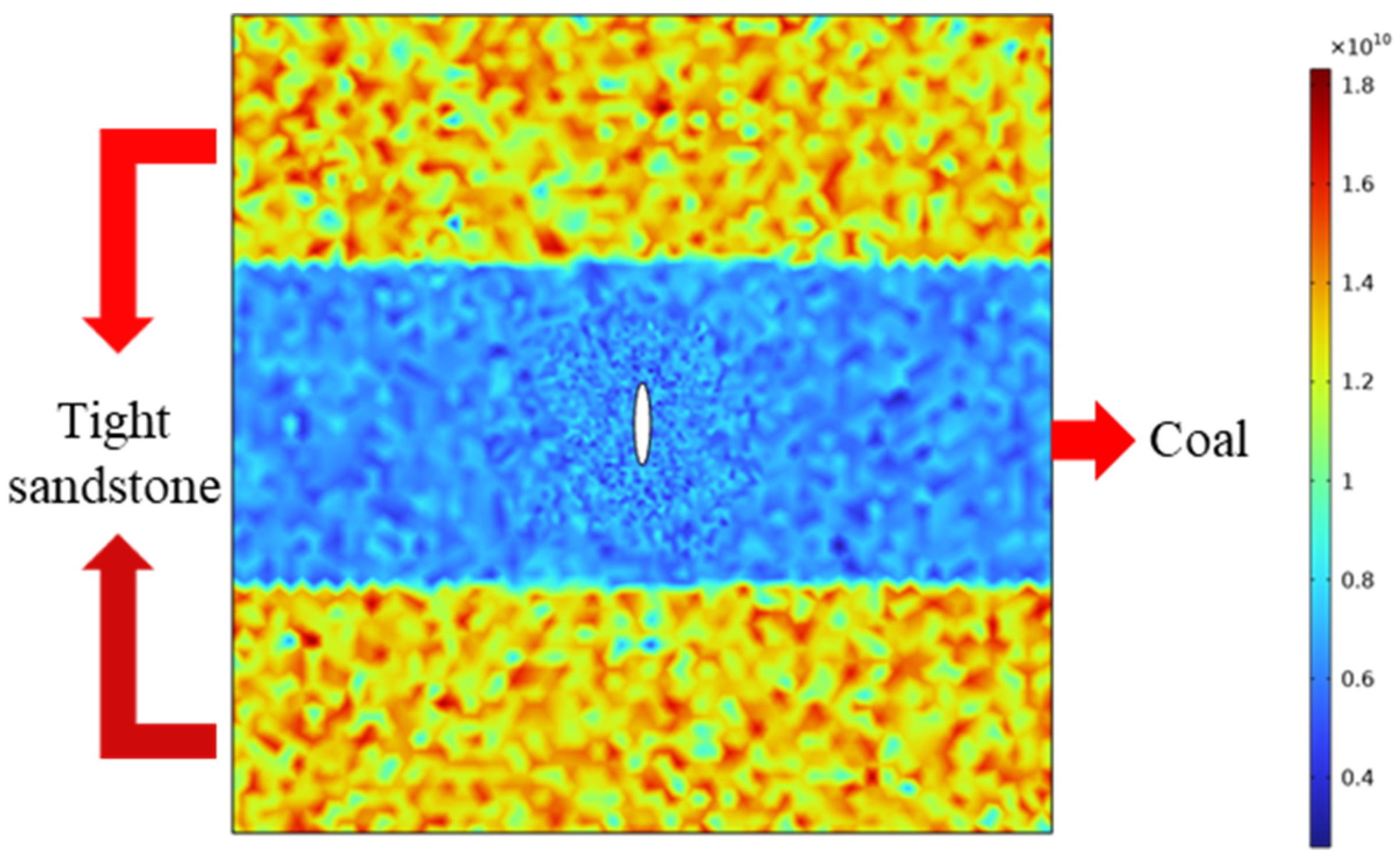
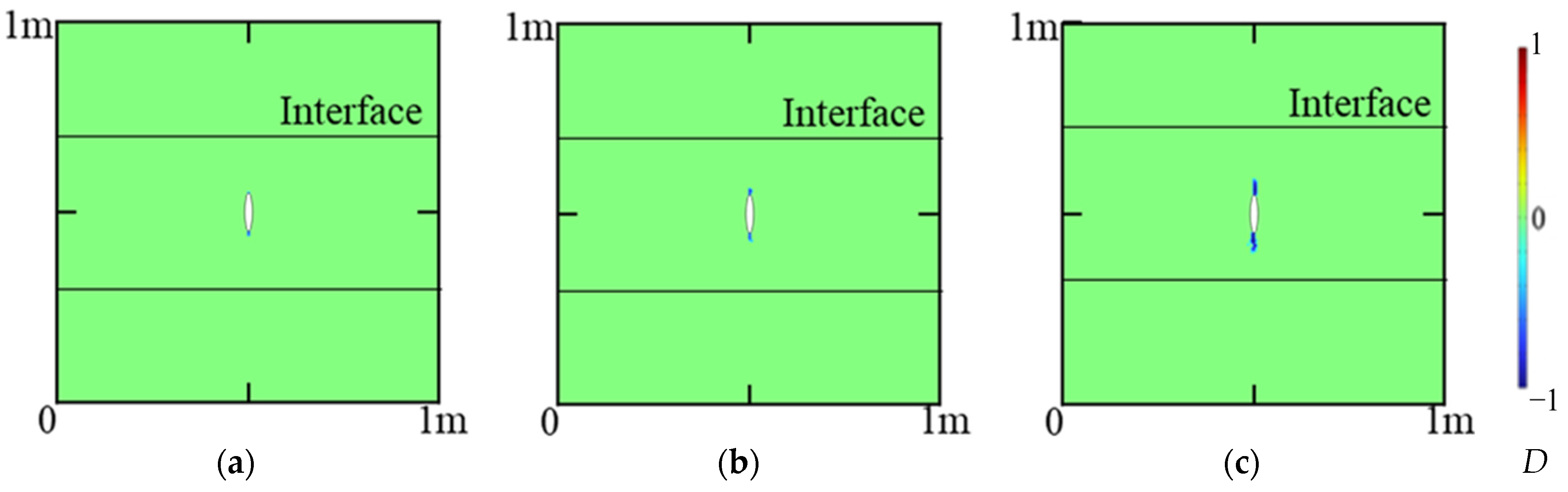
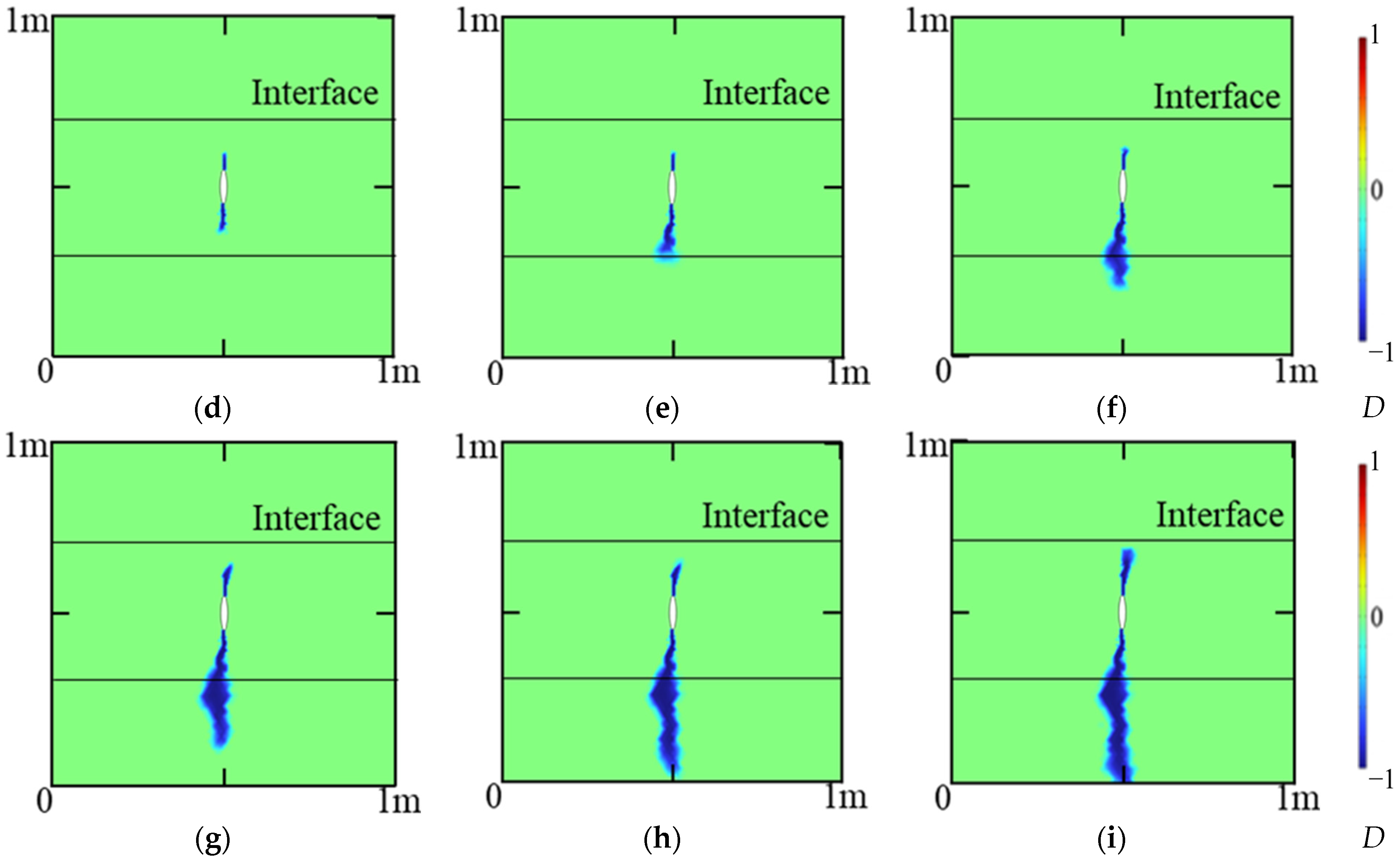
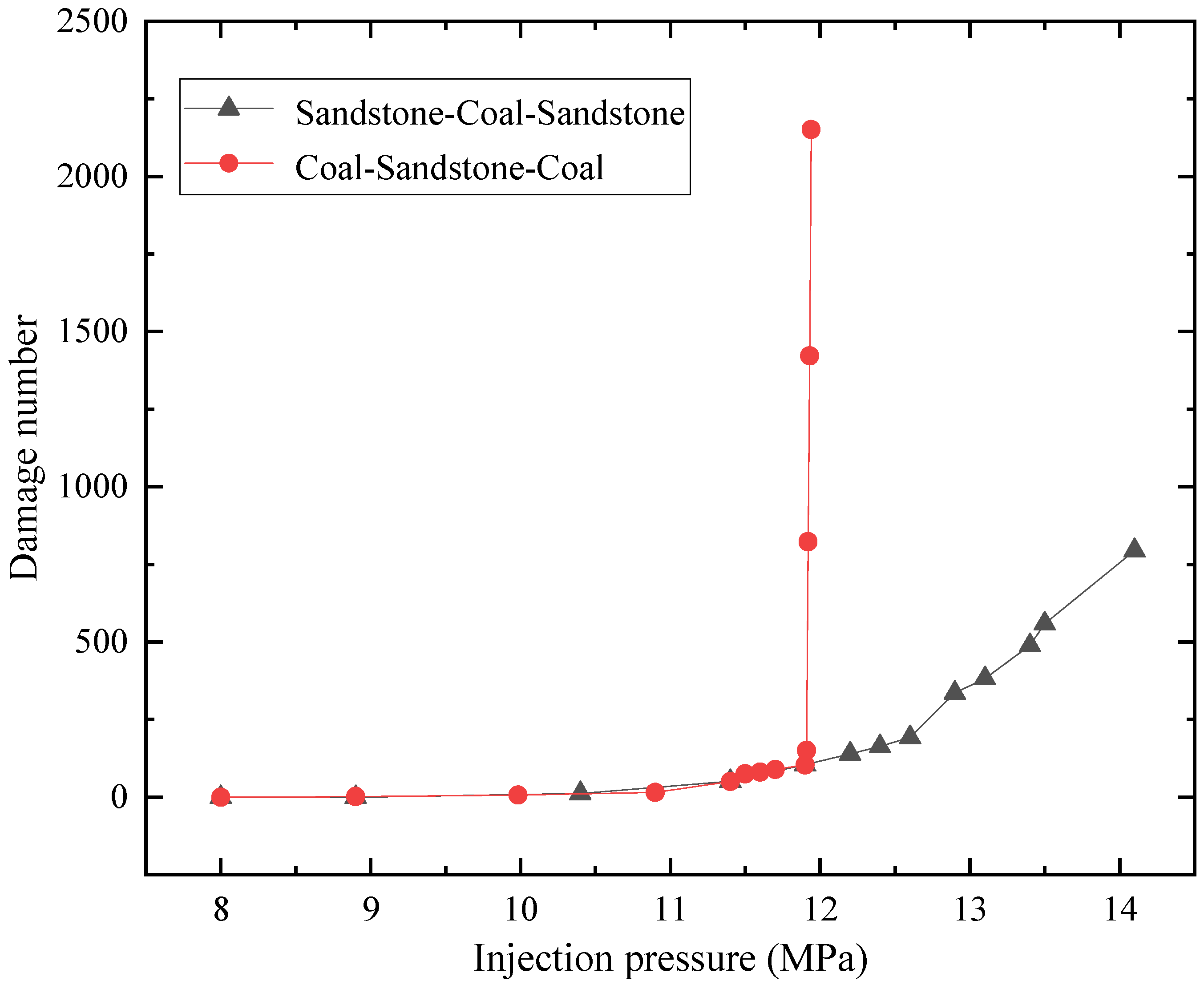
4.1. Fracture Propagation in a Coal-Sandstone–Coal Reservoir
4.2. Fracture Propagation in a Sandstone–Coal–Sandstone Reservoir
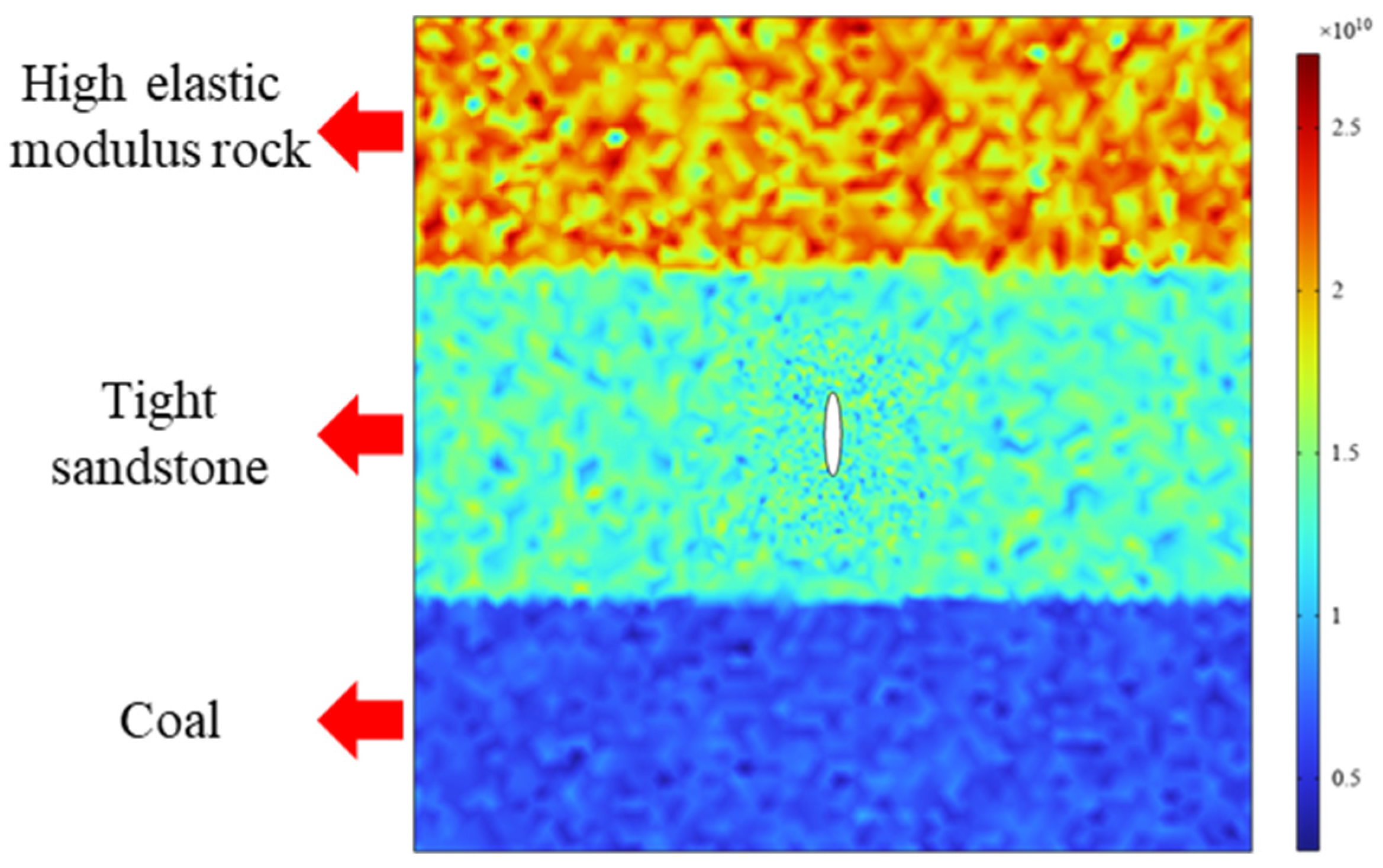
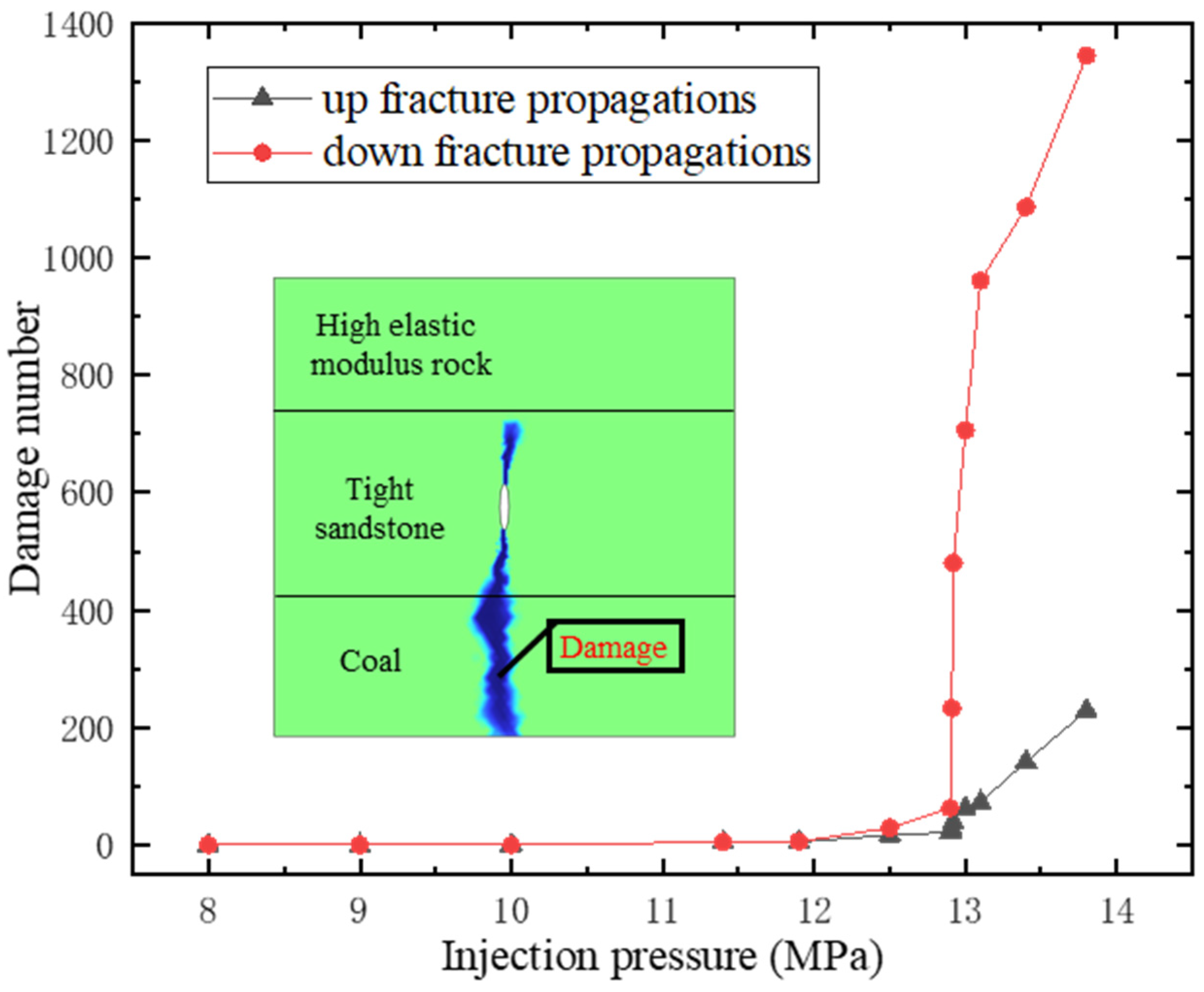
4.3. Fracture Propagation in High Elastic Modulus Rock-Sandstone–coal Reservoirs
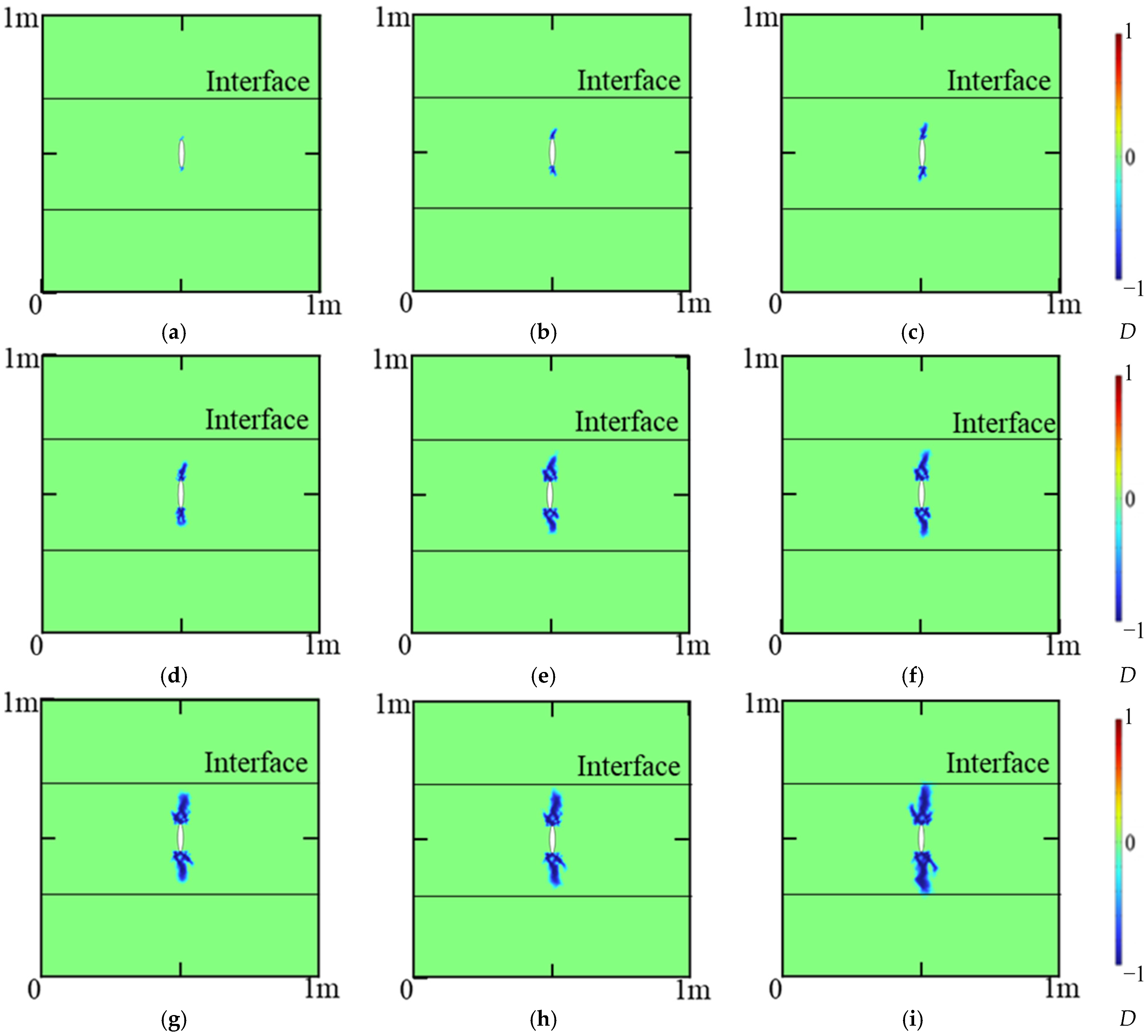
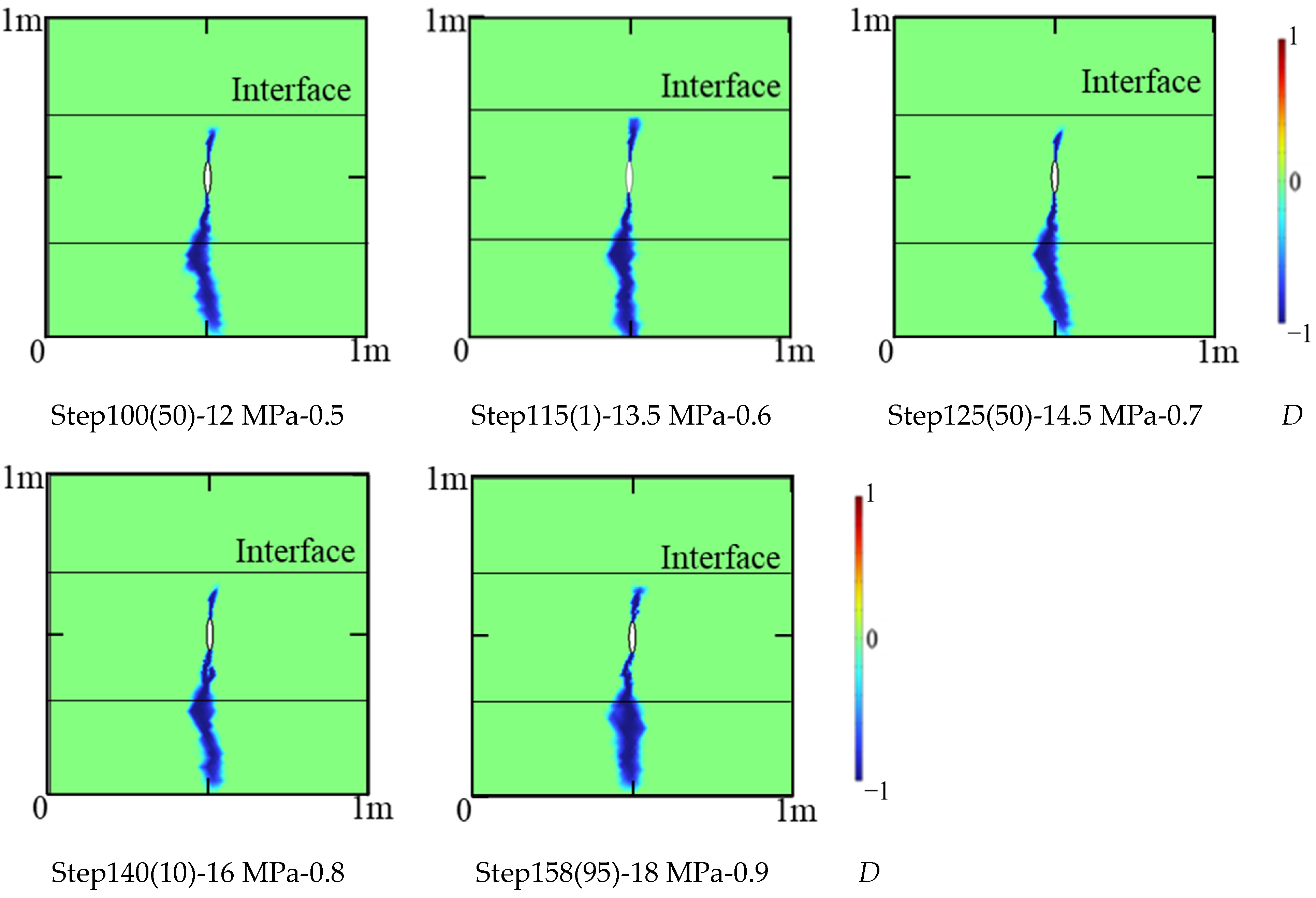
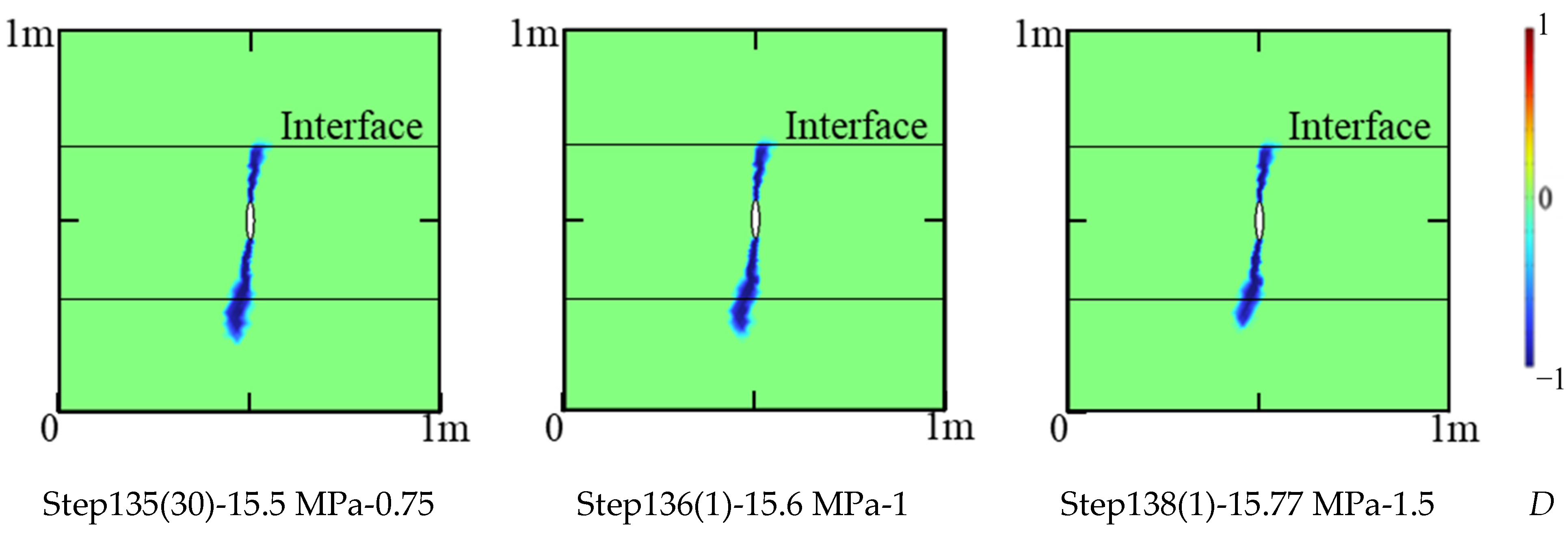
4.4. Fracture Propagation in Different Stress States
4.5. Fracture Propagation in Different Fracturing Fluid Viscosity
5. Discussion
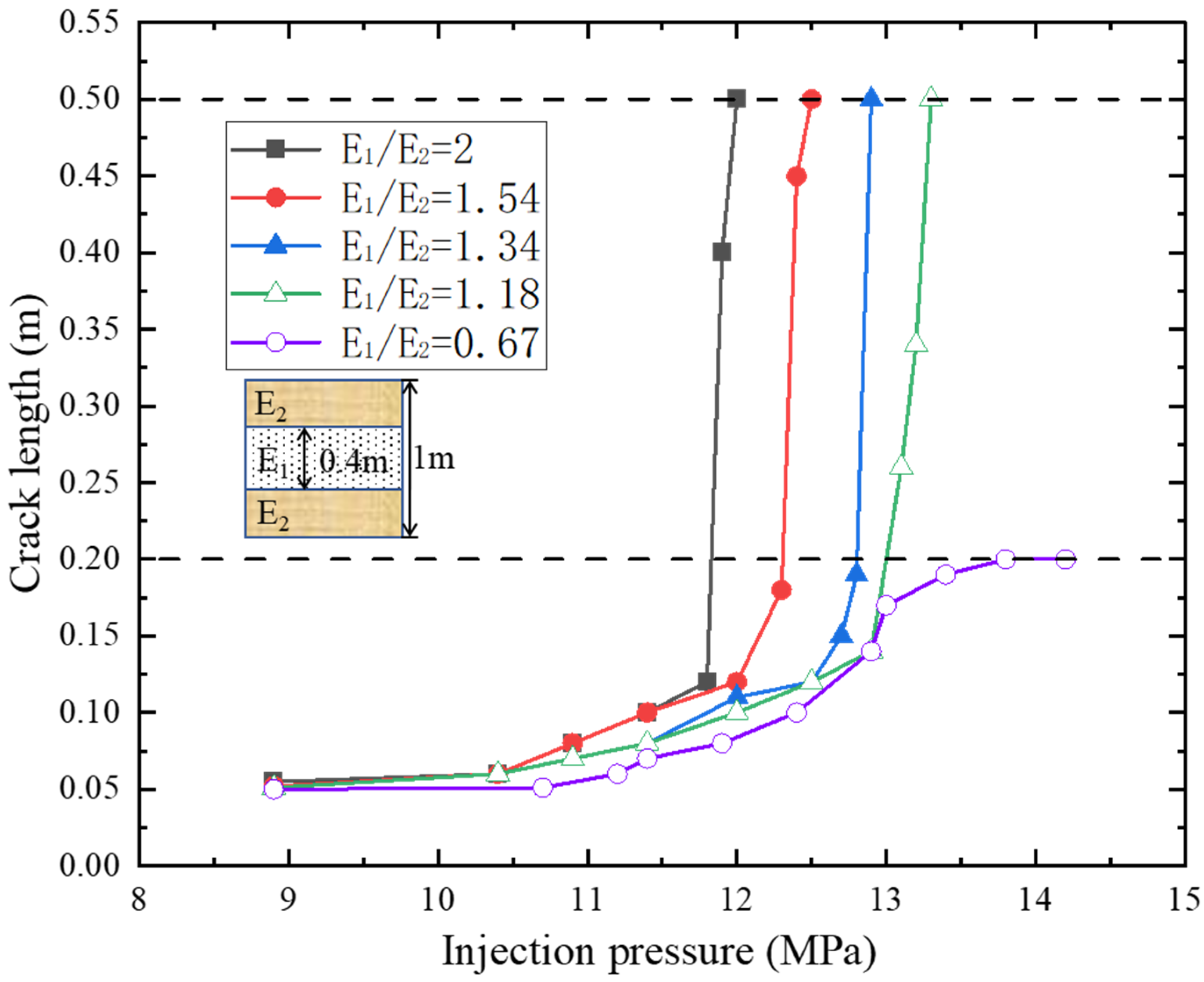
5.1. Influence of Elastic Modulus Difference between Adjacent Reservoirs on Fracture Propagation
5.2. Influence of Elastic Modulus Difference of Adjacent Reservoirs on Stress Intensity Factor
5.3. Influence of Elastic Modulus Difference of Adjacent Reservoirs on Damage
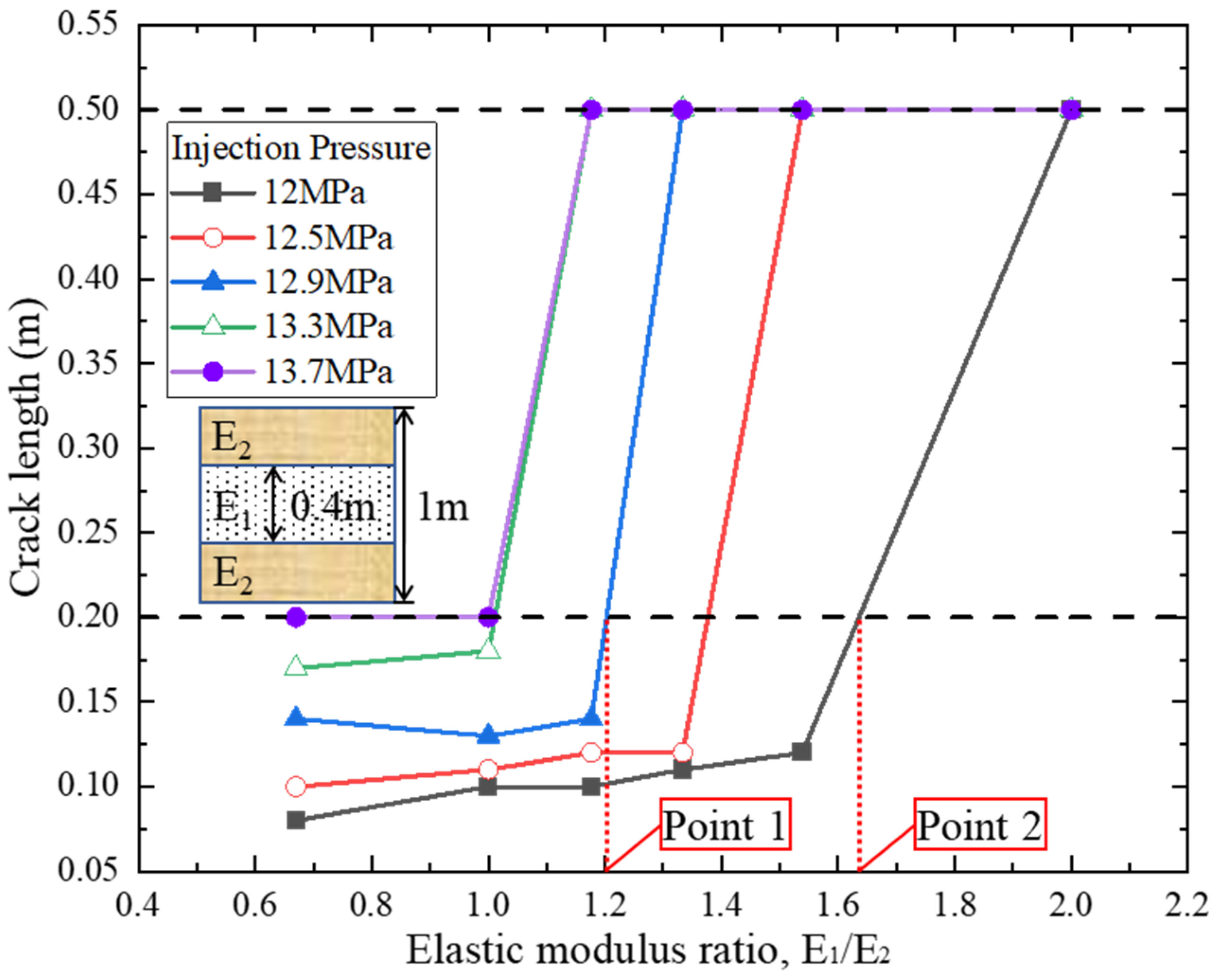
5.4. Effect of Elastic Modulus Difference of Adjacent Reservoirs on Fracture Length
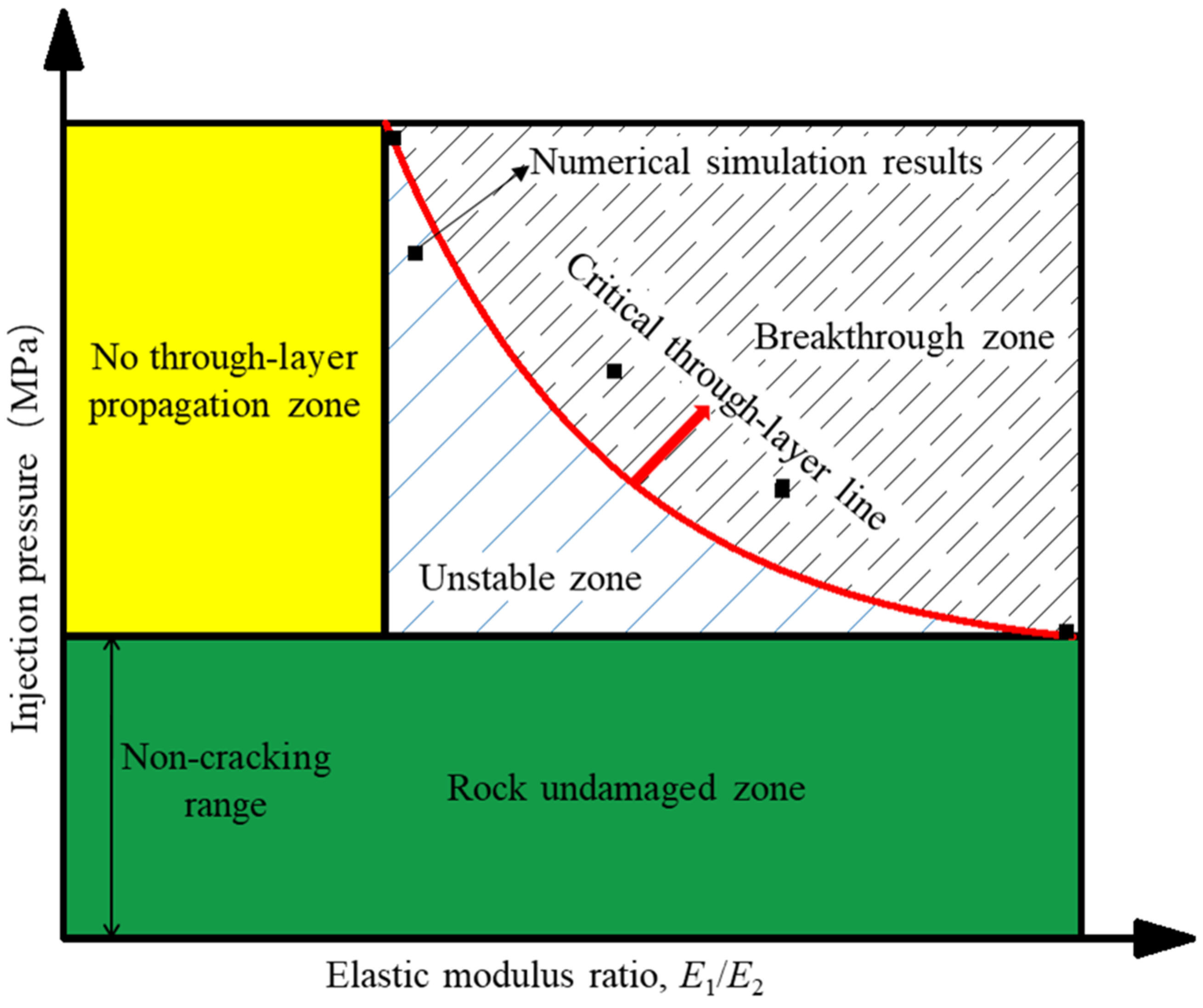
5.5. Conceptual Zoning for Hydraulic Fracture Propagation through Reservoir Interface
5.6. Influence of Stress State and Fracturing Fluid Viscosity on Fracture Propagation through Layers
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Xie, H.; Leung, C.; Wang, J.; Li, X. Advancing deep underground research through integration of engineering and science. Deep. Undergr. Sci. Eng. 2022, 1, 1–2. [Google Scholar] [CrossRef]
- Hu, L.; Wang, J.; Ali Karrech Li, X.; Zhao, P.; Liu, L. Exploring the frontiers of deep underground sciences and engineering—China Yunlong Lake Laboratory is striving to be the best. Deep. Undergr. Sci. Eng. 2022, 1, 130–136. [Google Scholar] [CrossRef]
- Li, Z.; Wang, S.; Li, L.; Zhang, J. Numerical investigation on interference of multiple hydraulic fractures in layered formation. Front. Earth Sci. 2022, 10, 865155. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, H.; Zhou, Z.; Ge, Z.; Chen, C.; Hou, Y.; Ye, M. Current status and effective suggestions for efficient exploitation of coalbed methane in China: A review. Energy Fuels 2021, 35, 9102–9123. [Google Scholar] [CrossRef]
- Ali, R.; Fahd, S.; Birol, D.; Mohamed, Y. A review on factors influencing the rock mechanics of the gas bearing formations. J. Nat. Gas Sci. Eng. 2020, 80, 103348. [Google Scholar]
- Zou, C.; Yang, Z.; Huang, S.; Ma, F.; Sun, Q.; Li, F.; Pan, S.; Tian, W. Resource types, formation, distribution and prospects of coal-measure gas. Pet. Explor. Dev. 2019, 46, 451–462. [Google Scholar] [CrossRef]
- Pouria, B.; Mohammad, B.; Alireza, G.; Sohrab, Z. A new technique to conduct hydraulic fracture design in coal bed methane reservoirs by incorporating stress variations. J. Pet. Sci. Eng. 2019, 174, 1208–1222. [Google Scholar]
- Vanessa, S.; Ayrton, R.; Raymond, J.; Suzanne, H.; Zhen, J. Modeling and economic analyses of graded particle injections in conjunction with hydraulic fracturing of coal seam gas reservoirs. SPE J. 2022, 27, 1633–1647. [Google Scholar]
- Wang, H.; Wu, Z.; Wang, Y.; Yu, R. Investigation on crack propagation perpendicular to mortar–rock interface: Experimental and numerical. Int. J. Fract. 2020, 226, 45–69. [Google Scholar] [CrossRef]
- Zhou, B.; Zhou, C.; Yu, X.; Chang, L.; Li, J.; Miao, X.; Ye, C.; Zhang, B. Investigation on the fatigue crack behavior of Zr702/TA2/Q345R mixed plate with a crack normal to interface. Fatigue Fract. Eng. Mater. Struct. 2019, 43, 20–35. [Google Scholar] [CrossRef]
- Zhou, B.; Zhou, L.; Chang, L.; Zhou, C.; Ye, C.; Zhang, B. Investigation on fatigue crack propagation law of the crack perpendicular to interface for Zr/Ti/steel mixed plate. Int. J. Press. Vessel. Pip. 2022, 195, 104594. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. The stress intensity factor and propagation of an inclined crack in the central layer of a mixed laminate under tension. Theor. Appl. Fract. Mech. 2018, 93, 128–136. [Google Scholar] [CrossRef]
- Zhong, X.; Li, X.; Lee, K. Analysis of a mode-I crack perpendicular to an imperfect interface. Int. J. Solids Struct. 2009, 46, 1456–1463. [Google Scholar] [CrossRef]
- Zhong, X.; Zhang, K. Fracture analysis of mode-II crack perpendicular to imperfect bimaterial interface. Appl. Math. Mech. 2012, 33, 357–370. [Google Scholar] [CrossRef]
- Wu, J.; Yang, X.; Song, Y.; Sun, Q.; Pei, Y. Study on a new inversion method for non-uniform distribution of rock material parameters. Bull. Eng. Geol. Environ. 2022, 81, 280. [Google Scholar] [CrossRef]
- Xia, B.; Li, Y.; Hu, H.; Luo, Y.; Peng, J. Effect of crack angle on mechanical behaviors and damage evolution characteristics of sandstone under uniaxial compression. Rock Mech. Rock Eng. 2022, 55, 6567–6582. [Google Scholar] [CrossRef]
- Xi, X.; Zoe, K.S.; Jackie, E.K.; Andrew, F.; Julien, M.; Katriona, E.; Christopher, I.M.; Yang, S. Mixed-mode fracture modelling of the near-wellbore interaction between hydraulic fracture and natural fracture. Rock Mech. Rock Eng. 2022, 55, 5433–5452. [Google Scholar] [CrossRef]
- Ju, M.; Li, X.; Li, X.; Zhang, G. A review of the effects of weak interfaces on crack propagation in rock: From phenomenon to mechanism. Eng. Fract. Mech. 2022, 263, 108297. [Google Scholar] [CrossRef]
- Mahmoud, K.; Alissar, Y.; Elsa, M. Propagation and geometry of multi-stage hydraulic fractures in anisotropic shales. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 124. [Google Scholar]
- Ren, Q.; Zhao, Y.; Zhu, X.; Zhou, Y.; Jiang, Y.; Wang, P.; Zhang, C. CDEM-based simulation of the 3D propagation of hydraulic fractures in heterogeneous Coalbed Methane reservoirs. Comput. Geotech. 2022, 152, 104992. [Google Scholar] [CrossRef]
- Tian, F.; Jin, Y.; Jin, F.; Ma, X.; Shi, L.; Zhang, J.; Qiu, D.; Zhang, Z. Multi-fracture synchronous propagation mechanism of multi-clustered fracturing in interlayered tight sandstone reservoir. Sustainability 2022, 14, 8768. [Google Scholar] [CrossRef]
- Dou, F.; Wang, J.G. A numerical investigation for the impacts of shale matrix heterogeneity on hydraulic fracturing with a two-dimensional particle assemblage simulation model. J. Nat. Gas Sci. Eng. 2022, 104, 104678. [Google Scholar] [CrossRef]
- Dou, F.; Wang, J.G.; Wang, H.; Hu, B.; Li, C. Discrete element analysis for hydraulic fracture propagations in laminated reservoirs with complex initial joint properties. Geofluids 2019, 2019, 3958583. [Google Scholar] [CrossRef]
- Luis, A.; Vargas, E.D.A., Jr.; Raquel, Q.; Glaucio, H. Simulation of hydraulic fracturing processes in rocks by coupling the lattice Boltzmann model and the Park-Paulino-Roesler potential-based cohesive zone mode. Int. J. Rock Mech. Min. Sci. 2018, 112, 339–353. [Google Scholar]
- Zhao, H.; Wang, X.; Liu, Z.; Yan, Y.; Yang, H. Investigation on the hydraulic fracture propagation of multilayers-commingled fracturing in coal measures. J. Pet. Sci. Eng. 2018, 167, 774–784. [Google Scholar] [CrossRef]
- Afşar, F.; Luijendijk, E. Quantifying a critical marl thickness for vertical fracture extension using field data and numerical experiments. Geosci. Front. 2019, 10, 2135–2145. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, J.; Hu, Y.; Zhang, S.; Huang, T.; Liu, X. Numerical simulation of multistage fracturing optimization and application in coalbed methane horizontal wells. Eng. Fract. Mech. 2020, 223, 106738. [Google Scholar] [CrossRef]
- Wang, K.; Tang, S.; Zhang, S.; Guo, Y.; Lin, D.; Niu, Z. Numerical simulation of fracture propagation characteristics of hydraulic fracturing in multiple coal seams, eastern Yunnan, China. Front. Earth Sci. 2022, 10, 854638. [Google Scholar] [CrossRef]
- Hadei, M.R.; Veiskarami, A. An experimental investigation of hydraulic fracturing of stratified rocks. Bull. Eng. Geol. Environ. 2020, 80, 491–506. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.G.; Gao, F.; Ju, Y.; Liu, J. Impact of water and nitrogen fracturing fluids on fracturing initiation pressure and flow pattern in anisotropic shale reservoirs. Comput. Geotech. 2017, 81, 59–76. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.G.; Gao, F.; Ju, Y. Impact of water, nitrogen and CO2 fracturing fluids on fracturing initiation pressure and flow pattern in anisotropic shale reservoirs. J. Nat. Gas Sci. Eng. 2017, 45, 291–306. [Google Scholar] [CrossRef]
- Cruz-González, O.L.; Rodríguez-Ramos, R.; Lebon, F.; Sabina, F.J. Modeling of imperfect viscoelastic interfaces in mixed materials. Coatings 2022, 12, 705. [Google Scholar] [CrossRef]
- Raffa, M.L.; Lebon, F.; Rizzoni, R. A micromechanical model of a hard interface with micro-cracking damage. Int. J. Mech. Sci. 2022, 216, 106974. [Google Scholar] [CrossRef]
- Hashemi, R. On the overall viscoelastic behavior of graphene/polymer nanomixeds with imperfect interface. Int. J. Mech. Sci. 2016, 105, 38–55. [Google Scholar]
- Chen, W.; Zhou, Y.; Lü, C.; Ding, H. Bending of multiferroic laminated rectangular plates with imperfect interlaminar bonding. Eur. J. Mech. A/Solids 2009, 28, 720–727. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Hou, B.; Zheng, X.; Guo, X.; Gao, J. Experiments and analysis on hydraulic sand fracturing by an improved true tri-axial cell. J. Pet. Sci. Eng. 2017, 158, 766–774. [Google Scholar] [CrossRef]
- Shen, J.; Li, K.; Zhang, H.; Shabbiri, K.; Hu, Q.; Zhang, C. The geochemical characteristics, origin, migration and accumulation modes of deep coal-measure gas in the west of Linxing block at the eastern margin of Ordos Basin. J. Nat. Gas Sci. Eng. 2021, 91, 103965. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, C.; Qin, Y.; Zhang, B. Effect factors on co-mining of sandstone gas and coalbed methane in coal series and threshold of parameter in Linxing block, Ordos Basin. Nat. Gas Geosci. 2017, 28, 479–487. [Google Scholar]
- Li, Y.; Yang, J.; Pan, Z.; Meng, S.; Wang, K.; Niu, X. Unconventional natural gas accumulations in stacked deposits: A discussion of upper paleozoic coal-bearing strata in the east margin of the Ordos Basin, China. Acta Geol. Sin. Engl. Ed. 2019, 93, 111–129. [Google Scholar] [CrossRef]
- Li, Y.; Cao, D.; Meng, S.; Niu, X.; Wu, P.; Xu, H.; Liu, J. Permeability and elastic parameters under different pressures of tight gas sandstones in eastern Ordos basin, China. J. Nat. Gas Sci. Eng. 2016, 35, 362–371. [Google Scholar] [CrossRef]
- Cheng, J.; Li, R.; Qin, X.; Li, D.; Zhao, B.; Li, J.; Wu, X.; Wang, N. Impact of diagenetic facies on mechanical properties of sandstone rock in low-permeability reservoirs: A case study of the Upper Paleozoic gas reservoir in east Ordos Basin. Acta Pet. Sin. 2016, 37, 1256–1264. [Google Scholar]
- Zhang, G.; Wang, D.; Zeng, Q.; Yang, H.; Li, Z.; Zhao, Z.; Guo, S. Characteristics of coal-measure source rock and gas accumulation belts in marine-continental transitional facies fault basins: A case study of the oligocene deposits in the Qiongdongnan Basin located in the northern region of the South China Sea. Energy Explor. Exploit. 2019, 37, 1752–1778. [Google Scholar]
- Wang, J.; DElsworth Wu, Y.; Liu, J.; Zhu, W.; Liu, Y. The influence of fracturing fluids on fracturing processes: A comparison between water, oil and SC-CO2. Rock Mech. Rock Eng. 2017, 51, 299–313. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, Q.; Zhang, J.; Li, W.; Zhou, Z.; Liu, W. A numerical gas fracturing model of coupled thermal, flowing and mechanical effects. Comput. Mater. Contin. 2020, 65, 2123–2141. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Y.; Tang, J.; Zhou, Z.; Liao, Y. Experimental study on fracture initiation and propagation in shale using supercritical carbon dioxide fracturing. Fuel 2016, 190, 370–378. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, W.; Li, L.; Wei, C.; Yan, B.; Li, S. Multi-fracture interactions during two-phase flow of oil and water in deformable tight sandstone oil reservoirs. J. Rock Mech. Geotech. Eng. 2020, 12, 821–849. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.G.; Gao, F.; Wang, X. Numerical study of fracture network evolution during nitrogen fracturing processes in shale reservoirs. Energies 2018, 11, 2503. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, Y.; Li, L.; Wei, C.; Zhang, X.; Qin, C.; Song, X. Simulations on hydraulic fracture propagation of coal-rock combination in deep underground. Hazard Control Tunn. Undergr. Eng. 2019, 1, 96–108. [Google Scholar]
- He, J.; Lin, C.; Li, X.; Wan, X. Experimental investigation of crack extension patterns in hydraulic fracturing with shale, sandstone and granite cores. Energies 2016, 9, 1080. [Google Scholar] [CrossRef]
- Gai, D.; Zhu, W.; Wei, C.; Niu, L. Pulse fracturing model based on damage mechanics and its numerical simulation. J. Min. Saf. Eng. 2016, 33, 945–950. [Google Scholar]
- Tan, P.; Jin, Y.; Han, K.; Zheng, X.; Hou, B.; Gao, J.; Chen, M.; Zhang, Y. Vertical propagation behavior of hydraulic fractures in coal measure strata based on true triaxial experiment. J. Pet. Sci. Eng. 2017, 158, 398–407. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals Series and Products; Academic Press: New York, NY, USA, 1980. [Google Scholar]
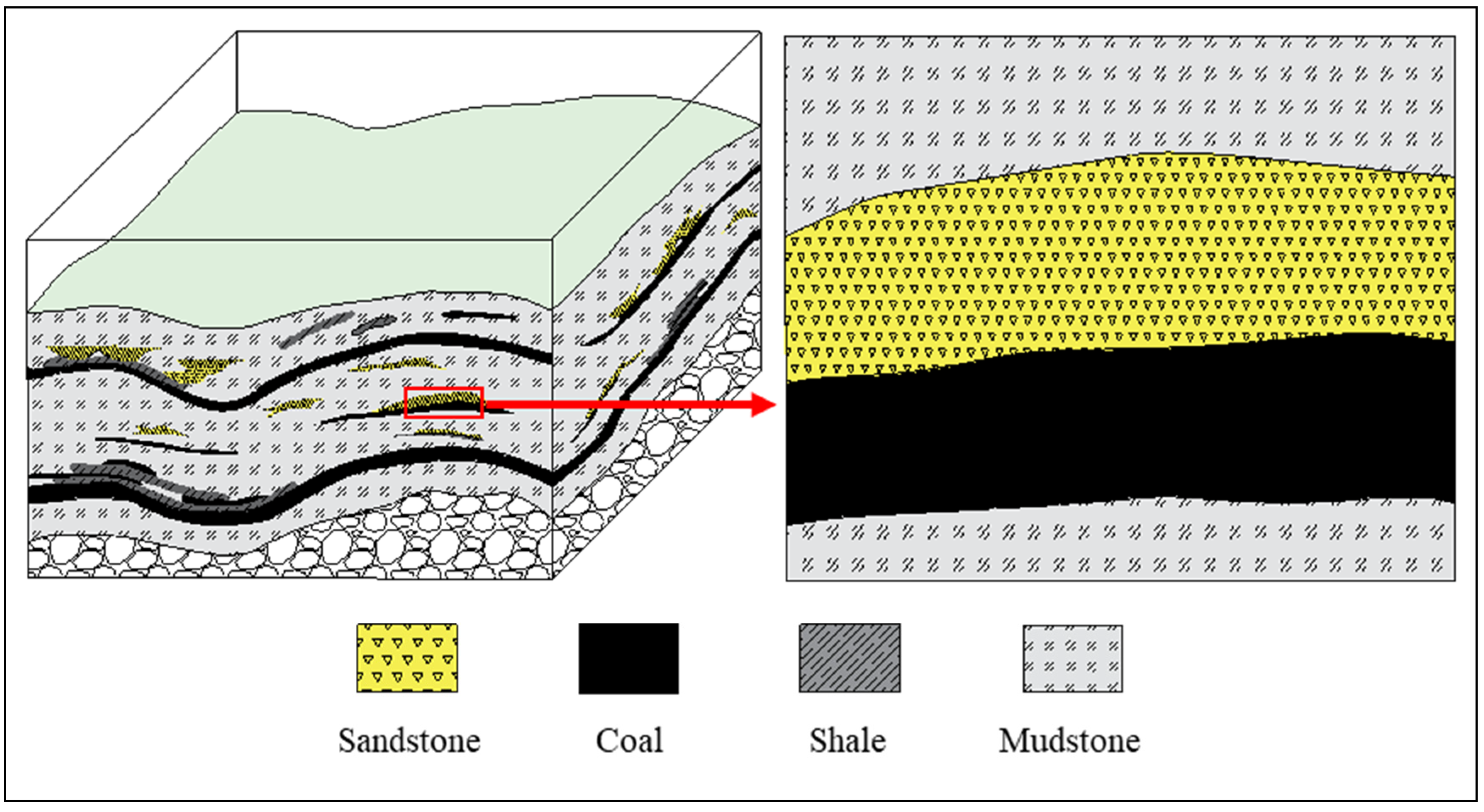

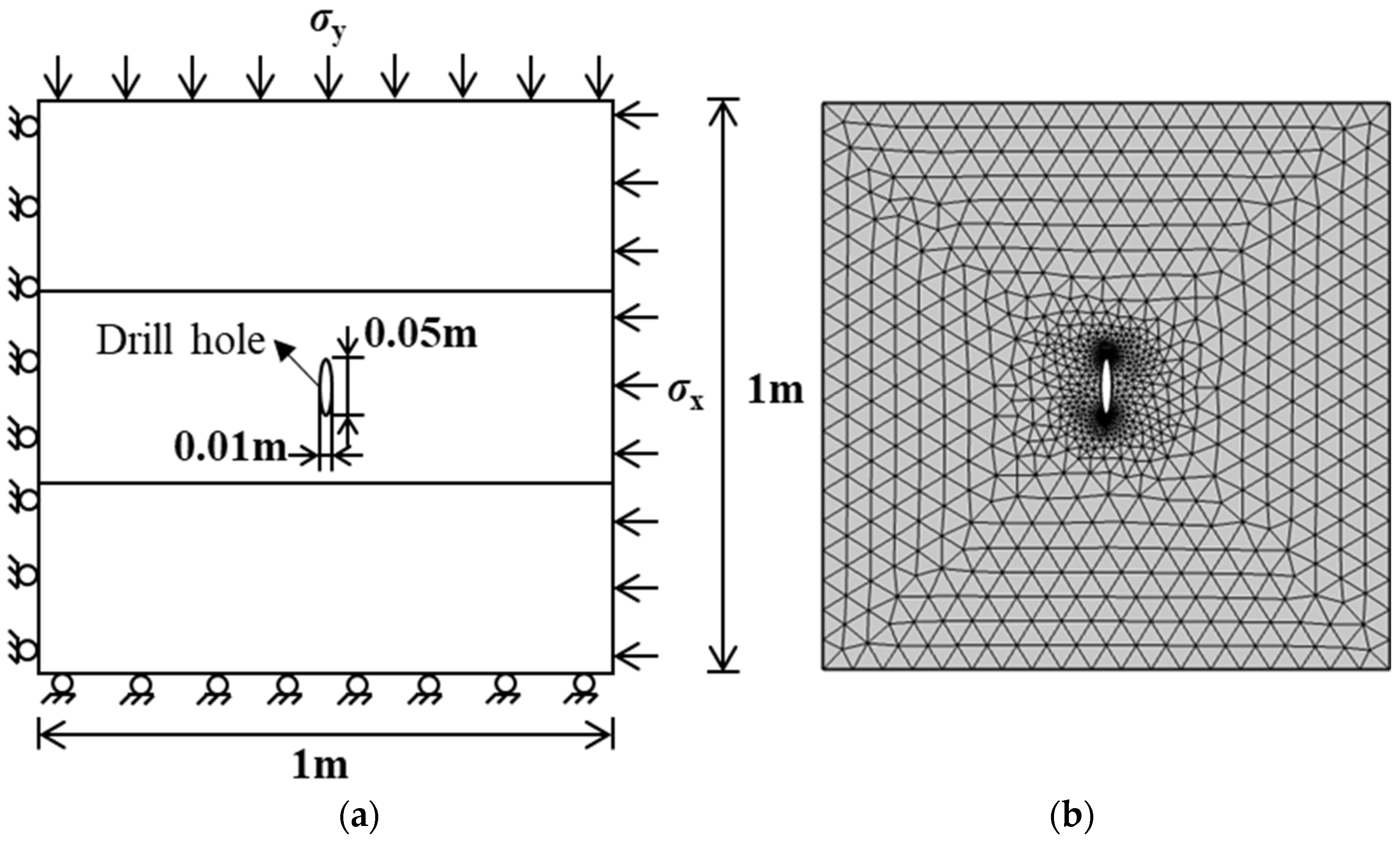
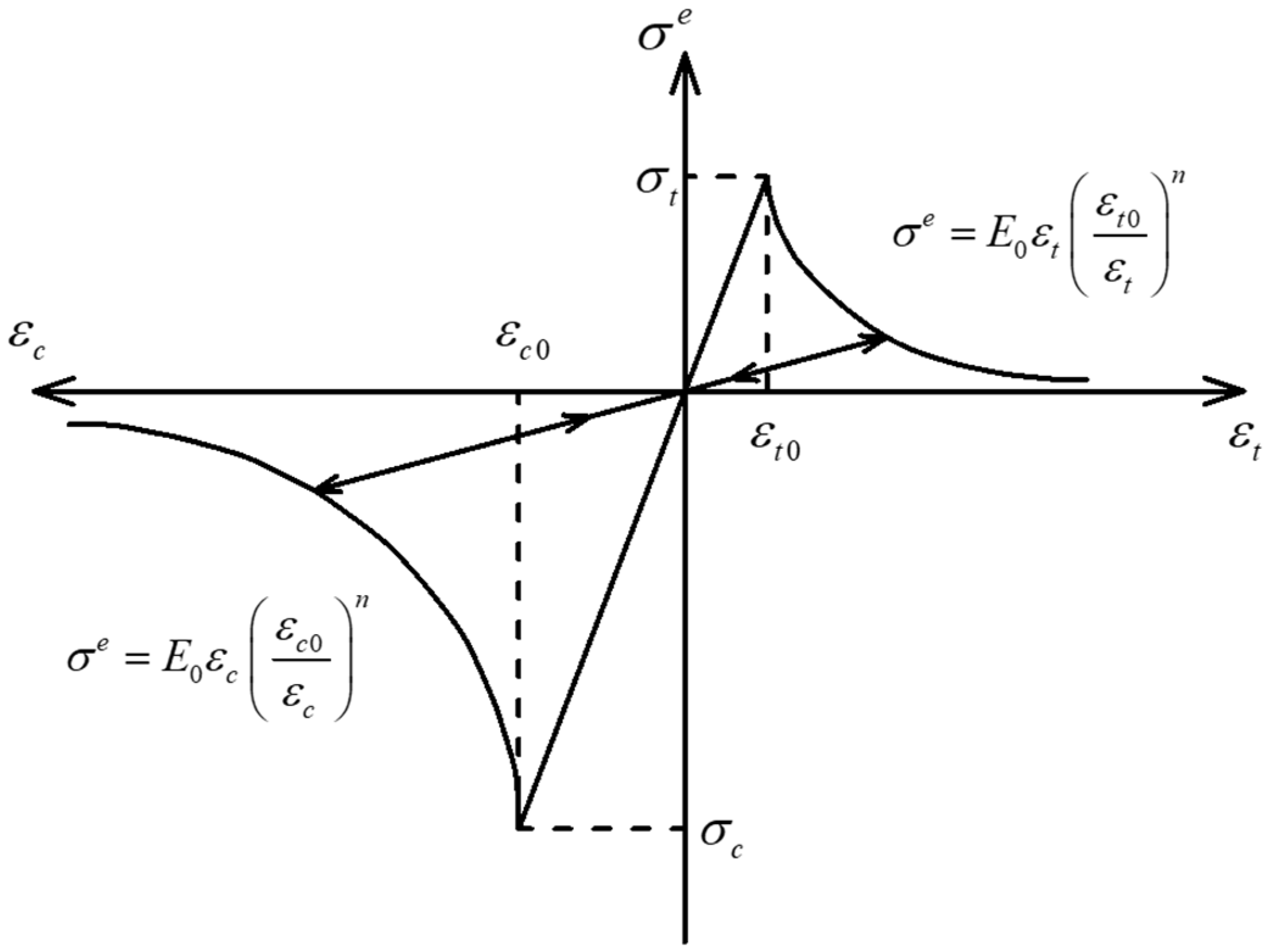
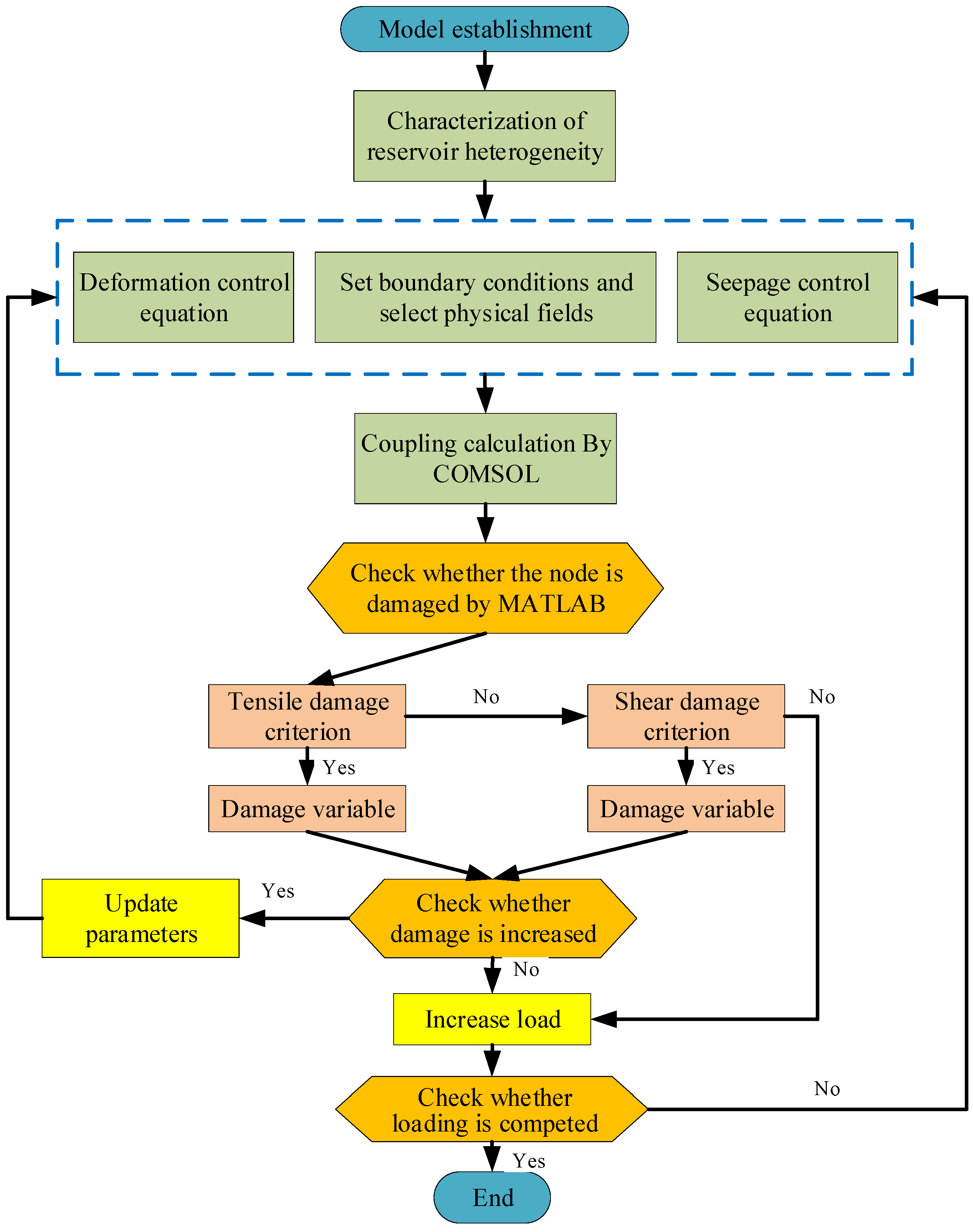

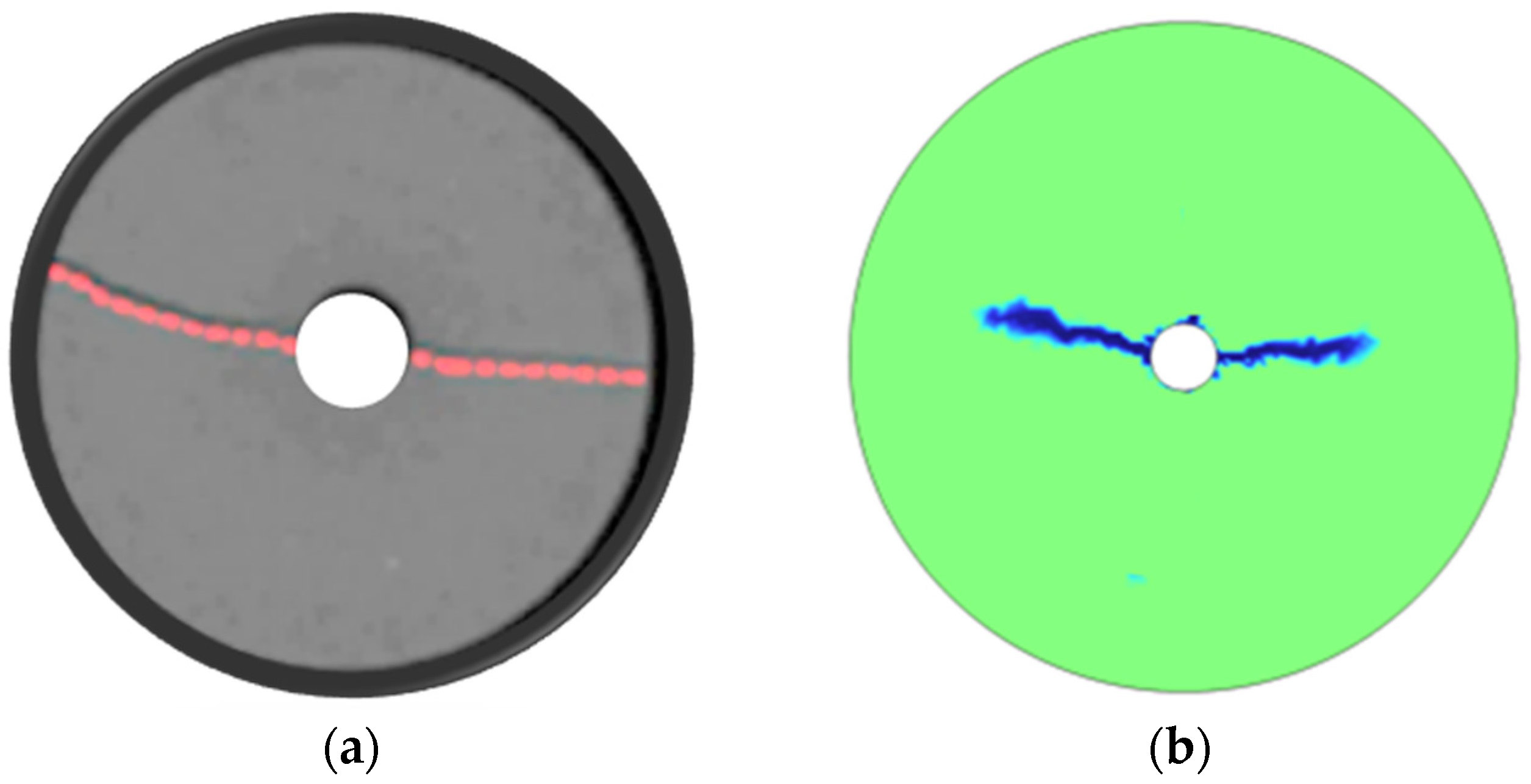
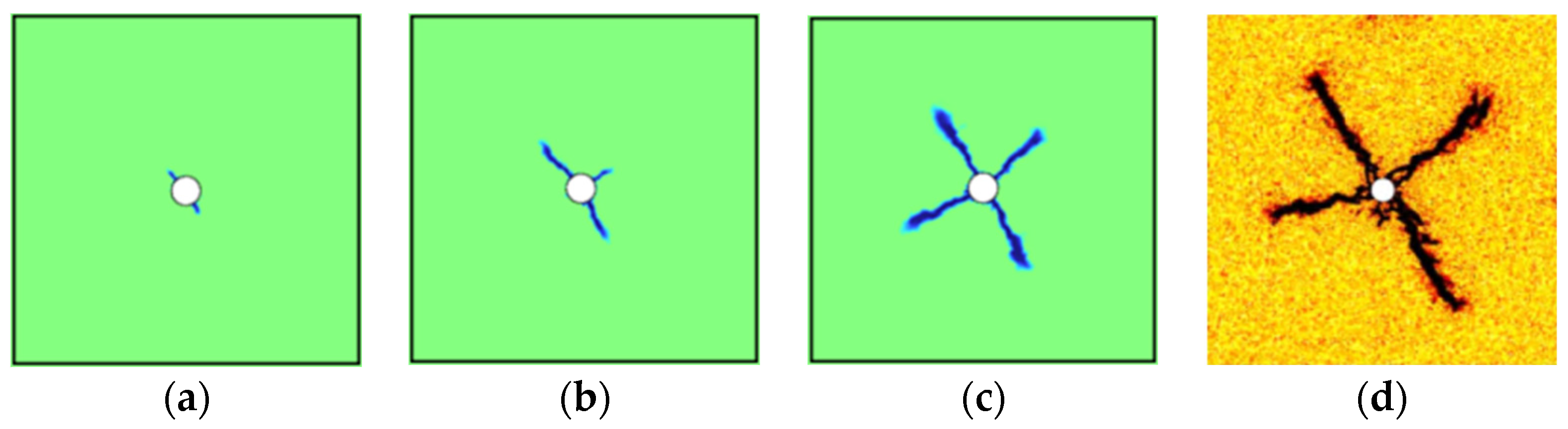
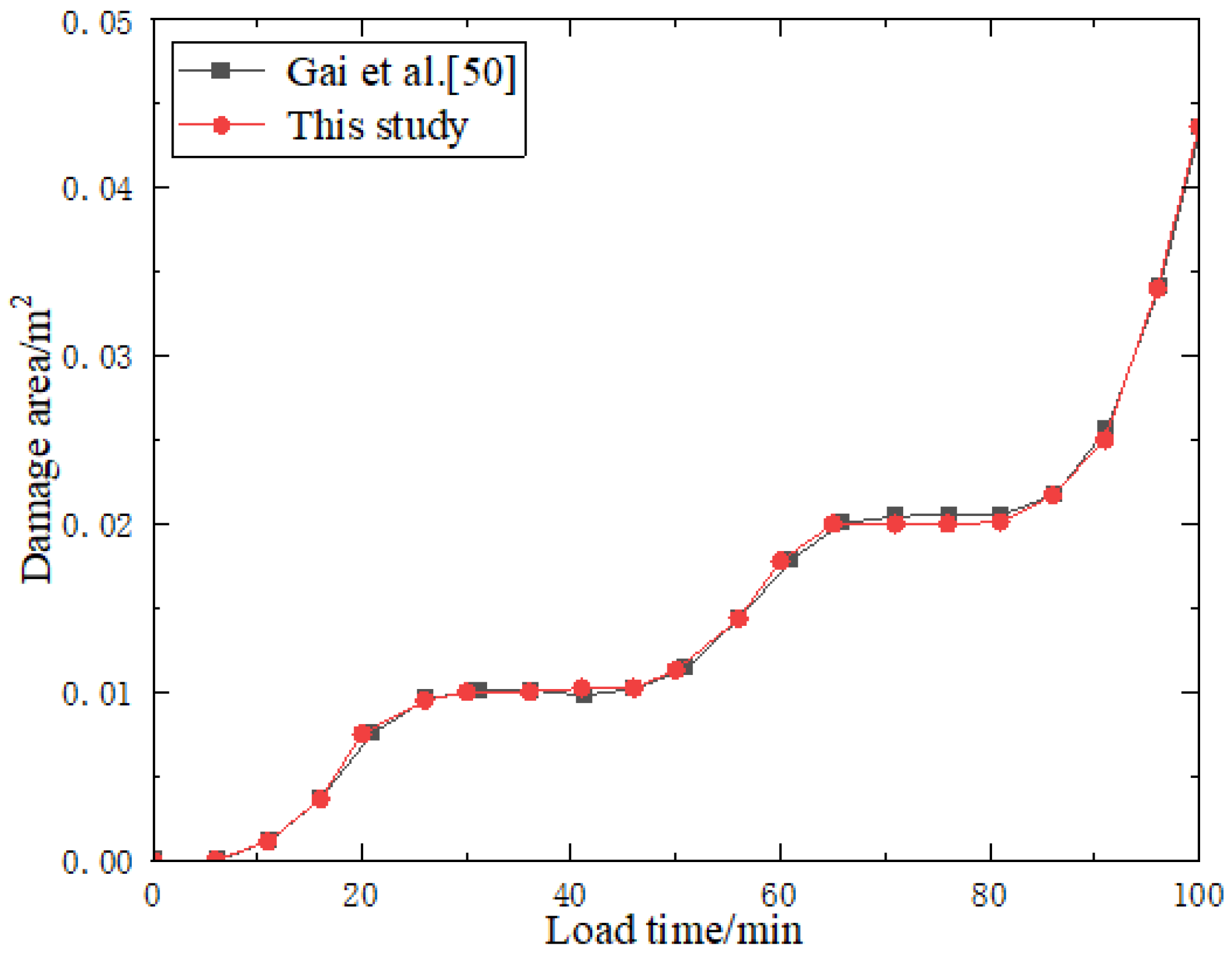
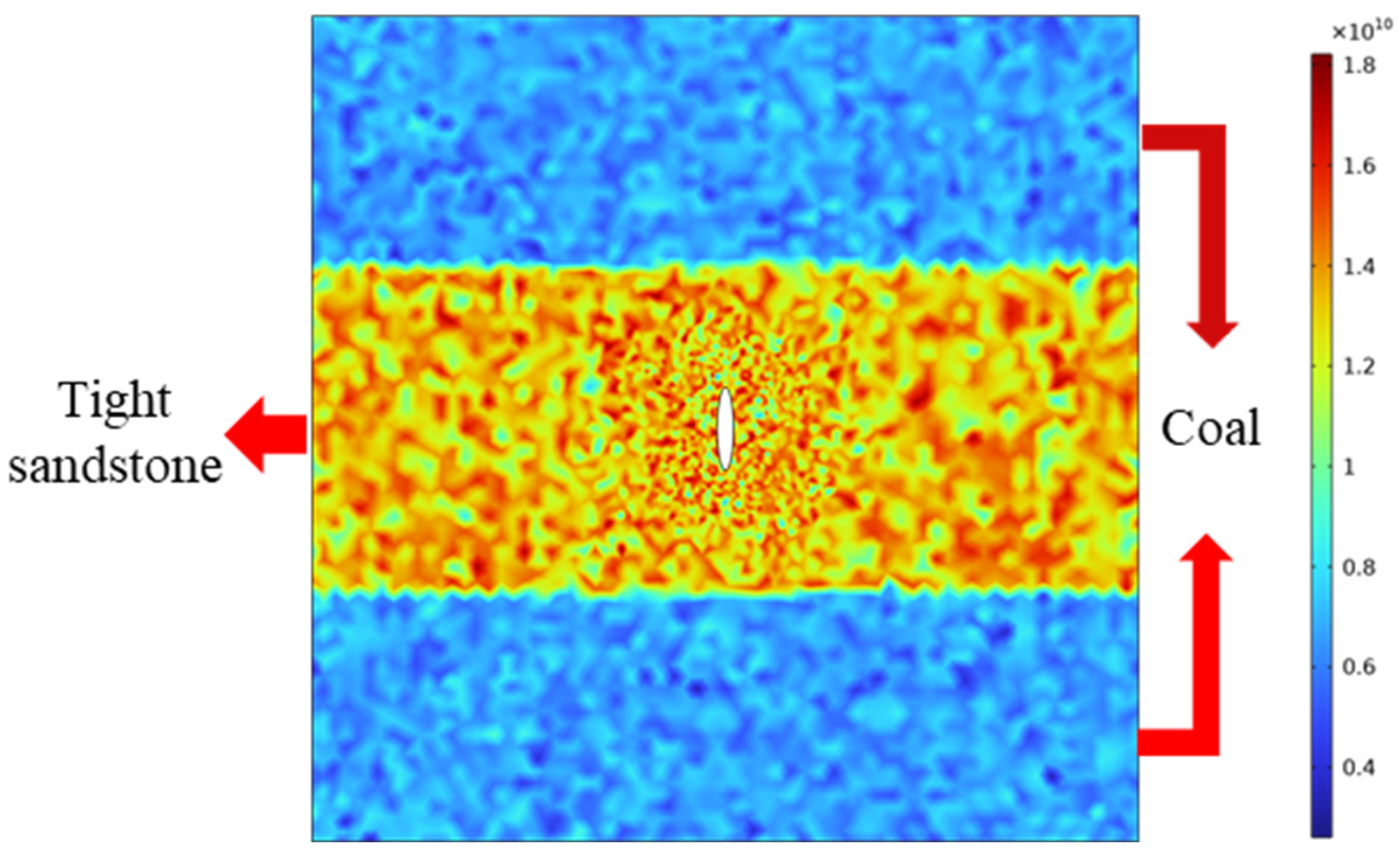
| Lithology | Coal | Tight Sandstone |
|---|---|---|
| Elastic modulus (GPa) | 7.2 | 14 |
| Poisson’s ratio | 0.4 | 0.2 |
| Compressive strength (MPa) | 10.53 | 63.89 |
| Tensile strength (MPa) | 1.053 | 6.389 |
| Initial permeability (m2) | 7.9 × 10−17 | 7.9 × 10−16 |
| Density (kg/m3) | 1250 | 2000 |
| Internal friction angle (°) | 25 | 30 |
| Rock | Young’s Modulus (GPa) | Poisson’s Ratio | In situ Stress σv/σh (MPa) | Fluid Viscosity (MPa·s) |
|---|---|---|---|---|
| Shale | 40.6 | 0.12 | 18/12 | 3 |
| Rock | Uniaxial Compressive Strength (GPa) | Density (g/cm3) | Tensile Strength (MPa) | Fluid Viscosity (MPa·s) |
|---|---|---|---|---|
| Sandstone | 65 | 2.45 | 6.4 | 1 |
| Rock | Elastic Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | Density (kg·m−3) |
|---|---|---|---|---|
| Coal | 1 | 0.15 | 1.3 | 1800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Wang, J.; Liang, W.; Sun, R. An Analytical and Numerical Analysis for Hydraulic Fracture Propagation through Reservoir Interface in Coal-Measure Superimposed Reservoirs. Sustainability 2023, 15, 4597. https://doi.org/10.3390/su15054597
Li P, Wang J, Liang W, Sun R. An Analytical and Numerical Analysis for Hydraulic Fracture Propagation through Reservoir Interface in Coal-Measure Superimposed Reservoirs. Sustainability. 2023; 15(5):4597. https://doi.org/10.3390/su15054597
Chicago/Turabian StyleLi, Peibo, Jianguo Wang, Wei Liang, and Rui Sun. 2023. "An Analytical and Numerical Analysis for Hydraulic Fracture Propagation through Reservoir Interface in Coal-Measure Superimposed Reservoirs" Sustainability 15, no. 5: 4597. https://doi.org/10.3390/su15054597
APA StyleLi, P., Wang, J., Liang, W., & Sun, R. (2023). An Analytical and Numerical Analysis for Hydraulic Fracture Propagation through Reservoir Interface in Coal-Measure Superimposed Reservoirs. Sustainability, 15(5), 4597. https://doi.org/10.3390/su15054597







