Power Flow Optimization Strategy of Distribution Network with Source and Load Storage Considering Period Clustering

Abstract

The large-scale grid connection of new energy will affect the optimization of power flow. In order to solve this problem, this paper proposes a power flow optimization strategy model of a distribution network with non-fixed weighting factors of source, load and storage. The objective function is the lowest cost, the smallest voltage deviation and the smallest power loss, and many constraints, such as power flow constraint, climbing constraint and energy storage operation constraint, are also considered. Firstly, the equivalent load curve is obtained by superimposing the output of wind and solar turbines with the initial load, and the best k value is obtained by the elbow rule. The k-means algorithm is used to cluster the equivalent load curve in different periods, and then the fuzzy comprehensive evaluation method is used to determine the weighting factor of the optimization model in each period. Then, the particle swarm optimization algorithm is used to solve the multi-objective power flow optimization model, and the optimal strategy and objective function values of each unit output in the operation period are obtained. Finally, IEEE33 is used as an example to verify the effectiveness of the proposed model through two cases: a fixed proportion method to determine the weighting factor, and this method to determine the weighting factor. The proposed method can improve the economy and reliability of distribution networks.

1. Introduction

As the power grid continues to develop in a more efficient, flexible and sustainable direction [1,2], the large-scale grid connection of distributed new energy has become an inevitable trend [3,4], increasing the difficulty of multi-objective power flow optimization (DNMPFO) of distribution networks [5,6,7].

At present, scholars at home and abroad have carried out relevant research on DNMPFO. Reference [8] generated a typical wind-light-load scenario based on fuzzy C-means clustering algorithm, and established a new energy planning model with the goal of maximizing the total installed capacity of distribution networks connected to scenery, but energy storage was not involved in the model. Reference [9] clustered wind speed and irradiance, and proposed a two-level optimal allocation model. The upper model took the comprehensive income as the goal, and the lower model took the minimum sum of network loss and voltage deviation as the goal, and adopted the planning-optimization solution strategy of genetic algorithm-interior point method, but energy storage is not considered in this reference either. Reference [10] established a mathematical model of interval power flow optimization (PFO) of an AC/DC hybrid system with a DC power flow controller based on interval and affine arithmetic, and used a non-dominated sequencing genetic algorithm to solve the model. However, the cost of unit operation is not considered in the model. Reference [11] modeled the uncertainty of wind and solar power generation, established a multi-objective optimization model of a battery energy storage system coordinated with demand response, and used a non-sequential genetic algorithm to solve it. However, photovoltaic units are not involved in this reference. Reference [12] proposed a multi-objective optimization hierarchical strategy of a distribution network considering the integration of distributed power generation and electric vehicles, which was solved by a genetic algorithm, but the wind turbine unit was not considered in the model. Considering the correlation, reference [13] simulated a 33-node distribution network, and the results showed that although the cost and network loss decrease, the voltage deviation increased slightly. Among the existing references on power flow optimization of distribution networks, there are very few references considering new energy and energy storage such as wind and solar, and none of them involve time period clustering, which needs further study.

For the DNMPFO problem with source load storage (SLS), this paper proposes a time-phased PFO model of a distribution network that takes into account many constraints, and uses a particle swarm optimization algorithm to solve the model. Finally, the paper takes a IEEE33-bus system as an example to carry out simulation analysis on the Matlab software (Version is R2016a) to verify the effectiveness of the proposed model in solving power flow optimization problems. The main contributions of this work are summarized as follows:

(1)

Based on the k-means clustering method, the equivalent load curve is clustered in different periods, so as to dynamically determine the weight coefficient of the objective function according to the periods;

(2)

A solution method based on particle swarm optimization is proposed, which can effectively solve the model.

(3)

Based on the proposed power flow optimization method of distribution network considering time period clustering, the power flow optimization of the IEEE33 system in a certain area is analyzed, and the objective function values are all decreased, thus improving the economy and security of the distribution network.

2. Multi-Objective Power Flow Optimization Model of Distribution Network with Source and Load Storage

The DNMPFO model includes wind turbine (WT), photovoltaic unit (PV), micro gas turbine (MG) and energy storage system (ESS). In order to make the optimization effect of power flow better, in addition to the total economic cost, voltage offset and power loss should also be considered. Since the model includes WT and PV with uncertain characteristics, it may affect the stability of the power grid, and PFO is an important link to ensure the stability, safety and economic operation of the power grid.

2.1. Establishment of Objective Function

(1)

Objective function $F_1$: the lowest total cost [14,15].

$$F_1=\min \left(C_f+C_m+C_{p,pur}+C_h\right)$$

(1)

where $C_f$ is the unit fuel cost. Since PV and WT are clean energy, the fuel cost is zero. The fuel cost of MG is calculated according to Equation (2), ten thousand yuan; $C_m$ is the operation and maintenance cost, calculated according to Equation (3), ten thousand yuan. Because the structure of MG is convenient for monitoring and replacement repair, its operation and maintenance cost is not considered; $C_{p,pur}$ is the cost of purchasing electricity from the superior power grid, calculated according to Equation (4), ten thousand yuan; $C_h$ is the pollutant emission control cost, calculated according to Equation (5), ten thousand yuan.

$$C_f={10}^4·{\displaystyle \mathcal{\sum }_{t=1}^T{\displaystyle \mathcal{\sum }_{i=1}^{N_{\mathrm{MG}}}\frac{c_g{P}_{\mathrm{unit},i}}{s_g{\eta }_{\mathrm{MG}}}}}$$

(2)

where $c_g$ is the natural gas price, $\mathrm{yuan}/{\mathrm{m}}^3$; $s_g$ is the calorific value of natural gas, $\mathrm{kW}·\mathrm{h}/{\mathrm{m}}^3$; $N_{\mathrm{MG}}$ is the number of MG; $P_{\mathrm{unit},i}$ is the output power of the ith unit, $\mathrm{kW}$; and ${\eta }_{\mathrm{MG}}$ is the conversion efficiency of MG.

$$C_m={10}^4·{\displaystyle \mathcal{\sum }_{t=1}^T{\displaystyle \mathcal{\sum }_{i=1}^J{c}_{om}}}{P}_{\mathrm{unit},i}(t)$$

(3)

where $J$ is the number of units; and $c_{om}$ is the operation and maintenance cost of the unit power, $\mathrm{yuan}/\mathrm{kW}$.

$$C_{p,pur}={10}^4·{\displaystyle \mathcal{\sum }_{t=1}^{T}p\left(t\right)P_{pur}\left(t\right)}$$

(4)

where $p\left(t\right)$ is the electricity price at time t, $\mathrm{yuan}/\mathrm{kW}$; and $P_{pur}\left(t\right)$ is the power purchased at time t, kW.

$$C_h={10}^4\cdot \left({\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_{\mathrm{MG}}}\frac{c_{1,{\mathrm{CO}}_2}{c}_{cet}{P}_{\mathrm{unit},i}(t)}{{\eta }_{\mathrm{MG}}}}}\right)+{10}^4\cdot \left({\displaystyle \sum _{t=1}^T{c}_{2,{\mathrm{CO}}_2}{c}_{cet}(1+\epsilon )P_{\mathrm{pur}}(t)}\right)$$

(5)

where $c_{{1,\mathrm{CO}}_2}$ and $c_{{2,\mathrm{CO}}_2}$ are, respectively, the ${\mathrm{CO}}_2$ emission coefficients of natural gas and coal-fired power plant combustion, $\mathrm{kg}/\mathrm{kW}·\mathrm{h}$; $c_{cet}$ is the equivalent carbon tax, $\mathrm{yuan}/\mathrm{kg}$; and is the line loss rate of the power grid, %.

(2)

Objective function $F_2$: the node voltage deviation is the smallest; that is, the voltage distribution is the most reasonable [16].

$$F_2=\min {\displaystyle \mathcal{\sum }_{t=1}^T{\displaystyle \mathcal{\sum }_{i=1}^n\left|\frac{U_{i,t}-U_N}{U_N}\right|}}$$

(6)

where $n$ is the number of independent nodes of the distribution network; $t$ is the period mark; $T$ is the number of whole day periods; $U_{i,t}$ is the voltage amplitude of the ith node during t period, $\mathrm{kV}$; and $U_N$ is the rated voltage of the ith node, kV.

(3)

Objective function $F_3$: minimum power loss.

$$F_3=\min {\displaystyle \mathcal{\sum }_{t=1}^T{\displaystyle \mathcal{\sum }_{k=1}^b\left(P_k\left(t\right)-P_k^{\prime }\left(t\right)\right)}}\Delta t$$

(7)

where $b$ is the number of branches; $P_k\left(t\right)$ and $P_k^{\prime }\left(t\right)$ are, respectively, the head power and end power of branch k, $\mathrm{kW}$; and $\Delta t$ is a run time period, $\mathrm{h}$.

2.2. Constraints

The optimization strategy needs to satisfy equality constraints such as power flow constraint and power balance constraint, and inequality constraints such as bus voltage constraint and climbing constraint.

2.2.1. Power Flow Constraint

For the operation of a distribution network, it is necessary to meet certain power flow constraints [17]:

$$\left\{\begin{array}{l}{P}_{\mathrm{in},i}(t)=e_{i,t}{\displaystyle \sum _{j=1}^n(G_{ij}{e}_{j,t}-B_{ij}{f}_{j,t})}+f_{i,t}{\displaystyle \sum _{j=1}^n(G_{ij}{f}_{j,t}+B_{ij}{e}_{j,t})}\\ Q_{\mathrm{in},i}(t)=f_{i,t}{\displaystyle \sum _{j=1}^n(G_{ij}{e}_{j,t}-B_{ij}{f}_{j,t})}-e_{i,t}{\displaystyle \sum _{j=1}^n(G_{ij}{f}_{j,t}+B_{ij}{e}_{j,t})}\end{array}\right.$$

(8)

where $P_{\mathrm{in},i}$ and $Q_{\mathrm{in},i}$ are, respectively, the active power ($\mathrm{kW}$) and reactive power ($\mathrm{kVar}$) injected into the distribution network by node i; $e_{i,t}$ and $j_{i,t}$ are, respectively, the real part and imaginary part of the voltage of node i at time t; $e_{j,t}$ and $j_{j,t}$ are, respectively, the real part and imaginary part of the voltage of node j at time t; $G_{ij}$ and $B_{ij}$ are, respectively, the real part and imaginary part of elements in node admittance matrix, Ω.

2.2.2. Power Balance Constraints

The sum of the output of all units minus the load power and power loss is equal to the power injected into the grid [18], with the following constraints:

$$\left\{\begin{array}{c}{P}_{\mathrm{in},i}(t)=P_{\mathrm{g},i}(t)+P_{\mathrm{WT},i}(t)+P_{\mathrm{PV},i}(t)+P_{\mathrm{ESS},i}^{\mathrm{dch}}(t)-P_{\mathrm{ESS},i}^{\mathrm{ch}}(t)+P_{\mathrm{MG},i}(t)-P_{\mathrm{Load},i}(t)-P_{\mathrm{Loss}}\\ Q_{\mathrm{in},i}(t)=Q_{\mathrm{g},i}\left(t\right)+Q_{\mathrm{MG},i}\left(t\right)-Q_{\mathrm{Load},i}\left(t\right)-Q_{\mathrm{Loss}}\end{array}\right.$$

(9)

where $P_{g,i}$ and $Q_{g,i}$ are, respectively, the active power ($\mathrm{kW}$) and reactive power ($\mathrm{kVar}$) of the power supply on node i; $P_{\mathrm{MG},i}$ and $Q_{\mathrm{MG},i}$ are, respectively, the active power ($\mathrm{kW}$) and reactive power ($\mathrm{kVar}$) generated by the gas turbine on node i; $P_{\mathrm{ESS},i}^{\mathrm{dch}}$ and $P_{\mathrm{ESS},i}^{\mathrm{ch}}$ are, respectively, the discharge and charging power of the energy storage device on node i; $P_{\mathrm{Load},i}$ and $Q_{\mathrm{Load},i}$ are, respectively, the active load ($\mathrm{kW}$) and reactive load ($\mathrm{kVar}$) of node i; and $P_{\mathrm{Loss}}$ and $Q_{\mathrm{Loss}}$ are, respectively, the active power loss ($\mathrm{kW}$) and reactive power loss ($\mathrm{kVar}$).

2.2.3. Bus Voltage Constraint

The bus voltage needs to meet the following constraints:

$$U_{i,\min }\le U_i\left(t\right)\le U_{i,\max }$$

(10)

where $U_{i,\max }$ and $U_{i,\min }$, respectively, represent the maximum and minimum value of the voltage amplitude of the ith node, kV.

2.2.4. Unit Output Constraint

The unit output needs to meet the following constraints:

$$P_{i,\min }\le P_i\left(t\right)\le P_{i,\max }$$

(11)

where $P_{i,\max }$ and $P_{i,\min }$, respectively, represent the maximum and minimum value of the active output of the ith unit, kW.

2.2.5. Energy Storage Operation Constraints

The output of the energy storage device during operation meets the following constraints [19]:

$$P_{\mathrm{ESS}}^{\min }\le P_{\mathrm{ESS}}\left(t\right)\le P_{\mathrm{ESS}}^{\max }$$

(12)

where $P_{\mathrm{ESS}}\left(t\right)$, $P_{\mathrm{ESS}}^{\max }$ and $P_{\mathrm{ESS}}^{\min }$, respectively, represent the output power, the maximum value of the output power and the minimum value of the output power of ESS at time t, kW.

In order to prevent overcharging and discharging from affecting the battery life, the overall state of charge (SOC) of ESS is constrained:

$$\left\{\begin{array}{c}\mathrm{SOC}(t)=(1-\gamma ){\mathrm{SOC}}_0+{\displaystyle \sum _{t=1}^T{P}_{\mathrm{ESS}}(t)}\Delta t\\ {\mathrm{SOC}}_{\min }\le \mathrm{SOC}(t)\le {\mathrm{SOC}}_{\max }\end{array}\right.$$

(13)

where $\mathrm{SOC}(t)$ is the SOC value of ESS at time t, $\mathrm{kW}·\mathrm{h}$; $\gamma$ is the self-discharge rate of electric energy storage; and ${\mathrm{SOC}}_0$, ${\mathrm{SOC}}_{\min }$ and ${\mathrm{SOC}}_{\max }$ are, respectively, the initial value, minimum value and maximum value of SOC, $kW·h$.

2.2.6. Climbing Constraint

According to the operation characteristics of MG, its active power regulation rate (namely climbing rate) is constrained [20]:

$$R_{\mathrm{down}}\le \frac{P_{\mathrm{MG},t}\le P_{\mathrm{MG},t-1}}{\Delta t}\le R_{\mathrm{up}}$$

(14)

where $R_{\mathrm{down}}$ and $R_{\mathrm{up}}$, respectively, represent the downward and upward climbing speed of MG, $\mathrm{kW}/\mathrm{h}$; and $P_{\mathrm{MG},t}$ and $P_{\mathrm{MG},t-1}$, respectively, represent the output of MG at time t and time t−1, $\mathrm{kW}$.

2.2.7. Branch Current Constraint

The branch current needs to meet the following constraints:

$$\left|I_k\left(t\right)\right|\le I_{k,\max }$$

(15)

where $I_{k,\max }$ represents the allowable maximum value of branch current, $\mathrm{A}$.

2.3. Power Flow Optimization Mathematical Model

Firstly, the objective functions are normalized [21], and then the multi-objective power flow optimization model of distribution network is established. Set $F_n^{\prime }$ as the normalized objective function:

$$F_n^{\prime }=\frac{F_n}{F_{n,\max }}$$

(16)

where $F_n$ is the objective function, $n=1,2,3$; and $F_{n,\max }$ is, respectively, the maximum value of $F_n$.

The multi-objective power flow optimization model of distribution network is as follows:

$$\min F=f_1{F}_1^{\prime }+f_2{F}_2^{\prime }+f_3{F}_3^{\prime }$$

(17)

where $f_1$, $f_2$, $f_3$ are, respectively, the weighting factors of $F_1^{\prime }$, $F_2^{\prime }$, and $F_3^{\prime }$, and meet $f_1+f_2+f_3=1$ [22].

3. Determination of Weighting Factors of Optimization Model Based on k-Means Clustering

In this paper, a k-means clustering algorithm is used to cluster the periods to determine the weighting factor of each period.

3.1. k-Means Clustering Analysis

k-means is a partition-based clustering algorithm [23], k represents clustering into k clusters, and means represents taking the average value of data in each cluster as the center of the cluster, also called centroid. The main steps are as follows:

Step (1) Randomly select $k$. sample points as the initial clustering center;

Step (2) Calculate the distance from each sample point to the “cluster center”, and divide each sample point into the nearest cluster. The measurement strategy usually used in this step is the Euclidean distance [24], whose calculation formula is as follows:

$$d(x,y)=\sqrt{{(x_1-y_1)}^2+{(x_2-y_2)}^2+\cdots +{(x_n-y_n)}^2}={\displaystyle \mathcal{\sum }_{i=1}^n\sqrt{{(x_n-y_n)}^2}}$$

(18)

Step (3) Calculate the center point of each cluster. If the center point obtained is the same as the previous one, output it; otherwise, repeat step (2) with the newly obtained center point as the initial point.

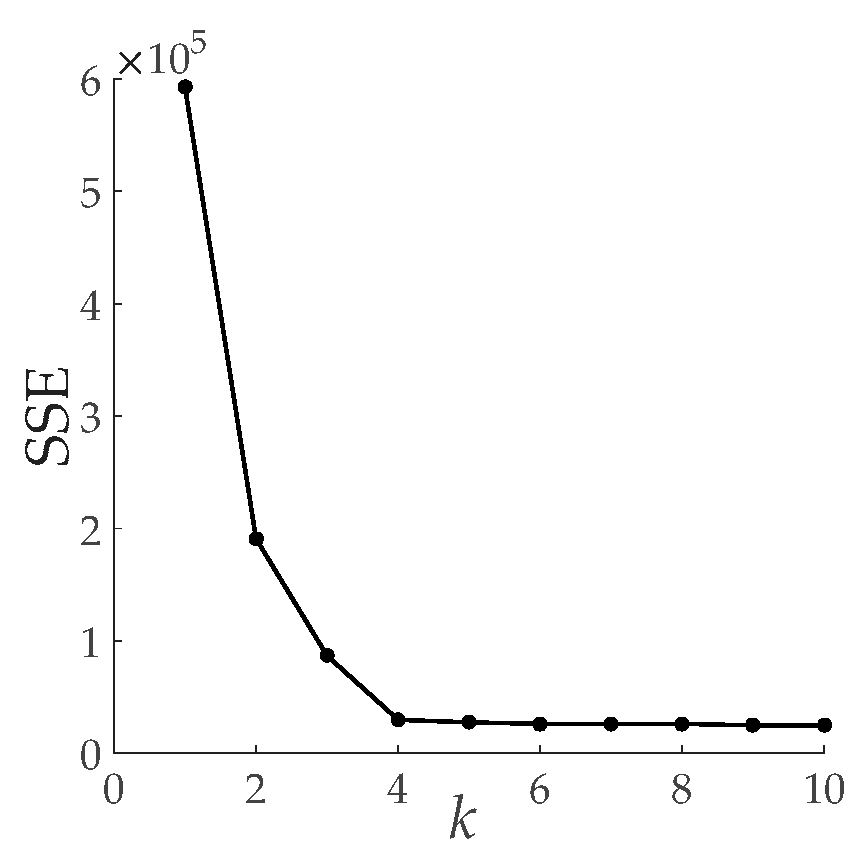
3.2. Elbow Rule Determines the Best Clustering Number k

The determination of clustering number k is very important to the clustering quality [25]. The larger the k value, the better the clustering effect, but the longer the calculation time. The traditional k value is obtained through experience and lacks objectivity, so it is necessary to choose the appropriate k value. In this paper, the elbow rule is adopted to ensure the accuracy of k value selection. When Euclidean distance is used as the metric, K-means takes the sum of squares for error (SSE) (also called the degree of distortion) as the target to measure the clustering quality, and its calculation formula is shown in Equation (19).

$$\mathrm{SSE}={{\displaystyle {\mathcal{\sum }}_{i=1}^k{\displaystyle {\mathcal{\sum }}_{p\in C_i}\left|p-m_i\right|}}}^2$$

(19)

where $k$ represents the number of clusters; $C_i$ represents the ith cluster; $p$ represents the sample point in $C_i$; and $m_i$ represents the mean value of all data in the ith cluster.

As the k value increases, the number of samples contained in each cluster decreases, and the distance from the sample to its center will be closer, so the average distortion degree will decrease [26]. For data with a certain degree of differentiation, when reaching a certain critical point, the distortion degree will be greatly improved, and then slowly decreased, and this critical point will be considered as the best k value.

3.3. Determination of Weighting Factor

In this paper, the PV output, WT output and load output of a day are superimposed to obtain the equivalent load curve, and then the period of the equivalent load curve is clustered, and then the fuzzy comprehensive evaluation method (FCE) is used to determine the weighting factor of the optimization model in each period under the condition of equivalent load [27]. Then, compare it with the weighting factor determined by the fixed proportion method (FPM) (see Equation (22)) to establish two schemes for the weighting factor. The calculation formula is as follows:

$$f_n=\frac{f_n^{\prime }}{{\displaystyle \mathcal{\sum }_{n=1}^{N_F}{f}_n^{\prime }}}$$

(20)

where $f_n^{\prime }$ is the weighted value of exceeding the standard, calculated according to Equation (21); and N_F is the number of objective functions.

$$f_n^{\prime }=\frac{C_n}{C_{an,n}}$$

(21)

where $C_n$ is actual value of the nth factor, $n=1,2,3$; and $C_{an,n}$ is the maximum value of the nth factor.

In this paper, $C_n$ takes the average value of factors in each case, and $C_{an,n}$ takes the maximum value of factors in each case.

$$f_n=\frac{1}{N_F}$$

(22)

4. Solution of Mathematical Model

The particle swarm optimization (PSO) is used to solve the model established in this paper. In PSO, multiple particles in the search space guide the update of speed and position according to the global optimization and individual optimization, and co-evolve to find the optimal solution of the problem [28]. The speed update equation is as follows [29]:

$$V_{i,d}^{t+1}=\omega V_{i,d}^t+r_1{c}_1(P_{i,d}^t-x_{i,d}^t)+r_2{c}_2(G_{i,d}^t-x_{i,d}^t)$$

(23)

where $V_{i,d}^t$ is the velocity of the ith particle in the tth iteration; $r_1$ and $r_2$, respectively, represent random numbers evenly distributed in (0,1); $c_1$ is a self-learning factor; $c_2$ is a global learning factor; and $\omega$ is the inertia weighting factor.

The location update formula is as follows:

$$X_{i,d}^{t+1}=X_{i,d}^t+V_{i,d}^{t+1}$$

(24)

where $X_{i,d}^t$ is the position of the ith particle in the tth iteration.

Considering the security of the power system, this paper gives the output constraints of each unit to calculate the objective function value at each time. In order to avoid the PSO algorithm falling into local optimization, this paper dynamically improves the inertia weight $\omega$ and learning factors $c_1$ and $c_2$ [30,31], which are, respectively, shown in Equations (25) and (26).

$$\omega =a+\frac{(a-b)g^d}{g_{\max }^d}$$

(25)

where $a$ and $b$ are the maximum and minimum values of inertia weight $\omega$; $g$ is the current iteration number; $g_{\max }$ is the maximum number of iterations; and $d$ is a parameter.

$$\left\{\begin{array}{c}{c}_1=\frac{(e_1-e_2)g^d}{g_{\max }^d}+e_2\\ c_2=\frac{(f_1-f_2)g^d}{g_{\max }^d}+f_2\end{array}\right.$$

(26)

where $e_1$ and $e_2$ are the maximum and minimum values of $c_1$; $f_1$ and $f_2$ are the maximum and minimum values of $c_2$.

5. Analysis of Example

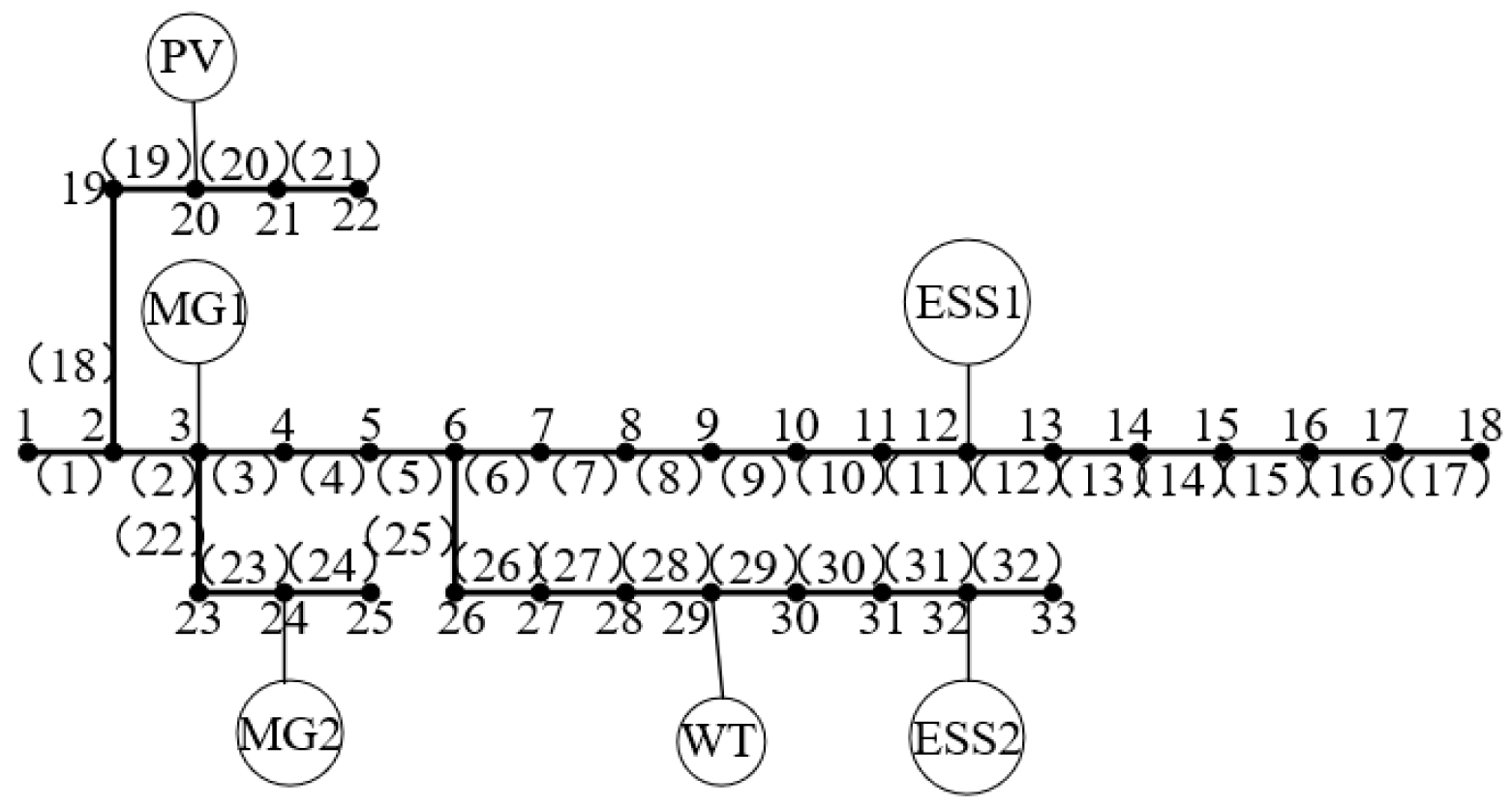
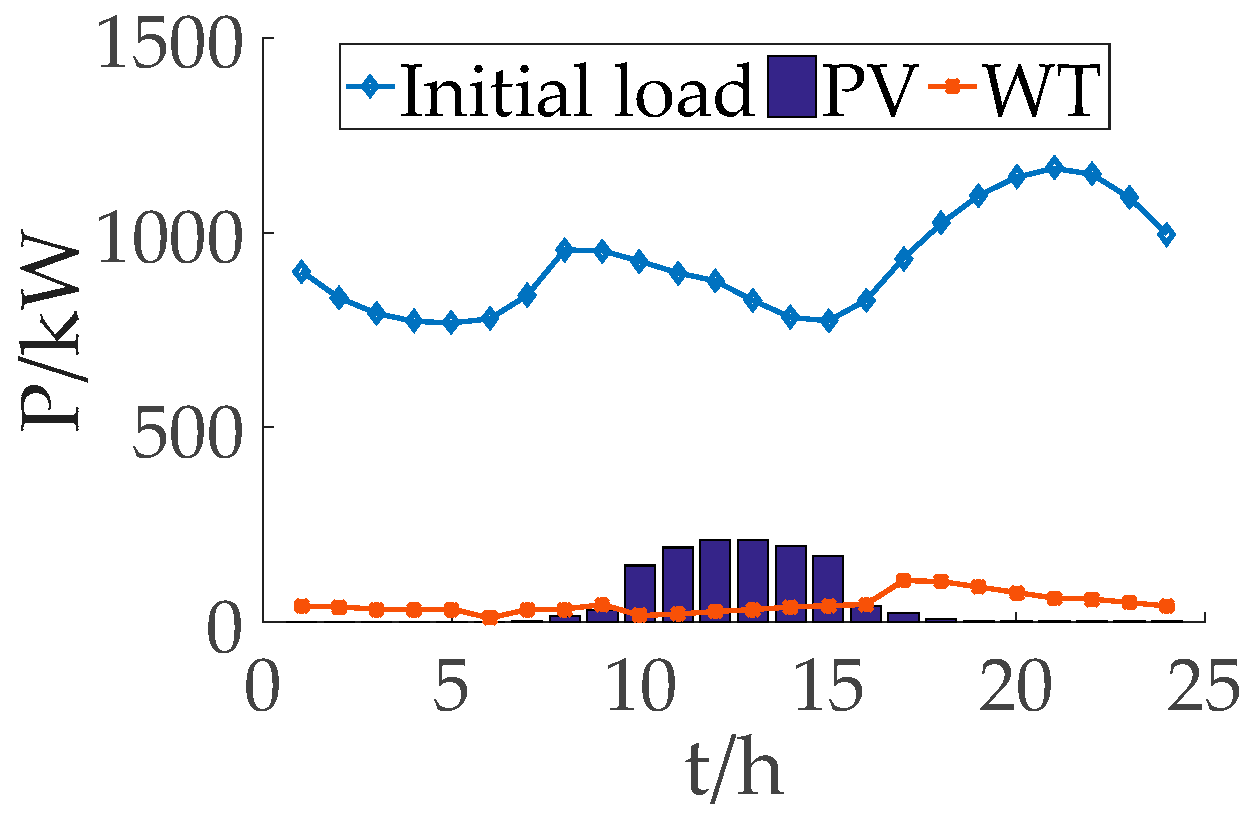
5.1. Basic Data

This paper simulates and analyzes the distribution network shown in Figure 1. ESS is connected to 12 and 32 nodes; MG is connected to 3 and 24 nodes; PV is connected to 20 nodes; and WT is connected to 29 nodes. See Reference [6] for the network parameters. Voltage reference value $U_B=12.66 \mathrm{kV}$ and power reference value $S_B=1 \mathrm{MVA}$. The specified voltage (per unit value) shall not be lower than 0.95 and not higher than 1.05; the upper limit of the branch current is 20A; the upper limit of MG active output is 300 kW, the lower limit is 100 kW, and the climbing speed $R_{\mathrm{down}}$, $R_{\mathrm{up}}$ is, respectively, −20 and 20 $\mathrm{kW}/\mathrm{h}$; and the maximum discharge power of the ESS is 250 kW, the maximum charging power is 200 kW, and the self-discharge rate $\gamma$ of the electric energy storage is 0.001. ${\mathrm{SOC}}_0$, ${\mathrm{SOC}}_{\min }$, ${\mathrm{SOC}}_{\max }$ is, respectively, 80, 40 and 160 $\mathrm{kW}\cdot \mathrm{h}$. Select PV, WT and load data of a certain area for analysis (see Figure 2). The time-of-use electricity price is shown in

Table 1. Time-of-use electricity price.

Period	$\mathbf{Electricity} \mathbf{Price} (\mathbf{Yuan}/\mathrm{kW}\cdot \mathrm{h})$
0:00–4:00	0.2294
4:00–8:00	0.0287
8:00–12:00	0.4932
12:00–16:00	0.9462
16:00–20:00	0.3823
20:00–24:00	0.4251

. See

Table 2. Coefficient setting in power generation cost.

Parameter	Value
cg	0.9462
sg	0.3823
ηMG	0.4251

,

Table 3. Setting of coefficient in operation cost.

Unit Type	$\mathbf{Value} \mathbf{of} {\mathit{c}}_{\mathit{o}\mathit{m}}$
PV	0.3456
WT	0.5386
ESS	0.2610

and

Table 4. Coefficient setting in environmental protection cost.

Parameter	Value
$c_{1,{\mathrm{CO}}_2}$	0.19
$c_{2,{\mathrm{CO}}_2}$	0.80
$c_{cet}$	0.30
ε	0.001

for each cost coefficient in objective function $F_1$. The DNMPFO strategy based on the PSO algorithm proposed in this paper is used to optimize the power flow of the distribution network for 24 h in this example to verify the effectiveness of the proposed model.

5.2. Analysis of Power Flow Optimization Results Based on PSO

Firstly, K-means is used to cluster the equivalent load curve in different periods, so as to dynamically determine the weighting factor. Then, the optimization model established in Section 2 is solved based on PSO, and the power flow optimization results include unit output results, voltage results and network loss results.

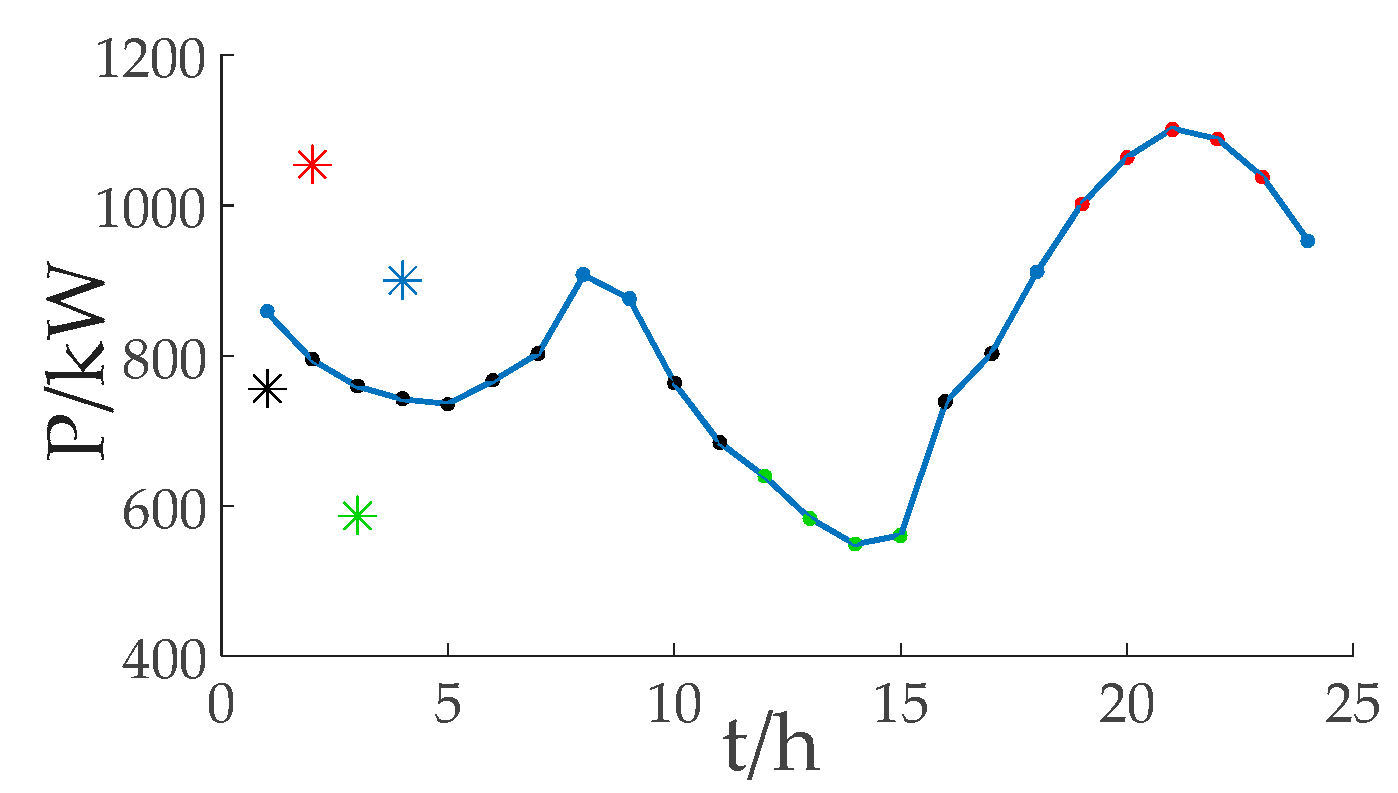
5.2.1. Time-Interval Clustering Results of Equivalent Load Curve

In this paper, the PSO algorithm is used to solve the DNMPFO model. The maximum number of iterations is set to 200, the search space dimension is 96, the number of particles is set to 50, and the inertia weight ω and learning factors $c_1, c_2$ are shown in

Table 5. Parameter settings.

Parameter	Value
$a$	0.9
$b$	0.4
$d$	2.0
$e_1,f_2$	0.5
$e_2,f_1$	2.5

.

Because the outputs of PV and WT can be regarded as negative loads, the equivalent load of the system can be obtained by subtracting the output of PV and WT from the initial load of the system (Figure 3).

Cluster analysis of the equivalent load curve: firstly, the SSE curve is obtained by the elbow rule (see Figure 4). It can be found that after k = 4, the improvement of SSE tends to be slow obviously, that is, k = 4 is the critical point, so 4 is taken as the best k value.

Then, the equivalent load curve is clustered by K-means, and the following clustering results can be obtained (see Figure 5).

As can be seen from the above figure, the period can be clustered into the following four segments (

Table 6. Period clustering result of equivalent load.

Period Sequence	Time Period
Period 1	12:00~15:00
Period 2	2:00~7:00, 10:00~11:00, 16:00~17:00
Period 3	24:00~1:00, 8:00~9:00, 18:00
Period 4	19:00~23:00

).

5.2.2. Determination of Power Flow Optimization Scheme

$C_n$ and $C_{an,n}$ are shown in

Table 7. Actual value and maximum allowable value of each period.

Parameter	Period 1	Period 2	Period 3	Period 4
$C_1$ (ten thousand yuan)	4.5833	2.9135	3.2874	4.1105
$C_2$$(\mathrm{kV}$)	0.9729	1.2616	1.3901	1.7288
$C_3$$(\mathrm{kW}·\mathrm{h}$)	0.0691	0.1134	0.1393	0.2092
$C_{an,1}$ (ten thousand yuan)	5.0894	4.5857	3.6964	4.4428
$C_{an,2}$$(\mathrm{kV}$)	1.1313	1.5232	1.5409	1.8572
$C_{an,3}$$(\mathrm{kW}·\mathrm{h}$)	0.0921	0.1559	0.1739	0.2421

.

According to Equation (21), the overweight weight of each objective function in each period can be calculated (

Table 8. Weighted value of each time period exceeding the standard.

Parameter	Period 1	Period 2	Period 3	Period 4
$f_1^{\prime }$	0.8383	0.9043	0.5760	0.5809
$f_2^{\prime }$	0.7310	0.7969	0.7608	0.9567
$f_3^{\prime }$	0.7545	0.8189	0.7977	0.9615

).

According to the normalization of Equation (20), the weighting factor of each objective function in each time period can be obtained, which is shown in

Table 9. Weighting factor of each period.

Parameter	Period 1	Period 2	Period 3	Period 4
$f_1$	0.3607	0.3588	0.2699	0.2324
$f_2$	0.3146	0.3162	0.3564	0.3828
$f_3$	0.3247	0.3249	0.3737	0.3847

.

In this paper, the following optimization schemes are set up: the weighting factor determined by FPM is adopted in the whole period, which is set as scheme 1; The weighting coefficient determined by FCE is adopted in each period, which is set as scheme 2, and then the two schemes are compared and analyzed with those before optimization.

5.2.3. DNMPFO Results under Different Schemes

(1)

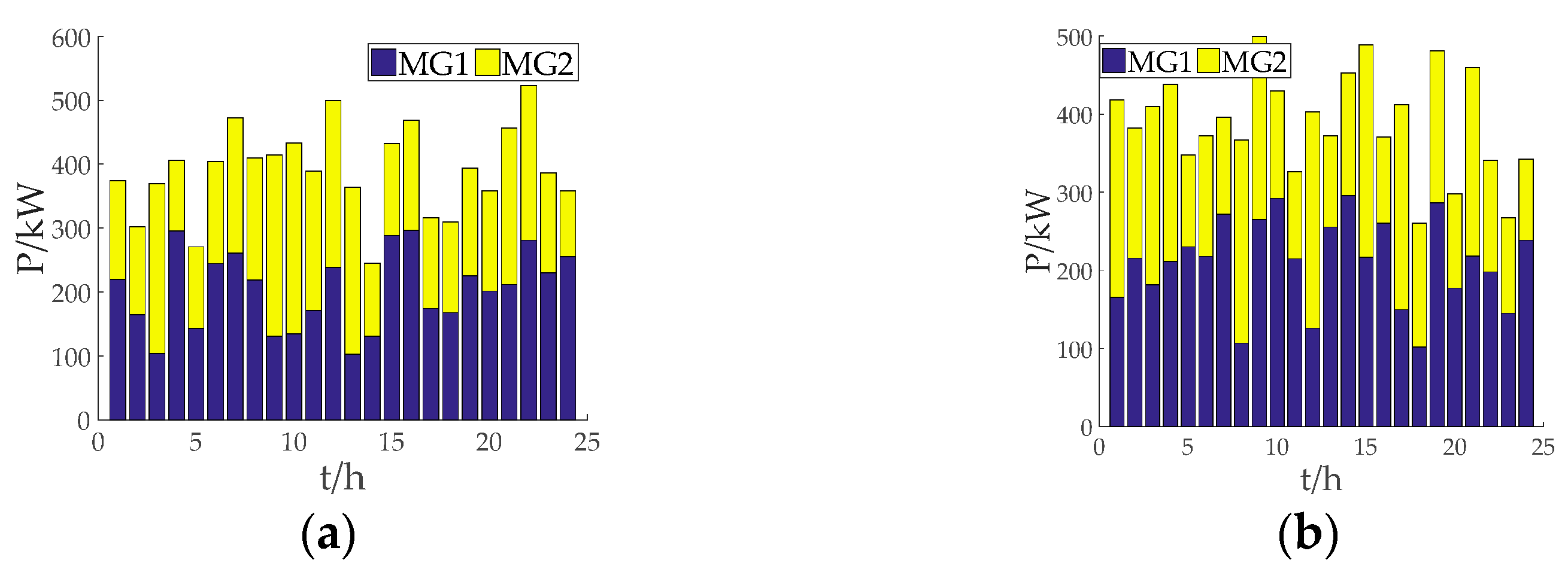
Units Output results under each scheme

The output results of MG and ESS are shown in Figure 6 and Figure 7, respectively.

(2)

Voltage results under each scheme

The voltage results are shown in Figure 8.

(3)

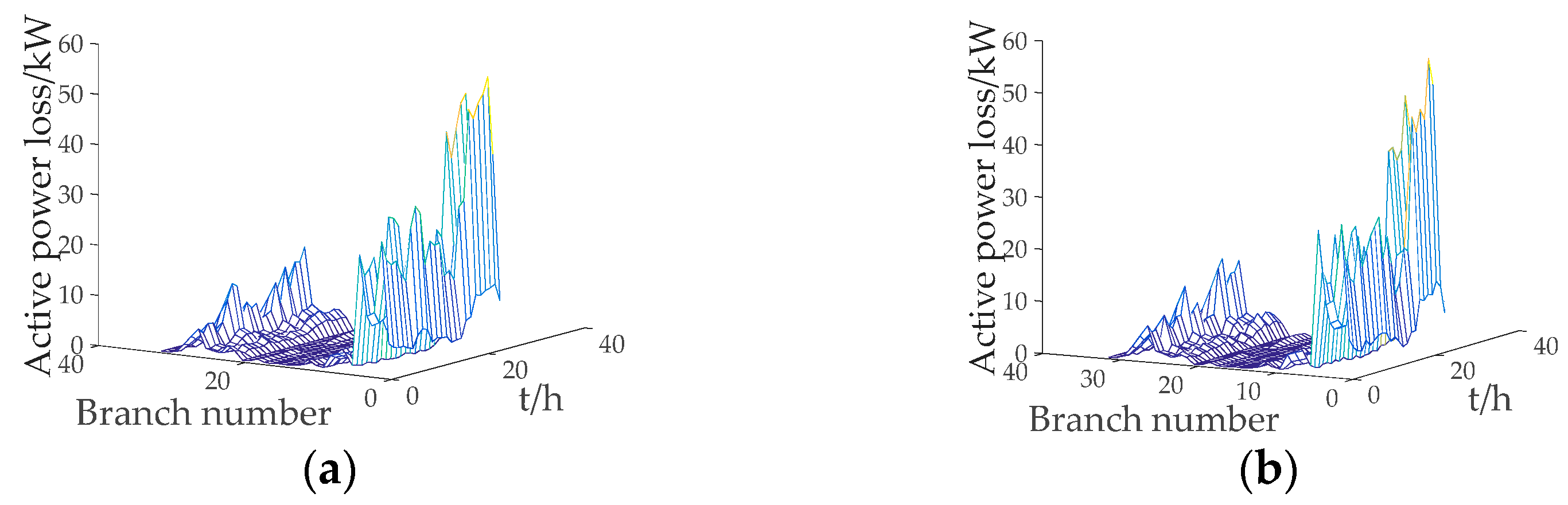
Network loss results under each scheme

The network loss results are shown in Figure 9.

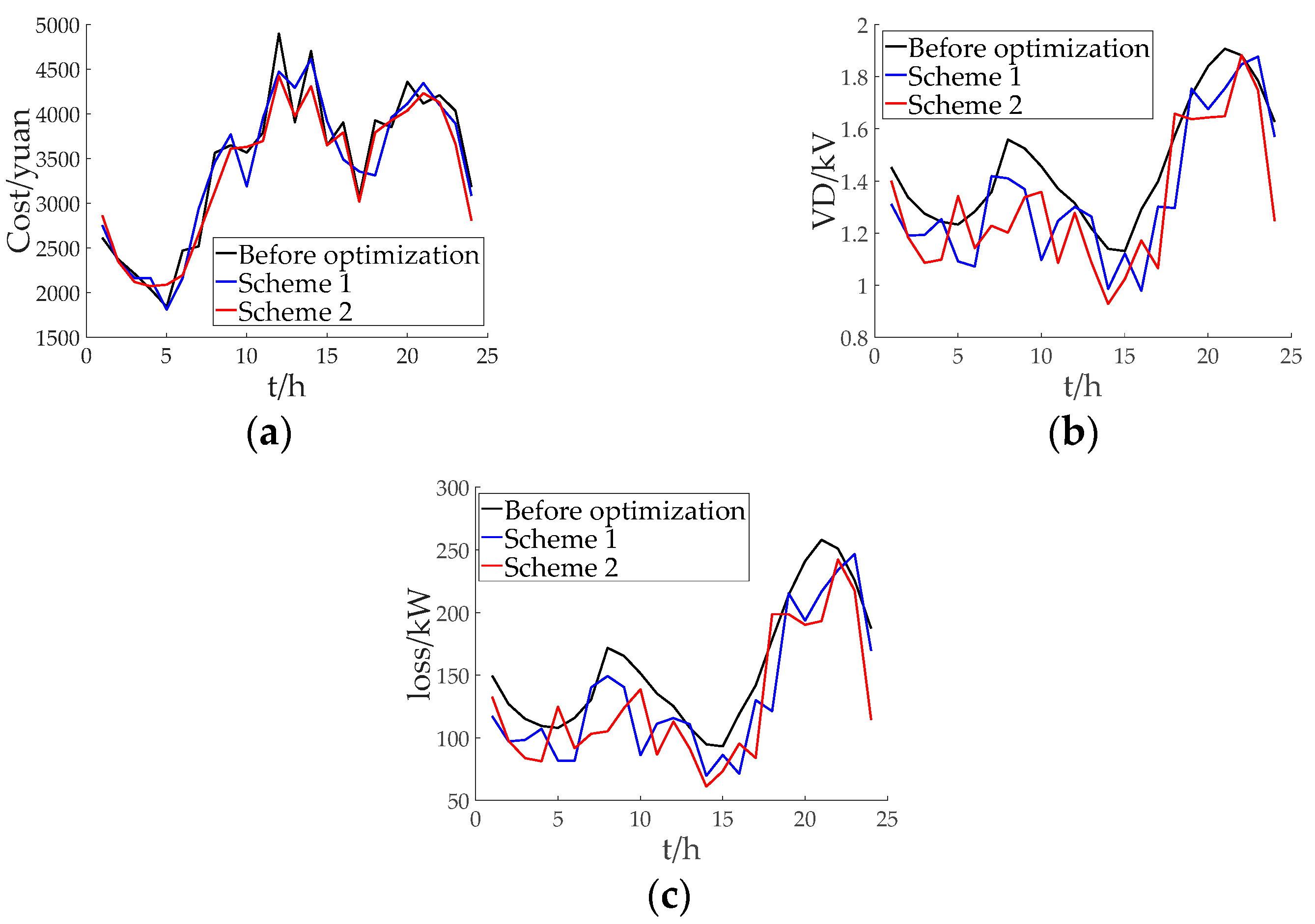
(4)

Comparison results of different schemes

The comparison results of different schemes are shown in Figure 10.

The results of each objective function before optimization, after optimization through scheme 1 and after optimization through scheme 2 are shown in

Table 10. Objective function values under different schemes.

Type	Before Optimization	Scheme 1	Scheme 2
Total cost (ten thousand yuan)	82,333.3	81,673.9	80,176.9
Total VD $\left(\mathrm{kV}\right)$	34.9305	32.3813	31.4875
Total power loss $\left(\mathrm{kW}·\mathrm{h}\right)$	3716.2	3190.2	3041.6

.

The results are analyzed in combination with Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 and Table 10.

Scheme 1: The total output of MG is higher at 7:00, 12:00, 16:00 and 21:00; ESS1 is in a state of discharge most of the time, with more discharge at 7:00~8:00 and 16:00~17:00; and ESS2 is more charged at 7~9:00, 17:00 and 23:00. The three indexes have been effectively improved compared with those before optimization, which verifies the effectiveness of the model established in this paper. Among them, the total cost decreased by 0.80%, the voltage offset decreased by 7.30% and the power loss decreased by 14.15%.

Scheme 2: The total output of MG is higher at 9:00, 15:00 and 19:00; the charging power of ESS1 reaches the limit at 8:00; ESS2 is in a state of discharge most of the time; and the discharging power reaches the maximum at 4:00. The improvement effect of the three indexes is better than that of scheme 1, which verifies the effectiveness of the strategy of determining the weight coefficient by time clustering and FCE adopted in this paper. Among them, the total cost decreased by 2.62%, the voltage offset decreased by 9.86% and the power loss decreased by 18.15%.

The MG output in scheme 2 is more than that in scheme 1, and the energy storage output is more concentrated. Both schemes conform to the law that the energy storage battery is charged at low load and discharged at peak load, thus realizing the balance between power production and consumption.

6. Conclusions

In this paper, the DNMPFO model is established, and the model is solved by PSO algorithm. The effectiveness of this method is verified based on an IEEE33-bus system. The conclusions are as follows.

(1)

When establishing the DNMPFO model, taking the lowest total cost, the lowest voltage deviation and the lowest power loss including fuel cost, operation and maintenance cost, power purchase cost and pollutant emission control cost as objective functions, and comprehensively considering multiple constraints such as power flow constraint, climbing constraint and energy storage operation constraint, it can be more in line with the actual operation situation of distribution network, and the comprehensive optimization effect is better;

(2)

K-means clustering is used to divide the equivalent load after the superposition of PV, WT and load output for 24 h a day into different periods, and FCE is used to dynamically determine the weighting factor of each period, so that the determination of the weighting factor is more reasonable and the subsequent optimization effect is better;

(3)

The results of PSO algorithm show that the calculation results of this strategy can effectively reduce the economic cost, improve the voltage deviation and reduce the power loss, thus improving the economy and reliability of power grid operation.