Using Machine Learning to Predict the Performance of a Cross-Flow Ultrafiltration Membrane in Xylose Reductase Separation
Abstract
1. Introduction
Background
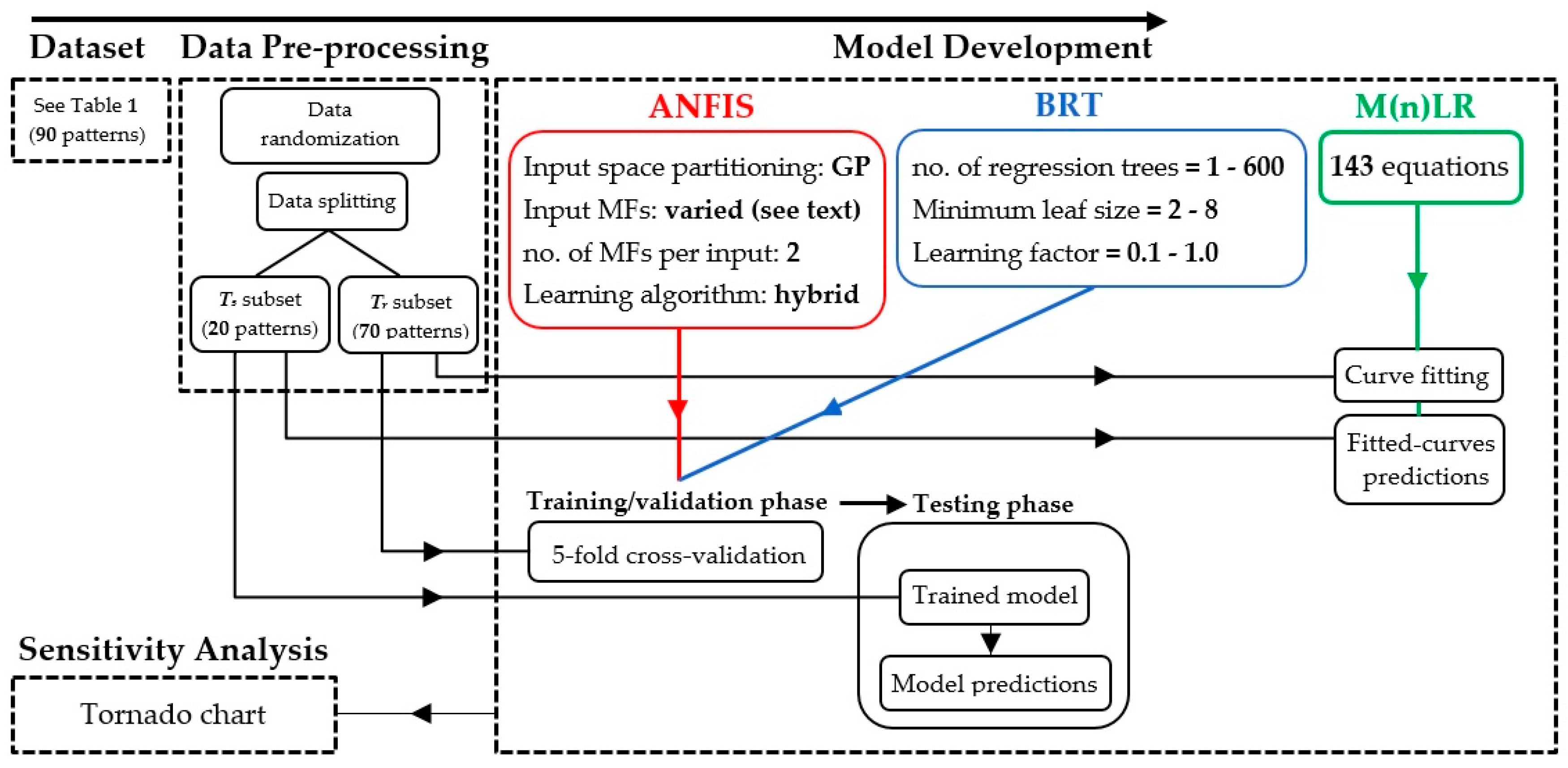
2. Methodology
2.1. Dataset
2.2. Modeling Approaches
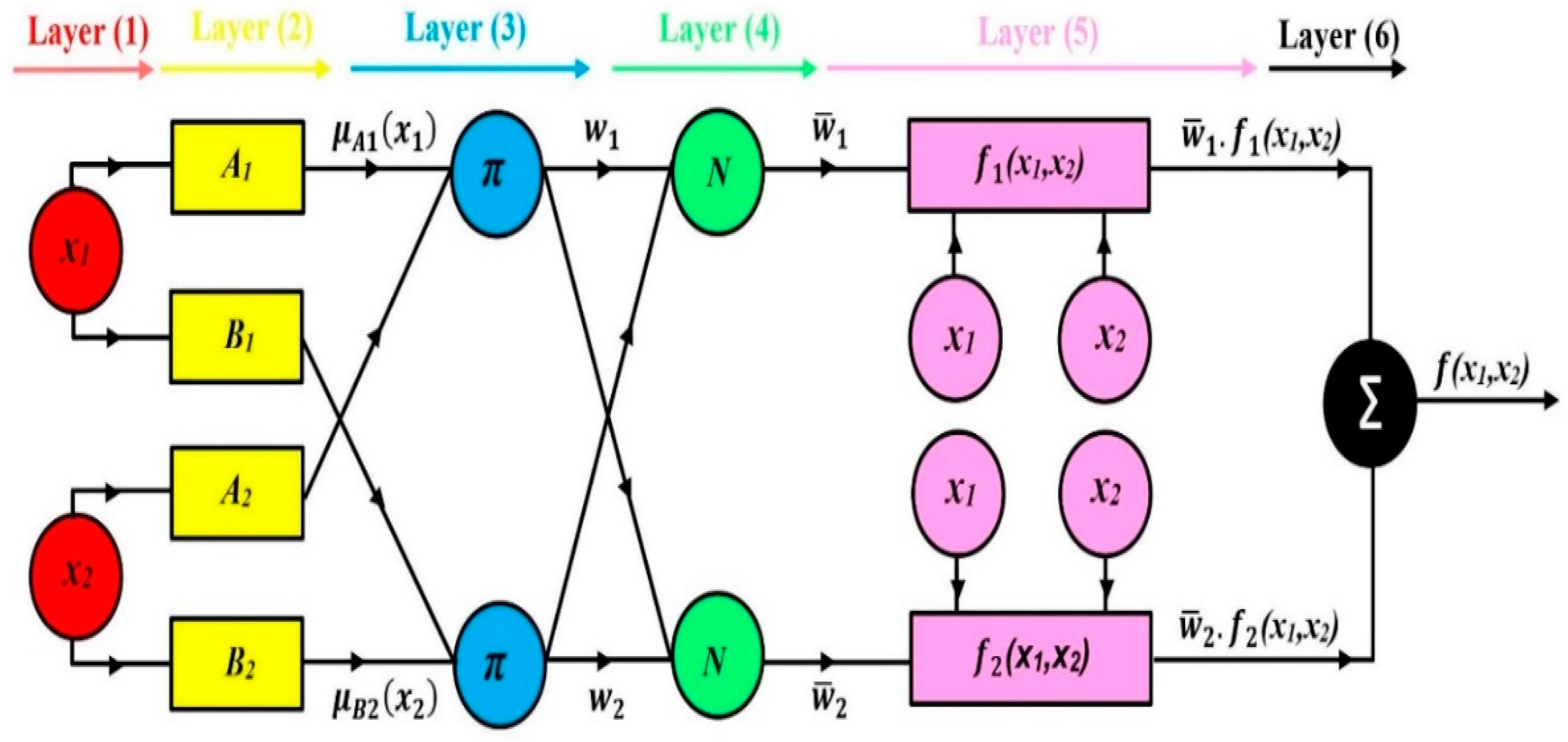
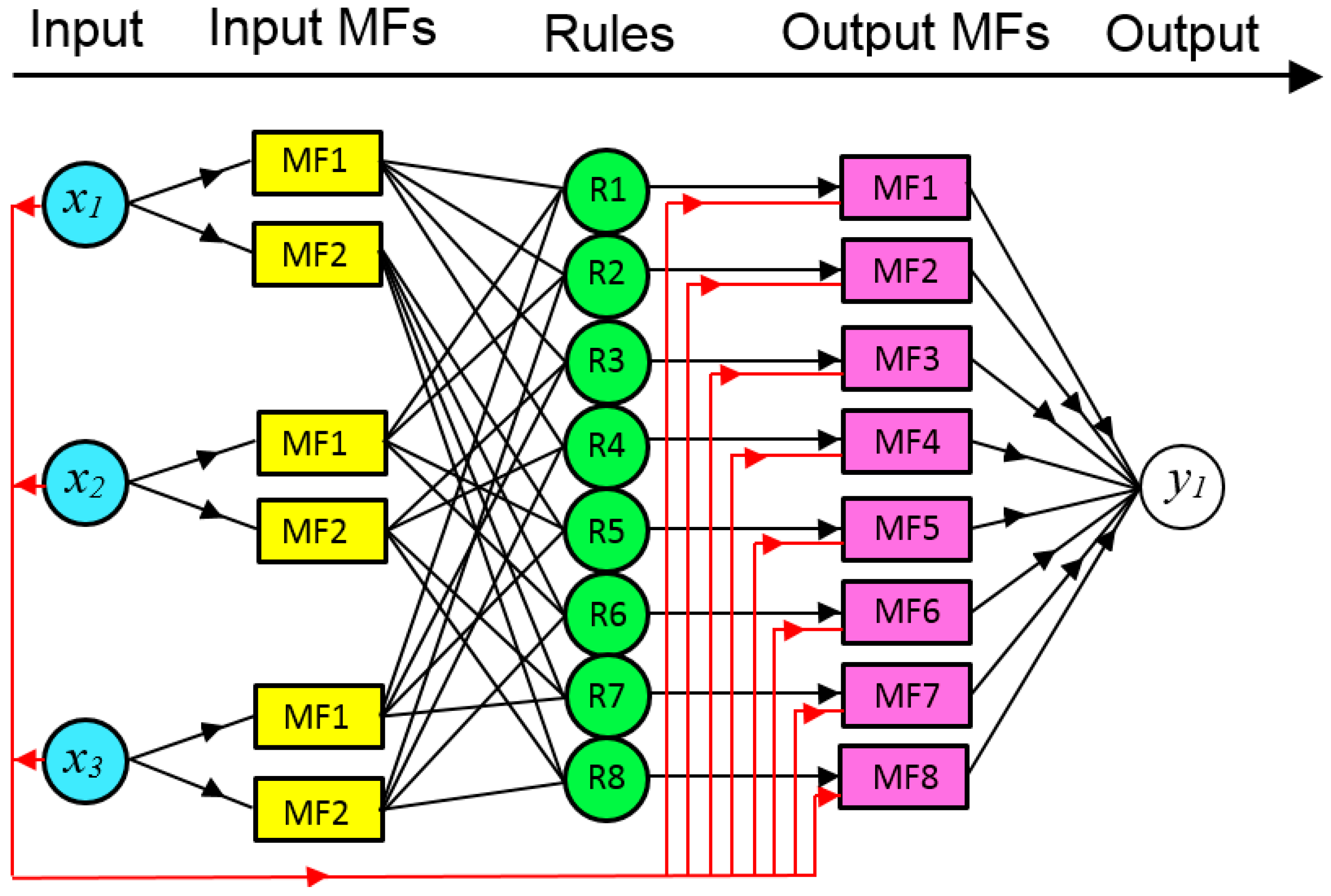
2.2.1. ANFIS Model
- ANFIS-GP
- ANFIS Parameters
- (1)
- Forward pass: The input signals go forward through the network, layer by layer, until the defuzzification layer wherein the LSE method is applied to determine the consequent parameters while the antecedent parameters remain constant.
- (2)
- Backward pass: The error signals are back propagated from the output layer to the input layer and gradient descent is used to adjust the antecedent parameters, while the consequent parameters remain constant.
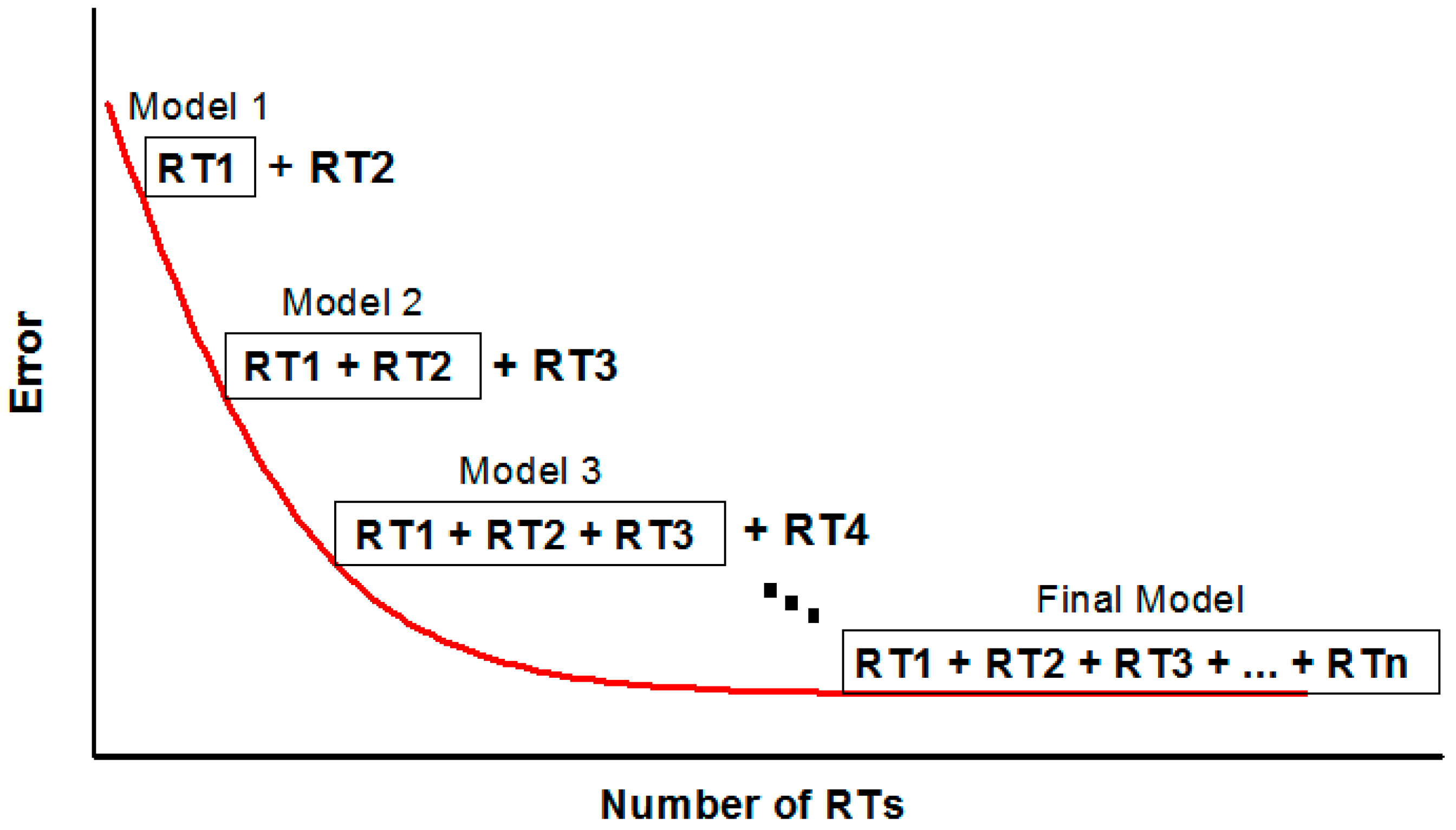
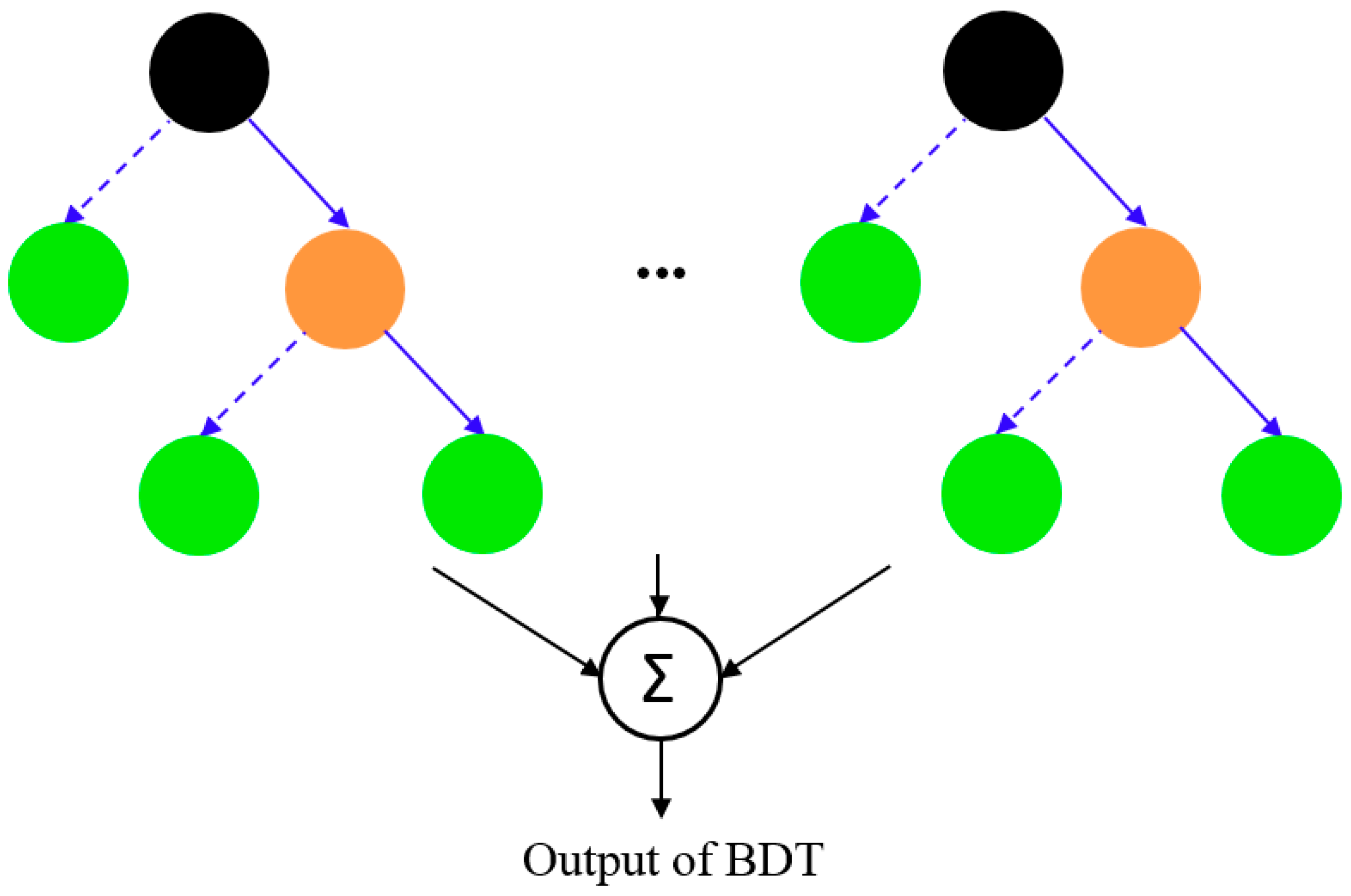
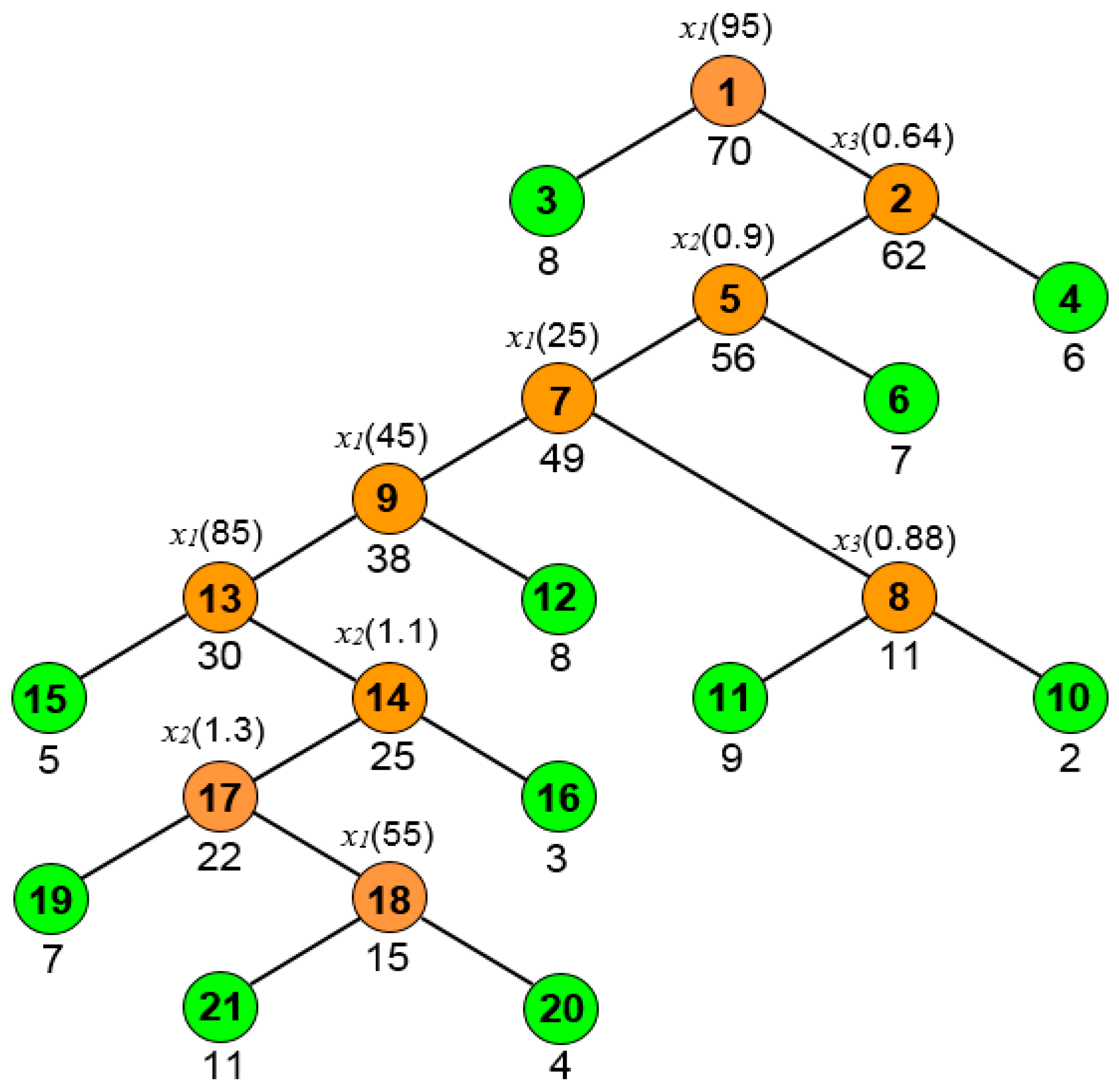
2.2.2. Boosted Regression Trees
- RT Algorithm
- Boosting
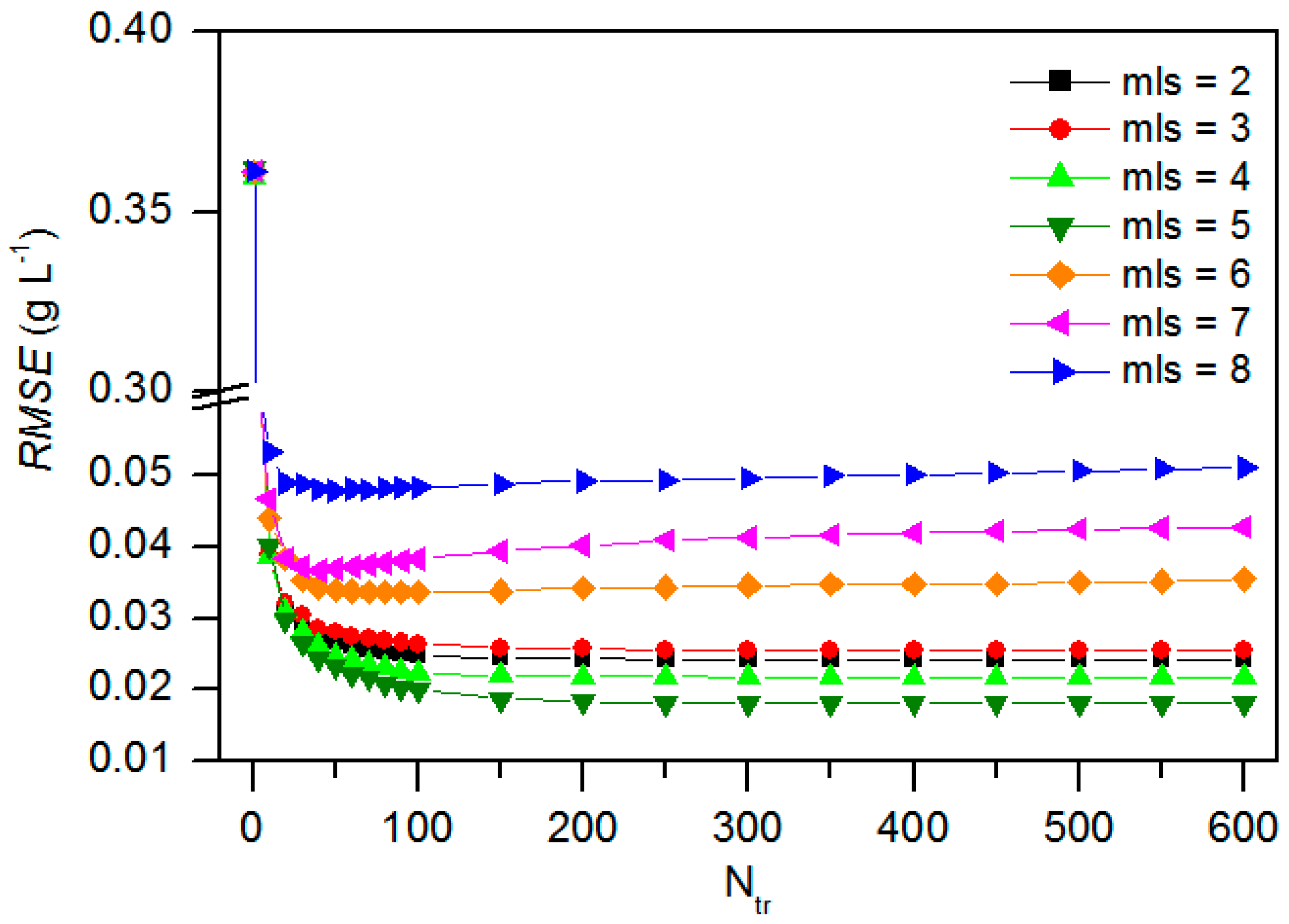
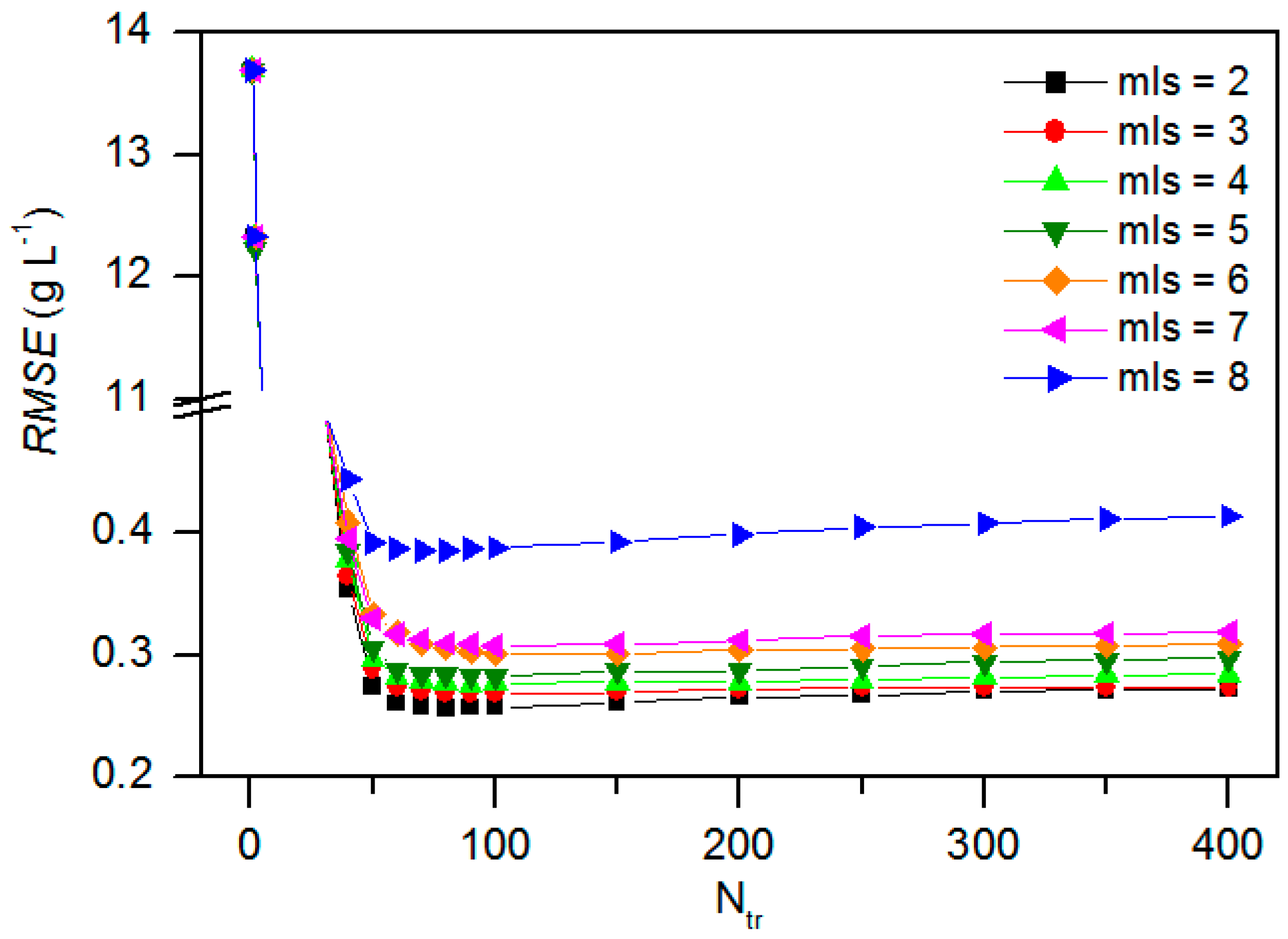
- BRT Tuning Parameters
2.2.3. Multiple Regression Analysis
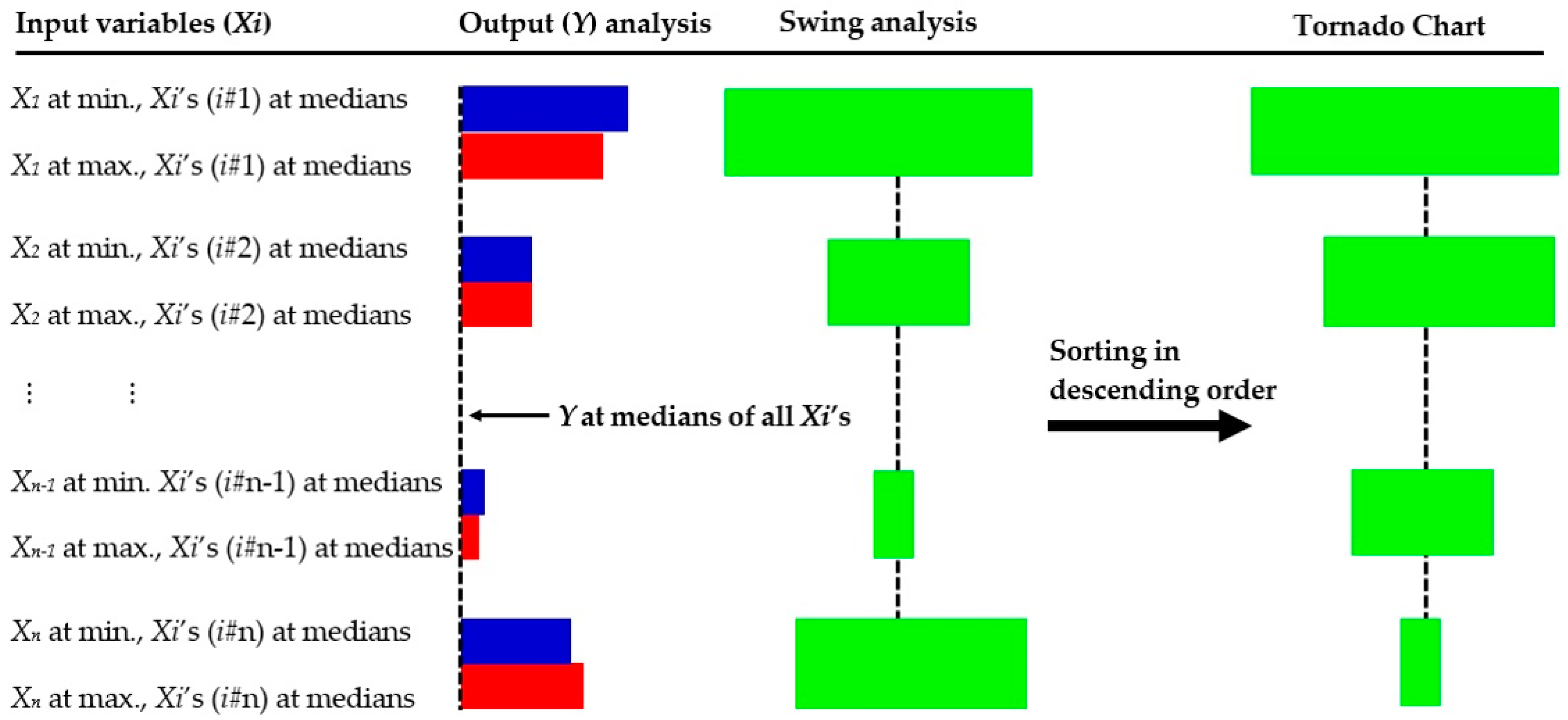
2.2.4. Sensitivity Analysis
3. Results and Discussions
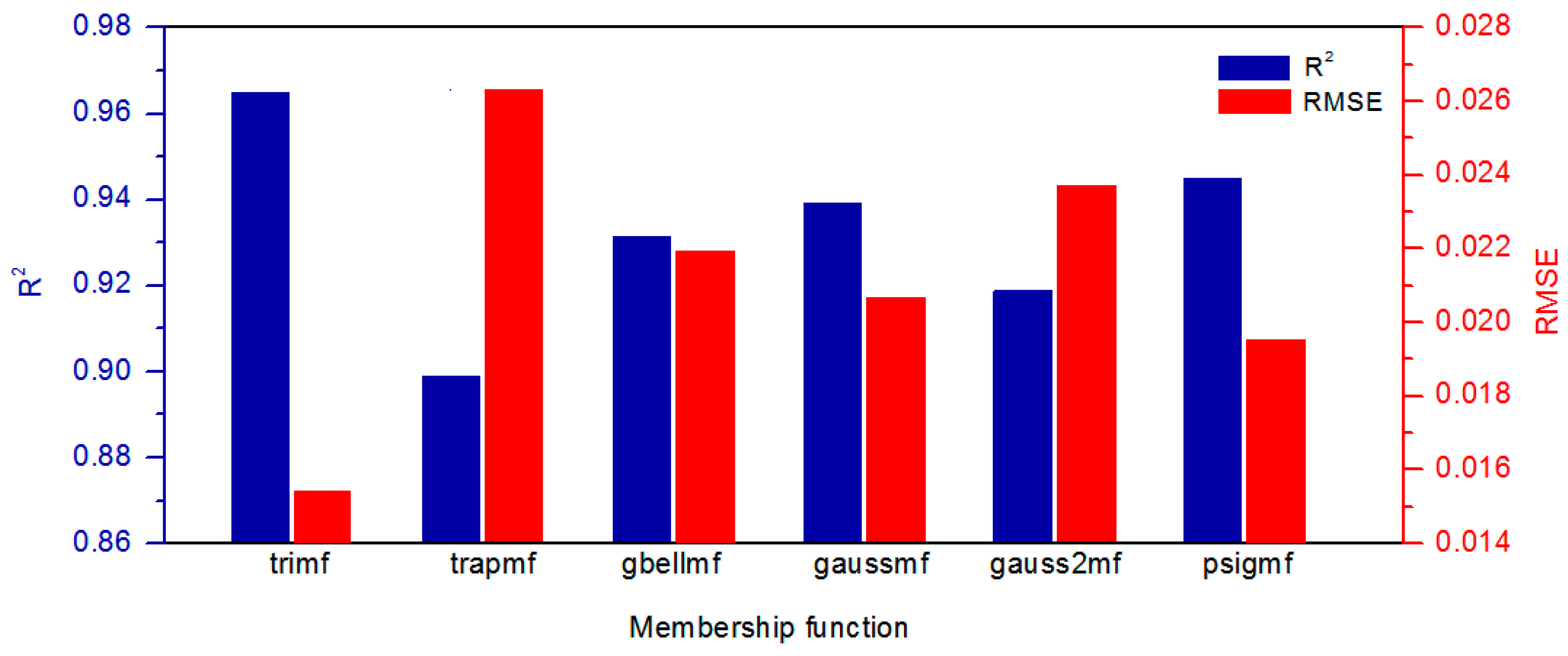
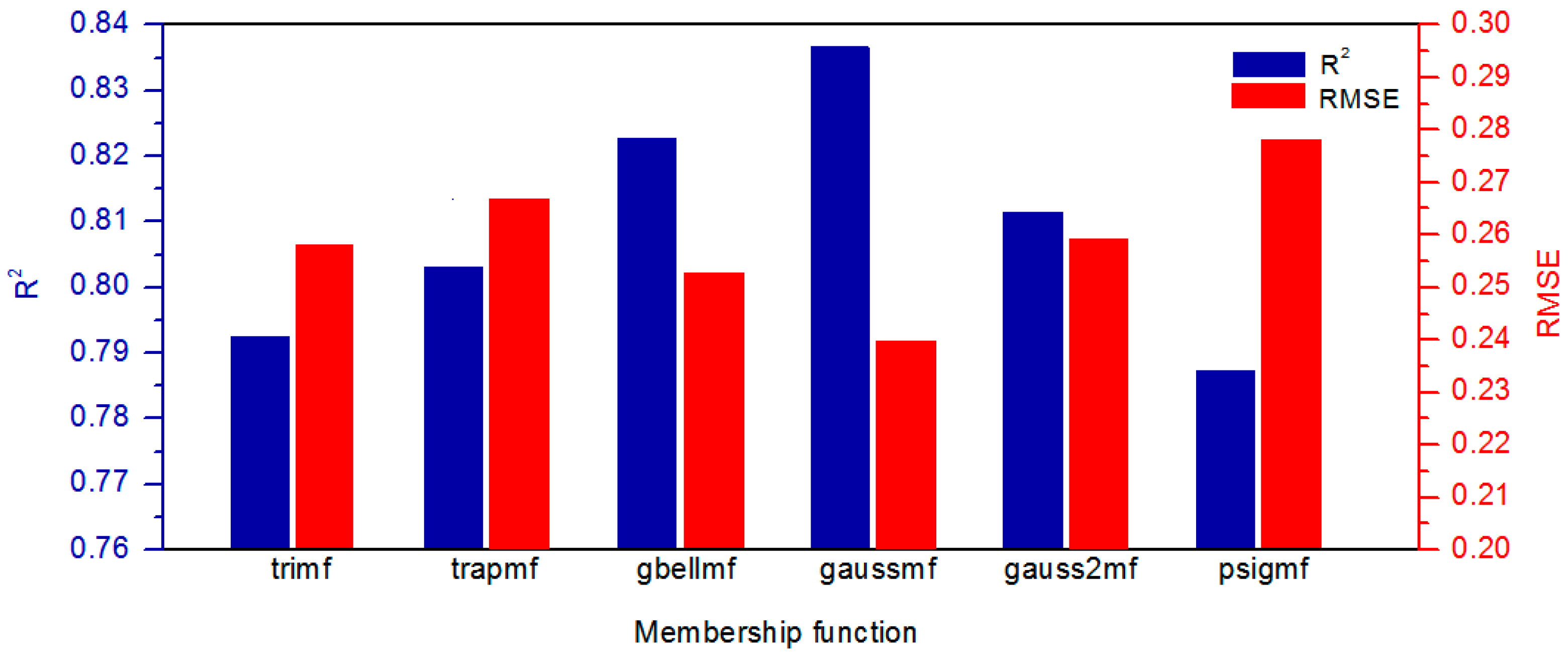
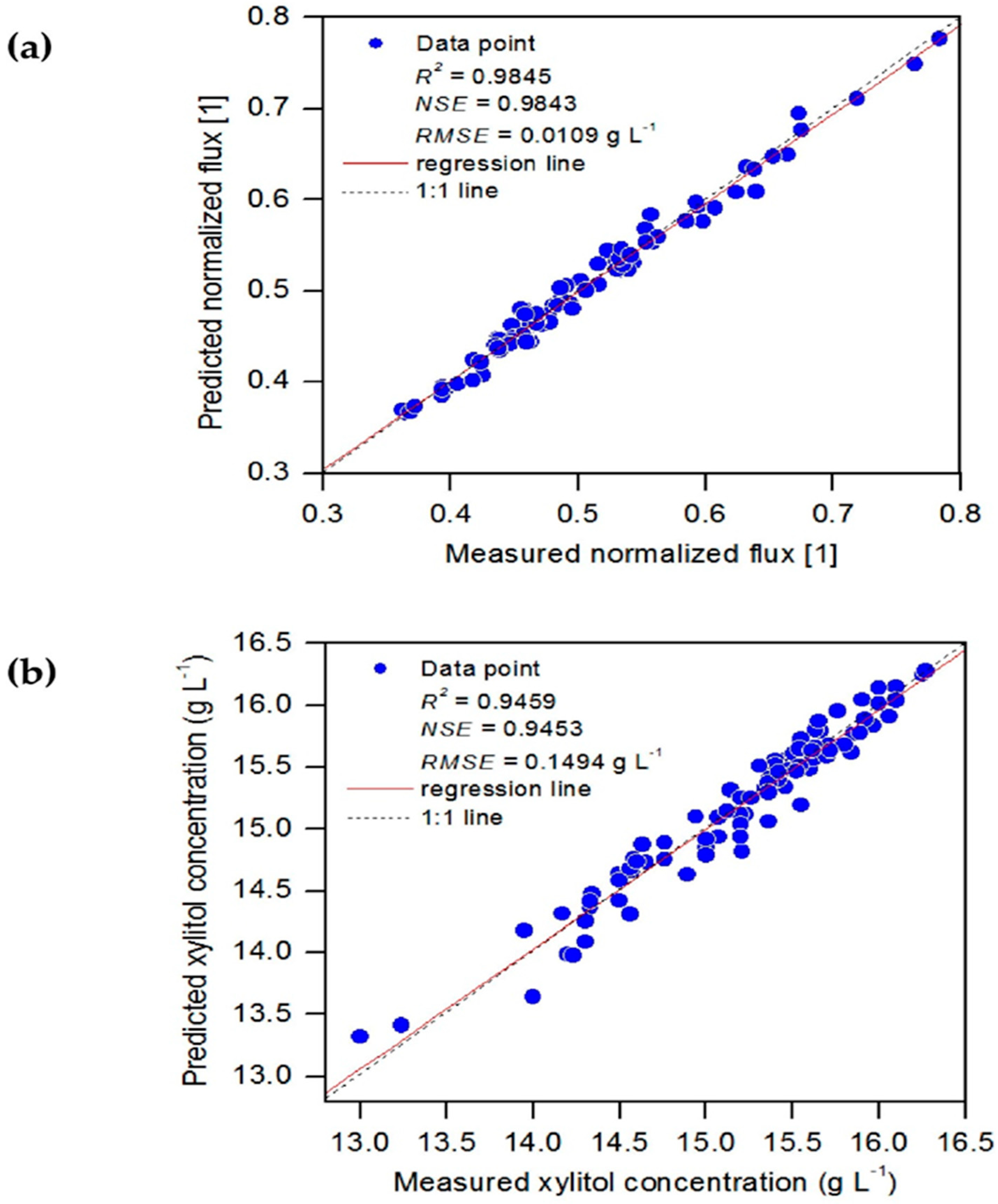
3.1. Evaluation of ANFIS-GP Model
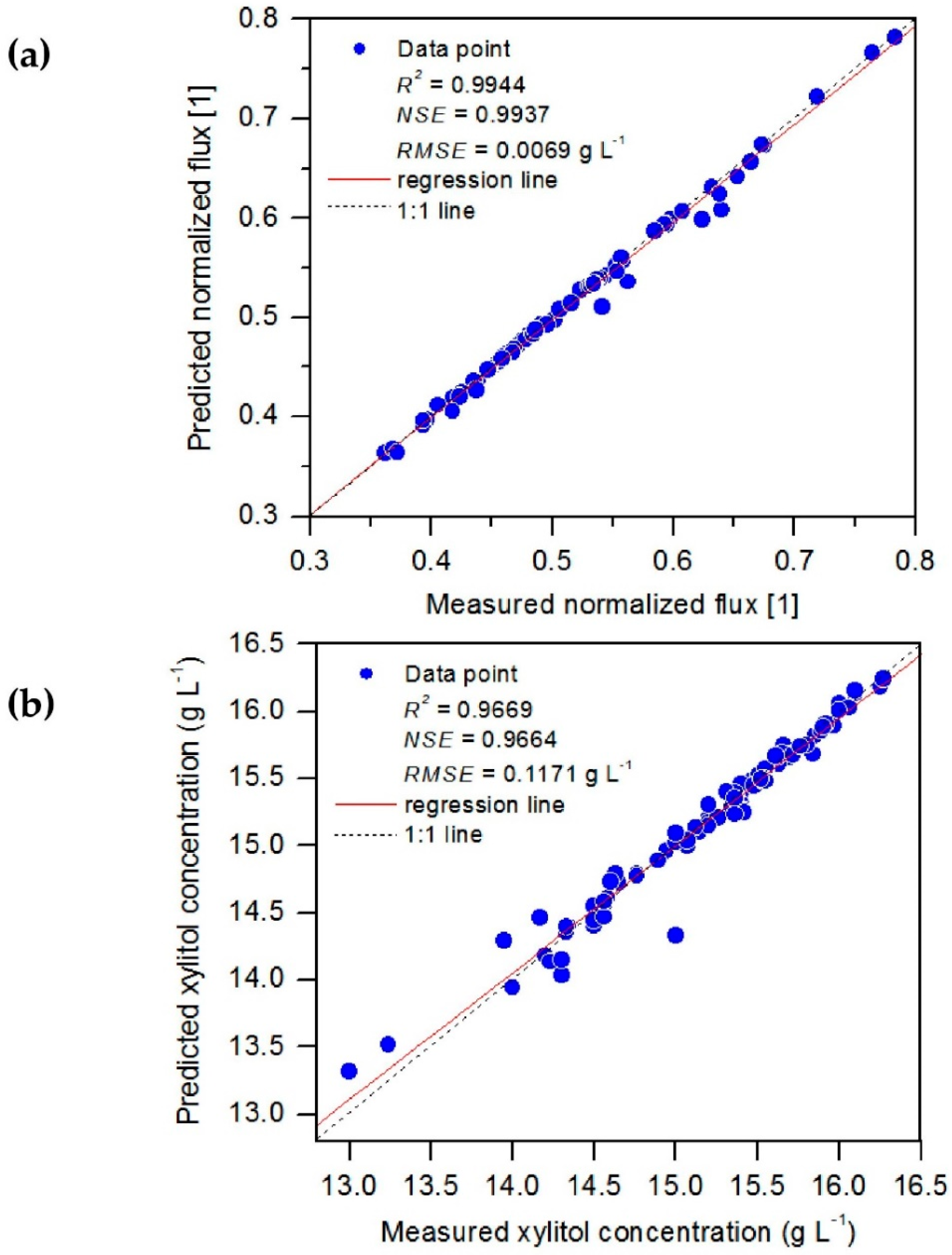
3.2. Evaluation of BRT Model
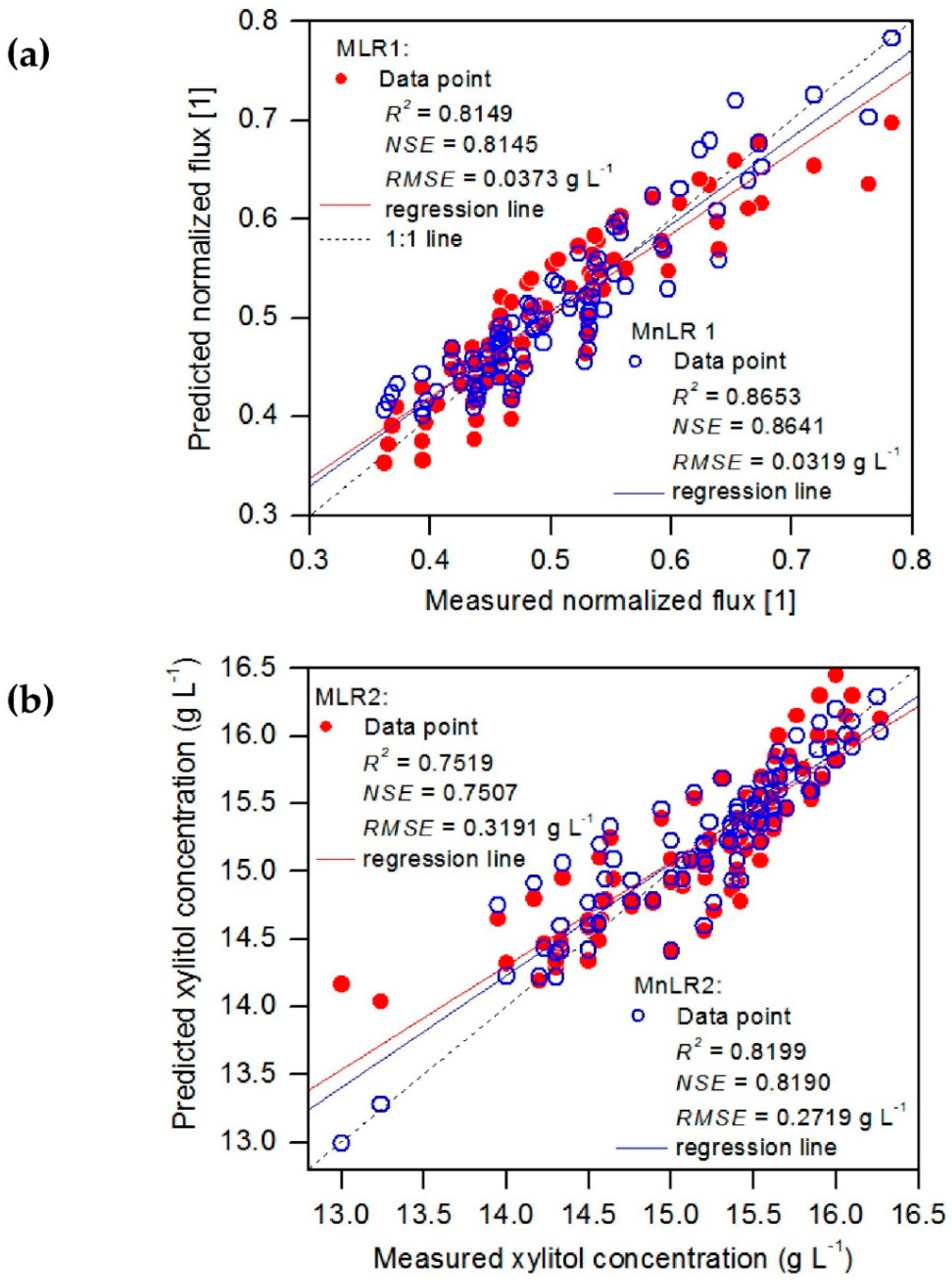
3.3. Evaluation of Regression Models
y1 = −0.0019x1 + 0.2167x2 + 0.1745x3 + 0.1845
y2 = −0.0150x1 + 1.5183x2 + 0.9941x3 + 13.2684
3.4. Comparison of the Models
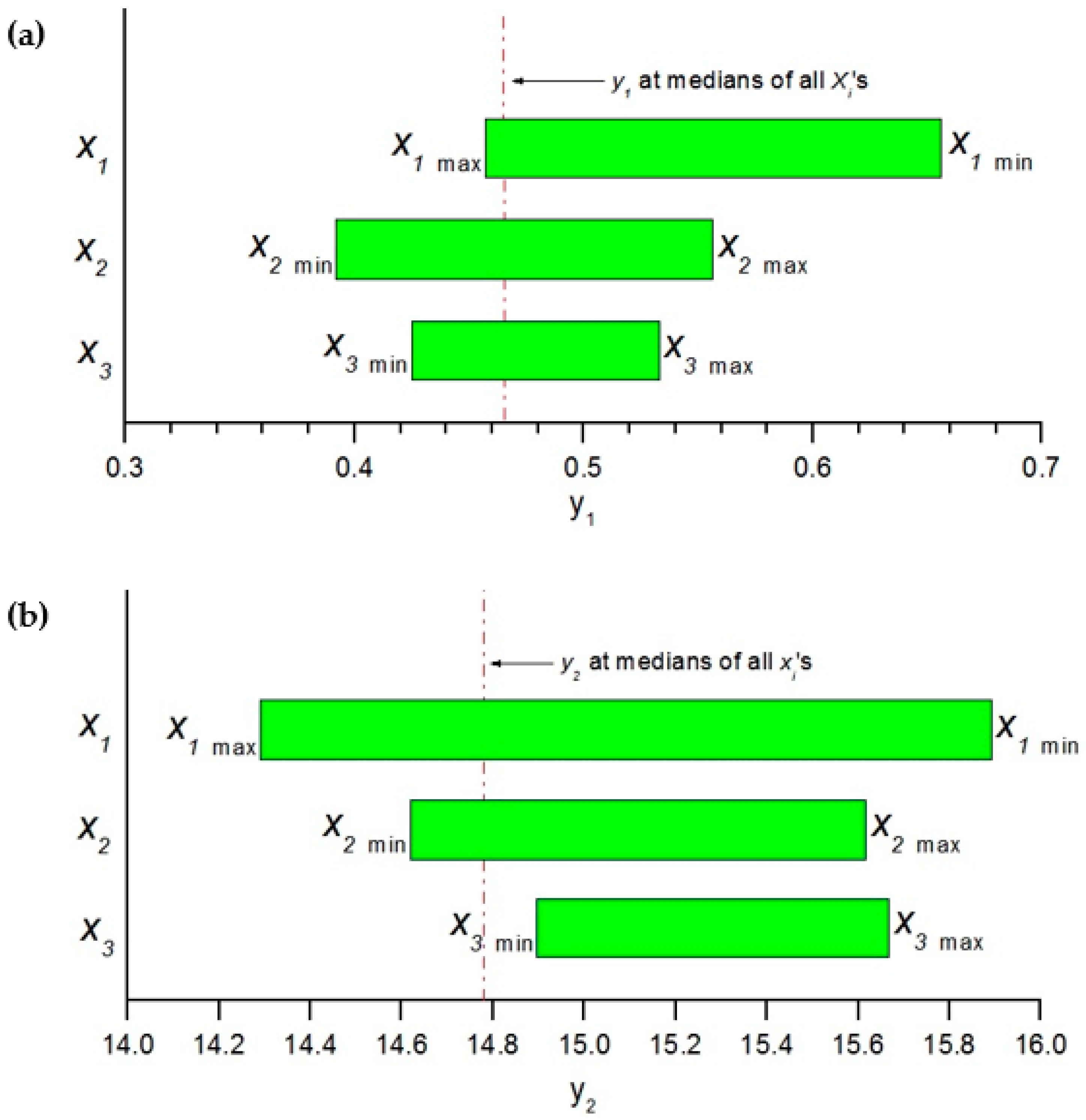
3.5. Sensitivity Analysis for Model BRT
3.6. Model Calibration and Validation Need
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AKR | aldo-keto reductase |
| ALR | aldehyde reductase |
| ANFIS-GP | adaptive neuro-fuzzy inference system based on grid partitioning on the input space |
| ANN | artificial neural network |
| Ai, Bi | fuzzy sets pertaining to input variable xi |
| ai, bi, ci | antecedent parameters corresponding to the i-th output function |
| BP | backpropagation |
| BRT | boosted regression tree |
| c | cut-off point |
| CF-UF | cross-flow ultrafiltration |
| CV | cross-validation |
| FBPNN | feedforward backpropagation neural network |
| FIS | fuzzy inference system |
| fi | output function of the i-th fuzzy rule |
| GP | grid partitioning |
| GUI | graph user interface |
| gaussmf | Gaussian membership function |
| gauss2mf | combination of two Gaussian membership function |
| gbellmf | generalized bell-shaped membership function |
| LSE | least squared estimation |
| M | number of membership functions assigned to each input |
| MF | membership function |
| MLR | multiple linear regression |
| mls | minimum leaf size |
| MnLR | multiple nonlinear regression |
| N | number of inputs to the ANFIS model |
| NA | number of antecedent parameters |
| NC | number of consequent parameters |
| NR | number of fuzzy rules |
| n | total number of observations |
| NADPH | reduced form of nicotinamide adenine dinucleotide phosphate (donor of hydrogen atoms) |
| NSE | Nash–Sutcliffe efficiency coefficient |
| P | number of input MFs |
| psigmf | product of two sigmoidal membership function |
| R2 | coefficient of determination |
| RMSE | root mean squared error |
| r | vector of residuals |
| RT | regression tree |
| SSR | sum of squared residuals |
| trapmf | trapezoidal membership function |
| trimf | triangular membership function |
| UF | ultrafiltration |
| wi | synaptic weight assigned to the signal leaving the i-th neuron with the hid den layer |
| XR | xylose reductase |
| x1 | FT (filtration time; min) |
| x2 | TMP (transmembrane pressure; bar) |
| x3 | CFV (cross-flow velocity; cm s−1) |
| y1 | normalized flux (i.e., ratio of the permeate flux to the pure water flux) |
| y2 | xylitol concentration (g L−1) |
| yip | model-predicted value for the i-th observation |
| averaged value of yi | |
| output value computed at xi set to its minimum value | |
| output value computed at xi set to its maximum value | |
| μji (xi) | membership function of j-th fuzzy set associated with input variable xi |
| α | learning rate (step size or shrinkage factor) |
References
- Jez, J.M.; Penning, T.M. The aldo-keto reductase (AKR) superfamily: An update. Chem. Biol. Interact. 2001, 130–132, 499–525. [Google Scholar] [CrossRef]
- Krishnan, S.; Nasrullah, M.; Kamyab, H.; Suzana, N.; Munaim, M.S.A.; Wahid, Z.A.; Ali, I.H.; Salehi, R.; Chaiprapat, S. Fouling characteristics and cleaning approach of ultrafiltration membrane during xylose reductase separation. Bioprocess Biosyst. Eng. 2022, 45, 1125–1136. [Google Scholar] [CrossRef]
- Azizah, N. Biotransformation of xylitol production from xylose of lignocellulose biomass using xylose reductase enzyme: Review. J. Food Life Sci. 2019, 3, 103–112. [Google Scholar]
- Umai, D.; Kayalvizhi, R.; Kumar, V.; Jacob, S. Xylitol: Bioproduction and applications-A review. Front. Sustain. 2022, 3, 826190. [Google Scholar] [CrossRef]
- Lugani, Y.; Sooch, B.S. Fermentative production of xylitol from a newly isolated xylose reductase producing Pseudomonas putida BSX-46. LWT-Food Sci. Technol. 2020, 134, 109988. [Google Scholar] [CrossRef]
- Narisetty, V.; Castro, E.; Durgapal, S.; Coulon, F.; Jacob, S.; Kumar, D.; Awasthi, M.K.; Pant, K.K.; Parameswaran, B.; Kumar, V. High level xylitol production by Pichia fermentans using non-detoxified xylose-rich sugarcane bagasse and olive pits hydrolysates. Bioresour. Technol. 2021, 342, 126005. [Google Scholar] [CrossRef]
- Saha, B.C.; Kennedy, G.J. Production of xylitol from mixed sugars of xylose and arabinose without co-producing arabitol. Biocatal. Agric. Biotechnol. 2020, 29, 101786. [Google Scholar] [CrossRef]
- Lugani, Y.; Puri, M.; Sooch, B.S. Recent insights, applications and prospects of xylose reductase: A futuristic enzyme for xylitol production. Eur. Food Res. Technol. 2021, 247, 921–946. [Google Scholar] [CrossRef]
- Ho, N.W.Y.; Lin, F.P.; Huang, S.; Andrewst, P.C.; Tsao, G.T. Purification, characterization, and amino terminal sequence of xylose reductase from Candida shehatae. Enzym. Microb. Technol. 1990, 12, 33–39. [Google Scholar] [CrossRef]
- Eryasar, K.; Karasu-Yalcin, S. Evaluation of some lignocellulosic byproducts of food industry for microbial xylitol production by Candida tropicalis. 3 Biotech 2016, 6, 202. [Google Scholar] [CrossRef]
- Ariyan, M.; Uthandi, S. Xylitol production by xylose reductase over producing recombinant Escherichia coli M15. Madras Agric. J. 2019, 106, 205–209. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Sung, B.H. Isolation and characterization of the stress-tolerant Candida tropicalis YHJ1 and evaluation of its xylose reductase for xylitol production from acid pre-treatment wastewater. Front. Bioeng. Biotechnol. 2019, 7, 12. [Google Scholar] [CrossRef]
- Walsh, M.K.; Khliaf, H.F.; Shakir, K.A. Production of xylitol from agricultural waste by enzymatic methods. Am. J. Agric. Biol. Sci. 2018, 13, 1–8. [Google Scholar] [CrossRef]
- Kklaif, H.F.; Nasser, J.M.; Shakir, K.A. Production of xylose reductase and xylitol by Candida guilliermondii using wheat straw hydrolysates. Iraqi J. Agric. Sci. 2020, 51, 1653–1660. [Google Scholar]
- Quehenberger, J.; Reichenbach, T.; Baumann, N.; Rettenbacher, L.; Divne, C.; Spadiut, O. Kinetics and predicted structure of a novel xylose reductase from Chaetomium thermophilum. Int. J. Mol. Sci. 2019, 20, 185. [Google Scholar] [CrossRef]
- Mouro, A.; dos Santos, A.A.; Agnolo, D.D.; Gubert, G.F.; Bon, E.P.S.; Rosa, C.A.; Fonseca, C.; Stambuk, B.U. Combining xylose reductase from Spathaspora arborariae with xylitol dehydrogenase from Spathaspora passalidarum to promote xylose consumption and fermentation into xylitol by Saccharomyces cerevisiae. Fermentation 2020, 6, 72. [Google Scholar] [CrossRef]
- Woodyer, R.; Simurdiak, M.; van der Donk, W.A.; Zhao, H. Heterologous expression, purification, and characterization of a highly active xylose reductase from Neurospora crassa. Appl. Environ. Microbiol. 2005, 71, 1642–1647. [Google Scholar] [CrossRef]
- Mueller, M.; Wilkins, M.R.; Banat, I.M. Production of xylitol by the thermotolerant Kluyveromyces marxianus IMB strains. Bioprocess. Biotech. 2011, 1, 1000102e. [Google Scholar] [CrossRef]
- Dasgupta, D.; Ghosh, D.; Bandhu, S.; Agrawal, D.; Suman, S.K.; Adhikari, D.K. Purification, characterization and molecular docking study of NADPH dependent xylose reductase from thermotolerant Kluyveromyces sp. IIPE453. Process Biochem. 2016, 51, 124–133. [Google Scholar] [CrossRef]
- Krishnan, S.; Suzan, B.N.; Wahid, Z.A.; Nasrullah, M.; Munaim, M.S.A.; MD Din, M.F.B.; Taib, S.M.; Li, Y.Y. Optimization of operating parameters for xylose reductase separation through ultrafiltration membrane using response surface methodology. Biotechnol. Rep. 2020, 27, e00498. [Google Scholar] [CrossRef]
- Desiriani, R.; Kresnowati, M.T.A.P.; Wenten, I.G. Membrane-based downstream processing of microbial xylitol production. Int. J. Technol. 2017, 8, 1393–1401. [Google Scholar] [CrossRef]
- Conidi, C.; Drioli, E.; Cassano, A. Membrane-based agro-food production processes for polyphenol separation, purification and concentration. Curr. Opin. Food Sci. 2018, 23, 149–164. [Google Scholar] [CrossRef]
- Cordova, A.; Astudillo, C.; Illanes, A. Membrane technology for the purification of enzymatically produced oligosaccharides. In Separation of Functional Molecules in Food by Membrane Technology; Elsevier: Amsterdam, The Netherlands, 2019; pp. 113–153. [Google Scholar]
- Mukherjee, S. Isolation and purification of industrial enzymes: Advances in enzyme technology. Adv. Enzym. Technol. (Biomass Biofuels Biochem.) 2019, 41–70. [Google Scholar] [CrossRef]
- Michaels, A.S. New separation techniques for the CPI. Chem. Eng. Process. 1968, 64, 31–42. [Google Scholar]
- Vilker, V.L.; Colton, C.K.; Smith, K.A.; Green, D.L. The osmotic pressure of concentrated protein and lipoprotein solutions and its significance to ultrafiltration. J. Membr. Sci. 1984, 20, 63–77. [Google Scholar] [CrossRef]
- Bellara, S.R.; Cui, Z. A Maxwell-Stefan approach to modeling the cross flow ultrafiltration of protein solutions in tubular membranes. Chem. Eng. Sci. 1998, 53, 2153–2166. [Google Scholar] [CrossRef]
- Wesselingh, J.A.; Vonk, P. Ultrafiltration of a large polyelectrolyte. J. Membr. Sci. 1995, 99, 21–27. [Google Scholar] [CrossRef]
- Ahmad, A.L.; Chong, M.F.; Bhatia, S. Ultrafiltration modeling of multiple solutes system for continuous cross flow process. Chem. Eng. Sci. 2006, 61, 5057–5069. [Google Scholar] [CrossRef]
- Karasu, K.; Yoshikawa, S.; Kentish, S.E.; Stevens, G.W. A model for cross flow filtration of dairy whey based on the rheology of the compressible cake. J. Membr. Sci. 2009, 341, 252–260. [Google Scholar] [CrossRef]
- Landman, K.A.; Sirakoff, C.; White, L.R. Dewatering of flocculated suspensions by pressure filtration. Phys. Fluids Fluid Dyn. 1991, 3, 1495–1509. [Google Scholar] [CrossRef]
- Landman, K.A.; White, L.R.; Eberl, M. Pressure filtration of flocculated suspensions. AIChE J. 1995, 41, 1687–1700. [Google Scholar] [CrossRef]
- Lawrence, N.D. Characterisation and Performance of Ultrafiltration Membranes in the Dairy Industry. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 1998. [Google Scholar]
- Nguyen, T.A.; Yoshikawa, S.; Karasu, K.; Ookawara, S. A simple combination model for filtrate flux in cross flow ultrafiltration of protein suspension. J. Membr. Sci. 2012, 403–404, 84–93. [Google Scholar] [CrossRef]
- Kirschner, A.Y.; Cheng, Y.H.; Paul, D.R.; Field, R.W.; Freeman, B.D. Fouling mechanisms in constant flux cross flow ultrafiltration. J. Membr. Sci. 2019, 574, 65–75. [Google Scholar] [CrossRef]
- Hermia, J. Constant pressure blocking filtration laws—Application of power-law non-Newtonian fluids. Trans. Am. Inst. Chem. Eng. 1982, 60, 183–187. [Google Scholar]
- Field, R.W.; Wu, J.J. Modeling of permeability loss in membrane filtration: Re-examination of fundamental fouling equations and their link to critical flux. Desalination 2011, 283, 68–74. [Google Scholar] [CrossRef]
- Cheryan, M. Ultrafiltration and Microfiltration Handbook; CRC Press: Roca Raton, FL, USA, 1998. [Google Scholar]
- Krippl, M.; Durauer, A.; Duerkoa, M. Hybrid modeling of cross filtration: Predicting the flux evolution and duration of ultrafiltration processes. Sep. Purif. 2020, 248, 117064. [Google Scholar] [CrossRef]
- Sargolzaei, J.; Saghatoleslami, N.; Mosavi, S.M.; Khoshnoodi, M. Comparative study of artificial neural network (ANN) and statistical methods for predicting the performance of ultrafiltration process in the milk industry. Iran J. Chem. Chem. Eng. 2006, 25, 67–76. [Google Scholar]
- Teodosiu, C.; Pastravanu, O.; Macoveanu, M. Neural network models for ultrafiltration and backwashing. Water Res. 2000, 34, 4371–4380. [Google Scholar] [CrossRef]
- Wei, A.L.; Zeng, G.M.; Huang, G.H.; Liang, J.; Li, X.D. Modeling of a permeate flux of cross-flow membrane filtration of colloidal suspensions: A wavelet network approach. Int. J. Environ. Sci. Technol. 2009, 6, 395–406. [Google Scholar] [CrossRef]
- Bowen, W.R.; Jones, M.G.; Yousef, H.N.S. Prediction of the rate of cross flow membrane ultrafiltration of colloids: A neural network approach. Chem. Eng. Sci. 1998, 53, 3793–3802. [Google Scholar] [CrossRef]
- Hussain, W.; Merigo, J.M.; Reza, M.R. Predictive intelligence using ANFIS-induced OWAWA for complex stock market prediction. Int. J. Intell. Syst. 2022, 37, 4586–4611. [Google Scholar] [CrossRef]
- Al-qaness, M.A.A.; Ewees, A.A.; Fan, H.; Abualigah, L.; Abd Elaziz, M. Boosted ANFIS model using augmented marine predator algorithm with mutation operators for wind power forecasting. Appl. Energy 2022, 314, 118851. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its application to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Zivkovic, M.; Bacanin, N.; Venkatachalam, K.; Nayyar, A.; Djordjevic, A.; Strumbeger, I.; Al-Turjman, F. COVID-19 cases prediction by using hybrid machine learning and beetle antennae search approach. Sustain. Cities Soc. 2021, 66, 102669. [Google Scholar] [CrossRef]
- Salehi, R.; Chaiprapat, S. Predicting H2S emission from gravity sewer using an adaptive neuro-fuzzy inference system. Water Qual. Res. J. 2022, 57, 20–39. [Google Scholar] [CrossRef]
- Khaled, B.; Abdellah, A.; Noureddine, D.; Salim, H.; Sabeha, A. Modelling of biochemical oxygen demand from limited water quality variable by ANFIS using two partition methods. Water Qual. Res. J. 2018, 53, 24–40. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing (A Computational Approach to Learning and Machine Intelligence); Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Karim, R.; Dilwar, F.; Siddique, R.A. Predictive modeling of surface roughness in MQL assisted turning of SiC-Al alloy composites using artificial neural network and adaptive neuro fuzzy inference system. J. Adv. Res. Manuf. Mater. Sci. Metall. Eng. 2018, 5, 12–28. [Google Scholar]
- Keneni, B.M. Evolving Rule Based Explainable Artificial Intelligence for Decision Support System of Unmanned Aerial Vehicles. Master’s Thesis, University of Toledo, Electrical and Computer Science Engineering Department, Toledo, OH, USA, 2018. [Google Scholar]
- Clemente, L. ANFIS Modelling of PIV Tests. Master’s Thesis, Department of Chemical and Materials Engineering, Polytechnic of Turin, Turin, Italy, 2019. [Google Scholar]
- Deo, R.C.; Downs, N.J.; Adamowski, J.F.; Parisi, A.V. Adaptive neuro-fuzzy inference system integrated with solar zenith angle for forecasting sub-tropical photo-synthetically active radiation. Food Energy Secur. 2019, 8, e00151. [Google Scholar] [CrossRef]
- Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.W. Prediction of hydropower generation using grey wolf optimization adaptive neuro-fuzzy inference system. Energies 2019, 12, 289. [Google Scholar] [CrossRef]
- Belvederesi, C.; Dominic, J.A.; Hassan, Q.K.; Gupta, A.; Achari, G. Predicting river flow using an Al-based sequential adaptive neuro-fuzzy inference system. Water 2020, 12, 1622. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Carty, D.M. An Analysis of Boosted Regression Trees to Predict the Strength Properties of Wood Composites. Master’s Thesis, Graduate School at Tennessee Research Creative Exchange, University of Tennessee, Knoxville, TN, USA, 2011. [Google Scholar]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in Epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar]
- Chang, Y. Economic forecasting by a piecewise regression tree method. Int. J. Manag. Appl. Sci. 2017, 3, 12–15. [Google Scholar]
- Koc, Y.; Eyduran, E.; Akbulut, O. Application of regression tree method for different data from animal science. Pak. J. Zool. 2017, 49, 599–607. [Google Scholar] [CrossRef]
- Naumets, S.; Lu, M. Investigation into explainable regression trees for construction engineering applications. J. Constr. Eng. Manag. 2021, 147, 04021084. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Chapman and Hall/CRC: London, UK, 1984. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Application in R; Springer Science + Business Media: New York, NY, USA, 2013. [Google Scholar]
- Das, S. Reconstruction of Gamma-Ray Direction Using Boosted Decision Trees and the Disp Parameter. Master’s Thesis, Department of Physics, McGill University, Montreal, QC, Canada, 2019. [Google Scholar]
- Akalin, A. Computational Genomics with R; Chapman and Hall/CRC: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Ceballos-Santos, S.; González-Pardo, J.; Carslaw, D.C.; Santurtún, A.; Santibáñez, M.; Fernández-Olmo, I. Meteorological normalisation using boosted regression trees to estimate the impact of COVID-19 restrictions on air quality levels. Int. J. Environ. Res. Public Health 2021, 18, 13347. [Google Scholar] [CrossRef]
- Mehta, M.; Agrawal, R.; Rissanen, J. SLIQ: A fast scalable classifier for data mining. In International Conference on Extending Database Technology; Springer: Berlin, Heidelberg, 1996. [Google Scholar] [CrossRef]
- Sutton, C.D. Classification and regression trees, bagging, and boosting. Handb. Stat. 2005, 24, 303–329. [Google Scholar]
- Bastos, J. Credit Scoring with Boosted Decision Trees; CEMAPRE, School of Economics and Management (ISEG), Technical University of Lisbon: Lisbon, Portugal, 2008. [Google Scholar]
- Roe, B.P.; Yang, H.J.; Zhu, J.; Liu, Y.; Stancu, I.; McGregor, G. Boosted decision trees as an alternative to artificial neural networks for particle identification. Nucl. Instrum. Methods Phys. Res. A 2005, 543, 577–584. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: NewYork, NY, USA, 2001. [Google Scholar]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Freund, Y. Boosting a week learning algorithm by majority. Inf. Comput. 1995, 121, 256–285. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999, 14, 771–780. (In Japanese) [Google Scholar]
- Ridgeway, G. The state of boosting. Comput. Sci. Stat. 1999, 31, 172–181. [Google Scholar]
- Latif, S.D. Developing a boosted decision tree regression prediction model as a sustainable tool for compressive strength of environmentally friendly concrete. Environ. Sci. Pollut. Res. 2021, 28, 65935–65944. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Zhu, C.; Lu, Y.; Zhu, Z. Towards optimization of boosting models for formation lithology identification. Math. Probl. Eng. 2019, 13, 5309852. [Google Scholar] [CrossRef]
- Carslaw, D.C.; Taylor, P.J. Analysis of air pollution data at a mixed source location using boosted regression trees. Atmos. Environ. 2009, 43, 3563–3570. [Google Scholar] [CrossRef]
- Fedotenkova, M. Extraction of Multivariate Components in Brain Signals Obtained during General Anesthesia. Ph.D. Thesis, Faculty of science and technology, University of Lorraine, Nancy, France, 2016. [Google Scholar]
- Salehi, R.; Lestari, R.A.S. Predicting the performance of a desulfurizing bio-filter using an artificial neural network (ANN) model. Environ. Eng. Res. 2021, 26, 200462. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Eschenbach, T.G. Spiderplots versus tornado diagrams for sensitivity analysis. Interfaces 1992, 22, 40–46. [Google Scholar] [CrossRef]
- Bassam, A.; Tzuc, M.; Soberanis, M.E.; Ricalde, L.J.; Cruz, B. Temperature estimation for photovoltaic array using an adaptive neuro fuzzy inference system. Sustainability 2017, 9, 1399. [Google Scholar] [CrossRef]
- Tran, Q.H.; Huh, J.; Nguyen, V.B.; Kang, C.; Ahn, J.H.; Park, I.J. Sensitivity analysis for ship-to-shore container crane design. Appl. Sci. 2018, 8, 1667. [Google Scholar] [CrossRef]


| CFV = 0.58 cm s−1 | CFV = 0.70 cm s−1 | CFV = 0.82 cm s−1 | ||||||||||||
| Exp. code | TMP (bar) | FT (min) | y1 | y2 (g L−1) | Exp. code | TMP (bar) | FT (min) | y1 | y2 (g L−1) | Exp. code | TMP (bar) | FT (min) | y1 | y2 (g L−1) |
| E1 | 1.2 | 10 | 0.5321 | 15.51 | E2 | 1.2 | 10 | 0.5976 | 15.66 | E3 | 1.2 | 10 | 0.6397 | 15.80 |
| 20 | 0.4865 | 15.48 | 20 | 0.5439 | 15.61 | 20 | 0.5623 | 15.84 | ||||||
| 30 | 0.4586 | 15.34 | 30 | 0.4859 | 15.52 | 30 | 0.5157 | 15.70 | ||||||
| 40 | 0.4351 | 15.12 | 40 | 0.4553 | 15.36 | 40 | 0.4906 | 15.62 | ||||||
| 50 | 0.4232 | 15.00 | 50 | 0.4478 | 15.20 | 50 | 0.4940 | 15.45 | ||||||
| 60 | 0.4253 | 14.89 | 60 | 0.4497 | 15.07 | 60 | 0.4764 | 15.40 | ||||||
| 70 | 0.4054 | 14.56 | 70 | 0.4467 | 14.76 | 70 | 0.4781 | 15.37 | ||||||
| 80 | 0.3967 | 14.23 | 80 | 0.4397 | 14.50 | 80 | 0.4718 | 15.26 | ||||||
| 90 | 0.3932 | 14.00 | 90 | 0.4387 | 14.33 | 90 | 0.4684 | 15.20 | ||||||
| 100 | 0.3937 | 13.00 | 100 | 0.4365 | 14.30 | 100 | 0.4673 | 15.00 | ||||||
| CFV = 1.20 cm s−1 | CFV = 1.06 cm s−1 | TMP = 0.8 bar | ||||||||||||
| Exp. code | TMP (bar) | FT (min) | y1 | y2 (g L−1) | Exp. code | TMP (bar) | FT (min) | y1 | y2 (g L−1) | Exp. code | CFV (cm s−1) | FT (min) | y1 | y2 (g L−1) |
| E4 | 1.2 | 10 | 0.7643 | 16.27 | E5 | 1.2 | 10 | 0.6639 | 15.97 | E6 | 1.06 | 10 | 0.5296 | 15.40 |
| 20 | 0.6753 | 16.10 | 20 | 0.5572 | 15.71 | 20 | 0.4820 | 15.23 | ||||||
| 30 | 0.6381 | 16.00 | 30 | 0.5233 | 15.31 | 30 | 0.4570 | 15.00 | ||||||
| 40 | 0.5923 | 15.92 | 40 | 0.5018 | 15.14 | 40 | 0.4183 | 14.65 | ||||||
| 50 | 0.5529 | 15.85 | 50 | 0.4808 | 14.94 | 50 | 0.4176 | 14.60 | ||||||
| 60 | 0.5343 | 15.63 | 60 | 0.4674 | 14.63 | 60 | 0.3932 | 14.58 | ||||||
| 70 | 0.5319 | 15.55 | 70 | 0.4585 | 14.57 | 70 | 0.3723 | 14.56 | ||||||
| 80 | 0.5307 | 15.54 | 80 | 0.4634 | 14.34 | 80 | 0.3685 | 14.50 | ||||||
| 90 | 0.5318 | 15.40 | 90 | 0.4593 | 14.17 | 90 | 0.3652 | 14.20 | ||||||
| 100 | 0.5287 | 15.42 | 100 | 0.4572 | 13.95 | 100 | 0.3622 | 13.24 | ||||||
| TMP = 1.0 bar | TMP = 1.4 bar | TMP = 1.6 cm s−1 | ||||||||||||
| Exp. code | CFV (cm s−1) | FT (min) | y1 | y2 (g L−1) | Exp. code | CFV (cm s−1) | FT (min) | y1 | y2 (g L−1) | Exp. code | CFV (cm s−1) | FT (min) | y1 | y2 (g L−1) |
| E7 | 1.06 | 10 | 0.5941 | 15.66 | E8 | 1.06 | 10 | 0.7188 | 16.10 | E9 | 1.06 | 10 | 0.7832 | 16.25 |
| 20 | 0.5412 | 15.61 | 20 | 0.6320 | 16.06 | 20 | 0.6732 | 16.00 | ||||||
| 30 | 0.5165 | 15.52 | 30 | 0.6072 | 15.89 | 30 | 0.6532 | 15.90 | ||||||
| 40 | 0.4953 | 15.36 | 40 | 0.5532 | 15.72 | 40 | 0.6238 | 15.76 | ||||||
| 50 | 0.4618 | 15.20 | 50 | 0.5395 | 15.60 | 50 | 0.5844 | 15.65 | ||||||
| 60 | 0.4482 | 15.07 | 60 | 0.5064 | 15.46 | 60 | 0.5583 | 15.63 | ||||||
| 70 | 0.4371 | 14.76 | 70 | 0.4841 | 15.55 | 70 | 0.5367 | 15.55 | ||||||
| 80 | 0.4382 | 14.50 | 80 | 0.4591 | 15.36 | 80 | 0.5347 | 15.54 | ||||||
| 90 | 0.4359 | 14.33 | 90 | 0.4586 | 15.20 | 90 | 0.5328 | 15.40 | ||||||
| 100 | 0.4382 | 14.30 | 100 | 0.4573 | 15.21 | 100 | 0.5320 | 15.42 | ||||||
| Model Output | Model | R2 | NSE | Unit | RMSE |
|---|---|---|---|---|---|
| Normalized flux | BRT1 | 0.9944 | 0.9937 | 1 | 0.0069 |
| ANFIS-GP1 | 0.9845 | 0.9843 | 1 | 0.0109 | |
| MnLR1 | 0.8653 | 0.8641 | 1 | 0.0319 | |
| MLR1 | 0.8149 | 0.8145 | 1 | 0.0373 | |
| Xylitol concentration | BRT2 | 0.9669 | 0.9664 | 1 | 0.1171 |
| ANFIS-GP2 | 0.9459 | 0.9453 | 1 | 0.1494 | |
| MnLR2 | 0.8199 | 0.8190 | 1 | 0.2719 | |
| MLR 2 | 0.7519 | 0.7507 | 1 | 0.3191 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehi, R.; Krishnan, S.; Nasrullah, M.; Chaiprapat, S. Using Machine Learning to Predict the Performance of a Cross-Flow Ultrafiltration Membrane in Xylose Reductase Separation. Sustainability 2023, 15, 4245. https://doi.org/10.3390/su15054245
Salehi R, Krishnan S, Nasrullah M, Chaiprapat S. Using Machine Learning to Predict the Performance of a Cross-Flow Ultrafiltration Membrane in Xylose Reductase Separation. Sustainability. 2023; 15(5):4245. https://doi.org/10.3390/su15054245
Chicago/Turabian StyleSalehi, Reza, Santhana Krishnan, Mohd Nasrullah, and Sumate Chaiprapat. 2023. "Using Machine Learning to Predict the Performance of a Cross-Flow Ultrafiltration Membrane in Xylose Reductase Separation" Sustainability 15, no. 5: 4245. https://doi.org/10.3390/su15054245
APA StyleSalehi, R., Krishnan, S., Nasrullah, M., & Chaiprapat, S. (2023). Using Machine Learning to Predict the Performance of a Cross-Flow Ultrafiltration Membrane in Xylose Reductase Separation. Sustainability, 15(5), 4245. https://doi.org/10.3390/su15054245







