Contribution of Air Management to the Energy Efficiency of Water Pipelines
Abstract
1. Introduction
2. Water–Air Flows in Pipelines
3. Discharge Reduction Due to Entrapped Air
3.1. Governing Equations Neglecting Water Depth in the Channel Flow
3.2. Governing Equations Considering Water Depth in the Channel Flow
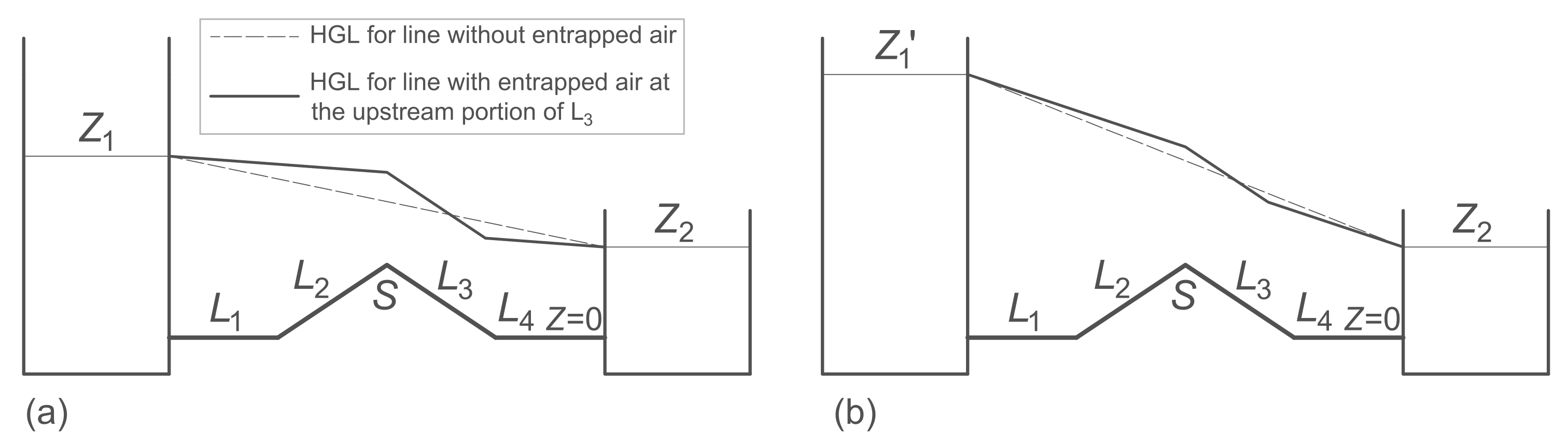
3.3. Discharge Reduction due to Entrapped Air Pocket at a System’s High Point
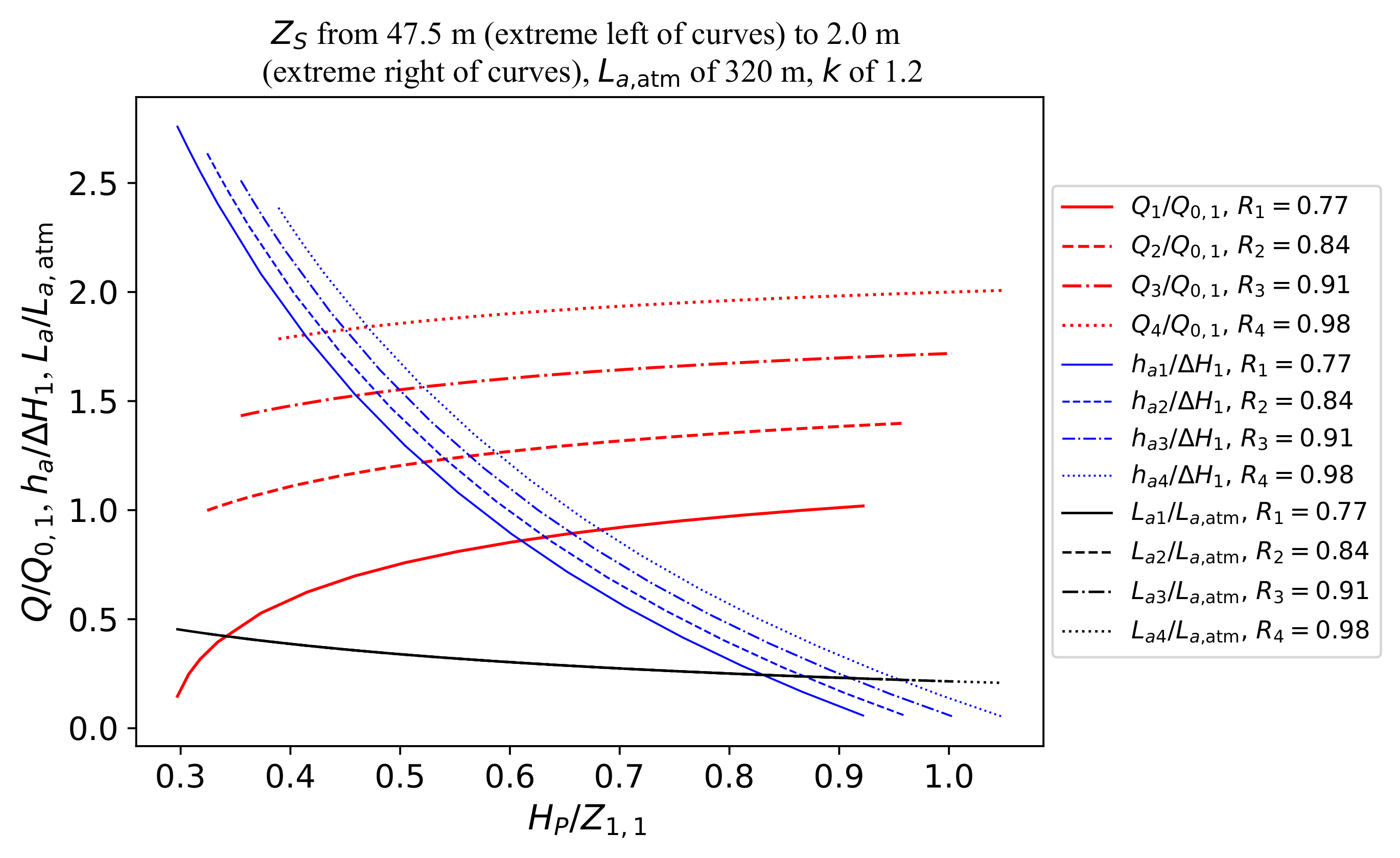
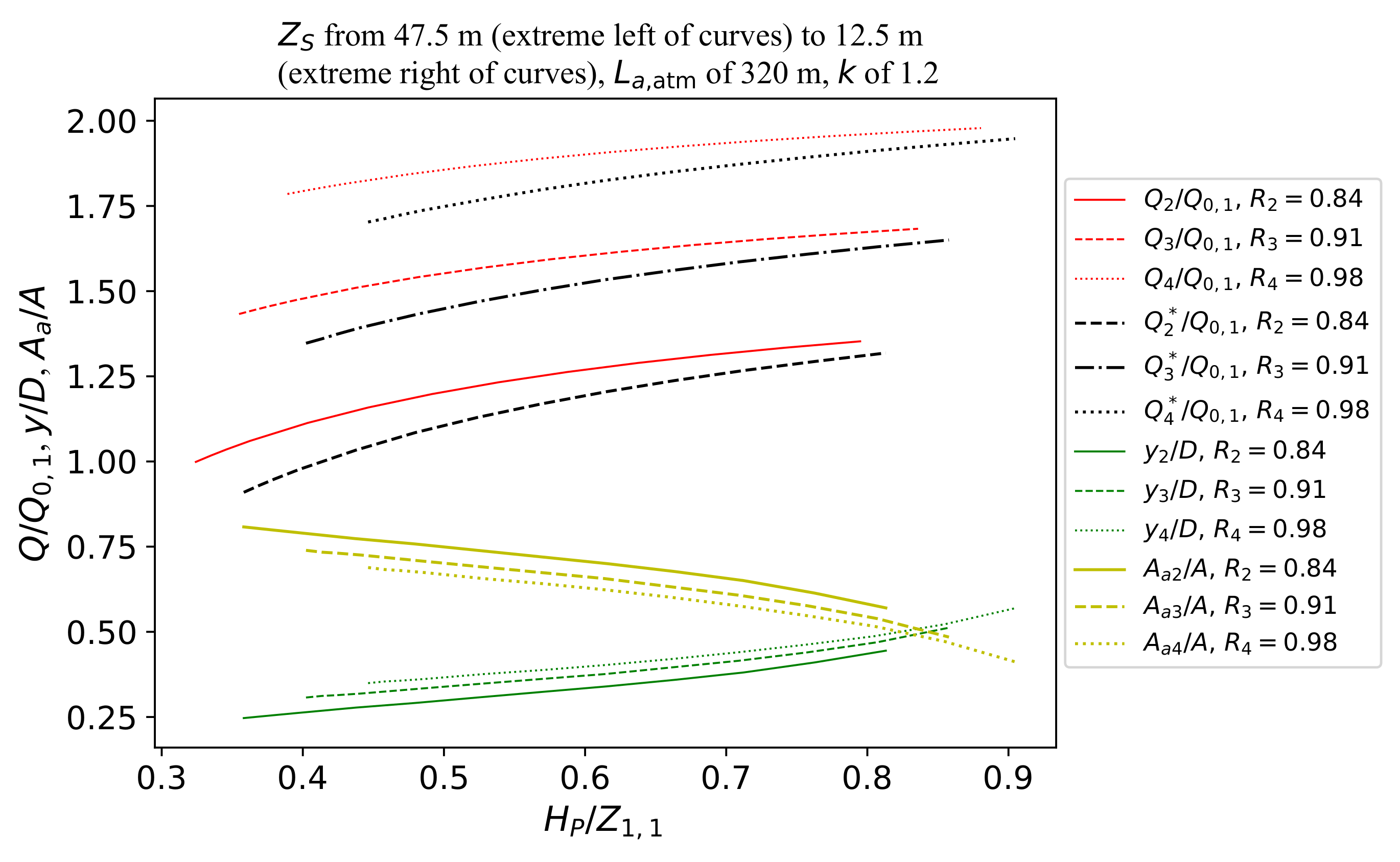
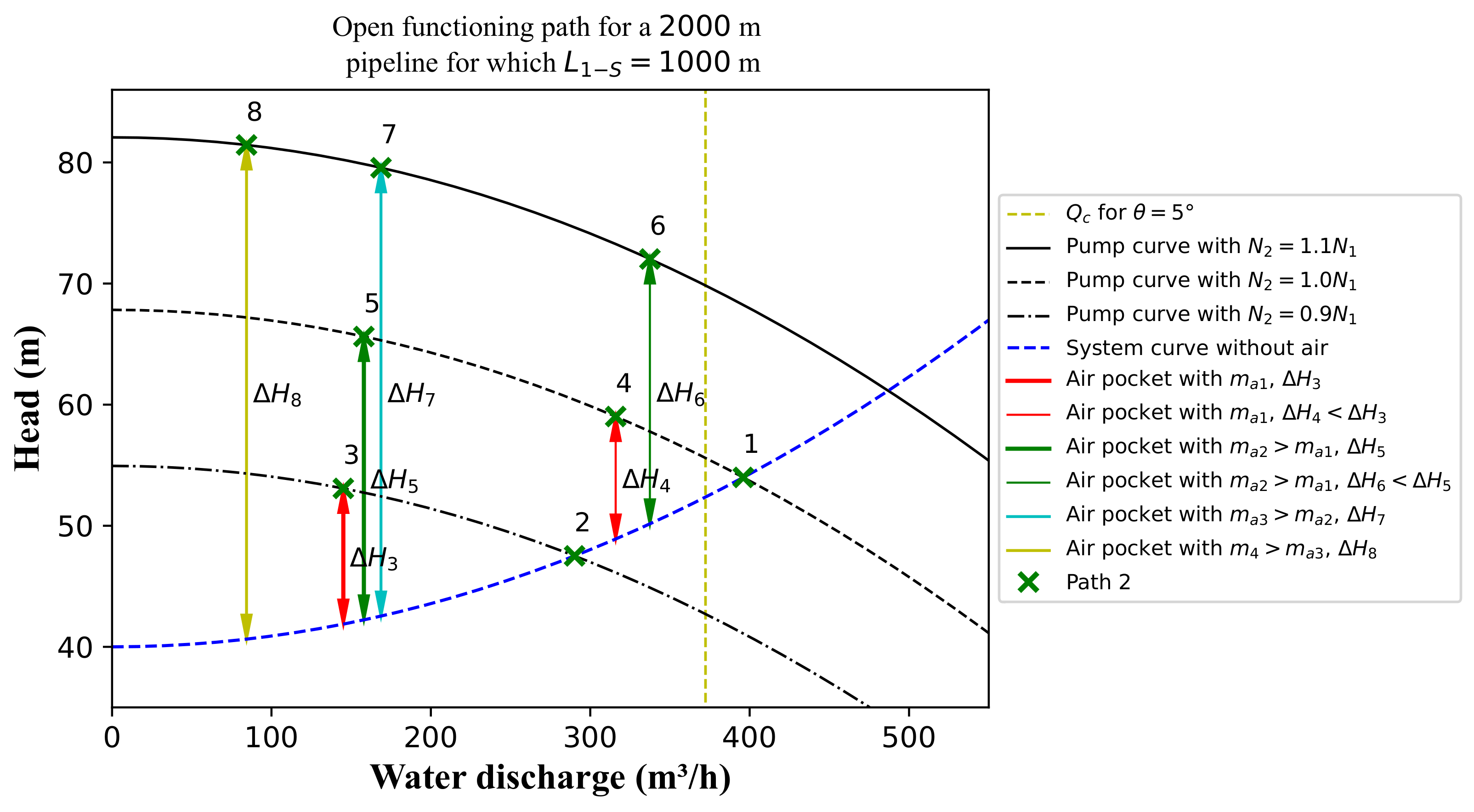
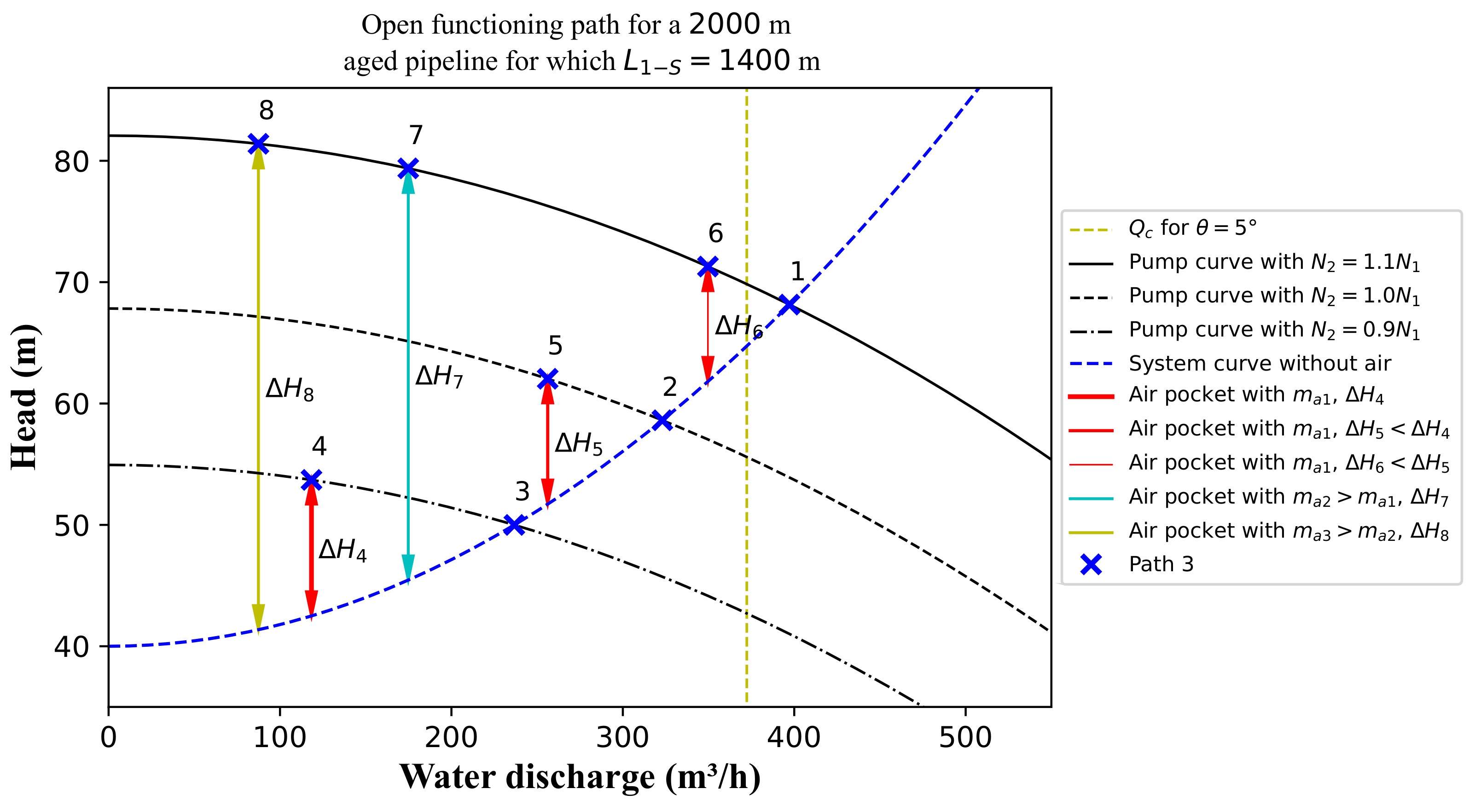
3.4. Evolution of Discharge Reduction in the Context of Air Entrapment
Energy Considerations
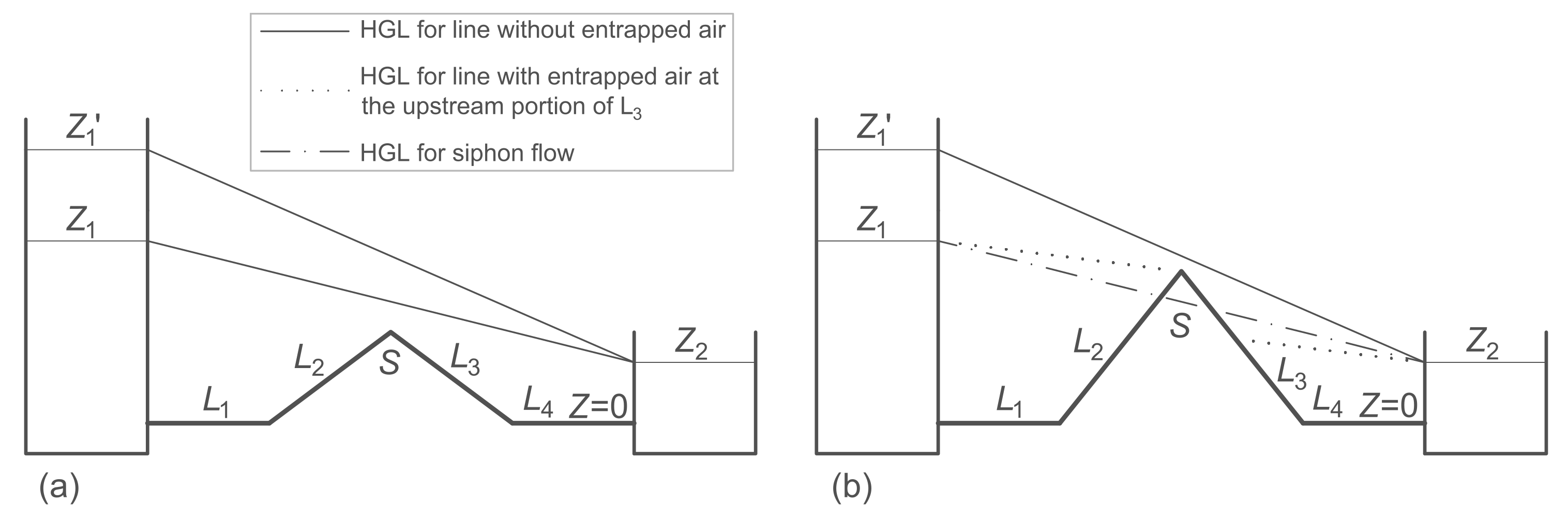
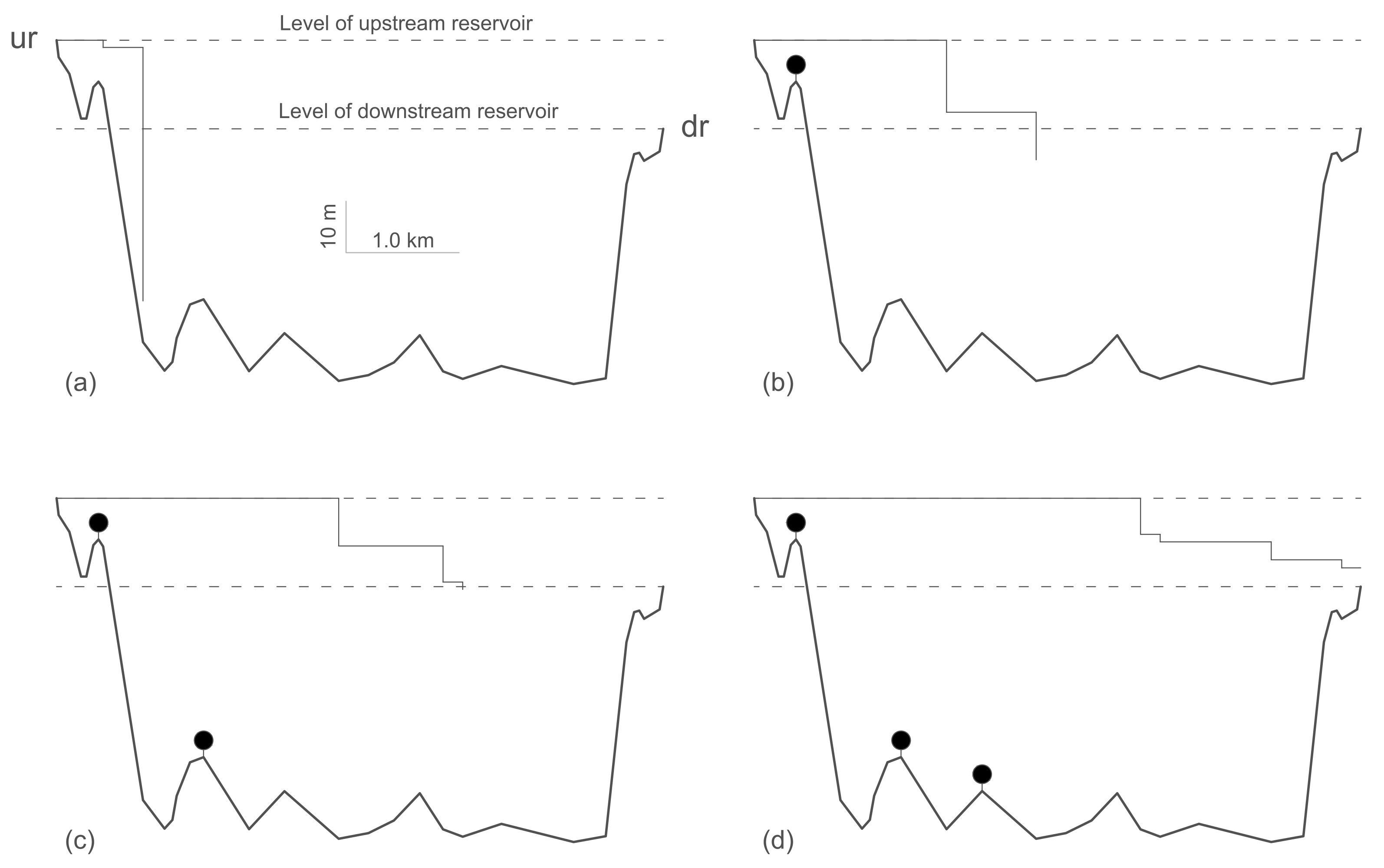
3.5. Siphon Flow and Associated Air Entrapment Risks
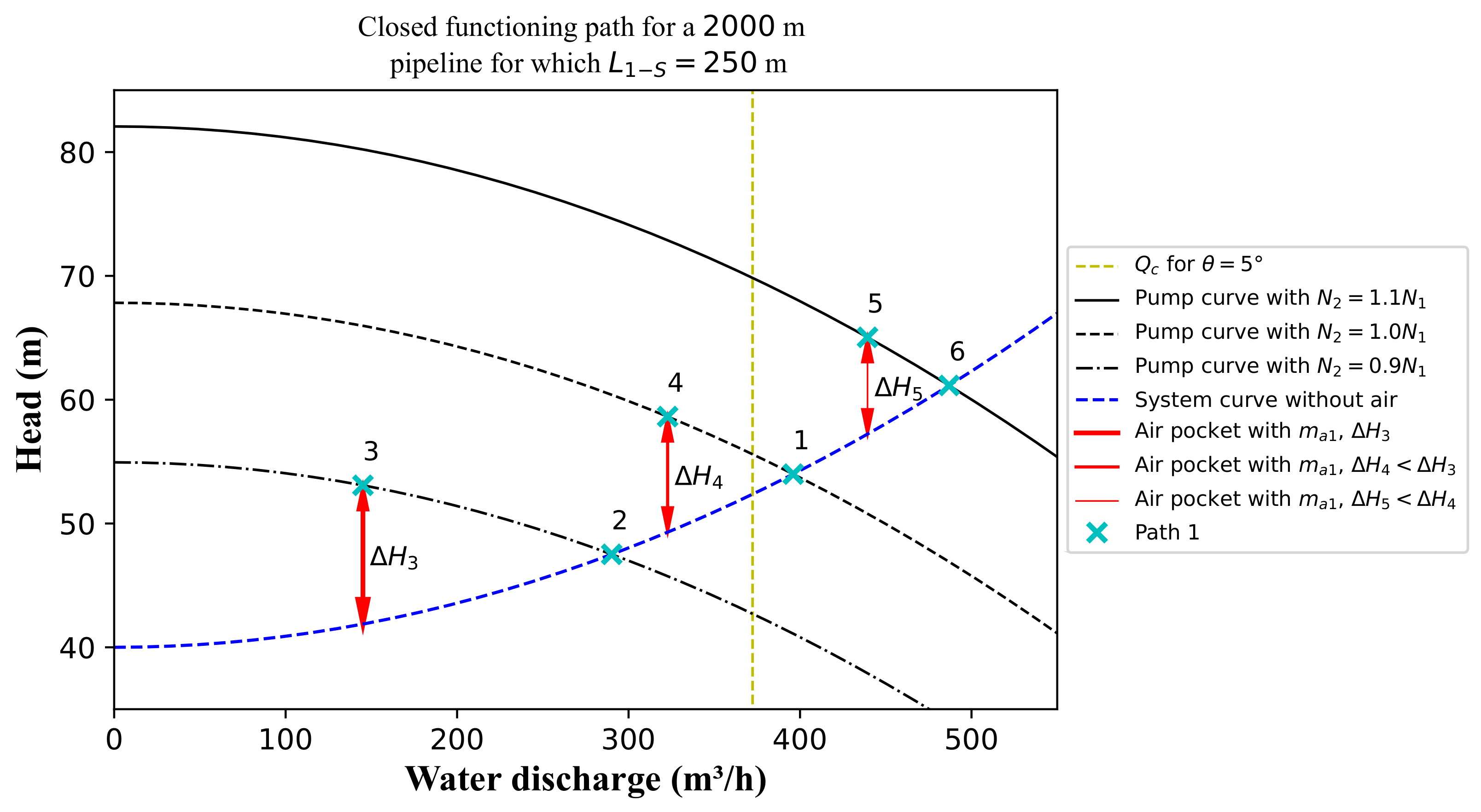
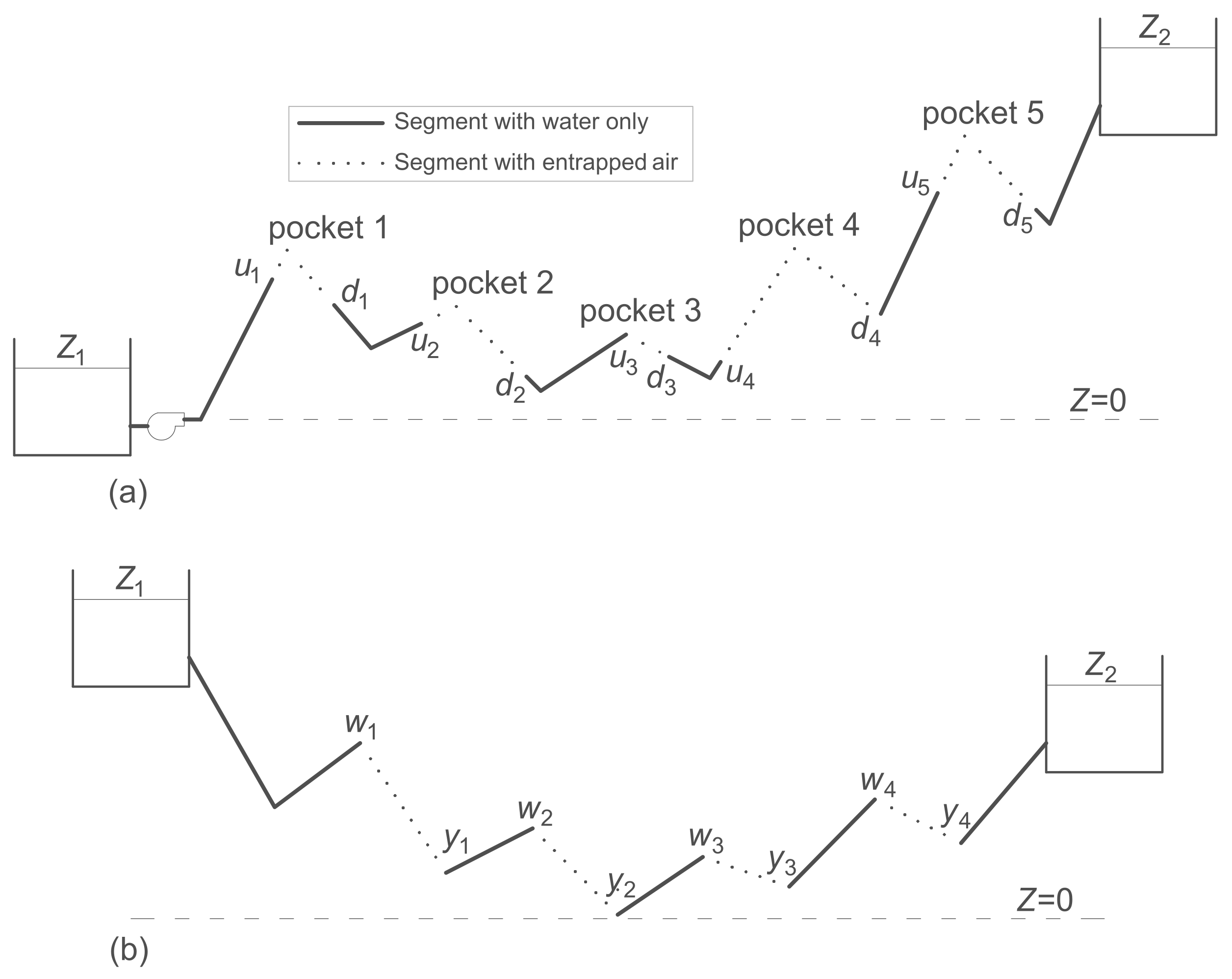
3.6. Air-Binding in Pipelines
4. Air Management Strategies
4.1. Hydraulic Removal of Air
4.2. Application of Air Valves
5. Conclusions
- The proclivity of a pipeline to the deleterious effects of entrapped air may significantly change over time. Initially well-behaved systems may get chronic air-related problems if not well maintained and adjusted to new operational circumstances.
- Air valves should be carefully selected, sized, located, and maintained to allow the necessary air exchanges in a pipeline system in its varied operating conditions during its lifespan.
- It is often difficult to identify the size and location of air pockets in a pipeline. Nevertheless, from their effects, operators might be able to infer their presence.
- Entrapped air pockets can result in appreciable pumping inefficiency and conveyance capacity reduction.
- The water conveyance reduction caused by unaddressed air pockets can put the serviceability of the system at risk.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Latin Symbols | |
| A | pipe cross-sectional area () |
| cross-sectional area occupied by the air pocket () | |
| cross-sectional area occupied by the water phase () | |
| a | coefficient of the pump curve that characterizes its shape () |
| C | polytropic constant neglecting water depth in the channel flow |
| polytropic constant considering water depth in the channel flow | |
| c | coefficient of the pump curve associated with the pump’s shut-off head (m) |
| D | pipe diameter (m) |
| Eo | Eötvös number |
| f | friction factor |
| g | acceleration due to gravity () |
| net available head for water conveyance (m) | |
| net available head for pipeline with j locations with air valve protection (m) | |
| head at the high point (m) | |
| shut-off head (m) | |
| head-loss caused by an entrapped air pocket (m) | |
| k | polytropic exponent |
| L | pipeline length (m) |
| length of the first segment of the pipeline (m) | |
| length of the second segment of the pipeline (m) | |
| length of the third segment of the pipeline (m) | |
| length of the fourth segment of the pipeline (m) | |
| distance between the upstream reservoir and the high point (m) | |
| air pocket length (m) | |
| air pocket length under atmospheric pressure (m) | |
| air pocket mass (kg) | |
| N | number of descending pipe segments with entrapped air |
| pump’s rated rotational speed (rpm) | |
| pump’s actual rotational speed (rpm) | |
| n | Manning roughness coefficient (s) or dimensionless air pocket volume |
| air pocket pressure (Pa) | |
| atmospheric pressure (Pa) | |
| Q | water discharge (/s) |
| water discharge for gravity line with | |
| critical water discharge for air removal by hydraulic means (/s) | |
| water discharge considering the water depth in the channel flow (/s) | |
| R | relative rotational speed |
| hydraulic radius (m) | |
| V | air pocket volume () |
| critical velocity for air removal by hydraulic means (m/s) | |
| y | water depth in the channel flow (m) |
| elevation of the upstream reservoir (m) | |
| increased elevation of upstream reservoir (m) | |
| elevation of the downstream reservoir (m) | |
| elevation of the downstream end of the ith air pocket (m) | |
| elevation of the high point (m) | |
| elevation of the upstream end of the ith air pocket (m) | |
| elevation of the upstream end of the ith descending pipe segment (m) | |
| elevation of the downstream end of the ith descending pipe segment (m) | |
| Greek Symbols | |
| coefficient that characterizes the shape of the critical velocity equation | |
| coefficient of the critical velocity equation related to the horizontal pipe | |
| specific weight of water (N/) | |
| additional head-loss caused by entrapped air pocket at point i (m) | |
| elevation difference between m and m | |
| inclination of the descending pipe segment (rad) | |
| angle formed by the water surface (rad) | |
| Acronyms | |
| ARV | air-release valve |
| AVV | air/vacuum valve |
| AWWA | American Water Works Association |
| CAV | combination air valve |
| dr | downstream reservoir |
| HGL | hydraulic grade line |
| SDG | Sustainable Development Goals |
| ur | upstream reservoir |
| VB | vacuum breaker |
References
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Hamzekhani, H.; Mousavi, S.J.; Vesal, M. Water–energy nexus–based economic optimization of water supply projects. J. Water Resour. Plann. Manag. 2021, 147, 04021044. [Google Scholar] [CrossRef]
- Ferroukhi, R.; Nagpal, D.; Lopez-Peña, A.; Hodges, T.; Mohtar, R.H.; Daher, B.; Mohtar, S.; Keulertz, M. Renewable Energy in the Water, Energy and Food Nexus; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2015. [Google Scholar]
- Abdeldayem, O.M.; Ferràs, D.; van der Zwan, S.; Kennedy, M. Analysis of unsteady friction models used in engineering software for water hammer analysis: Implementation case in WANDA. Water 2021, 13, 495. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Brunone, B.; Meniconi, S.; Ramos, H.M.; Covas, D.I.C. Efficient computational fluid dynamics model for transient laminar flow modeling: Pressure wave propagation and velocity profile changes. J. Fluids Eng. 2018, 140, 011102. [Google Scholar] [CrossRef]
- American Water Works Association (AWWA). Manual of Water Supply Practices M51—Air Valves: Air–Release, Air/Vacuum and Combination, 2nd ed.; AWWA: Denver, CO, USA, 2016. [Google Scholar]
- Kühnen, J.; Song, B.; Scarselli, D.; Budanur, N.B.; Riedl, M.; Willis, A.P.; Avila, M.; Hof, B. Destabilizing turbulence in pipe flow. Nat. Phys. 2018, 14, 386–390. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Mora-Meliá, D.; Iglesias-Rey, P.L. Hydraulic modeling during filling and emptying processes in pressurized pipelines: A literature review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Ramos, H.M.; Fuertes-Miquel, V.S.; Tasca, E.; Coronado-Hernández, O.E.; Besharat, M.; Zhou, L.; Karney, B. Concerning dynamic effects in pipe systems with two–phase flows: Pressure surges, cavitation, and ventilation. Water 2022, 14, 2376. [Google Scholar] [CrossRef]
- Lauchlan, C.S.; Escarameia, M.; May, R.W.P.; Burrows, R.; Gahan, C. Air in Pipelines: A Literature Review; HR Wallingford: Oxfordshire, UK, 2005. [Google Scholar]
- Zhou, L.; Liu, D.; Karney, B. Investigation of hydraulic transients of two entrapped air pockets in a water pipeline. J. Hydraul. Eng. 2013, 139, 949–959. [Google Scholar] [CrossRef]
- Martins, S.C. Dinâmica da Pressurização de Sistemas Hidráulicos com Ar Aprisionado. Ph.D. Thesis, Instituto Superior Técnico, Universidade Técnica de Lisboa, Lisbon, Portugal, 2013. [Google Scholar]
- Pozos, O.; Sanchez, A.; Rodal, E.A.; Fairuzov, Y.V. Effects of water–air mixtures on hydraulic transients. Can. J. Civ. Eng. 2010, 37, 1189–1200. [Google Scholar] [CrossRef]
- Adamkowski, A. Case study: Lapino powerplant penstock failure. J. Hydraul. Eng. 2001, 127, 547–555. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.E.; Steffler, P.M. Transient flow in a rapidly filling horizontal pipe containing trapped air. J. Hydraul. Eng. 2002, 128, 625–634. [Google Scholar] [CrossRef]
- Pozos, O.; Gonzalez, C.A.; Giesecke, J.; Marx, W.; Rodal, E.A. Air entrapped in gravity pipeline systems. J. Hydraul. Res. 2010, 48, 338–347. [Google Scholar] [CrossRef]
- Vasconcelos, J.G.; Wright, S.J. Geysering generated by large air pockets released through water–filled ventilation shafts. J. Hydraul. Eng. 2011, 137, 543–555. [Google Scholar] [CrossRef]
- Aguirre-Mendoza, A.M.; Oyuela, S.; Espinoza-Román, H.G.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Paternina-Verona, D.A. 2D CFD modeling of rapid water filling with air valves using OpenFOAM. Water 2021, 13, 3104. [Google Scholar] [CrossRef]
- Aguirre-Mendoza, A.M.; Paternina-Verona, D.A.; Oyuela, S.; Coronado-Hernández, O.E.; Besharat, M.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Ramos, H.M. Effects of orifice sizes for uncontrolled filling processes in water pipelines. Water 2022, 14, 888. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Derpich, I.; Fuertes-Miquel, V.S.; Coronado-Hernández, J.R.; Gatica, G. Assessment of steady and unsteady friction models in the draining processes of hydraulic installations. Water 2021, 13, 1888. [Google Scholar] [CrossRef]
- Hurtado-Misal, A.D.; Hernández-Sanjuan, D.; Coronado-Hernández, O.E.; Espinoza-Román, H.; Fuertes-Miquel, V.S. Analysis of sub–atmospheric pressures during emptying of an irregular pipeline without an air valve using a 2D CFD model. Water 2021, 13, 2526. [Google Scholar] [CrossRef]
- Tasca, E.; Karney, B.; Fuertes-Miquel, V.S.; Dalfré Filho, J.G.; Luvizotto, E., Jr. The crucial importance of air valve characterization to the transient response of pipeline systems. Water 2022, 14, 2590. [Google Scholar] [CrossRef]
- Li, X.; Wang, T.; Zhang, Y.; Guo, P. Study on the factors influencing air valve protection against water hammer with column separation and rejoinder. J. Water Supply Res. Technol.-Aqua 2022, 71, 949–962. [Google Scholar] [CrossRef]
- Escarameia, M. Investigating hydraulic removal of air from water pipelines. Water Manag. 2007, 160, 25–34. [Google Scholar] [CrossRef]
- Pozos, O. Investigation on the Effects of Entrained Air in Pipelines. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2007. [Google Scholar]
- Pothof, I.; Clemens, F. On elongated air pockets in downward sloping pipes. J. Hydraul. Res. 2010, 48, 499–503. [Google Scholar] [CrossRef]
- Pothof, I.; Clemens, F. Experimental study of air–water flow in downward sloping pipes. Int. J. Multiph. Flow 2011, 37, 278–292. [Google Scholar] [CrossRef]
- Pothof, I.; Schuit, A.; Clemens, F. Influence of surface tension on air–water flows. J. Hydraul. Eng. 2013, 139, 44–50. [Google Scholar] [CrossRef]
- Ramezani, L.; Karney, B.; Malekpour, A. Encouraging effective air management in water pipelines: A critical review. J. Water Resour. Plann. Manag. 2016, 142, 04016055. [Google Scholar] [CrossRef]
- Edmunds, R.C. Air binding in pipes. J. Am. Water Work. Assoc. 1979, 71, 272–277. [Google Scholar] [CrossRef]
- Richards, R.T. Air binding in water pipelines. J. Am. Water Work. Assoc. 1962, 54, 719–730. [Google Scholar] [CrossRef]
- Sorensen, D.K. Energy savings in water and wastewater transmission systems through the use of air valves. In Proceedings of the Pipelines 2017: Condition Assessment, Surveying, and Geomatics, Phoenix, AZ, USA, 6–9 August 2017. [Google Scholar]
- United Nations General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development (A/RES/70/1); United Nations: New York, NY, USA, 2015; Available online: https://undocs.org/A/RES/70/1 (accessed on 5 December 2022).
- Barnea, D.; Shoham, O.; Taitel, Y. Flow pattern transition for gas–liquid flow in horizontal and inclined pipes. Int. J. Multiph. Flow 1980, 6, 217–225. [Google Scholar] [CrossRef]
- Zheng, G.; Brill, J.P.; Taitel, Y. Slug flow behavior in a hilly terrain pipeline. Int. J. Multiph. Flow 1994, 20, 63–79. [Google Scholar] [CrossRef]
- Pozos, O.; Giesecke, J.; Marx, W.; Rodal, E.A.; Sanchez, A. Experimental investigation of air pockets in pumping pipeline systems. J. Hydraul. Res. 2010, 48, 269–273. [Google Scholar] [CrossRef]
- Kalinske, A.A.; Robertson, J.M. Closed conduit flow. Trans. Am. Soc. Civ. Eng. 1943, 108. [Google Scholar] [CrossRef]
- Malekpour, A.; Karney, B.; Nault, J. Physical understanding of sudden pressurization of pipe systems with entrapped air: Energy auditing approach. J. Hydraul. Eng. 2016, 142, 04015044. [Google Scholar] [CrossRef]
- Porto, R.M. Hidráulica Básica, 4th ed.; Escola de Engenharia de São Carlos, Universidade de São Paulo: São Carlos, Brazil, 2006. [Google Scholar]
- Ramezani, L.; Karney, B.; Malekpour, A. The challenge of air valves: A selective critical literature review. J. Water Resour. Plann. Manag. 2015, 141, 04015017. [Google Scholar] [CrossRef]
- Koelle, E. Adutoras—Acessórios; Sabesp: São Paulo, Brazil, 1981. [Google Scholar]
- Malekpour, A.; She, Y. Air pocket detection in water and wastewater conveyance pipelines using inverse transient analysis. In Proceedings of the Pipelines 2018: Condition Assessment, Construction, and Rehabilitation, Toronto, ON, Canada, 15–18 July 2018. [Google Scholar]
- Kalinske, A.A.; Bliss, P.H. Removal of air from pipelines by flowing water. Civ. Eng. 1943, 13. [Google Scholar]
- Kent, J.C. The Entrainment of Air by Water Flowing in Circular Conduits with Downgrade Slopes. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1952. [Google Scholar]
- Falvey, H.T. Air–Water Flow in Hydraulic Structures—Engineering Monograph No. 41; Water and Power Resources Service: Denver, CO, USA, 1980. [Google Scholar]
- Liu, T.; Yang, J. Experimental studies of air pocket movement in a pressurized spillway conduit. J. Hydraul. Res. 2013, 51, 265–272. [Google Scholar] [CrossRef]
- Wisner, P.E.; Mohsen, F.N.; Kouwen, N. Removal of air from water lines by hydraulic means. J. Hydraul. Div. 1975, 101, 243–257. [Google Scholar] [CrossRef]
- Ramezani, L.; Daviau, J. The challenge of air valve selection in pumping systems. In Proceedings of the Pipelines 2021: Design, Online, 3–6 August 2021. [Google Scholar]
- McPherson, D.L. Air valve sizing and location: A prospective. In Proceedings of the Pipelines 2009: Infrastructure’s Hidden Assets, San Diego, CA, USA, 15–19 August 2009. [Google Scholar]
- Lescovich, J.E. Locating and sizing air-release valves. J. Am. Water Work. Assoc. 1972, 64, 457–461. [Google Scholar] [CrossRef]

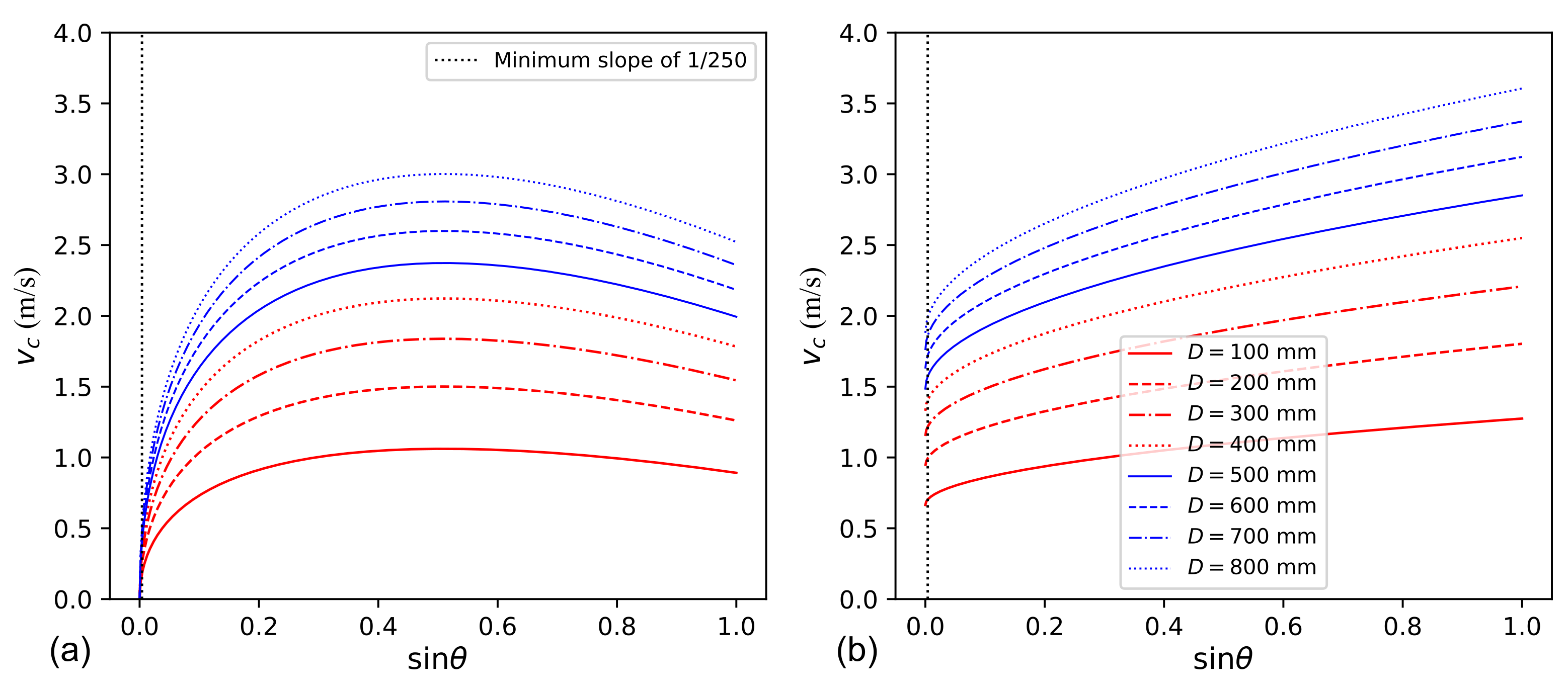
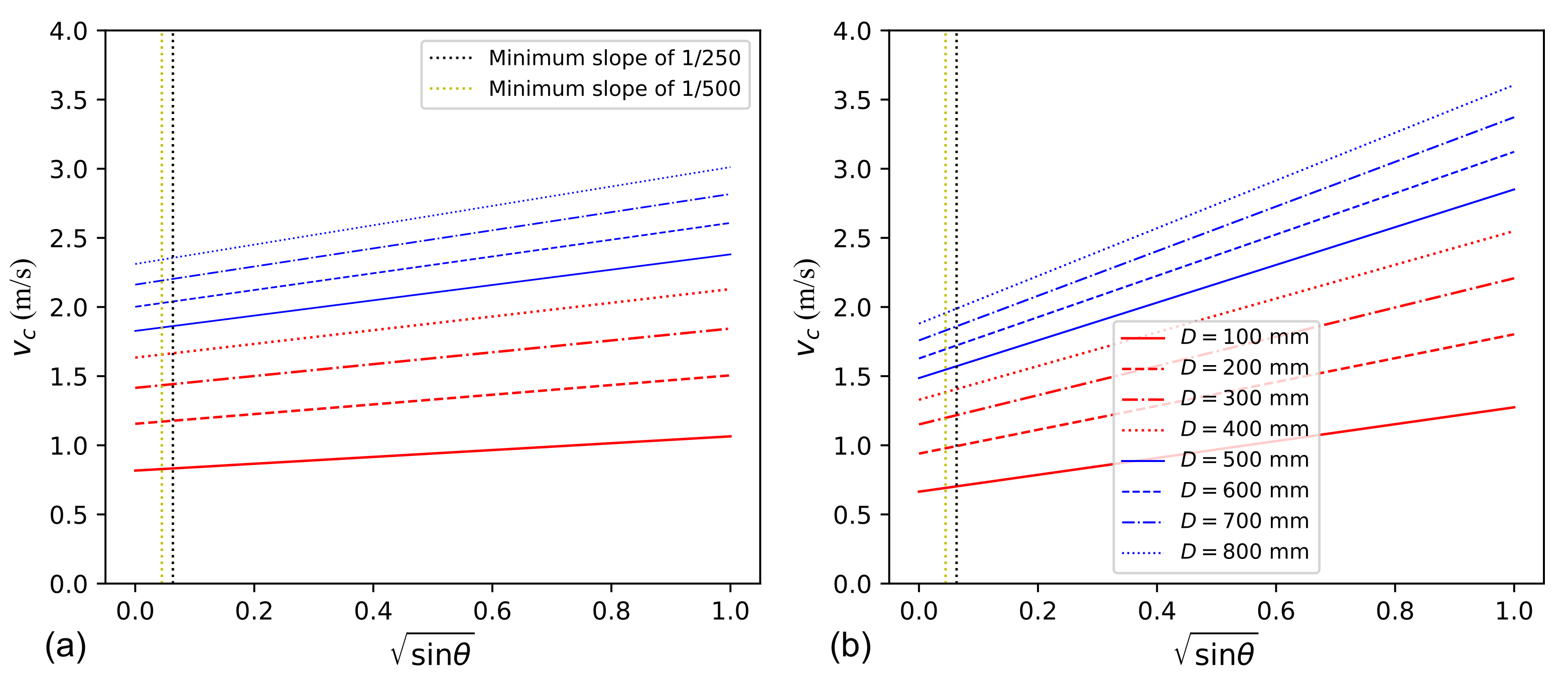
| Pipe Diameter (mm) | Inclination of Descending Pipe Segment | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |
| 100 | 0.7 | 0.8 | 0.8 | 0.9 | 0.9 | 0.9 | 0.9 | 1.0 | 1.0 | 1.0 | 1.0 |
| 150 | 0.8 | 1.0 | 1.0 | 1.1 | 1.1 | 1.1 | 1.2 | 1.2 | 1.2 | 1.2 | 1.3 |
| 200 | 0.9 | 1.1 | 1.2 | 1.2 | 1.3 | 1.3 | 1.3 | 1.4 | 1.4 | 1.4 | 1.4 |
| 250 | 1.1 | 1.2 | 1.3 | 1.4 | 1.4 | 1.5 | 1.5 | 1.5 | 1.6 | 1.6 | 1.6 |
| 300 | 1.2 | 1.3 | 1.4 | 1.5 | 1.5 | 1.6 | 1.6 | 1.7 | 1.7 | 1.7 | 1.8 |
| 400 | 1.3 | 1.6 | 1.7 | 1.7 | 1.8 | 1.8 | 1.9 | 1.9 | 2.0 | 2.0 | 2.0 |
| 500 | 1.5 | 1.7 | 1.8 | 1.9 | 2.0 | 2.1 | 2.1 | 2.2 | 2.2 | 2.2 | 2.3 |
| 600 | 1.6 | 1.9 | 2.0 | 2.1 | 2.2 | 2.3 | 2.3 | 2.4 | 2.4 | 2.5 | 2.5 |
| 700 | 1.8 | 2.1 | 2.2 | 2.3 | 2.4 | 2.4 | 2.5 | 2.6 | 2.6 | 2.7 | 2.7 |
| 800 | 1.9 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.7 | 2.8 | 2.8 | 2.9 |
| 900 | 2.0 | 2.3 | 2.5 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.0 | 3.0 | 3.1 |
| 1000 | 2.1 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 3.0 | 3.1 | 3.1 | 3.2 | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tasca, E.; Besharat, M.; Ramos, H.M.; Luvizotto, E., Jr.; Karney, B. Contribution of Air Management to the Energy Efficiency of Water Pipelines. Sustainability 2023, 15, 3875. https://doi.org/10.3390/su15053875
Tasca E, Besharat M, Ramos HM, Luvizotto E Jr., Karney B. Contribution of Air Management to the Energy Efficiency of Water Pipelines. Sustainability. 2023; 15(5):3875. https://doi.org/10.3390/su15053875
Chicago/Turabian StyleTasca, Elias, Mohsen Besharat, Helena M. Ramos, Edevar Luvizotto, Jr., and Bryan Karney. 2023. "Contribution of Air Management to the Energy Efficiency of Water Pipelines" Sustainability 15, no. 5: 3875. https://doi.org/10.3390/su15053875
APA StyleTasca, E., Besharat, M., Ramos, H. M., Luvizotto, E., Jr., & Karney, B. (2023). Contribution of Air Management to the Energy Efficiency of Water Pipelines. Sustainability, 15(5), 3875. https://doi.org/10.3390/su15053875









