Modelling Road Work Zone Crashes’ Nature and Type of Person Involved Using Multinomial Logistic Regression
Abstract
:1. Introduction
1.1. Framework and Objectives
1.2. Literature Review
2. Method
2.1. Multinomial Logistic Regression
- Y is the qualitative dependent variable for a model where the response variable assumes m response categories (for this case m = 3, with codes 0, 1 and 2).
- X is the matrix of independent variables (explanatory variables).
- β0, β1 and β2 are the logistic regression coefficient vectors for the response category m.
2.2. Data Processing
- (a)
- Records coded as ‘Undefined’ in report fields A3: Crash type (with property damage only, fatalities, serious or minor injuries); A4: Crash nature (run of road, collision or run over pedestrians); A6: Gender and/or Date of birth; B2.1: Road horizontal geometry (straight or curved); B2.2: Road vertical geometry (level, slope or hump); B2.4: Road crash location (on the track, side, sidewalk, dedicated track or parking lot); B2.5: Road intersection (outside the intersection, at a level or uneven intersection); B4.1: Pavement type (unpaved, bituminous, concrete or stone); B4.2: Pavement condition (good, regular or bad); B4.4: Pavement grip condition (dry and clean, humid, wet, etc.); and B5.1: Markings on the pavement (no marks or barely visible, with markings separating the direction of traffic or with markings separating the direction and lanes of traffic).
- (b)
- Records without location data (no information in field A2).
- (c)
- Records of drivers under the age allowed by law to drive (field A6).
- (d)
- Records with no information about the year of license to drive (field E1.3).
3. Models and Discussion
3.1. Model 1: WZ Crash Nature
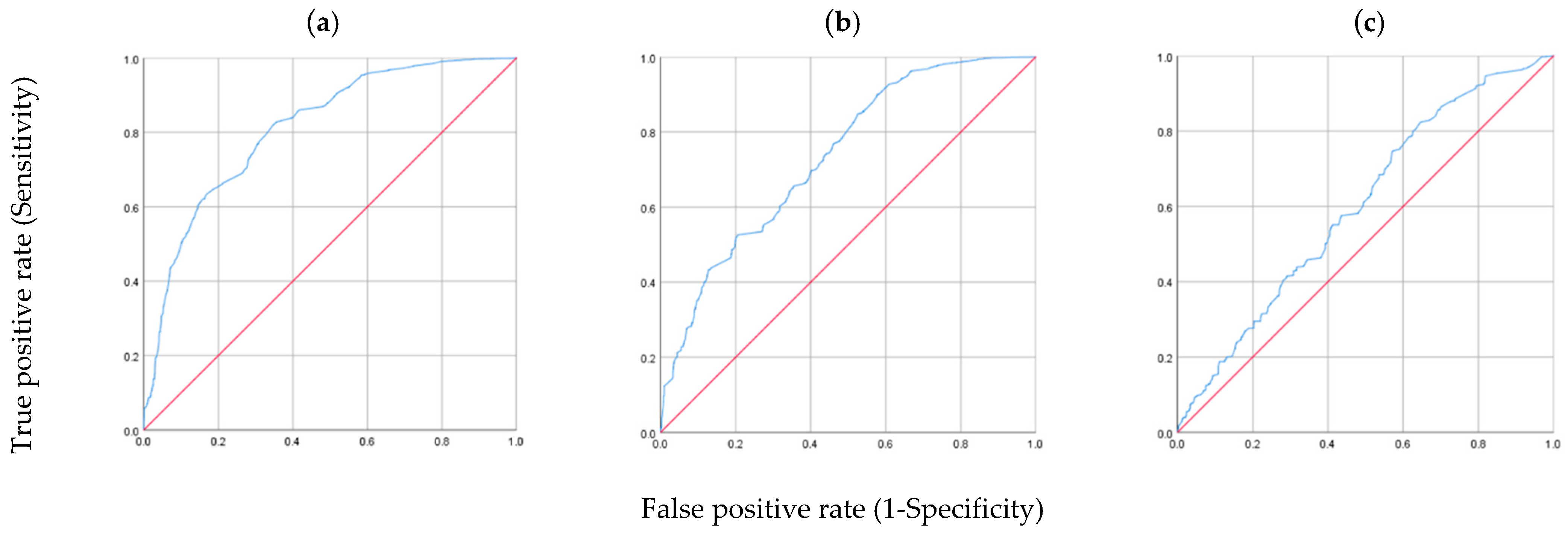
3.1.1. Results
3.1.2. Analysis of Results
3.2. Model 2: Type of Person Involved in WZ Crashes
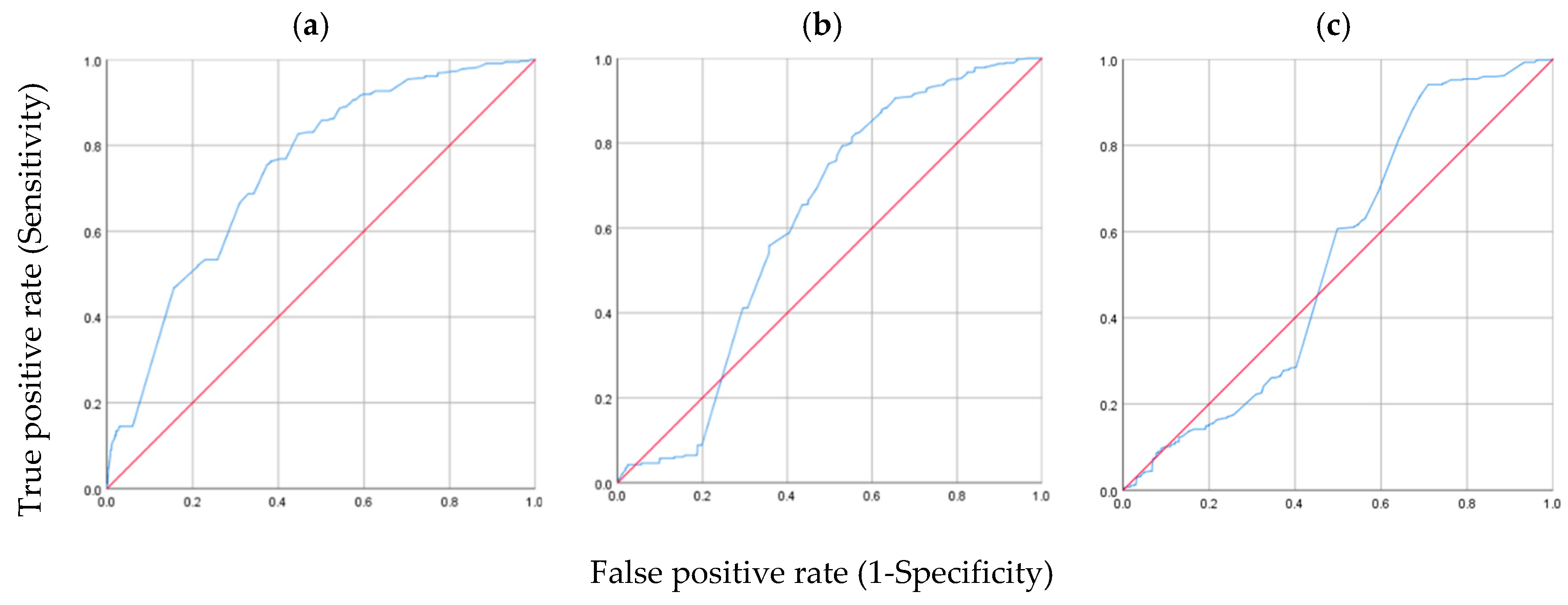
3.2.1. Results
3.2.2. Analysis of Results
3.3. Discussion of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- OECD-ITF. Road Safety Annual Report 2020. Available online: https://www.itf-oecd.org/sites/default/files/docs/irtad-road-safety-annual-report-2020_0.pdf (accessed on 9 November 2022).
- United Nations. A/RES/70/1 Transforming Our World: The 2030 Agenda for Sustainable Development Trans-Forming Our World: The 2030 Agenda for Sustainable Development Preamble. 2015. Available online: https://sdgs.un.org/sites/default/files/publications/21252030%20Agenda%20for%20Sustainable%20Development%20web.pdf (accessed on 9 November 2022).
- United Nations. A/RES/74/299 Improving Global Road Safety. 2020. Available online: https://digitallibrary.un.org/record/3879711?ln=en (accessed on 9 November 2022).
- WHO. Global Status Report on Road Safety 2018. Available online: https://www.who.int/publications/i/item/9789241565684 (accessed on 9 November 2022).
- WHO. The Top 10 Causes of Death. 2020. Available online: https://www.who.int/news-room/fact-sheets/detail/the-top-10-causes-of-death (accessed on 10 November 2022).
- WHO. Road Traffic Injuries. 2022. Available online: https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries (accessed on 10 November 2022).
- Ambros, J.; Turek, R.; Elgner, J.; Křivánková, Z.; Valentová, V. Effectiveness evaluation of section speed control in Czech motorway work zones. Safety 2020, 6, 38. [Google Scholar] [CrossRef]
- La Torre, F.; Domenichini, L.; Nocentini, A. Effects of stationary work zones on motorway crashes. Saf. Sci. 2017, 92, 148–159. [Google Scholar] [CrossRef]
- Silverstein, C.; Schorr, J.; Hamdar, S.H. Work zones versus nonwork zones: Risk factors leading to rear-end and sideswipe collisions. J. Transp. Saf. Secur. 2016, 8, 310–326. [Google Scholar] [CrossRef]
- Yang, H.; Ozbay, K.; Ozturk, O.; Xie, K. Work zone safety analysis and modeling: A state-of-the-art review. Traffic Inj. Prev. 2015, 16, 387–396. [Google Scholar] [CrossRef]
- Ullman, G.; Ullman, B.; Finley, M. Analysis of crashes at active night work zones. In Proceedings of the Transportation Research Board 85th Annual Meeting, Washington, WA, USA, 22–26 January 2006. [Google Scholar]
- Meng, Q.; Weng, J.; Qu, X. A probabilistic quantitative risk assessment model for the long-term work zone crashes. Accid. Anal. Prev. 2010, 42, 1866–1877. [Google Scholar] [CrossRef] [PubMed]
- Santos, B.; Trindade, V.; Polónia, C.; Picado-Santos, L. Detecting risk factors of road work zone crashes from the information provided in police crash reports: The case study of Portugal. Safety 2021, 7, 12. [Google Scholar] [CrossRef]
- Khattak, A.; Rodriguez, D.; Targa, F.; Rocha, M. Understanding the Role of Truck-Driver, Occupational and High-Risk Roadway Factors in Truck-Involved Collisions; CURS Report No. 2003-04; CURS: Nashville, TN, USA, 2003. [Google Scholar]
- Khattak, A.; Targa, F. Injury severity and total harm in truck-involved work zone crashes. Transp. Res. Rec. 2004, 1877, 106–116. [Google Scholar] [CrossRef]
- Qi, Y.; Srinivasan, R.; Teng, H.; Baker, R. Frequency of Work Zone Accidents on Construction Projects: Final Report C-01-61. 2005. Available online: https://rosap.ntl.bts.gov/view/dot/16159 (accessed on 21 November 2022).
- Li, Y.; Bai, Y. Fatal and injury crash characteristics in highway work zones. In Proceedings of the Transportation Research Board 87th Annual Meeting, Washington, WA, USA, 13–17 January 2008. [Google Scholar]
- Li, Y.; Bai, Y. Comparison of characteristics between fatal and injury accidents in the highway construction zones. Saf. Sci. 2008, 46, 646–660. [Google Scholar] [CrossRef]
- Elghamrawy, T. Optimizing Work Zone Practices for Highway Construction Projects. Ph.D. Thesis, University of Illinois, Champaign, IL, USA, 2011. [Google Scholar]
- Yang, H.; Ozbay, K.; Ozturk, O.; Yildirimoglu, M. Modeling work zone crash frequency by quantifying measurement errors in work zone length. Accid. Anal. Prev. 2013, 55, 192–201. [Google Scholar] [CrossRef] [PubMed]
- Osman, M.; Paleti, R.; Mishra, S.; Golias, M. Analysis of injury severity of large truck crashes in work zones. Accid. Anal. Prev. 2016, 97, 261–273. [Google Scholar] [CrossRef] [PubMed]
- Osman, M.; Paleti, R.; Mishra, S. Analysis of passenger-car crash injury severity in different work zone configurations. Accid. Anal. Prev. 2018, 111, 161–172. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.; Du, G.; Ma, L. Driver injury severity analysis for two work zone types. Proc. Inst. Civ. Eng.-Transp. 2016, 169, 97–106. [Google Scholar] [CrossRef]
- Sze, N.; Song, Z. Factors contributing to injury severity in work zone related crashes in New Zealand. Int. J. Sustain. Transp. 2019, 13, 148–154. [Google Scholar] [CrossRef]
- Li, Y.; Bai, Y. Highway work zone risk factors and their impact on crash severity. J. Transp. Eng. 2009, 135, 694–701. [Google Scholar] [CrossRef]
- Ashqar, H.; Shaheen, Q.; Ashur, S.; Rakha, H. Impact of risk factors on work zone crashes using logistic models and Random Forest. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–21 September 2021. [Google Scholar] [CrossRef]
- Weng, J.; Meng, Q. Analysis of driver casualty risk for different work zone types. Accid. Anal. Prev. 2011, 43, 1811–1817. [Google Scholar] [CrossRef] [PubMed]
- Bédard, M.; Guyatt, G.; Stones, M.; Hirdes, J. The independent contribution of driver, crash, and vehicle characteristics to driver fatalities. Accid. Anal. Prev. 2002, 34, 717–727. [Google Scholar] [CrossRef]
- Harb, R.; Radwan, E.; Yan, X.; Pande, A.; Abdel-Aty, M. Freeway work-zone crash analysis and risk identification using multiple and conditional logistic regression. J. Transp. Eng. 2008, 134, 203–214. [Google Scholar] [CrossRef]
- Santos, B.; Picado-Santos, L. Impact assessment of road work zones in operating conditions, safety and user costs. In Pavement and Asset Management, 1st ed.; Crispino, M., Ed.; CRC Press/Balkema Taylor & Francis: London, UK, 2019; pp. 595–604. ISBN 978-0-367-20989-6. [Google Scholar]
- Santos, B.; Picado-Santos, L.; Trindade, V. Using binary logistic regression to explain the impact of accident factors on work zone crashes. In Proceedings of the RSS 2017—Road Safety & Simulation International Conference, The Hague, The Netherlands, 17–19 October 2017. [Google Scholar]
- Abdulhafedh, A. Road traffic crash data: An overview on sources, problems, and collection methods. J. Transp. Technol. 2017, 7, 206–219. [Google Scholar] [CrossRef]
- Hosmer, D.; Lemeshow, S.; Sturdivant, R. Applied Logistic Regression, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Washington, S.; Karlaftis, M.; Mannering, F.; Anastasopoulos, P. Statistical and Econometric Methods for Transportation Data Analysis, 3rd ed.; Chapman & Hall/CRC: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Marôco, J. Análise Estatística Com o SPSS Statistics, 6th ed.; ReportNumber—Análise e gestão de informação, Lda; Biblioteca Nacional de Portugal: Pêro Pinheiro, Portugal, 2014. [Google Scholar]
- Chen, J.; Lewis, B.; Marathe, A.; Marathe, M.; Swarup, S.; Vullikanti, A. Individual and collective behavior in public health epidemiology. Handb. Stat. 2017, 36, 329–365. [Google Scholar] [CrossRef]
- Fávero, L.; Belfiore, P.; Silva, F.; Chan, B. Análise de Dados: Modelagem Multivariada Para Tomada de Decições, 3rd ed.; Elsevier: Rio de Janeiro, Brasil, 2009; ISBN 9788535230468. [Google Scholar]
- Bham, G.; Javvadi, B.; Manepalli, U. Multinomial logistic regression model for single-vehicle and multivehicle collisions on urban U.S. highways in Arkansas. J. Transp. Eng. 2012, 138, 786–797. [Google Scholar] [CrossRef]
- Osborne, J. Best Practices in Logistic Regression; SAGE Publications, Ltd.: Thousand Oaks, CA, USA, 2017. [Google Scholar] [CrossRef]
- Pituch, K.; Stevens, J. Applied Multivariate Statistics for the Social Sciences: Analyses with SAS and IBM’s SPSS, 6th ed.; Taylor and Francis: Oxfordshire, UK, 2015. [Google Scholar] [CrossRef]
- Hensher, D.; Stopher, P. Behavioural Travel Modelling; Taylor and Francis Inc.: London, UK, 2021. [Google Scholar] [CrossRef]
- Long, J. Regression Models for Categorical and Limited Dependent Variables, 1st ed.; SAGE Publications: Thousand Oaks, CA, USA, 1997; ISBN 9780803973749. [Google Scholar]
- Hoffmann, R. Análise de Regressão: Uma Introdução à Econometria; Escola Superior de Agricultura Luiz de Queiroz: Piracicaba, Brazil, 2017. [Google Scholar] [CrossRef]
- Miles, J. Tolerance and variance inflation factor. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Sze, N.; Wong, S.; Lee, C. The likelihood of achieving quantified road safety targets: A binary logistic regression model for possible factors. Accid. Anal. Prev. 2014, 73, 242–251. [Google Scholar] [CrossRef] [PubMed]
- Harrel, F., Jr. Regression Modeling Strategies—With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis, 2nd ed.; Springer Series in Statistics; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- IBM Corp. IBM SPSS Statistics for Windows; IBM Corp.: Armonk, NY, USA, 2017. [Google Scholar]
- Autoridade Nacional de Segurança Rodoviária (ANSR). Boletim Estatístico de Acidentes de Viação, Portugal. 2014. Available online: http://www.ansr.pt/Estatisticas/BEAV/Documents/BEAV.pdf (accessed on 9 November 2022).
- Pahukula, J.; Hernandez, S.; Unnikrishnan, A. A time of day analysis of crashes involving large trucks in urban areas. Accid. Anal. Prev. 2015, 75, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Roque, C.; Moura, F.; Lourenço-Cardoso, J. Detecting unforgiving roadside contributors through the severity analysis of ran-off-road crashes. Accid. Anal. Prev. 2015, 80, 262–273. [Google Scholar] [CrossRef]
- Tay, R.; Choi, J.; Kattan, L.; Khan, A. A multinomial logit model of pedestrian-vehicle crash severity. Int. J. Sustain. Transp. 2011, 5, 233–249. [Google Scholar] [CrossRef]
- Vieira, A. Analysis of Road Work Zone Crash Data Using Multinomial Logistic Regression. Master’s Thesis, University of Beira Interior, Covilhã, Portugal, 2019. [Google Scholar]
| Reference | Year | Method | Scope |
|---|---|---|---|
| Khattak et al. [14] | 2003 | Ordered probit Linear regression | Heavy vehicle involvement Injury severity and frequency |
| Khattak et al. [15] | 2004 | Ordered probit | Heavy vehicle involvement Injury severity |
| Qi et al. [16] | 2005 | Ordered probit | Rear-end collisions Crash severity |
| Li & Bai [17,18,25] | 2006–2009 | Logistic regression Crash frequency analysis | Fatal and injury crashes Human factors |
| Meng et al. [12] | 2010 | Probabilistic quantitative risk assessment: regression model, event tree, consequence estimation models | Long-term WZ Casualty risk Crash severity |
| Elghamrawy et al. [19] | 2011 | Ordered logistic regression | Fatal and injury crashes Crash severity and cost |
| Yang et al. [20] | 2013 | Negative binomial regression | Crash frequency Single vehicle Drivers’ injury severity |
| Osman et al. [21] | 2016 | Multinomial logit Nested logit Ordered logit Generalized ordered logit | Heavy vehicle involvement Injury severity |
| Osman et al. [22] | 2018 | Mixed generalized ordered probit | Injury severity of passenger-car crashes |
| Santos et al. [13,30,31] | 2017–2021 | Logistic regression Probit regression | Type of crash Contributing factor Driver age group |
| Ashqar et al. [26] | 2021 | Crash frequency analysis Logistic regression Machine learning Random Forest algorithm | Crash severity |
| Reference | Khattak et al. [14] | Khattak et al. [15] | Qi et al. [16] | Li & Bai [17,18,25] | Meng et al. [12] | Elghamrawy [19] | Yang et al. [20] | Osman et al. [21] | Osman et al. [22] | Santos et al. [13,30,31] | Ashqar et al. [26] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Category and variables | Year | 2003 | 2004 | 2005 | 2006–2009 | 2010 | 2011 | 2013 | 2016 | 2018 | 2017–2021 | 2021 |
| Temporal: hour and minutes (a), day of the week (b), month (c) | a, b, c | a, b | (a) | (a, b) | ||||||||
| Road environment conditions: light (a), weather (b), road surface (c) | a, b | a, b | a, b, c | a, b, c | a | a, b, c | a, b, c | b, c | a, b, c | a, b, c | ||
| Road and WZ conditions: road class (a), road geometry (b), road configuration (1) (c), number of lanes (d), lane width (e), intersection (f), bridge (g), pavement type (h), rural/urban (i), AADT/peak hour (j), speed limit (k), WZ type (2) (l), WZ marked with sign/cones (m), access/traffic control device (n), pedestrian/pedestrian worker (o), WZ activity (ongoing) (p), WZ duration (q), WZ length (r), type of work being done (s), WZ effect on the roadway (3) (t) | c, k, l, m, n, o, p, q, s, t | c, k, l, m, n, p, s, t | a, b, f, l, n, o, q, s, t | a, b, d, h, i, k, n | i, j, q, r | a, c, d, e, f, j, k, l, n | b, j, k | b, d, f, g, i, j, k, n, o, t | a, b, d, g, i, k, n, o, t | b, f, i, k | a, b, d, f, k, l, m, p | |
| Driver: age (a), gender (b), physical condition (c), illegal behaviours/poor judgment (d), driving under the influence (alcohol, drugs, etc.) (e), driver’s vision obstruction (f) | a, b, c, d, e, f | d, e, f | a, b, d, e | a, e | b, e | a, d, e | ||||||
| Vehicle: type (a), age (b), estimated speed at impact (c) | a c | a | a | a | a | a b c | ||||||
| Crash information: crash location (4) (a), n.º of vehicles involved (b), n.º of persons involved (c), HV involvement (d), motorcycle involvement (e), crash type/severity (f), contributing factors (g), pre-collision actions (h), first/most harmful event (i) | a, b, c, d, f, h, i | a, b, c, d, f, i | a, b, d, g | a, b, f, g, h | b, d, f | b, c, d, f, g | d, f, g, h | a, b | a, b, d | d, e, g, h | a | |
| Year | N.º of Records Coded as ‘Undefined’ in Field B4.3 | N.º of WZ Crashes (1) | N.º of Drivers Involved | N.º of Passengers Involved | N.º of Pedestrians Involved | Total N.º of Persons Involved |
|---|---|---|---|---|---|---|
| 2010 | 1558 | 830 | 1263 | 336 | 116 | 1715 |
| 2011 | 968 | 706 | 1107 | 247 | 97 | 1451 |
| 2012 | 424 | 544 | 814 | 162 | 93 | 1069 |
| 2013 | 419 | 511 | 755 | 192 | 91 | 1038 |
| 2014 | 364 | 451 | 650 | 145 | 72 | 867 |
| 2015 | 320 | 462 | 694 | 143 | 75 | 912 |
| Total | 4053 | 3504 | 5283 | 1225 | 544 | 7052 |
| Dependent Variable | Code | Categories | N | % | Tolerance | VIF |
| Crash nature | 0 | Run over pedestrians | 957 | 13.6% | ||
| 1 | Run-off-road | 1851 | 26.2% | |||
| 2 | Collision | 4244 | 60.2% | |||
| Independent variables | Code | Categories | N | % | Tolerance | VIF |
| N. of persons involved in the crash (Covariate) | X1 | 1 person involved (1) | 1167 | 16.5% | 0.853 | 1.172 |
| 2 persons involved (2) | 2992 | 42.4% | ||||
| 3 persons involved (3) | 1656 | 23.5% | ||||
| 4 persons involved (4) | 832 | 11.8% | ||||
| 5 persons involved (5) | 405 | 5.8% | ||||
| Fatality | X2 | No (0) | 6982 | 99.0% | 0.969 | 1.031 |
| Yes (1) | 70 | 1.0% | ||||
| Seriously injured | X3 | No (0) | 6813 | 96.6% | 0.915 | 1.093 |
| Yes (1) | 239 | 3.4% | ||||
| Slightly injured | X4 | No (0) | 2802 | 39.7% | 0.868 | 1.152 |
| Yes (1) | 4250 | 60.3% | ||||
| Road environment (urban) | X5 | No (0) | 2650 | 37.6% | 0.914 | 1.094 |
| Yes (1) | 4402 | 62.4% | ||||
| Horizontal geometric design (alignment) | X6 | No (0) | 1884 | 26.7% | 0.978 | 1.023 |
| Yes (1) | 5168 | 73.3% | ||||
| Pav. grip condition (dry and clean) | X7 | No (0) | 2431 | 34.5% | 0.970 | 1.031 |
| Yes (1) | 4621 | 65.5% | ||||
| Passenger car | X8 | No (0) | 1575 | 22.3% | 0.907 | 1.103 |
| Yes (1) | 5477 | 77.7% | ||||
| Driver action (running straight) | X9 | No (0) | 2183 | 31.0% | 0.938 | 1.067 |
| Yes (1) | 4869 | 69.0% | ||||
| Pedestrian worker victim action (in WZ) | X10 | No (0) | 6965 | 98.8% | 0.958 | 1.043 |
| Yes (1) | 87 | 1.2% | ||||
| Excessive speed for prevailing conditions | X11 | No (0) | 6563 | 93.1% | 0.969 | 1.032 |
| Yes (1) | 489 | 6.9% | ||||
| Valid values Missing values Total values Subpopulation | 7052 0 7052 535 a | 100% 0% | ||||
| Step | Action | Variable Code | Model Fitting Criteria | Effect Selection Tests | ||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | −2Log Likelihood | Chi-Square a | df | Sig. (p-Value) | |||
| 0 | Entered | Intercept | 7206.624 | 7220.346 | 7202.624 | |||
| 1 | Entered | X1 | 5118.382 | 5145.826 | 5110.382 | 2092.242 | 2 | <0.001 |
| 2 | Entered | X9 | 4412.906 | 4454.073 | 4400.906 | 709.475 | 2 | <0.001 |
| 3 | Entered | X4 | 3965.229 | 4020.118 | 3949.229 | 451.677 | 2 | <0.001 |
| 4 | Entered | X5 | 3658.287 | 3726.897 | 3638.287 | 310.943 | 2 | <0.001 |
| 5 | Entered | X10 | 3508.108 | 3590.441 | 3484.108 | 154.179 | 2 | <0.001 |
| 6 | Entered | X3 | 3398.055 | 3494.110 | 3370.055 | 114.052 | 2 | <0.001 |
| 7 | Entered | X6 | 3288.628 | 3398.405 | 3256.628 | 113.427 | 2 | <0.001 |
| 8 | Entered | X8 | 3180.663 | 3304.162 | 3144.663 | 111.965 | 2 | <0.001 |
| 9 | Entered | X7 | 3124.939 | 3262.161 | 3084.939 | 59.724 | 2 | <0.001 |
| 10 | Entered | X11 | 3081.704 | 3232.647 | 3037.704 | 47.235 | 2 | <0.001 |
| 11 | Entered | X2 | 3053.036 | 3217.702 | 3005.036 | 32.668 | 2 | <0.001 |
| Model | Model Fitting Criteria | Likelihood Ratio Tests | ||||
|---|---|---|---|---|---|---|
| AIC | BIC | −2Log Likelihood | Chi-Square | df | Sig. (p-Value) | |
| Intercept only | 7206.624 | 7220.346 | 7202.624 | |||
| Final | 5118.382 | 5145.826 | 5110.382 | 2092.242 | 22 | <0.001 |
| Goodness-of-fit | ||||||
| Pseudo R-Square | Pseudo R2 | |||||
| Cox and Snell | 0.449 | |||||
| Nagelkerke | 0.532 | |||||
| McFadden | 0.321 | |||||
| Effect | AIC of Reduced Model | BIC of Reduced Model | −2Log Likelihood | Chi-Squre | df | Sig. (p-Value) |
|---|---|---|---|---|---|---|
| Intercept | 3053.036 | 3217.702 | 3005.036 a | 0.000 | 0 | |
| X1 | 4418.717 | 4569.660 | 4374.717 | 1369.681 | 2 | <0.001 |
| X2 | 3081.704 | 3232.647 | 3037.704 | 32.668 | 2 | <0.001 |
| X3 | 3172.531 | 3323.475 | 3128.531 | 123.495 | 2 | <0.001 |
| X4 | 3575.313 | 3726.257 | 3531.313 | 526.277 | 2 | <0.001 |
| X5 | 3330.868 | 3481.811 | 3286.868 | 281.832 | 2 | <0.001 |
| X6 | 3144.972 | 3295.915 | 3100.972 | 95.935 | 2 | <0.001 |
| X7 | 3101.301 | 3252.245 | 3057.301 | 52.265 | 2 | <0.001 |
| X8 | 3166.438 | 3317.381 | 3122.438 | 117.401 | 2 | <0.001 |
| X9 | 3580.781 | 3731.724 | 3536.781 | 531.744 | 2 | <0.001 |
| X10 | 3189.141 | 3340.084 | 3145.141 | 140.104 | 2 | <0.001 |
| X11 | 3096.417 | 3247.360 | 3052.417 | 47.381 | 2 | <0.001 |
| Crash Nature a | β | Std. Error | Wald | df | Sig. b (p-Value) | Exp(β) c (Odds Ratio) | 95% Conf. Interval for Exp(B) | ||
|---|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | ||||||||
| Run-off-road | Intercept | 9.314 | 0.749 | 154.439 | 1 | 0.000 | |||
| X1 | −1.233 | 0.046 | 726.329 | 1 | <0.001 | 0.291 | 0.266 | 0.319 | |
| X2 (=0) | −1.975 | 0.339 | 33.830 | 1 | <0.001 | 0.139 | 0.071 | 0.270 | |
| X3 (=0) | −2.257 | 0.202 | 125.050 | 1 | <0.001 | 0.105 | 0.070 | 0.155 | |
| X4 (=0) | −1.753 | 0.097 | 328.494 | 1 | <0.001 | 0.173 | 0.143 | 0.209 | |
| X5 (=0) | 0.264 | 0.075 | 12.298 | 1 | <0.001 | 1.302 | 1.123 | 1.508 | |
| X6 (=0) | 0.626 | 0.076 | 67.960 | 1 | <0.001 | 1.870 | 1.611 | 2.170 | |
| X7 (=0) | 0.456 | 0.073 | 39.449 | 1 | <0.001 | 1.577 | 1.368 | 1.819 | |
| X8 (=0) | 0.032 | 0.082 | 0.151 | 1 | 0.698 | 1.032 | 0.879 | 1.213 | |
| X9 (=0) | −1.046 | 0.091 | 132.227 | 1 | <0.001 | 0.351 | 0.294 | 0.420 | |
| X10 (=0) | −2.472 | 0.599 | 17.023 | 1 | <0.001 | 0.084 | 0.026 | 0.273 | |
| X11 (=0) | −0.574 | 0.129 | 19.816 | 1 | <0.001 | 0.563 | 0.438 | 0.725 | |
| Running over pedestrians | Intercept | 6.012 | 0.785 | 58.723 | 1 | 0.000 | |||
| X1 | −1.182 | 0.065 | 335.410 | 1 | <0.001 | 0.307 | 0.270 | 0.348 | |
| X2 (=0) | −0.842 | 0.417 | 4.074 | 1 | 0.044 | 0.431 | 0.190 | 0.976 | |
| X3 (=0) | −0.739 | 0.239 | 9.536 | 1 | 0.002 | 0.478 | 0.299 | 0.763 | |
| X4 (=0) | 0.653 | 0.091 | 51.973 | 1 | <0.001 | 1.922 | 1.609 | 2.295 | |
| X5 (=0) | −1.714 | 0.128 | 178.035 | 1 | <0.001 | 0.180 | 0.140 | 0.232 | |
| X6 (=0) | −0.358 | 0.106 | 11.344 | 1 | 0.001 | 0.699 | 0.568 | 0.861 | |
| X7 (=0) | −0.197 | 0.091 | 4.671 | 1 | 0.031 | 0.821 | 0.687 | 0.982 | |
| X8 (=0) | −1.228 | 0.128 | 92.221 | 1 | <0.001 | 0.293 | 0.228 | 0.376 | |
| X9 (=0) | 1.395 | 0.087 | 254.695 | 1 | <0.001 | 4.036 | 3.400 | 4.790 | |
| X10 (=0) | −4.426 | 0.542 | 66.671 | 1 | <0.001 | 0.012 | 0.004 | 0.035 | |
| X11 (=0) | 0.985 | 0.270 | 13.360 | 1 | <0.001 | 2.679 | 1.579 | 4.544 | |
| Predicted | ||||
|---|---|---|---|---|
| Observed | Collision | Run of Road | Run over Pedestrian | Percent Correct |
| Collision | 3540 | 506 | 198 | 83.4% |
| Run-off-road | 556 | 1248 | 47 | 67.4% |
| Run over pedestrian | 571 | 10 | 376 | 39.3% |
| Percent correct | 66.2% | 25.0% | 8.8% | 73.2% |
| Dependent Variable | Code | Categories | N | % | Tolerance | VIF |
| Crash nature | 0 | Pedestrian | 544 | 7.7% | ||
| 1 | Passenger | 1225 | 17.4% | |||
| 2 | Driver | 5283 | 74.9% | |||
| Independent variables | Code | Categories | N | % | Tolerance | VIF |
| N. of persons involved in the crash (Covariate) | X1 | 1 person involved (1) | 1167 | 16.5% | 0.948 | 1.054 |
| 2 persons involved (2) | 2992 | 42.4% | ||||
| 3 persons involved (3) | 1656 | 23.5% | ||||
| 4 persons involved (4) | 832 | 11.8% | ||||
| 5 persons involved (5) | 405 | 5.8% | ||||
| Fatality | X2 | No (0) | 6982 | 99.0% | 0.995 | 1.005 |
| Yes (1) | 70 | 1.0% | ||||
| Seriously injured | X3 | No (0) | 6813 | 96.6% | 0.992 | 1.008 |
| Yes (1) | 239 | 3.4% | ||||
| Road environment (urban) | X4 | No (0) | 2650 | 37.6% | 0.937 | 1.067 |
| Yes (1) | 4402 | 62.4% | ||||
| Horizontal geometric design (alignment) | X5 | No (0) | 1884 | 26.7% | 0.984 | 1.016 |
| Yes (1) | 5168 | 73.3% | ||||
| Pav. grip condition (dry and clean) | X6 | No (0) | 2431 | 34.5% | 0.981 | 1.020 |
| Yes (1) | 4621 | 65.5% | ||||
| Heavy vehicle involvement | X7 | No (0) | 6704 | 95.1% | 0.984 | 1.016 |
| Yes (1) | 348 | 4.9% | ||||
| Working weekday | X8 | No (0) | 1813 | 25.7% | 0.991 | 1.009 |
| Yes (1) | 5239 | 74.3% | ||||
| Valid values | 7052 | 100% | ||||
| Missing values | 0 | 0% | ||||
| Total values | 7052 | |||||
| Subpopulation | 226 a | |||||
| Step | Action | Variable Code | Model Fitting Criteria | Effect Selection Tests | ||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | -2Log Likelihood | Chi-Square a | df | Sig. (p-Value) | |||
| 0 | Entered | Intercept | 2690.999 | 2704.721 | 2686.999 | |||
| 1 | Entered | X1 | 1895.983 | 1923.427 | 1887.983 | 799.016 | 2 | <0.001 |
| 2 | Entered | X4 | 1725.956 | 1767.122 | 1713.956 | 174.027 | 2 | <0.001 |
| 3 | Entered | X3 | 1633.382 | 1688.271 | 1617.382 | 96.573 | 2 | <0.001 |
| 4 | Entered | X8 | 1566.389 | 1634.999 | 1546.389 | 70.993 | 2 | <0.001 |
| 5 | Entered | X7 | 1517.454 | 1599.787 | 1493.454 | 52.934 | 2 | <0.001 |
| 6 | Entered | X5 | 1485.635 | 1581.690 | 1457.635 | 35.819 | 2 | <0.001 |
| 7 | Entered | X2 | 1459.336 | 1569.113 | 1427.336 | 30.299 | 2 | <0.001 |
| 8 | Entered | X6 | 1450.037 | 1573.536 | 1414.037 | 13.299 | 2 | <0.001 |
| Model | Model Fitting Criteria | Likelihood Ratio Tests | ||||
|---|---|---|---|---|---|---|
| AIC | BIC | -2Log Likelihood | Chi-Square | df | Sig. (p-Value) | |
| Intercept only | 2690.999 | 2704.721 | 2686.999 | |||
| Final | 1450.037 | 1573.536 | 1414.037 | 1272.962 | 16 | <0.001 |
| Goodness-of-fit | ||||||
| Pseudo R-Square | Pseudo R2 | |||||
| Cox and Snell | 0.165 | |||||
| Nagelkerke | 0.217 | |||||
| McFadden | 0.126 | |||||
| Effect | AIC of Reduced Model | BIC of Reduced Model | -2Log Likelihood | Chi-Squre | df | Sig. (p-Value) |
|---|---|---|---|---|---|---|
| Intercept | 1450.037 | 1573.536 | 1414.037 a | 0.000 | 0 | |
| X1 | 2179.746 | 2289.523 | 2147.746 | 733.709 | 2 | <0.001 |
| X2 | 1476.190 | 1585.967 | 1444.190 | 30.153 | 2 | <0.001 |
| X3 | 1552.724 | 1662.501 | 1520.724 | 106.687 | 2 | <0.001 |
| X4 | 1673.644 | 1783.421 | 1641.644 | 227.607 | 2 | <0.001 |
| X5 | 1478.061 | 1587.838 | 1446.061 | 32.024 | 2 | <0.001 |
| X6 | 1459.336 | 1569.113 | 1427.336 | 13.299 | 2 | <0.001 |
| X7 | 1496.907 | 1606.684 | 1464.907 | 50.870 | 2 | <0.001 |
| X8 | 1509.464 | 1619.241 | 1477.464 | 63.427 | 2 | <0.001 |
| Type of Person Involved a | β | Std. Error | Wald | df | Sig. b (p-Value) | Exp(β) c (Odds Ratio) | 95% conf. Interval for Exp(B) | ||
|---|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | ||||||||
| Passenger | Intercept | −7.548 | 0.627 | 144.972 | 1 | 0.000 | |||
| X1 | 0.780 | 0.057 | 184.951 | 1 | <0.001 | 2.182 | 1.950 | 2.442 | |
| X2 (=0) | 2.150 | 0.483 | 19.795 | 1 | <0.001 | 8.588 | 3.330 | 22.146 | |
| X3 (=0) | 1.434 | 0.230 | 38.994 | 1 | <0.001 | 4.197 | 2.676 | 6.584 | |
| X4 (=0) | 1.914 | 0.157 | 148.787 | 1 | <0.001 | 6.782 | 4.986 | 9.225 | |
| X5 (=0) | 0.734 | 0.135 | 29.719 | 1 | <0.001 | 2.084 | 1.600 | 2.714 | |
| X6 (=0) | 0.429 | 0.119 | 12.945 | 1 | <0.001 | 1.535 | 1.215 | 1.939 | |
| X7 (=0) | 1.789 | 0.284 | 39.806 | 1 | <0.001 | 5.983 | 3.432 | 10.429 | |
| X8 (=0) | 1.016 | 0.138 | 53.909 | 1 | <0.001 | 2.763 | 2.106 | 3.624 | |
| Driver | Intercept | −2.781 | 0.430 | 41.928 | 1 | 0.000 | |||
| X1 | −0.030 | 0.052 | 0.346 | 1 | 0.556 | 0.970 | 0.876 | 1.074 | |
| X2 (=0) | 1.980 | 0.321 | 38.095 | 1 | <0.001 | 7.243 | 3.862 | 13.583 | |
| X3 (=0) | 2.043 | 0.182 | 125.901 | 1 | <0.001 | 7.712 | 5.398 | 11.019 | |
| X4 (=0) | 1.812 | 0.146 | 154.502 | 1 | <0.001 | 6.124 | 4.602 | 8.150 | |
| X5 (=0) | 0.465 | 0.119 | 15.351 | 1 | <0.001 | 1.592 | 1.262 | 2.009 | |
| X6 (=0) | 0.306 | 0.102 | 8.946 | 1 | 0.003 | 1.358 | 1.111 | 1.659 | |
| X7 (=0) | 0.551 | 0.188 | 8.610 | 1 | 0.003 | 1.735 | 1.201 | 2.508 | |
| X8 (=0) | 0.606 | 0.125 | 23.454 | 1 | <0.001 | 1.833 | 1.434 | 2.342 | |
| Predicted | ||||
|---|---|---|---|---|
| Observed | Pedestrian | Passenger | Driver | Percent Correct |
| Pedestrian | 26 | 6 | 512 | 4.8% |
| Passenger | 4 | 204 | 1017 | 16.7% |
| Driver | 19 | 230 | 5034 | 95.3% |
| Percent correct | 0.7% | 6.2% | 93.1% | 74.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, A.; Santos, B.; Picado-Santos, L. Modelling Road Work Zone Crashes’ Nature and Type of Person Involved Using Multinomial Logistic Regression. Sustainability 2023, 15, 2674. https://doi.org/10.3390/su15032674
Vieira A, Santos B, Picado-Santos L. Modelling Road Work Zone Crashes’ Nature and Type of Person Involved Using Multinomial Logistic Regression. Sustainability. 2023; 15(3):2674. https://doi.org/10.3390/su15032674
Chicago/Turabian StyleVieira, Adriana, Bertha Santos, and Luís Picado-Santos. 2023. "Modelling Road Work Zone Crashes’ Nature and Type of Person Involved Using Multinomial Logistic Regression" Sustainability 15, no. 3: 2674. https://doi.org/10.3390/su15032674
APA StyleVieira, A., Santos, B., & Picado-Santos, L. (2023). Modelling Road Work Zone Crashes’ Nature and Type of Person Involved Using Multinomial Logistic Regression. Sustainability, 15(3), 2674. https://doi.org/10.3390/su15032674








