Abstract
In recent years, intensive water use combined with global climate change has increased fluctuations in freshwater lake levels, hydrological characteristics, water quality, and water ecosystem balance. To provide a sustainable management plan in the long term, deep learning models (DL) can provide fast and reliable predictions of lake water levels (LWLs) in challenging future scenarios. In this study, artificial neural networks (ANNs) and four recurrent neural network (RNN) algorithms were investigated to predict LWLs that were applied in time series such as one day, five days, ten days, twenty days, one month, two months, and four months ahead. The results show that the performance of the Long Short-Term Memory (LSTM) model with a prediction of 60 days is in the very good range and outperforms the benchmark, the Naïve Method, by 78% and the ANN at the significance level (p < 0.05) with an RMSE = 0.1762 compared to other DL algorithms. The RNN-based DL algorithms show better prediction performance, specifically, for long time horizons, 57.98% for 45 days, 78.55% for 60 days, and 58% for 120 days, and it is better to use a prediction period of at least 20 days with an 18.45% performance increase to take advantage of the gated RNN algorithms for predicting future water levels. Additionally, microcystin concentration was tightly correlated with temperature and was most elevated between 15 and 20 m water depths during the summer months. Evidence on LWL forecasting and microcystin concentrations in the context of climate change could help develop a sustainable water management plan and long-term policy for drinking water lakes.
1. Introduction
Depending on climatic, geographic, geological, social, and economic factors, each location has its own water quality and quantity challenges. Additionally, ongoing global warming and meteorological patterns are likely to disrupt the temporal and spatial balance of water, leading to freshwater scarcity and impeding the achievement of the United Nations Sustainable Development Goals around the world. Modeling studies suggest that there will be a paradigm shift in the distribution of freshwater on the planet by 2050 [1,2]. Therefore, a sound water management plan, developed using reliable forecasting models, is essential for implementing sustainable water use and conserving water resources in a given basin or region.
Turkey experiences frequent droughts that significantly reduce surface and groundwater resources, including wetlands and lakes [3,4]. Drought conditions affect standing water bodies when there is a reduction in surface runoff and in stream inputs. Droughts typically coincide with hot weather, which causes evaporation to increase significantly during dry periods. The effects of drought include a decrease in water levels in what is usually a very fertile littoral zone. This can leave aquatic fauna (e.g., mussels, snails, and flora) stranded in the area. The increased water temperature associated with drought can lead to stratification, increased salinity, and reduced oxygen levels. In some cases, the combination of high temperatures with low oxygen may lead to the extinction of fish species [5].
Uncontrolled drinking water supplies and inadequately managed water reservoirs pose a significant threat to developing and densely populated cities. Lake Sapanca, for example, is an important source of fresh water supply for the cities of Sakarya and Kocaeli and is also used by several bottled water companies for commercial purposes. The prospects of the reservoir appear to be affected by climate change and recent droughts, which could negatively impact several parts of the region and its ecosystems [6], as well as water quality associated with cyanobacteria and microcystin [7]. Because of the multitude of factors that affect the surface area of a lake, one of the most critical hydrologic problems is estimating the water level of a lake before it reaches its threshold. Hydrological models have certain limitations in terms of providing accurate predictive results [8] due to the complex nature of hydrological and meteorological variables as well as the temporal and spatial properties of an individual catchment. Therefore, it is vital to develop more reliable predictive models that can accurately and reliably estimate the future water level of a lake.
There are two different approaches for LWL prediction in the literature. The most prominent approach follows the physical process, and the emerging approach focuses on data-driven methodologies, which focus on historical datasets to predict future values. Data-driven methods simulate the LWL in addition to the factors affecting it using scientific computer models. Different types of models have been developed to promote specific cases. For instance, Chang and Chang evaluated the model with Support Vector Regression (SVR) and an Adaptive Neuro-Fuzzy Inference System (ANFIS) [9]. Liu et al. presented a multivariate conditional model based on copulas to predict water level and improve spatial precipitation estimation [10]. Wang et al. applied SVR to simulate the causality between LWL and the quantity of water discharged from the reservoir [11]. Statistical methods and Artificial Intelligence (AI) techniques are two common data-driven approaches to solving LWL prediction problems [12]. These methods include multiple regression, pattern recognition, neural network techniques, time series methods, and probability features [13].
During the recent decade, a variety of contemporaneous techniques have been applied to compare the predictive performance of the algorithms. For example, Ghorbani et al. investigated the ability of the Genetic Programming (GP) and ANN models to predict LWLs in Australia, and reported accurate predictions with good agreement [14]. To predict LWLs at Lake Urmia in Iran, Talebizadeh and Moridnejad employed the ANN and ANFIS [15]. The ANFIS algorithm has better accuracy compared to the ANN model, as shown by the uncertainty analysis. In another study, neural network, neural fuzzy, and GP models were applied to estimate the LWL on a daily basis [16]. The results showed that each of the three models accurately predicted the LWL. Buyukyildiz et al. developed a series of AI models, Multilayer Perceptron (MLP), hybridized SVR with Particle Swarm Optimization (PSO), a Radial Basis Neural Network, and ANFIS, to predict LWLs [17]. Their results show that the hybrid model SVR-PSO is a reliable predictive model. Similarly, for three upstream rivers on the east coast of Malaysia, water levels for the next five hours were successfully estimated using an ANN [18]. To predict the LWL, Yadav and Eliza used a Support Vector Machine (SVM) and Wavelet [19]. The results of the study showed that the model implemented to predict future values of the reservoir was more accurate compared to regression models. Despite the successful attempts to use machine learning (ML) methods in these studies, there are certain inherent limitations in the algorithms used in the literature [20]. For instance, in ANNs, the rules that could explain underlying methods are not given. In terms of fuzzy logic, setting precise, fuzzy enrollment limitations and parameters can be difficult and the fuzzy justification is not always correct. Regression models show that as the number of variables increases, their accuracy decreases. The regression models work better when there are fewer variables. Lastly, training a deep learning model requires a lot of computing power, which leads to the need for powerful GPUs and a large amount of RAM. Another potential drawback is an overfitting issue that arises when a model performs poorly on newly untrained data after being overtrained on training data.
The most used time series prediction model with statistical analysis that is conducted by scholars for lake level prediction is the Autoregressive Integrated Moving Average (ARIMA) model [21,22]. It can be expressed in several ways, including as Moving Average (MA), Autoregressive (AR), or hybrid AR or MA, known as Autoregressive Moving Average (ARMA) or Seasonal Autoregressive Integrated Moving Average (SARIMA) [23]. The SARIMA model, on the other hand, has the advantage of requiring fewer model features to explain the structure of time series that exhibit nonstationarity in seasons and between seasons [24]. Unlike ML methods, which often require multiple features as input, this is an important simplification [22]. The artificial neural network (ANN) algorithm is a widely used ML method for water flow modeling, water quality assessment, and water level prediction in the field of hydrology and water resources [18,25,26,27]. In addition, some research papers have presented a hybrid ANN-ARIMA model [28,29].
Review of the aforementioned studies shows that various models for LWL prediction have different findings and highlight their estimation uncertainty. Some scholars have used time series techniques for predicting various areas such as energy price, stock price, and corporate sales forecasts, which are critical to the global economy [30,31], including weather, environment, hydrology, and geological phenomena [32,33] in recent years. Nearly all of them concluded that the time series forecasting methods provide more accurate results compared to the benchmark models.
The recurrent neural network (RNN)-based deep learning (DL) approach is proposed in this paper as a state-of-art technique for examining the LWL that would improve the prediction performance. DL networks, which differ from conventional approaches in that they allow computer models consisting of numerous layers to learn representations of data consisting of multiple levels of abstraction, replicate the functioning of the human brain [34]. The approach of DL has been used for object recognition, speech recognition, and visual object recognition including genomics and drug discovery [35]. The extraordinary success of supervised RNN-based DL algorithms for conducting recognition studies directed the use of RNN-based algorithms in multivariate time series studies. The LWL studies also have time series data due to their nature and attract hydrologists to exploit the power of these DL algorithms in their future time series prediction studies. However, the application of DL models for LWLs is limited and is the focus of this study in order to overcome several drawbacks of the available approaches to predict LWLs, such as the large number of input variables and their uncertainty. The motivation behind this study is to provide an effective prediction technique for water managers to handle drinking water supply availability in lakes before reaching an alarming level. The limited water supply in lakes not only causes frequent drought experiences and water shortages, but also causes a decrease in water quality.
In this work, novel gated RNN-based algorithms are used to build a model that can predict the future LWL to support drought mitigation and reservoir management. In addition, this study aims to help fill the gap in the literature regarding the selection of DL models and the evaluation of the performance of LWL prediction algorithms by using Naïve Benchmarks and the Diebold–Mariano test. As far as the authors are aware, there is no other study that focuses on the comparison between algorithms for multivariate prediction studies with different time lags.
2. Materials and Methods
2.1. Case Study Area
Lake Sapanca extends between the latitudes of 40°41′–40°44′ E and the longitudes of 30°09′–30°20′ N in the northwestern part of Turkey (Figure 1). It is located between two cities: the western part of the lake is in Kocaeli and the eastern end is within the provincial border of Sakarya. It is a 16 km (east–west) and 5 km (north–south) long tectonic fresh water source that provides the drinking water needs of both cities. It has a surface area of 46 km2 and a reasonable depth of 30 m. It has a volume of about 1.3 billion m3. The greatest depth of the lake basin is 54 m, and its catchment area is 250 km2 [36]. The Lake is surrounded by southern mountains and northern hills.
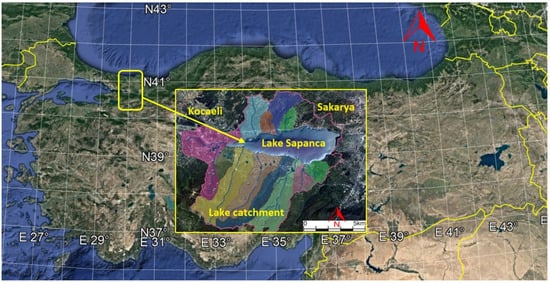
Figure 1.
Lake Sapanca area and its catchment with river basins.
The transitional climate found in the Sapanca basin is influenced by the Black Sea and Mediterranean climates. While the basin exhibits characteristics of both the Black Sea and Mediterranean climates, it may also display elements of a continental climate due to its interaction with an intermediary air system. Despite the warm and rainy winters experienced in the basin, summers are comparatively less hot and dry than what is typically observed in the Mediterranean region.
Figure 1 depicts the catchment area of Lake Sapanca and its sub-basins, which consist of 12 streams that inflow to Lake Sapanca. The lake has a controlled outflow with Cark Creek, which regulates the maximum LWL to prolong water retention in the lake. The seasonal precipitation, water withdrawal, and surface outflow results in inter-annual LWL variations of 2.28 m, between 29.90 and 32.18 m above sea level. The lake is noteworthy because it supplies potable water to the provinces of Sakarya and Kocaeli. It is also believed that the lake basin will eventually meet the bottled water needs of Istanbul. Although the basin area does not include any industrial regions, 23% of the basin area is used as cultivated land mainly covered by ornamentals and fruit orchards, and 9.5% is used as settlement land. The remaining basin area is covered by 65% of forest land and 2.5% as natural land. The water needs of urban, agricultural, and industrial sectors have caused Lake Sapanca basin’s water quantity and quality to worsen. Whereas the mean growth rate of the population in Turkey is 0.8%, the population growth rate of the basin has increased from 1.5% to 3.5% in the last 20 years [37]. The rapid growth in the population of the basin is adversely affecting the quantity and quality of the water. Despite the fact that the lake is in a transitional stage from oligotrophic to mesotrophic, its ecological status is deteriorating as the water level drops below the lake’s surface discharge during droughts, and point and nonpoint runoff flows in from numerous sources [20]. The lake’s ecological state deteriorates primarily as a result of unchecked agricultural operations and household wastewater leakages in the vicinity. In addition, the droughts that periodically occur cause the lake’s water quality and quantity to deteriorate [6].
2.2. Dataset Description
Several characteristics are used in the literature to evaluate future LWLs. The most commonly used features in the literature are precipitation (17%), LWL, and evaporation [20]. Other major features used by researchers include discharge [38], temperature [39], inflow [40], streamflow and humidity [41], wind speed and solar radiation [42], and volume and area [43].
The State Hydraulic Works and Turkish State Meteorological Service, through their river monitoring program for Lake Sapanca, provided the data examined for this study. LWL, maximum temperature, minimum temperature, average temperature, precipitation, and withdrawal were the features that were supplied (Table 1). Among these, withdrawal feature includes water withdrawal for industrial, agricultural, and domestic use. Measurements were taken daily between 2012 and 2023, with occasional missing data. The interpolation technique was used to complete the missing data.

Table 1.
Dataset Features.
Time series data are a collection of values generated over a period of time in continuous or discrete time units. Numerous research has demonstrated the effectiveness of time series prediction as a control and early warning system. Time series prediction seeks to forecast upcoming changes across time at observation locations. The dataset employed in this research, as shown in Figure 2, is a typical multivariate time series that typically contains real-valued LWL and meteorological information in addition to water removal from the reservoir. One can spot abnormalities in the LWL, meteorological, and hydrological data by carefully examining the graph. However, only annual and seasonal patterns of change are seen in the temperature data. Distribution data from LWL are compatible to meteorological data, especially in annual precipitation. Additionally, water withdrawals show an increasing trend over time (Figure 2).
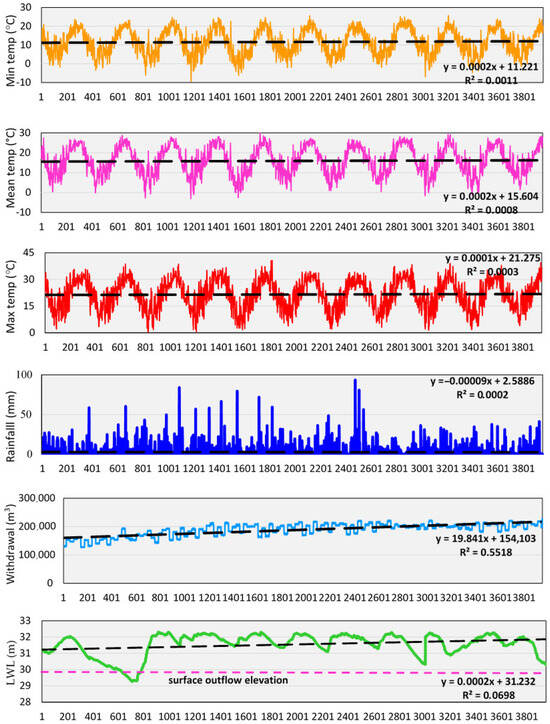
Figure 2.
Time series plots of daily meteorological data, water withdrawals, and lake water level for Lake Sapanca from 11 October 2012 through 4 August 2023. (x-axis: data rows in sequence.)
As shown in Figure 2, during prolonged drought, the LWL drops below the discharge elevation at the surface, which is 29.90 m above sea level in Lake Sapanca. Data from LWL indicate that in years of low precipitation, LWL decreases. Higher precipitation in the last decade (2015–2018) coincides with LWLs above the lake’s discharge elevation. In addition, higher maximum temperatures and low precipitation in recent years reduce LWLs to the surface runoff elevation during dry periods (Figure 2). Low precipitation also increases water demand, while low temperatures decrease water use. In addition, increasing population and industrialization are related to water withdrawal from the lake. Therefore, multivariate time series data that include freshwater demand and meteorological characteristics are critical for predicting lake water levels.
2.3. Data Preprocessing
The dataset was created on a daily basis with monthly stacks and converted to a time series format to be used as a predictive model. The dataset contains several missing points that prevent the model from running. Although the dataset has small gaps, some columns contain large blanks. The large gaps that are located either at the beginning or at the end of the dataset were removed from the dataset. Other missing data were interpolated using the linear method. Among the features, maximum temperature, minimum temperature, average temperature, and withdrawal do not have any missing values. The only missing values are included in the features of precipitation (0.7%) and water level (3.03%). Therefore, the dataset can be used for an RNN-based neural network study with minimal bias with the interpolation method due to its negligible missingness rate. No outlier was detected using the interquantile range method and expert opinions. The data were used after the necessary preprocessing steps had been performed.
Due to the sequential nature of time series, the data should be used to assign the training, validation, and test sets. The daily hydrological and meteorological data collected at the lake basin from 11 October 2012 to 4 August 2023 were used to train, validate, and test the algorithms. The dataset was divided into training, validation, and test sets with 60%, 20%, and 20% proportions, respectively, to cover the high/low values in the training and test subsets to determine the optimal pattern for the data and to improve the model’s validity. To avoid overfitting and to include all seasons in the dataset, dry and wet seasons were included in all sets created. The lag values used in the study are 1, 5, 10, 20, 30, 45, 60, and 120. The lag values were determined considering the seasonal cycles in terms of wet and dry seasons. After 120 days, the LWL values arrive for the next seasonal cycle, which causes the Naïve Method to become overly optimistic.
2.4. Model Descriptions
The RNN is the ancestor of gated recurrent-based networks. Due to time delays during the backpropagation error in the learning stage of the RNN-based network, it was established as a remedy for the gradient explosion issue. At each time step, gated RNNs predict the label of an activity. To predict an activity label, any number of previous time steps can be merged. The gated RNN model networks have been shown to be a significant model in the past and are capable of learning from sequential inputs. They can effectively learn from sequences of different lengths and capture long-term dependencies.
There are 4 different gated RNN networks used in this study: LSTM, GRU, Stacked LSTM, and Bidirectional LSTM.
The gates and feedback loops used by LSTM are self-trained using the input data. By incorporating a gate mechanism, the LSTM network, a particular architecture created to simulate dynamic temporal and spatial sequences, is able to more precisely resolve long-range dependencies [12]. The LSTM network is made up of a number of memory blocks connected by layers made up of a collection of memory cells with recurrent connections (Figure 3). LSTM has three multiplicative units: input, output, and forget gates. Through the hyperbolic tangent function, sigmoid function, and regulatory filter, the input gate transforms the information. The forget gate erases the less important information. The output gate selects the pertinent data from the active cell. The LSTM layer uses the following mathematical operation to determine the output variable [20]:
where ft is the forgotten variable, it the input variable, and ot the output variable. Xt indicates the values that the feature receives at t time, and ht−1 is the output cell of the previous cell. Inside the LSTM cell, memory is indicated by ct−1. W is the weight matrix, and B is the term bias. The sigmoid function (σ), the hyperbolic tangent function (tanh), processes the Xt variable and the h variable from the previous learning.
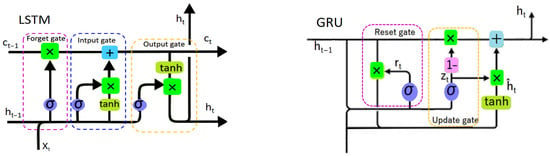
Figure 3.
Basic structure of LSTM and GRU algorithms.
While GRU has two gates, it requires less memory and runs faster than LSTM. GRU is computationally more efficient than LSTM because the structure is simpler and more straightforward. The input gate and the forgetting gate are combined into one update gate and simplified (Figure 3). GRU has two activation functions and one tanh function. Therefore, GRU is able to build a long-term memory similar to the LSTM, but has the advantage of having fewer parameters and a faster training speed than the LSTM. GRU uses the following equations to determine the output variables [20]:
where tanh and σ are the hyperbolic tangent and logistic sigmoid functions, respectively, and r and z are vectors for the activation values of the update and reset gates, respectively. Wr, Ur, Wz, Uz, Wc, Uc represent the weight matrix.
The RNN is the ancestor of gated recurrent-based networks. Due to time delays during backpropagation error in the learning process of the RNN model network, gated structures were established as a remedy for the gradient explosion problem [44]. At each time step, gated RNN networks predict the label of an activity. To predict an activity label, any number of previous time steps can be merged [45]. The gated RNN model networks have proven to be a significant model in the past and are capable of learning from sequential inputs. They can effectively learn from sequences of different lengths and capture long-term dependencies [46]. Stacked LSTM is a variant of LSTM with multiple LSTM layers containing multiple memory cells that give the model the ability to capture the structure of time series and combine the learned representation of previous layers while providing a higher level of abstraction for the final results [47]. This structure contributes to the model’s ability to learn higher-level temporal representations, but can lead to degradation problems due to the low convergence rate of the LSTM layers, although this error is different from the vanishing gradient problem. Another variation of the LSTM is the Bidirectional LSTM, in which the input currents of the LSTM flow in both directions so that information from both the input and output sides can be used [48]. The use of both forward and reverse information improves the accuracy of this model and supports improved learning for long-term dependency data.
where hn = new state, in = input, hn−1 = output of past state, hn+1 = output of future state, and the ⊗ symbol represents the concatenation operation.
Lastly, the RNN algorithms are also compared against ANN, which is the most used neural network algorithm for LWL studies [20]. A massively parallel-distributed information processing system called an ANN mimics the function of the neuron network in the human brain. Human learning is a result of neurons, and ANNs employ this important feature for ML.
An NN is made up of several nodes, or basic processing units. The mathematical functions and network architecture make up the ANNs. The architecture is made up of the arrangement of nodes in a specific way. Typically, the nodes are organized in layers that facilitate the flow of information from the input layer to the output layer. Between the input and output layers, there may be multiple hidden levels. The network’s capacity to represent more complicated events is enhanced by the hidden layers.
2.5. Hyperparameters
This study uses the Tensorflow Keras (2.11.0) libraries to implement the proposed different RNN-based networks, with Tensorflow as the backend [49]. The implementation of ANN, LSTM, GRU, Stacked LSTM, and Bidirectional LSTM layers in the algorithm uses the sequential approach. The loss function is set as “MAE” and the optimizer as “Adam” since these hyperparameters do not have a significant impact on the performance of the algorithm. However, the hyperparameters such as neuron number, epoch, batch size, number of previous time steps, and number of layers are optimized. The hyperparameters in the algorithms that have the best performance are briefly listed in Table 2.

Table 2.
Optimized hyperparameter values of algorithms.
The optimized hyperparameter values in Table 2 are different for the different algorithms. However, all RNN-based algorithms performed the best when the number of layers was 2 and the prediction period was 60 days.
2.6. Evaluation Metrics
A significant number of researchers in the literature prefer Root Mean Squared Error (RMSE), Mean Squared Error, Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), R2, or R as evaluation metrics to compare their algorithms with the base model or with other algorithms [20]. These metrics account for more than 50% of the evaluation metrics in the literature. On the other hand, there are less favorable evaluation metrics used by some researchers, including Nash–Sutcliffe Efficiency [42], accuracy [50], Mean Relative Error [20], and Percent Bias [51].
The goal of model performance determination is to verify the accuracy and precision of the proposed model and to determine the difference rate so that it can be used with confidence [52]. The evaluation metrics chosen for this study are RMSE and MAPE. The RMSE value shows the root of the squares of the average differences between predicted and observed values. Lower RMSE values indicate higher model performance and better correlation between observed and predicted values. Equation (10), discussed in more detail below, was used as a performance measure in the evaluation of the model.
where “Σ” stands for sum, Pi is the expected value for the dataset’s ith observation, Qi is the actual value for that observation, and “n” denotes sample size.
The exactness of a forecasting approach is determined by a statistic called Mean Absolute Percentage Error (MAPE). In order to determine how accurate the predicted quantities are in relation to the actual numbers, the value represents the mean of the absolute percentage errors for every value in a dataset. MAPE necessitates the usage of data values apart from zero and is frequently useful for large-scale data analysis. MAPE is a simple metric; a 10% MAPE indicates that, irrespective of whether the variance was positive or negative, the average difference between the expected and actual amounts was 10%. Lower MAPE values indicate higher model performance and better correlation between observed and predicted values. The MAPE formula used to calculate the error rate is in Equation (11)
where “Σ” stands for sum, Xi is the expected value for the dataset’s ith observation, Yi is the actual value for that observation, and “m” denotes sample size.
Although the performance of the model is evaluated using the RMSE and MAPE values, the comparison of forecast accuracy is made using the Naïve Method. The Naïve Benchmark is one of the most commonly used method for comparing time series forecasting models because it is easy to compute and understand [53]. In this approach, each forecast is equated to the last observed value for the intended time step. The performance of the algorithm is considered successful if the RMSE or MAPE value is lower than the RMSE or MAPE results of the Naïve Method. The reason for such a comparison is that the RMSE or MAPE values for earlier time steps are always lower than for further time steps due to their proximity to the actual values. For this reason, the performance of further time periods (i.e., 60 days and 120 days) cannot be compared using only the RMSE or MAPE values themselves. To compare all time values, performance is evaluated using the percentage increase in RMSE compared to the RMSE score or difference in MAPE values over the Naïve Method.
where Yt is the forecast value at time t and Yt−n is the value at the previous nth day
To determine whether the proposed algorithms are successful enough to be used as a prediction method, the prediction results of the algorithms are also compared. The Diebold–Mariano significance test was used to control the algorithm differences and their significance at p-value < 0.05, as described by Van der Heijden et al. [53]. If the p-value of the test is less than 0.05, the prediction accuracies are significantly different from each other. This approach gives the impression that the sophisticated procedure is only recommended if it is significantly better than the benchmark, not only if it has better accuracy statistics. This also implies that there is a significant difference between the prediction results and that the proposed algorithms cannot be used interchangeably.
A graphical representation of the entire modelling process with the flowchart applied to predict LWL in this study is shown in Figure 4.
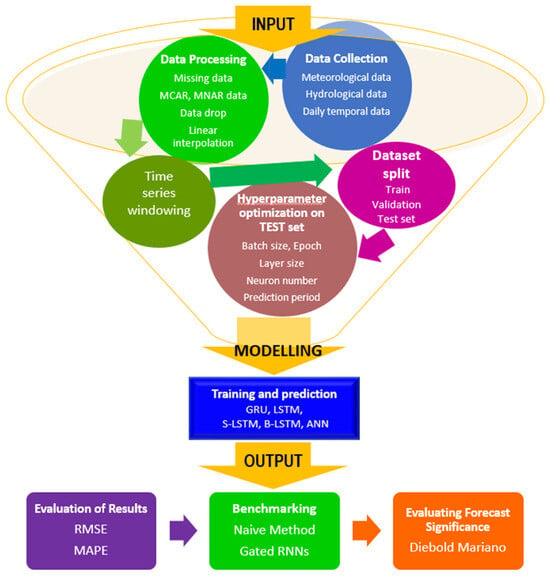
Figure 4.
Flowchart of LWL modelling.
2.7. Water Quality Indicator
In freshwater habitats, temperature and light intensity are the most important meteorological factors determining algal photosynthesis and algal blooms [54]. Toxin production behavior of freshwater algal species is strongly influenced by environmental conditions. As an indicator of biological water quality, monthly microcystin measurement data at various depths from the surface to 20 m during the period from March 2019 to April 2023 were subjected to statistical analysis. Computer-based models require long-term data to make more reliable and accurate predictions for the future. Therefore, the Mann–Kendall trend analysis test is used with environmental time series. In this test, the null hypothesis assumes that there is no trend and the alternative hypothesis assumes that there is a trend. Furthermore, Spearman rank correlation analysis was applied to determine the relationship between key meteorological parameters and the concentration of the cyanobacterial growth byproduct microcystin since microcystin concentrations did not follow a normal distribution.
3. Results
This study uses the ANN and four different RNN-based deep learning algorithms to compare their forecasting accuracy from day 1 to day 120 ahead, based on RMSE and MAPE values, the Naïve Method, and Diebold–Mariano test results. The ANN, LSTM, GRU, Stacked LSTM, and Bidirectional LSTM algorithms were successfully trained and validated, and compared with test data consisting of 3004 lines to evaluate the model’s reliability for the unknown dataset. Table 3 presents the performance of LWL prediction of the investigated ANN and RNN algorithms from day 1 to day 120 ahead forecasting. These results show that all investigated ANN and RNN algorithms showed excellent prediction accuracy in the 1 day to 10 day ahead prediction scenario with RMSE values of <0.1 m. On the other hand, in the 60 day ahead scenarios, the LSTM algorithm had the best performance value for training and testing with an RMSE = 0.1762 m, while in the 120 day ahead scenarios, GRU showed the best performance with an RMSE score of 0.3838 m (Table 3). In contrast, the Stacked LSTM and Bidirectional LSTM models did not show additional performance in terms of prediction accuracy over LSTM. In summary, the LSTM model is significantly efficient considering its high accuracy among other advanced models, specifically for long-term predictions such as a 60 days ahead forecast, due to the architectural benefits of the process of parameter tuning and its migration to different tasks. GRUs are easier to train and faster to run than LSTMs, but they may not be as effective at storing and accessing long-term dependencies. Since it is necessary to know the next timestamp in advance for a Bidirectional LSTM, it is more appropriate for offline applications [55]. On the other hand, the performance difference between Stacked LSTM and LSTM comes from additional dimensions for next value prediction other than the time dimension.

Table 3.
The performance of ANN and RNN-based algorithms for predicting lake water level with increasing time intervals, RMSE results. (Metric is based on m.)
Additionally, the RMSE values describing the prediction error rates of time series algorithms were compared using the Naïve Method, and the algorithms that performed better than the Naïve Method were identified as successful algorithms for predicting future LWL values. The Naïve Benchmark comparison results of algorithms are presented in Table 4 from day 1 to day 120 forecasting. The higher value for each investigated algorithm to each prediction period indicates higher performance and good predictive power. Based on the Naïve Method benchmark, the algorithm performances increased up to the 60 days ahead predictions, then decreased for the 120 days ahead predictions. As an average, the performance of GRU was higher for all investigated periods, whereas Stacked LSTM had a lower average performance value, followed by the Bidirectional LSTM algorithms.

Table 4.
Benchmark performance comparison of algorithms; figures indicate improvement in RMSE values over Naïve Method.
The variabilities between Naïve Benchmark comparison scores are much more apparent than for RMSE values (Table 4). The decreasing performance goes down to −24.26%, which indicates that it would be disadvantageous to use the RNN-based algorithm for predicting that specific period. The results also show that the RMSE results of some algorithms are close to those of the Naïve Method, especially for the predictions of 5 and 10 days. Therefore, the algorithms were tested even more to find if it is necessary to use these algorithms for future LWL values. The results show an increase in performance of at least 18.45% (Stacked LSTM) when the prediction horizon is set to 20 days or more. Based on the Naïve Method comparison, LSTM showed the highest performance with a 78.55% improvement over the Naïve Method at 60 day ahead forecasting. It is also worth noting that ANN is the only algorithm that performed better than the Naïve Method in the 1 day prediction period.
The performances of ANN and RNN-based algorithms were also tested using MAPE as an evaluation metric. A similar pattern was observed in the MAPE results when considering the results in the RMSE values because as the time horizon extends to further time periods, the model performance decreases. This pattern indicates there needs to be additional evaluation criteria for model performance results between different time periods. For this reason, the results in Table 5 were calculated further by taking differences between the Naïve Method results and the algorithms’ results (Table 6).

Table 5.
The performance of ANN and RNN-based algorithms for predicting lake water level with increasing time intervals, MAPE results. (%).

Table 6.
Benchmark performance comparison of algorithms; figures indicate difference of MAPE values compared with Naïve Method.
Table 6 reveals the performance differences that indicate the performance improvement in models in terms of the Naïve Method. As can be seen in the table, none of the models perform better when compared with the Naïve Method in the 1 day and 5 day prediction periods. However, as the time period increases, the performance improvement also increases. The best performance is observed for the GRU algorithm in the 120 day prediction period with a 0.85 points performance increase in the MAPE. The MAPE results are occasionally compatible with the RMSE results, but the MAPE results indicate that in order to achieve the advantage of RNN-based algorithms, the models should focus on at least a 30 day ahead prediction. In addition, the ANN algorithm is advantageous when used in the 30 day and 60 day prediction period according to the results.
The performance of ANN, LSTM, GRU, Stacked LSTM, and Bidirectional LSTM for LWL, and their observed and estimated values compared with the Naïve Method for the day 1 to day 120 ahead scenarios are presented in Figure A1, Figure A2, Figure A3 and Figure A4. It can be seen from Figure A1 that the observed and simulated lines are generally distributed closely for each investigated model, showing that all ANN and RNN algorithms have high simulation performance at day 1. However, as the forecasting time extends from day 1 to day 120, the observed, estimated, and Naïve Method lines diverge for each of the algorithms.
Figure A1 shows the 1 day and 5 days prediction results of the ANN and gated RNN algorithms and the comparison with the observed and Naïve Method values. The prediction results of all the studied algorithms are quite similar to each other and to the Naïve Method for the 1 day and 5 days prediction (Figure A1), indicating good training, validation, and prediction. Figure A2 shows the prediction results of the ANN and gated RNN algorithms for 10 and 20 days ahead and the comparison with the observed values and the Naïve Method. Compared to the Naïve Method, all tested algorithms had a similar prediction trend for 10 days ahead, but all algorithms outperformed the Naïve Method in their predictions for 20 days ahead. When forecasting 10 and 20 days ahead, the GRU achieved the best results (Figure A2), showing a lower RMSE (Table 3) and a higher performance improvement compared with the Naïve Method (Table 4).
When comparing the performance results of the algorithms for day 30, Stacked LSTM and Bidirectional LSTM produced a similar prediction performance to LSTM and GRU, whereas for day 45 prediction, the GRU, Stacked LSTM, and LSTM algorithms produced a similar performance to Bidirectional LSTM (Figure A3, Table 4).
Figure A4 shows the 60 and 120 day forecast results of the ANN and gated RNN algorithms and the comparison with the observed values and the Naive Method. The 60th day was the culminating point for the prediction performance of the tested algorithms, and LSTM performed better for LWL at the 60 day prediction based on the RMSE and Naïve Method values. Although all tested algorithms performed well in 60 day prediction (Table 4), LSTM provided the closest prediction values to the observed values of LWL 60 days in advance compared with the other methods, as shown in Figure A4. For the 120 day ahead predictions, there was a significant decrease in values for the studied algorithms compared to the Naïve Method, with the exception of GRU. Although the prediction performance was low, the GRU algorithm provided a statistically similar prediction performance for day 60 and day 120. These results show that the GRU algorithm may still be superior to the other algorithms in terms of prediction accuracy with higher Naïve values. However, the degree of agreement between the predicted value and the actual value is not very good and exceeds the actual value.
As a summary, Figure A1, Figure A2, Figure A3 and Figure A4 show that the tested algorithms predicted LWL at a statistically acceptable level for up to 120 days. Among the proposed algorithms, the LSTM algorithm was clearly superior in tracking the nonlinear behavior of Lake Sapanca over a 60-day period with the smallest RMSE (0.1762 m) and a higher performance ratio compared to the Naïve Method result (78.55%). Thus, when a model is needed for long-term forecasting LWL, the LSTM-based DL algorithm can help to automate and manage LWL to implement more effective water management strategies. It is optimal for 60-day forecasts of LWL.
The Diebold–Mariano test values to determine the statistical significance of two separate prediction results are summarized in Table 7. It can be noted that the RNN algorithms did not show significant superiority for the 1-day, 5-days, and 10-days LWL forecasting over the Naïve Method. However, the Naïve Method and the GRU algorithm for 5 days gave a p-value of 0.031, indicating the GRU algorithm’s superior result is significant compared with the Naïve Method to predict the next 5 days. The same is true for predicting the next 10 days using the LSTM and GRU algorithms. However, when the prediction significances of LSTM and GRU are tested, the p-value is lower than 0.05, indicating that GRU must be used to predict the next 10 days.

Table 7.
Forecast difference results of Naïve Method, ANN, and RNN algorithms based on Diebold–Mariano (DM) test for increasing day intervals from day 1 to day 120 (p-value ≤ 0.05 indicates the significance of the DM test results, Green boxes indicate significantly different prediction results with distinct tones, red boxes indicate insignificant results).
From Table 4, it can be seen that, for day 20 predictions, the best performance improvement comes from the GRU algorithm. Accordingly, the p-values are significant (p < 0.05) based on the Diebold–Mariano test (Table 7), which confirms the superiority of GRU. Regarding the Naïve Method comparison (Table 4) and the Diebold–Mariano (Table 7) test results, only the GRU algorithm should be preferred to predict the LWL for the next 20 days.
Similarly, GRU, LSTM, and Stacked LSTM gave a p-value of less than 0.05 in the Diebold–Mariano tests compared to the Naïve Method for predicting the next 30 days LWL. On the other hand, the predictive performance of Bidirectional LSTM was not significant compared to the Naïve Method as the p-value is greater than 0.05.
According to the Naïve Method comparison, GRU performed better than the other algorithms in the 45-day forecast (Table 4). Table 7 further confirms that the predictions of GRU algorithms have a significant p-value compared to the Naïve Method. Moreover, the p-values are more remarkable than 0.05 when GRU is compared with Stacked LSTM and Bidirectional LSTM, indicating that the GRU algorithm can be used interchangeably with the Stacked LSTM and Bidirectional LSTM algorithms.
The results of the Diebold–Mariano test show that the accuracy of the prediction results and the stability of the performance of the LSTM algorithm are significantly better, with a p-value of less than 0.05 (Table 7). Considering the results of the RMSE, Naïve Method, and Diebold–Mariano test, only the LSTM algorithm should be preferred for predicting the next 60 days to obtain a more reliable and accurate prediction of the future dynamics of LWL.
It is clear that the implemented ANN and RNN algorithms provide a relatively accurate prediction pattern when the prediction values are compared with the observed data for the 120 day prediction (Table 7), even though the magnitude of the Naïve Method benchmark result is reduced compared to the 60 day prediction. In addition to the benchmark, the Naïve Method, the GRU algorithm has the significant best performance for the 120 day forecast considering the Diebold–Mariano test results compared to the other algorithms (Table 7), indicating that the GRU algorithm is more efficient at forecasting the next 120 days of LWL.
From the obtained results for LWL prediction from day 1 to day 120, we can see that: (1) Day 60 predictions provide the most optimized LWL detection based on high Naïve Benchmark performance comparison values. (2) The best performance of the investigated algorithms can change in terms of the selected prediction periods. (3) The LSTM algorithm can better predict LWL for 60 days in advance with higher accuracy, which allows water managers to take action. In addition, it is worth noting that the Bidirectional LSTM and Stacked LSTM algorithms contribute to the forecast with little or no performance increase for the short prediction period of less than 20 days.
Among the features, the most important one to affect the output was determined as withdrawal using the Mutual Information technique. The importance levels can be ordered as withdrawal, average temperature, minimum temperature, maximum temperature, and precipitation (Figure 5).
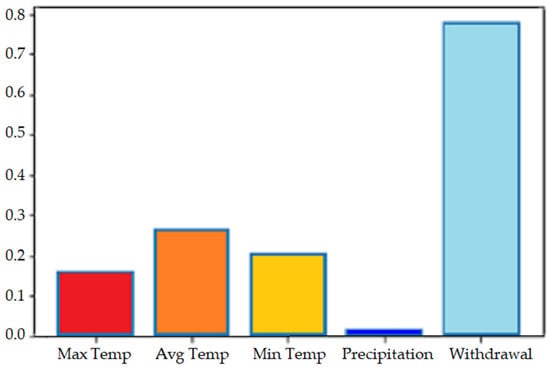
Figure 5.
Variable importance.
Accurate LWL prediction is a necessity, not only to prevent possible drought conditions but also possible water quality effects. Therefore, this study conducted extra work to observe the relationship between microcystin concentrations previously observed during low LWL periods. In addition to the LWL effect, this study investigated the relationship for the maximum temperature, mean temperature, minimum temperature, precipitation, light intensity, and evaporation. This experiment was conducted in order to reveal their importance so as to predict LWL in advance and be able to take measurable actions in advance.
To begin with, the microcystin concentrations at the surface, 1 m, 5 m, 10 m, 15 m, and 20 m were measured over the period of 2019–2023 to understand the relationship between the changing meteorological situation and water quality was affected by algal growth. The microcystin concentration in all sampled depths showed approximately the same increasing pattern over time, except for the samples collected from the depth of 15 m (Figure 6). The variations in Figure 6 indicate there is an increasing trend of microcystin for the surface water, 1 m, 5 m, 10 m, and 20 m depths. However, the trend is decreasing for the 15 m depth. The microcystin level was almost similar for each depth of the first 10 m; however, significant differences were recorded in the spring and autumn, specifically, vertically mixing periods. During the summer, the microcystin concentration stayed relatively low (<0.5 µg/L) or at an undetectable level from May to October. The highest concentrations were observed during the winter period from November to April with a significant fluctuation, which coincided with the mixing period. By contrast, the microcystin concentrations were higher at the sampling depths of 15 and 20 m. The microcystin was recorded at all sampling times during the experimental period. In general, the concentrations were below the 2 µg/L for both sampling depths; however, the highest concentrations of around 8 µg/L were recorded during the summer stratification phase (June to August). For the two years 2020 and 2021, the microcystin concentration was the lowest (with <3.31 µg/L), especially for 2021 (<1.61 µg/L).
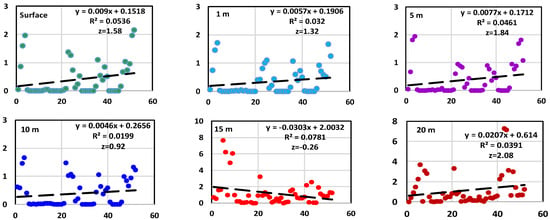
Figure 6.
Linear trend of microcystin concentration in the water column at different depths from surface to 20 m from 21 March 2019 to 12 April 2023. (x-axis: data rows in sequence, y-axis: microcystin concentration).
The nonparametric Mann–Kendall test shows that the microcystin concentration decreases monotonically at a depth of 15 m and increases at the other depths. However, only the microcystin concentration at 20 m depth was significant at the 95% confidence limit with a z-value of 2.08 (Figure 6), indicating an increasing positive trend in the microcystin data time series that dominates at this depth.
Due to temporal and spatial variability, it is difficult to obtain sufficient input data needed for data-driven predictive models to analyze and learn the relationships between microcystin and meteorological parameters, i.e., temperature, precipitation associated with algal proliferation, and microcystin concentration. To better understand the changing meteorological parameters on microcystin concentration, Spearman correlations were evaluated using monthly microcystin data collected from raw water before water treatment. From Figure 7, the significant positive contribution of temperature on microcystin concentration is evident. Light intensity also has a positive effect on microcystin concentration. On the other hand, the water level of the lake had no significant effect on the microcystin concentration.
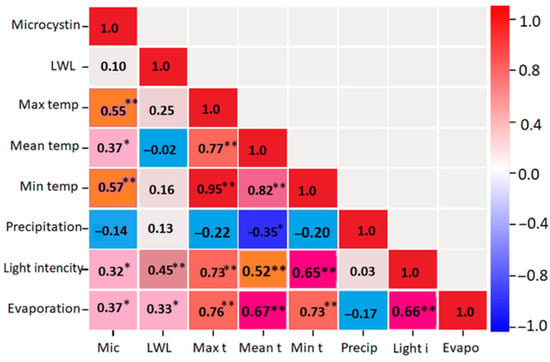
Figure 7.
Spearman rank correlation between microcystin and meteorological parameters (** p < 0.01, * p < 0.05).
The degree of association differs in terms of the features in Figure 7. The minimum temperature, maximum temperature, mean temperature, and evaporation have a moderate correlation with microcystin [56]. In addition, light intensity has a weak correlation. On the other hand, the LWL and precipitation have a very weak correlation with microcystin. The results provide a better understanding that the water quality is rarely affected by the level of water. However, the temperature, which is one of the indicators for predicting LWL, affects the water quality. Thus, it can be concluded that LWL does not directly affect the water quality, but the effect is indirect through the consideration of temperature values.
4. Discussion
Based on the experimental result of this case study that applies ANN and RNN-based deep learning algorithms for lake water level prediction, it is possible to forecast the next 120 days with a smaller RMSE (0.3838 m), reasonable Naïve Benchmark comparison value (58.00%), and significant Diebold–Mariano test results (p < 0.05). However, compared with other models, the prediction result based on LSTM proposed in this study is optimal for the next 60 days LWL forecasting with a smaller RMSE (0.1762 m), the highest Naïve Benchmark comparison value (78.55%), and a significant Diebold–Mariano test p-value (<0.003). The goal of this study is to compare the impact of various climates and comprehend how new AI techniques behave and perform on various event forecasting tasks. The prediction performance of the investigated ANN and RNN algorithms aligns with previous research based on the RMSE and the Naïve Method. Using ANN and SVM, Yoon et al. predicted the groundwater levels in the nearshore aquifer in Donghae City, Korea, for two wells with RMSE values of 0.13 m and 0.136 m, respectively [57]. The objective of their research was to create and evaluate data-driven time series forecasting models for the short-term fluctuations in groundwater levels in a coastal aquifer caused by tidal influence and precipitation recharge. However, their study lacks a comparison of the proposed algorithms with the baseline models and other algorithms from DL. Therefore, the performance of the models cannot be evaluated for predicting water levels. The algorithms are also not evaluated against basic benchmark methods such as the Naïve Method, which raises the question of whether it is necessary to create fancy DL algorithms for LWL prediction. Thus, this study could be a milestone for further water level studies that attempt to develop every single DL algorithm available in the field of data science.
Hrnjica, B. and Bonacci found that the LSTM and RNN algorithms performed better than the traditional ANN algorithms on datasets with a given number of features and a time scale of one month [58]. They also found that the feed-forward neural network and LSTM models performed better than the traditional time series forecasting models based on ARIMA and other similar techniques. The objective of their study was motivated by the realization that traditional regression and statistical techniques were insufficiently effective at predicting stochastic events such as water level. In contrast to traditional models, Lee et al. showed that the LSTM model better reproduces the variability and correlation structure of the broader time scale as well as the important statistics of the original time domain [59]. Applying the LSTM into stochastic simulation and determining if the long-term trends of known hydroclimatological indicators can be replicated was the main objective of their work. The improved representation of long-term variability is critical for water managers as they rely on these data to plan and manage future water resources. In the future, the performance improvement over the Naïve Benchmark can be tested with other novel models, such as attention-based algorithms or other derivatives. However, the recent attempt to use an attention-based algorithm showed that it did not perform better than a recurrent network [60].
The main hypothesis of the present study is confirmed by the fact that RNN-based algorithms achieve better predictive performance of LWL when using long-term daily data from a decade and improve predictive accuracy for 60-day forecasts (Table 4). The trends of observations and model predictions in Figure A1 through Figure A4 suggest that the potential performance of RNN algorithms can also be extended beyond 120-day forecasts by incorporating more data into the models. The LSTM model network has demonstrated its ability to learn from sequential data in the past and has been shown to be a useful model. It can effectively learn from sequences of varied durations, capturing long-term dependencies. [35]. To confirm the results of this paper, Zhu et al. studied 69 lakes in Poland for 30 day ahead water level prediction and concluded that the recurrent DL models performed similarly to attention-based recurrent DL models in terms of predictive performance [60]. The results of the LSTM algorithm between its variants, namely the Stacked LSTM and the Bidirectional LSTM, in the present study show that there is no significant difference in predicting less than 30 days ahead. The LSTM algorithm requires long observation datasets and the selection and optimization of hyperparameters, learning rate, and number of epochs to achieve correct prediction results [20]. For example, Morovati et al. reported a better prediction performance of LSTM when using daily recorded data over 20 years [61]. The results obtained for LSTM in this study are consistent with these findings. The findings also show that the LSTM algorithm reflects well when compared to the fluctuation trend of the real LWL value. This is due to the use of a gated structure in the LSTM model, so the LSTM algorithm is good at extracting short-term temporal correlations. However, due to the cyclic periods of water level variations, the performance increase drops when it reaches the next LWL cycle after 60 days. The better performance of RNN algorithms compared to the Naïve Method is also due to the successful optimization of hyperparameters in the RNN networks.
Another important aspect is that although the prevailing opinion suggests using all available DL algorithms to find the algorithm that performs best according to the RMSE or MAPE results, the results of the algorithms do not seem to differ significantly with respect to the Diebold–Mariano test. Therefore, in order to suggest a better performing algorithm, the statistical difference must be shown in addition to the RMSE or MAPE results [53], and in some cases, the ANN and gated RNN derivatives, as indicated in the Results section, do not appear to have statistical significance and can be used interchangeably.
The fluctuations in LWL are associated with meteorological processes and anthropogenic activities, which lead to a nonlinear and complex system. In this context, the study has several limitations due to its nature. One of the limitations is that the results depend on the geographical location. The experiment was conducted at Lake Sapanca in the northeastern Marmara region of Turkey. This location has characteristics of both Black Sea and Mediterranean climates. Therefore, the results may change in regions with different climate characteristics. Another limitation of the study is that the dataset produced by the Turkish Meteorological Service contains several missing data for selected parameters. Although it is possible to interpolate missing data, the results with interpolated data rows may produce a biased LWL value. The results could change with a dataset containing complete records for a longer period without missing data. In addition, there are limitations to the study in that there is an insufficient amount of data, especially for some features. In practice, there may not be a chance to gather all the features from the field. The potential feature(s) may not be represented to the algorithm and the potential feature(s) may even increase the model prediction performance. In addition, in the case of there being very few available features, the prediction performance could be underrepresented. However, in the case of there being too many features, it may cause the model to overfit. Therefore, a balance between overrepresentation and underrepresentation must be provided. Thus, it is further suggested to apply other appropriate preprocessing methods to improve the predictive performance of the RNN DL models with different time horizons. In the future, the LWL prediction could be practiced by using GIS methods with a satellite dataset. The performance difference between time series prediction and prediction with image data could be compared with the Naïve Method Benchmark. In addition, in terms of the availability of more features, the researchers can conduct sensitivity analysis and uncertainty analysis to eliminate some of the features to prevent possible overfitting issues.
Several well-known nutrient inputs and relatively less known meteorological parameters, together with hydrological disturbances, cause excessive growth of cyanobacteria in freshwater ecosystems, which degrade water quality with their toxins. Extreme heat waves are becoming more common as global and regional warming continues and are expected to become the norm in future scenarios. Microcystin concentration correlated positively with temperature variables (max, min, and mean, p < 0.01), including evaporation and light intensity (p < 0.05), and not significantly with precipitation (negative correlation), which is directly related to LWL (Figure 7). Significant correlations between meteorological parameters and microcystin concentrations in freshwater bodies have been reported previously [7]. Light intensity in the metalimnion zone leads to greater development of cyanobacteria and the presence of large amounts of microcystins, posing potential problems for the use of water resources [62]. Since freshwater lakes are used as drinking water sources, proper water and algae management is necessary to ensure a clean and safe water supply. The use of tap water is restricted when large amounts of algae are found in water reservoirs because various water treatment problems can occur, such as clogged treatment systems, a bad odor, color in the water, and regulated toxic substances such as microcystin. Predicting the correlation of algal blooms with easily measured meteorological or hydrological parameters in advance and taking rapid response actions to algal growth can minimize damage and ensure uninterrupted production of purified water.
5. Conclusions
Monitoring and forecasting lake water levels is one of the most important tasks to ensure sustainable water resource management, safeguard water quality, and maintain watershed balance in the face of global climate change. The gated RNN-based algorithms are powerful modeling techniques for future forecasting and were tested in this study to obtain more accurate estimates of water level changes in lakes. The gated RNN algorithms correctly adapt to changing input conditions, such as adjustments in water demand policy during reservoir operation. The fact that the gated RNN structure accounts for the nonlinear dynamics of the problem throughout the dataset, means that it can be used to explain why gated RNNs perform better than conventional approaches in predicting reservoir levels. With respect to the RMSE, the results demonstrated here show the ability of the models used to understand the nonlinear behavior of LWLs.
The modeling results support the following findings:
- The results of the algorithms can be compared, and although there could be different but similar results, the algorithms can be used interchangeably.
- Overall, the GRU algorithm performs better than other gated RNN algorithms because it has a lower RMSE. However, it does not perform better in all time periods, so the algorithm needs to be replaced by another one to achieve better results for LWL prediction cases further in the future.
- Gated RNN-based algorithms appear to have higher RMSE results as the prediction horizon increases, indicating poorer performance in lower prediction time periods. A more accurate comparison is possible using the Naïve Method, and the percentage increase could provide a healthier result for comparing algorithm results with different prediction time periods. Although the prediction may differ from the actual values as the time period increases, the performance increase is much higher compared to the Naïve Benchmark, making it more attractive for use in LWL prediction cases.
In addition, this study also examined the relationship between global warming and microcystin levels in freshwater lakes and demonstrated a clear relationship with meteorological data. However, more research is needed in this area to close the gap between LWL predictions with different geographical locations using the same available features, algal growth, and microcystin levels.
Overall, the prediction results suggest that the proposed RNN algorithms can be successfully used to predict the future state of LWL for drinking water resource management leading to the achievement of sustainability under changing climatic conditions.
Author Contributions
Conceptualization, S.O.; methodology, S.O.; software, S.O.; validation, S.O.; formal analysis, S.O.; investigation, S.O.; resources, S.O.; data curation, S.O.; writing—original draft preparation, S.O.; writing—review and editing, S.O. and S.O.Y.; visualization, S.O.; supervision, S.O.Y.; project administration, S.O. and S.O.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from The State Hydraulic Works for water level and withdrawal features, and the Turkish State Meteorological Service for maximum temperature, average temperature, minimum temperature, and precipitation features, which are governmental institutions for water administration and meteorological services in Turkey. The data are available from the authors with the permission of The State Hydraulic Works and Turkish State Meteorological Service.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
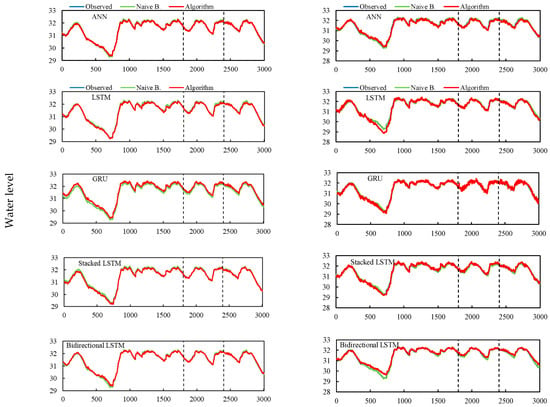
Figure A1.
One day (left side) and 5 days (right side) ahead prediction results. The vertical dashed lines indicate the train set-validation set-test set, respectively.
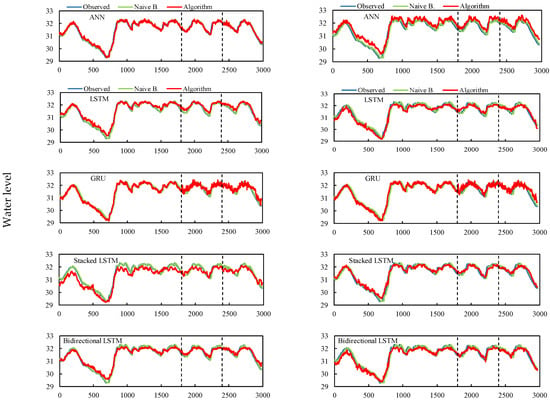
Figure A2.
Ten days (left side) and 20 days (right side) ahead prediction results. The vertical dashed lines indicate the train set-validation set-test set, respectively.
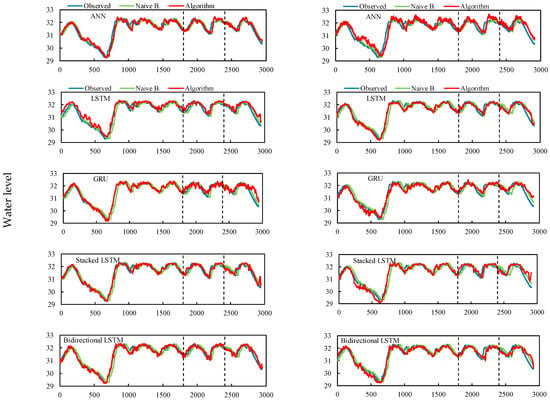
Figure A3.
Thirty days (left side) and 45 days (right side) ahead prediction results. The vertical dashed lines indicate the train set-validation set-test set, respectively.
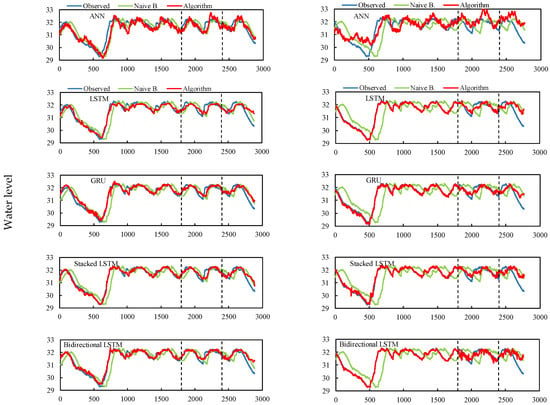
Figure A4.
Sixty days (left side) and 120 days (right side) ahead prediction results. The vertical dashed lines indicate the train set-validation set-test set, respectively.
References
- Paul, N.; Elango, L. Predicting future water supply-demand gap with a new reservoir, desalination plant and waste water reuse by water evaluation and planning model for Chennai megacity, India. Groundw. Sustain. Dev. 2018, 7, 8–19. [Google Scholar] [CrossRef]
- Castillo-Botón, C.; Casillas-Pérez, D.; Casanova-Mateo, C.; Moreno-Saavedra, L.M.; Morales-Díaz, B.; Sanz-Justo, J.; Gutiérrez, P.A.; Salcedo-Sanz, S. Analysis and prediction of dammed water level in a hydropower reservoir using machine learning and persistence-based techniques. Water 2020, 12, 1528. [Google Scholar] [CrossRef]
- Soylu Pekpostalci, D.; Tur, R.; Danandeh Mehr, A.; Vazifekhah Ghaffari, M.A.; Dąbrowska, D.; Nourani, V. Drought monitoring and forecasting across Turkey: A contemporary review. Sustainability 2023, 15, 6080. [Google Scholar] [CrossRef]
- Yeşilköy, S.; Şaylan, L. Spatial and temporal drought projections of northwestern Turkey. Theor. Appl. Climatol. 2022, 149, 1–14. [Google Scholar] [CrossRef]
- Bond, N.R.; Lake, P.S.; Arthington, A.H. The impacts of drought on freshwater ecosystems: An Australian perspective. Hydrobiologia 2008, 600, 3–16. [Google Scholar] [CrossRef]
- Duru, U. Shoreline change assessment using multi-temporal satellite images: A case study of Lake Sapanca, NW Turkey. Environ. Monit. Assess. 2017, 189, 385. [Google Scholar] [CrossRef]
- Novais, M.H.; Penha, A.M.; Catarino, A.; Martins, I.; Fialho, S.; Lima, A.; Palma, P. The usefulness of ecotoxicological tools to improve the assessment of water bodies in a climate change reality. Sci. Total Environ. 2023, 901, 166392. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Chang, F.J.; Chang, Y.T. Adaptive neuro-fuzzy inference system for prediction of water level in reservoir. Adv. Water Resour. 2006, 29, 1–10. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, X.; Guan, Y. A multivariate conditional model for streamflow prediction and spatial precipitation refinement. J. Geophys. Res. Atmos. 2015, 120, 10–116. [Google Scholar] [CrossRef]
- Wang, M.; Dai, L.; Dai, H.; Mao, J.; Liang, L. Support vector regression based model for predicting water level of Dongting Lake. J. Drain. Irrig. Mach. Eng. 2017, 35, 954–961. [Google Scholar]
- Zhang, X.; Liu, P.; Zhao, Y.; Deng, C.; Li, Z.; Xiong, M. Error correction-based forecasting of reservoir water levels: Improving accuracy over multiple lead times. Environ. Model. Softw. 2018, 104, 27–39. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Khatibi, R.; Aytek, A.; Makarynskyy, O.; Shiri, J. Sea water level forecasting using genetic programming and comparing the performance with artificial neural networks. Comput. Geosci. 2010, 36, 620–627. [Google Scholar] [CrossRef]
- Talebizadeh, M.; Moridnejad, A. Uncertainty analysis for the forecast of lake level fluctuations using ensembles of ANN and ANFIS models. Expert Syst. Appl. 2011, 38, 4126–4135. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Nikoofar, B. Forecasting daily lake levels using artificial intelligence approaches. Comput. Geosci. 2012, 41, 169–180. [Google Scholar] [CrossRef]
- Buyukyildiz, M.; Tezel, G.; Yilmaz, V. Estimation of the change in lake water level by artificial intelligence methods. Water Resour. Manag. 2014, 28, 4747–4763. [Google Scholar] [CrossRef]
- Lukman, Q.A.; Ruslan, F.A.; Adnan, R. 5 Hours ahead of time flood water level prediction modelling using NNARX technique: Case study terengganu. In Proceedings of the 2016 7th IEEE Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 8 August 2016; IEEE: New York, NY, USA, 2016; pp. 104–108. [Google Scholar] [CrossRef]
- Yadav, B.; Eliza, K. A hybrid wavelet-support vector machine model for prediction of lake water level fluctuations using hydro-meteorological data. Measurement 2017, 103, 294–301. [Google Scholar] [CrossRef]
- Ozdemir, S.; Yaqub, M.; Yildirim, S.O. A systematic literature review on Lake water level prediction models. Environ. Model. Softw. 2023, 163, 105684. [Google Scholar] [CrossRef]
- Yu, Z.; Lei, G.; Jiang, Z.; Liu, F. ARIMA modelling and forecasting of water level in the middle reach of the Yangtze River. In Proceedings of the 2017 4th International Conference on Transportation Information and Safety (ICTIS), Banff, AB, Canada, 8–10 August 2017; IEEE: New York, NY, USA, 2017; pp. 172–177. [Google Scholar]
- Viccione, G.; Guarnaccia, C.; Mancini, S.; Quartieri, J. On the use of ARIMA models for short-term water tank levels forecasting. Water Supply 2020, 20, 787–799. [Google Scholar] [CrossRef]
- Azad, A.S.; Sokkalingam, R.; Daud, H.; Adhikary, S.K.; Khurshid, H.; Mazlan, S.N.A.; Rabbani, M.B.A. Water level prediction through hybrid SARIMA and ANN models based on time series analysis: Red hills reservoir case study. Sustainability 2022, 14, 1843. [Google Scholar] [CrossRef]
- Fang, T.; Lahdelma, R. Evaluation of a multiple linear regression model and SARIMA model in forecasting heat demand for district heating system. Appl. Energy 2016, 179, 544–552. [Google Scholar] [CrossRef]
- Altunkaynak, A. Forecasting surface water level fluctuations of Lake Van by artificial neural networks. Water Resour. Manag. 2007, 21, 399–408. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Improving streamflow forecast using optimal rain gauge network-based input to artificial neural network models. Hydrol. Res. 2018, 49, 1559–1577. [Google Scholar] [CrossRef]
- Nouri, H.; Ildoromi, A.; Sepehri, M.; Artimani, M. Comparing three main methods of artificial intelligence in flood estimation in Yalphan catchment. Geogr. Environ. Plan. 2019, 29, 35–50. [Google Scholar] [CrossRef]
- Khandelwal, I.; Adhikari, R.; Verma, G. Time series forecasting using hybrid ARIMA and ANN models based on DWT decomposition. Procedia Comput. Sci. 2015, 48, 173–179. [Google Scholar] [CrossRef]
- Phan, T.T.H.; Nguyen, X.H. Combining statistical machine learning models with ARIMA for water level forecasting: The case of the Red river. Adv. Water Resour. 2020, 142, 103656. [Google Scholar] [CrossRef]
- Sethia, A.; Raut, P. Application of LSTM, GRU and ICA for stock price prediction. In Information and Communication Technology for Intelligent Systems, Proceedings of ICTIS 2018, Padang, Indonesia, 25–26 July 2018; Springer Singapore: Singapore, 2019; Volume 2, pp. 479–487. [Google Scholar] [CrossRef]
- Anupa, A.; Sugathadasa, R.; Herath, O.; Thibbotuwawa, A. Artificial neural network based demand forecasting integrated with federal funds rate. Appl. Comput. Sci. 2021, 17, 34–44. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Gharabaghi, B. A reliable linear method for modeling lake level fluctuations. J. Hydrol. 2019, 570, 236–250. [Google Scholar] [CrossRef]
- Xiang, Z.; Demir, I. Distributed long-term hourly streamflow predictions using deep learning–A case study for State of Iowa. Environ. Model. Softw. 2020, 131, 104761. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, R.; Yang, X.; Wang, J.; Latif, A. Extraction of urban water bodies from high-resolution remote-sensing imagery using deep learning. Water 2018, 10, 585. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Akkoyunlu, A.; Akiner, M.E. Pollution evaluation in streams using water quality indices: A case study from Turkey’s Sapanca Lake Basin. Ecol. Indic. 2012, 18, 501–511. [Google Scholar] [CrossRef]
- Population Growth (Annual %)—Turkiye. Available online: https://data.worldbank.org/indicator/SP.POP.GROW?locations=TR (accessed on 8 March 2023).
- Jiang, F.; Dong, Z.; Wang, Z.A.; Zhu, Y.; Liu, M.; Luo, Y.; Zhang, T. Flood forecasting using an improved NARX network based on wavelet analysis coupled with uncertainty analysis by Monte Carlo simulations: A case study of Taihu Basin, China. J. Water Clim. Change 2021, 12, 2674–2696. [Google Scholar] [CrossRef]
- Nourani, V.; Tootoonchi, R.; Andaryani, S. Investigation of climate, land cover and lake level pattern changes and interactions using remotely sensed data and wavelet analysis. Ecol. Inform. 2021, 64, 101330. [Google Scholar] [CrossRef]
- Tsao, H.H.; Leu, Y.G.; Chou, L.F.; Tsao, C.Y. A method of multi-stage reservoir water level forecasting systems: A case study of Techi hydropower in Taiwan. Energies 2021, 14, 3461. [Google Scholar] [CrossRef]
- Obringer, R.; Nateghi, R. Predicting urban reservoir levels using statistical learning techniques. Sci. Rep. 2018, 8, 5164. [Google Scholar] [CrossRef]
- Guyennon, N.; Salerno, F.; Rossi, D.; Rainaldi, M.; Calizza, E.; Romano, E. Climate change and water abstraction impacts on the long-term variability of water levels in Lake Bracciano (Central Italy): A Random Forest approach. J. Hydrol. Reg. Stud. 2021, 37, 100880. [Google Scholar] [CrossRef]
- Dinka, M.O. Estimation of groundwater contribution to Lake Basaka in different hydrologic years using conceptual netgroundwater flux model. J. Hydrol. Reg. Stud. 2020, 30, 100696. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Supervised Sequaence Labelling; Springer: Berlin/Heidelberg, Germany, 2012; pp. 5–13. [Google Scholar]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries. IEEE Trans. Ind. Electron. 2017, 65, 6730–6739. [Google Scholar] [CrossRef]
- Ojo, S.O.; Owolawi, P.A.; Mphahlele, M.; Adisa, J.A. Stock market behaviour prediction using stacked LSTM networks. In Proceedings of the 2019 International Multidisciplinary Information Technology and Engineering Conference (IMITEC), Vanderbijlpark, South Africa, 21–22 November 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Kang, H.; Yang, S.; Huang, J.; Oh, J. Time series prediction of wastewater flow rate by bidirectional LSTM deep learning. Int. J. Control Autom. Syst. 2020, 18, 3023–3030. [Google Scholar] [CrossRef]
- Gulli, A.; Pal, S. Deep Learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Paul, S.; Oppelstrup, J.; Thunvik, R.; Magero, J.M.; Ddumba Walakira, D.; Cvetkovic, V. Bathymetry development and flow analyses using two-dimensional numerical modeling approach for Lake Victoria. Fluids 2019, 4, 182. [Google Scholar] [CrossRef]
- Nhu, V.H.; Shahabi, H.; Nohani, E.; Shirzadi, A.; Al-Ansari, N.; Bahrami, S.; Miraki, S.; Geertsema, M.; Nguyen, H. Daily water level prediction of Zrebar Lake (Iran): A comparison between M5P, random forest, random tree and reduced error pruning trees algorithms. ISPRS Int. J. Geo-Inf. 2020, 9, 479. [Google Scholar] [CrossRef]
- Zheng, F.; Maier, H.R.; Wu, W.; Dandy, G.C.; Gupta, H.V.; Zhang, T. On lack of robustness in hydrological model development due to absence of guidelines for selecting calibration and evaluation data: Demonstration for data-driven models. Water Resour. Res. 2018, 54, 1013–1030. [Google Scholar] [CrossRef]
- Van der Heijden, T.; Lago, J.; Palensky, P.; Abraham, E. Electricity price forecasting in European Day Ahead Markets: A greedy consideration of market integration. IEEE Access 2021, 9, 119954–119966. [Google Scholar] [CrossRef]
- Albay, R.A.; Köker, L.; Gürevin, C.; Albay, M. Planktothrix rubescens: A perennial presence and toxicity in Lake Sapanca. Turk. J. Bot. 2014, 38, 782–789. [Google Scholar]
- Sahar, A.; Han, D. An LSTM-based indoor positioning method using Wi-Fi signals. In Proceedings of the 2nd International Conference on Vision, Image and Signal Processing, Las Vegas, NV, USA, 27–29 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Fowler, J.; Cohen, L.; Jarvis, P. Practical Statistics for Field Biology; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Yoon, H.; Jun, S.C.; Hyun, Y.; Bae, G.O.; Lee, K.K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Hrnjica, B.; Bonacci, O. Lake level prediction using feed forward and recurrent neural networks. Water Resour. Manag. 2019, 33, 2471–2484. [Google Scholar] [CrossRef]
- Lee, T.; Shin, J.Y.; Kim, J.S.; Singh, V.P. Stochastic simulation on reproducing long-term memory of hydroclimatological variables using deep learning model. J. Hydrol. 2020, 582, 124540. [Google Scholar] [CrossRef]
- Zhu, S.; Ji, Q.; Ptak, M.; Sojka, M.; Keramatfar, A.; Chau, K.W.; Band, S.S. Daily water-level forecasting for multiple polish lakes using multiple data-driven models. Geogr. J. 2023, 189, 357–369. [Google Scholar] [CrossRef]
- Morovati, K.; Nakhaei, P.; Tian, F.; Tudaji, M.; Hou, S. A Machine learning framework to predict reverse flow and water level: A case study of Tonle Sap Lake. J. Hydrol. 2021, 603, 127168. [Google Scholar] [CrossRef]
- Boscaini, A.; Brescancin, F.; Cerasino, L.; Fedrigotti, C.; Anna, F.E.; Salmaso, N. Vertical and horizontal distribution of the microcystin producer Planktothrix rubescens (Cyanobacteria) in a small perialpine reservoir. Adv. Oceanogr. Limnol. 2017, 8, 208–221. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).