Abstract
Site quality evaluation is an important foundation for decision-making and planning in forest management and provides scientific decision support and guidance for the sustainable development of forests and commercial plantations. Site index and site form models were constructed and subsequently compared utilizing fir (Cunninghamia lanceolata) plantations in Nanping City, Fujian Province, China. This papers aim was to construct a site quality classification model, conduct further analysis on the effects of different site factors on the quality of the site, and achieve an assessment of site quality for Chinese fir plantations. An algebraic difference approach was used to establish a site index model and a site form model for Chinese fir in Fujian Province. The suitability of the two models was compared using model accuracy analysis and partial correlation, and the optimal model was chosen for classifying the site quality of the stands. On this basis, a site quality classification model was established using the random forest algorithm, and the importance of each site factor was determined through importance ranking in terms of their impact on site quality. Within the study area, the R2 of the site index model results was 0.581, and the R2 values of the five site form models based on different reference breast diameters, ranked from high to low, were 0.894, 0.886, 0.884, 0.880, and 0.865. The bias correlation coefficient between site form and stand volume was 0.71, and the bias correlation coefficient between site index and stand volume was 0.52. The results confirmed that the site form model is better suited for evaluating the site quality of Chinese fir plantations. The random forest-based site form classification model had a high classification accuracy with a generalization accuracy of 0.87. The factors that had the greatest impact on site form were altitude, canopy closure, and slope gradient, whereas landform had the smallest impact on site form. These results can provide a reference for the evaluation of the site quality of plantations and natural forests in southern China to ensure the long-term sustainable use of forest resources.
1. Introduction
Site quality refers to the production potential of a given forest or other vegetation type at a specific site [1,2,3]. Site quality evaluation can assess the potential for forest growth and development, including factors such as soil quality, climatic conditions, water availability, etc., and the sustainable use and development of forests can be achieved through scientific assessment and the integrated use of the results of site quality evaluation [4,5]. Forest site quality not only has an important impact on forest site growth and harvest and forest management decisions but is also an important means to understand the forest growth environment and the impact of the environment on forest productivity, providing a reliable basis for achieving scientific afforestation and forest management [6]. The methods of site quality evaluation are divided into direct and indirect evaluation methods [7]. Among them, the site index as a direct assessment method is the most commonly used method for site quality evaluation, and it is expressed using the average height of the dominant trees of the stand at a given reference age [8]. The site index assesses the relative site of different trees in a forest by measuring the dominant tree height of different trees at a reference age. Forest stands with higher site index in the same study area reflect their high-quality soil composition and ecological condition [9]. However, determining uneven-aged forests within planted forests is also challenging because each plot usually contains trees of different ages, and it is time-consuming to survey each tree individually. Therefore, indirect methods are often used instead of using a reference age. Given the relative simplicity, convenience, and accuracy of the DBH determination method, some scholars have proposed the site form method and the dominant height of the site at breast height should be used to express the quality of the site; in this case, the site form method is proposed as an alternative to the site index method [10].
The site form method has been controversial since it was first proposed. Many scholars have evaluated the site quality of certain areas based on site form and concluded that the method has valid results for measuring the site quality of different forest species, whereas others have come to the opposite conclusion [10,11,12,13,14,15,16]. Vanclay et al. [10] were the first to apply site form to the evaluation of heterogeneous coniferous forests in Queensland, Australia; they established a tree height-and-diameter equation based on an exponential relationship. The results of the study demonstrated that site form and site index showed a linear correlation, and site form could be used instead of site index for the site quality evaluation of mixed forests. Herrera-Fernández et al. [11] applied site form to evaluate broadleaf forest site quality in neotropical secondary rainforests and showed that site form is a potentially useful indicator of broadleaf forest site quality in neotropical secondary rainforests. Padilla-Martínez et al. [12] applied site form to evaluate sites in a temperate heterogeneous multispecies forest in Durango, Mexico and found that site form can better evaluate site quality. Ahmadi et al. [13] used the free statistical programming language “R” to fit a sequential logistic regression model of standing terrain on soil and topographic variables, and the results indicated that standing terrain appears to be a potentially useful indicator of site quality. Castano-Santamaría et al. [14] applied site form to a natural beech forest in northwestern Spain and estimated site quality by fitting a dynamic equation, showing a significant relationship between site form and site index and that site form was a good assessment of site quality. However, the results of some research have shown that the evaluation of site quality by site form lacks some basis. For example, Buda et al. [15] showed, in a study of sugar maple trees in central Ontario, that site quality was independent of site form and any site variables associated with sugar maple height growth; they also found that using site form to indicate site quality was inadequate. Wang et al. [16] tested the validity of using tree height at a specific diameter at breast height as an indicator of site quality by using stand ecology and trunk analysis data for subboreal spruce dominated by white spruce in British Columbia; they found that the height of dominant trees at a specific diameter was not an adequate measure of site quality. Therefore, one of the major reasons for the controversy of the site form model is the inconsistency in the determination of the base diameter at breast height in the current domestic and international literature. Due to the inconsistent results from previous studies and the fact that whether site form has a better effect of site evaluation in fir plantations has not been reported, in this study, we conducted comparative experiments between the site index and the site form models, and chose the optimal model with higher reliability as the classification criterion, and further verified the feasibility of the site form method in the present study area.
In site quality evaluation, the site factor is an expression of site quality in forestland, and some literature show that the site factor and the understory vegetation factor have a key decision role in site quality. Yu et al. [17] used a quantitative theoretical model to establish a regression model of the relationship between the maximum growth rate at breast height and the site factors; the site factors had a greater influence on the growth rate at breast height in fir plantations, and thus, the quality of the site in the study area can be effectively evaluated. Abrudan et al. [18] studied the influence of the site factors on the composition and structure of seminatural mixed forests of beech, silver fir, and Norway spruce in northwestern Romania, showing that slope gradient and altitude have a strong influence on site size and are key factors in the evaluation of site quality. Wang et al. [19] also showed that altitude, slope gradient, soil thickness, and soil type among the site factors were the main factors affecting the high growth of larch trees in northern China. Scholars have also used the site factors and constructed regression models with site indices to predict the site quality of forestland. Chen et al. [20] made accurate predictions of quaking aspen productivity by establishing a multiple linear regression model with the site index method and climate variables, altitude, slope direction, slope position, soil properties, or foliar nutrients as predictors. Tian et al. [21] used a random forest algorithm to construct a model based on site factors and age to estimate the volume growth of larch and oak plantations and its influencing factors. Niall et al. [22] were able to predict the site quality of Irish spruce by establishing a site index prediction model with climate, site conditions, and soil properties as the predictor variables, but no studies using site factors to predict site form have been reported. In addition, the construction of such models mostly relies on multivariate statistics-based models; however, the relationship between forest growth and site factors is usually complex and nonlinear, and traditional linear or simple nonlinear modeling methods generally simplify the assumptions, making it difficult to achieve the desired results; moreover, the model design and prediction accuracy still have many shortcomings. Compared with traditional statistical models, random forest algorithms can handle high-dimensional data well with complex nonlinear interactions and deeply mine valuable information in the data; hence, these algorithms can reveal new relationships and laws in the data and are widely used in forestry theory and production research. Ma et al. [23] proposed a new vegetation index method using the random forest algorithm to estimate the forest stock on Helan Mountain, Ningxia. Wang et al. [24] used a random forest algorithm to explore the relationship between forest productivity and stand and climate factors. Jiang et al. [25] modeled the intra-annual wood formation dynamics of a fir forest with central subtropical climate characteristics by using a random forest algorithm. Yang et al. [26] used a mixed-effects random forest algorithm to describe the height–diameter relationship of Caribbean trees. If we can take advantage of the random forest algorithm to explore the relationship between site factors and site form, it can provide a more credible basis for site factors to be used for site quality evaluation, which is critical to establishing sustainable management of fir plantations.
As a primary lumber species in China, fir can be used as a good plant for a windbreak forest and for environmental management, which can reduce land erosion and improve soil quality. In this study, we used a fir plantation in the Fujian Province, China as an example and constructed a site index model and a site form model based on the base age and base diameter at breast height, respectively, to analyze the possibility of site form for fir plantation site quality evaluation from different perspectives. On this basis, a random forest-based fir site quality classification model was established to explore the influence of each key site factor on the site quality of fir plantations and to reveal the nonlinear relationship between each site factor and the site quality of stands.
2. Materials and Methods
2.1. Study Area
Nanping City is located in the northern part of Fujian Province (Figure 1), with relatively high terrain (117°00′–119°25′ E, 26°30′–28°20′ N), with an average annual temperature of about 17–21 °C. The summer is hot, with the highest temperature reaching over 30 °C, and the winter is cooler, with an annual average precipitation of 1000–2000 mm, which is typical of a monsoon climate.
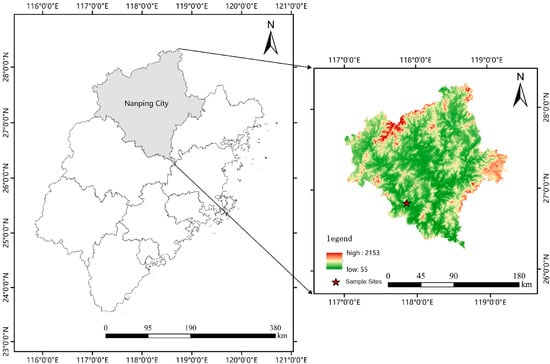
Figure 1.
The study area map of Nanping City, Fujian Province.
2.2. Data
The study data were obtained from the first-class inventory data of fir plantation forests in Nanping City, Fujian Province, which contained 64 fixed remeasurement sample plots of the 4th, 5th, 6th, and 7th consecutive national forest inventory of pure fir plantation forests. The sample plots were retested every 5 years, and 264 observations were obtained after excluding the abnormal data of tree height, age, and diameter at breast height. All sample plots were not nursed with mesquite. The data mainly included site data and stand growth data, where stand data included altitude, slope gradient, slope direction, slope position, soil thickness, and landform. Slope position was divided into ridge, upper, middle, lower, valley, and flat land, and slope direction was divided into north, northeast, east, southeast, south, southwest, west, northwest, and no slope direction. The landforms were divided into middle mountains, low mountains, and hills. The stand growth data mainly included age, average site diameter at breast height, average site height, and site volume, and the summary of growth data and site factors are shown in Table 1 and Table 2.

Table 1.
The growth factor statistics of Chinese fir plantations in Nanping City.

Table 2.
The site factor statistics of Chinese fir plantations in Nanping City.
2.3. Data Preprocessing
Given that the site index and site form models in this study required stand dominance height data and there were no mean stand dominance height data in the first category of inventory data, the mean wood-dominance height model of y = 0.9706x + 1.0735 was used, (x represents the mean tree height, y represents the dominant tree height) and R2 = 0.97 was constructed using standard plot survey data from the same study area to predict the dominant tree height in the first category of inventory sample plots. The basic information of the standard plot survey data is shown in Table 3.

Table 3.
The basic information on standard plot survey data.
2.4. Establishment of the Site Index Model and Site Form Model
2.4.1. Guidance Curve Selection
In the cluster of stand dominant height curves, there is an average height growth curve representing the change in stand dominant height with stand age under moderate stand conditions, which is called a guide curve [27,28,29]. Theoretical growth equations are often used in the selection of guidance curves. The theoretical growth equation is a model derived from the study of biological growth models by making some assumptions based on biological principles, establishing differential equations about the size of the organism, predicting its growth trend, and solving and substituting its initial conditions; in forestry, it can provide a scientific and reasonable explanation of the growth trend of trees [30,31]. In this study, five theoretical growth equations commonly used in forest growth simulations at home and abroad were selected as the basic equations [32], and the expressions of each equation are shown in Table 4.

Table 4.
The theoretical growth equation.
2.4.2. Determination of Base Age and Base Diameter at Breast Height
Given that fir plantations in Fujian Province generally reach maturity after 20 years, the base age of fir in this study was set at 20 years. The methods for determining the base diameter at breast height have inconsistencies, i.e., finding the diameter at breast height that tends to be stable and sensitive to the differences in stand. From domestic and international studies, several main methods can determine the base diameter at breast height as follows:
- (1)
- Half of the natural mature diameter at breast height [1];
- (2)
- The most frequent diameter breast height (DBH) value in the sample site survey data is the base DBH [10];
- (3)
- Establish a diameter-at-breast-age model and take the diameter at the base age as the base diameter at breast [33];
- (4)
- Establish the height–breast diameter model of logistic equation and find the inflection point, the point where the second-order derivative is 0, that is, the point where the tree height growth trend changes, and the corresponding horizontal coordinate is the reference diameter at breast height [34];
- (5)
- Take the average of the above four methods [35].
2.4.3. Construction of the Site Index Model and Site Form Model
The site index is the dominant tree height at the base age [36], and the site form is the height of the dominant tree at the base diameter at breast height [12]. In this study, we choose the optimal guidance curve as the base equation for the site index model and the site form model and used the algebraic difference approach (ADA) to derive the site index model and the site form model using the Schumacher equation as an example. ADA is one of the common methods used to establish forest stand site indices. Its principle is to select a theoretical growth equation as the basic equation and select one parameter in the equation as the element elimination parameter, thus elimination of the equation to obtain a difference equation including two groups of dependent and independent variables [37,38]. The expressions of each model are shown in Equations (1) and (2).
where T denotes the mean age of the dominant tree, T0 denotes the base age, HT denotes the dominant height at age T, D denotes the mean diameter at breast height, D0 denotes the base diameter, HD denotes the dominant height at breast diameter D, and b is a parameter.
In this study, the site index model is denoted by E0, and the site form models corresponding to the five different base DBH methods were E1, E2, E3, E4, and E5. The site index model (E0) and the site form model (E1, E2, E3, E4, E5) were fitted using Origin 2021 software. This study compares and analyzes the fitting results of five types of base DBH site form models and selects the best model as the result of this site form model.
2.5. Principle and Process of the Random Forest Stand Classification Model
2.5.1. Principle of the Random Forest Classification Model
Random forest is a classical, integrated, learning algorithm that integrates multiple decision trees and makes decisions by voting or averaging. It can effectively reduce the risk of overfitting and improve the robustness and generalization ability of the model and can effectively deal with nonlinearity, interactivity, and covariance [39,40]. In addition, random forests can be used for regression, classification, and prediction and to measure the importance of variables.
The training process of random forest can be summarized as follows: a certain number of samples are randomly selected from the original data with release as the new training set, a process called bootstrap sampling. For each sample, a random selection of features is used to train the decision tree model and the test sample is predicted by voting or averaging multiple decision trees. In practical applications, random forest models can be used for classification and regression problems and can handle many types of data, including numeric, category type, or text type. The construction process of the random forest model is shown in Figure 2.
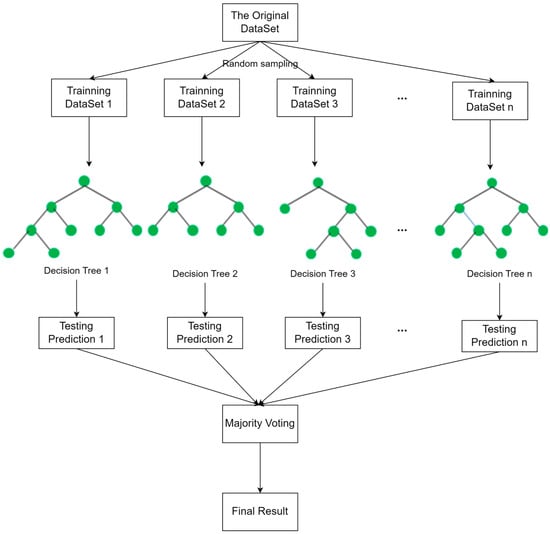
Figure 2.
The principles of random forest modeling.
The random forest model has two important custom parameters: “n_estimators” and “max_depth”, where “n_esitmators” is the number of trees in the forest, i.e., the number of base evaluators; the larger the “n_esitmators” is, the better the model tends to be. However, accordingly, any model has decision boundaries, and after a certain level of “n_esitmators”, the accuracy of the random forest tends not to rise or starts to fluctuate, and the larger the “n_estimators”, the more computation and memory are needed, and the longer the training time will be; the default value of “n_estimators” is 100. In this study, the optimal value of “n_estimators” is 50, “max_depth” is the maximum depth of the decision tree, and the default is not limited. If the model has more samples and more features, then the common value can be between 10 and 100. In this study, the optimal value of “max_depth” is 20.
2.5.2. Importance Evaluation of Random Forest Variables
When using random forest for classification, the mean decrease impurity (MDI) method can be used to evaluate the importance of each feature. The core idea of the MDI approach is to measure the number of times a feature is used to partition data in a random forest and the size of its contribution to model impurity at each partition. The MDI method is based on feature importance evaluation in each tree in the random forest, and the MDI method is a common feature selection method that can evaluate the importance of features by calculating the impurity reduction of each feature in all the split points in the tree. Specifically, for each feature, we can calculate the average impurity reduction of the split points it involves in all trees and then divide it by the number of split points involved in the feature to obtain the MDI value of the feature. A higher MDI value means that the feature has a greater impact on the classification result, and vice versa. The percentage importance of each feature in the random forest classification can be obtained by dividing the MDI value of each feature by the sum of the MDI values of all features, i.e., the proportion of each feature. The formula is as follows:
where denotes the MDI value of each feature, pi denotes the importance percentage, f denotes the feature whose importance is to be evaluated, denotes the number of trees in the random forest, T denotes the number of decision trees, Nt denotes the set of nodes in tree t, Sti is the split feature selected by node , denotes the impurity of node , and is the impurity of tree t. denotes whether the feature selected by node i is f. If yes, the item is 1; otherwise, it is 0. is the importance of each individual feature, nfeatures denotes the number of features.
2.5.3. Random Forest Classification Model Process
The steps to build a fir site form classification and prediction model are as follows [41]:
- (1)
- Determine the measure of fir site rank;
- (2)
- Preprocess the sample data and divide them into training and test samples in the ratio of 8:2;
- (3)
- Use the training samples to build a random forest model;
- (4)
- Input the test samples into the trained model and derive the classification results;
- (5)
- Evaluate and rank the importance of site factors affecting fir growth and analyze the influence of single factors on fir growth.
The importance of the factors affecting the growth of fir was assessed and ranked, and the influence of single factors on the growth of fir was analyzed. Figure 3 shows the flowchart of model construction.
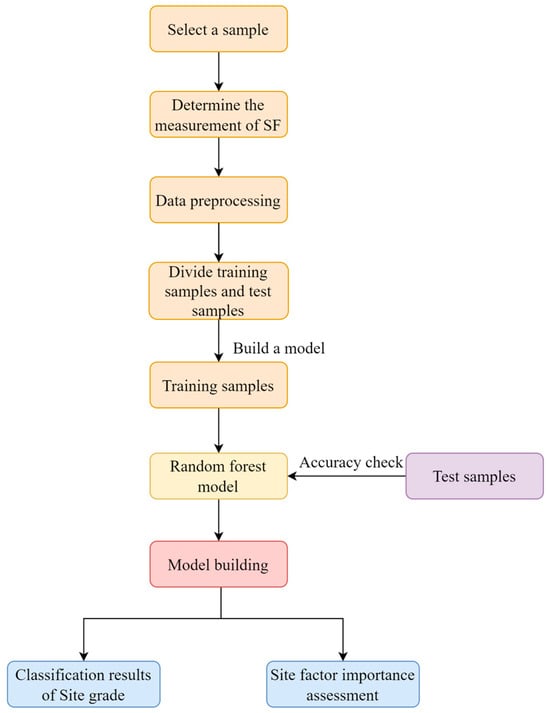
Figure 3.
The flowchart of model construction.
2.6. Model Evaluation Metrics
2.6.1. Site Quality Model Evaluation Indicators
The test of the model is based on two main points: the biological meaning of the model and parameters and the actual fit of the model as characterized by statistical indicators. In this study, the three statistical indicators of the coefficient of determination (R2), root mean square error (RMSE), and mean absolute error (MAE), which are commonly used in regression analysis, were used to evaluate the quality of the model fit. R2 and RMSE were calculated using fitted samples. The closer R2 is to 1, the smaller the RMSE is, which means that the model is better. MAE is calculated using independent test sample data; the smaller the value is, the better the model prediction. The formula for calculating each indicator is as follows:
where R2 is the coefficient of determination, RMSE is the root mean square error, MAE is the mean absolute error, n is the number of samples, and , Yi, Ŷi are the mean value of the dominant height, the measured value of the dominant height sample, and the model predicted value of all sample sites, respectively.
2.6.2. Random Forest Classification Model Evaluation Metrics
Model evaluation metrics for multiple classifications in this study refers to the method of defining dichotomous classifications, which can be obtained similar to the dichotomous confusion matrix. FjPi for incorrectly predicting the true classification j as classification i, TiPi for correctly predicting the true classification i as classification i. For example, when we observe a category i, we consider the remaining n − i categories as counter examples in binary classification so that we can calculate TPi, FNi, FPi, TNi for category i. Using the above method, we can obtain n binary confusion matrices and calculate the accuracy, error rate, accuracy, and completeness of the n binary confusion matrices.
The following confusion matrix visualizes the predictions for each category, with each column representing the predicted value, each row representing the actual category, and the last column representing the sample size for each category, with the structure shown in Table 5.

Table 5.
Confused matrix of predictive results.
According to the confusion matrix, the following metrics can be obtained to evaluate the classification model: classification accuracy, which is the probability that the true classified samples are correctly classified; precision, which is the degree of truthfulness of the situation where the classification results in true classified samples; and recall, which is the probability that the true classified samples are identified. The accuracy metric (Accuracy) is usually used to measure the performance of the model. The experimental data are divided into training samples and test samples at a ratio of 8:2. The training samples are used to build the model and the test samples are used to check the accuracy of the model.
3. Results
3.1. Fitting Results of the Guidance Curve
Guidance curves were fitted using Origin 2021 software. The results of the fitting of the guide curve are shown in Figure 4. Table 6 and Table 7 show the fitting results of the tree height–age equation and tree height–breast diameter equation, respectively. From the fitting indices, the best fitting results of both were the Schumacher’s equation for tree height, which were higher than the other four equations. Moreover, the values of RMSE and MAE of the model were smaller than the other four equations. Therefore, the study used the Schumacher equation for the construction of the site index and the site form models.
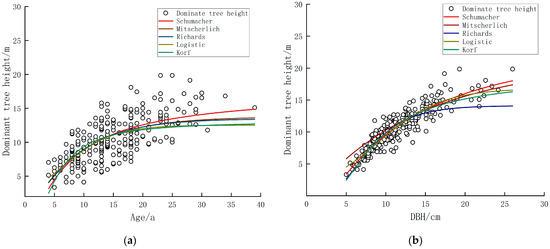
Figure 4.
Fitting results of the guide curves: (a) stand height−age orientation curves; (b) stand height–DBH orientation curves.

Table 6.
Statistics of parameters and fit test indicators of the theoretical equation of tree height−age.

Table 7.
Statistics of parameters and fit test indicators of the theoretical equation of tree height−diameter at breast height.
3.2. Results of the SI Model and the SF Models
The results of different base diameters of the breast height determination methods for fir trees are shown in Table 8. To reduce the impact of errors on the experimental results, the Schumacher equation was used as the base equation. The model fitting results parameters b, R2, RMSE, and MAE are shown in Table 9. Comparing the elevated site form models reveals that the E5 model was the best fit among the five models. Therefore, the E5 model was selected as the result of the site form model for the follow-up study. Substituting the parameters b of the site index model into Equation (1), which has a base age of 20, yields an expression for the E0 model as Equation (11), and substituting the parameters b of the optimal site form and the base DBH into Equation (2) yields an expression for the E5 model as Equation (12).

Table 8.
Five methods of calculating reference DBH for fir plantation.

Table 9.
SI and SF model fitting parameters.
The distribution of site index and site form reflects the differences in resources and terrain conditions across the same stand. By looking at the distribution of site index and site form, it is more intuitive to see which model is better able to reflect the stand quality of a forest site. In order to interpret the distribution of the site index model and the site form model more intuitively, Figure 5 was constructed, from which it can be seen that there is a strong linear trend in some of the values of the site index compared to the five site form models. Since each sample site has unique soil characteristics, vegetation composition, climatic conditions, etc., if there is an obvious trend in the values of the site index and site form, these individual differences may be disregarded, resulting in a failure to accurately assess and utilize the characteristics and potentials between the sample sites. Although there is no obvious difference in R2 between the five site form models, there is a partial difference in the distribution of the values due to the difference in base diameters at breast height (DBH).
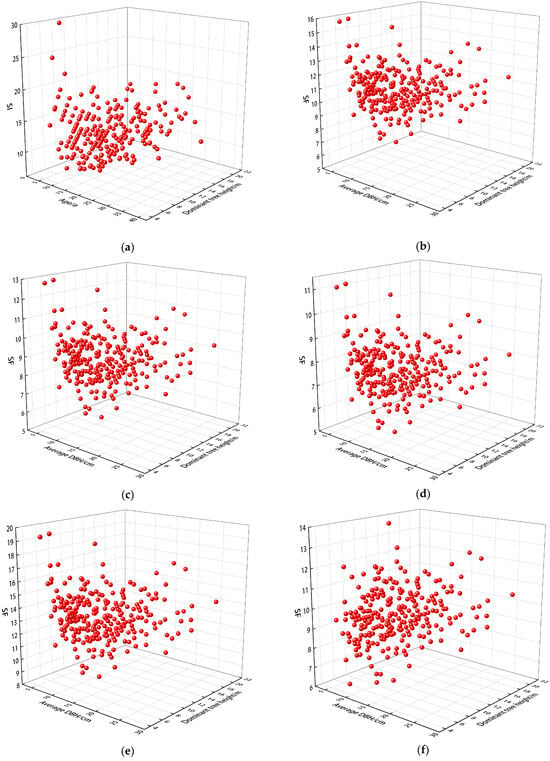
Figure 5.
SI and SF model results: (a) SI model; (b–f) correspond to SF models modeled as E1, E2, E3, E4, and E5, respectively.
3.3. Comparative Analysis of SF and SI Models
The residuals of the site index model (E0) and the site form model (E1, E2, E3, E4, E5) with predicted values of dominant tree height are shown in Figure 6. The values of parameter b were substituted into Equations (1) and (2), respectively, to obtain the site index and site form for each sample site. The R2, RMSE, and MAE of the results of the site index and site form models were then compared, and residual analysis was performed on both. The results showed that all five site form models outperform the site index model. The partial correlation coefficients of site form, site index, and stand volume were analyzed using SPSS 25.0 software, controlling for constant age and density, and the results are shown in Table 10. The results showed that site form, site index, and stand volume were all significantly and positively correlated, and the bias correlation between site form and stand volume was greater than that between site index and stand volume.
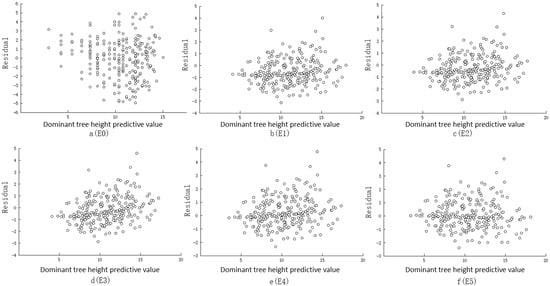
Figure 6.
SI and SF model residuals: (a) residual plots of the site index model; (b–f) residual plots of the site form model.

Table 10.
The results of skewed correlation analysis of SF and stand volume and SI and stand volume.
3.4. Random Forest-Based Site Form Model
- (1)
- Site grade division
The SF of fir can be calculated in accordance with Equation (4), and the frequency statistics of SF are shown in Table 11. The nine types of site form within the fir subdivision of Nanping City, have indices ranging from 6 to 14. There was an uneven distribution of the number of fir trees within the different site forms; the number of site forms in 8, 9, 10, and 11 was higher, accounting for 0.91 of the totals, and the number of other site forms was lower. In view of the fact that the accuracy of the final classification model will be affected by the numerous standings, the sites in this study were classified into three categories based on the frequency distribution of the site in the data: 11–14 as Class I with a frequency of 52, which is an excellent site quality class; 9–10 as Class II with a frequency of 170, which is a medium-standing quality class; and 6–8 as Class III with a frequency of 42, which is considered a poor-quality site class.

Table 11.
SF frequency distribution of Chinese fir in Fujian Province.
- (2)
- Data oversampling processing
When using machine learning methods for real-world problems, imbalances in the dataset can affect model performance. Among the 264 training samples in this experiment, there are 42 samples of SF class I, 170 samples of SF class II, and 52 samples of SF class III. The number of samples of the middle class is more than the number of samples of the other two classes. To avoid bias in the classification results due to the imbalance of data, the experiment should balance the samples. Oversampling (adding samples from a few classes) and undersampling (deleting samples from most classes) are two approaches often used for data balancing. Given the small sample size in this study, oversampling was used. The sample size of the three classes balanced by the SMOTE algorithm remains the same. The balanced data are shown in Table 12.

Table 12.
The number of samples before and after data balance.
- (3)
- Results of the SF classification model
The eight site factors of altitude, slope gradient, slope direction, slope position, canopy closure, soil thickness, soil type, and landform were used as input variables, and the SF grades were used as the output variable. The classification of the predicted data is reported as shown in Table 13. The classification accuracy of the model is 0.87, indicating that the prediction results are more satisfactory.

Table 13.
Performance of classification models for classification levels I, II, and III in the study area.
3.5. Variable Importance Assessment
With regard to the weight of the influence of the site factor characteristic variables on the site form, this study uses the relative importance of the variables for description. Figure 7 shows that among the eight site factors, altitude and canopy closure had the greatest effect on fir growth, respectively, followed by soil thickness, slope gradient, slope direction, slope position and soil taxon. The factor with the least effect on the growth of fir was landform.
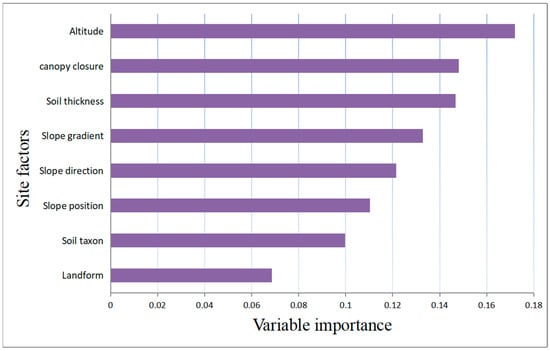
Figure 7.
The relative importance of variables affecting site form.
4. Discussion
4.1. Comparison with Other Studies
The results of the importance ranking showed that among the many site factors, altitude and canopy closure had the greatest effect on fir growth, followed by soil thickness and slope gradient, while the influence of landforms on the site quality was smaller. Scholars have also used site factors and constructed regression models with the site index method to achieve the use of site factors to predict the site quality of forestland. Wang et al. [19] evaluated site quality by establishing a site index model for plantation forests under different stand conditions, and the results showed that the main limiting factors for the high growth of larch trees in northern China were altitude, slope gradient, soil thickness, and soil type. Zhang et al. [42] established a nonlinear mixed-effects high-diameter model with the interaction of site density and site index, and the results showed that the interaction of site density and site index could significantly improve the prediction accuracy of the high-diameter model of long white larch. Some literature also showed that site factors have a strong correlation with site quality. Qiao et al. [43] showed that the climate–radial growth relationship of Changbai larch was strongly influenced by altitude and slope gradient. Related studies showed that the steeper the slope gradient, the worse the quality of the site due to the influence of slope gradient on the microclimate of the site and that places with fairly steep slope gradients are often located on the windward side with a thin soil layer, which is not conducive to fir growth [44]. As the altitude increases, the intensity of solar radiation becomes stronger, but the moisture content in the air decreases due to the drop in temperature, which makes the moisture in the soil also decrease; therefore, altitude is an important factor affecting the quality of the site [45]. The change in slope gradient has a certain effect on solar radiation, soil fertility, and temperature; thus, slope gradient has a greater impact on the growth of fir.
Ma et al. [46] showed that topography and wood density were the main drivers of productivity allocation. Canopy closure of the recipient forest was considered the most important factor to be negatively associated with bamboo expansion; moso bamboo expansion showed significant variation when facing different stands, and site characteristics (canopy closure, canopy height, etc.) were the main variables affecting moso bamboo expansion. Several studies also demonstrated that the canopy closure of the site indirectly affects the vegetation site conditions [47]. Canopy closure is the embodiment of stand density. The change in canopy closure can indirectly affect changes in solar radiation, stand air humidity, the growth environment of undergrowth vegetation, soil physical and chemical conditions, and the types and activity intensity of microorganisms in the soil. There are many studies that have indicated that soil thickness and humus layer thickness have relatively important effects on site quality [48,49,50].
Some fir species are more adaptable to landforms and can grow under various landform conditions; moreover, fir landforms in Nanping City have fewer types, which are divided into only three categories: middle mountains, low mountains, and hills, and belong to areas with gentle terrain, in which case the growth of fir is less affected by the landforms. Therefore, the influence of landforms on the site quality is smaller in this study.
This finding indicates that the effect of site factors on the site form is basically the same as the effect on the site, and the site form can better reflect the stand condition; in addition, it can better reflect the relationship between site performance and tree species growth. Overall, the site form of this study can replace the site index as an indicator for fir site quality evaluation, which is consistent with the findings of Vanclay et al. [10], Padilla-Martínez et al. [12], and Castano-Santamaría et al. [14].
4.2. Strengths and Limitations of This Study
Site form represents the relationship between dominant stand height and diameter at breast height (DBH), which requires the identification of a base DBH at which tree height growth tends to stabilize and which is sensitive to differences in site quality. However, the methods for determining the base DBH are not consistent. The commonly used methods for determining the diameter at breast height are taking half of all the natural mature diameters at breast height, i.e., using the diameter at breast height value that occurs more frequently in the sample site survey data as the base diameter at breast height, establishing a DBH–age model, and establishing a tree height–DBH model. To reduce uncertainty, in this study, the four methods proposed in the literature and the average value of the four methods were used as the base diameter at breast height to obtain five site form models, and the optimal site form model was selected by comparing R2, RMSE, and MAE. Given that the age of heterogeneous forests is difficult to determine, whereas the determination of diameter at breast height is simpler, more convenient, more accurate, and easier to obtain, the site form can be applied in the evaluation of the site quality of heterogeneous natural forests, thus avoiding the limitation brought by age, meaning the site quality is more accurately evaluated.
This study addresses the difficulty of obtaining stand age by modeling site quality as represented by site form. Most of the previous site quality models focused on constructing a site index model, which requires stand age as an important variable; however, stand age is difficult to obtain in actual production practice applications. In this study, we used diameter at breast height (DBH) instead of age to evaluate site quality, which is innovative in practical application.
Given the numerous site factors, measuring all the site factors in the study is impossible, and determining which factors are candidates for preliminary judgment is difficult. The selection of site factors is a multi-attribute fuzzy decision problem, and the selection of site factors in the current study is often subjective based on experience. The site factors used to build the site quality evaluation model are often relatively single and fail to reflect the results of the interaction between the four aspects of the site in terms of geomorphology, climate, soil, and understory vegetation. The relationship between the factors is complex, and the key factors are often difficult to find; therefore, a breakthrough in the theory and method of the study is needed. In addition, the unevenness of experimental data is the main reason why the above factors failed to delineate the standing quality of fir trees clearly, and plantation forests may be located in specific locations; therefore, the site factors affecting the growth of fir trees are not consistent with the findings of other pieces of literature [51,52,53]. The results of this study are only applicable to the study area; thus, we also need to verify the applicability of the results to other areas. The site form may also be related to forest type, competition, and other factors such as geographic location and climate, and these inferences must be verified by relevant experiments and are a future research direction for achieving sustainable forest development.
5. Conclusions
This study focused on examining the fir plantations in Nanping City, Fujian Province, China. The Algebraic Difference Approach (ADA) was employed to establish the fir site index and the site form model. Subsequently, the optimal model (site form) was selected for sample plot classification using comparative analysis. The random forest algorithm was utilized to construct a site quality classification model based on site factors. The importance ranking was then employed to determine the weight of each individual factor on site quality. In addition, we selected the data of fir plantations in Qingyuan County, Zhejiang Province for model validation, and the model validation results were good. Our specific conclusions are as follows:
- (1)
- The simulation results of using the site form method for site grade classification are more favorable in the study area. Therefore, the use of the site form method for site quality assessment is more advantageous than the site index method;
- (2)
- The correlation between site form and stand volume was greater than the correlation between site index and stand volume;
- (3)
- A site quality classification model with site factors was developed using the random forest algorithm, which has a high classification accuracy and can classify the site quality of forestland with a given site factor;
- (4)
- Using the variable importance assessment function of the random forest model, we analyzed the degree of influence of eight site factors on the site form, and the results of the study showed that the influence of the site factors on the site form was basically the same as that of the woodland, which further indicates that it is feasible to use the site form method to evaluate site quality.
Modeling applications see Supplementary Materials.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su152115587/s1, Modeling applications.
Author Contributions
Conceptualization, W.G.; Methodology, W.G., Y.G. and C.D.; Validation, W.G.; Formal analysis, W.G. and S.M.; Resources, C.D.; Data curation, C.D.; Writing—original draft preparation, W.G.; Writing—review and editing, W.G. and S.L.; Visualization, W.G., J.S. and S.M.; Supervision, C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Zhejiang Province (grant. number LQ21C160004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meng, X.Y. Forest Measurements, 3rd ed.; China Forestry Publishing House: Beijing, China, 2006. [Google Scholar]
- Shugart, H.H.; Foster, A.; Wang, B.; Druckenbrod, D.; Ma, J.Y.; Lerdau, M.; Saatchi, S.; Yang, X.; Yan, X.D. Gap models across micro- to mega-scales of time and space: Examples of Tansley’s ecosystem concept. For. Ecosyst. 2020, 7, 18. [Google Scholar] [CrossRef]
- Rozendaal, D.M.A.; Bongers, F.; Aide, T.M.; Alvarez-Dávila, E.; Ascarrunz, N.; Balvanera, P.; Becknell, J.M.; Bentos, T.V.; Brancalion, P.H.S.; Cabral, G.A.L.; et al. Biodiversity Recovery of Neotropical Secondary Forests. Sci. Adv. 2019, 5, eaau3114. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wu, B.; Chen, D.; Qi, Y. Using Machine Learning to Assess Site Suitability for Afforestation with Particular Species. Forests 2019, 10, 739. [Google Scholar] [CrossRef]
- Finley, K.; Zhang, J. Climate Effect on Ponderosa Pine Radial Growth Varies with Tree Density and Shrub Removal. Forests 2019, 10, 477. [Google Scholar] [CrossRef]
- Yousefpour, R.; Temperli, C.; Jacobsen, J.B.; Thorsen, B.J.; Meilby, H.; Lexer, M.J.; Lindner, M.; Bugmann, H.; Borges, J.G.; Palma, J.H.N.; et al. A Framework for Modeling Adaptive Forest Management and Decision Making under Climate Change. Ecol. Soc. 2017, 22, 40. [Google Scholar] [CrossRef]
- Clutter, J.L.; Fortson, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management: A Quantitative Approach; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1983. [Google Scholar]
- Batho, A.; García, O. De Perthuis and the origins of site index: A historical note. FBMIS 2006, 1, 1–10. [Google Scholar]
- Cheng, R.; Zhang, J.; Wang, X.; Ge, Z.; Zhang, Z. Predicting the Growth Suitability of Larix Principis-Rupprechtii Mayr Based on Site Index under Different Climatic Scenarios. Front. Plant Sci. 2023, 14, 1097688. [Google Scholar] [CrossRef]
- Vanclay, J.K.; Henry, N.B. Assessing site productivity of indigenous cypress pine forest in southern Queensland. Commonw. For. Rev. 1988, 67, 53–64. [Google Scholar]
- Herrera-Fernández, B.; Campos, J.J.; Kleinn, C. Site productivity estimation using height-diameter relationships in Costa Rican secondary forests. For. Syst. 2004, 13, 295–303. [Google Scholar]
- Padilla-Martínez, J.R.; Paul, C.; Corral-Rivas, J.J.; Husmann, K.; Diéguez-Aranda, U.; von Gadow, K. Evaluation of the Site Form as a Site Productive Indicator in Temperate Uneven-Aged Multispecies Forests in Durango, Mexico. Plants 2022, 11, 2764. [Google Scholar] [CrossRef]
- Ahmadi, K.; Alavi, S.J.; Kouchaksaraei, M.T. Constructing site quality curves and productivity assessment for uneven-aged and mixed stands of oriental beech (Fagus oriental Lipsky) in Hyrcanian forest, Iran. For. Sci. Technol. 2017, 13, 41–46. [Google Scholar]
- Javier, C.-S.; Lopez-Sanchez Carlos, A.; Jose, R.O.; Marcos, B.-A. Development of a site form equation for predicting and mapping site quality. A case study of unmanaged beech forests in the Cantabrian range (NW Spain). For. Ecol. Manag. 2023, 529, 120711. [Google Scholar]
- Buda, N.J.; Wang, J.R. Suitability of two methods of evaluating site quality for sugar maple in central Ontario. For. Chron. 2006, 82, 733–744. [Google Scholar] [CrossRef]
- Wang, G.G. Is height of dominant trees at a reference diameter an adequate measure of site quality? For. Ecol. Manag. 1998, 112, 49–54. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, M.; Yang, H.; Chen, C. An NFI-based site quality evaluation of Chinese fir plantation. J. Sustain. For. 2020, 39, 137–152. [Google Scholar] [CrossRef]
- Abrudan, I.V.; Mather, R.A. The influence of site factors on the composition and structure of semi-natural mixed-species stands of beech (Fagus sylvatica), silver fir (Abies alba) and Norway spruce (Picea abies) in the Upper Draganul Watershed of North-West Romania. Forestry 1999, 72, 87–94. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, D.; Jiang, F.; Bai, Y.; Zhang, Z.; Huang, X. A site index model for larix principis-rupprechtii plantation in Saihanba, north China. J. Appl. Ecol. 2015, 26, 3413–3420. [Google Scholar]
- Chen, H.Y.H.; Klinka, K.; Kabzems, R.D. Site index, site quality, and foliar nutrients of trembling aspen: Relationships and prediction. Can. J. For. Res. 1998, 28, 1743–1755. [Google Scholar] [CrossRef]
- Tian, H.; Zhu, J.; He, X.; Chen, X.; Jian, Z.; Li, C.; Ou, Q.; Li, Q.; Huang, G.; Liu, C.; et al. Using machine learning algorithms to estimate stand volume growth of Larix and Quercus forests based on national-scale Forest Inventory data in China. For. Ecosyst. 2022, 9, 100037. [Google Scholar] [CrossRef]
- Farrelly, N.; Ní Dhubháin, Á.; Nieuwenhuis, M. Site Index of Sitka Spruce (Picea sitchensis) in Relation to Different Measures of Site Quality in Ireland. Can. J. For. Res. 2011, 41, 265–278. [Google Scholar] [CrossRef]
- Ma, T.; Hu, Y.; Wang, J.; Beckline, M.; Pang, D.; Chen, L.; Ni, X.; Li, X. A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China. Remote Sens. 2023, 15, 1853. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.; Sophan, C.; Zhang, J.; Duan, A. Disentangling the effects of stand and climatic variables on forest productivity of Chinese fir plantations in subtropical China using a random forest algorithm. Agricul. For. Meteorol. 2021, 304–305, 108412. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, X.; Zhang, J.; Sophan, C. Comparing the random forest algorithm with other modelling approaches to capture the complex patterns of intra-annual wood formation of Chinese fir with different ages. Dendrochronologia 2023, 77, 126043. [Google Scholar] [CrossRef]
- Yang, S.I.; Brandeis, T.J.; Helmer, E.H.; Oatham, M.P.; Heartsill-Scalley, T.; Marcano-Vega, H. Characterizing height-diameter relationships for Caribbean trees using mixed-effects random forest algorithm. For. Ecol. Manag. 2022, 524, 120507. [Google Scholar] [CrossRef]
- Filho, A.M.; Netto, S.P.; Machado, S.A.; Corte, A.P.D.; Behling, A. Site Classification for Eucalyptus sp. in a Tropical Region of Brazil. An. Acad. Bras. Ciênc. 2023, 95, e20200038. [Google Scholar] [CrossRef]
- Mitsuda, Y.; Tsutsumi, H. Comparing Methods for Developing Site Index Prediction Model of Sugi (Cryptomeria japonica) Planted Stand. FORMATH 2018, 17, 17.004. [Google Scholar] [CrossRef]
- Lumbres, R.I.C.; Seo, Y.O.; Son, Y.M.; Doyog, N.D.; Lee, Y.J. Height-Age Model and Site Index Curves for Acacia mangium and Eucalyptus pellita in Indonesia. For. Sci. Technol. 2018, 14, 91–96. [Google Scholar]
- Luo, J.; Zhang, M.; Zhou, X.; Chen, J.; Tian, Y. Tree Height and DBH Growth Model Establishment of Main Tree Species in Wuling Mountain Small Watershed. IOP Conf. Ser. Earth Environ. Sci. 2018, 108, 042003. [Google Scholar] [CrossRef]
- Xu, H.; Sun, Y.; Wang, X.; Fu, Y.; Dong, Y.; Li, Y. Nonlinear Mixed-Effects (NLME) Diameter Growth Models for Individual China-Fir (Cunninghamia lanceolata) Trees in Southeast China. PLoS ONE 2014, 9, e104012. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Z.; Ma, W. Analysis of Tree Species Suitability for Plantation Forests in Beijing (China) Using an Optimal Random Forest Algorithm. Forests 2022, 13, 820. [Google Scholar] [CrossRef]
- Huang, S.; Titus, S.J. An index of site productivity for uneven-aged or mixed-species stands. Can. J. For. Res. 1993, 23, 558–562. [Google Scholar] [CrossRef]
- Raptis, D.I.; Kazana, V.; Kazaklis, A.; Stamatiou, C. Mixed-Effects Height–Diameter Models for Black Pine (Pinus Nigra Arn.). For. Manag. Trees 2021, 35, 1167–1183. [Google Scholar] [CrossRef]
- Shen, J.; Lei, X.; Lei, Y.; Li, Y. Comparison between site index and site form for site quality evaluation of Larix olgensis plantation. J. Beijing For. Univ. 2018, 40, 1–8. [Google Scholar]
- Dais, G.; Kitikidou, K.; Milios, E. Site Index Curves for Abies borisii-regis Mattf. and Fagus sylvatica L. Mixed Stands in Central Greece. Sustainability 2023, 15, 10349. [Google Scholar] [CrossRef]
- Guo, Y.; Han, Y.; Wu, B.; Yang, L. Study on Modelling of Site Quality Evaluation and its Dynamic Update Technology for Plantation Forests. Nat. Environ. Pollut. Technol. 2013, 12, 591–597. [Google Scholar]
- Zobel, J.M.; Schubert, M.R.; Granger, J.J. Shortleaf Pine (Pinus echinata) Site Index Equation for the Cumberland Plateau, USA. For. Sci. 2022, 68, 259–269. [Google Scholar] [CrossRef]
- Xu, C.; Xu, D.; Liu, Z.; Li, Y.; Li, N.; Chartier, R.; Chang, J.; Wang, Q.; Wu, Y.; Li, N. Estimating Hourly Average Indoor PM2.5 Using the Random Forest Approach in Two Megacities, China. Build. Environ. 2020, 180, 107025. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, Y.; Lee, D.L.; Cui, W. iForest: Interpreting Random Forests via Visual Analytics. IEEE Trans. Vis. Comput. Graph. 2019, 25, 407–416. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, L.; Sharma, R.P.; He, X.; Zhang, H.; Feng, L.; Zhou, Z. A Nonlinear Mixed-Effects Height-Diameter Model with Interaction Effects of Stand Density and Site Index for Larix olgensis in Northeast China. Forests 2021, 12, 1460. [Google Scholar] [CrossRef]
- Qiao, J.; Sun, Y. Effects of Altitude and Slope on the Climate–Radial Growth Relationships of Larix olgensis A. Henry in the Southern Lesser Khingan Mountains, Northeast China. Ecol. Process. 2022, 11, 46. [Google Scholar] [CrossRef]
- Song, J. Discussion of the relationship between Chinese fir growth and environmental conditions. West. China Technol. 2008, 7, 54–55. [Google Scholar]
- Wu, C.; Chen, D.; Sun, X.; Zhang, S. Influence of Altitude and Tree Class on Climate-Growth Relationships in a Larch Plantation in Subtropical China. J. For. Res. 2023, 34, 1869–1880. [Google Scholar] [CrossRef]
- Ma, S.P.; Wang, X.P.; Wang, X.M.; Sun, H.Z.; Guo, Z.W. Relative influence of environmental, stand factors and functional traits on allocation of forest productivity during the restoration of subtropical forests in central China. For. Ecol. Manag. 2021, 482, 118814. [Google Scholar] [CrossRef]
- Watt, M.S.; Kimberley, M.O.; Dash, J.P.; Harrison, D. Spatial prediction of optimal final stand density for even-aged plantation forests using productivity indices. Can. J. For. Res. 2017, 47, 527–535. [Google Scholar] [CrossRef]
- Dong, C.; Chen, Y.; Lou, X.; Min, Z.; Bao, J. Site Quality Classification Models of Cunninghamia Lanceolata Plantations Using Rough Set and Random Forest West of Zhejiang Province, China. Forests 2022, 13, 1312. [Google Scholar] [CrossRef]
- Guner, S.T. Relationships between Site Index and Ecological Variables of Oriental Beech Forest in the Marmara Region of Turkey. Fresenius Environ. Bull. 2021, 30, 6920–6927. [Google Scholar]
- Sacewicz, W.A.; Bijak, S. Effect of selected soil properties on site index of oak stands in the Miezyrzec Forest District. Sylwan 2018, 162, 3–11. [Google Scholar]
- Fang, J.-Y.; Shen, Z.-H.; Cui, H.-T. Ecological characteristics of mountains and research issues of mountain ecology. Biodiv. Sci. 2004, 12, 10–19. [Google Scholar]
- Körner, C. The Use of ‘Altitude’ in Ecological Research. Trends Ecol. Evol. 2007, 22, 569–574. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, S.; Chhin, S.; Zhang, X.; He, P.J. Modelling site index of Chinese fir plantations using a random effects model across regional site types in Hunan province, China. For. Ecol. Manag. 2019, 446, 143–150. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).