A Review of Optimization for Corrugated Boards

Abstract

This paper presents a comprehensive review of optimization practices in the corrugated board industry, which has recently experienced significant interest in using optimization methodologies driven by sustainable demands and increasing computational capabilities. The authors cover different review perspectives, including historical context, manufacturing applications, design optimization, and numerical optimization algorithms used. The main findings of this study indicate that the corrugated board industry has experienced a shift from trial-and-error and expert-driven approaches to data-centric strategies, particularly since the beginning of the 21st century. Interestingly, the industry has also adopted Multi-Disciplinary Optimization techniques from other fields, which demonstrates the importance of knowledge convergence across sectors. However, due to the complex nature of corrugated boards—including materials, design, and manufacturing processes—there is still much research to be done in this area. This work provides guidance for future research directions and encourages innovation and improvement in corrugated board optimization practices. In particular, the strong developments of material models for paper in recent years will boost the use of optimization tools in this field.

1. Introduction

The remarkable strides in globalization, alongside the robust upswing in e-commerce, pharmaceutical, cosmetics, food, and beverage industries, have precipitated an unprecedented demand for efficient and sustainable packaging solutions [1,2]. The market dynamics in 2021 underscored the surging importance of this sector, estimated at USD 199.8 billion and forecasted to burgeon to a staggering USD 254.5 billion by 2026, registering a Compound Annual Growth Rate (CAGR) of 5.0% [1,3,4]. Amid this evolving landscape, the paper and paperboard packaging sector, specifically corrugated boards, has emerged as a vital component in addressing this demand [5].

Corrugated boards, credited to the inventive genius of Albert L. Jones in 1871 [6], persistently revolutionized the packaging industry [7]. Lightweight, with excellent weight-specific stiffness and great strength properties [8,9], corrugated boards play a pivotal role in constructing robust boxes and containers for the safe transportation and protection of goods at a lower cost [10]. The increasing concerns surrounding environmental pollution further accentuate the importance of corrugated boards. Predominantly made from cellulose [11]—a renewable resource—these packaging materials are highly ecological. They serve as a viable and preferred alternative to their non-biodegradable counterparts, mainly plastic [12].

Despite the advantages offered by corrugated boards, the fiercely competitive landscape and ever-increasing market demands necessitate continuous improvement and innovation. Consequently, the optimization of corrugated boards has surfaced as a cardinal concern for manufacturers [5,12].

In fact, in an era marked by raw material scarcity, climate change, and escalating global needs for food, energy, water, and materials, the significance of optimization cannot be overstated. It presents an opportunity for manufacturers to leverage resources judiciously, promote sustainability, and enhance the overall efficiency of the packaging industry. Optimization facilitates an understanding of the behavior of corrugated boards under diverse loading conditions, paving the way for designs that maximize strength and durability while minimizing environmental impact [13].

Furthermore, customized optimization strategies are invaluable for navigating the complex trade-offs between different objectives, such as reducing waste, minimizing cost, and improving product performance [14]. Therefore, the multi-objective optimization of corrugated boards is more than a strategic advantage—it is a critical component of sustainable industrial practice.

The existence of a state-of-the-art review related to optimization in corrugated boards would be of the utmost importance to assist the corrugated board industry better. However, after an analysis of the available literature, a review of the optimization strategies to tackle corrugated board-related problems, considering a critical analysis of potential research gaps in the topic, was yet to be published.

This paper is then intended to perform a historical and critical review of optimization for corrugated board problems and to analyze the research gaps and future directions, tackling such a gap in the literature.

More specifically, the authors formulate three research questions that will be discussed at the end of the review:

RQ1.

What is the current landscape of optimization methodologies in the corrugated board industry, and how do these methodologies contribute to the economic and environmental outcomes?

RQ2.

How have these methodologies evolved, and what are the key drivers behind these changes?

RQ3.

What current state-of-the-art limitations may lead to potential trends that can be anticipated in optimizing corrugated boards?

The present work is organized as follows: Section 2 provides an elucidative background on the main concepts surrounding optimization and corrugated boards. Section 3 describes the methodology adopted for the search and selection of the papers considered in the current review. Section 4, the pivotal part of this research, is a comprehensive state-of-the-art review highlighting the latest advances and applications of optimization techniques specific to corrugated boards. Section 5 explores the limitations and potential areas for improvement in the current realm of optimization applied to corrugated boards. Key conclusions are drawn from the research in Section 6, concisely synthesizing the main insights and future research perspectives.

Figure 1 represents the overview of the structure of the paper more in detail. Based on a pre-analysis of the available literature, the authors propose to divide the review section (Section 4) into five sub-sections:

• The early stages of optimization of corrugated boards.
• Advances of optimization in the design and manufacturing of corrugated boards.
• Design optimization of the structure.
• Optimization objectives.
• Numerical optimization algorithms used in the context of corrugated boards.

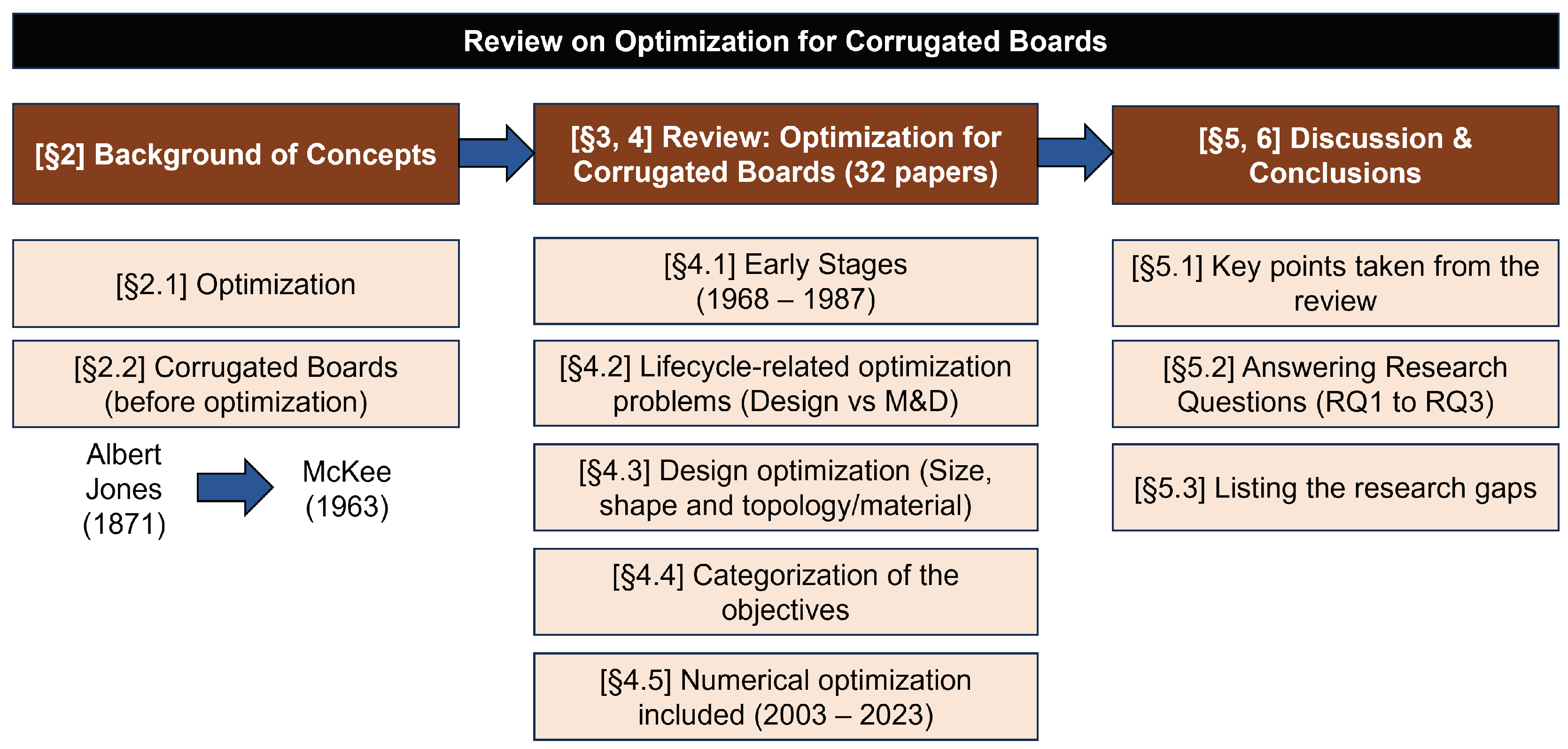
2. Background of Concepts

2.1. Optimization—Definition and Strategies

“Optimization” can be defined as the process of obtaining the maxima or minima in a set of available alternatives [15]. Its wide-ranging implications and consequences make it crucial in practically all engineering fields [16]. As technology advances and knowledge expands, techniques for optimization have been continuously evolving and improving [17], providing engineers with increasingly sophisticated tools to enhance efficiency, effectiveness, and overall performance in various domains.

In the context of single optimization, only one objective function is considered to minimize. Let N be the number of design variables and $\mathbf{X}$ = $\{x_1,\cdots ,x_N\}$ and $f\left(\mathbf{X}\right)$ such an objective function. The number of inequality constraints is given by $n_g$ and the inequality constraints are $g_i\left(\mathbf{X}\right),i=1,\cdots ,n_g$. Moreover, the number of equality constraints is given by $n_h$ and $h_j\left(\mathbf{X}\right),j=1,\cdots ,n_h$, are the equality constraints. $\mathbf{X}\in {\mathcal{S}}^N$, where ${\mathcal{S}}^N=[x_{1_L},x_{1_U}]\times \cdots \times [x_{N_L},x_{N_U}]$ is the search space. The standard form of a single-objective, constrained optimization problem is given in (1):

$$\begin{array}{cc}\mathrm{Minimize}:\hfill & f\left(\mathbf{X}\right)\hfill \\ \mathrm{Subject}\mathrm{to}:\hfill & g_i\left(\mathbf{X}\right)\le 0,i=1,\cdots ,n_g\hfill \\ \hfill & h_j\left(\mathbf{X}\right)=0,j=1,\cdots ,n_h\hfill \\ \hfill & x_{k_L}\le x_k\le x_{k_U},k=1,\cdots ,N\hfill \end{array}$$

(1)

Determining objectives and constraints can be achieved through explicit or implicit functions. Side constraints can be easily and effectively handled through direct implementation. The optimal solution ${\mathbf{X}}^{*}$ involves identifying the combination of values that achieve the best objective function while satisfying equality, inequality, and side constraints.

When maximization problems occur, those can be transformed into minimization problems by inverting the signal of the objective function $f\left(\mathbf{X}\right)$. Once looking at the optimal ${\mathbf{X}}^{*}$, one might be interested in $f\left({\mathbf{X}}^{*}\right)$, which represents the maximum value of f.

Engineering problems can also have multiple objectives. If this is the case, they are known as multi-objective optimization problems [18]. Those can be related to the minimization of objectives, maximization of objectives, or both situations in the same problem. Converting to a problem where all the objectives are minimized is processed as above.

There are two main methods for dealing with multi-objective optimization problems: Pareto dominance and scalarization [19]. Pareto dominance involves defining a set of solutions called the Pareto set, which dominates all other solutions within the search space. This also means that no element of the Pareto set can dominate any other element of it. Dominance is determined by a mathematical statement, as shown in (2), where ${\mathbf{X}}_{\mathbf{1}},{\mathbf{X}}_{\mathbf{2}}\in {\mathcal{S}}^N$ [20].

$${\mathbf{X}}_{\mathbf{1}}\prec {\mathbf{X}}_{\mathbf{2}}\iff \forall i=1,\cdots ,n_f:f_i\left({\mathbf{X}}_{\mathbf{1}}\right)\le f_i\left({\mathbf{X}}_{\mathbf{2}}\right)\mathrm{and}\exists i\in \{1,\cdots ,n_f\}:f_i\left({\mathbf{X}}_{\mathbf{1}}\right)<f_i\left({\mathbf{X}}_{\mathbf{2}}\right)$$

(2)

The Pareto set is a set with multiple valid solutions. One of the advantages of having a Pareto set is that the end user can choose an adequate solution. The set can also be used to calculate niches of solutions, which can have a tremendous impact on balancing exploitation and exploration. On the other hand, scalarization is an easier, sometimes more efficient approach, where various objectives are combined in a single fitness function to transform the problem into a single optimization problem.

Implicit functions can be preferred for numerical simulations, such as finite element simulations. In such numerical simulations, only embedded approximations are assumed. Therefore, those are more accurate and, consequently, preferable. However, complex simulations can pose a challenge and be time-consuming. In these cases, simplifying a model in order to reduce its computational evaluation time can be preferable against accuracy. One common approach for computational efficiency is using surrogate models, also denominated as metamodels. Among them, some of the most known are Artificial Neural Networks [21], Response Surface Modelling [22], and the Kriging method [23]. A very attractive advantage of using surrogate models is that gradient-based algorithms can be easily implemented since derivatives are easily computed. They improve the overall optimization process computational power even more. These models can also handle variables restricted to integer or discrete values [24], which may prove difficult for some local algorithms but can be solved by most global algorithms.

When it comes to solving optimization problems, there are various techniques available. The selection of a specific technique depends on its complexity and suitability for the problem at hand. Traditional methods involve calculating the evaluation function’s gradient, such as Newton’s method and Quasi-Newton methods. However, modern engineering problems are often very complex. In this context, two major approaches are usually considered.

The first approach is employing gradient-free algorithms, usually metaheuristics, which are more useful in such kinds of problems. These methods, including Genetic Algorithms (GA) [25], Ant Colony Optimization (ACO) [26], and Particle Swarm Optimization (PSO) [27], among others, work by modifying instances of design variables, such as chromosomes in GA. In PSO, individual instances called particles move through the search space based on social and individual cognitions. Although both GA and PSO have convergence issues, variations, and alternatives have been published to address these problems.

In multi-objective optimization, Sharma and Kumar [28] examined various metaheuristic-based methods for optimizing multiple objectives. Among these methods, Non-Dominated Sorting Genetic Algorithm-II (NSGA-II) [29] and Multi-objective Particle Swarm Optimization (MOPSO) [30], which are adaptations of GA and PSO, are two of them. Researchers have also developed hybrid approaches that combine the strengths of both GA and PSO, such as the one described in [31].

A second approach arises when surrogate models for the objective function become available or when metaheuristics prove to be computationally demanding. This usually involves the utilization of gradient-based algorithms, with Stochastic Gradient Descent (SGD) [32] and Adam optimizer [33] being the most commonly used, and the dataset taken from the simulation prepared to be used for training and test purposes.

Stochastic Gradient Descent (SGD) is a variant of the Gradient Descent [34]. The fundamental concept of SGD lies in its use of a single, randomly selected training example to calculate the gradient at each step instead of using the entire data set. This can be an advantage compared to Gradient Descent because the latter uses the entire dataset for training purposes, which can be computationally demanding. SGD can be even more effective when conjugated with Momentum [34,35], used to accelerate convergence and avoid local minima. Momentum works by adding a fraction of the direction of the previous step to a current step. This serves the purpose of increasing the speed of descent in persistent directions, which in turn leads to faster convergence. At the same time, it also helps to smooth out the updates, thus reducing the oscillations and noise that can occur with SGD.

Adam (Adaptive Moment Estimation) is a method for efficient stochastic optimization that only requires first-order gradients with little memory requirement. It is an extension to SGD, combining the best properties of the AdaGrad [36] and RMSProp [37] algorithms to provide an optimization algorithm that can handle sparse gradients and noisy data. Adam uses estimations of the first and second moments of the gradient to adaptively change the learning rate for different parameters.

Despite such advantages of numerical optimization overall, the reality is that its complexity often deters its application in practice. Some approaches in the literature go so far as to employ manual iterations. For instance, instead of traditionally using numerical optimization algorithms, some authors consider a list of values for the design variables to evaluate [38]. These are not purely produced throughout iterations using a specific algorithm but rather from the specialist’s knowledge. Moreover, the stopping criterion is often set so that the process stops once an improvement is observed compared to previous findings. Because these differences apply, only a few iterations or even a single iteration of the improvement process are performed. As such, evidence of mathematical convergence to the true optimum is typically absent.

Manual iteration is an older method, but it is still vital nowadays. For instance, optimizing hyperparameters in machine learning algorithms by using manual iterations is still a common approach [38]. This is because there are usually numerous parameters and algorithms that require the expertise of a specialist for large datasets and specific applications, and it is still a feasible approach compared to finding a general optimization approach for all problems. It should be emphasized that the latter is unattainable according to the No Free Lunch Theorem [39].

2.2. Corrugated Boards—An Overview

Corrugated board is a type of material that is commonly used to make boxes and containers for transporting and protecting goods. It is made up of layers, including a wavy core called a flute and face sheets called liners, which affect the strength of the material [13]. The architecture of a corrugated board is integral to its utility in packaging. The flute, or the wavy inner layer, gives the material its unique combination of strength and flexibility. Encased by flat liner layers, the flute’s orientation largely dictates the board’s mechanical characteristics. Most fibers run along the paper web, also known as the machine direction (MD) [5,13], leading to stiffer properties along this axis. The direction perpendicular to MD, known as the cross direction (CD), generally exhibits weaker mechanical properties [5,13]. This inherent imbalance is mitigated by the take-up factor of the corrugated layers, which effectively distributes the material’s tensile strength.

The orthotropic nature of corrugated boards results in varied mechanical properties across different directions. Predominantly, the elasticity moduli in both the machine and cross directions ($E_{MD}$ and $E_{CD}$) and the compressive strength in the cross direction (${SCT}_{CD}$) constitute the most crucial characteristics [5].

It is a well-known fact that corrugated boards boast exceptional mechanical properties [8,9]. They offer an outstanding weight-specific stiffness and possess remarkable strength properties, making them lightweight and more affordable than their predecessors, wooden crates and boxes, that were widely utilized for shipping and transportation until the end of the 19th century but which were prone to damage and difficult to manage in terms of waste [7].

Corrugated boards were introduced in 1871 by Albert L. Jones [6]. They were initially used for packing delicate glassware. Two years later, Henry Norris recognized the transformative potential of this innovation and acquired Jones’s patent [7], leading to the widespread use of corrugated fluting for glassware packing. The development trajectory of corrugated boards was further enriched by Oliver Long’s dual patents, which pioneered a core of shredded material followed by fluted paper [7].

This innovative evolution took a decisive turn as the industry began to harness the true potential of corrugated boards for mass production. The corrugated board industry experienced a significant shift in the 1910s as more companies began producing it after the expiration of the original patents [7].

As corrugated boards assumed the throne of the packaging world, they began to be treated not just as a packaging solution but as an engineering material [40]. Due to their tendency to buckle under pressure and weight, they present a unique challenge that has spurred research and development efforts. The strength and stability of boxes made from corrugated boards have become a crucial focus, particularly in situations where stacking is required and the bottom box needs to demonstrate adequate compression strength.

As the packaging industry grew in complexity and scale, the lack of consistency in the quality and performance of corrugated boards produced by different manufacturers started to become more evident [7]. This inconsistency posed significant problems for businesses relying on these materials for packaging and shipping. Disparities in product quality could lead to product damage during transport, resulting in financial losses and reduced customer satisfaction.

As a response to these challenges, industry stakeholders began to develop and adopt standards to regulate the production and use of corrugated boards. The Technical Association of the Pulp and Paper Industry (TAPPI), one of the leading organizations for standards development in this industry, was then founded in 1915 [41], and the development of many standards for paper and paperboard products started around this time. One of those standards is related to flute types, which typically range from A to F [42], with A-flute offering excellent shock absorption and F-flute providing superior printing surface. Beyond the standardization of flute types, other critical aspects of corrugated boards have also been standardized. These include standards for:

• Bursting strength [43,44]: A measure of the board’s resistance to rupture under pressure, important for ensuring the packaging can withstand handling and transport.
• Edge crush test (ECT) [45,46]: A measure of the plate’s stacking strength, which indicates how much weight a box made of the material can support before collapsing.
• Flat crush test (FCT) [47,48]: A measure of the material’s rigidity and resistance to crushing when it is flat.
• Moisture content and resistance [49,50,51]: These ensure that the board can withstand varying degrees of humidity without losing its structural integrity.
• Stiffness [52,53]: This ensures the corrugated board has the necessary rigidity to hold shape under load.
• Box Compression Test (BCT) [54,55]: A measure of how much force a box can withstand before it collapses. This test is essential for determining the overall strength of the final corrugated box, and it helps manufacturers and packagers determine the weight and content limits for a given box.

These and other standards have been essential in maintaining the quality, reliability, and functionality of corrugated boards across the globe. They continue to evolve as the industry adapts to new challenges and innovations.

Attempts also started to be made in the 1950s to predict the compression strength of corrugated containers. These efforts ranged from empirical formulas identifying paper, board, and box parameters to finite element simulations. One notable outcome of these efforts was the formula proposed by McKee [56], an analytical tool published in 1963 that has continued to provide simple solutions for standard boxes. The McKee formula can be stated as follows:

$$BCT=a·EC{T}^b·{\left(\sqrt{S_{B,MD}·S_{B,CD}}\right)}^{1-b}{Z}^{2b-1}$$

(3)

where a and b are empirical constants, Z is the perimeter of the box, and $S_B$ is the bending stiffness of the corrugated board in the machine direction (MD) and in the cross-machine direction (CD).

The McKee formula is widely used in corrugated board-related research due to its simplicity and practicability. Despite its limitations, it was a significant stepping stone in the evolution of corrugated board technology. Subsequent studies have expanded on this foundation, incorporating box dimensions, modifying constants, and exponents, and considering Poisson’s ratio [57,58,59,60].

Improving manufacturing and transportation processes is also key to quality improvement, consequently reducing costs and improving customer satisfaction. By making production more efficient and cost-effective, packaging can be made cheaper and less prone to damage during transportation. This would result in faster delivery times and longer-lasting packaging.

As the world becomes more environmentally conscious, the corrugated board industry faces new challenges. Waste management is a growing concern, as even though corrugated boards are made from recyclable materials, they can still contribute to waste if not properly managed. The industry must promote recycling and reusability while also reducing the amount of material used in the first place. This ’lightweight’ approach can result in significant savings in costs, energy, and raw materials and is an important step towards sustainability. The industry is also looking to find more sustainable inks, adhesives, and other materials for corrugated board manufacturing, to further promote environmental stewardship.

Today, there are various methods—experimental, analytical, and numerical—that can help estimate the strength of corrugated boards more accurately. These methods also offer ways to optimize the composition and use of corrugated materials, reducing waste in their production. This marks a significant shift from the simple formulas of the past, such as the McKee formula, to the complex computational models of today. This brings us to the present literature review.

3. Methodology and General Overview

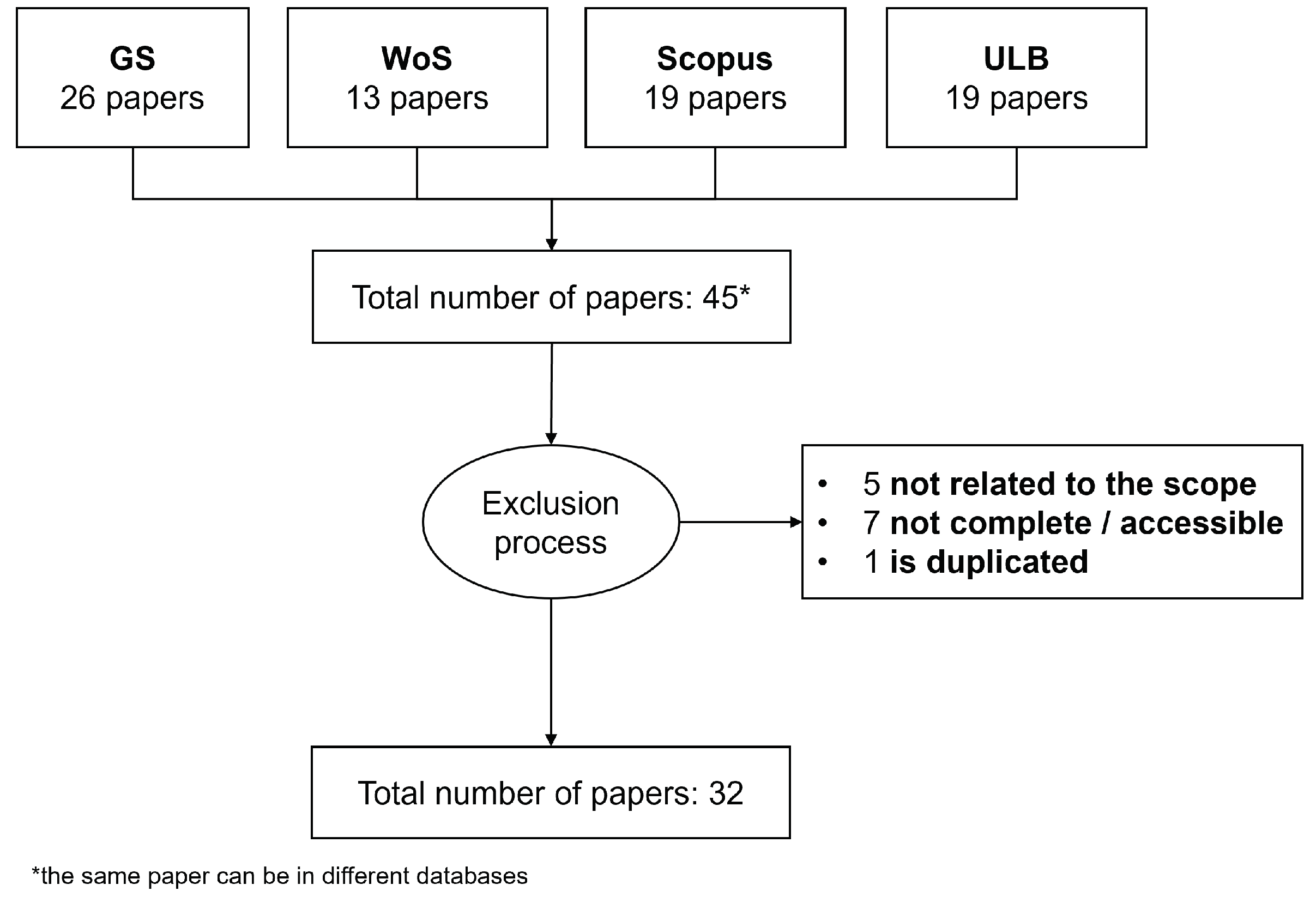
3.1. Databases and Keywords

To ensure a comprehensive understanding and to collate the most relevant studies, multiple databases were revised using a set of carefully selected keywords.

Google Scholar (GS) served as one of the sources of articles, with searches emphasizing titles containing words related to optimization. This included terms such as “optimization”, “optimum”, “optimal”, and “optimisation”. These optimization-related terms were combined with specific corrugated materials nomenclature like "Corrugated board", “Corrugated cardboard”, “Corrugated paperboard”, “Corrugated box”, “Corrugated boxes”, “Corrugated fiberboard”, and “Corrugated fibreboard”. Variations of the English “optimization” and “Corrugated fiberboard” expressions (American versions) were searched to ensure more papers were included in the review.

The interlibrary services offered by the university library of Technische Universität Darmstadt (ULB) were another essential resource. Here, searches were performed using both English and German terms. Keywords such as “Optimierung” (optimization), “optimal”, and “optimum” were combined with “Wellpappe” (corrugated board). These services were crucial for the development of the current review since most of the evaluated papers were not available in Google Scholar or not even mentioned in it.

Further deep dives into scholarly content were executed on databases like Scopus and Web of Science (WoS). In both of these databases, titles were filtered with a combination of optimization descriptors along with the various types of corrugated materials, matching the structure used in the previous databases.

During this literature collection process, some keyword combinations, especially those with “Fluted paperboards” and other similar terms, yielded no results across the databases. As a result, these terms were excluded from the final list of searches.

3.2. Limitations

There is the possibility of the literature review being incomplete with other works due to the following reasons:

• It is possible that more English terms similar to those mentioned are being discarded.
• There might exist other libraries and databases that consider other papers that are not detected by Google Scholar, Scopus, Web of Science, and ULB.
• Despite the capability of the considered databases to detect papers written in languages other than English but using English keywords, this paper is limited by these databases’ own limitations of not finding other non-English written papers.
• It is also possible that “optimization”-related keywords are present in the body of the papers despite not being mentioned in the title. However, the authors are considering that optimization must be mentioned in the title so that it can be considered an optimization-related paper.
• Words such as “minimization” and “maximization” that are related to the optimization topic are not used, not only because there are multiple combinations of such words but also because they are not so widely used as “optimization”.

Nevertheless, the authors are confident that the found set of papers corresponds to the main publications on the research of optimization of corrugated boards; therefore, it is a very significant sample representing the advances in the field.

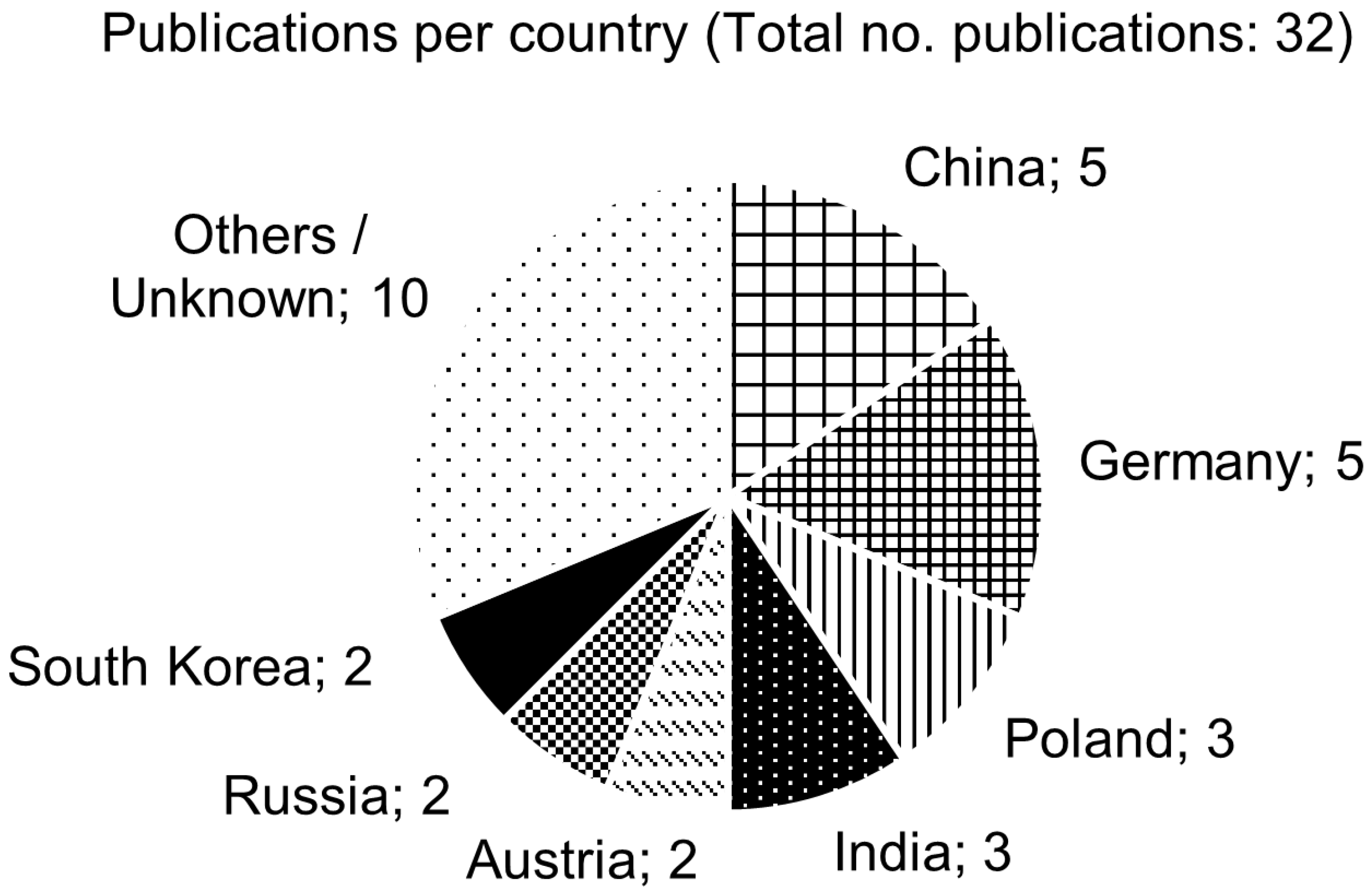
3.3. First Analysis of the Available Literature

Searching for papers related to optimization and corrugated boards resulted in a total of 45 papers from different countries and written in different languages. From those:

• Five publications are excluded because they are not related to the scope of the current review, despite having the necessary keywords.
• Seven other publications are excluded because they are not complete or not accessible (due to policies that do not allow public consultation).
• One other publication is duplicated (i.e., with double reference) from another publication that is already considered in the final set of papers.

After the exclusion process, a total of 32 publications are analyzed in the next section. This preliminary analysis is graphically summarized in Figure 2.

Major countries whose researchers that are referenced in this review belong to a research institution of said countries are China (5), Germany (5), Poland (3), India (3), Austria (2), Russia (2), and South Korea (2). Other countries are also represented with one publication each: Romania, Bulgaria, Turkey, Slovakia, Indonesia, Sweden, Taiwan, USA, Argentina, Japan, and Finland. A pie chart representative of this analysis is presented in Figure 3.

All papers (including the excluded papers) were published after the publication of the McKee formula in 1963, more precisely since 1968. There is a set of papers that will be mentioned in the current work in the subsection “Early stages” that were published before 1992. New approaches in the field of optimization started appearing in 2003, especially at a time when surrogate models started being commonly explored among researchers and at a time with more powerful simulation tools and more computational power available. Although the number of publications per year has never steadily grown over the years, it is evident that more papers in the field have been published since 2003 than before. Figure 4 is a plot with the total number of publications per year along the time until 2023.

4. Literature Review on the Optimization of Corrugated Boards

This section is divided into five parts. The first part focuses on the initial papers published in the field, while the remaining four are categorized based on the lifecycle phases, design optimization types, objectives, and the presence of numerical optimization. To make it easier for the reader, Figure 5 illustrates the main categories of the publications selected for further analysis.

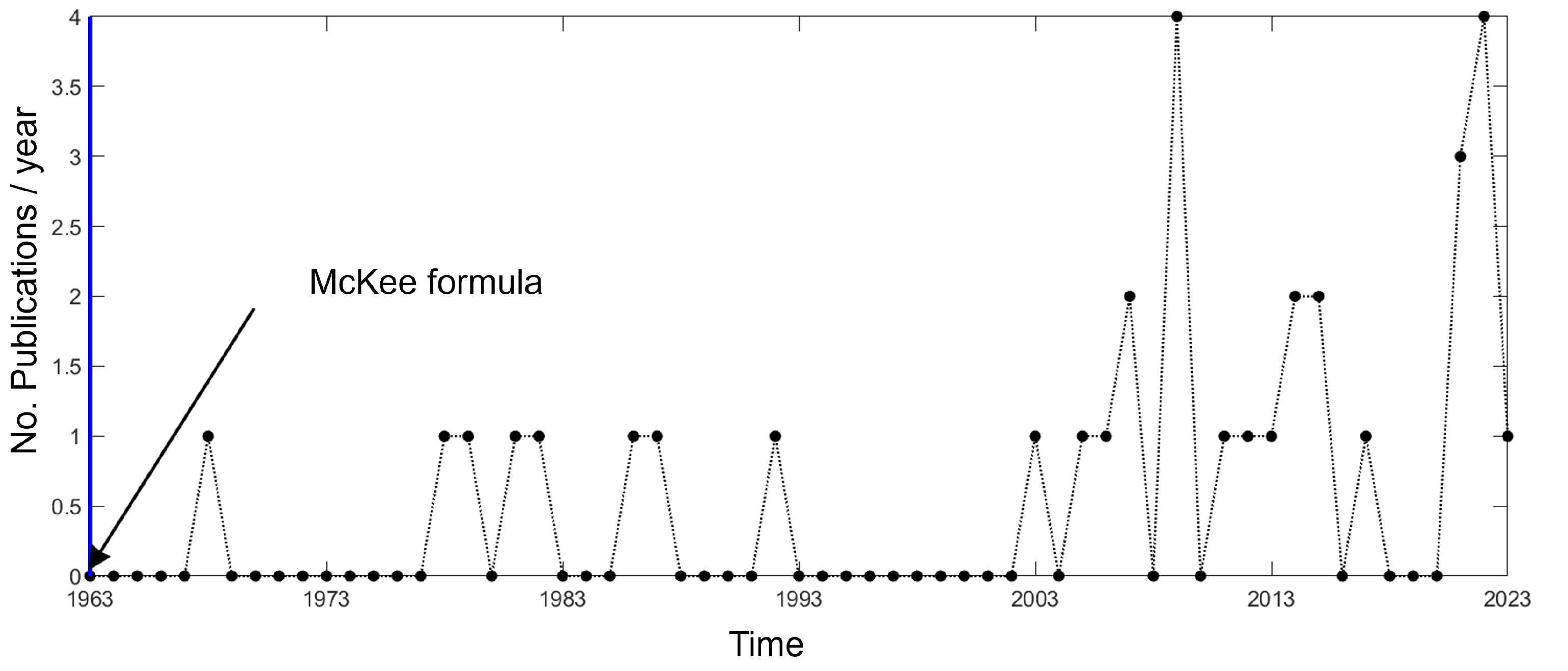
4.1. Early Stages

McKee was one of the earliest influential papers on the optimization of corrugated boards. His work in 1963 [56] centered on deriving a simpler formula to model the top-load compression strength of vertical flute boxes using board properties and box dimensions. Although this paper did not specifically deal with optimization, it highlighted the importance of edgewise compression strength and its empirical correlation with properties governing flexural stiffness.

As early as 1968, Langaard [61] presented the first-ever optimization approach in board construction, primarily focusing on compressive resistance. Guided by robust statistical analysis, the study sought to align with an economic mindset, leveraging both ECT and BCT values while keeping efficiency—minimizing board thickness and maximizing fluting proportion. Langaard emphasized the balance between performance metrics and material efficiency. The study was a clarion call for designs that were not just robust but also sustainable and cost-effective. It then made a significant contribution to the literature because it motivated further research, especially from an optimization perspective. A similar work was also published in 1969 by the same author [62].

A decade later, in 1978, P. Seyffert [63] pivoted towards a broader operational purview. The study introduced a holistic optimization approach, leveraging the prowess of an optimization system called “VERWEL”, with the aim to turbocharge corrugated board production processes. This ambitious methodology sought to juggle multiple facets of the production process, from order structures to the intricacies of corrugated boards. The study’s objective was to optimize every possible element, ensuring reduced waste and setup changes while maximizing utilization, sales, and overall production efficiency. It motivated further research related to manufacturing improvement in order to optimize processes related to the production of corrugated boards, whose publications are discussed in the present review.

In 1979, M.W. Johnson et al. [64] focused on the relationship between fiber distribution and the strength of singlewall corrugated fiberboards. This study used both empirical and theoretical methods to better understand the strength of short columns when faced with local buckling. The result was an empirical stress–strain formula that provided a foundation for understanding the strength of singlewall fiberboards. This formula had significant design implications, as it allowed for the optimal fiber distribution to be determined. This not only increased resistance to edgewise compression but also protected the boards from structural weaknesses such as local buckling.

The early 1980s saw the first explorational optimization study of adhesives in corrugated boards. In 1981, a research paper [65] embarked on the task of unraveling the optimal processing methodologies for corrugated-board glue. The article showcased how refining the adhesive process could lead to more durable and defect-free corrugated boards, emphasizing the importance of a high-quality adhesive process in both manufacturing and distribution. It leads to an increased lifespan of the final product.

Building on the adhesive-focused discourse, in 1982, Durinda and Obetko [66] took a deep dive into adhesive optimization for corrugated boards. They underscored a regression analysis originated by the balance between gelatinization temperatures, apparent viscosity, and adhesive properties. By shedding light on these nuanced relationships, the study highlighted the potential for designers to craft corrugated boards that were not only economically viable but also excelled in performance.

Different problems and optimization solutions continued appearing. In another paper published in 1986, Kainulainen [67] delved into the nuanced relationship between the composition of corrugated boards and the compression resistance of the finished boxes. Taking advantage of linear regression analysis, this study assessed the influence of specific variables like basis weight and fluting properties on the compression strength of boxes. Understanding the relationship between board composition and box strength allows for better design of corrugated boxes. Manufacturers can then produce boxes tailored for specific strength requirements, ensuring the safety and integrity of enclosed products.

One year later, another study emerged by Vogelpohl and Hohmann [68], offering an in-depth examination of corrugated board’s quality and processing outcomes. A facet of this research was its spotlight on the role of storage conditions, especially humidity and temperature, and their impacts on corrugated board processability. The study established correlations between bending resistances, groove strength, and various other influential variables. This research, with its holistic approach, had sweeping implications for manufacturing, such as quality assurance and reduced waste. A key takeaway was the interdependence between optimized groove positioning and storage conditions in producing high-quality corrugated boards.

The evolution of optimization in corrugated boards, as evident from these early-stage papers, was multifaceted. While some of the regression analysis and design optimization methodologies that were reviewed in this subsection were inspired by the McKee simplified formula, the need for surrogate models, such as Response Surface Methodology (RSM) and more formal optimization and FE analysis-related problems are starting to be discussed from the beginning of the next century.

Table 1. Summary of the papers presented in the subsection “early stages”.

Ref.	Authors (Year)	Novelty	Objectives (Category)	Design Variables	Lifecycle
[61,62]	Langaard (1968)	Optimization of corrugated boards based on the McKee equation (first approach)	Mechanical Properties	Type and quality of the corrugated board	Design
[63]	P. Seyffert (1978)	Introduction of VERWEL	Time	Product order-related data	M&D
[64]	M. W. Johnson et al. (1979)	Formulation of a theory for short-column strength of the local buckling, Empirical stress–strain analysis	Mechanical Properties	Strain of the material	Design
[65]	Goldschmidt AG (1981)	Increase glue quality to achieve minimum defects	Mechanical Properties	Chemical concentrations; shear forces applied during mixing; temperature during the gelatinization process	M&D
[66]	Durinda and Obetko (1982)	Design of experiments for adhesives, with the purpose of saving manufacturing costs, while increasing efficiency in production and quality of the products	Cost	Gelatination temperature, apparent viscosity	Design
[67]	Kainulainen (1986)	Maximization of the compression resistance	Mechanical Properties	Basis weight, properties of fluting	Design
[68]	Vogelpohl and Hohmann (1987)	Maximization of the grooveability, bending resistance, and uniformity of moisture content in storage and minimization of cover damage during grooving, variability in grooving outcomes, and moisture loss during storage	Mechanical Properties	Gap width in relation to board thickness, type of corrugated board, groove profile used, storage conditions, especially humidity levels, creasing tool profile and the gap width	M&D

summarizes the papers presented in this subsection on early optimization developments for corrugated boards.

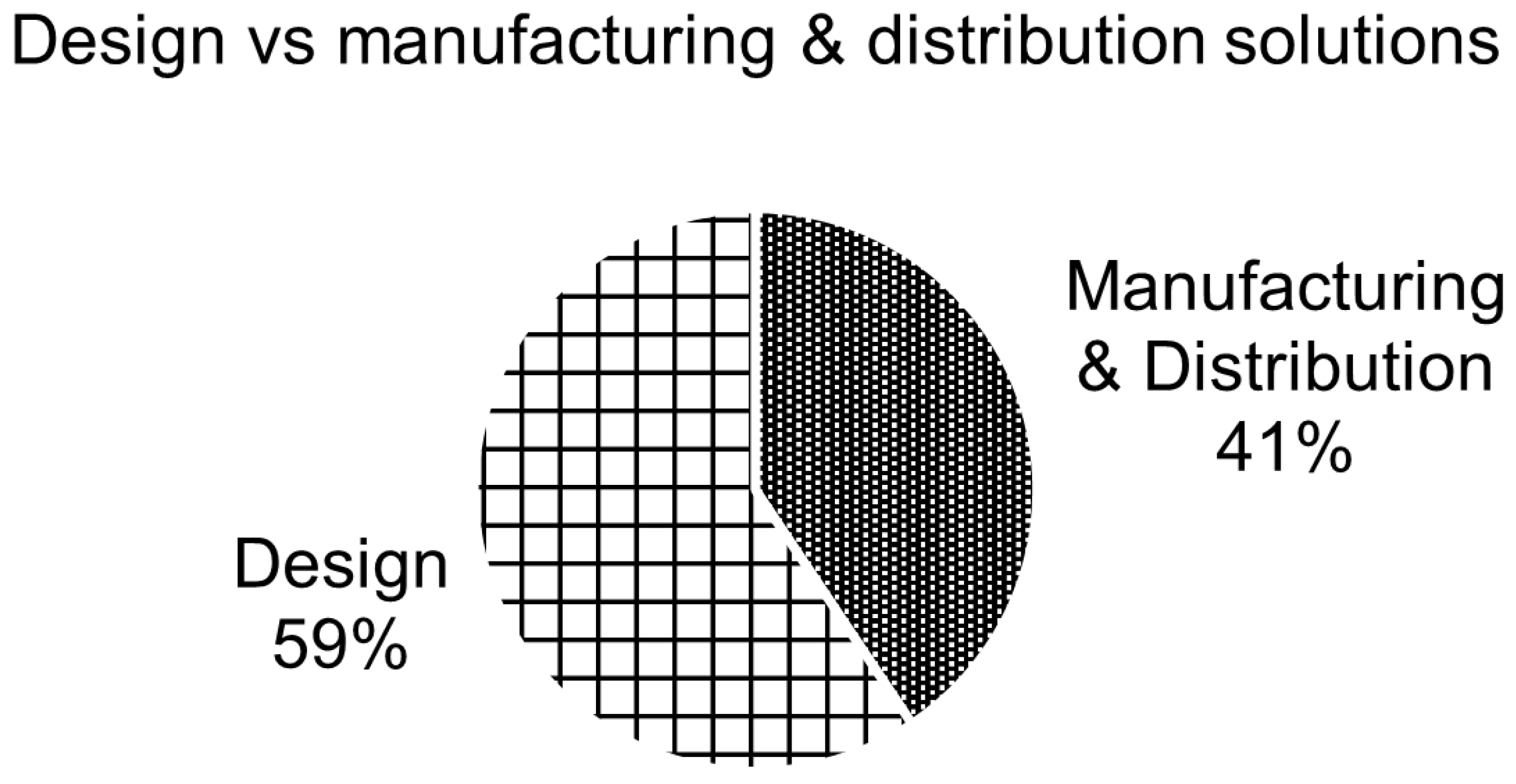
4.2. Design vs. Manufacturing and Distribution

Previous research on corrugated boards has shown that there are two main categories of studies: those focused on designing the boards and those focused on optimizing their manufacture. A pie chart in Figure 6 illustrates the distribution of papers between these two categories.

In addition to the studies mentioned earlier, recent papers on manufacturing and distribution optimization from corrugated boards have focused on specific variables, such as reducing water waste, raw material waste, and electricity consumption.

For instance, the study conducted by Cho and Um [69] delves into the optimal operational settings for producing microflute corrugated paperboards on a small scale. The main objective is to improve the board’s physical characteristics, particularly its strength and shock absorption capacity, which are vital indicators of its durability and effectiveness. Through this research, a more efficient and quality-focused approach to production can be established. This study is one of the few reviewed that objectively considers shock absorption capacity and offers solutions to interested readers.

A patent for an advanced method and system focused on optimizing the cutting area efficiency of corrugated boards was made by Tian et al. [70]. The core aim of this process is to strategically cut paper pieces, with a particular emphasis on minimizing the waste of raw materials. The cornerstone of this methodology is deeply rooted in computational geometry, space partitioning, and heuristic optimization techniques. By optimizing the cutting process, manufacturers can potentially produce more product units from the same amount of raw material, thus driving up production efficiency and decreasing environmental waste.

Kubera and Tyczyński [71] offer a comprehensive analysis of the optimal use of corrugated boards in transport packaging. By employing the capabilities of Cape Pack Palletizing and Packaging Design Software, the study specifically zeroes in on the fitment of individual packages within a corrugated box. The objective here is to achieve enhanced packaging efficiency, ensuring that the volume is minimized both during the production process and in storage settings without compromising the integrity and protection afforded by the corrugated transport packages. The suggested solution is crucial in minimizing package usage and material waste.

In the publication written by Mahakalkar et al. [72], optimizing the corrugated box production process through the combined application of dimensional analysis and RSM is carried out. The core methodology involves employing RSM for modeling the corrugated box production process and leveraging statistical approximation of the response variables using Buckling Pis as independent variables. This approach forms a comprehensive model of the production process, giving special emphasis to the role of Buckling Pis in understanding and predicting outcomes. In manufacturing, this research stands as a cornerstone. It not only holds promise for heightened efficiency and product quality but also underscores the significance of integrating advanced statistical and analytical tools in the modern manufacturing landscape.

Musielak [73] examines the utilization within corrugated board plants, emphasizing the avenues of optimization. By leveraging the capabilities of a Surrogated Model alongside the advanced predictive powers of Artificial Neural Networks (ANN), the research delves into the relationships between electricity consumption, corrugated board plant modules, corrugator speeds, and flute types. This study has a potential impact because it provides a methodology to be conducted by interested stakeholders.

Karabacakoğlu and Tezakıl [74] delve into the electrocoagulation of corrugated box industrial effluents using Response Surface Methodology (RSM), facilitated by tools such as Design-Expert and Pareto analysis. A novel aspect of this research is the dual focus on both maximizing the Chemical Oxygen Demand (COD) removal efficiency and concurrently minimizing energy consumption, contrasting the conventional approach that singularly emphasizes COD maximization. The design variables under consideration include current density, time, and stirring speed. In the context of manufacturing, this research holds importance as it offers an innovative solution to effluent treatment in the corrugated box industry. The emphasis on energy conservation alongside effective wastewater treatment can usher in cost reductions, enhance sustainability, and position manufacturers to better meet environmental standards and regulations.

Beyond exploring manufacturing problems, some authors have also explored the design optimization problems of corrugated boards. For instance, Wang et al. [75] embark on a comprehensive exploration of the shock absorption properties of packages by refining and enhancing the procedure for selecting appropriate corrugated boards. The authors used advanced methodologies such as ANOVA and polynomial regression models to model the relationship between design variables and the objective variable. A significant emphasis is placed on understanding the environmental conditions impacting the board’s performance, particularly the role of humidity. Through rigorous testing and data analysis, the research seeks to develop a robust prediction model, with parameters including drop height, static stress, and cushion thickness. This study can be especially important for stakeholders who want to perform quality prediction of packages by considering shock absorption properties during the design phase.

Other design-related studies are explored in the next subsection.

Table 2. Summary of the papers presented in the subsection “Design vs. Manufacturing and Distribution”.

Ref.	Authors (Year)	Novelty	Objectives (Category)	Design Variables	Lifecycle
[69]	Cho and Um (2007)	Changing operation conditions in manufacture to improve physical properties of the product	Mechanical Properties	Operational conditions	M&D
[70]	Tian et al. (2021)	Cutting methodology to reduce cutting waste	Cost	Raw material	M&D
[71]	Kubera and Tyczyński (2009)	Fitting packages in a corrugated box	Volume	Production process and storage	M&D
[72]	Mahakalkar et al. (2015)	Use of Buckling Pis for an application in the production process	N/A	Buckling Pis	M&D
[73]	Musielak (2014)	Usage of ANN for minimization of electricity consumption for a corrugator	Cost	Corrugated board plant modules, corrugator speed and flute type	M&D
[74]	Karabacakoğlu and Tezakıl (2023)	Added energy consumption as an objective beyond Chemical Oxygen Demand (COD) related to corrugated board production	Cost	Current density, time, stirring speed	M&D
[75]	Wang et al. (2021)	Improvement of the procedure for selecting a corrugated board by measuring shock absorption characteristics	Mechanical Properties	Prediction model (hyperparameters)—input: drop height; static stress; cushion thickness; output—impact strength	Design

is a summary of the new papers presented in the current subsection.

4.3. Design Optimization of the Corrugated Boards

In similar fields of design optimization, three major types of problems exist: size, shape, and topology [18,76,77]. Usually, research papers are categorized as such by looking at the design variables. In size optimization, parameters such as height, thickness, and width of the board or only related to either liners or flutes are considered design variables. In shape optimization, the shape and curvature of the liners and flute are considered to be changed and are explicitly referred to as design variables. Topology optimization, usually associated with a more complex problem, is related to changing the format of the board considerably. The latter considers not only the material design but also the number of walls. Due to the nature of the problem, the optimization problem becomes dimensionally dynamic along the iterations, so most topology optimization problems in other application domains are solved numerically using an approach with more than one step, one for each vector of design variables. A schematic representation of this common categorization, adapted to corrugated boards, is illustrated in Figure 7.

A solution for one of the possible size optimization problems was proposed by Mikami et al. [78]. It focuses on geometric variables such as the radius of curvature, glue width, flute weight, take-up factor, and the angle between the liner and the flute. The core objective of the investigation, which is carried out via experimentation, is to ascertain the combination of these variables that yields the maximum strength when subjected to edgewise compression. Although improving maximum strength is a common goal in the early stages, it is essential for the industry to detail the problem and state the design variables. This helps to understand the applicability of the obtained design and allows other researchers to compare or suggest designs based on different variables.

From the observed publications, those that deal with topology optimization problems only aim at modifying the material of the board. In total, there are only four publications related to this category. Two of them only consider the change of adhesive, with the study by Durinda and Obetko [66] being the first of them. Litovski et al. [79] presented in 2003 a detailed investigation into optimizing paper production for corrugated boards by incorporating Chemical–Mechanical Pulp (CMP). Utilizing a statistical regression model, the research establishes a nuanced correlation between variables, facilitated by a D-optimal experimental design. Central to the optimization approach is a focus on the intrinsic properties of the material, with primary performance metrics being breaking length, burst index, and flat crunch resistance index. The study’s methodologies center around adjusting the amount of chemical–mechanical pulp and manipulating the freeness level of the fiber material to achieve optimal paper characteristics. The industry can benefit from the resulting region of interest (30 to 60% of CMP and between 20 to 40 degrees Schopper–Riegler) in order to make a more informed decision about the material parameterization to apply.

Another study focusing on material design was published by Ihwah et al. [80]. It delves into the intricacies of raw material proportion optimization in the creation of handicraft paper, uniquely sourced from Pinang fiber and repurposed corrugated board. Through the adept application of a surrogate model, particularly the RSM, the study seeks to find the optimal proportion of these materials to produce superior paper quality. Key performance indicators in this endeavor are gram weight, tensile strength, tear strength, and water absorbency, all of which are intrinsically linked to the proportion of the raw materials utilized in the paper-making process. This approach helps stakeholders measure the potential impact of corrugated board recycling and consider its limitations.

On the other hand, Park et al. [81] explored different types of corrugating adhesives and their impact on the physical and strength properties of the corrugated board. This research would be useful to improve the quality of corrugated boards used for archival purposes. This is achieved by comparing the properties of the developed corrugated board with imported ones and by evaluating the adhesion strength under various conditions of storage and curing temperatures. Changing the types of corrugating adhesives experimentally is done as a way to increase the strength of the structure. Therefore, it is also considered a solution for a material design optimization problem.

Despite not belonging to any of the referred categories, there is also an optimization work published by Song et al. [82] related to the optimum design of a finite element in the context of FEM and the design of corrugated boards. The new finite element model was developed by adopting an orthotropic material constitutive model to capture the information of the peak load, looking at considering the non-linear properties of the board.

Table 3. Summary of the papers presented in the subsection “Design Optimization of the corrugated boards”.

Ref.	Authors (Year)	Novelty	Objectives (Category)	Design Variables	Design Opt. (Category)
[78]	Mikami et al. (2005)	Maximum strength by considering several design parameters	Mechanical Properties	Geometric values (radius of curvature, glue width, flute weight, take-up factor, angle between liner and medium theta)	Size
[79]	Litovski et al. (2003)	Consideration of D-optimal experimental design for optimization	Mechanical Properties	Amount of chemical-mechanical pulp, freeness level of the fiber material	Topology (Material)
[80]	Ihwah et al. (2021)	Usage of the response surface methodology for material selection by optimizing the proportion of raw material	Mechanical Properties	Proportion of raw material	Topology (Material)
[81]	Park et al. (2009)	Development of a suitable design for corrugated board for archival quality containers	N/A	Types of corrugating adhesives used and the conditions of storage and curing temperatures	Topology (Material)
[82]	Song et al. (2017)	FEM element optimization for modelling corrugated boards	N/A	N/A	N/A

summarizes the papers in this subsection, with the final column indicating the subcategory of design optimization for each paper.

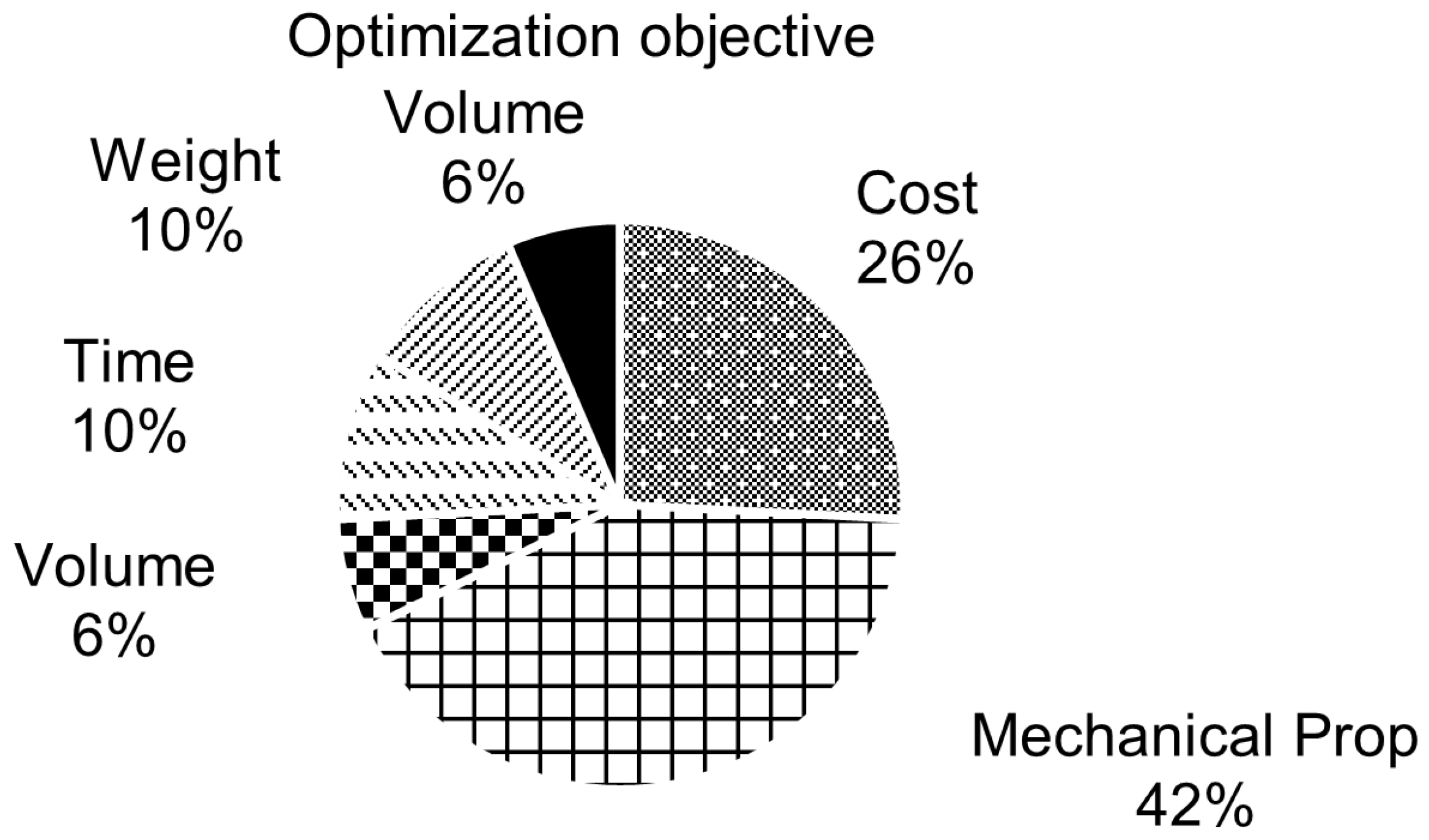
4.4. Optimization Objectives

The current review also categorizes publications according to the objective. There are five categories that are considered: improvement of the mechanical properties, minimization of the weight, reduction of production cost, minimization of the volume of the container, and minimization of the production and operational time. An example for each of them is given.

Multiple works focused on increasing the mechanical properties related to corrugated boards, but Neidoni et al. [83] have also developed their experimental approach to optimize corrugated boxes in the presence of perforations, which is a specific aspect that was not studied before. The goal is to increase the compressive strength of the box, in line with the research path already lined in earlier stages. Despite the novel presentation of the problem, whose solution can become promising in the future, the greatest limitation of the given solution is related to the lack of numerical representation of the problem and further numerical optimization.

A comprehensive examination of the production logistics system specific to corrugated box manufacturing was presented by Li et al. [84], which may be of particular interest to production and project managers aiming to reduce operational time. The study applies a blend of theoretical methods and advanced optimization technologies to refine the production logistics of corrugated boxes. Key methodologies employed include a weighted checklist—created by aggregating the product of importance coefficients with solution marks—and techniques to reduce the mass transfer of honeycomb panels and frequent handling of semi-manufacturers.

In another perspective, Yuan et al. [85] aimed at achieving minimization of the weight of the structure. They developed a numerical simulation approach and a mathematical model to optimize the structure size of the UV-type corrugated board. The optimization approach involves evaluating the structure by direct use of ANSYS software for mechanical analysis, i.e., without any surrogate model. However, a gradual transition to a simplified model of the 11 U-shaped flute-shape corrugated board from the V-shaped set of material properties is approached. A SHELL181 element is used for the Finite Element Method (FEM) [86]. This is one of the few studies that consider ANSYS for simulation, followed by manual iterations for optimization. Despite of the novel advances, numerical optimization approaches and considerations of surrogate models are still needed.

In the realm of optimal packaging, Kalyankar et al. [87] propose the minimization of the volume of the package, providing an in-depth exploration into the optimization and design of corrugated sheet box sizes specifically tailored for an industrial component. With the aid of Finite Element Analysis, the research primarily focuses on the minimization of box size and clearance, aiming to fine-tune the packaging to its most compact and efficient dimensions. The study underscores key design parameters like compression, tensile load, and buckling considerations.

Similarly to the previously mentioned works with respect to waste minimization, Mrówczyński et al. [5,88] also aimed to improve the sustainable management of natural resources while searching for the optimal design. The critical load of the packaging walls, ECT, and BCT, which are also a function of the design parameters of the board, are optimized in the context of a five-layer corrugated board. It uses a sensitivity analysis using random initialization of optimization hyperparameters to understand the influence of each design variable. Despite the aforementioned approach not being an optimization methodology by itself, it may be useful to reduce the number of evaluations necessary to achieve an optimized solution. The grammage of the corrugated board layers is maintained during the optimization process. The solution presented can serve as a reference for manufacturers and researchers interested in minimizing material waste on corrugated boards.

Figure 8 is another pie chart, this time with respect to the characterization present in the current subsection. It is possible to observe that most of the research papers are related to the improvement of the mechanical properties of the structure (p<0.005, binomial test).

Table 4. Summary of the papers presented in the subsection “Optimization objectives”.

Ref.	Authors (Year)	Novelty	Objectives (Category)	Design Variables	Lifecycle
[83]	Neidoni et al. (2009)	Experimental approach to optimize perforations	Mechanical Properties	Type, dimensions, position of the perforations on the corrugated board boxes	Design
[84]	Li et al. (2012)	Minimize the mass transfer of honeycomb panels and the frequent handling of semi manufacturers	Time	Workshop layout by using parameters	M&D
[85]	Yuan et al. (2014)	Use of numerical simulation and mathematical modeling to optimize the structure size of UV-type corrugated board	Weight	Dimensions, structural parameters of the corrugated board	Design
[87]	Kalyankar et al. (2015)	Minimization of box size and clearance by using FEM	Volume	Box design parameters	Design
[5,88]	Mrówczyński et al. (2022)	Sensitivity analysis for the optimal selection of the components of a five-layer corrugated board was studied	Cost	Edge crush resistance, critical load of the packaging walls, and packaging load capacity	Design

is a summary of the papers presented in this subsection.

4.5. Numerical Optimization

Until now, all the mentioned papers were supported by expert knowledge, the classical design of experiments, heuristic optimization, or even via trial and error. However, none of them were subjected to a numerical optimization procedure. Moreover, despite some of the modern works using surrogate models in order to computationally simplify the evaluation function, which also involves the use of numerical optimization, those are not used further in the context of numerical optimization to solve the minimization problem whose associated surrogate model poses for simplification.

The importance of including numerical optimization against manual iterations is related to better confidence in the optimal solution and less dependence on expert knowledge. Most of the time, employing numerical optimization can be of utmost interest where relying on expert knowledge can sometimes introduce biases or where solutions obtained through numerical methods can be consistently reproduced. Moreover, as the complexity of the problem grows, the number of parameters and variables might increase exponentially, making manual iteration infeasible. Numerical optimization can handle large datasets and high-dimensional problems more efficiently.

However, in the context of corrugated boards, there are only five publications, also published since the 2000s, that consider a numerical optimization procedure. Those are detailed in the following paragraphs.

In 2006, the first numerical algorithms were applied in the context of corrugated boards. Rodríguez and Vecchietti [89] aimed at targeting the pervasive cutting stock problem faced by the industry. This problem, known for its discrete, combinatory, and non-convex nature, poses a significant challenge. The research explores the capabilities of Mixed Integer Non-Linear Programming (MINLP) and compares it with the utilization of a surrogate model and Mixed Integer Linear Programming (MILP). The overarching aim is to identify the most efficient cutting patterns that yield minimum waste, ensuring the best use of primary stock material.

Daxner et al. [90] used a numerical optimization method to improve the design of a corrugated board, aiming at minimizing the weight of the board by considering normal density properties. In 2007, this publication became the first to consider minimizing the weight of such structures. Evaluation of the constraints and weight is done by using ANSYS. The optimization approach involves the use of finite element unit cell buckling analyses and a semi-analytical method. The latter consists of an analytical expression that is firstly derived from simplifications to calculate the strength of the structure and a numerical optimization approach that uses “NMinimze” function from Mathematica software to solve such optimization problems. Leveraging an FE model to predict buckling more accurately is also done by using “fminbound” and “fmin_cobyla” from the SciPy library of Python to solve the unit cell buckling optimization problem.

Two years later, aiming at reducing the overall cost of the manufacturing process of production of corrugated boxes, Protalinskii and Kokuev [91] explored a dynamic programming method where a set of manufacturing controls are optimized with respect to the coolant and the amount of heat carrier. In such a numerical optimization approach, local descent algorithms are used with initial random choice, where the direction of the search for optimal control is taken from the end of the process. A penalty is proposed to handle violated constraints related to existing manufacturing regulations.

In 2011, aiming at proposing the extension of the optimization approach proposed by Daxner et al. [90], another study [92] was published by the same authors, whose resulting optimal solution led to an achieved reduction of 18.7% of the weight. The results from both papers can serve as a reference for further analysis from industry and research perspectives, particularly for those interested in minimizing board weight and in numerical optimization.

Already in 2022, Zhang et al. [93] developed a multi-objective strategy that is based on scalarization in order to optimize the design of sinusoidal corrugated sheet-filled sandwich tubes. The weights for scalarization were obtained via sensitivity analysis. This approach calculates the sensitivity of each factor to the objective function at different levels to obtain the optimal factor level combination scheme. Objectives are represented by different response variables, namely Specific Energy Absorption (SEA), Peak Crushing Force (PCF), Mean Crushing Force (MCF), and Coupling Force Efficiency (CFE). The goal is to maximize SEA, MCF, and CFE while minimizing PCF. Despite the work can give some hints to being used in the research of corrugated board, the materials used may have different mechanical properties, which may give very different results. Also, it considers tubes instead of boxes, which may limit the application of the findings.

In that same year, Kalita et al. [94] undertook a meticulous numerical analysis using Response Surface Methodology (RSM) and Genetic Algorithm (GA) to optimize the design of corrugated packages specifically tailored for the apple industry. Recognizing that the dimensions of these packages are constrained by pallet sizes, the research concentrates on minimizing package deformation. The key variables under consideration include the package’s length, width, height, size of length stiffener, and size of width stiffener. The study also gives due consideration to the guidelines stipulated by the Bureau of Indian Standards (BIS), ensuring that the optimized packages meet the requisite minimum safety requirements. The way standards and requirements are handled here can serve as a reference for the industry and researchers investigating numerical optimization.

Table 5. Summary of the papers presented in the subsection “Numerical Optimization”.

Ref.	Authors (Year)	Numerical Algorithm Used	Objectives (Category)	Design Variables	Lifecycle
[89]	Rodríguez and Vecchietti (2006)	MINLP and MILP	Cost	Cutting patterns	M&D
[90]	Daxner et al. (2007)	COBYLA and Brent’s method	Weight	Width of the board, the height of the unit cell, and the thickness of the liners and fluting.	Design
[91]	Protalinskii and Kokuev (2009)	Local descent; a penalty is proposed to handle violated constraints	Cost	Dimensions, structural parameters of the corrugated board	M&D
[92]	Daxner et al. (2011)	COBYLA and Brent’s method	Weight	Width of the board, the height of the unit cell, and the thickness of the liners and fluting	Design
[93]	Zhang et al. (2022)	Finite Differences	Mechanical Properties	Sine wave parameters amplitude and the period, thicknesses of the inner, outer and sine layers	Design
[94]	Kalita et al. (2022)	Genetic Algorithm (and RSM as a surrogate model)	Mechanical Properties	Length, width, height, size of length stiffener, size of width stiffener	Design

summarizes the numerical algorithms used in the papers of this subsection.

5. Discussion of the Results Found

5.1. What Are the Main Common Findings throughout the Literature?

The evolution of research on the optimization of corrugated boards over time reveals a clear demarcation between early works and those published in the 21st century. Initially, optimization approaches were primarily rooted in experimentation, expert knowledge, and the traditional design of experiments. These foundational methods provided essential insights into the mechanical and functional aspects of corrugated boards. However, once transitioned into the 21st century, there was a noticeable shift toward adopting numerical optimization procedures, which became more prevalent in recent publications. These modern techniques, often complemented by software platforms, are more data-driven. Nevertheless, there are still modern works relying on experimental studies to perform optimization.

A distinctive trend in the optimization literature of corrugated boards is the adaptation and integration of novel findings from other scientific and engineering domains. Concepts like Multidisciplinary Design Optimization (MDO), which originated in 1965 [95], found their way into the corrugated board research field with the publication of Langaard [61], reshaping traditional methodologies. Similarly, the emergence and rising significance of surrogate models and FEM since the early 2000s have played an influential role in shaping modern research trajectories, with the works of, for instance, [72,90]. These external influences have undeniably enriched the depth and breadth of optimization strategies applied to corrugated boards.

While the methods and tools adopted in the research have evolved, it is notable that the problems under investigation have constantly shifted as well. For instance, while early-stage papers address the improvement of mechanical properties [61], weight and cost started to be more evident objectives since 2007 [70,90]. This dynamic nature suggests that as solutions were found for older challenges, new issues emerged, necessitating novel approaches. Even in later publications, the problems tackled were not mere reiterations of past challenges but rather fresh perspectives or deeper dives into previously uncharted territories of corrugated board optimization.

The improvement of the mechanical properties of corrugated boards stands out among other objectives. From addressing basic mechanical concerns to intricate perforation optimization, there has been a continuous pursuit to enhance the structural integrity and load-bearing capacities of these boards. This focus is indicative of the core importance of strength and resilience in the corrugated board industry.

Furthermore, with environmental issues gaining prominence worldwide, researchers have turned their attention towards optimizing corrugated boards in a sustainable way. This involves managing resources responsibly, reducing waste, and making efficient use of raw materials. The focus on sustainability and optimization is a recurring theme in the field, demonstrating the industry’s dedication to ecological responsibility.

Several publications have focused on improving the production and distribution of corrugated boards. They aim to streamline logistics and reduce operational time to boost efficiency in the manufacturing and supply chain sectors. The industry’s primary goal is to meet consumer demands promptly while maintaining high-quality standards.

Another recurring objective throughout the literature is the minimization of the weight and volume of corrugated boards and packages. The emphasis here aligns with the industry’s need to produce lightweight, compact, yet robust packaging solutions, ensuring cost-effectiveness and ease of transport.

Moreover, the integration of software platforms like ANSYS in the research process marked a significant leap in the optimization techniques used. The ability to simulate, model, and iterate designs virtually opened doors to more nuanced and intricate optimization avenues. This shift also reduced dependency on exhaustive physical experiments, making the research process more efficient and expansive.

Perhaps the most interesting fact is that despite the advancements in technology and methodologies, numerical optimization procedures made a relatively late entry into the corrugated board research scene. With only a handful of publications since 2003 adopting these advanced procedures, it points to either the complexity of integrating these methods or a gradual acknowledgment of their potential benefits.

Lastly, the literature on corrugated board optimization is a testament to the interdisciplinary nature of research. Borrowing methodologies from fields like optimization and engineering, the research on corrugated boards has grown to be a confluence of varied techniques, aiming to achieve optimal design and functionality. This collaborative approach ensures that the field remains dynamic, evolving, and ever-relevant.

5.2. The Research Questions

RQ1. What is the current landscape of optimization methodologies in the corrugated board industry, and how do these methodologies contribute to the economic and environmental outcomes?

The current landscape of optimization methodologies in the corrugated board industry is diverse and increasingly sophisticated. While the classical design of experiments and expert knowledge-driven approaches dominated earlier works, the 21st century has seen an upsurge in computational methods, like FEM, surrogate models, and numerical algorithms. The objectives of these methodologies range from improving mechanical properties and reducing weight, cost, and volume to enhancing production efficiency. Economically, the methodologies drive cost savings by optimizing production logistics, minimizing waste, and refining designs to achieve more with less material. Environmentally, streamlined designs lead to reduced material usage and waste generation, which contributes to a smaller carbon footprint and reduced environmental degradation. An optimized production process, which decreases operational times and wastage, also indirectly promotes energy conservation.

Nevertheless, due to the complexity of the topic, there is no predominant optimization methodology. As the industry grapples with diverse requirements ranging from structural integrity and cost-effectiveness to environmental sustainability, it continually seeks to integrate and adapt methodologies that best fit the problem at hand. Consequently, a holistic, adaptable approach, rather than a singular dominant method, seems to be the industry’s response to the intricate optimization demands.

RQ2. How have these methodologies evolved, and what are the key drivers behind these changes?

Historically, the optimization methodologies for corrugated boards were simpler, more experimental, and often relied on trial and error. However, with the dawn of the 21st century, there has been a clear shift towards more advanced, data-driven approaches. This evolution can be attributed to several key drivers. One of them is related to the rise of computational tools, software like ANSYS, and capabilities such as FEM, which have enabled detailed simulations and analyses that were not previously feasible. Another explanation is that the corrugated board industry has borrowed insights and techniques from other fields. For example, Multi-Disciplinary Optimization (MDO) methodologies, surrogate models, and other advanced optimization techniques that originated in diverse domains have found their way into corrugated board optimization. Lastly, the growing emphasis on sustainability and cost-effectiveness has compelled industries, including corrugated board manufacturers, to seek optimization methods that minimize waste, reduce material use, and streamline production processes.

RQ3. What current state-of-the-art limitations may lead to potential trends that can be anticipated in optimizing corrugated boards?

One primary observation is the industry’s over-reliance on FEM and a narrow focus on size and material optimization. This indicates a potential shift towards embracing a broader spectrum of optimization approaches in the near future, encompassing not just size and material optimization but also shape and topology optimization. Additionally, there is an evident under-representation of environmental considerations in current practices, which, given global sustainability movements, suggests a likely trajectory toward more eco-centric optimization methods.

Furthermore, the current methodologies often operate in silos, narrowly focusing on specific optimization goals without addressing the holistic picture. The future might see a growing interest in multi-objective optimization, considering not just mechanical properties or weight reduction but also factors like recyclability, production efficiency, and risk management. This holistic approach would aim to achieve a balanced harmony between economic benefits, performance efficiency, and sustainability, representing a more comprehensive optimization strategy for the corrugated board industry.

5.3. The Gaps—And Research Directions

Although there have been recent studies published, the authors have identified several limitations in the current literature:

• It is clear that researchers have yet to fully explore the potential of corrugated boards in terms of weight reduction and safety enhancement. Despite a handful of studies on the subject, there appears to be a lack of consensus and focus on design optimization. Highlighting the benefits of corrugated boards could prove invaluable in establishing them as a reliable alternative to other materials in various structures and physical products. Therefore, it is imperative that more research is conducted in this area to realize the potential of corrugated boards fully. Future research directions: to establish new optimization strategies to reduce corrugated boards’ weight and enhance the design safety.
• There has been a significant amount of research conducted on weight minimization through different optimization approaches in applications such as composite structures [18]. These approaches include size, shape, and topology optimization. However, studies related to corrugated boards only focus on size and material optimization, and shape and topology optimization are not explored. Future research directions: to establish and tackle shape and topology optimization problems.
• The No Free Lunch Theorem [39] underscores the importance of a diversified optimization approach. Yet, the trend in corrugated board optimization research often showcases a heavy leaning toward expert-driven knowledge and a singular optimization strategy. This narrow approach potentially overlooks innovative solutions that a multifaceted, adaptive strategy could yield. Future research directions: to explore applying other optimization approaches by changing the algorithm or seeking surrogate models.
• While the FEM has proven invaluable in many engineering applications, its dominance in the realm of corrugated board weight minimization research is a double-edged sword. Sole reliance on FEM implies that the accuracy and reliability of optimization solutions are contingent upon the precision of the model. Exploring alternative or supplementary modeling techniques could enhance the robustness of the findings and their applicability in real-world scenarios. Future research directions: to explore the robustness of the simulation models and optimized solutions by exploring techniques in robust optimization.
• A discernible gap in the literature is the lack of emphasis on identifying future research directions. Such omissions might stifle the continuity and progression of knowledge in the field. Addressing limitations and articulating future research avenues not only fosters academic rigor but also galvanizes further exploration, ensuring the subject remains dynamic. Future research directions: to describe guidelines for future improvements.
• Given the complexity of real-world applications, it is often imperative to juggle multiple design objectives simultaneously. The noticeable absence of multi-objective design optimization in the literature suggests a missed opportunity. Incorporating such methodologies, especially in the context of customized solutions and robust optimization, could elevate the practical utility and adaptability of corrugated board designs. Future research directions: to more accurately apply and discuss such application of multi-objective optimization techniques.
• Factors such as environmental conditions, fire risks, and manufacturing defects profoundly influence the efficacy of any material in practical applications. The oversight of these critical variables in many studies indicates a somewhat myopic research perspective. Addressing these overlooked factors could not only bridge the prevailing research gap but also enrich the holistic understanding of corrugated board optimization in diverse conditions. Future research directions: to address new objectives that can also improve the sustainability related to the corrugated boards.
• One of the overarching gaps is the lack of a consolidated research framework. Such a framework would encompass standardized problems, methodologies, and assessment metrics, promoting consistency across studies. By working within a unified paradigm, researchers can build upon previous findings more effectively, propelling the field forward with cumulative knowledge. Future research directions: to enhance collaboration between the scientific community working in the field of the optimization of corrugated boards in order to work on standard problems instead of specific cases.
• Lastly, while theoretical advancements are crucial, there is an impending need to bridge the gap between theoretical research and its practical implications. Translational research, which focuses on turning academic findings into tangible, real-world applications, is vital. Such an approach would ensure that innovations in corrugated board optimization find their rightful place in industries and commercial products, maximizing their societal impact. Future research directions: to manage and monitor problems occurring from the application of the optimized solution or potential changes occurring in the objective function over time.

To summarize, there are several areas of research that need to be explored in the optimization of corrugated boards. These gaps present challenges as well as opportunities for groundbreaking advancements. By addressing these gaps through diverse optimization approaches and interdisciplinary collaborations, researchers can enrich academic knowledge and revolutionize practical applications. It is crucial for researchers, practitioners, and industries to work together and take advantage of these opportunities to ensure that corrugated board optimization reaches its full potential in both theory and practice.

6. Conclusions

Assessing the latest advancements in optimization for corrugated boards, this study represents the first review of its kind based on the available literature. Despite the existence of corrugated boards since 1871, optimization methods have only been employed in recent years, since 1968. The study suggests that the introduction of MDO, the available computational power, and the novelty of optimization algorithms were key drivers in pioneering advances in the MDO field of corrugated boards.

However, there are still too many manual iterations in optimization methodologies. The review suggests that this is not only related to the complexity of the problems but also to the lack of evidence from other works and experimentation. Optimization algorithms are also only employed late in corrugated boards compared to other MDO fields.

The analysis suggests that more research is required to comprehend the complete potential of corrugated boards. This can be achieved by exploring new optimization techniques, such as those based on Pareto dominance and crowding distance concepts, to address multi-objective problems. Additionally, other design methodologies should be considered, such as modifying the theoretical problem to account for uncertainties that are typically present in practical applications. The complete list of research gaps is available in Section 5.3 of this paper for further consideration by interested readers.

Future studies should use the list of research gaps as a reference for providing guidance to further research on the topic. The scientific community interested in solving sustainability problems related to corrugated boards can benefit from this list.