Vector Quantized Variational Autoencoder-Based Compressive Sampling Method for Time Series in Structural Health Monitoring
Abstract
:1. Introduction
2. Compressive Sampling and Block Compressive Sampling
3. Modified Block CS with VQ-VAE
3.1. VQ-VAE Model with a Naïve Multitask Implementation
3.2. DNN-Based CS Algorithm
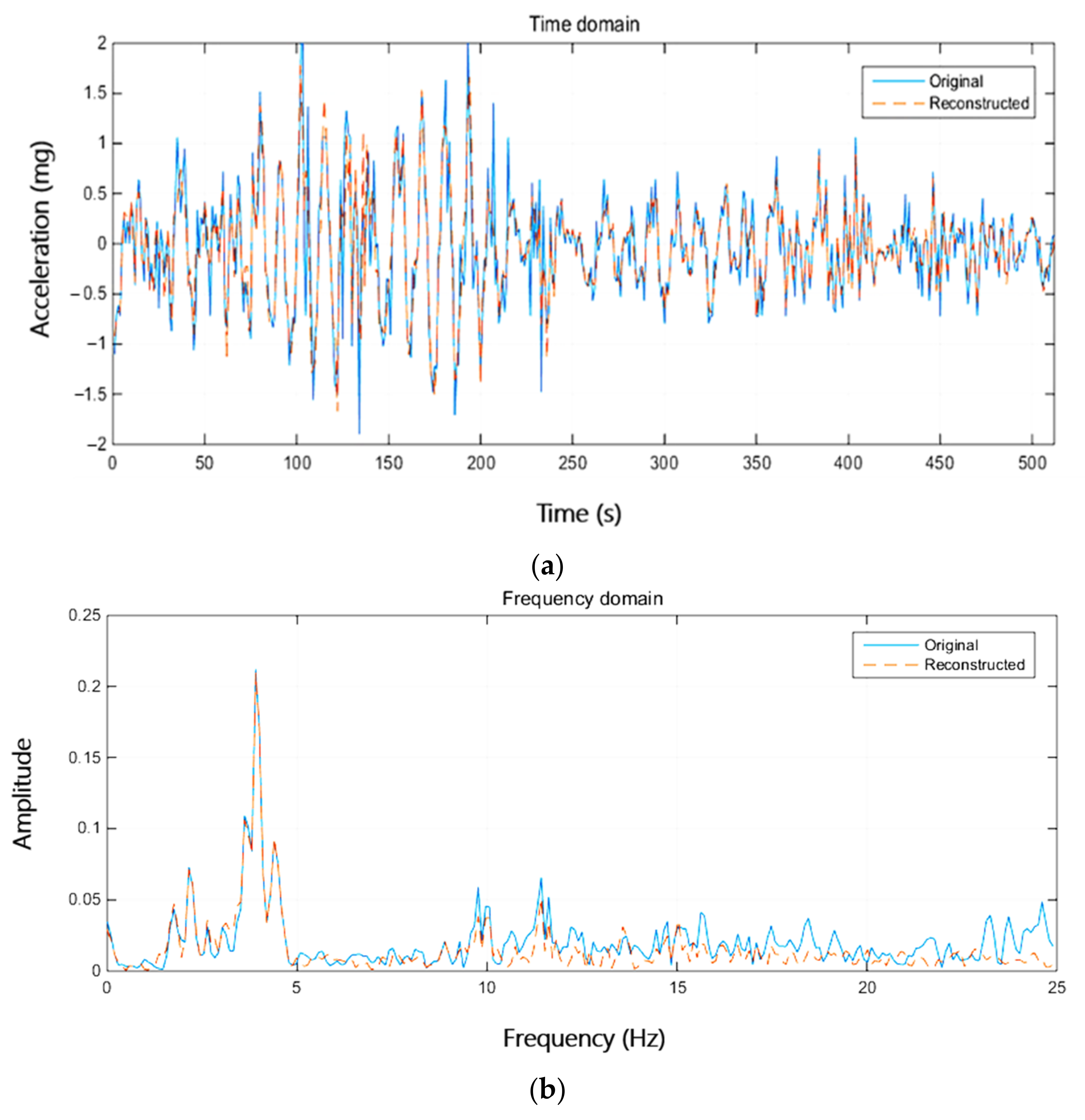
4. Results
4.1. Performance Metric
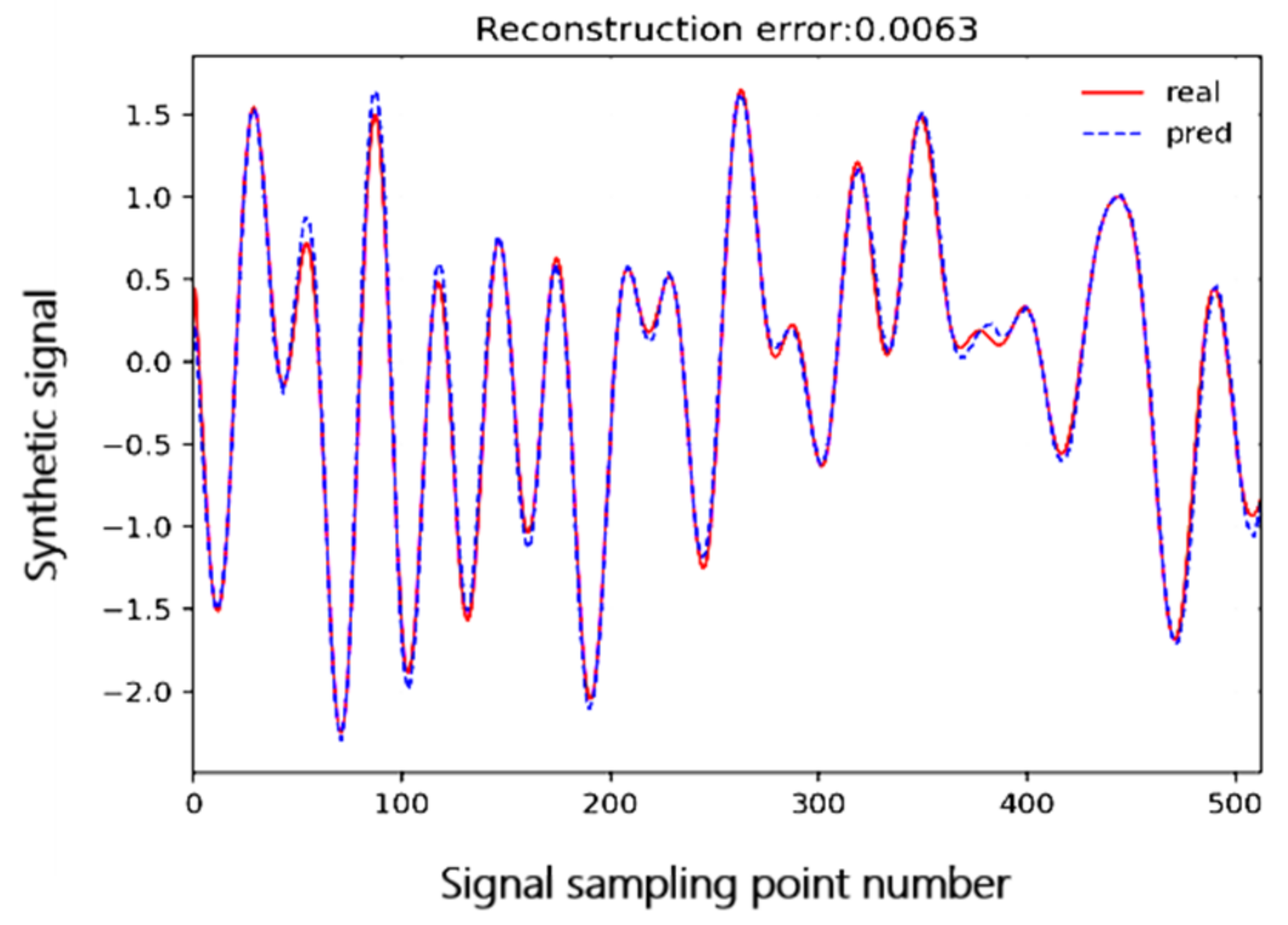
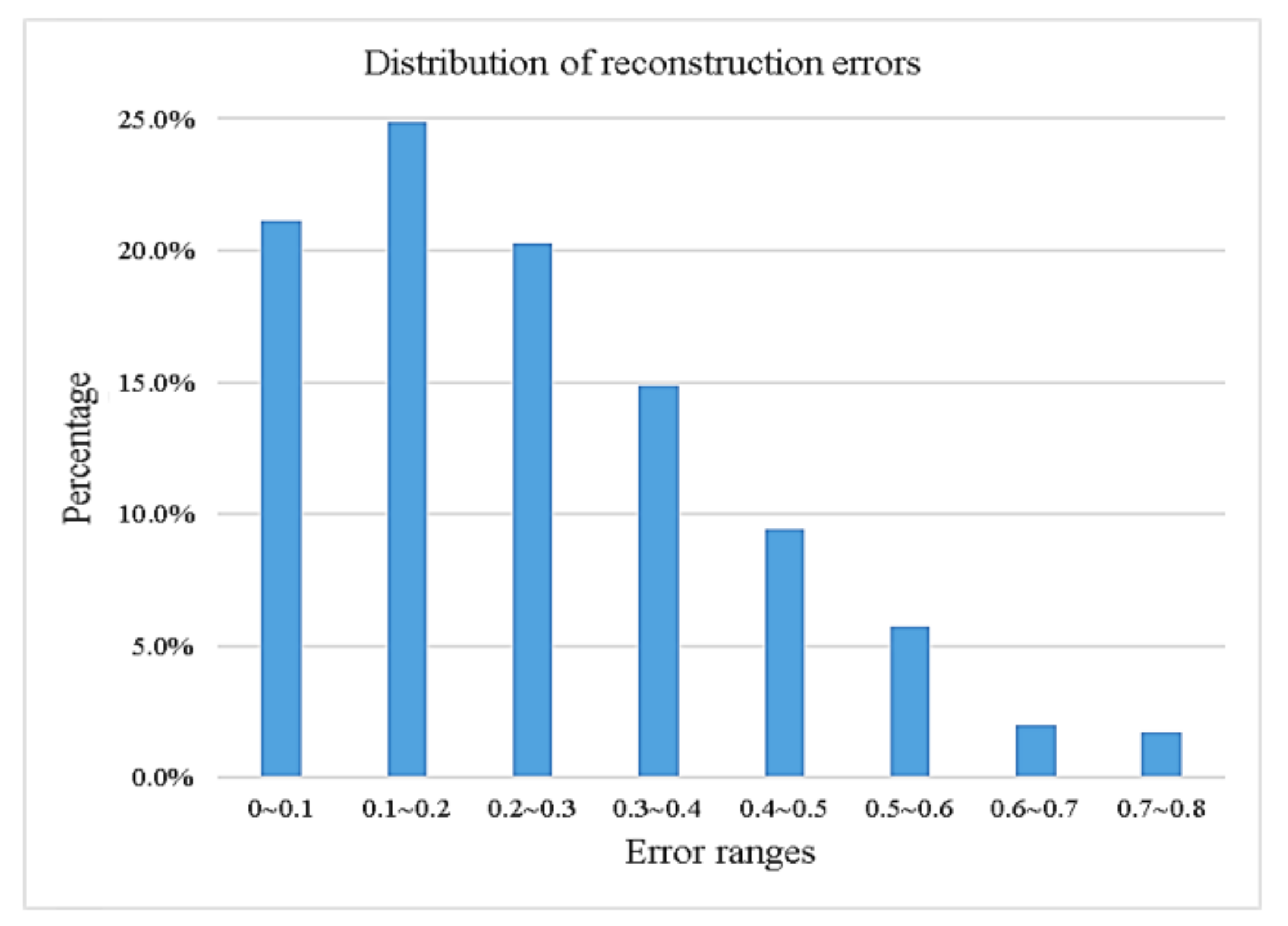
4.2. Test on Synthetic Data
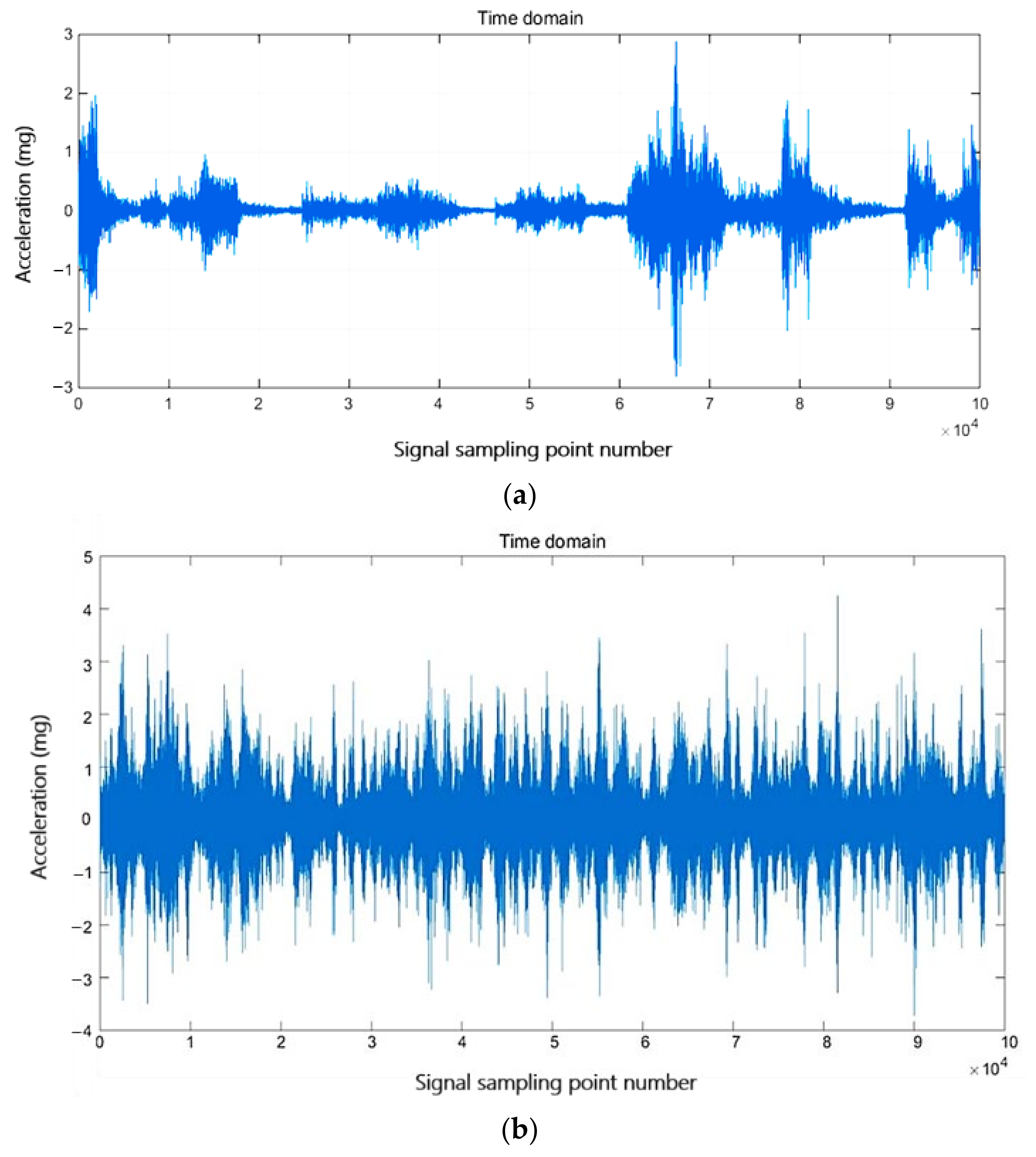
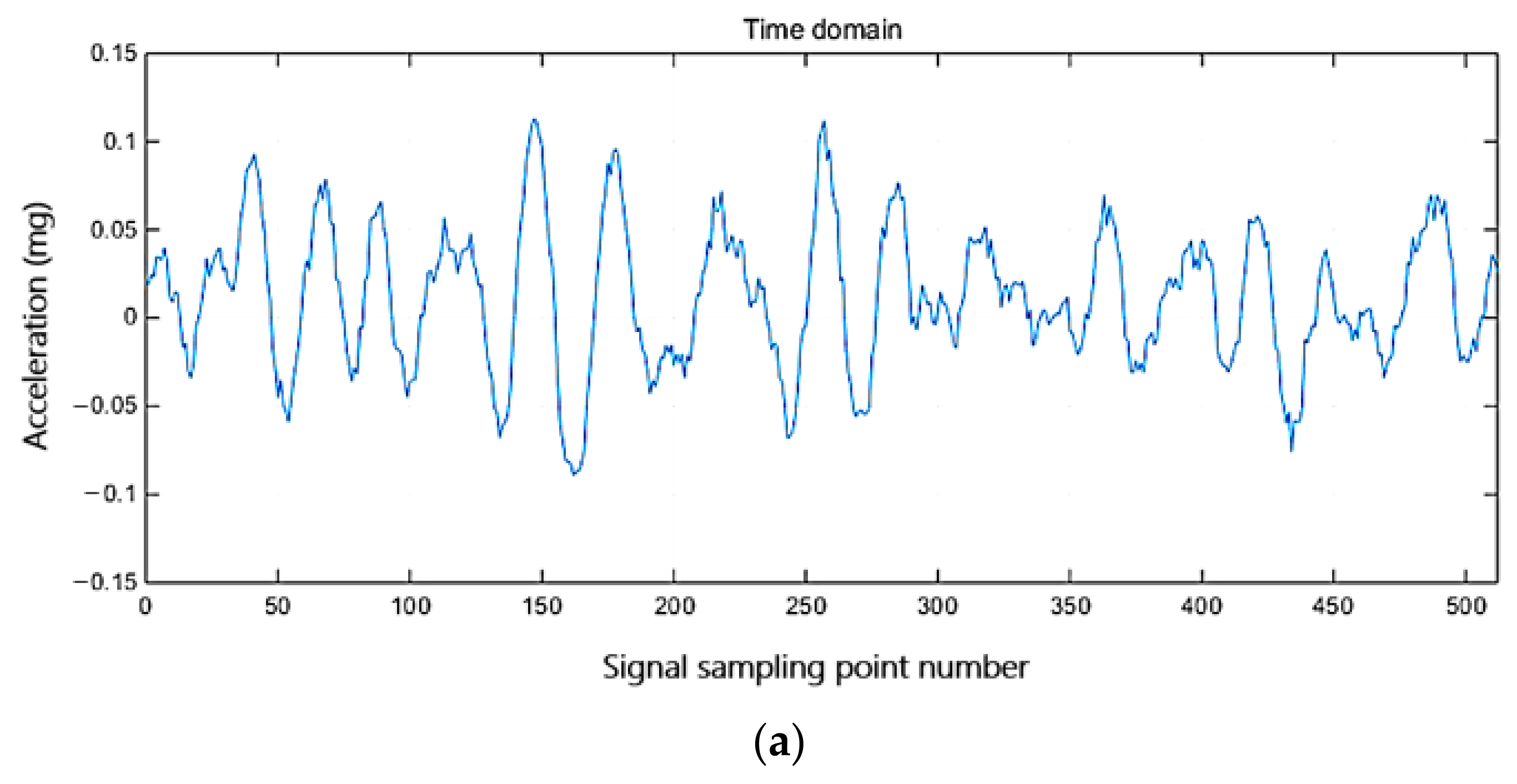
4.3. Test on Real SHM Data
4.3.1. Sensitivity to Hyperparameters in Block CS
4.3.2. Sensitivity to Noise Contamination
4.3.3. Sensitivity to Residual Blocks and Skip Connections
4.3.4. Comparison of Different CS Algorithms
5. Conclusions
- (1)
- Based on the vector quantized–variational autoencoder model with a naïve multitask paradigm (VQ-VAE-M), a one-dimensional compressive sampling signal reconstruction method is established. This method uses VQ-VAE-M to learn the data characteristics of the signal, replaces the “hard constraint” of sparsity to realize the compressive sampling signal reconstruction and so eliminate the need to select the appropriate sparse basis for the signal. VQ-VAE-M embeds and maintains one or more codebooks in the latent space to reconstruct signal. The unique bottleneck structure improves the depth of the network, and the two-tier network structure enriches the details of the reconstructed signal. In addition, the model combined with the block random Gaussian projection matrix can preserve the spatial position features between the elements in the signal as much as possible in both the compression and reconstruction stages, which greatly reduces the difficulty of decoupling in decompression and reconstruction, and ensures the quality and speed of signal reconstruction.
- (2)
- The superimposed sinusoidal synthetic signal (sparse enough in the frequency domain) and Yonghe Bridge acceleration signal (not sparse enough on both the cosine basis and wavelet basis) are used to verify the performance of the proposed method, which is compared with the other compressive sampling methods. The results show that the proposed method obviously has better performance, that is, higher reconstruction quality, faster reconstruction speed, enabling to reconstruct signal at a higher compression ratio, and no need to select the appropriate sparse basis for the signal.
- (3)
- The characteristics and advantages of the block random Gaussian projection matrix are analyzed. The matrix can preserve the spatial features between the elements in the signal, which is not only conducive to decoupling, but also to extracting the overall characteristics of adjacent signals. In addition, the reconstruction performance of this method in complex environment is also investigated. Even if the environment excitation is more complex, the method can still reconstruct the information of the low-frequency components of the signal effectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Waveform Transposed Convolution Neural Networks
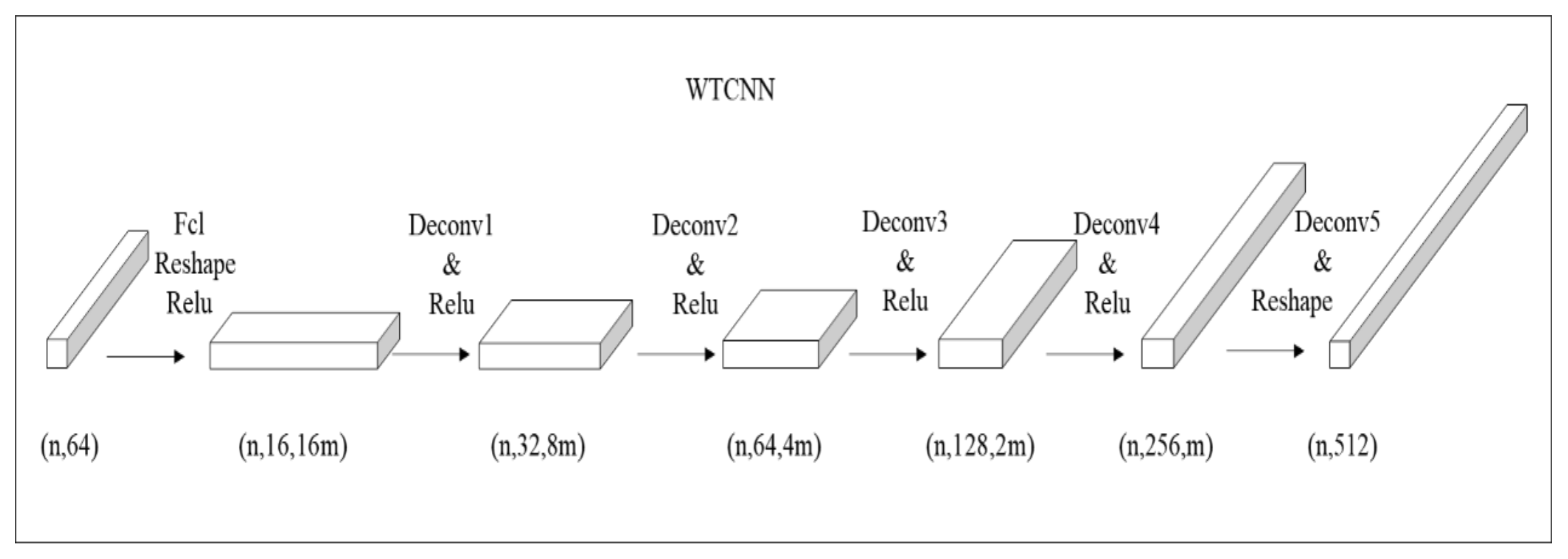
Appendix B. WaveGAN
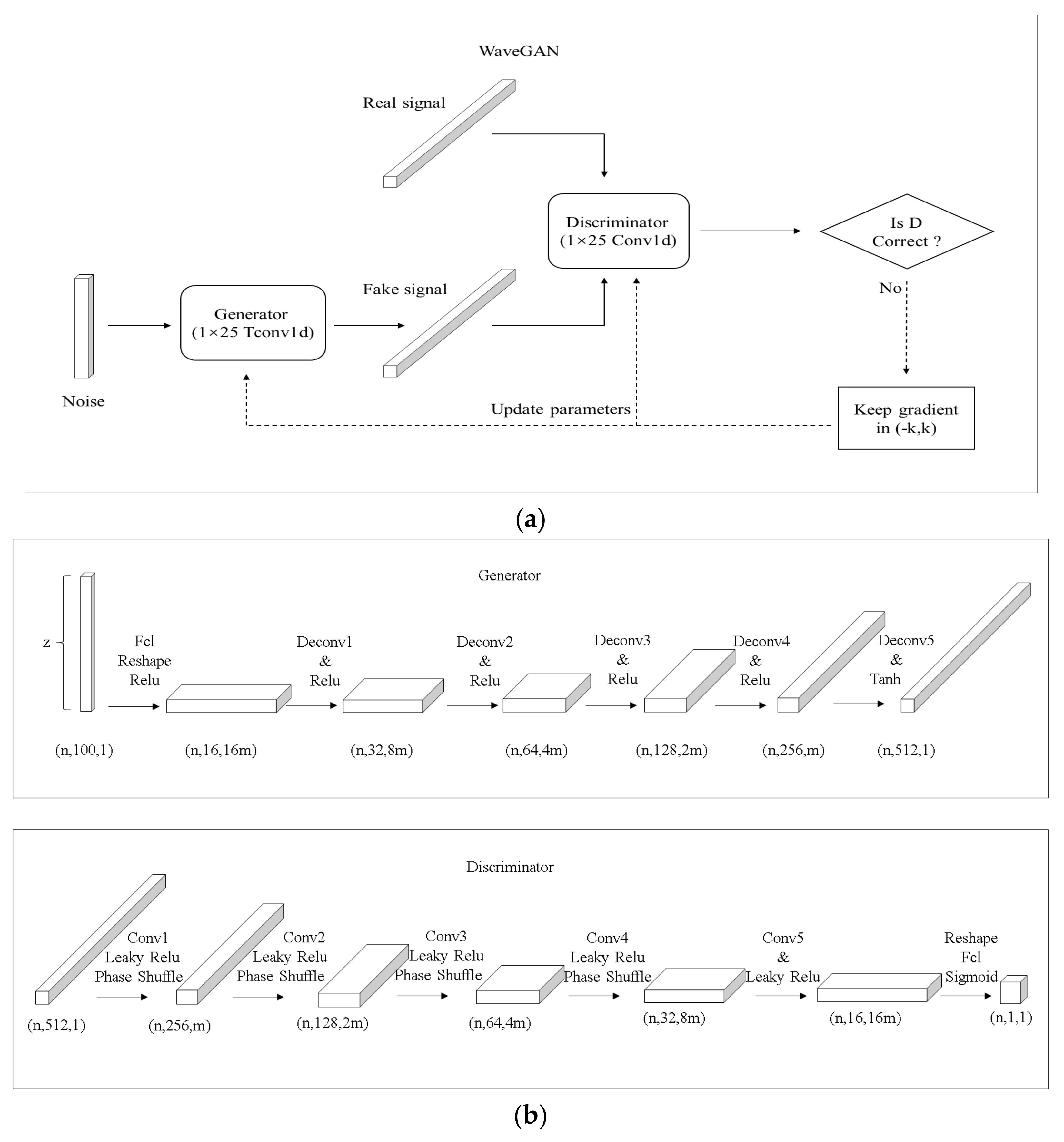
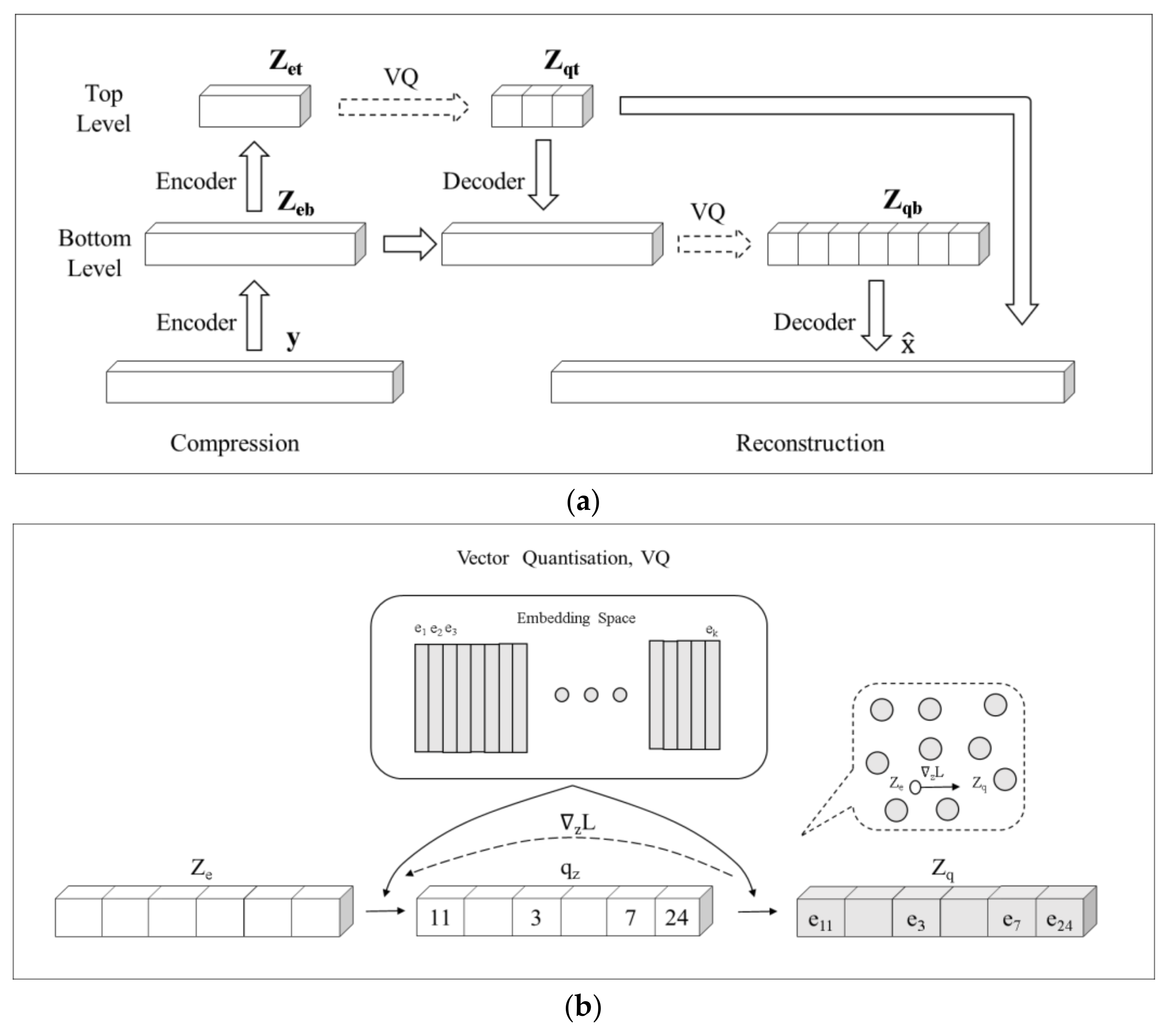
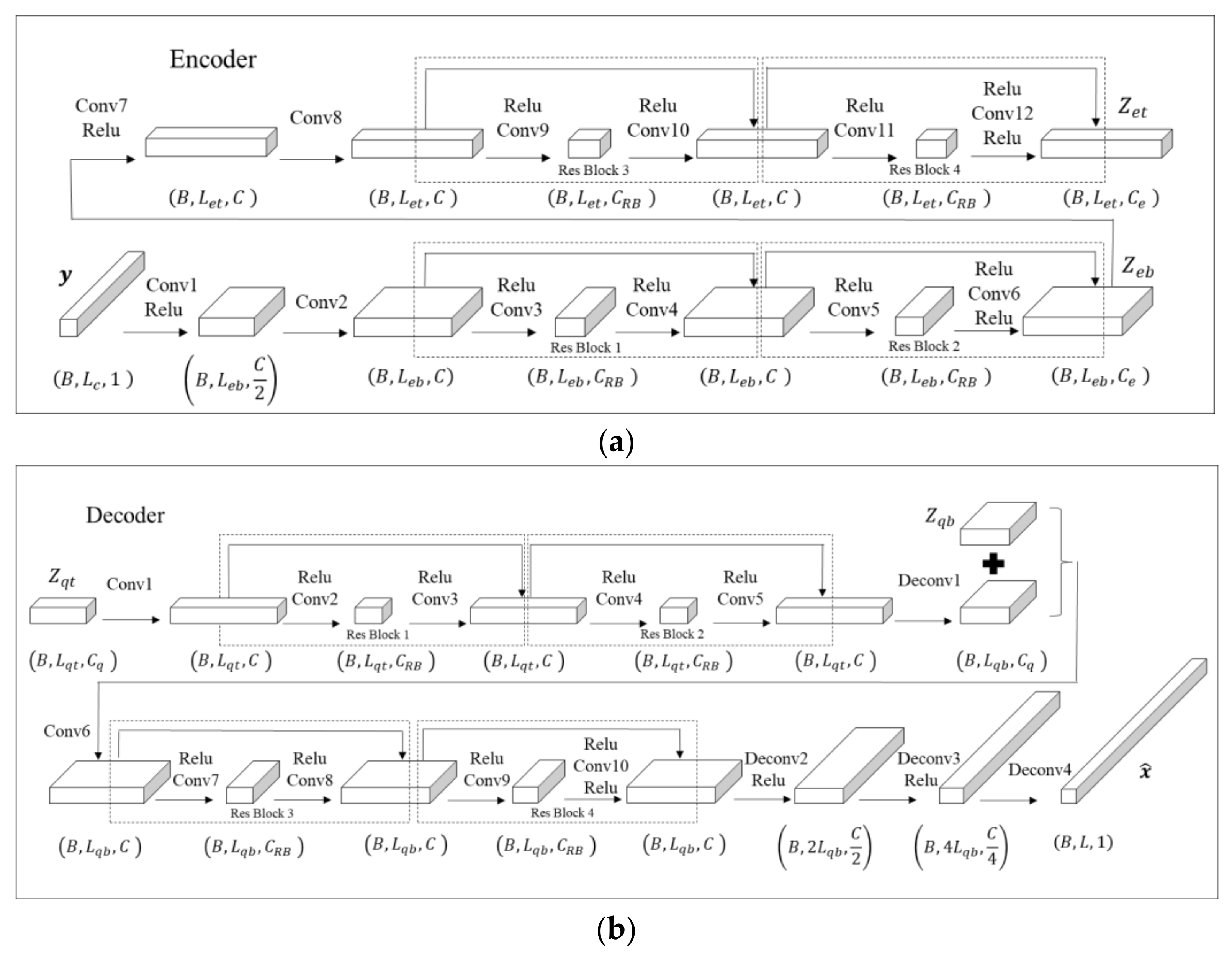
Appendix C. Vector Quantized–Variational AutoEncoder
References
- Li, Q.; Gao, J.; Beck, J.L.; Lin, C.; Li, H. Probabilistic outlier detection for robust regression modeling of structural response for high-speed railway track monitoring. Struct. Health Monit. 2023, 14759217231184584. [Google Scholar] [CrossRef]
- Song, J.; Zhang, S.; Tong, F.; Tong, F.; Yang, J.; Zeng, Z.; Yuan, S. Outlier Detection Based on Multivariable Panel Data and K-Means Clustering for Dam Deformation Monitoring Data. Adv. Civ. Eng. 2021, 2021, 3739551. [Google Scholar] [CrossRef]
- Liu, T.; Xu, H.; Ragulskis, M.; Cao, M.; Ostachowicz, W. A data-driven damage identification framework based on transmissibility function datasets and one-dimensional convolutional neural networks: Verification on a structural health monitoring benchmark structure. Sensors 2020, 20, 1059. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.A.; Dai, Y.; Ma, Z.G.; Ni, Y.Q.; Tang, J.Q.; Xu, X.Q.; Wu, Z.Y. Towards probabilistic data-driven damage detection in SHM using sparse Bayesian learning scheme. Struct. Control Health Monit. 2022, 29, e3070. [Google Scholar] [CrossRef]
- Wang, Q.A.; Wang, C.B.; Ma, Z.G.; Chen, W.; Ni, Y.Q.; Wang, C.F.; Yan, B.G.; Guan, P.X. Bayesian dynamic linear model framework for structural health monitoring data forecasting and missing data imputation during typhoon events. Struct. Health Monit. 2022, 21, 2933–2950. [Google Scholar] [CrossRef]
- Wang, Q.A.; Dai, Y.; Ma, Z.G.; Wang, J.F.; Lin, J.F.; Ni, Y.Q.; Ren, W.X.; Jiang, J.; Yang, X.; Yan, J.R. Towards high-precision data modeling of SHM measurements using an improved sparse Bayesian learning scheme with strong generalization ability. Struct. Health Monit. 2023, 14759217231170316. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, Z.; Li, S.; Li, H. Strain features and condition assessment of orthotropic steel deck cable-supported bridges subjected to vehicle loads by using dense FBG strain sensors. Smart Mater. Struct. 2017, 26, 104007. [Google Scholar] [CrossRef]
- Sony, S.; Dunphy, K.; Sadhu, A.; Capretz, M. A systematic review of convolutional neural network-based structural condition assessment techniques. Eng. Struct. 2021, 226, 111347. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, Y.; Meng, L.; Qin, Z.; Yang, F.; Li, A. Bayesian Multiple Linear Regression and New Modeling Paradigm for Structural Deflection Robust to Data Time Lag and Abnormal Signal. IEEE Sens. J. 2023, 23, 19635–19647. [Google Scholar]
- Zhang, H.; Ding, Y.; Li, A.; Qin, Z.; Chen, B.; Zhang, X. State-monitoring for abnormal vibration of bridge cables focusing on non-stationary responses: From knowledge in phenomena to digital indicators. Measurement 2022, 205, 112418. [Google Scholar]
- Wang, Q.A.; Zhang, C.; Ma, Z.G.; Ni, Y.Q. Modelling and forecasting of SHM strain measurement for a large-scale suspension bridge during typhoon events using variational heteroscedasic Gaussian process. Eng. Struct. 2021, 251, 113554. [Google Scholar] [CrossRef]
- Huang, Y.; Beck, J.L.; Wu, S.; Li, H. Bayesian compressive sensing for approximately sparse signals and application to structural health monitoring signals for data loss recovery. Probabilistic Eng. Mech. 2016, 46, 62–79. [Google Scholar] [CrossRef]
- Huang, Y.; Beck, J.L.; Wu, S.; Li, H. Robust Bayesian compressive sensing for signals in structural health monitoring. Comput. -Aided Civ. Infrastruct. Eng. 2014, 29, 160–179. [Google Scholar] [CrossRef]
- Jogin, M.; Madhulika, M.S.; Divya, G.D.; Meghana, R.K.; Apoorva, S. Feature Extraction using Convolution Neural Networks (CNN) and Deep Learning. In Proceedings of the 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 18–19 May 2018. [Google Scholar]
- Shaheen, F.; Verma, B.; Asafuddoula, M. Impact of Automatic Feature Extraction in Deep Learning Architecture. In Proceedings of the 2016 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, QLD, Australia, 1–3 December 2017. [Google Scholar]
- Hatir, M.E.; Ince, I. Lithology mapping of stone heritage via state-of-the-art computer vision. J. Build. Eng. 2021, 34, 101921. [Google Scholar] [CrossRef]
- Hatır, E.; Korkanç, M.; Schachner, A.; Ince, I. The deep learning method applied to the detection and mapping of stone deterioration in open-air sanctuaries of the Hittite period in Anatolia. J. Cult. Herit. 2021, 51, 37–49. [Google Scholar] [CrossRef]
- Bora, A.; Jalal, A.; Price, E.; Dimakis, A.G. Compressed sensing using generative models. In Proceedings of the International Conference on Machine Learning (PMLR), Amsterdam, The Netherlands, 7–10 July 2017. [Google Scholar]
- Huang, Y.; Zhang, H.Y.; Li, H.; Wu, S. Recovering compressed images for automatic crack segmentation using generative models. Mech. Syst. Signal Process. 2021, 146, 107061. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Wu, S.; Huang, Y.; Li, H. Robust multitmask compressive sampling via deep generative models for crack detection in structural health monitoring. Struct. Health Monit. 2023, 14759217231183663. [Google Scholar] [CrossRef]
- Dave, V.V.; Jalal, A.; Soltanolkotabi, M.; Price, E.; Vishwanath, S.; Dimakis, A.G. Compressed Sensing with Deep Image Prior and Learned Regularization. arXiv 2018, arXiv:1806.06438. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep Image Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Iliadis, M.; Spinoulas, L.; Katsaggelos, A.K. Deep fully-connected networks for video compressive sensing. Digit. Signal Process. 2018, 72, 9–18. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, J. Content-Aware Scalable Deep Compressed Sensing. IEEE Trans. Image Process. 2022, 31, 5412–5426. [Google Scholar] [CrossRef]
- Wang, Z.F.; Wang, Z.H.; Zeng, C.Z.; Yu, Y.; Wan, X.K. High-Quality Image Compressed Sensing and Reconstruction with Multi-scale Dilated Convolutional Neural Network. Circuits Syst. Signal Process. 2023, 42, 1593–1616. [Google Scholar] [CrossRef]
- Yang, G.; Yu, S.; Dong, H.; Slabaugh, G.; Dragotti, P.L.; Ye, X.J.; Liu, F.D.; Arridge, S.; Keegan, J.; Guo, Y.K.; et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans. Med. Imaging 2018, 37, 1310–1321. [Google Scholar] [CrossRef]
- Ni, F.T.; Zhang, J.; Noori, M.N. Deep learning for data anomaly detection and data compression of a long-span suspension bridge. Comput.-Aided Civ. Infrastruct. Eng. 2019, 35, 685–700. [Google Scholar] [CrossRef]
- Fan, G.; Li, J.; Hao, H. Lost data recovery for structural health monitoring based on convolutional neural networks. Struct. Control Health Monit. 2019, 26, e2433. [Google Scholar] [CrossRef]
- Lei, X.; Sun, L.; Xia, Y. Lost data reconstruction for structural health monitoring using deep convolutional generative adversarial networks. Struct. Health Monit. 2020, 20, 2069–2087. [Google Scholar] [CrossRef]
- Chai, X.L.; Fu, J.Y.; Gan, Z.; Lu, Y.; Zhang, Y.S. An image encryption scheme based on multi-objective optimization and block compressed sensing. Nonlinear Dyn. 2022, 108, 2671–2704. [Google Scholar] [CrossRef]
- Mousavi, A.; Baraniuk, R.G. Learning to invert: Signal recovery via deep convolutional networks. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Yao, H.T.; Dai, F.; Zhang, D.M.; Zhang, Y.D.; Tian, Q.; Xu, C.S. DR2-Net: Deep Residual Reconstruction Network for Image Compressive Sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. ReconNet non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Donahue, C.; McAuley, J.; Puckette, M. Adversarial Audio Synthesis. arXiv 2018, arXiv:1802.04208. [Google Scholar]
- Oord, A.v.d.; Vinyals, O.; Kavukcuoglu, K. Neural Discrete Representation Learning. In Proceedings of the Conference and Workshop on Neural Information Processing Systems (NeurIPS), Long Beach Convention Center, Long Beach, CA, USA, 4–9 December 2018. [Google Scholar]
- Razavi, A.; Oord, A.v.d.; Vinyals, O. Generating Diverse High-Fidelity Images with VQ-VAE-2. In Proceedings of the Conference and Workshop on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Gan, L. Block Compressed Sensing of Natural Images. In Proceedings of the 2007 15th International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007. [Google Scholar]
- Palangi, H.; Ward, R.; Deng, L. Distributed Compressive Sensing: A Deep Learning Approach. IEEE Trans. Signal Process. 2016, 64, 4504–4518. [Google Scholar] [CrossRef]
- Su, K.; Fu, H.; Do, B.; Cheng, H.; Wang, H.F.; Zhang, D.Y. Image denoising based on learning over-complete dictionary. In Proceedings of the 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Chongqing, China, 29–31 May 2012. [Google Scholar]
- Zhou, F.; Tan, J.; Fan, X.Y.; Zhang, L. A novel method for sparse channel estimation using super-resolution dictionary. EURASIP J. Adv. Signal Process. 2014, 2014, 29. [Google Scholar] [CrossRef]
- Madbhavi, R.; Srinivasan, B. Enhancing Performance of Compressive Sensing-based State Estimators using Dictionary Learning. In Proceedings of the International Conference on Power Systems Technology (POWERCON), Kuala Lumpur, Malaysia, 12–14 September 2022. [Google Scholar]
- Liu, S.; Zhang, G.; Soon, Y.T. An Over-Complete Dictionary Design Based on GSR for SAR Image Despeckling. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 2230–2234. [Google Scholar] [CrossRef]
- Neddell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Ji, S.H.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Prechelt, L. Early Stopping—But When? In Neural Networks: Tricks of the Trade; Orr, G., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 1524, pp. 55–69. [Google Scholar]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Y.; Luo, T.; Xiao, Y.; Ma, Z. Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks. arXiv 2019, arXiv:1901.06523. [Google Scholar] [CrossRef]


| Methods | Emean | E1 | E2 | t (s) | ttrain (min) |
|---|---|---|---|---|---|
| VQ-VAE-M | 0.003 | 1.0 | 1.0 | 0.038 | 2.967 |
| WaveGAN | 0.155 | 0.0938 | 0.8516 | 4.743 | 56.15 |
| VQ-VAE | 0.02 | 1.0 | 1.0 | 0.329 | 2.333 |
| DB | Emean | E1 | E2 | t (s) |
|---|---|---|---|---|
| 8 | 0.039 | 0.882 | 0.985 | 0.014 |
| 16 | 0.100 | 0.641 | 0.849 | 0.014 |
| 32 | 0.110 | 0.662 | 0.818 | 0.013 |
| 64 | 0.116 | 0.613 | 0.803 | 0.014 |
| 128 | 0.306 | 0.156 | 0.344 | 0.013 |
| 256 | 0.580 | 0.072 | 0.162 | 0.013 |
| 512 | 0.768 | 0.056 | 0.133 | 0.013 |
| Emean | E1 | |||
|---|---|---|---|---|
| Multi-Blocks | Block | Multi-Blocks | Block | |
| 1 | 0.136 | 0.136 | 0.699 | 0.699 |
| 2 | 0.129 | 0.096 | 0.653 | 0.737 |
| 4 | 0.066 | 0.076 | 0.791 | 0.766 |
| 8 | 0.066 | 0.068 | 0.790 | 0.786 |
| 16 | 0.058 | 0.064 | 0.821 | 0.800 |
| 32 | 0.053 | 0.062 | 0.831 | 0.800 |
| 64 | 0.040 | 0.060 | 0.882 | 0.815 |
| Methods | Emean | E1 | E2 | t (s) | ttrain (min) |
|---|---|---|---|---|---|
| VQ-VAE-M | 0.038 | 0.882 | 0.987 | 0.013 | 18.501 |
| (VQ-VAE-M)E | 0.043 | 0.867 | 0.964 | 0.011 | 20.362 |
| (VQ-VAE-M)D | 0.049 | 0.838 | 0.956 | 0.011 | 21.034 |
| Methods | Emean | E1 | E2 | t (s) | ttrain (min) |
|---|---|---|---|---|---|
| VQ-VAE-M | 0.034 | 0.892 | 0.977 | 0.013 | 14.312 |
| (VQ-VAE-M)E | 0.038 | 0.877 | 0.946 | 0.011 | 16.031 |
| (VQ-VAE-M)D | 0.043 | 0.862 | 0.941 | 0.011 | 16.647 |
| Methods | Emean | E1 | E2 | t (s) | ttrain (min) |
|---|---|---|---|---|---|
| VQ-VAE-M | 0.021 | 0.936 | 1.000 | 0.013 | 12.148 |
| (VQ-VAE-M)E | 0.025 | 0.911 | 0.972 | 0.011 | 14.025 |
| (VQ-VAE-M)D | 0.029 | 0.895 | 0.964 | 0.011 | 14.507 |
| Methods | Emean | E1 | E2 | t (s) |
|---|---|---|---|---|
| BP | 0.475 | 0 | 0 | 0.172 |
| CoSaMP | 3.501 | 0 | 0 | 0.191 |
| GPSR | 0.437 | 0 | 0.020 | 0.042 |
| BCS | 0.499 | 0 | 0.050 | 0.067 |
| BCS-IPE | 0.466 | 0.010 | 0.060 | 1.251 |
| MLP | 0.051 | 0.854 | 0.944 | 0.016 |
| WTCNN | 0.050 | 0.862 | 0.964 | 0.012 |
| VQ-VAE-M | 0.038 | 0.882 | 0.987 | 0.013 |
| WaveGAN | 0.553 | 0.110 | 0.190 | 4.732 |
| VQ-VAE | 0.453 | 0.569 | 0.685 | 2.574 |
| Methods | Emean | E1 | E2 | t (s) |
|---|---|---|---|---|
| BP | 0.364 | 0 | 0 | 0.178 |
| CoSaMP | 0.417 | 0.020 | 0.170 | 0.250 |
| GPSR | 0.310 | 0 | 0.250 | 0.022 |
| BCS | 0.338 | 0.040 | 0.290 | 0.095 |
| BCS-IPE | 0.325 | 0.060 | 0.330 | 1.504 |
| MLP | 0.048 | 0.859 | 0.913 | 0.017 |
| WTCNN | 0.043 | 0.874 | 0.956 | 0.011 |
| VQ-VAE-M | 0.034 | 0.892 | 0.977 | 0.013 |
| WaveGAN | 0.434 | 0.170 | 0.210 | 6.722 |
| VQ-VAE | 0.460 | 0.149 | 0.526 | 2.586 |
| Methods | Emean | E1 | E2 | t (s) |
|---|---|---|---|---|
| BP | 0.304 | 0 | 0.060 | 0.190 |
| CoSaMP | 0.293 | 0.070 | 0.360 | 0.301 |
| GPSR | 0.250 | 0.020 | 0.390 | 0.013 |
| BCS | 0.268 | 0.150 | 0.390 | 0.097 |
| BCS-IPE | 0.266 | 0.150 | 0.410 | 2.000 |
| MLP | 0.032 | 0.895 | 0.979 | 0.016 |
| WTCNN | 0.023 | 0.918 | 0.997 | 0.011 |
| VQ-VAE-M | 0.021 | 0.936 | 1.000 | 0.013 |
| WaveGAN | 0.365 | 0.180 | 0.210 | 7.005 |
| VQ-VAE | 0.194 | 0.595 | 0.733 | 2.623 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, G.; Ji, Z.; Zhong, Q.; Huang, Y.; Han, K. Vector Quantized Variational Autoencoder-Based Compressive Sampling Method for Time Series in Structural Health Monitoring. Sustainability 2023, 15, 14868. https://doi.org/10.3390/su152014868
Liang G, Ji Z, Zhong Q, Huang Y, Han K. Vector Quantized Variational Autoencoder-Based Compressive Sampling Method for Time Series in Structural Health Monitoring. Sustainability. 2023; 15(20):14868. https://doi.org/10.3390/su152014868
Chicago/Turabian StyleLiang, Ge, Zhenglin Ji, Qunhong Zhong, Yong Huang, and Kun Han. 2023. "Vector Quantized Variational Autoencoder-Based Compressive Sampling Method for Time Series in Structural Health Monitoring" Sustainability 15, no. 20: 14868. https://doi.org/10.3390/su152014868
APA StyleLiang, G., Ji, Z., Zhong, Q., Huang, Y., & Han, K. (2023). Vector Quantized Variational Autoencoder-Based Compressive Sampling Method for Time Series in Structural Health Monitoring. Sustainability, 15(20), 14868. https://doi.org/10.3390/su152014868










