Diagnostics of Early Faults in Wind Generator Bearings Using Hjorth Parameters
Abstract
:1. Introduction
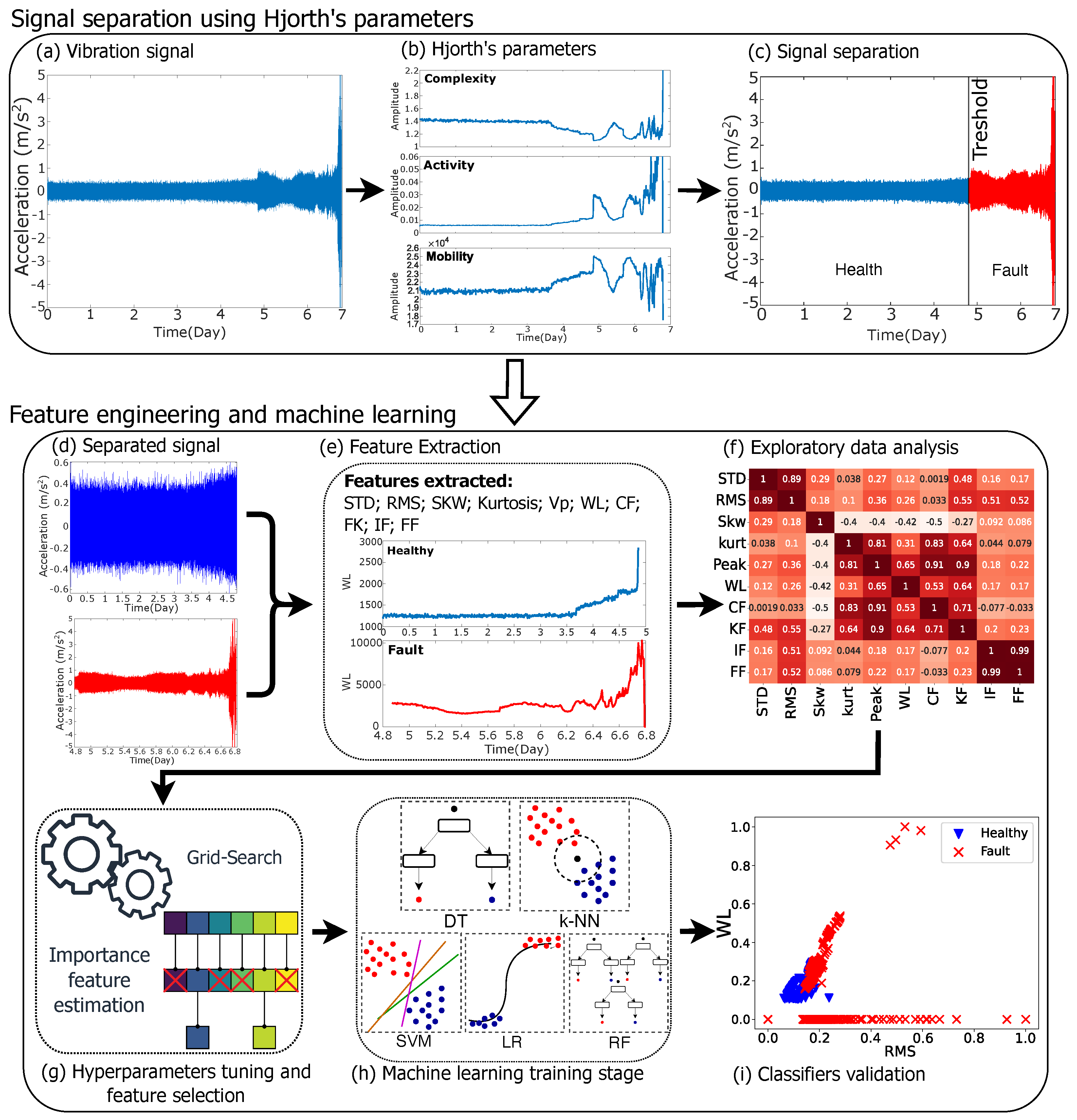
2. Methodology
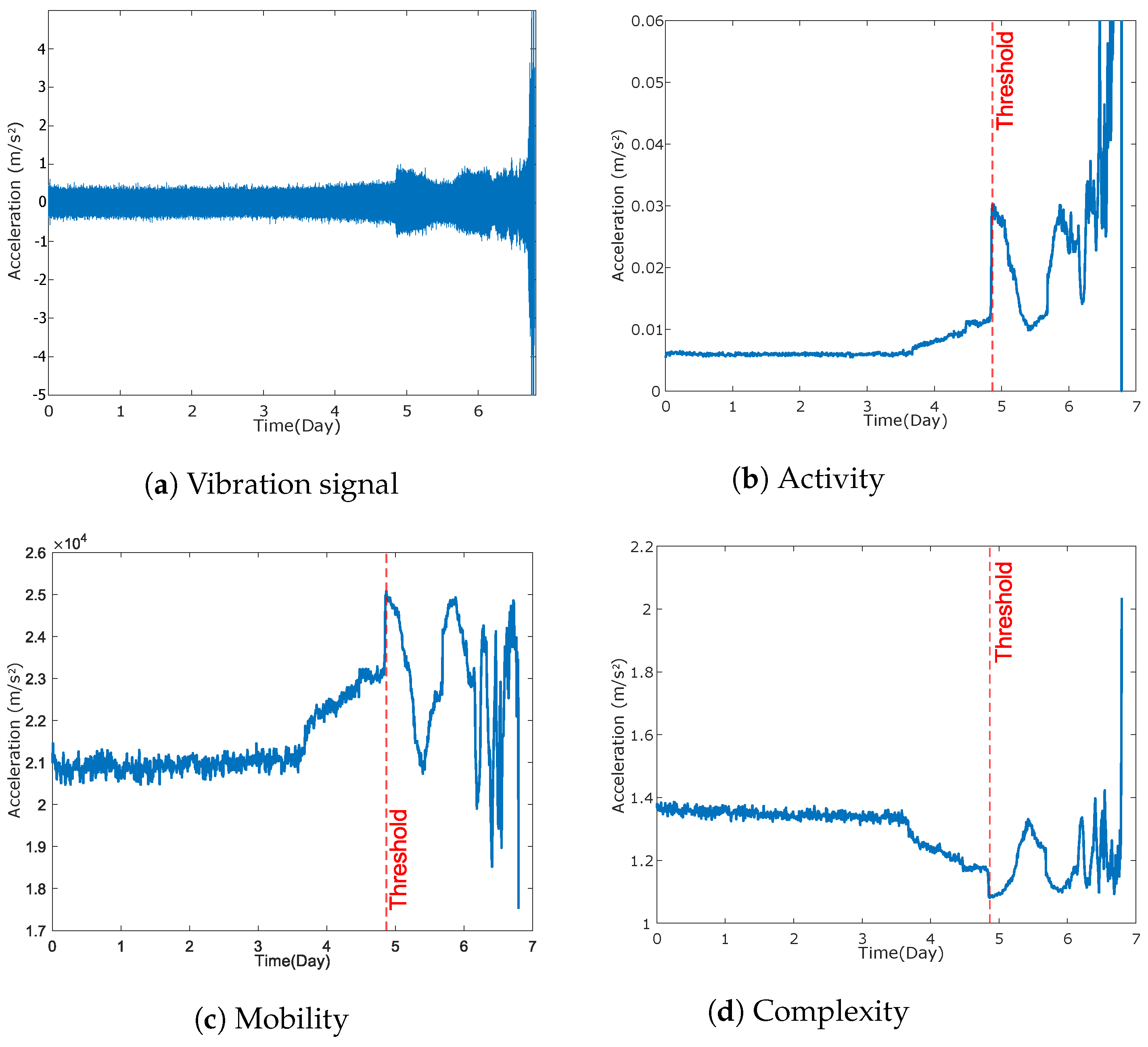
2.1. Hjorth’s Parameters
- Activity is defined as the zeroth-order spectral moment (), given by Equation (1), and is expressed by the variance () of the signal amplitude (y), representing the surface envelope of the power spectrum in the time domain.
- Mobility represents the second-order spectral moment (), expressed by Equation (2), as the square root of the ratio between the variance () of the first-order derivative of the signal () and the variance of the signal. A measure of the standard deviation of the slope compared to the standard deviation of the amplitude is established, often known as the mean frequency.The fact that mobility is a slope measure relative to the mean makes it dependent solely on the waveform shape.
- Complexity is given by the fourth-order spectral moment (), defined by Equation (3), as the square root of the ratio between the variance () of the second-order derivative of the signal amplitude () and the variance of the first-order derivative of the signal. A measure of the similarity of the waveform under study to a sinusoidal wave is established, expressing a change in the frequency of the analyzed signal.
2.2. Feature Engineering and Machine Learning
2.2.1. Feature Extraction
- The standard deviation (STD) is given by Equation (4), where N represents the number of points composing the signal, represents the mean value of the signal amplitude, and is the amplitude of the signal at point i, with the SDT being a measure of data dispersion around the mean value.
- The root mean square (RMS) is expressed by Equation (5), quantifying the average power contained in the signal, serving as a metric for detecting vibration levels yet not being sensitive to early-stage faults.
- The skewness (SKW) assesses how far the signal distribution deviates from a normal distribution, and faults can lead to an increase in signal skewness, as expressed by Equation (6).
- Kurtosis is a measure of the data concentration around the central tendency measures of a normal distribution, given by Equation (7).
- The peak value () checks for the highest absolute value of the signal, given by Equation (8), where X represents the signal amplitude, and an increase in its value may indicate the occurrence of faults.
- The waveform length (WL) provides information about the signal frequency, calculated by Equation (9), where P represents the number of signal points and represents the difference between the amplitude of the current sample i and that of the next sample.
- The crest factor (CF) aims to overcome the limitation encountered by the RMS value for sensitivity to early-stage faults, expressed by Equation (10), which is the division of the peak value by the RMS value.The peak value has a greater sensitivity to early-stage faults, but as the fault progresses, the RMS value increases faster than the peak value, causing the CF value to decrease in the later stages.
- The factor K (FK) aims to combine the sensitivity of the peak value for early-stage faults and the sensitivity of the RMS value for later-stage fault detection. It is expressed as the product of the two metrics, as in Equation (11).
- The impulse factor (IF) compares the maximum value of the signal to the signal’s mean and is expressed by Equation (12), where represents the signal’s mean value.
- The form factor (FF), given by Equation (13), is defined as the ratio between the RMS value and the mean value of the signal, becoming dependent on the signal’s shape and independent of the signal’s dimensions.
2.2.2. Machine Learning
- Logistic regression (LR) is a statistical method for binary classification that employs input variables to calculate the probability of an event occurring. Utilizing the logistic function to convert values to probabilities ranging from 0 to 1, LR is useful for categorical and binary classification problems [25].
- Decision tree (DT) is a method that predicts outcomes by generating a tree-like structure of decisions based on input features. It divides data into subsets recursively, beginning with the root node, using features that best separate between classes. Leaf nodes represent the result of the predictions. DTs are interpretable, applicable to different fields, and facilitate the hierarchical visualization of decision-making processes [26].
- Random forest (RF) is a DT ensemble-based classification method. Since the decision trees in the RF are generated independently from random samples, there is a low association between the trees. Afterward, voting takes place using the classifications generated by each tree, and the class with the most votes is used to predict the presented sample [27].
- The support vector machine (SVM) algorithm searches for the optimal hyperplane for class separation, and various hyperplanes can be used to divide classes [28]. Nonetheless, the optimal hyperplane is determined by utilizing the most similar samples between the classes, which are the coordinates from which the support vectors are derived. The objective is to maximize distances in both directions to identify the hyperplane with the most significant separation, providing superior generalization [29].SVM can classify datasets that are not linearly separable by utilizing a kernel that determines the relationship between higher-dimensional data to identify the separability plane [30].
- The k-nearest neighbors (k-NN) classifier is based on the distance between the new sample to be classified and the other samples. The class of the new sample is determined by the majority class among the nearest neighbors. The parameter k specifies the number of closest points (neighbors) observed during classification, where small k values can lead to less stable results. In contrast, larger k values produce more stable results with increased errors. The Euclidean, Manhattan, or Minkowski functions can compute the distance between points [31].
3. Experimental Setup and Dataset
4. Results and Discussion
4.1. Signal Separation
4.2. Classification
4.3. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CF | Crest factor |
| CWRU | Case Western Reserve University |
| DT | Decision tree |
| EEG | Electroencephalogram |
| EFS | Exhaustive feature selection |
| FF | Form factor |
| ICP | Integrated circuit piezoelectric |
| IF | Impulse factor |
| IMS | Intelligent maintenance systems |
| k-NN | k-nearest neighbors |
| LR | Logistic regression |
| RF | Random forest |
| RMS | Root mean square |
| SKW | Skewness |
| STD | Standard deviation |
| SVM | Support vector machine |
| WL | Waveform length |
References
- Hutchinson, M.; Zhao, F. GWEC Global Wind Report; Hutchinson, M., Zhao, F., Eds.; GWEC: Brussels, Belgium, 2023. [Google Scholar]
- Attallah, O.; Ibrahim, R.A.; Zakzouk, N.E. CAD system for inter-turn fault diagnosis of offshore wind turbines via multi-CNNs & feature selection. Renew. Energy 2023, 203, 870–880. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Jiang, B.; Pillay, P.; Rakheja, S. A Comprehensive Review on Signal-Based and Model-Based Condition Monitoring of Wind Turbines: Fault Diagnosis and Lifetime Prognosis. Proc. IEEE 2022, 110, 754–806. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Signal based condition monitoring techniques for fault detection and diagnosis of induction motors: A state-of-the-art review. Mech. Syst. Signal Process. 2020, 144, 106908. [Google Scholar] [CrossRef]
- Vaimann, T.; Belahcen, A.; Kallaste, A. Necessity for implementation of inverse problem theory in electric machine fault diagnosis. In Proceedings of the IEEE International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015; pp. 380–385. [Google Scholar] [CrossRef]
- Spyropoulos, D.V.; Mitronikas, E.D. A Review on the Faults of Electric Machines Used in Electric Ships. Adv. Power Electron. 2013, 2013, 216870. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Measurement 2020, 149, 107002. [Google Scholar] [CrossRef]
- Nabhan, A.; Ghazaly, N.; Samy, A.; Mousa, M.O. Bearing Fault Detection Techniques—A Review. Turk. J. Eng. Sci. Technol. 2015, 3. [Google Scholar]
- Duan, Z.; Wu, T.; Guo, S.; Shao, T.; Malekian, R.; Li, Z. Development and trend of condition monitoring and fault diagnosis of multi-sensors information fusion for rolling bearings: A review. Int. J. Adv. Manuf. Technol. 2018, 96, 803–819. [Google Scholar] [CrossRef]
- Gundewar, S.K.; Kane, P.V. Condition Monitoring and Fault Diagnosis of Induction Motor. J. Vib. Eng. Technol. 2021, 9, 643–674. [Google Scholar] [CrossRef]
- Tama, B.A.; Vania, M.; Lee, S.; Lim, S. Recent advances in the application of deep learning for fault diagnosis of rotating machinery using vibration signals. Artif. Intell. Rev. 2023, 56, 4667–4709. [Google Scholar] [CrossRef]
- Gnanasekaran, S.; Jakkamputi, L.; Thangamuthu, M.; Marikkannan, S.K.; Rakkiyannan, J.; Thangavelu, K.; Kotha, G. Condition Monitoring of an All-Terrain Vehicle Gear Train Assembly Using Deep Learning Algorithms with Vibration Signals. Appl. Sci. 2022, 12, 10917. [Google Scholar] [CrossRef]
- KiranKumar, M.V.; Lokesha, M.; Kumar, S.; Kumar, A. Review on Condition Monitoring of Bearings using vibration analysis techniques. IOP Conf. Ser. Mater. Sci. Eng. 2018, 376, 012110. [Google Scholar] [CrossRef]
- Souza, W.A.; Alonso, A.M.; Bosco, T.B.; Garcia, F.D.; Gonçalves, F.A.; Marafão, F.P. Selection of features from power theories to compose NILM datasets. Adv. Eng. Inform. 2022, 52, 101556. [Google Scholar] [CrossRef]
- Toma, R.N.; Prosvirin, A.E.; Kim, J.M. Bearing Fault Diagnosis of Induction Motors Using a Genetic Algorithm and Machine Learning Classifiers. Sensors 2020, 20, 1884. [Google Scholar] [CrossRef] [PubMed]
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset with Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Wang, H.; Yue, W.; Wen, S.; Xu, X.; Haasis, H.D.; Su, M.; Liu, P.; Zhang, S.; Du, P. An improved bearing fault detection strategy based on artificial bee colony algorithm. CAAI Trans. Intell. Technol. 2022, 7, 570–581. [Google Scholar] [CrossRef]
- Pacheco-Chérrez, J.; Fortoul-Díaz, J.A.; Cortés-Santacruz, F.; María Aloso-Valerdi, L.; Ibarra-Zarate, D.I. Bearing fault detection with vibration and acoustic signals: Comparison among different machine leaning classification methods. Eng. Fail. Anal. 2022, 139, 106515. [Google Scholar] [CrossRef]
- Shen, S.; Lu, H.; Sadoughi, M.; Hu, C.; Nemani, V.; Thelen, A.; Webster, K.; Darr, M.; Sidon, J.; Kenny, S. A physics-informed deep learning approach for bearing fault detection. Eng. Appl. Artif. Intell. 2021, 103, 104295. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Hjorth, B. EEG analysis based on time domain properties. Electroencephalogr. Clin. Neurophysiol. 1970, 29, 306–310. [Google Scholar] [CrossRef]
- Jacopo, C.C.M.; Matteo, S.; Riccardo, R.; Marco, C. Analysis of NASA Bearing Dataset of the University of Cincinnati by Means of Hjorth’s Parameters. In Archivio Istituzionale della Ricerca; Università di Modena e Reggio Emilia: Reggio Emilia, Italy, 2018. [Google Scholar]
- Vitor, A.L.; Goedtel, A.; Barbon, S.; Bazan, G.H.; Castoldi, M.F.; Souza, W.A. Induction motor short circuit diagnosis and interpretation under voltage unbalance and load variation conditions. Expert Syst. Appl. 2023, 224, 119998. [Google Scholar] [CrossRef]
- Mazziotta, M.; Pareto, A. Normalization methods for spatio-temporal analysis of environmental performance: Revisiting the Min–Max method. Environmetrics 2022, 33, e2730. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. CATENA 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Souza, W.A.; Marafão, F.P.; Liberado, E.V.; Simões, M.G.; Da Silva, L.C.P. A NILM Dataset for Cognitive Meters Based on Conservative Power Theory and Pattern Recognition Techniques. J. Control Autom. Electr. Syst. 2018, 29, 742–755. [Google Scholar] [CrossRef]
- Saravanan, S.; Reddy, N.M.; Pham, Q.B.; Alodah, A.; Abdo, H.G.; Almohamad, H.; Al Dughairi, A.A. Machine Learning Approaches for Streamflow Modeling in the Godavari Basin with CMIP6 Dataset. Sustainability 2023, 15, 12295. [Google Scholar] [CrossRef]
- Guenther, N.; Schonlau, M. Support Vector Machines. Stata J. Promot. Commun. Stat. Stata 2016, 16, 917–937. [Google Scholar] [CrossRef]
- Jiang, P.; Li, R.; Liu, N.; Gao, Y. A novel composite electricity demand forecasting framework by data processing and optimized support vector machine. Appl. Energy 2020, 260, 114243. [Google Scholar] [CrossRef]
- Chowdhury, S.; Schoen, M.P. Research Paper Classification using Supervised Machine Learning Techniques. In Proceedings of the 2020 Intermountain Engineering, Technology and Computing (IETC), Orem, UT, USA, 2–3 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Yesilbudak, M.; Ozcan, A. kNN Classifier Applications in Wind and Solar Energy Systems. In Proceedings of the 2022 11th International Conference on Renewable Energy Research and Application (ICRERA), Istanbul, Turkey, 18–21 September 2022; pp. 480–484. [Google Scholar] [CrossRef]
- Fayed, H.A.; Atiya, A.F. Speed up grid-search for parameter selection of support vector machines. Appl. Soft Comput. 2019, 80, 202–210. [Google Scholar] [CrossRef]
- Mantovani, R.G.; Rossi, A.L.; Alcobaça, E.; Vanschoren, J.; de Carvalho, A.C. A meta-learning recommender system for hyperparameter tuning: Predicting when tuning improves SVM classifiers. Inf. Sci. 2019, 501, 193–221. [Google Scholar] [CrossRef]
- Venkatesh, B.; Anuradha, J. A Review of Feature Selection and Its Methods. Cybern. Inf. Technol. 2019, 19, 3–26. [Google Scholar] [CrossRef]
- Got, A.; Moussaoui, A.; Zouache, D. Hybrid filter-wrapper feature selection using whale optimization algorithm: A multi-objective approach. Expert Syst. Appl. 2021, 183, 115312. [Google Scholar] [CrossRef]
- Sathianarayanan, B.; Singh Samant, Y.C.; Conjeepuram Guruprasad, P.S.; Hariharan, V.B.; Manickam, N.D. Feature-based augmentation and classification for tabular data. CAAI Trans. Intell. Technol. 2022, 7, 481–491. [Google Scholar] [CrossRef]
- Gousseau, W.; Antoni, J.; Girardin, F.; Griffaton, J. Analysis of the Rolling Element Bearing data set of the Center for Intelligent Maintenance Systems of the University of Cincinnati. In Proceedings of the CM2016, Charenton, France, 10–12 October 2016. [Google Scholar]
- Sun, B.; Liu, X. Bearing early fault detection and degradation tracking based on support tensor data description with feature tensor. Appl. Acoust. 2022, 188, 108530. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Qin, X.; Sun, Y. A two-stage fault diagnosis methodology for rotating machinery combining optimized support vector data description and optimized support vector machine. Measurement 2022, 200, 111651. [Google Scholar] [CrossRef]
- Shao, K.; He, Y.; Xing, Z.; Du, B. Detecting wind turbine anomalies using nonlinear dynamic parameters-assisted machine learning with normal samples. Reliab. Eng. Syst. Saf. 2023, 233, 109092. [Google Scholar] [CrossRef]
- Liu, C.; Gryllias, K. A semi-supervised Support Vector Data Description-based fault detection method for rolling element bearings based on cyclic spectral analysis. Mech. Syst. Signal Process. 2020, 140, 106682. [Google Scholar] [CrossRef]
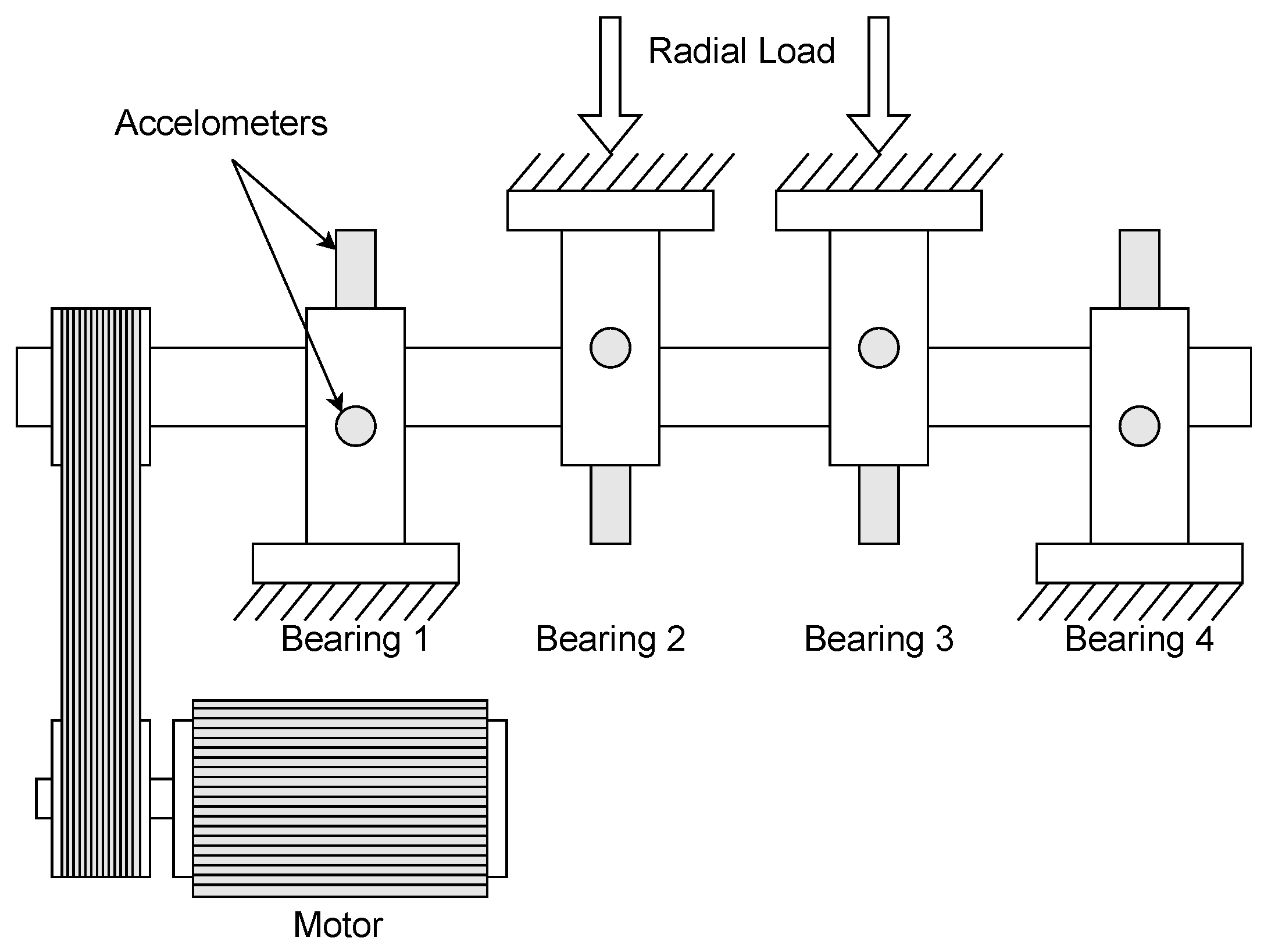

| Quantity of Samples | Bearing Fault | Fault Location | |
|---|---|---|---|
| Experiment 1 | 2156 | Bearing 3 Bearing 4 | Inner race Roll |
| Experiment 2 | 984 | Bearing 1 | Outer race |
| Experiment 3 | 4448 | Bearing 3 | Outer race |
| Day of Fault | Number of Healthy Samples | Number of Faulty Samples | |
|---|---|---|---|
| Bearing 3—Experiment 1 | 33 | 1910 | 246 |
| Bearing 4—Experiment 1 | 25 | 1540 | 616 |
| Bearing 1—Experiment 2 | 4.8 | 704 | 280 |
| Classifier | Hyperparameter | Tested Values | Selected |
|---|---|---|---|
| LR | C | 0.2, 2, 20, 80 | 0.2 |
| Penalty | L2, Elasticnet | L2 | |
| Solver | lbfgs, liblinear, sag, saga | lbfgs | |
| DT | Criterion | Gini, Entropy | Entropy |
| Tree depth | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 | 10 | |
| Data points to split a node | 8, 10, 12 | 10 | |
| Tree depth | 10, 20, 30 | 10 | |
| Attributes to split a node | 2, 3 | 3 | |
| RF | Data points to split a node | 8, 10, 12 | 10 |
| Minimum allowed data in a leaf | 3, 4, 5 | 3 | |
| Number of trees | 100, 150, 200, 250 | 100 | |
| C | 0.1, 5, 10, 20, 50 | 50 | |
| SVM | Kernel coefficient | 0.001, 0.01, 0.1, 1 | 1 |
| Kernel | RBF, Linear | RBF | |
| k-NN | Number of neighbors (k) | 3, 5, 7, 9, 11 | 11 |
| Weights | Uniform, Distance | Distance | |
| Metric | Minkowski, Euclidian, Manhattan | Minkowski |
| Classifier | |||||
|---|---|---|---|---|---|
| Metric | LR | DT | RF | SVM | -NN |
| Accuracy | 0.82 | 0.98 | 0.99 | 0.97 | 0.98 |
| Precision | 0.85 | 0.98 | 0.98 | 0.97 | 0.98 |
| Recall | 0.58 | 0.96 | 0.98 | 0.94 | 0.96 |
| F1 score | 0.59 | 0.97 | 0.98 | 0.95 | 0.97 |
| 2.54 | 3.98 | 122.64 | 25.62 | 0.73 | |
| 0.0007 | 0.001 | 0.015 | 0.072 | 0.011 | |
| Classifier | |||||
|---|---|---|---|---|---|
| Metric | LR | DT | RF | SVM | -NN |
| Accuracy | 0.84 | 0.99 | 0.99 | 0.97 | 0.99 |
| Precision | 0.91 | 0.98 | 0.99 | 0.97 | 0.98 |
| Recall | 0.61 | 0.98 | 0.99 | 0.94 | 0.98 |
| F1 score | 0.63 | 0.98 | 0.99 | 0.96 | 0.98 |
| 2.49 | 3.38 | 105.05 | 22.41 | 0.73 | |
| 0.0019 | 0.0022 | 0.023 | 0.051 | 0.012 | |
| Classifier | Features |
|---|---|
| LR | STD and |
| DT | WL and FF |
| RF | RMS and WL |
| SVM | STD and WL |
| k-NN | RMS and WL |
| Classifier | |||||
|---|---|---|---|---|---|
| Metric | LR | DT | RF | SVM | k-NN |
| Accuracy | 0.82 () | 0.98 () | 0.98 () | 0.96 () | 0.98 () |
| Precision | 0.86 () | 0.97 () | 0.98 () | 0.96 () | 0.97 () |
| Recall | 0.56 () | 0.96 () | 0.97 () | 0.92 () | 0.97 () |
| F1 score | 0.56 () | 0.97 () | 0.97 () | 0.94 () | 0.97 () |
| 0.77 () | 1.21 () | 89.52 () | 24.33 () | 0.51 () | |
| 0.001 () | 0.002 () | 0.018 () | 0.065 () | 0.004 () | |
| Classifier | |||||
|---|---|---|---|---|---|
| Metric | LR | DT | RF | SVM | k-NN |
| Accuracy | 0.82 () | 0.98 () | 0.99 () | 0.96 () | 0.98 () |
| Precision | 0.91 () | 0.98 () | 0.98 () | 0.96 () | 0.98 () |
| Recall | 0.57 () | 0.97 () | 0.98 () | 0.93 () | 0.97 () |
| F1 score | 0.58 () | 0.97 () | 0.98 () | 0.94 () | 0.98 () |
| 0.81 () | 1.24 () | 86.14 () | 24.39 (⇑ 4.8%) | 0.53 (⇓ 27.4%) | |
| 0.001 () | 0.002 () | 0.025 () | 0.060 () | 0.004 (⇓ 55.5%) | |
| Method | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| Our approach | 0.98 | 0.98 | 0.97 | 0.98 |
| WPD-STDD [38] | 1.00 | 1.00 | – | – |
| KNN [38] | 0.97 | 0.97 | – | – |
| COM-GOA-SVDD [39] | 0.92 | 0.90 | 1.00 | 0.94 |
| GMPOP [40] | 0.99 | – | 1.00 | – |
| CSC—NSVDD [41] | 0.99 | 0.99 | 0.99 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, A.C.; Souza, W.A.; Barbara, G.V.; Castoldi, M.F.; Goedtel, A. Diagnostics of Early Faults in Wind Generator Bearings Using Hjorth Parameters. Sustainability 2023, 15, 14673. https://doi.org/10.3390/su152014673
Santos AC, Souza WA, Barbara GV, Castoldi MF, Goedtel A. Diagnostics of Early Faults in Wind Generator Bearings Using Hjorth Parameters. Sustainability. 2023; 15(20):14673. https://doi.org/10.3390/su152014673
Chicago/Turabian StyleSantos, Arthur C., Wesley A. Souza, Gustavo V. Barbara, Marcelo F. Castoldi, and Alessandro Goedtel. 2023. "Diagnostics of Early Faults in Wind Generator Bearings Using Hjorth Parameters" Sustainability 15, no. 20: 14673. https://doi.org/10.3390/su152014673
APA StyleSantos, A. C., Souza, W. A., Barbara, G. V., Castoldi, M. F., & Goedtel, A. (2023). Diagnostics of Early Faults in Wind Generator Bearings Using Hjorth Parameters. Sustainability, 15(20), 14673. https://doi.org/10.3390/su152014673









