Transient Stability Analysis for Grid-Forming VSCs Based on Nonlinear Decoupling Method
Abstract
:1. Introduction
- (1)
- The development of a comprehensive full-order large-signal model for grid-forming VSCs, including a truncated model that captures the quadratic nonlinear terms through Taylor expansion, thereby fully representing the nonlinear characteristics of VSCs.
- (2)
- The implementation of a nonlinear decoupling method utilizing coupling factors to decouple the high-order nonlinear model into multiple low-order modes. Through the adjustment of the inner and outer control parameters, a thorough analysis of the transient stability of grid-forming VSCs is conducted under the influence of significant disturbances. Additionally, the analysis conclusions are validated through HIL experiments.
2. Principle of Nonlinear Decoupling Method
2.1. Model Representation of High-Order Systems
2.2. Linear Decoupling of Nonlinear System Model
2.3. Nonlinear Decoupling Process
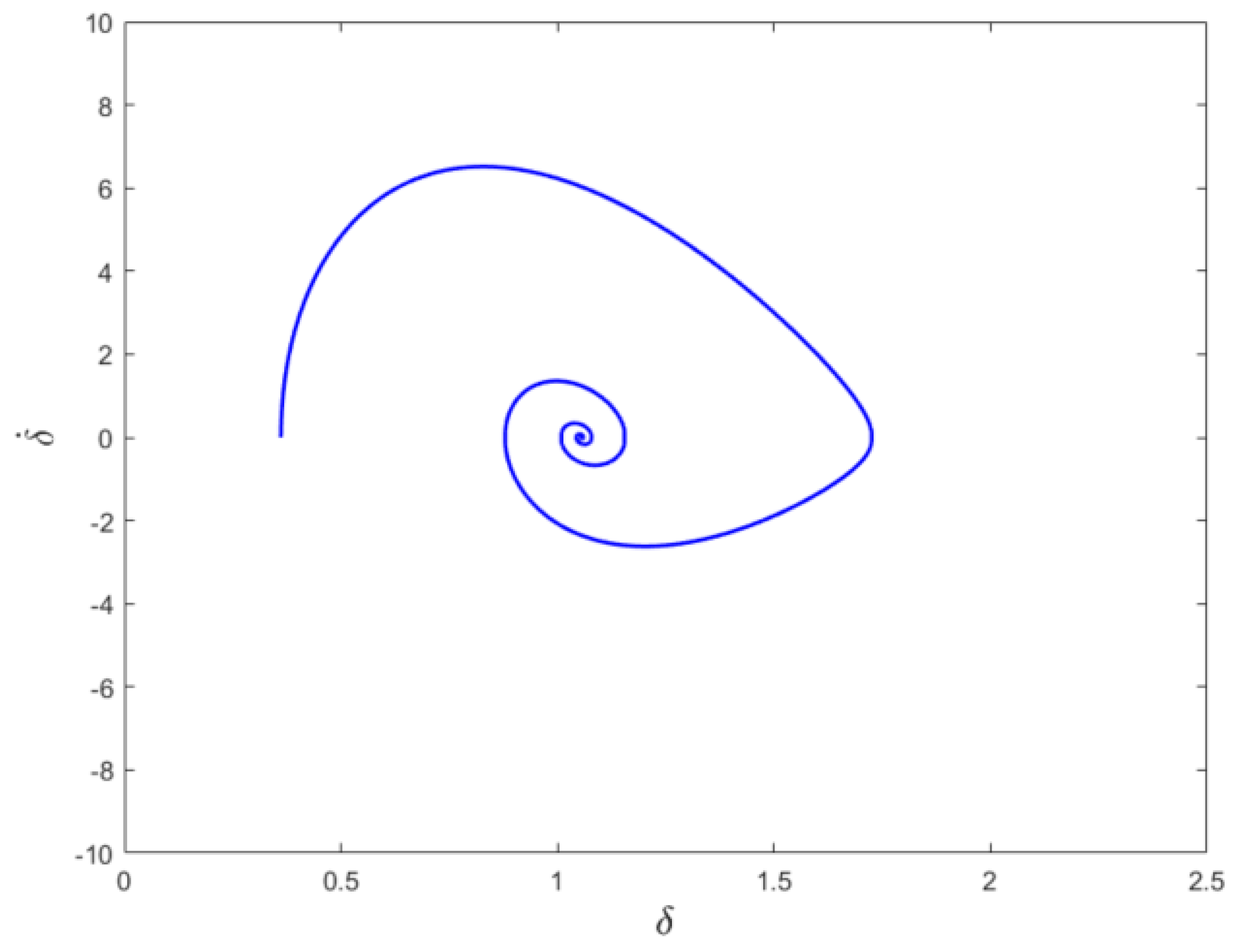
2.4. Transient Stability Analysis
3. Transient Stability for Grid-Forming VSCs
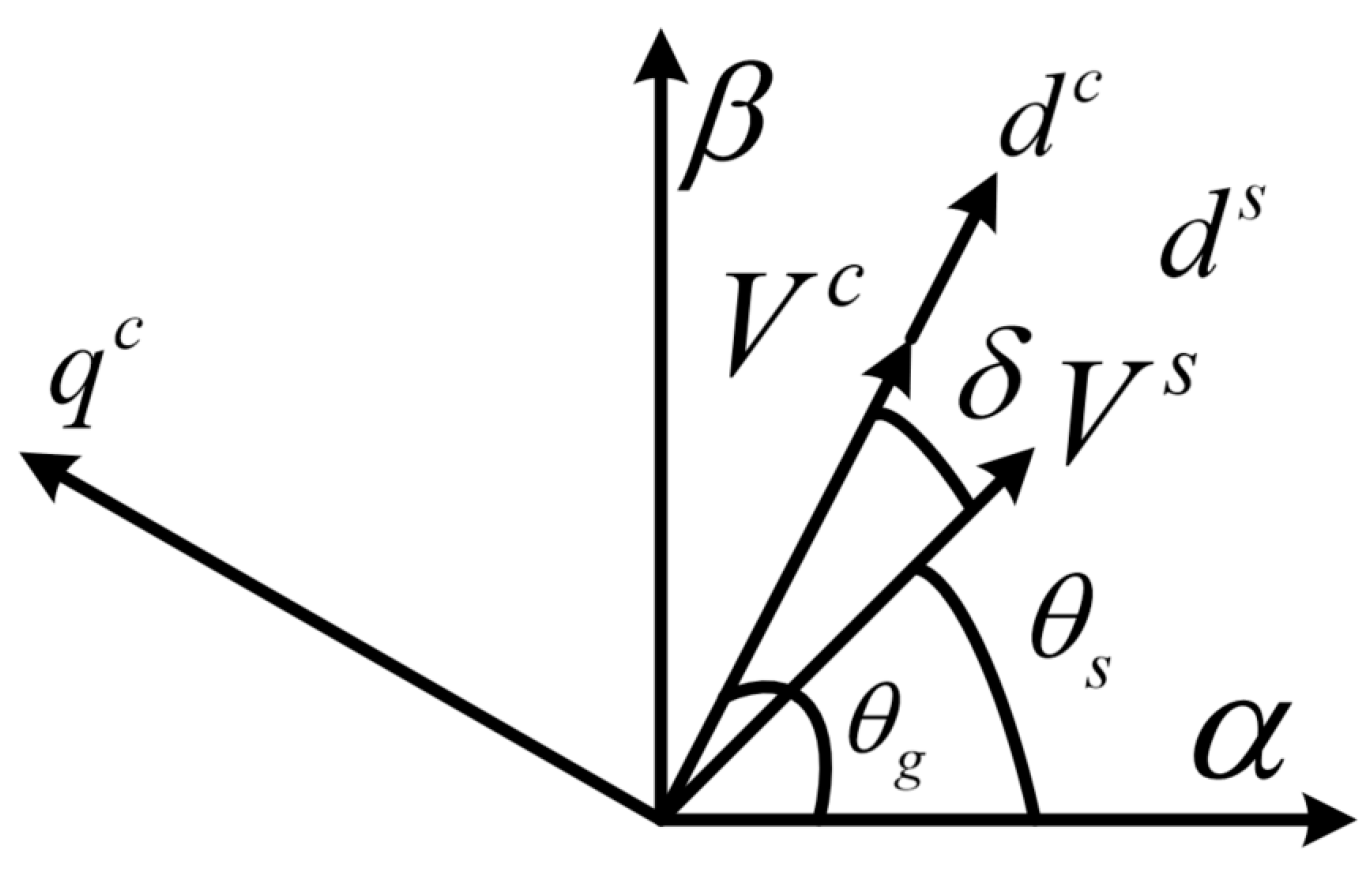
3.1. Principle of VSG Control
3.2. Model of the VSG Control Strategy
3.3. Transient Stability Analysis for Grid-Forming VSCs
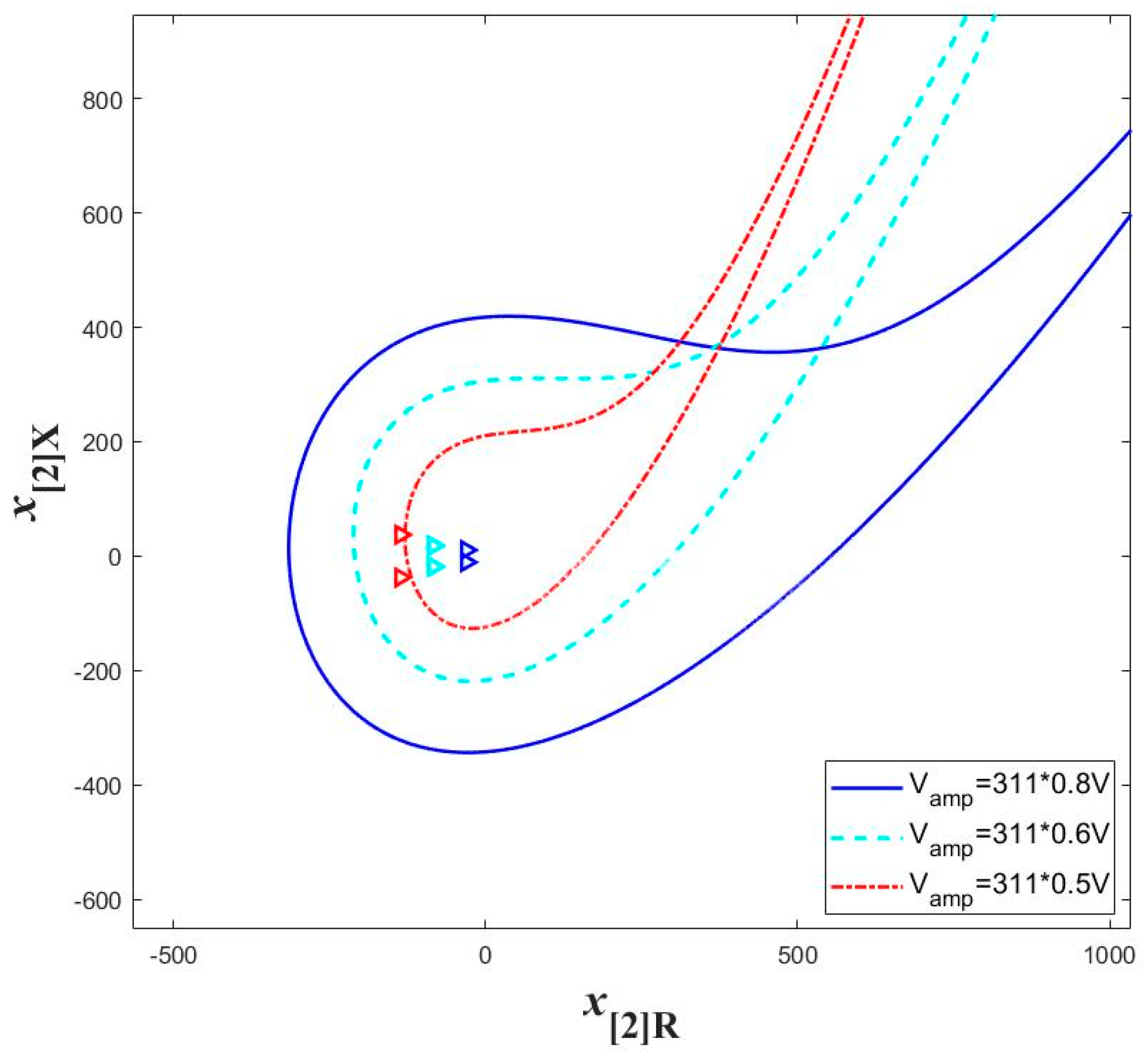
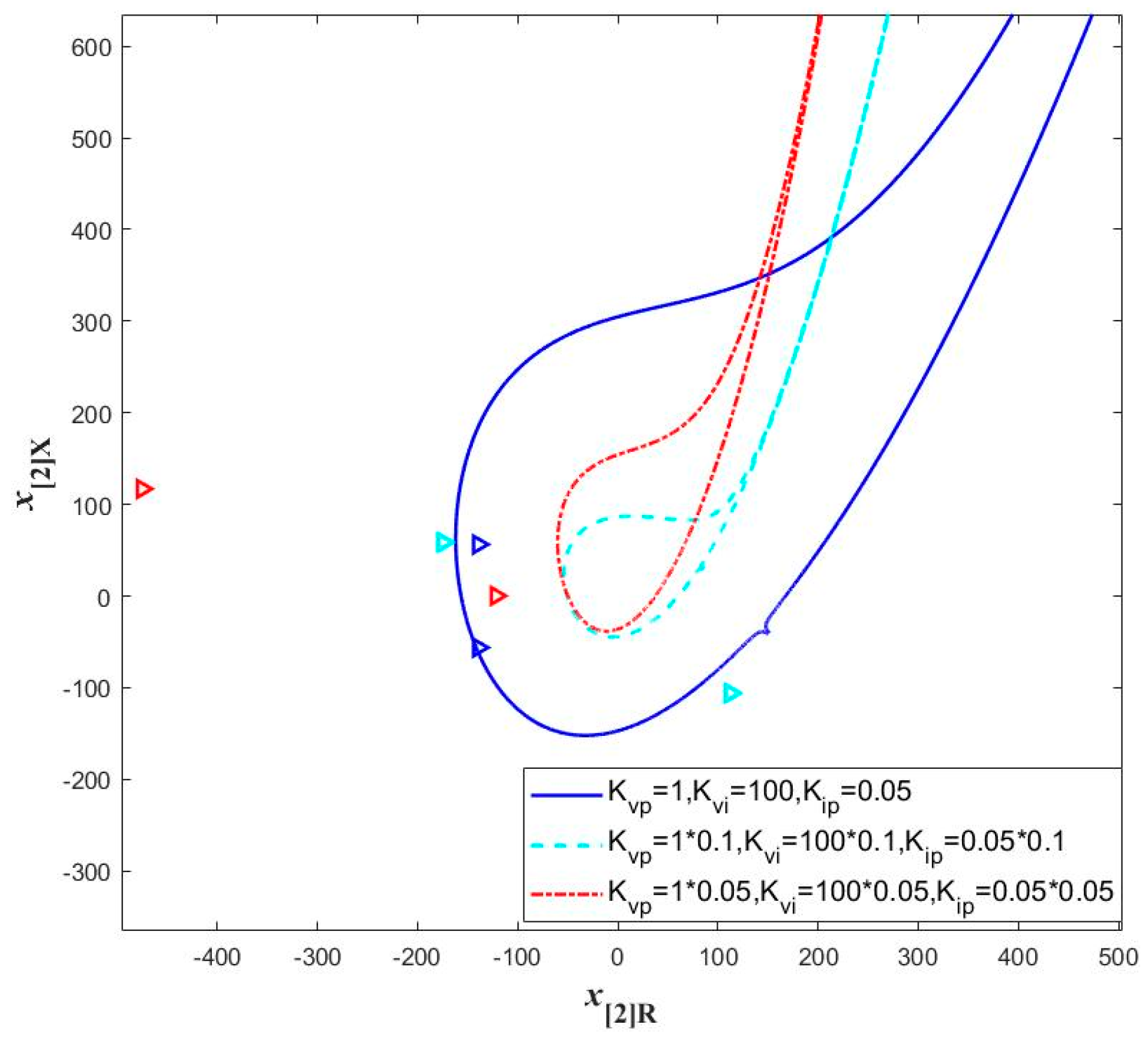
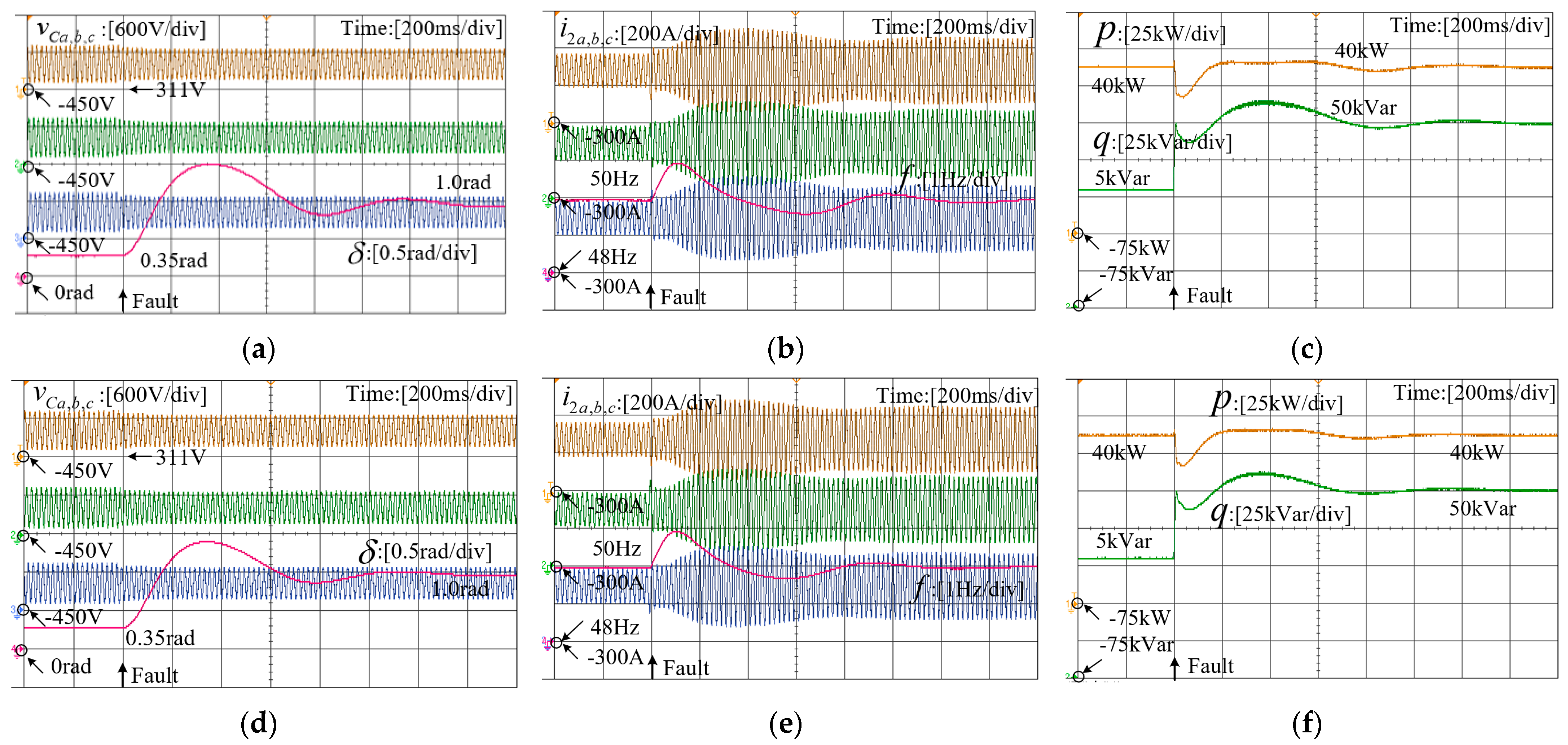
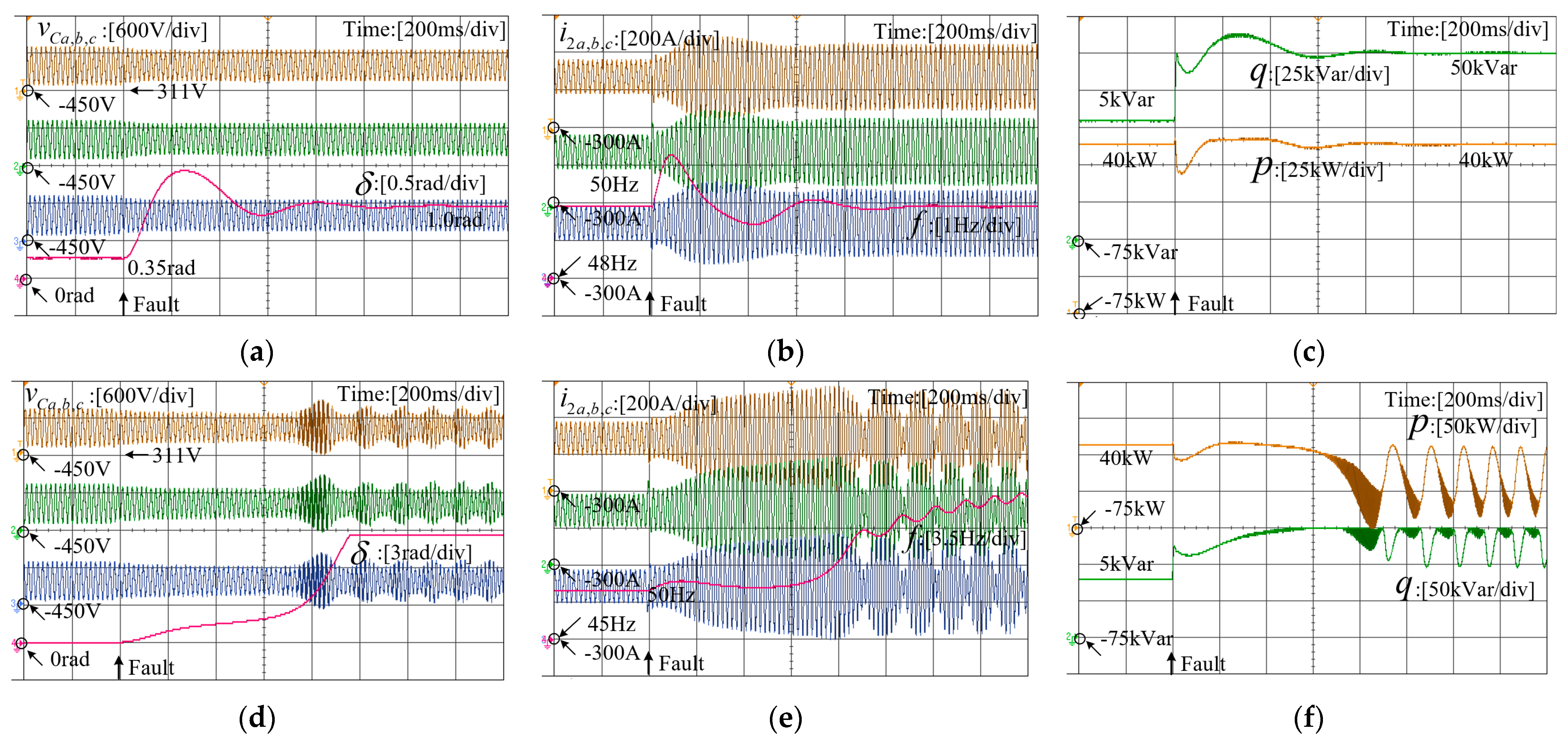
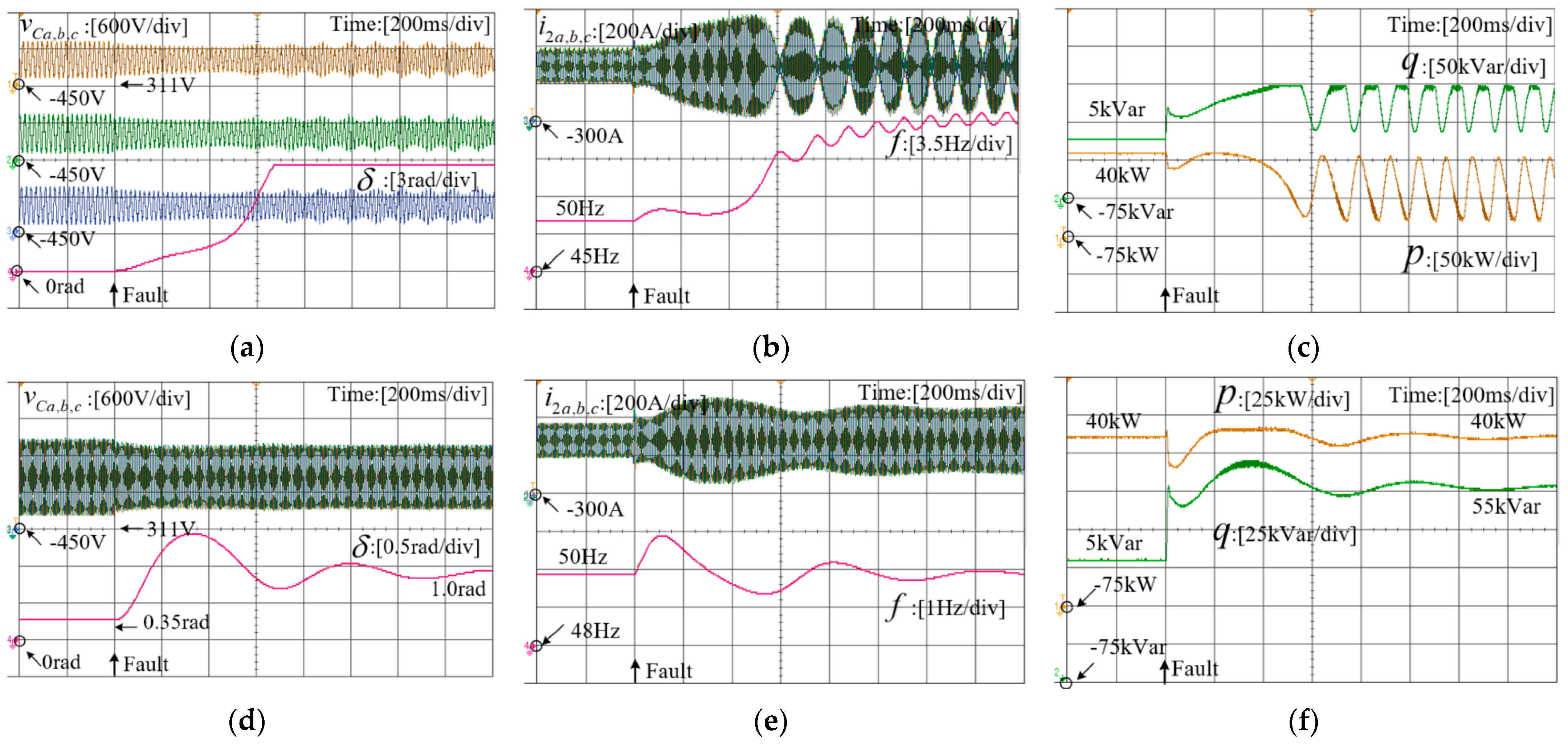
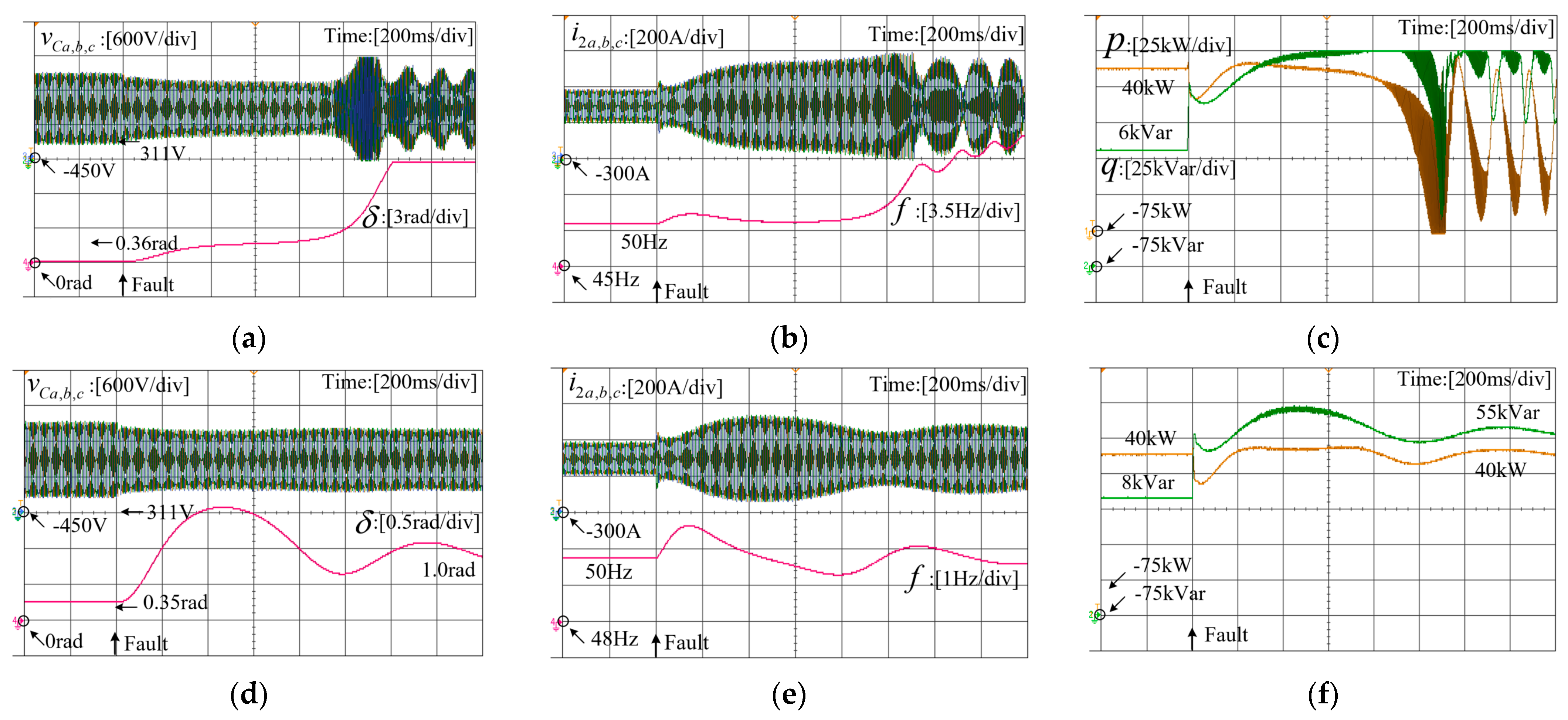
3.4. Typical Cases for Transient Stability Analysis
4. Discussions
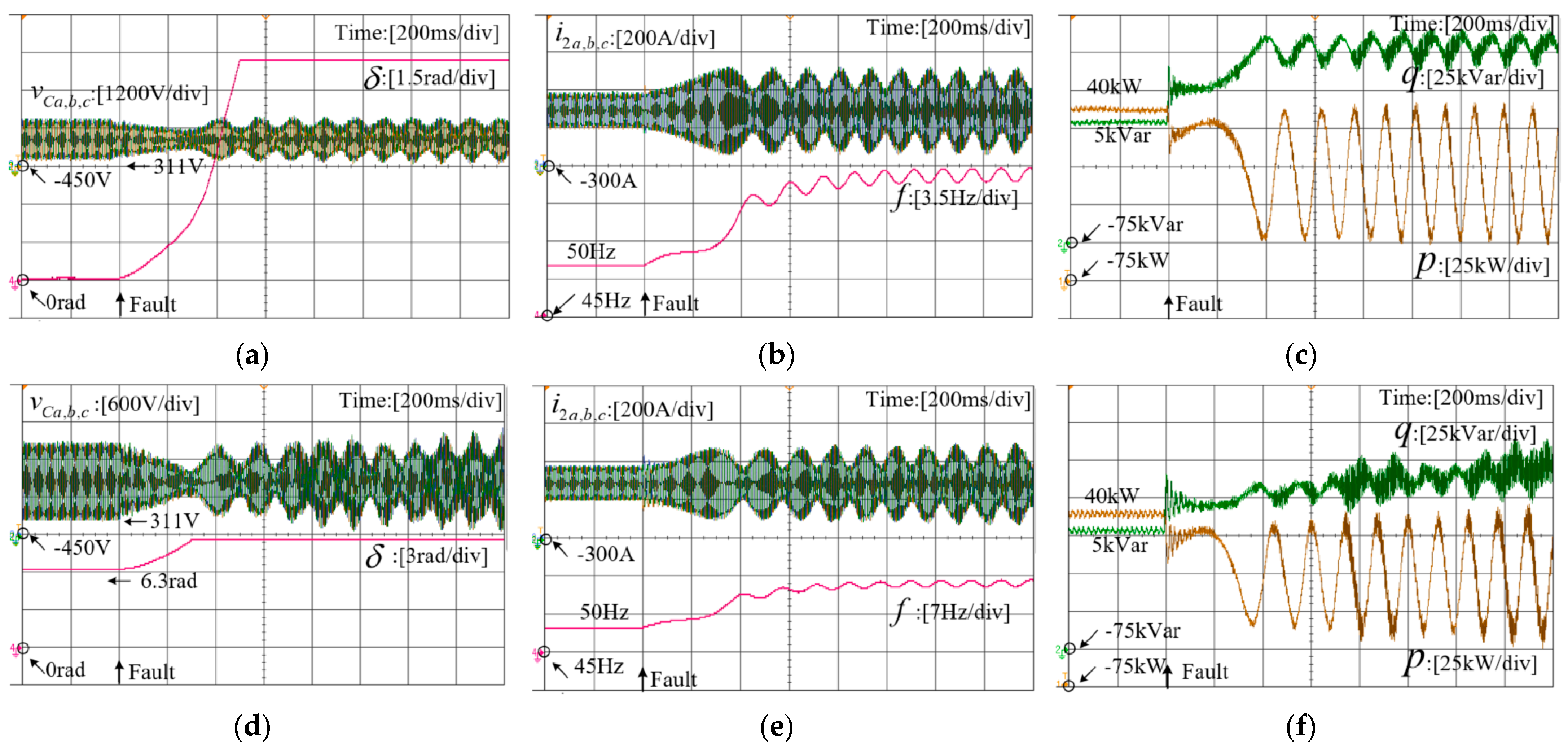
5. HIL Experiment Verification
6. Conclusions
- (1)
- The transient stability of grid-forming inverters diminishes with increasing voltage-amplitude drop in the grid. In essence, a larger magnitude of voltage drop in the grid corresponds to a higher likelihood of transient instability occurring in the system.
- (2)
- The analysis demonstrates that the damping parameters and inertia parameters within the active power loop exert varying influences on the transient stability of grid-forming VSCs. A larger damping parameter effectively mitigates power-angle fluctuations, facilitating the restoration of steady-state operation points. Conversely, a higher inertia parameter narrows the ROA of the critical mode, thereby diminishing the system’s transient stability.
- (3)
- Furthermore, the impact of parameters in the reactive power loop on transient stability was also examined. An increased voltage-drop coefficient and reactive power reference value are shown to enhance transient stability.
- (4)
- In the existing literature, the transient stability analysis of grid-forming VSCs relies on establishing a quasi-steady-state model that exclusively focuses on the outer control loop. This approach is relatively accurate when there is a significant difference in bandwidth between the inner and outer loops. However, current methods completely disregard the impact of the inner control loop, rendering them unable to analyze the transient stability of the system when the inner loop parameters change. In this paper, the method for developing the quasi-steady-state model based on the existing literature is presented. Subsequently, the existing method is used to analyze the transient stability with the same parameters, and the obtained results are compared with the stability analysis results of the full-order model adopted in this paper. The comparison indicates that the proposed method offers a more comprehensive approach to transient analysis for grid-forming VSC systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- D’Adamo, I.; Mammetti, M.; Ottaviani, D.; Ozturk, I. Photovoltaic systems and sustainable communities: New social models for ecological transition. The impact of incentive policies in profitability analyses. Renew. Energy 2023, 202, 1291–1304. [Google Scholar] [CrossRef]
- Olabi, A.G.; Obaideen, K.; Abdelkareem, M.A.; AlMallahi, M.N.; Shehata, N.; Alami, A.H.; Mdallal, A.; Hassan, A.A.M.; Sayed, E.T. Wind Energy Contribution to the Sustainable Development Goals: Case Study on London Array. Sustainability 2023, 15, 4641. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Gupta, M.K.; Yadav, J.; Jain, A. solar tree-based water pumping for assured irrigation in sustainable Indian agriculture environment. Sustain. Prod. Consum. 2022, 33, 15–27. [Google Scholar] [CrossRef]
- Kumar, R.; Pachauri, R.K.; Badoni, P.; Bharadwaj, D.; Mittal, U.; Bisht, A. Investigation on parallel hybrid electric bicycle along with issuer management system for mountainous region. J. Clean. Prod. 2022, 362, 132430. [Google Scholar] [CrossRef]
- Raupp, I.P.; da Paz, L.R.L.; da Serra Costa, F.; de Matos, D.F.; Garcia, K.C. Key challenges of sustainable hydropower in the context of energy transition: A Brazilian contribution. In Renewable Energy Production and Distribution; Jeguirim, M., Dutournié, P., Eds.; Academic Press: Cambridge, MA, USA, 2023; Volume 2, pp. 315–349. [Google Scholar]
- Costa, J.; Kilajian, A.; Kadyrzhanova, A. Hydropower Sustainability Assessment. Comprehensive Renewable Energy, 2nd ed.; Letcher, T.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 202–224. [Google Scholar]
- Kondrakhin, V.P.; Martyushev, N.V.; Klyuev, R.V.; Sorokova, S.N.; Efremenkov, E.A.; Valuev, D.V.; Mengxu, Q. Mathematical Modeling and Multi-Criteria Optimization of Design Parameters for the Gyratory Crusher. Mathematics 2023, 11, 2345. [Google Scholar] [CrossRef]
- Meera, C.S.; Sunny, S.; Singh, R.; Sairam, P.S.; Kumar, R.; Emannuel, J. Automated precise liquid transferring system. In Proceedings of the 2014 IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; pp. 1–6. [Google Scholar]
- Xia, Y.; Wei, W.; Yu, M.; Wang, X.; Peng, Y. Power Management for a Hybrid AC/DC Microgrid With Multiple Subgrids. IEEE Trans. Power Electron. 2018, 33, 3520–3533. [Google Scholar] [CrossRef]
- Xia, Y.; Wei, W.; Yu, M.; Peng, Y.; Tang, J. Decentralized Multi-Time Scale Power Control for a Hybrid AC/DC Microgrid With Multiple Subgrids. IEEE Trans. Power Electron. 2018, 33, 4061–4072. [Google Scholar] [CrossRef]
- Popella, H.; Hennig, T.; Kaiser, M.; Massmann, J.; Müller, L.; Pfeiffer, R. Necessary development of inverter-based generation with grid forming capabilities in Germany. In Proceedings of the 20th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants (WIW 2021), Hybrid Conference, Berlin, Germany, 29–30 September 2021; pp. 125–129. [Google Scholar]
- Noguchi, T.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Xia, Y.; Wei, W.; Long, T.; Blaabjerg, F.; Wang, P. New Analysis Framework for Transient Stability Evaluation of DC Microgrids. IEEE Trans. Smart Grid 2020, 11, 2794–2804. [Google Scholar] [CrossRef]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-Synchronization Stability of Converter-Based Resources—An Overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Yang, P.; Xia, Y.; Yu, M.; Wei, W.; Peng, Y. A Decentralized Coordination Control Method for Parallel Bidirectional Power Converters in a Hybrid AC–DC Microgrid. IEEE Trans. Ind. Electron. 2018, 65, 6217–6228. [Google Scholar] [CrossRef]
- Wen, B.; Dong, D.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Impedance-Based Analysis of Grid-Synchronization Stability for Three-Phase Paralleled Converters. IEEE Trans. Power Electron. 2016, 31, 26–38. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Small-Signal Stability Assessment of Power Electronics Based Power Systems: A Discussion of Impedance- and Eigenvalue-Based Methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of PLL-Synchronized Voltage-Source Converters. IEEE Trans. Power Electron. 2020, 35, 3573–3589. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Tsinghua University; Geng, H.; Ma, S. Transient Stability Analysis of Grid-Tied Converters Considering PLL’s Nonlinearity. CPSS Trans. Power Electron. Appl. 2019, 4, 40–49. [Google Scholar] [CrossRef]
- Tang, Y.; Tian, Z.; Zha, X.; Li, X.; Huang, M.; Sun, J. An Improved Equal Area Criterion for Transient Stability Analysis of Converter-Based Microgrid Considering Nonlinear Damping Effect. IEEE Trans. Power Electron. 2022, 37, 11272–11284. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters With Grid-Forming Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient Angle Stability of Virtual Synchronous Generators Using Lyapunov’s Direct Method. IEEE Trans. Smart Grid 2019, 10, 4648–4661. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Blaabjerg, F. Effects of Virtual Resistance on Transient Stability of Virtual Synchronous Generators Under Grid Voltage Sag. IEEE Trans. Ind. Electron. 2022, 69, 4754–4764. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Han, H.; Fu, S.; Luo, S.; Shi, G. A Modified VSG Control Scheme With Virtual Resistance to Enhance Both Small-Signal Stability and Transient Synchronization Stability. IEEE Trans. Power Electron. 2023, 38, 6005–6014. [Google Scholar] [CrossRef]
- Ge, P.; Tu, C.; Xiao, F.; Guo, Q.; Gao, J. Design-Oriented Analysis and Transient Stability Enhancement Control for a Virtual Synchronous Generator. IEEE Trans. Ind. Electron. 2023, 70, 2675–2684. [Google Scholar] [CrossRef]
- Koditschek, D.; Narendra, K. The stability of second-order quadratic differential equations. IEEE Trans. Autom. Control 1982, 27, 783–798. [Google Scholar] [CrossRef] [Green Version]
- Tian, T.; Kestelyn, X.; Thomas, O.; Amano, H.; Messina, A.R. An Accurate Third-Order Normal Form Approximation for Power System Nonlinear Analysis. IEEE Trans. Power Syst. 2018, 33, 2128–2139. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.-C. Small-Signal Modeling and Parameters Design for Virtual Synchronous Generators. IEEE Trans. Ind. Electron. 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Bao, C.; Li, W.; Wang, X. Optimized Controller Design for LCL-Type Grid-Connected Inverter to Achieve High Robustness Against Grid-Impedance Variation. IEEE Trans. Ind. Electron. 2015, 62, 1537–1547. [Google Scholar] [CrossRef]





| Method | Description | Application | Advantages | Disadvantages |
|---|---|---|---|---|
| Equal area criterion (EAC) [23] | Evaluates stability by comparing the areas of transient response curves | Analyzes transient stability of second-order models | Intuitive and easy to apply | Only applicable to systems with simplified second-order models |
| Lyapunov method [25] | Constructs Lyapunov function to demonstrate asymptotic and local stability | Analyzes stability of high-order nonlinear systems | Provides mathematical proof of system stability | Constructing the Lyapunov function is challenging, and the results tend to be conservative |
| Normal form method [30] | Transforms system to linear decoupled form | Analyzes stability of high-order nonlinear systems | Stability analysis of the transformed system can be conducted with linear theory | Only the combination of linear modes can be considered, and the information about the system’s ROA cannot be obtained |
| The nonlinear decoupling method adopted in this paper | Transforms system to low-order modes to reflect transient stability | Analyzes stability of high-order nonlinear systems | Applicable to various high-order models | Computational complexity increases, and truncation error exists |
| Symbol | Parameters | Value |
|---|---|---|
| Reference of active and reactive power | 40 kW, 0 kVar | |
| Virtual inertia | 200 kg·m2 | |
| Damping coefficient | 800 (N·m·s)/rad | |
| Reactive-voltage droop coefficient | 800 Var/V | |
| The voltage of the DC side | 1000 V | |
| Inductance and capacitance | 5 mH, 200 uF, 4 mH | |
| Proportional and integral parameters | 1, 100, 0.005 |
| Parameters | Impact on Transient Stability |
|---|---|
| Voltage-amplitude sag | The greater the voltage magnitude drop, the more likely the system is to experience transient instability. |
| Active power control loop parameters | Increasing the damping coefficient contributes to transient stability in the system, while increasing the inertia coefficient may lead to transient instability in the system. |
| Reactive power control loop parameters | Increasing the voltage-reactive power droop coefficient and reactive power reference value helps to improve the transient stability of the system. |
| Inner loop control parameters | The control parameters of the current inner loop result in significant changes to the stability region of the system, and excessively small control parameters of the current inner loop may lead to transient instability in the system. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xia, Y.; Ni, Y.; Peng, Y.; Feng, Q. Transient Stability Analysis for Grid-Forming VSCs Based on Nonlinear Decoupling Method. Sustainability 2023, 15, 11981. https://doi.org/10.3390/su151511981
Li Y, Xia Y, Ni Y, Peng Y, Feng Q. Transient Stability Analysis for Grid-Forming VSCs Based on Nonlinear Decoupling Method. Sustainability. 2023; 15(15):11981. https://doi.org/10.3390/su151511981
Chicago/Turabian StyleLi, Yue, Yanghong Xia, Yini Ni, Yonggang Peng, and Qifan Feng. 2023. "Transient Stability Analysis for Grid-Forming VSCs Based on Nonlinear Decoupling Method" Sustainability 15, no. 15: 11981. https://doi.org/10.3390/su151511981
APA StyleLi, Y., Xia, Y., Ni, Y., Peng, Y., & Feng, Q. (2023). Transient Stability Analysis for Grid-Forming VSCs Based on Nonlinear Decoupling Method. Sustainability, 15(15), 11981. https://doi.org/10.3390/su151511981







