Numerical Simulation Analysis and Full-Scale Experimental Validation of a Lower Wall-Mounted Solar Chimney with Different Radiation Models
Abstract
:1. Introduction
2. Radiation Model Theory
3. Methodology
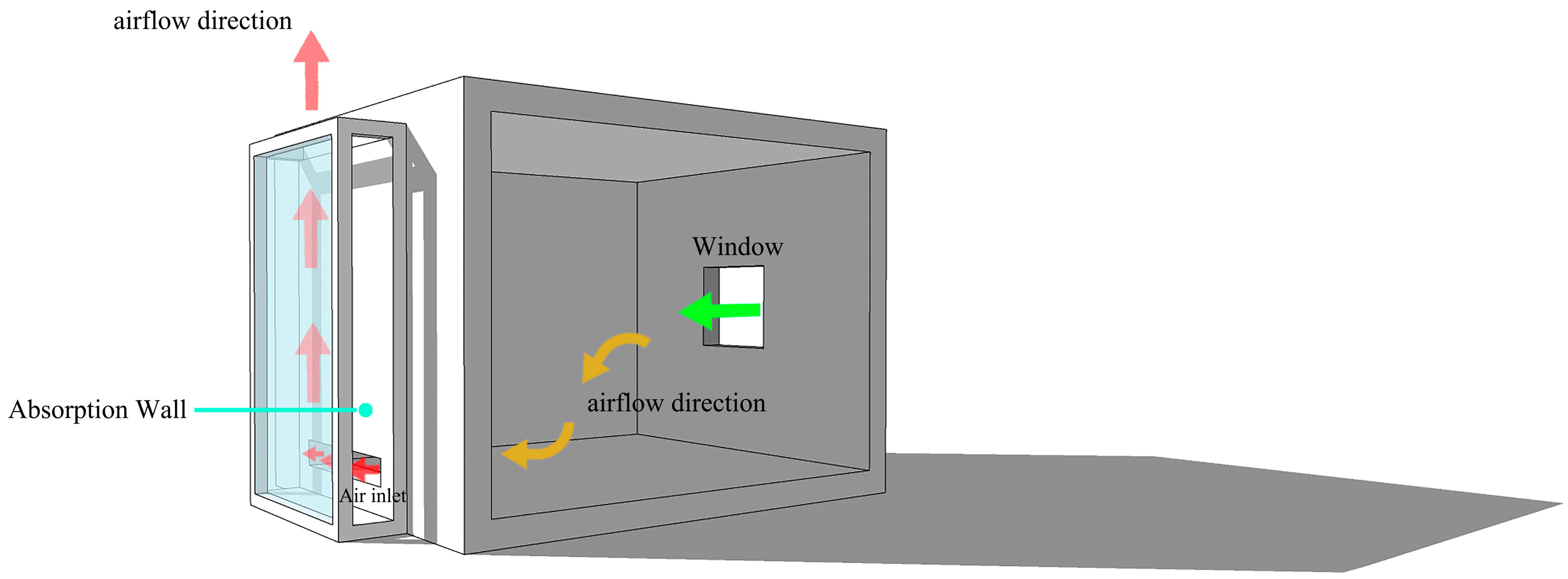
3.1. Physical Grid Model
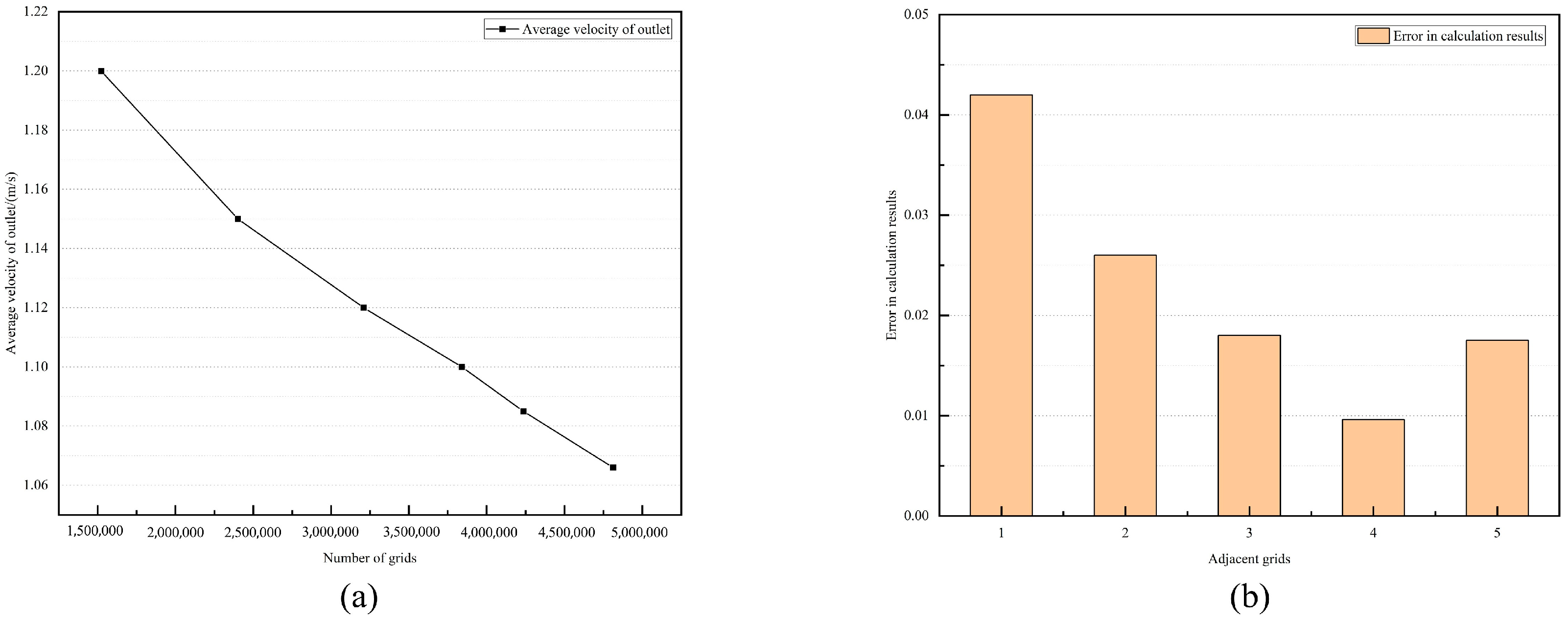
3.2. Grid-Independent Verification
3.3. Boundary Conditions and Turbulence Model
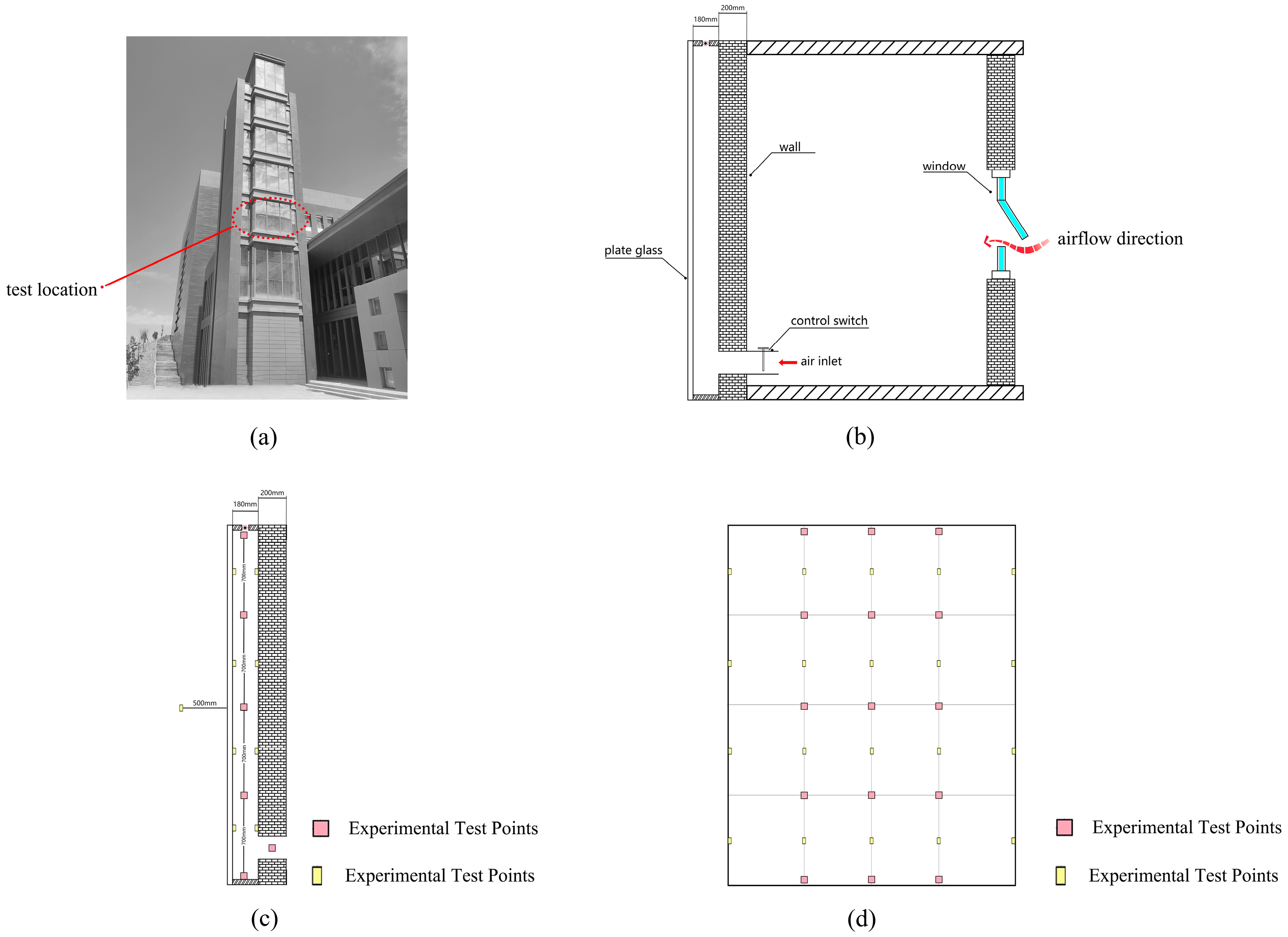
3.4. Full-Scale Experiments
4. Results and Discussion
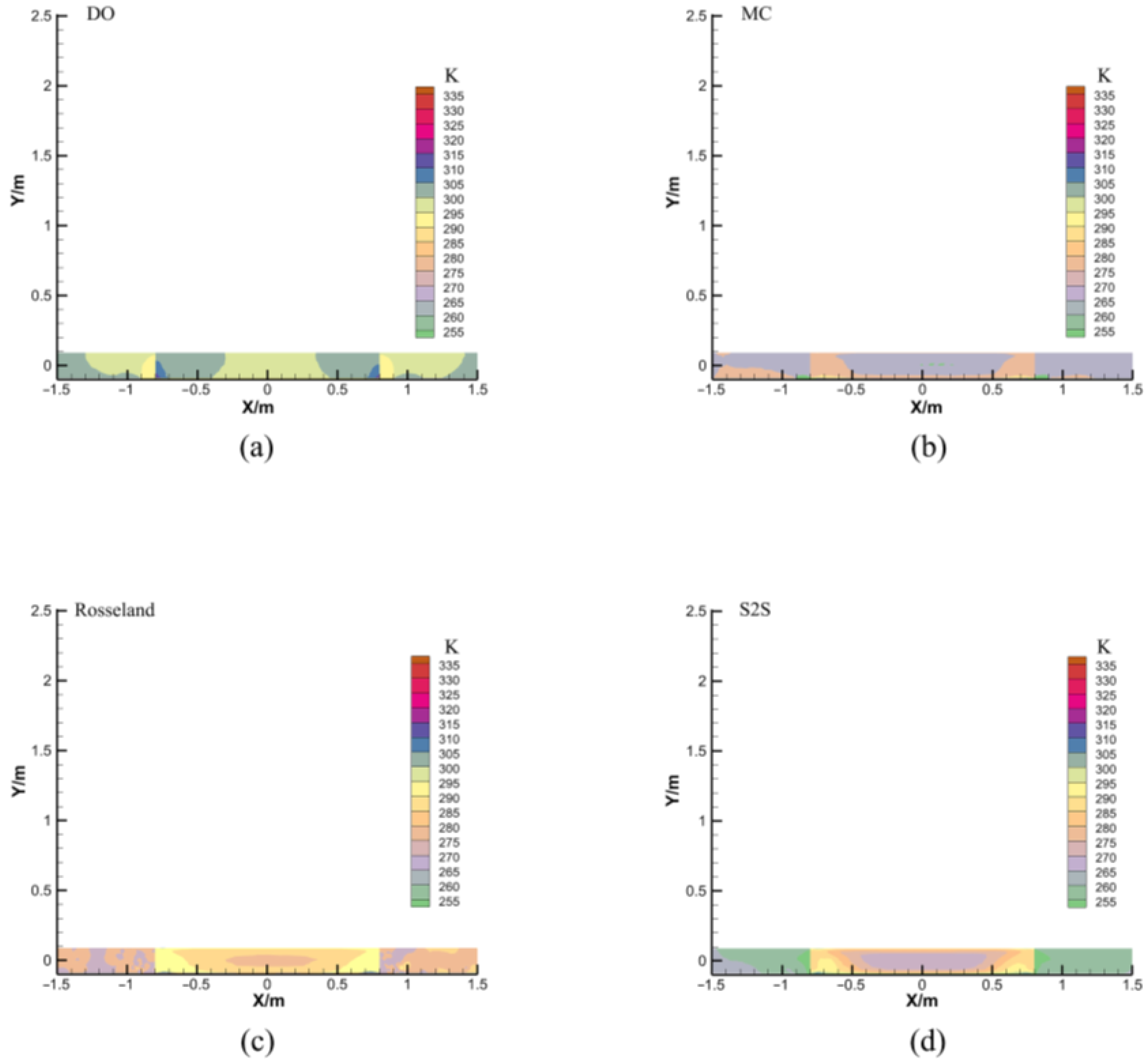
4.1. Specific Enthalpy at the Outlet and Turbulence Distribution at the Inlet
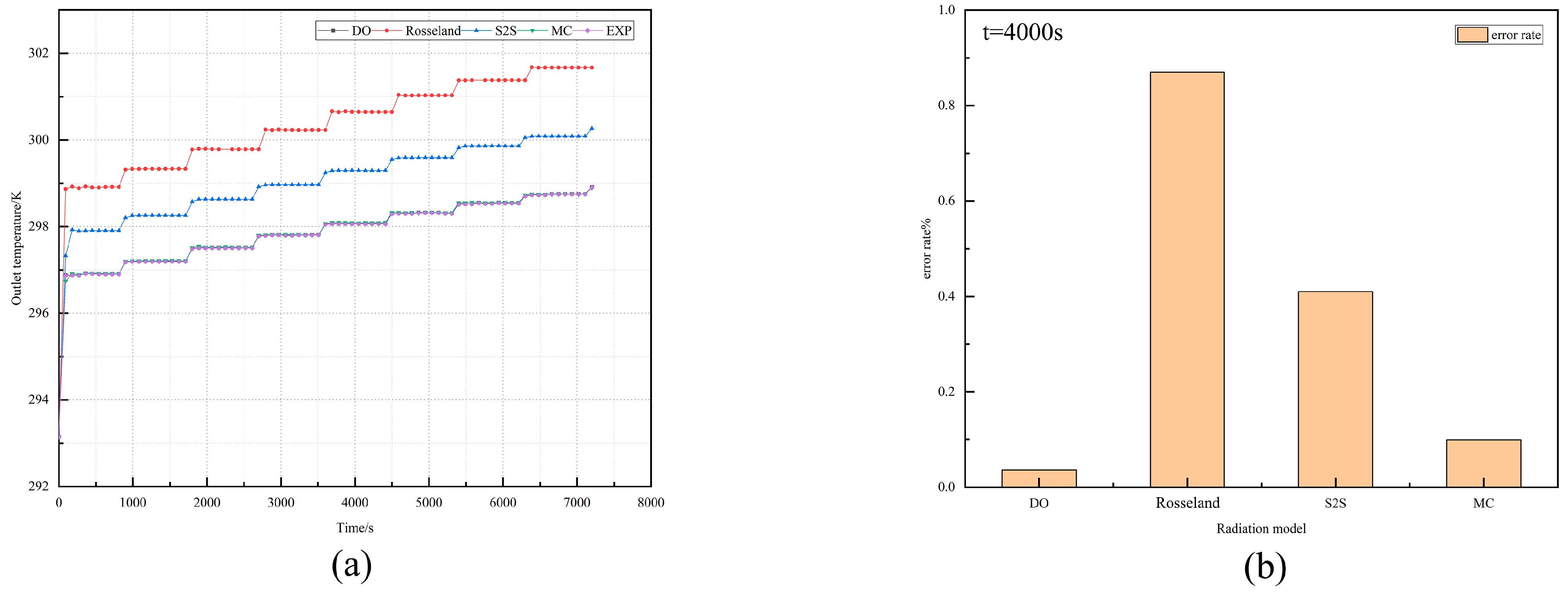
4.2. Comparison of Exit Velocity and Temperature Characteristics
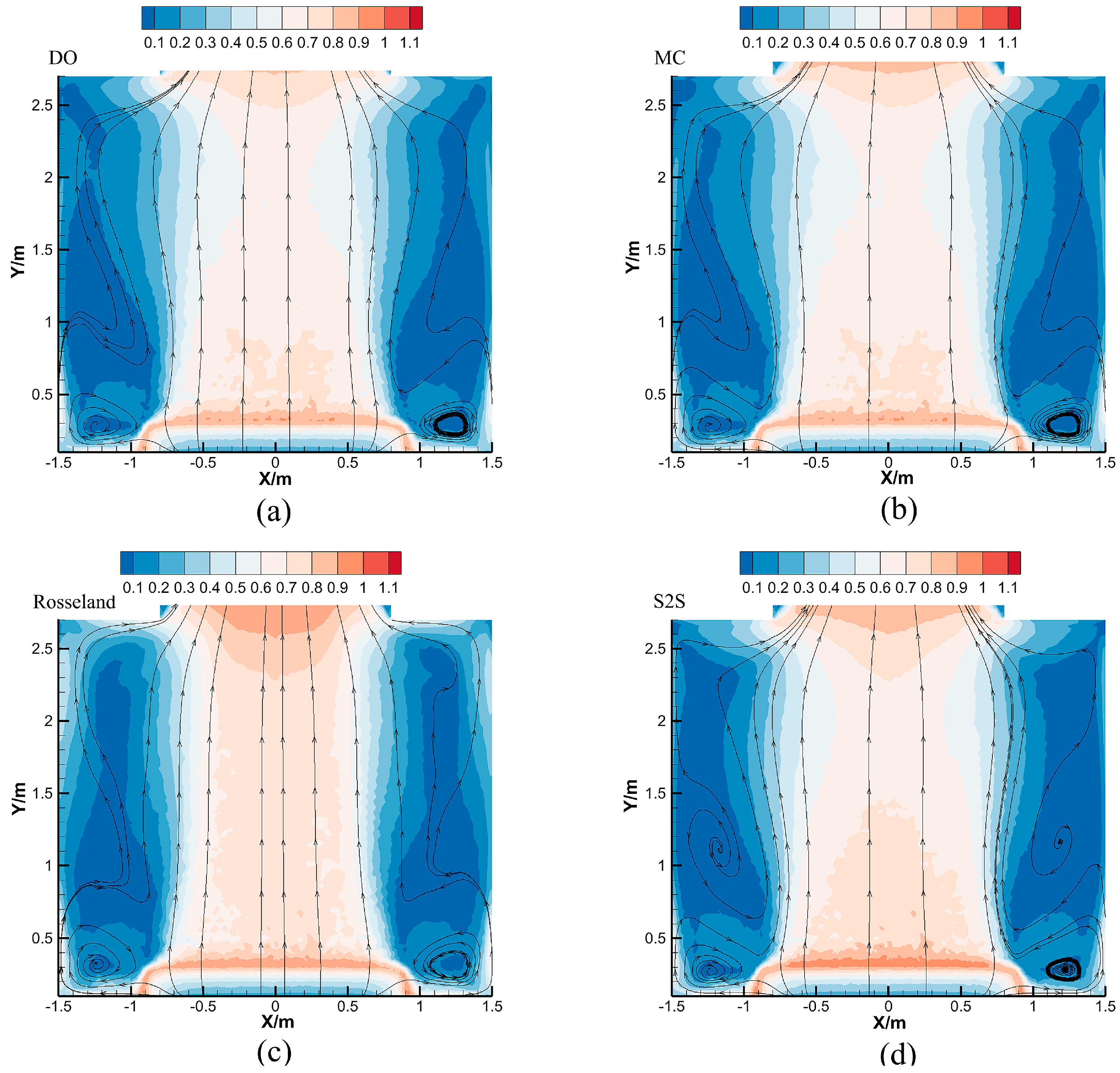
4.3. Internal Flow Field and Temperature Distribution
5. Conclusions
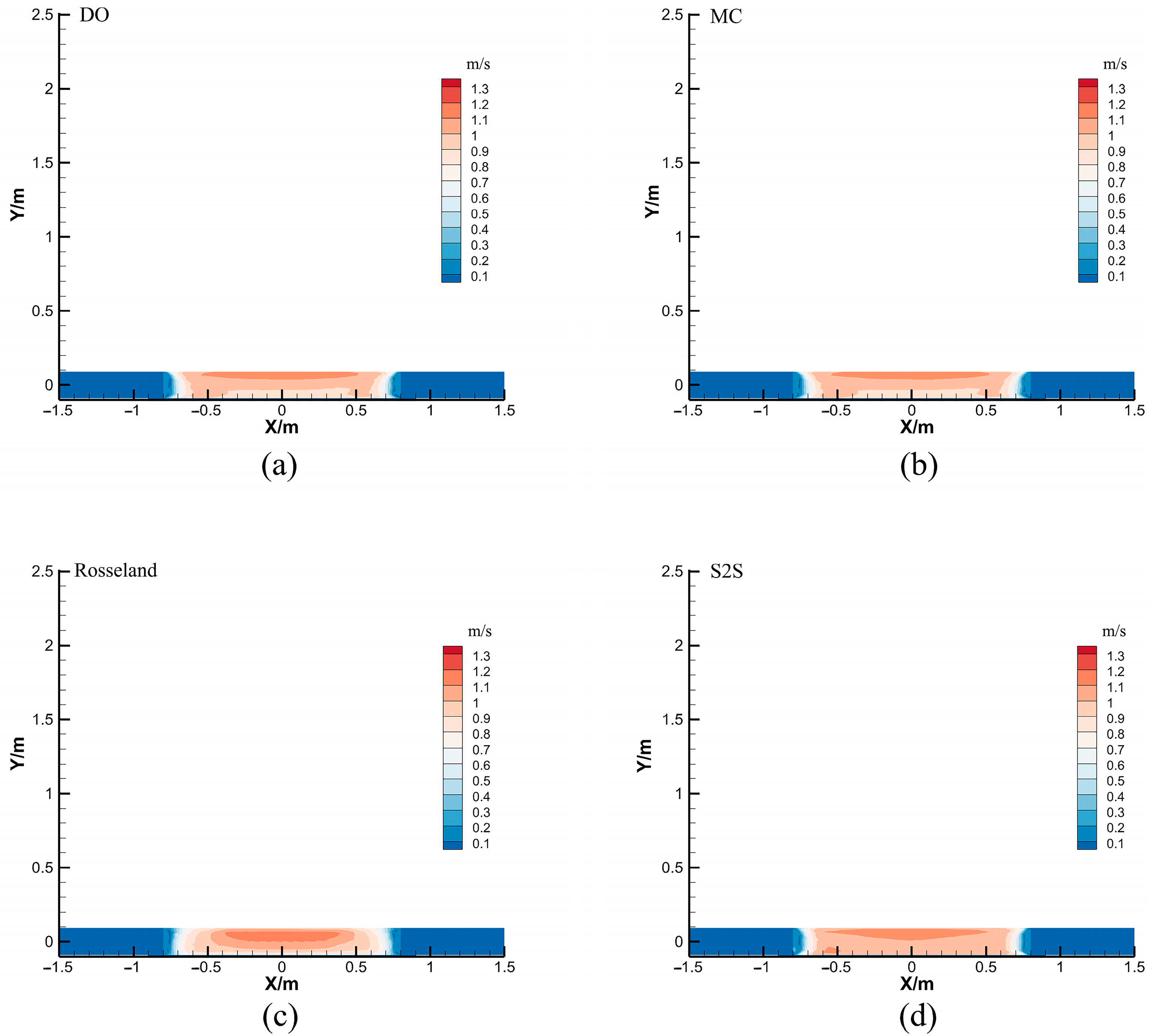
- The peak specific enthalpy of the S2S radiation model at the boundary on both sides of the outlet is 53.2%, 23.4%, and 54.2% higher than that of the DO, Rosseland, and MC radiation models.
- The S2S radiation model focuses only on the radiative heat transfer process at the surface of the walled solar chimney, ignoring the radiation effect within the air and, therefore, its predicted maximum turbulent fluid viscosity is higher than that of the MC and DO models by 16.87% and 8.44%, respectively.
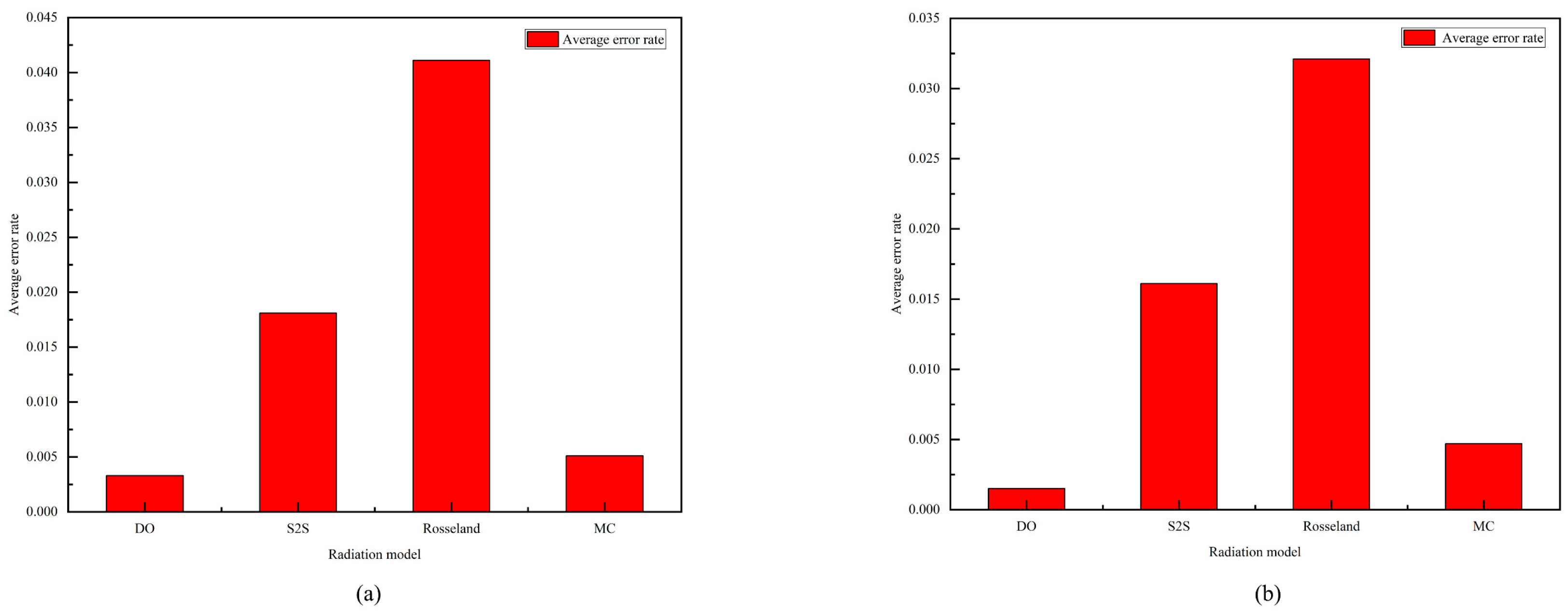
- The error between the DO radiation model and the experimental results in the mid-axis and glass cover directions is only 0.33% and 0.15%, respectively; the error of the MC radiation model in these two directions is 0.51% and 0.47%, respectively. Although the S2S radiation model also considers the surface radiative heat transfer inside the walled solar chimney, its simulation results disagree with the experimental results, with errors of 1.81% and 1.61% in the central axis and glass cover directions, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| absorption coefficient | |
| directional vector volume | |
| scattering coefficient | |
| phase functions | |
| position vector | |
| three-dimensional angle | |
| radiation intensity | |
| refraction rate | |
| k total radiant energy of the surface | |
| k surface transmitting power | |
| k surface reflectance | |
| the view factor between the k surface and j surface | |
| i radiant energy emitted by the surface | |
| constants | |
| constants | |
| constants | |
| turbulent kinetic energy from mean velocity gradients | |
| computational fluid dynamics | |
| buoyancy turbulent kinetic energy from force effects | |
| compressible turbulent pulsating expansion effect on total dissipation rate | |
| source terms | |
| effective viscosity | |
| fluid density | |
| turbulent dissipation rate | |
| turbulence kinetic energy | |
| DO | discrete ordinates radiation model |
| MC | Monte Carlo radiation model |
| Rosseland | Rosseland radiation model |
| S2S | surface-to-surface radiation model |
References
- Salehi, A.; Fayaz, R.; Bozorgi, M.; Asadi, S.; Costanzo, V.; Imani, N.; Nocera, F. Investigation of thermal comfort efficacy of solar chimneys under different climates and operation time periods. Energy Build. 2019, 205, 109528. [Google Scholar] [CrossRef]
- Fang, Z.C.; Wang, W.J.; Chen, Y.H.; Song, J.K. Structural and Heat Transfer Model Analysis of Wall-Mounted Solar Chimney Inlets and Outlets in Single-Story Buildings. Buildings 2022, 12, 1790. [Google Scholar] [CrossRef]
- Jiménez-Xamán, C.; Xamán, J.; Moraga, N.O.; Hernández-Pérez, I.; Zavala-Guillén, I.; Arce, J.; Jiménez, M.J. Solar chimneys with a phase change material for buildings: An overview using CFD and global energy balance. Energy Build. 2019, 186, 384–404. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Sreejaya, K.V.; Chikere, A.O. Experimental and numerical analysis of the influence of inlet configuration on the performance of a roof top solar chimney. Energy Build. 2018, 159, 89–98. [Google Scholar] [CrossRef]
- Khanal, R.; Lei, C. Solar chimney—A passive strategy for natural ventilation. Energy Build. 2011, 43, 1811–1819. [Google Scholar] [CrossRef]
- Jianliu, X.; Weihua, L. Study on solar chimney used for room natural ventilation in Nanjing. Energy Build. 2013, 66, 467–469. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, B.; Suhendri; Ao, X.; Cao, J.; Wang, Q.; Riffat, S.; Su, Y.; Pei, G. Applications of radiative sky cooling in solar energy systems: Progress, challenges, and prospects. Renew. Sustain. Energy Rev. 2022, 160, 112304. [Google Scholar] [CrossRef]
- Hou, Y.; Li, H.; Li, A. Experimental and theoretical study of solar chimneys in buildings with uniform wall heat flux. Sol. Energy 2019, 193, 244–252. [Google Scholar] [CrossRef]
- Zhong, H.-Y.; Sun, Y.; Shang, J.; Qian, F.-P.; Zhao, F.-Y.; Kikumoto, H.; Jimenez-Bescos, C.; Liu, X. Single-sided natural ventilation in buildings: A critical literature review. Build. Environ. 2022, 212, 108797. [Google Scholar] [CrossRef]
- Rezaei, L.; Saeidi, S.; Sápi, A.; Abdollahi Senoukesh, M.R.; Gróf, G.; Chen, W.-H.; Kónya, Z.; Klemeš, J.J. Efficiency improvement of the solar chimneys by insertion of hanging metallic tubes in the collector: Experiment and computational fluid dynamics simulation. J. Clean. Prod. 2023, 415, 137692. [Google Scholar] [CrossRef]
- Jiang, Z.; Kobayashi, T.; Yamanaka, T.; Sandberg, M. A literature review of cross ventilation in buildings. Energy Build. 2023, 291, 113143. [Google Scholar] [CrossRef]
- Soto, A.; Martínez, P.J.; Martínez, P.; Tudela, J.A. Simulation and experimental study of residential building with north side wind tower assisted by solar chimneys. J. Build. Eng. 2021, 43, 102562. [Google Scholar] [CrossRef]
- Zhang, H.; Tao, Y.; Nguyen, K.; Han, F.; Li, J.; Shi, L. A wall solar chimney to ventilate multi-zone buildings. Sustain. Energy Technol. Assess. 2021, 47, 101381. [Google Scholar] [CrossRef]
- Hussam, W.K.; Salem, H.J.; Redha, A.M.; Khlefat, A.M.; Al Khatib, F. Experimental and numerical investigation on a hybrid solar chimney-photovoltaic system for power generation in Kuwait. Energy Convers. Manag. X 2022, 15, 100249. [Google Scholar] [CrossRef]
- Bayareh, M. Exergy analysis of solar chimney power plants: A review. Sustain. Energy Technol. Assess. 2022, 53, 102568. [Google Scholar] [CrossRef]
- Maghrabie, H.M.; Abdelkareem, M.A.; Elsaid, K.; Sayed, E.T.; Radwan, A.; Rezk, H.; Wilberforce, T.; Abo-Khalil, A.G.; Olabi, A.G. A review of solar chimney for natural ventilation of residential and non-residential buildings. Sustain. Energy Technol. Assess. 2022, 52, 102082. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, Y.; Wang, F.; Wang, X. Enhancement of natural ventilation of a novel roof solar chimney with perforated absorber plate for building energy conservation. Appl. Therm. Eng. 2016, 107, 653–661. [Google Scholar] [CrossRef]
- Praveen, V.; Chandramohan, V.P. Numerical study on optimization of fillet size on the chimney base of solar updraft tower plant for enhanced performance. Therm. Sci. Eng. Prog. 2022, 34, 101400. [Google Scholar] [CrossRef]
- Kebabsa, H.; Said Lounici, M.; Daimallah, A. Numerical investigation of a novel tower solar chimney concept. Energy 2021, 214, 119048. [Google Scholar] [CrossRef]
- Abdelsalam, E.; Almomani, F.; Ibrahim, S.; Kafiah, F.; Jamjoum, M.; Alkasrawi, M. A Novel Design of a Hybrid Solar Double-Chimney Power Plant for Generating Electricity and Distilled Water. Sustainability 2023, 15, 2729. [Google Scholar] [CrossRef]
- Maia, C.B.; Castro Silva, J.d.O. CFD Analysis of a Small-Scale Solar Chimney Exposed to Ambient Crosswind. Sustainability 2022, 14, 5208. [Google Scholar] [CrossRef]
- Kong, J.; Niu, J.; Lei, C. A CFD based approach for determining the optimum inclination angle of a roof-top solar chimney for building ventilation. Sol. Energy 2020, 198, 555–569. [Google Scholar] [CrossRef]
- Yoo, S.; Oh, S.; Hachicha, A.A. Numerical simulation and performance evaluation of filter-equipped solar chimney power plants. Appl. Therm. Eng. 2023, 218, 119284. [Google Scholar] [CrossRef]
- Nguyen, Y.Q.; Wells, J.C. A numerical study on induced flowrate and thermal efficiency of a solar chimney with horizontal absorber surface for ventilation of buildings. J. Build. Eng. 2020, 28, 101050. [Google Scholar] [CrossRef]
- Guo, P.; Wang, S.; Lei, Y.; Li, J. Numerical simulation of solar chimney-based direct airside free cooling system for green data centers. J. Build. Eng. 2020, 32, 101793. [Google Scholar] [CrossRef]
- Saifi, N.; Settou, N.; Dokkar, B.; Negrou, B.; Chennouf, N. Experimental Study And Simulation Of Airflow In Solar Chimneys. Energy Procedia 2012, 18, 1289–1298. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, D. The Study on Numerical Simulation of Classrooms Using Hybrid Ventilation Under Different Solar Chimney Radiation. Procedia Eng. 2015, 121, 1083–1088. [Google Scholar] [CrossRef] [Green Version]
- Aligholami, M.; Khosroshahi, S.S.; Khosroshahi, A.R. Hydrodynamic and thermodynamic enhancement of a solar chimney power plant. Sol. Energy 2019, 191, 180–192. [Google Scholar] [CrossRef]
- Hu, G.; Schietekat, C.M.; Zhang, Y.; Qian, F.; Heynderickx, G.; Van Geem, K.M.; Marin, G.B. Impact of Radiation Models in Coupled Simulations of Steam Cracking Furnaces and Reactors. Ind. Eng. Chem. Res. 2015, 54, 2453–2465. [Google Scholar] [CrossRef]
- Zhang, H.; Tao, Y.; Zhang, G.; Tam, V.W.Y.; Fan, C.; Shi, L. Ventilation performance of solar chimney integrated into a multi-storey building. Sustain. Energy Technol. Assess. 2022, 54, 102868. [Google Scholar] [CrossRef]
- Torabi, M.R.; Hosseini, M.; Akbari, O.A.; Afrouzi, H.H.; Toghraie, D.; Kashani, A.; Alizadeh, A.a. Investigation the performance of solar chimney power plant for improving the efficiency and increasing the outlet power of turbines using computational fluid dynamics. Energy Rep. 2021, 7, 4555–4565. [Google Scholar] [CrossRef]
- Suhendri, S.; Hu, M.; Su, Y.; Darkwa, J.; Riffat, S. Performance evaluation of combined solar chimney and radiative cooling ventilation. Build. Environ. 2022, 209, 108686. [Google Scholar] [CrossRef]
- Fasel, H.F.; Meng, F.; Shams, E.; Gross, A. CFD analysis for solar chimney power plants. Sol. Energy 2013, 98, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Wang, T. Investigation of radiation models in entrained-flow coal gasification simulation. Int. J. Heat Mass Transf. 2013, 67, 377–392. [Google Scholar] [CrossRef]
- Najm, O.A.; Shaaban, S. Numerical investigation and optimization of the solar chimney collector performance and power density. Energy Convers. Manag. 2018, 168, 150–161. [Google Scholar] [CrossRef]
- Shahreza, A.R.; Imani, H. Experimental and numerical investigation on an innovative solar chimney. Energy Convers. Manag. 2015, 95, 446–452. [Google Scholar] [CrossRef]
- Dai, B.; Ma, J.; Zhu, D.; Liu, Q.; Chai, J. Thermal performance of a directional heat radiation device utilizing the Monte Carlo ray tracing method. Appl. Therm. Eng. 2022, 217, 119257. [Google Scholar] [CrossRef]
- Ayadi, A.; Driss, Z.; Bouabidi, A.; Abid, M.S. Experimental and numerical study of the impact of the collector roof inclination on the performance of a solar chimney power plant. Energy Build. 2017, 139, 263–276. [Google Scholar] [CrossRef]
- Zamora, B.; Kaiser, A.S. Numerical study on mixed buoyancy-wind driving induced flow in a solar chimney for building ventilation. Renew. Energy 2010, 35, 2080–2088. [Google Scholar] [CrossRef]
- Malek, M.; Izem, N.; Mohamed, M.S.; Seaid, M.; Wakrim, M. Numerical solution of Rosseland model for transient thermal radiation in non-grey optically thick media using enriched basis functions. Math. Comput. Simul. 2021, 180, 258–275. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, P.; Fang, Z.; Wang, W.; Chen, Y.; Li, K. Numerical Simulation Analysis and Full-Scale Experimental Validation of a Lower Wall-Mounted Solar Chimney with Different Radiation Models. Sustainability 2023, 15, 11974. https://doi.org/10.3390/su151511974
Yuan P, Fang Z, Wang W, Chen Y, Li K. Numerical Simulation Analysis and Full-Scale Experimental Validation of a Lower Wall-Mounted Solar Chimney with Different Radiation Models. Sustainability. 2023; 15(15):11974. https://doi.org/10.3390/su151511974
Chicago/Turabian StyleYuan, Ping, Zhicheng Fang, Wanjiang Wang, Yanhui Chen, and Ke Li. 2023. "Numerical Simulation Analysis and Full-Scale Experimental Validation of a Lower Wall-Mounted Solar Chimney with Different Radiation Models" Sustainability 15, no. 15: 11974. https://doi.org/10.3390/su151511974
APA StyleYuan, P., Fang, Z., Wang, W., Chen, Y., & Li, K. (2023). Numerical Simulation Analysis and Full-Scale Experimental Validation of a Lower Wall-Mounted Solar Chimney with Different Radiation Models. Sustainability, 15(15), 11974. https://doi.org/10.3390/su151511974





