Experimental Investigations on the Response of Bedload Sediment to Vibration
Abstract
1. Introduction
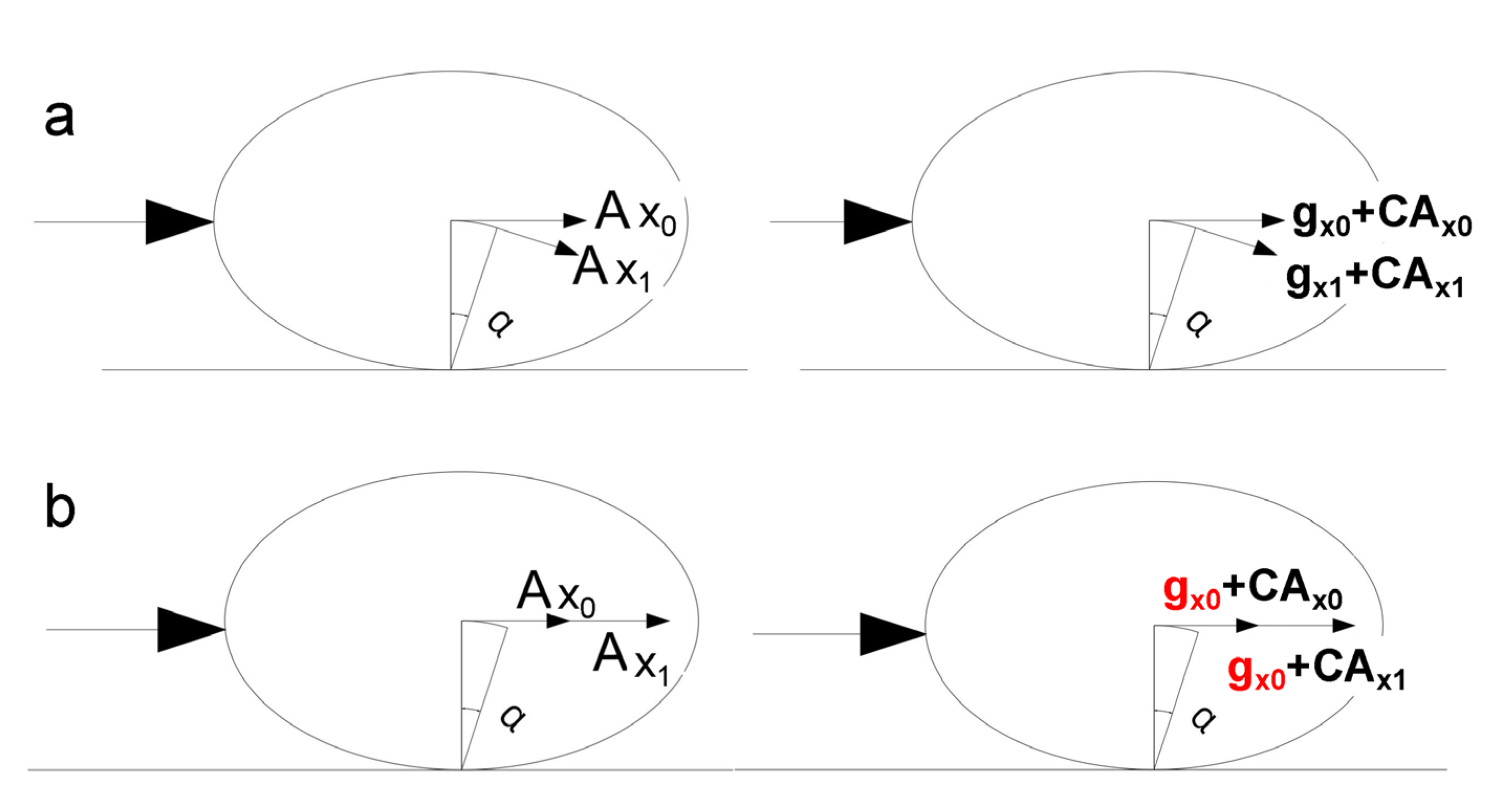
2. Kinetic Equation of Sediment Vibration
3. Materials and Methods
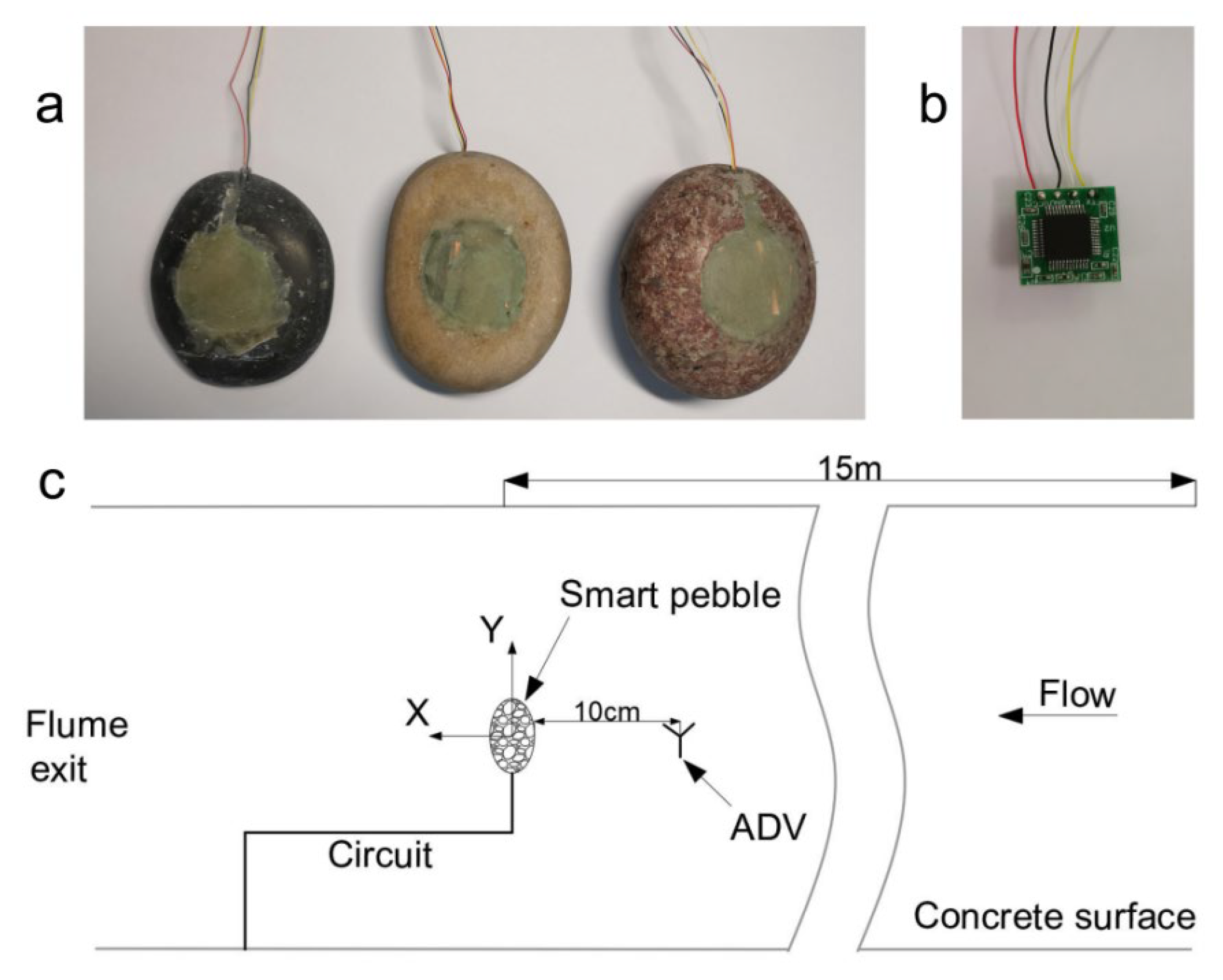
3.1. Design of Smart Pebble
3.2. Flume Bed Experiments
4. Results
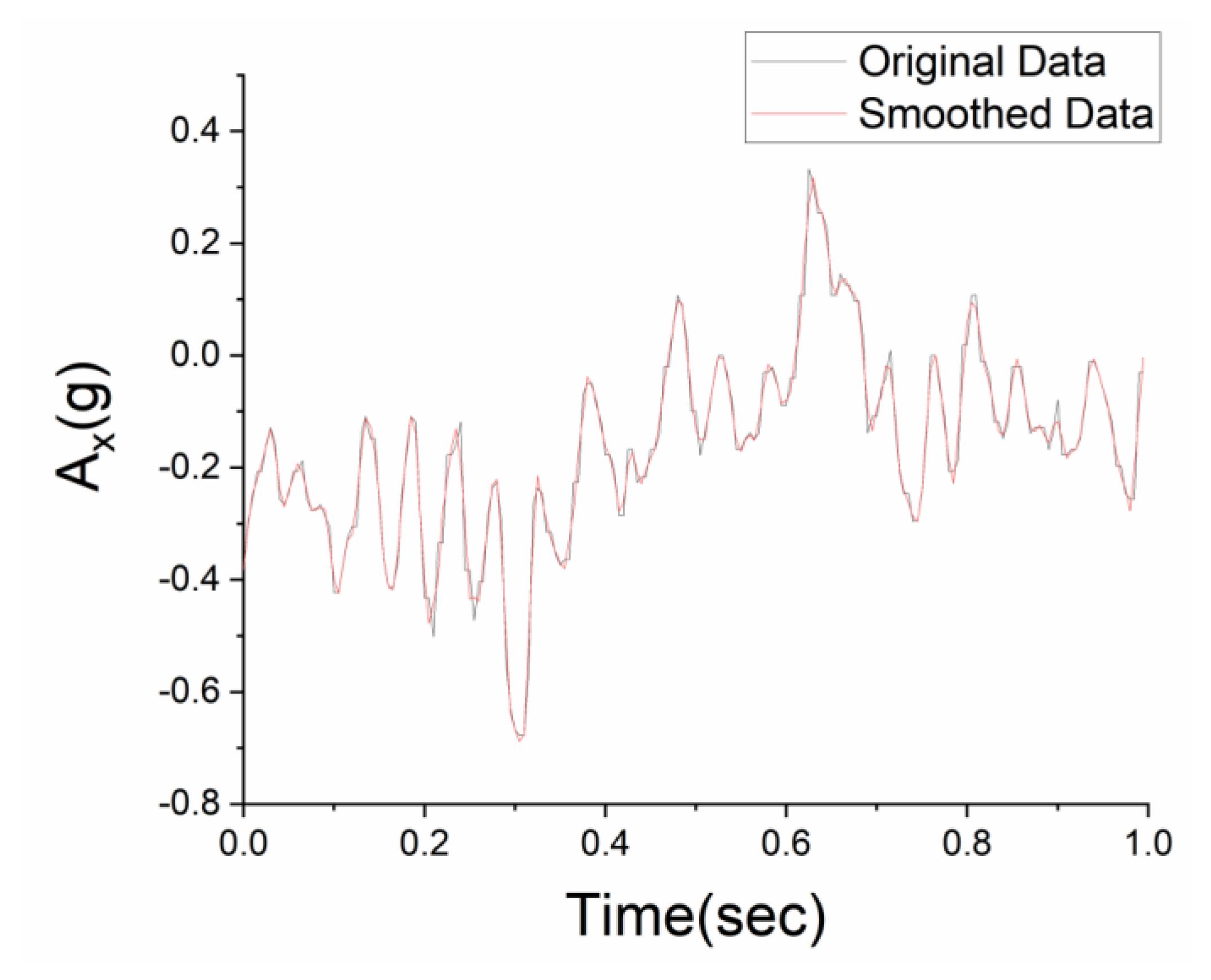
4.1. Pre-Processing of Data
4.2. Pebble Movement State Discrimination
- The motion state of smart pebble A: When the flow rate is Q2 = 32 L/h, for the five sets of measurement data, and gravitational acceleration remains unchanged, and pebble A is in a vibration state; in this situation, the near-bed velocity v = 29 cm/s is the vibration threshold of particle A. When the flow rate is Q5 = 53 L/h, the pebble at five measurement points moves in the direction of water flow by a combination of jumping and drifting; in this situation, the near-bed velocity (v = 37 cm/s) is the entrainment threshold of particle A. The smart pebble A tends to be flat because of its small height, resulting in an increase in uplift force and a decrease in gravity . Under the local transient turbulent force, it is very easy to drift or jump;
- The motion state of smart pebble B: When the flow rate is Q3 = 37 L/h, three measurement points are stationary and two measurement points experiences vibration, and pebble B begins to vibrate; in this situation, the near-bed velocity v = 32 cm/s is the vibration threshold of the particle B. When the flow rate is Q7 = 86 L/h, of the five measurement points, two rolling and three slowly pushing particle entrainments are identified; in this situation, the near-bed velocity (v = 44 cm/s) is the entrainment threshold of particle B;
- The motion state of smart pebble C: When the flow rate is Q3 = 37 L/h, measurement points are vibrating; in this situation, the near-bed velocity (v = 32 cm/s) is the vibration threshold of the particle C. When the flow rate is Q7 = 86 L/h, five measurement points of the pebble are directly rolling; in this situation, the near-bed velocity (v = 44 cm/s) is the entrainment threshold of particle C.
5. Discussion
5.1. Time Domain Characteristics of Particle Vibration
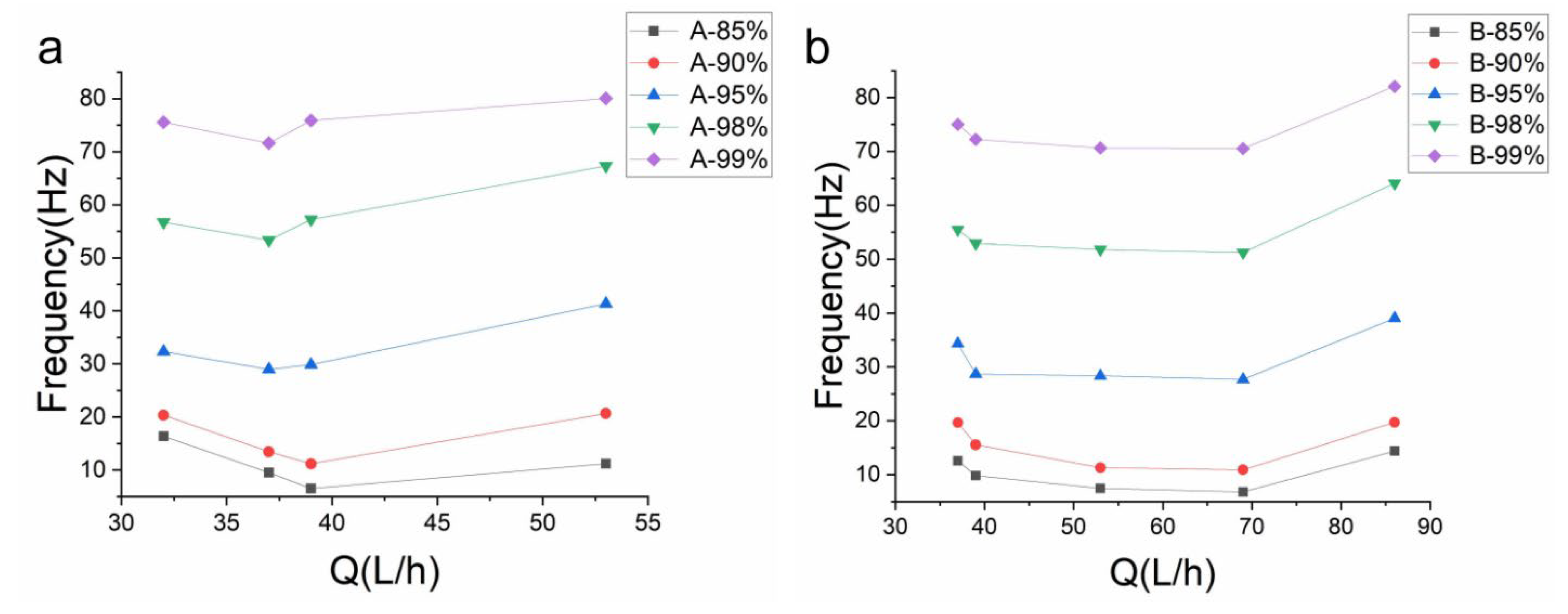
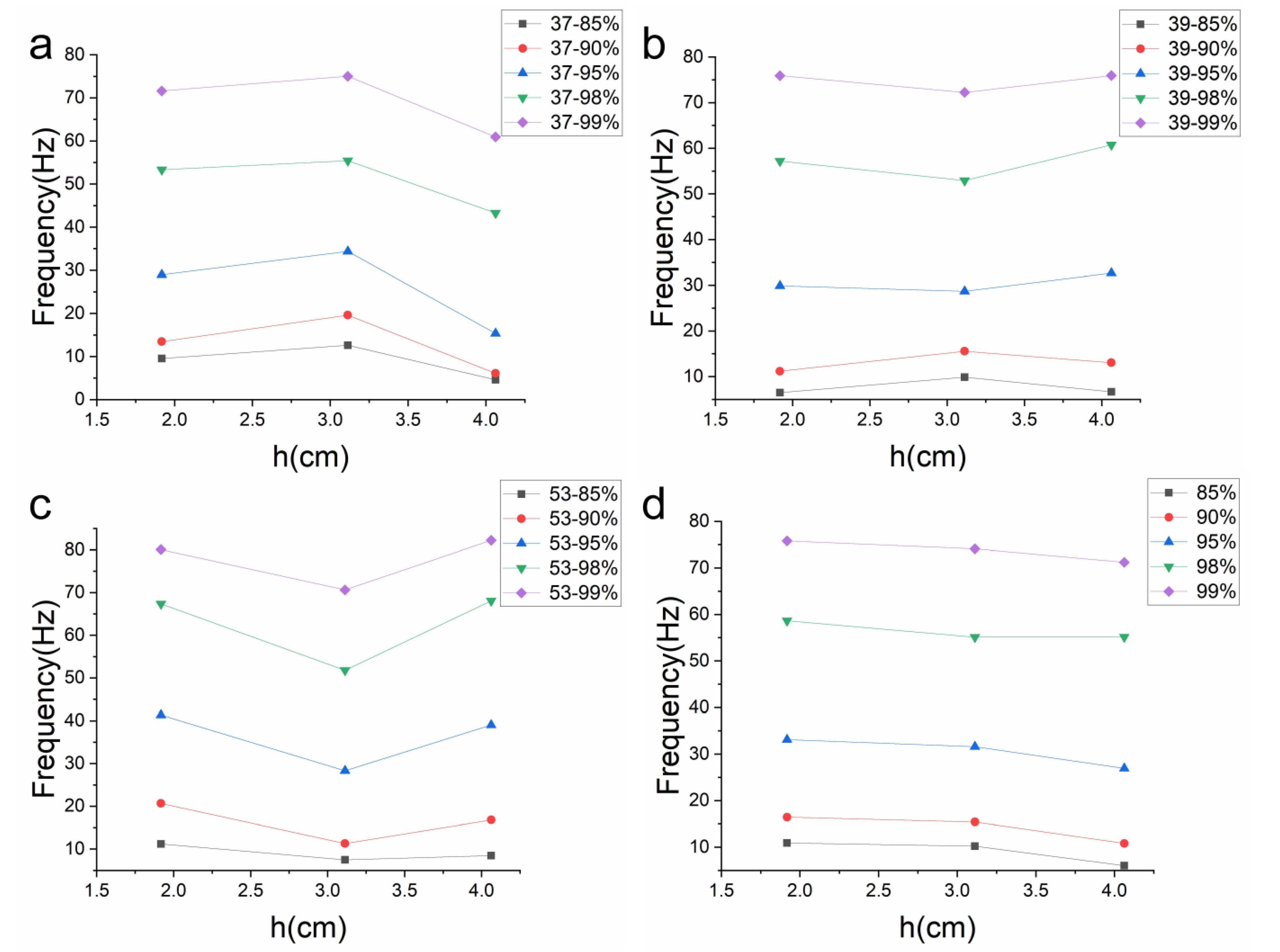
5.2. Spectral Characteristics of Particle Vibration
6. Conclusions
- The sediment motion belongs to the category of nonlinear dynamics. The height of the sediment also affects the magnitude of the lifting force drag force and gravity , and the relationship is nonlinear, so the final characterization of the sediment vibration is also nonlinear;
- The vibration intensity of pebbles A and B tended to increase before approaching the entrapment threshold, but weakened when approaching the entrapment threshold. In contrast, the vibration intensity of pebble C decreased and then increased, and rolled directly when approaching the entrainment threshold. The average vibration intensity of the pebbles increased with height;
- The distribution of the vibration intensity and frequency of pebbles at different heights under the same flow conditions does not follow a simple law;
- With an increase in flow rate, the vibration frequency of pebbles A and B showed an increasing trend before approaching the entrainment threshold, but decreased near the entrainment threshold. The vibration frequency of pebble C, on the other hand, decreased and then increased, and had no vibration frequency near the entrainment threshold. The average vibration frequency of pebbles decreased with increasing height;
- This paper is the first to explore the one-dimensional kinetic law of nudibranchs, which provides a reference for the study of the three-dimensional kinetic mechanism of nudibranchs in mountain rivers, and ultimately provides a theoretical guidance for the sustainable development and utilization of rivers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nelson, J.M.; Shreve, R.L.; McLean, S.R.; Drake, T.G. Role of Near-Bed Turbulence Structure in Bed Load Transport and Bed Form Mechanics. Water Resour. Res. 2010, 31, 2071–2086. [Google Scholar] [CrossRef]
- Celik, A.O. Experimental Investigation of the Role of Turbulence Fluctuations on Incipient Motion of Sediment. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2011. [Google Scholar]
- Lee, H.; Ha, M.Y.; Balachandar, S. Work-based criterion for particle motion and implication for turbulent bed-load transport. Phys. Fluids 2012, 24, 1–73. [Google Scholar]
- Amir, M.; Nikora, V.I.; Stewart, M.T. Pressure forces on sediment particles in turbulent open-channel flow: A laboratory study. J. Fluid Mech. 2014, 757, 458–497. [Google Scholar]
- Cecchetto, M.; Tregnaghi, M.; Bottacin-Busolin, A.; Tait, S.; Marion, A. Statistical Description on the Role of Turbulence and Grain Interference on Particle Entrainment from Gravel Beds. J. Hydraul. Eng. 2016, 143, 06016021. [Google Scholar] [CrossRef]
- Shih, W.; Diplas, P.; Celik, A.O.; Dancey, C. Accounting for the role of turbulent flow on particle dislodgement via a coupled quadrant analysis of velocity and pressure sequences. Adv. Water Resour. 2017, 101, 37–48. [Google Scholar]
- Prancevic, J.P.; Lamb, M.P. Particle friction angles in steep mountain channels. J. Geophys. Res. Earth Surf 2015, 120, 242–259. [Google Scholar]
- Diplas, P.; Dancey, C.L.; Celik, A.O.; Valyrakis, M.; Greer, K.; Akar, T. The role of impulse on the initiation of particle move-ment under turbulent flow conditions. Science 2008, 322, 717–720. [Google Scholar]
- Celik, A.O.; Diplas, P.; Dancey, C.L. Instantaneous pressure measurements on aspherical grain under threshold flow conditions. Fluid Mech. 2014, 741, 60–97. [Google Scholar] [CrossRef][Green Version]
- Celik, A.O.; Diplas, P.; Dancey, C.L. Instantaneous turbulent forces and impulse on a rough bed: Implications for initiation of bed material movement. Water Resour. Res. 2013, 49, 2213–2227. [Google Scholar]
- Valyrakis, M.; Diplas, P.; Dancey, C.L.; Greer, K.; Celik, A.O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res. 2010, 115, F02006. [Google Scholar]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res. Earth Surf. 2013, 118, 42–53. [Google Scholar]
- Garcia, C.; Cohen, H.; Reid, I.; Rovira, A.; Úbeda, X.; Laronne, J.B. Processes of initiation of motion leading to bedload transport in gravel-bed rivers. Geophys. Res. Lett. 2007, 34, 125–141. [Google Scholar]
- Maniatis, G.; Hoey, T.B.; Hassan, M.A.; Sventek, J. Calculating of Explicit Probability of Entrainment Based on Inertial Acceleration Measurements. J. Hydraul. Eng. 2017, 143, 04016097. [Google Scholar] [CrossRef]
- Ma, F. Law of Sediment Particle Movement and Nonlinear Analysis. Ph.D. Thesis, Tianjin University, Tianjin, China, 2012. [Google Scholar]
- Li, C.; Chen, D.; Ge, F.; Chen, Y. Fractional derivative modeling for suspended sediment in unsteady flows. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104971. [Google Scholar]
- Wang, X.K.; Ao, R.Z.; Fang, D. Nonlinearstudy on sediment incipient motion condition and itsmechanism. J. Yangtze River Sci. Inst. 1999, 16, 39–41. [Google Scholar]
- Yang, J.R.; Fang, D.; He, W.S.; Liu, X.N. Nonlinearstudy on transport rate of bed-load. J. Hydraul. Eng. 2003, 14, 36–40. [Google Scholar]
- He, W.S.; Cao, S.Y.; Lei, X.Z.; Liu, X.N. Nonlinear theory for incipient condition of sediment. J. Hydraul. Eng. 2004, 35, 28–32. [Google Scholar]
- Bai, Y.C.; Xu, H.J.; Xu, D.; Chiu-on, N.G. Nonlineardynamics of the process of bed-load transport. Chin. Sci. Technol. Sci. 2006, 36, 751–772. [Google Scholar]
- Yang, J.R.; Fang, D.; He, W.S.; Li, W.P. The nonlinearcusp-catastrophe model of incipient motion of non-uniform sediment. J. Hydraul. Eng. 2003, 34, 34–38. [Google Scholar]
- Xu, X.Y.; Zhang, G.; Zhou, S.; Wang, Y.; Chen, X.; Liu, Y. Formula of bedload sediment transport based on nonlinear theory. J. Hydroelectr. Eng. 2019, 38, 20–28. [Google Scholar]
- Akeila, E.; Salcic, Z.; Swain, A. Smart pebble for monitoring riverbed sediment transport. Sens.J. 2010, 10, 1705–1717. [Google Scholar] [CrossRef]
- Šolc, T.; Stefanovska, A.; Hoey, T.; Mikoš, M. Application of an instrumented tracer in an abrasion mill for rock abrasion studies. Stroj. Vestn. J. Mech. Eng 2012, 58, 263–270. [Google Scholar] [CrossRef]
- Maniatis, G.; Hoey, T.; Hodge, R.; Rickenmann, D.; Badoux, A. Inertial drag and lift forces for coarse grains on rough alluvial beds measured using in-grain accelerometers. Earth Surf. Dyn. 2020, 8, 1067–1099. [Google Scholar]
- Gronz, O.; Hiller, P.H.; Wirtz, S.; Becker, K.; Iserloh, T.; Seeger, M.; Brings, C.; Aberle, J.; Casper, M.C.; Ries, J.B. Smartstones: A small 9-axis sensor implanted in stones to track their movements. CATENA 2016, 142, 245–251. [Google Scholar]
- Dost, J.B.; Gronz, O.; Casper, M.C.; Krein, A. The potential of Smartstone probes in landslide experiments: How to read motion data. Nat. Hazards Earth Syst. Sci. 2020, 20, 3501–3519. [Google Scholar]
- Curley, E.; Valyrakis, M.; Thomas, R.; Adams, C.; Stephen, A. Smart Sensors To Predict Entrainment Of Freshwater Mussels: A New Tool In Freshwater Habitat Assessment. Sci. Total Environ. 2021, 787, 147586. [Google Scholar]
- AlObaidi, K.; Valyrakis, M. Linking the explicit probability of entrainment of instrumented particles to flow hydrodynamics. Earth Surf. Process. Landf. 2021, 46, 2448–2465. [Google Scholar] [CrossRef]
- Xie, Y.; Melville, B.W.; Shamseldin, A.Y.; Whittaker, C.N.; Yang, Y. Direct measurement of the inertial drag and lift forces on entrained coarse particles at various protrusion heights. Earth Surf. Process. Landf. 2021, 48, 371–385. [Google Scholar] [CrossRef]
- Wang, P.; Yuan, J.; Wang, M.; Wang, M. Sediment vibration characteristics based on accelerometer measurements. Sci. Rep. 2023, 13, 1205. [Google Scholar] [CrossRef]
- Williams, J.J.; Butterfield, G.R.; Clark, D.G. Aerodynamic entrainment threshold: Effects of boundary layer flow conditions. Sedimentology 1994, 41, 309–328. [Google Scholar] [CrossRef]






| Pebble Type | Length (cm) | Width(cm) | Height (cm) | Height/Width | Width/Length |
|---|---|---|---|---|---|
| A | 6.176 | 5.221 | 1.918 | 0.37 | 0.84 |
| B | 6.762 | 5.274 | 3.113 | 0.59 | 0.78 |
| C | 6.557 | 5.338 | 4.062 | 0.76 | 0.81 |
| Pebble Type | Q (L/h) | Velocity (cm/s) | Stationary Groups | Vibration Groups | Entrainment Groups | Movement Status |
|---|---|---|---|---|---|---|
| A | 30 | 28 | 5 | 0 | 0 | stationary |
| 32 | 29 | 0 | 5 | 0 | vibration | |
| 37 | 32 | 0 | 5 | 0 | vibration | |
| 39 | 34 | 0 | 5 | 0 | vibration | |
| 53 | 37 | 0 | 0 | 5 | entrainment | |
| B | 32 | 29 | 5 | 0 | 0 | stationary |
| 37 | 32 | 3 | 2 | 0 | vibration | |
| 39 | 34 | 1 | 4 | 0 | vibration | |
| 53 | 37 | 0 | 5 | 0 | vibration | |
| 69 | 41 | 0 | 5 | 0 | vibration | |
| 86 | 44 | 0 | 0 | 5 | entrainment | |
| C | 32 | 29 | 5 | 0 | 0 | stationary |
| 37 | 32 | 0 | 5 | 0 | vibration | |
| 39 | 34 | 0 | 5 | 0 | vibration | |
| 53 | 37 | 0 | 5 | 0 | vibration | |
| 69 | 41 | 0 | 5 | 0 | vibration | |
| 86 | 44 | 0 | 0 | 5 | entrainment |
| Pebble Type | Q (L/h) | Average Value | Mean Square Error | Maximum Value | Minimum Value |
|---|---|---|---|---|---|
| A | 32 | −1.53 | 2.16 | 3.10 | −6.61 |
| 37 | −0.37 | 6.99 | 22.29 | −20.40 | |
| 39 | 2.75 | 7.84 | 23.80 | −14.57 | |
| 53 | 1.40 | 5.05 | 24.15 | −8.15 | |
| B | 37 | 0.21 | 1.01 | 3.96 | −4.52 |
| 39 | −0.99 | 3.70 | 13.48 | −10.47 | |
| 53 | 3.96 | 6.52 | 30.66 | −14.88 | |
| 69 | −1.04 | 12.36 | 33.78 | −40.66 | |
| 86 | −1.958 | 4.49 | 8.79 | −15.03 | |
| C | 37 | 9.22 | 12.35 | 41.70 | −11.98 |
| 39 | −4.80 | 12.06 | 31.08 | −32.42 | |
| 53 | 6.02 | 9.14 | 47.18 | −11.39 | |
| 69 | 14.14 | 23.32 | 74.21 | −56.07 |
| Pebble Type | Q (L/h) | Energy Ratio | Freq. (Hz) | Energy Ratio | Freq. (Hz) | Energy Ratio | Freq. (Hz) | Energy Ratio | Freq. (Hz) | Energy Ratio | Freq. (Hz) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 32 | 85% | 16.36 | 90% | 20.36 | 95% | 32.33 | 98% | 56.72 | 99% | 75.57 |
| 37 | 85% | 9.52 | 90% | 13.46 | 95% | 28.97 | 98% | 53.34 | 99% | 71.62 | |
| 39 | 85% | 6.5 | 90% | 11.18 | 95% | 29.87 | 98% | 57.2 | 99% | 75.9 | |
| 53 | 85% | 11.18 | 90% | 20.66 | 95% | 41.35 | 98% | 67.34 | 99% | 80.06 | |
| Avg. | 85% | 10.89 | 90% | 16.42 | 95% | 33.13 | 98% | 58.65 | 99% | 75.79 | |
| B | 37 | 85% | 12.6 | 90% | 19.62 | 95% | 34.36 | 98% | 55.44 | 99% | 75.02 |
| 39 | 85% | 9.85 | 90% | 15.56 | 95% | 28.68 | 98% | 52.92 | 99% | 72.23 | |
| 53 | 85% | 7.46 | 90% | 11.31 | 95% | 28.31 | 98% | 51.8 | 99% | 70.64 | |
| 69 | 85% | 6.81 | 90% | 10.92 | 95% | 27.66 | 98% | 51.24 | 99% | 70.53 | |
| 86 | 85% | 14.42 | 90% | 19.7 | 95% | 39.06 | 98% | 64.06 | 99% | 82.09 | |
| Avg. | 85% | 10.23 | 90% | 15.42 | 95% | 31.61 | 98% | 55.09 | 99% | 74.10 | |
| C | 37 | 85% | 4.6 | 90% | 6.11 | 95% | 15.37 | 98% | 43.25 | 99% | 60.92 |
| 39 | 85% | 6.67 | 90% | 13.04 | 95% | 32.67 | 98% | 60.74 | 99% | 75.93 | |
| 53 | 85% | 8.47 | 90% | 16.81 | 95% | 39.03 | 98% | 68.08 | 99% | 82.23 | |
| 69 | 85% | 4.42 | 90% | 7.26 | 95% | 20.62 | 98% | 48.57 | 99% | 65.83 | |
| Avg. | 85% | 6.04 | 90% | 10.81 | 95% | 26.92 | 98% | 55.16 | 99% | 71.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Wang, P.; Wang, M.; Wang, M. Experimental Investigations on the Response of Bedload Sediment to Vibration. Sustainability 2023, 15, 11972. https://doi.org/10.3390/su151511972
Yuan J, Wang P, Wang M, Wang M. Experimental Investigations on the Response of Bedload Sediment to Vibration. Sustainability. 2023; 15(15):11972. https://doi.org/10.3390/su151511972
Chicago/Turabian StyleYuan, Jun, Pingyi Wang, Meili Wang, and Mi Wang. 2023. "Experimental Investigations on the Response of Bedload Sediment to Vibration" Sustainability 15, no. 15: 11972. https://doi.org/10.3390/su151511972
APA StyleYuan, J., Wang, P., Wang, M., & Wang, M. (2023). Experimental Investigations on the Response of Bedload Sediment to Vibration. Sustainability, 15(15), 11972. https://doi.org/10.3390/su151511972





