Impact Analysis of Smart Road Stud on Driving Behavior and Traffic Flow in Two-Lane Two-Way Highway
Abstract
1. Introduction
2. Literature Overview
2.1. Smart Road Stud
2.2. Two-Lane Two-Way Driving Behavior Characteristics
2.3. Microscopic Simulation
3. Materials and Methods
3.1. Overall Framework
3.2. The Visual Guide of Smart Road Stud System
3.3. Driving Simulator Experimental
3.3.1. Experimental Scenario
3.3.2. Participants
3.3.3. Procedure
3.4. Force-Based Microscopic Simulation
3.4.1. TAN-Based Overtaking Decision Model
3.4.2. Finite States Machine
3.4.3. Social Forces
3.4.4. Calibration
4. Results
4.1. Driving Simulator Results
4.1.1. Overtaking Frequency
4.1.2. Driving Characteristics
4.1.3. Overtaking Decision Characteristics
4.1.4. Tree Augmented Naive Bayes
4.2. Microscopic Simulation Results
4.2.1. Effects of the Rate of Trucks
4.2.2. Effects of the Rate of Road Section with Restricted Sight Distance
4.2.3. Smart Road Studs’ Effect on Traffic Conflict
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ou, H.; Tang, T.Q. Impacts of Moving Bottlenecks on Traffic Flow. Phys. A Stat. Mech. Its Appl. 2018, 500, 131–138. [Google Scholar] [CrossRef]
- Mao, G.; Hui, Y.; Ren, X.; Li, C.; Shao, Y. The Internet of Things for Smart Roads: A Road Map from Present to Future Road Infrastructure. IEEE Intell. Transp. Syst. Mag. 2022, 14, 66–76. [Google Scholar] [CrossRef]
- Le Roux, J.H.; Barnard, A.; Booysen, M.J. Remotely controllable wireless road stud network. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC), The Hague, The Netherlands, 6–9 October 2013; pp. 762–766. [Google Scholar]
- Shahar, A.; Brémond, R. Toward Smart Active Road Studs for Lane Delineation. In Proceedings of the TRA2014—Transport Research Arena: Transport Solutions: From Research to Deployment-Innovate Mobility, Mobilise Innovation! Paris, France, 14–17 April 2014. [Google Scholar]
- Reed, N. Driver Behaviour in Response to Actively Illuminated Road Studs: A Simulator Study; Project Report 143; Transport Research Laboratory: Crowthorne, UK, 2006. [Google Scholar]
- Villa, C.; Bremond, R.; Saint Jacques, E. Visibility and Discomfort Glare of LED Road Studs. Light. Res. Technol. 2015, 47, 945–963. [Google Scholar] [CrossRef]
- Samardzija, D.; Kovac, E.; Isailovic, D.; Miladinovic, B.; Katona, M. Road Nail: Intelligent Road Marking System Testbed. In Proceedings of the Second IEEE Vehicular Networking Conference, VVNC 2010, Jersey City, NJ, USA, 13–15 December 2010. [Google Scholar]
- Wang, H.; Sun, Y.; Quan, W.; Ma, X.; Ochieng, W.Y. Traffic Volume Measurement Based on a Single Smart Road Stud. Measurement 2022, 187, 110150. [Google Scholar] [CrossRef]
- Tao, Z.; Quan, W.; Wang, H. Innovative Smart Road Stud Sensor Network Development for Real-Time Traffic Monitoring. J. Adv. Transp. 2022, 2022, 8830276. [Google Scholar] [CrossRef]
- Lobjois, R.; Faure, V.; Désiré, L.; Benguigui, N. Behavioral and Workload Measures in Real and Simulated Driving: Do they Tell Us the Same Thing About the Validity of Driving Simulation? Saf. Sci. 2021, 134, 105046. [Google Scholar] [CrossRef]
- Toledo, T.; Koutsopoulos, H.N.; Ahmed, K.I. Estimation of Vehicle Trajectories with Locally Weighted Regression. Transp. Res. Rec. 2007, 1999, 161–169. [Google Scholar] [CrossRef]
- Li, D.; Pan, H. Two-Lane Two-Way Overtaking Decision Model with Driving Style Awareness Based on a Game-Theoretic Framework. Transp. A Transp. Sci. 2022, 19, 2076755. [Google Scholar] [CrossRef]
- Balal, E.; Cheu, R.L.; Sarkodie-Gyan, T. A Binary Decision Model for Discretionary Lane Changing Move Based on Fuzzy Inference System. Transp. Res. Part C-Emerg. Technol. 2016, 67, 47–61. [Google Scholar] [CrossRef]
- Xie, D.-F.; Fang, Z.-Z.; Jia, B.; He, Z. A Data-Driven Lane-Changing Model Based on Deep Learning. Transp. Res. Part C Emerg. Technol. 2019, 106, 41–60. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Golias, J.C. Bayesian Modeling of the Microscopic Traffic Characteristics of Overtaking in Two-Lane Highways. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 348–357. [Google Scholar] [CrossRef]
- Zhao, J.; Knoop, V.L.; Wang, M. Microscopic Traffic Modeling Inside Intersections: Interactions Between Drivers. Transp. Sci. 2022, 57, 135–155. [Google Scholar] [CrossRef]
- Zhao, J.; Knoop, V.L.; Sun, J.; Ma, Z.; Wang, M. Unprotected Left-Turn Behavior Model Capturing Path Variations at Intersections. In Proceedings of the 26th IEEE International Conference on Intelligent Transportation Systems (ITSC 2023), Bilbao, Spain, 24–28 September 2023. [Google Scholar]
- Kanagaraj, V.; Treiber, M. Self-Driven Particle Model for Mixed Traffic and Other Disordered Flows. Phys. A Stat. Mech. Its Appl. 2018, 509, 1–11. [Google Scholar] [CrossRef]
- Chao, Q.; Liu, P.; Han, Y.; Lin, Y.; Li, C.; Miao, Q.; Jin, X. A Calibrated Force-Based Model for Mixed Traffic Simulation. IEEE Trans. Vis. Comput. Graph 2021, 29, 1664–1677. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social Force Model for Pedestrian Dynamics. Phys. Rev. E 1995, 51, 4282–4286. [Google Scholar] [CrossRef] [PubMed]
- Anvari, B.; Bell, M.G.H.; Sivakumar, A.; Ochieng, W.Y. Modelling Shared Space Users via Rule-Based Social Force Model. Transp. Res. Part C Emerg. Technol. 2015, 51, 83–103. [Google Scholar] [CrossRef]
- Yang, D.; Zhou, X.; Su, G.; Liu, S. Model and Simulation of the Heterogeneous Traffic Flow of the Urban Signalized Intersection with an Island Work Zone. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1719–1727. [Google Scholar] [CrossRef]
- Delpiano, R.; Herrera, J.C.; Laval, J.; Coeymans, J.E. A Two-Dimensional Car-Following Model for Two-Dimensional Traffic Flow Problems. Transp. Res. Part C Emerg. Technol. 2020, 114, 504–516. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Zhang, H.M. A Unified Follow-the-Leader Model for Vehicle, Bicycle and Pedestrian Traffic. Transp. Res. Part B Methodol. 2017, 105, 315–327. [Google Scholar] [CrossRef]
- Johora, F.T.; Yang, D.; Muller, J.P.; Ozguner, U. On the Generalizability of Motion Models for Road Users in Heterogeneous Shared Traffic Spaces. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23084–23098. [Google Scholar] [CrossRef]
- Yoon, D.D.; Ayalew, B. Social Force Aggregation Control for Autonomous Driving with Connected Preview. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 1388–1393. [Google Scholar]
- Asaithambi, G.; Shravani, G. Overtaking Behaviour of Vehicles on Undivided Roads under Mixed Traffic Conditions. In Proceedings of the 20th International Conference of Hong Kong Society for Transportation Studies, Hong Kong, China, 12–14 December 2015. [Google Scholar]
- Hegeman, G.; Brookhuis, K.; Hoogendoorn, S. Opportunities of Advanced Driver Assistance Systems towards Overtaking. Eur. J. Transp. Infrastruct. Res. 2005, 5. [Google Scholar] [CrossRef]
- Castillo, E.; Menéndez, J.M.; Sánchez-Cambronero, S. Predicting Traffic Flow Using Bayesian Networks. Transp. Res. Part B Methodol. 2008, 42, 482–509. [Google Scholar]
- Vlahogianni, E.I.; Webber Jr, C.L.; Geroliminis, N.; Skabardonis, A. Statistical Characteristics of Transitional Queue Conditions in Signalized Arterials. Transp. Res. Part C Emerg. Technol. 2007, 15, 392–403. [Google Scholar] [CrossRef]
- Sun, J.; Liu, H.; Ma, Z. Modelling and Simulation of Highly Mixed Traffic Flow on Two-Lane Two-Way Urban Streets. Simul. Model. Pract. Theory 2019, 95, 16–35. [Google Scholar] [CrossRef]
- Qi, D.; Soffker, D. In Improved Driving Behaviors Prediction Based on Fuzzy Logic-Hidden Markov Model (FL-HMM). In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 2003–2008. [Google Scholar]
- Wang, J.F.; Chen, Y.; Dong, Z.K.; Gao, M.Y. Improved YOLOv5 Network for Real-Time Multi-Scale Traffic Sign Detection. Neural Comput. Appl. 2023, 35, 7853–7865. [Google Scholar] [CrossRef]
- Brockfeld, E.; Kuehne, R.D.; Wagner, P. Calibration and Validation of Microscopic Models of Traffic Flow. Transp. Res. Rec. J. Transp. Res. Board 2005, 1934, 179–187. [Google Scholar] [CrossRef]
- Jin, C.-J.; Knoop, V.L.; Jiang, R.; Wang, W.; Wang, H. Calibration and Validation of Cellular Automaton Traffic Flow Model with Empirical and Experimental Data. IET Intell. Transp. Syst. 2018, 12, 359–365. [Google Scholar] [CrossRef]
- Gray, R.; Regan, D.M. Perceptual Processes Used by Drivers during Overtaking in a Driving Simulator. Hum. Factors 2005, 47, 394–417. [Google Scholar] [CrossRef]
- Chen, J.; Bhat, M.; Jiang, S.; Zhao, D. Advanced Driver Assistance Strategies for a Single-Vehicle Overtaking a Platoon on the Two-Lane Two-Way Road. IEEE Access 2020, 8, 77285–77297. [Google Scholar] [CrossRef]




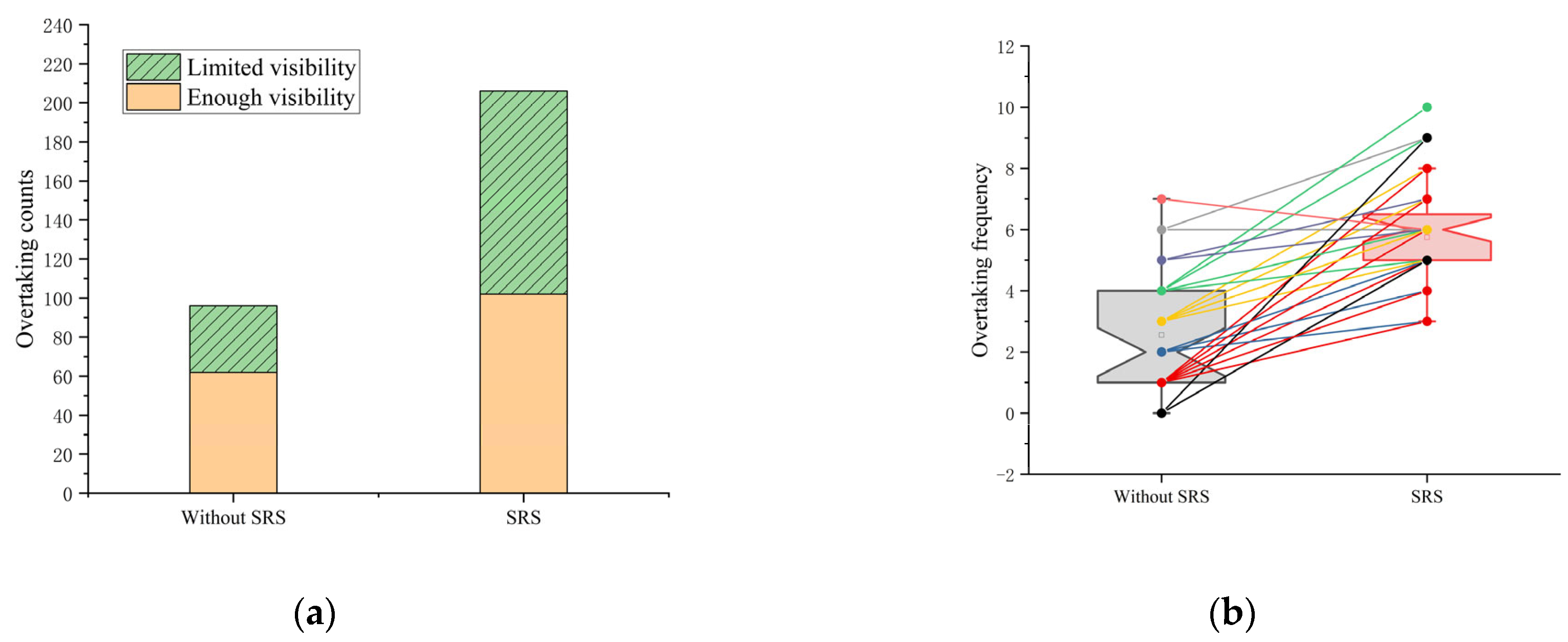
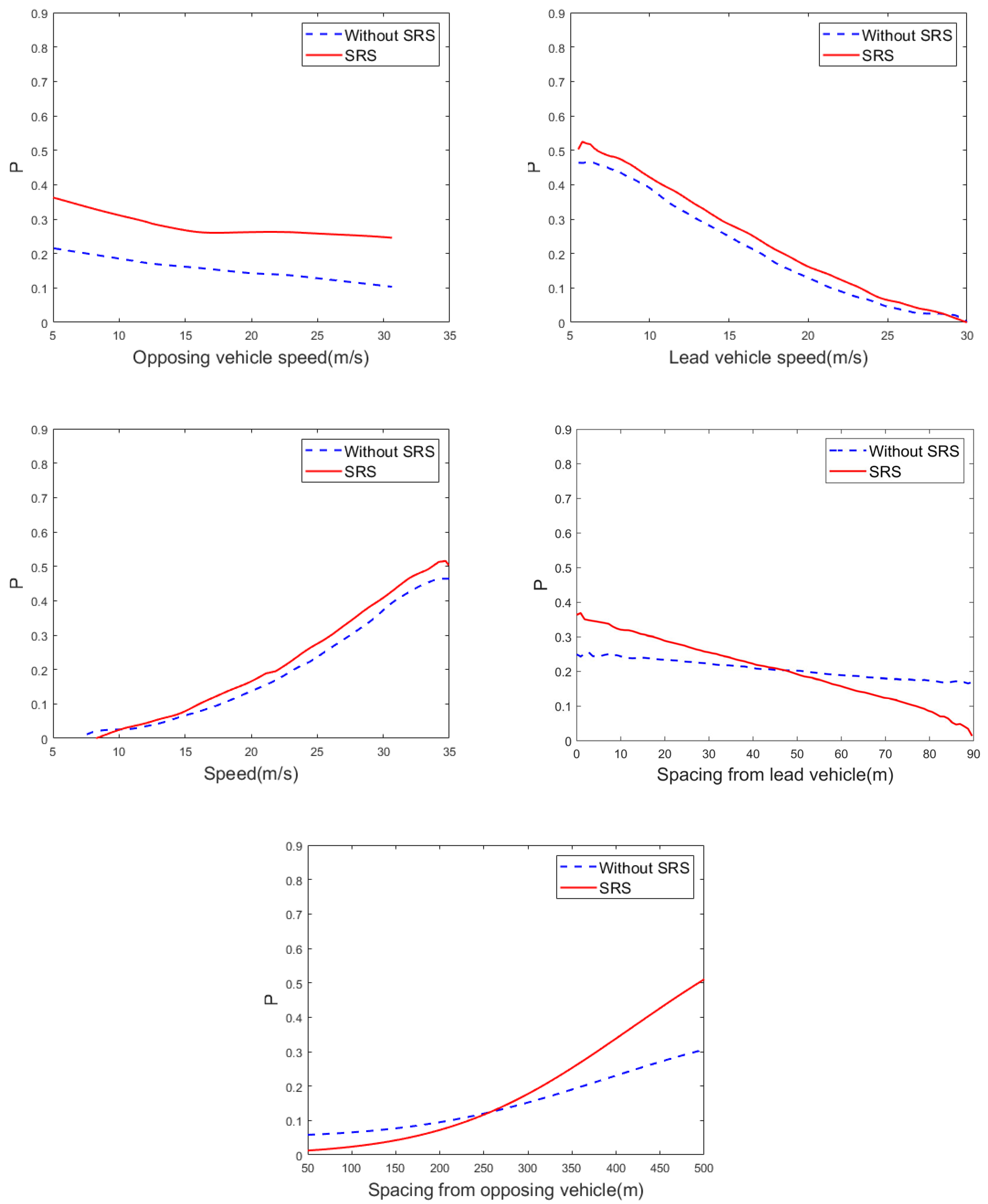
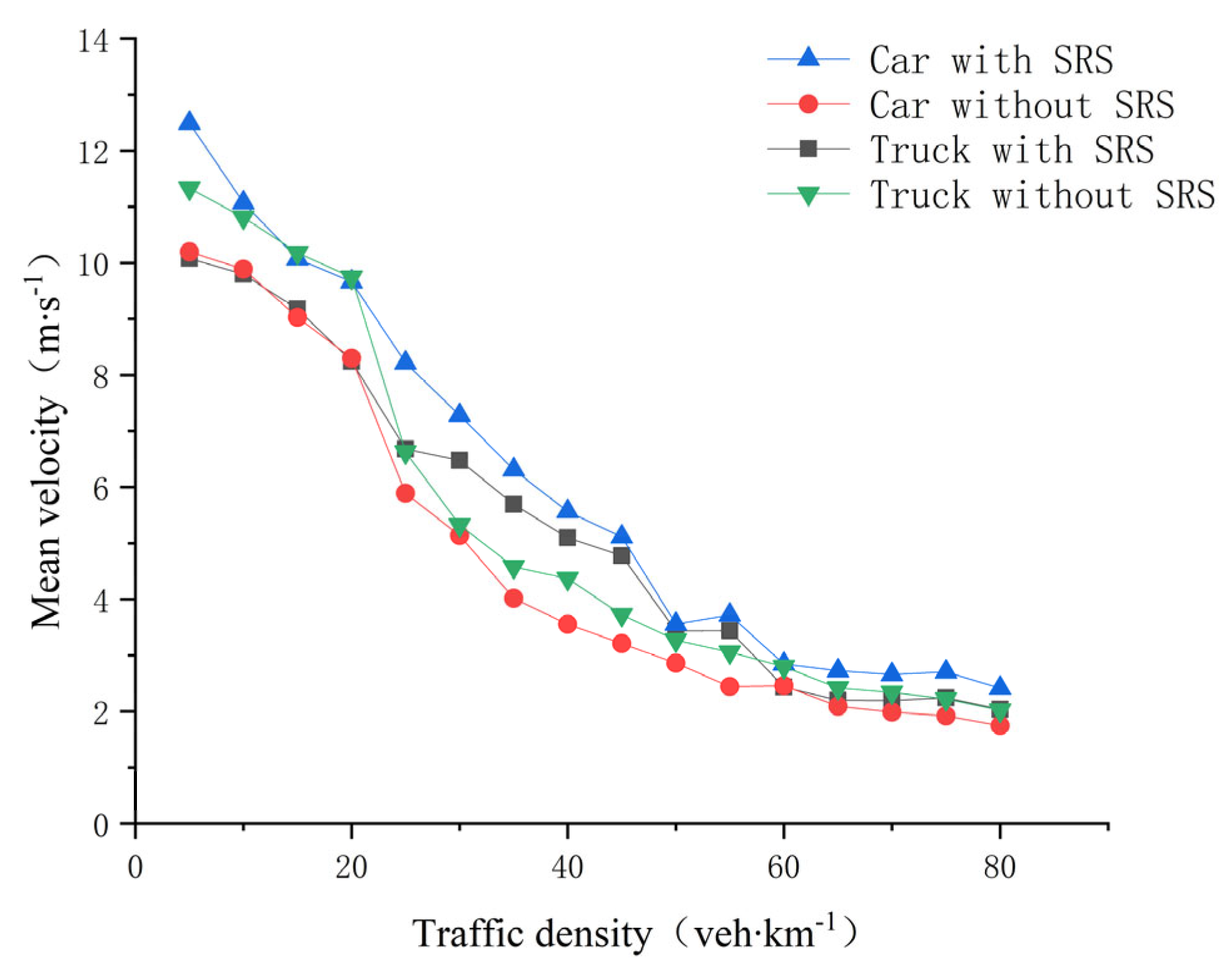


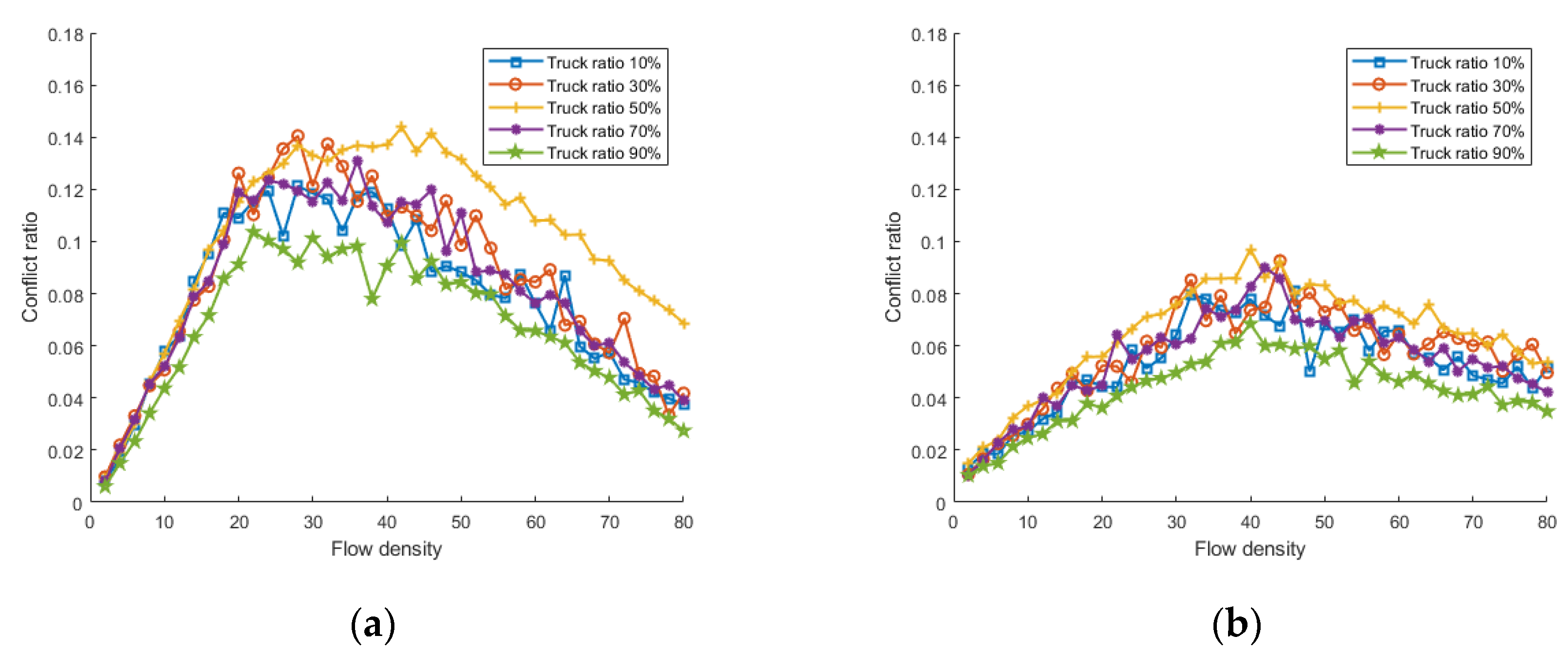
| Parameter | Truck | Car |
|---|---|---|
| 1.47 | 1.11 | |
| 4.31 | 2.25 | |
| 2.28 | 4.47 | |
| 0.76 | 1.25 | |
| 1.24 | 0.52 | |
| 0.92 | 1.13 | |
| 0.88 | 1.26 | |
| 4.51 | 2.95 | |
| 5.33 | 2.42 | |
| 41.5 | 55.2 | |
| 12 | 6 |
| Longitudinal Acceleration (m/s2) | Peak Lateral Acceleration1 (m/s2) | Peak Lateral Acceleration2 (m/s2) | Overtaking Distance (m) | ||
|---|---|---|---|---|---|
| Without SRS | Mean | 1.07 | 2.33 | 2.81 | 221.13 |
| Standard deviation | 0.45 | 1.17 | 0.99 | 58.14 | |
| With SRS | Mean | 1.08 | 2.10 | 2.97 | 212.23 |
| Standard deviation | 0.42 | 1.08 | 1.16 | 66.33 | |
| Wilcoxon | −0.27 | −0.81 | −0.14 | −0.09 | |
| Sig. | 0.782 | 0.416 | 0.887 | 0.927 | |
| Speed (km/h) | Lead Vehicle Speed (km/h) | Opposing Vehicle Speed (km/h) | Opposing Vehicle Spacing (m) | Spacing (m) | ||
|---|---|---|---|---|---|---|
| Without SRS | Mean | 56.79 | 47.38 | 51.14 | 305.41 | 22.29 |
| Standard deviation | 5.57 | 7.79 | 9.23 | 67.24 | 5.63 | |
| With SRS | Mean | 57.90 | 47.38 | 50.80 | 271.68 | 27.61 |
| Standard deviation | 6.88 | 8.05 | 10.17 | 26.81 | 16.15 | |
| Wilcoxon | −0.954 | −0.802 | 19.890 | −0.406 | −3.629 | |
| Sig. | 0.340 | 0.422 | 0.891 | 0.685 | 0.000 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Luo, Q.; Fan, J.; Ning, Q. Impact Analysis of Smart Road Stud on Driving Behavior and Traffic Flow in Two-Lane Two-Way Highway. Sustainability 2023, 15, 11559. https://doi.org/10.3390/su151511559
Li M, Luo Q, Fan J, Ning Q. Impact Analysis of Smart Road Stud on Driving Behavior and Traffic Flow in Two-Lane Two-Way Highway. Sustainability. 2023; 15(15):11559. https://doi.org/10.3390/su151511559
Chicago/Turabian StyleLi, Maosheng, Qian Luo, Jing Fan, and Qingyan Ning. 2023. "Impact Analysis of Smart Road Stud on Driving Behavior and Traffic Flow in Two-Lane Two-Way Highway" Sustainability 15, no. 15: 11559. https://doi.org/10.3390/su151511559
APA StyleLi, M., Luo, Q., Fan, J., & Ning, Q. (2023). Impact Analysis of Smart Road Stud on Driving Behavior and Traffic Flow in Two-Lane Two-Way Highway. Sustainability, 15(15), 11559. https://doi.org/10.3390/su151511559





