Cluster Analysis of Freeway Tunnel Length Based on Naturalistic Driving Safety and Comfort
Abstract
:1. Introduction
2. Methodology
3. Experiment
3.1. Participants and Vehicles
3.2. Instruments and Equipment
3.3. Experiment Road and Tunnel
- (1)
- Preview area (A): This area is the section where the driver is 200 m before the tunnel information sign to when he/she is one stopping sight distance from the tunnel entrance. This section extended from 500 m before the tunnel entrance to 110 m before the tunnel entrance.
- (2)
- Entrance area (B): This area is the section where the driver is one stopping sight distance before the tunnel entrance to him/her entering the tunnel (i.e., where the tunnel lighting environment no longer changes). This section extended from 110 m before the tunnel entrance to 200 m after the tunnel entrance.
- (3)
- Middle area (C): This area is the section of the tunnel where the lighting environment does not change. This section extended from 200 m after the tunnel entrance to 200 m before the tunnel exit.
- (4)
- Exit area (D): This area is the section where the lighting environment begins to change to where the driver is one stopping sight distance after the tunnel exit. This section extended to 200 m before the tunnel exit to 110 m after the tunnel exit.
- (5)
- Separation area (E): This area is the section where the driver is one stopping sight distance after the tunnel exit to when the tunnel no longer impacts the driver. This section extended from 110 m after the tunnel exit to 500 m after the tunnel exit.
3.4. Experimental Procedures
- (1)
- Provide unified training for participants; inform them of the precautions for experiment, and familiarize them with the experimental vehicle.
- (2)
- Install instruments and equipment for vehicles and participants; adjust the instruments and equipment to normal working conditions, and maintain consistency in the timing of the instruments and equipment.
- (3)
- The participant sits quietly in the car for 5 min to collect the participant’s resting physiological data.
- (4)
- The participant drives the vehicle through the experiment road and tunnel normally.
3.5. Data Analysis
4. Cluster Analysis of Tunnel Length
4.1. Subjective Evaluation of Participants
4.2. Clustering Algorithm
4.2.1. Euclidean Distance and the K-Means Algorithm
4.2.2. K-Shape Algorithm
- (1)
- Shape-based distance (SBD):
- (2)
- Time-series shape extraction:
- (3)
- Shape-based time series clustering:
4.2.3. DDTW+K-Means++ Algorithm
4.3. Clustering Results
- (1)
- Sum of squared error (SSE):
- (2)
- Davies–Bouldin index (DBI):
- (3)
- Compactness (CP):
- (4)
- Separation (SP):
- (1)
- Category 1: tunnel length of 54~466 m. A tunnel with a length of 450 m or less is defined as a short tunnel.
- (2)
- Category 2: tunnel length of 444~3962 m. A tunnel with a length of 450~4000 m is defined as a general tunnel.
- (3)
- Category 3: tunnel length of 4352~12,330 m. A tunnel with a length of 4000 m or more is defined as a long tunnel.
5. Cluster Analysis of Tunnel Length
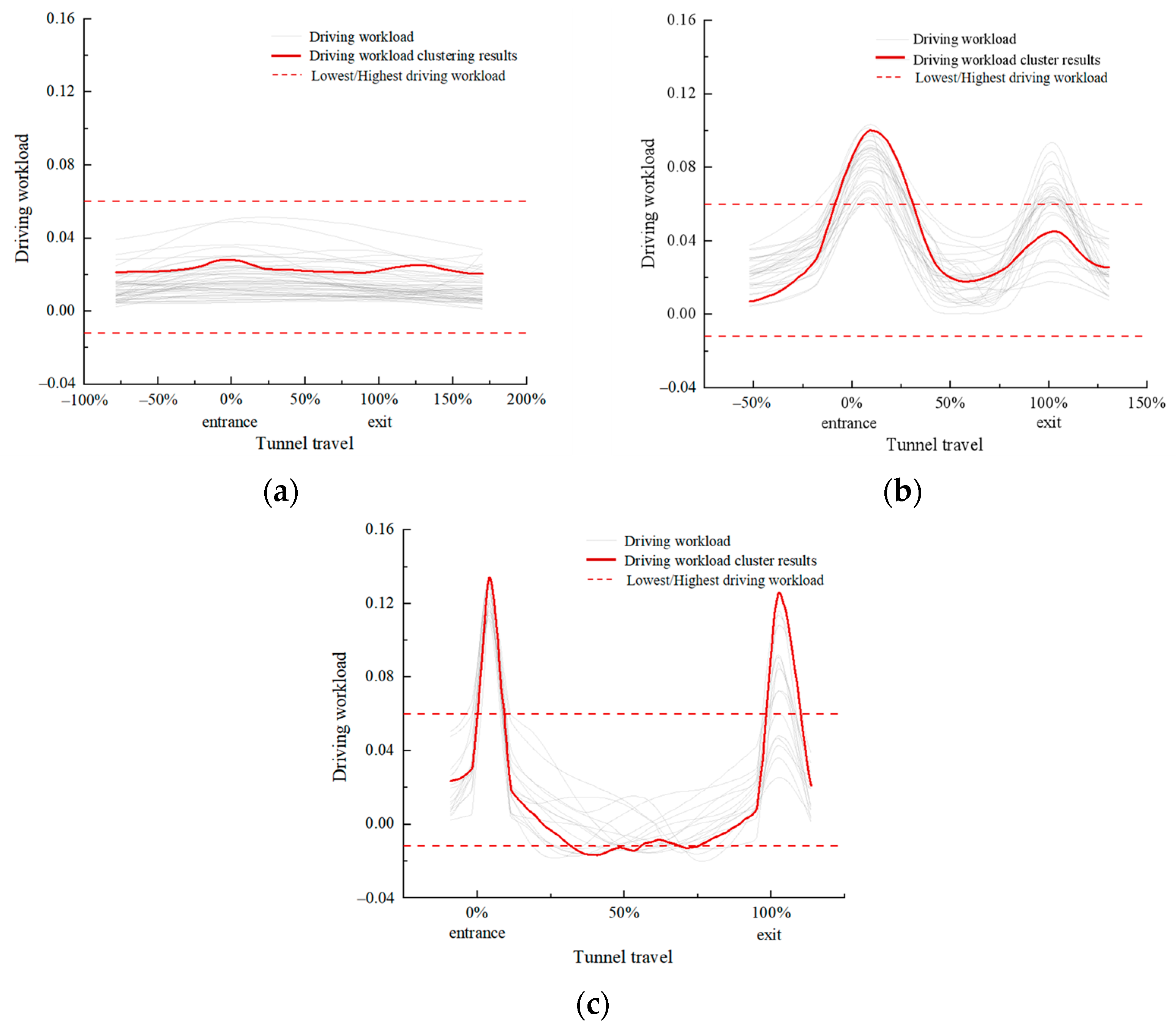
5.1. Short Tunnel
5.2. General Tunnel
5.3. Long Tunnel
6. Discussion
7. Conclusions
- The driving workload and vehicle speed characteristics of the 98 freeway tunnels of different lengths were obtained based on a naturalistic driving experiment involving 36 participants. The DDTW+K-means++ algorithm was used to cluster the tunnel lengths based on tunnel driving workload time series data. The results indicated that, in the tunnel operation stage, it is reasonable to divide tunnels into three categories according to their length (i.e., short tunnels were <450 m, general tunnels were 450~4000 m, and long tunnels were >4000 m).
- There were significant differences in the driving workload and vehicle running speed between the different categories of tunnels; the length of the tunnel had a positive correlation with the driving workload, while there was a negative correlation with the vehicle running speed. The range of changes in the driving workload and operation safety risks in the general tunnels and long tunnels were higher than those in the short tunnels.
- There were significant differences in the driving workload and vehicle running speed between the different sites in the tunnels. The road and environmental conditions were also important factors that affected the driving workload. The entrance area and exit area were the sections where the driving workload changed sharply and where the vehicle running speed was reduced, thus resulting in the adjacent sections of the vehicle running speed not being coordinated. Furthermore, the speed dispersion was large, thus increasing the risk of operational safety. Lastly, the driving workload in the middle area of the long tunnels was low; thus, there was more driving fatigue.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| Nomenclature | Meaning | Unit |
| Ai | HRV when driver i is driving normally | / |
| CCw(x,y) | A mutual correlation sequence of length 2m−1 | / |
| Ci | Set containing samples in category i | / |
| Cj | jth cluster | / |
| dist(Ci, xi) | Distance between Ci and xi | / |
| d(xi,Xi) | Distance between vector xi and cluster Xi | / |
| d(xi,xj) | Distance between two vectors xi, xj | / |
| d(xi,μi) | Distance of vector xi from cluster center μi of cluster Xi | / |
| d(μi,μj) | Distance between cluster centers μi, μj | / |
| Dx[x] | Derivative | / |
| ED | Euclidean distance | / |
| HF | High-frequency power | / |
| (i,j) | Euclidean distance wk of the time series data points xi and yj | / |
| k | Traffic volume | veh/km·ln |
| K | Number of categories | / |
| K0 | Length of the warping path | / |
| Kij | Driving workload of driver i at position j | / |
| LF | Low-frequency power | / |
| (LF/HF)ij | HRV of driver i at position j | / |
| M | m×n matrix | / |
| NCCc | Normalized cross-correlation coefficient | / |
| R | Sum of the dot products of the effective regions | / |
| SBD | Shape-based distance | / |
| Vij | Running speed when driver i is at position j | km/h |
| w | Maximum position of NCCc | / |
| W | Warping path | / |
| x = (x1,…,xm) | Time series x | / |
| y = (y1,…,ym) | Time series y | / |
| γ(i,j) | Total distance of the warping path accumulated up to row i and column j of the distance matrix | / |
| μj | Initial centroid of the jth cluster | / |
| μj* | Cluster center corresponding to the maximum squared similarity with all other time series | / |
Abbreviations
| Abbreviations | Meaning |
| CP | Compactness |
| DBI | Davies–Bouldin index |
| DDTW | Derivative dynamic time warping |
| DTW | Dynamic time warping |
| GPS | Global Positioning System |
| HR | Heart rate |
| HRG | Heart rate growth |
| HRV | Heart rate variability |
| M | Mean value |
| SD | Standard deviation |
| SP | Separation |
| SSE | Sum of squared error |
References
- Du, Z.; Wang, S.; Yang, L.; Ni, Y.; Jiao, F. Experimental study on the efficacy of retroreflective rings in the curved freeways tunnels. Tunn. Undergr. Space Technol. 2021, 110, 103813. [Google Scholar] [CrossRef]
- Wang, X.; Wen, R.; Cheng, K.; Yang, M. Evaluation and analysis of tunnel lighting service status based on driving safety. Traffic Inj. Prev. 2023, 24, 436–444. [Google Scholar] [CrossRef]
- Wang, K.; Hu, J.; Chen, R.; Wang, J. A study on the evacuation of an extra-long highway tunnel fire-A case study of Chengkai Tunnel. Sustainability 2023, 15, 4865. [Google Scholar] [CrossRef]
- Amundsen, F.H.; Ranes, G. Studies on traffic accidents in Norwegian road tunnels. Tunn. Undergr. Space Technol. 2000, 15, 3–11. [Google Scholar] [CrossRef]
- Ma, Z.; Shao, C.; Zhang, S. Characteristics of traffic accidents in Chinese freeway tunnels. Tunn. Undergr. Space Technol. 2009, 24, 350–355. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Wu, C.; Easa, S.; Lin, W.; Zheng, X. Effect of highway directional signs on driver mental workload and behavior using eye movement and brain wave. Accid. Anal. Prev. 2020, 146, 105705. [Google Scholar] [CrossRef]
- Lee, J.; Kirytopoulos, K.; Pervez, A.; Huang, H. Understanding drivers’ awareness, habits and intentions inside road tunnels for effective safety policies. Accid. Anal. Prev. 2022, 172, 106690. [Google Scholar] [CrossRef]
- Chen, J.; You, L.; Yang, M.; Wang, X. Traffic safety assessment and prediction under different lighting service states in road tunnels. Tunn. Undergr. Space Technol. 2023, 134, 105001. [Google Scholar] [CrossRef]
- Llopis, S.G. Traffic accidents in Spanish road tunnels. In Proceedings of the Institution of Civil Engineers-Transport; Thomas Telford Ltd.: London, UK, 2018; Volume 175, pp. 43–49. [Google Scholar] [CrossRef]
- Pena-Garcia, A. Sustainable tunnel lighting: One decade of proposals, advances and open points. Tunn. Undergr. Space Technol. 2021, 119, 104227. [Google Scholar] [CrossRef]
- Jiao, F.; Du, Z.; Zheng, H.; Wang, S.; Han, L.; Chen, C. Visual characteristics of drivers at different sections of an urban underpass tunnel entrance: An experimental study. Sustainability 2021, 13, 5224. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Q.; Zhang, P.; Zhong, Y.; Yue, X. Spatialtemporal characteristics of tunnel traffic accidents in China from 2001 to Present. Adv. Civ. Eng. 2019, 2019, 4536414. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Kang, X.; Wang, X.; Zhao, X.; Si, C. Research on spiral tunnel exit speed prediction model based on driver characteristics. Sustainability 2022, 14, 15736. [Google Scholar] [CrossRef]
- Kirytopoulos, K.; Kazaras, K.; Papapavlou, P.; Ntzeremes, P.; Tatsiopoulos, I. Exploring driving habits and safety critical behavioural intentions among road tunnel users: A questionnaire survey in Greece. Tunn. Undergr. Space Technol. 2017, 63, 244–251. [Google Scholar] [CrossRef]
- Wen, H.; Sun, J.; Zeng, Q.; Zhang, X.; Yuan, Q. The effects of traffic composition on freeway crash frequency by injury severity: A bayesian multivariate spatial modeling approach. J. Adv. Transport. 2018, 2018, 6964828. [Google Scholar] [CrossRef]
- Calvi, A.; De Blasiis, M.R.; Guattari, C. An empirical study of the effects of road tunnel on driving performance. Procedia Soc. Behav. Sci. 2012, 53, 1098–1108. [Google Scholar] [CrossRef]
- Calvi, A.; Amico, F.D. A study of the effects of road tunnel on driver behavior and road safety using driving simulator. Adv. Transp. Stud. 2013, 30, 57–76. [Google Scholar]
- Wang, S.; Du, Z.; Jiao, F.; Zheng, H.; Ni, Y. Drivers’ visual load at different time periods in entrance and exit zones of extra-long tunnel. Traffic Inj. Prev. 2020, 21, 539–544. [Google Scholar] [CrossRef]
- Feng, Z.; Yang, M.; Zhang, W.; Du, Y.; Bai, H. Effect of longitudinal slope of urban underpass tunnels on drivers’ heart rate and speed: A study based on a real vehicle experiment. Tunn. Undergr. Space Technol. 2018, 81, 525–533. [Google Scholar] [CrossRef]
- Yang, Y.; Du, Z.; Jiao, F.; Pan, F. Analysis of EEG characteristics of drivers and driving safety in undersea tunnel. Int. J. Environ. Res. Public Health 2021, 18, 9810. [Google Scholar] [CrossRef]
- Rendon-Velez, E.; van Leeuwen, P.M.; Happee, R.; Horváth, I.; van der Vegte, W.F.; de Winter, J.C.F. The effects of time pressure on driver performance and physiological activity: A driving simulator study. Transp. Res. Part F Traffic Psychol. Behav. 2016, 41, 150–169. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.; Shen, B.; Wang, L. Model of driver’s eye movement and ECG index under tunnel environment based on spatiotemporal data. J. Adv. Transport. 2020, 2020, 5215479. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Chen, J.; Easa, S.M.; Zheng, X.; Lin, W.; Peng, Y. Driving simulator study of the comparative effectiveness of monolingual and bilingual guide signs on Chinese highways. Transport. Res. F-Traf. 2020, 68, 67–78. [Google Scholar] [CrossRef]
- Pawar, N.M.; Velaga, N.R.; Sharmila, R.B. Exploring behavioral validity of driving simulator under time pressure driving conditions of professional drivers. Transp. Res. Part F Traffic Psychol. Behav. 2022, 89, 67–78. [Google Scholar] [CrossRef]
- Fu, X.; He, S.; Du, J.; Wang, X.; Ge, T. Variations in naturalistic driving behavior and visual perception at the entrances of short, medium, and long tunnels. J. Adv. Transport. 2020, 2020, 7630681. [Google Scholar] [CrossRef]
- Mashimo, H. State of the road tunnel safety technology in Japan. Tunn. Undergr. Space Technol. 2002, 17, 145–152. [Google Scholar] [CrossRef]
- British Standards Institution. Code of Practice for the Design of Road Lighting-Part 2: Lighting of Tunnels; BS 5489-2:2003+A1:2008; BSI Group Headquarters: London, UK, 2008. [Google Scholar]
- Kim, H.K.; Loennermark, A.; Ingason, H. Comparison of road tunnel design guidelines. In Proceedings of the Third International Symposium on Tunnel Safety and Security, Stockholm, Sweden, 12–14 March 2008. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Specifications for Design of Highway Tunnels-Section 1 Civil Engineering; JTG 3370.1-2018; China Communications Press: Beijing, China, 2019. [Google Scholar]
- Chen, X.; Guo, X. Research on Classification Methods for Operational Management of Highway Tunnels. Technol. Highw. Transp. 2010, 90, 121–123+128. [Google Scholar]
- Ma, S.; Hu, J.; Wang, R.; Qu, S. Study on the median opening length of a freeway work zone based on a naturalistic driving experiment. Appl. Sci. 2023, 13, 851. [Google Scholar] [CrossRef]
- Wei, W.; Fu, X.; Zhong, S.; Ge, H. Driver’s mental workload classification using physiological, traffic flow and environmental factors. Transp. Res. Part F Traffic Psychol. Behav. 2023, 94, 151–169. [Google Scholar] [CrossRef]
- Choi, K.-H.; Kim, J.; Kwon, O.S.; Kim, M.J.; Ryu, Y.H.; Park, J.-E. Is heart rate variability (HRV) an adequate tool for evaluating human emotions?—A focus on the use of the International Affective Picture System (IAPS). Psychiat. Res. 2017, 251, 192–196. [Google Scholar] [CrossRef]
- Wang, C.; Chan, Y.; Chu, S.; Yu, S. r-Reference points based k-means algorithm. Inform. Sci. 2022, 610, 204–214. [Google Scholar] [CrossRef]
- Paparrizos, J.; Gravano, L. k-Shape: Efficient and accurate clustering of time series. Sigmod. Rec. 2016, 45, 69–76. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Campana, B.; Mueen, A.; Batista, G.; Westover, B.; Zhu, Q.; Zakaria, J.; Keogh, E. Searching and mining trillions of time series subsequences under dynamic time warping. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD’ 12, Beijing, China, 12–16 August 2012. [Google Scholar]
- Keogh, E.J.; Pazzani, M.J. Derivative dynamic time warping. In Proceedings of the 2001 SIAM international Conference on Data Mining, Chicago, IL, USA, 5–7 April 2001. [Google Scholar]
- Baldassi, C. Recombinator-k-Means: An evolutionary algorithm that exploits k-Means plus plus for recombination. IEEE Trans. Evol. Comput. 2022, 26, 991–1003. [Google Scholar] [CrossRef]
- Meng, J.; Yu, Z.; Cai, Y.; Wang, X. K-Means++ clustering algorithm in categorization of glass cultural relics. Appl. Sci. 2023, 13, 4736. [Google Scholar] [CrossRef]
- Lee, Y.M.; Chong, S.Y.; Goonting, K.; Sheppard, E. The effect of speed limit credibility on drivers’ speed choice. Transp. Res. Part F Traffic Psychol. Behav. 2017, 45, 43–53. [Google Scholar] [CrossRef]
- Jung, S.; Qin, X. Data-Driven approach to weather-responsive speed management of road tunnel access zones. Transport. Res. Rec. 2022, 2676, 1–12. [Google Scholar] [CrossRef]
- Meng, Q.; Qu, X. Estimation of rear-end vehicle crash frequencies in urban road tunnels. Accident Anal. Prev. 2012, 48, 254–263. [Google Scholar] [CrossRef] [Green Version]
- Qin, P.; Wang, M.; Chen, Z.; Yan, G.; Yan, T.; Han, C.; Bao, Y.; Wang, X. Characteristics of driver fatigue and fatigue-relieving effect of special light belt in extra-long highway tunnel: A real-road driving study. Tunn. Undergr. Space Technol. 2021, 114, 103990. [Google Scholar] [CrossRef]







| Driving Workload Degree | Safety Level | Driving Workload |
|---|---|---|
| Highest | Highly risky (nervous) | Kij > 0.060 |
| Higher | Relatively risky (relatively nervous) | 0.030 < Kij ≤ 0.060 |
| Normal | Safe | –0.001 < Kij ≤ 0.030 |
| Lower | Relatively risky (relatively fatigued) | –0.012 < Kij ≤ –0.001 |
| Lowest | Highly risky (fatigue) | Kij ≤ –0.012 |
| Participants Status | Not Nervous and Not Fatigued | Only Nervous | Only Fatigued | Nervous and Fatigued |
|---|---|---|---|---|
| Participant Proportion | 28.2% | 48.1% | 3.6% | 20.1% |
| Number of Tunnel Classifications | 2 | 3 | 4 | 5 |
| Participant Proportion | 2.8% | 69.4% | 19.5% | 8.3% |
| K | 2 | 3 | 4 | 5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | A | B | C | A | B | C | A | B | C | A | B | C |
| SSE | 0.0098 | 0.0080 | 0.0076 | 0.0062 | 0.0052 | 0.0048 | 0.0058 | 0.0045 | 0.0042 | 0.0054 | 0.0038 | 0.0039 |
| DBI | 0.0102 | 0.0088 | 0.0084 | 0.0075 | 0.0056 | 0.0051 | 0.0062 | 0.0040 | 0.0041 | 0.0055 | 0.0041 | 0.0038 |
| CP | 0.0287 | 0.0198 | 0.0174 | 0.0187 | 0.0117 | 0.0101 | 0.0141 | 0.0099 | 0.0091 | 0.0124 | 0.0093 | 0.0084 |
| SP | 0.0245 | 0.0541 | 0.0654 | 0.0412 | 0.0765 | 0.0861 | 0.0346 | 0.0614 | 0.0645 | 0.0274 | 0.0511 | 0.0587 |
| Tunnel | Site | Maximum Speed (km/h) | Minimum Speed (km/h) | Running Speed (km/h) | Mean Speed (km/h) | SD | Speed Limit Compliance Rate |
|---|---|---|---|---|---|---|---|
| / | S | 102.54 | 66.01 | 96.94 | 88.13 | 10.28 | 23.61% |
| Short Tunnel | A | 95.86 | 59.95 | 86.98 | 80.04 | 10.09 | 45.52% |
| B | 83.68 | 49.61 | 74.44 | 64.40 | 9.79 | 90.63% | |
| D | 90.80 | 60.58 | 85.25 | 74.31 | 9.78 | 63.85% | |
| E | 96.54 | 63.06 | 86.82 | 78.29 | 9.90 | 51.02% | |
| General Tunnel | A | 95.80 | 58.05 | 84.89 | 76.83 | 10.40 | 62.57% |
| B | 81.65 | 48.43 | 70.89 | 61.82 | 9.36 | 93.86% | |
| C | 86.93 | 60.67 | 77.97 | 73.87 | 6.59 | 90.31% | |
| D | 87.14 | 53.42 | 73.76 | 65.50 | 8.98 | 86.74% | |
| E | 91.54 | 56.94 | 82.86 | 74.10 | 10.72 | 67.58% | |
| Long Tunnel | A | 94.77 | 56.55 | 84.88 | 76.65 | 10.84 | 65.87% |
| B | 82.65 | 46.43 | 69.01 | 60.86 | 9.03 | 95.88% | |
| C | 92.26 | 56.10 | 82.90 | 75.10 | 10.93 | 73.28% | |
| D | 86.29 | 50.66 | 69.93 | 64.10 | 8.77 | 93.75% | |
| E | 89.22 | 52.16 | 82.30 | 72.65 | 10.95 | 70.51% |
| Tunnel | Site | Maximum | Minimum | Mean | SD | Higher Risk Ratio | High Risk Ratio |
|---|---|---|---|---|---|---|---|
| / | S | 0.03541 | –0.00412 | 0.00614 | 0.00701 | 2.01% | 0.00% |
| Short Tunnel | A | 0.04957 | 0.00205 | 0.01631 | 0.00940 | 8.05% | 0.00% |
| B | 0.05125 | 0.00445 | 0.01825 | 0.01035 | 11.02% | 0.00% | |
| D | 0.05254 | 0.00513 | 0.01635 | 0.00939 | 10.06% | 0.00% | |
| E | 0.04445 | 0.00079 | 0.01387 | 0.00783 | 4.55% | 0.00% | |
| General Tunnel | A | 0.05857 | 0.00412 | 0.02509 | 0.00901 | 28.51% | 0.00% |
| B | 0.10306 | 0.00211 | 0.05760 | 0.02126 | 89.72% | 46.27% | |
| C | 0.05162 | 0.00021 | 0.01841 | 0.00981 | 11.73% | 0.00% | |
| D | 0.09316 | 0.00008 | 0.04677 | 0.01796 | 78.82% | 25.37% | |
| E | 0.05786 | 0.00756 | 0.02967 | 0.01036 | 44.09% | 0.00% | |
| Long Tunnel | A | 0.06384 | 0.00244 | 0.02467 | 0.01535 | 30.98% | 2.36% |
| B | 0.13396 | 0.00487 | 0.07944 | 0.03304 | 91.68% | 69.41% | |
| C | 0.05886 | –0.02064 | 0.00220 | 0.01470 | 51.72% | 21.20% | |
| D | 0.12596 | –0.00932 | 0.05834 | 0.03022 | 80.77% | 45.48% | |
| E | 0.07778 | 0.00124 | 0.03136 | 0.01695 | 47.62% | 6.88% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Hu, J.; Ma, E.; Li, W.; Wang, R. Cluster Analysis of Freeway Tunnel Length Based on Naturalistic Driving Safety and Comfort. Sustainability 2023, 15, 11914. https://doi.org/10.3390/su151511914
Ma S, Hu J, Ma E, Li W, Wang R. Cluster Analysis of Freeway Tunnel Length Based on Naturalistic Driving Safety and Comfort. Sustainability. 2023; 15(15):11914. https://doi.org/10.3390/su151511914
Chicago/Turabian StyleMa, Sen, Jiangbi Hu, Ershun Ma, Weicong Li, and Ronghua Wang. 2023. "Cluster Analysis of Freeway Tunnel Length Based on Naturalistic Driving Safety and Comfort" Sustainability 15, no. 15: 11914. https://doi.org/10.3390/su151511914
APA StyleMa, S., Hu, J., Ma, E., Li, W., & Wang, R. (2023). Cluster Analysis of Freeway Tunnel Length Based on Naturalistic Driving Safety and Comfort. Sustainability, 15(15), 11914. https://doi.org/10.3390/su151511914






