Life Insurance Prediction and Its Sustainability Using Machine Learning Approach
Abstract
:1. Introduction
2. Related Work
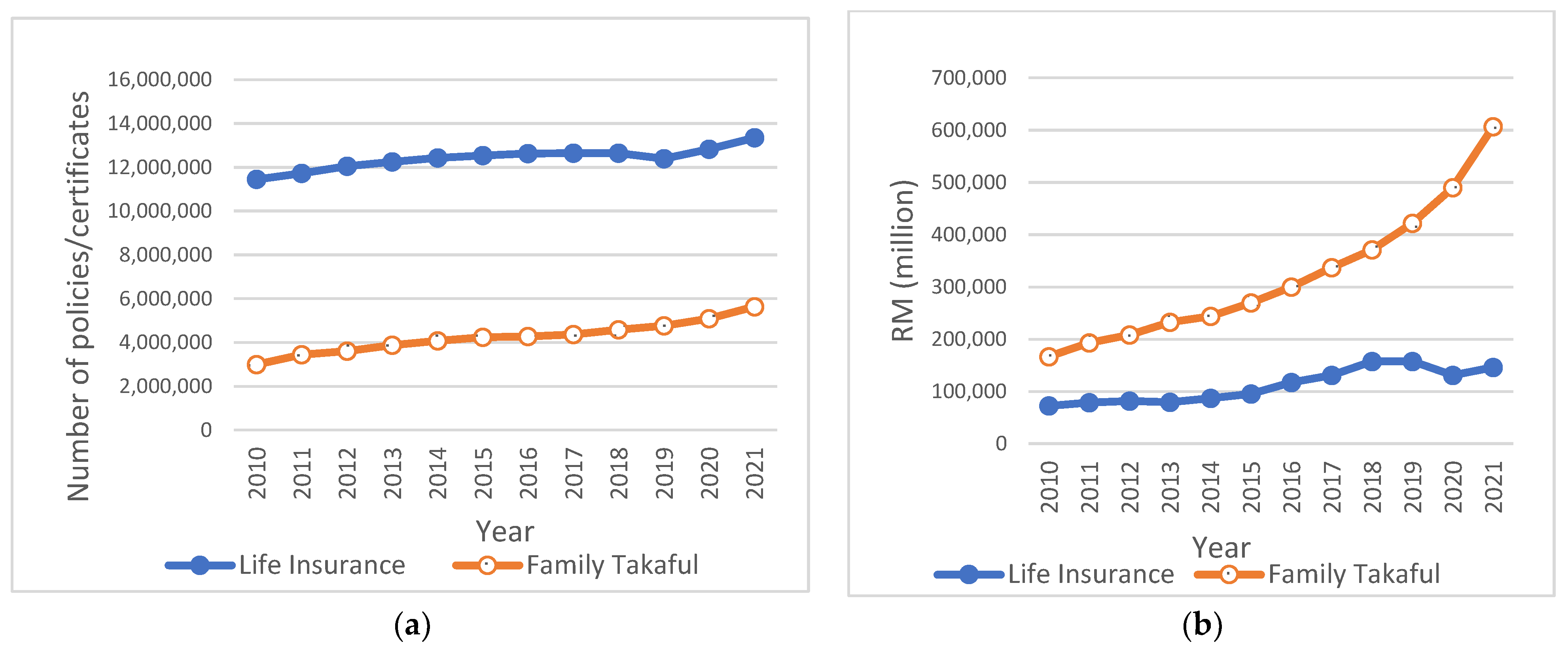
2.1. The Life Insurance Ownership
2.2. Data Mining
2.3. Life Insurance and Machine Learning
2.4. Sampling for Imbalanced Dataset
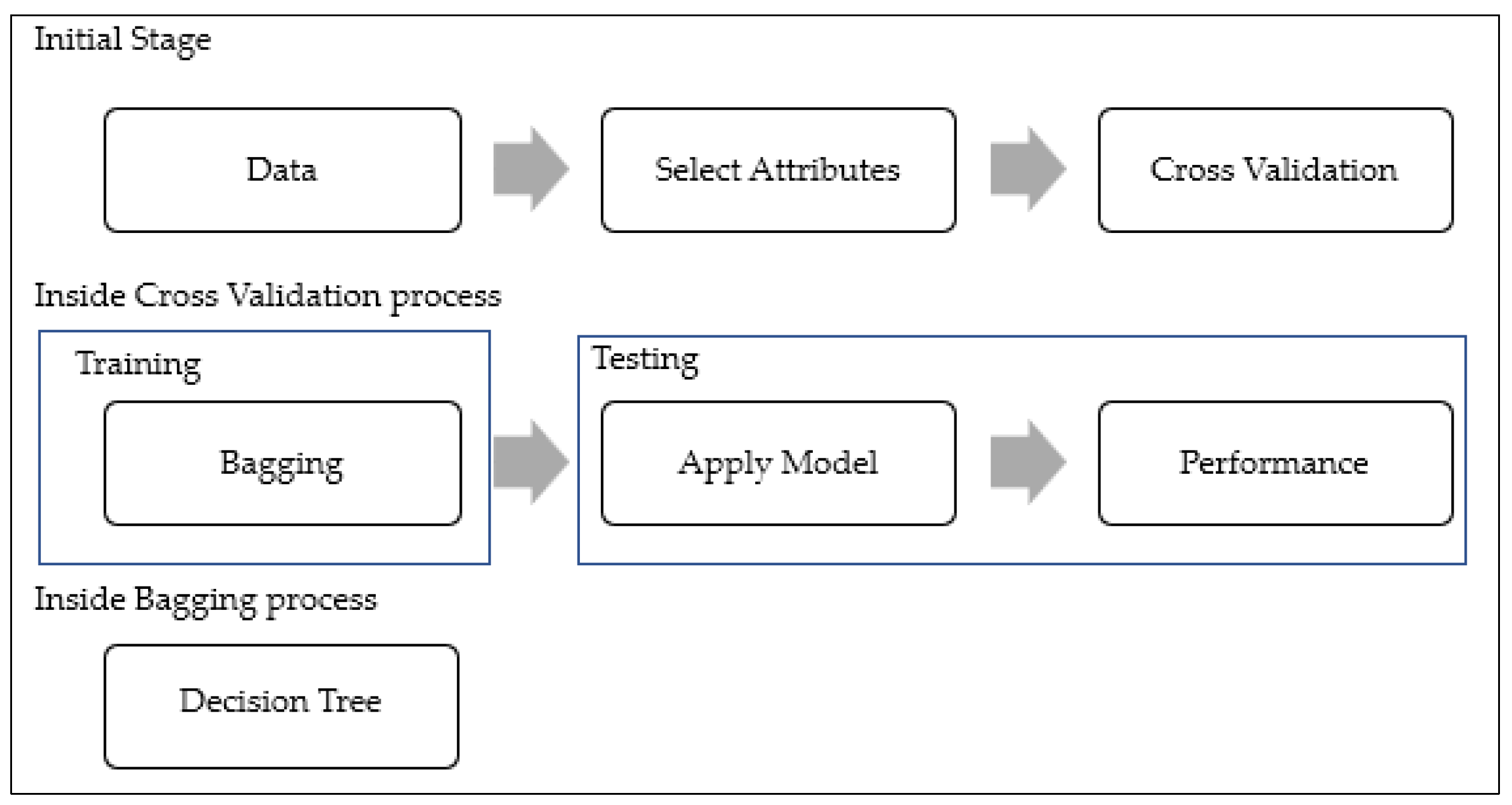
2.5. Ensemble Approaches (Bagging and Boosting)
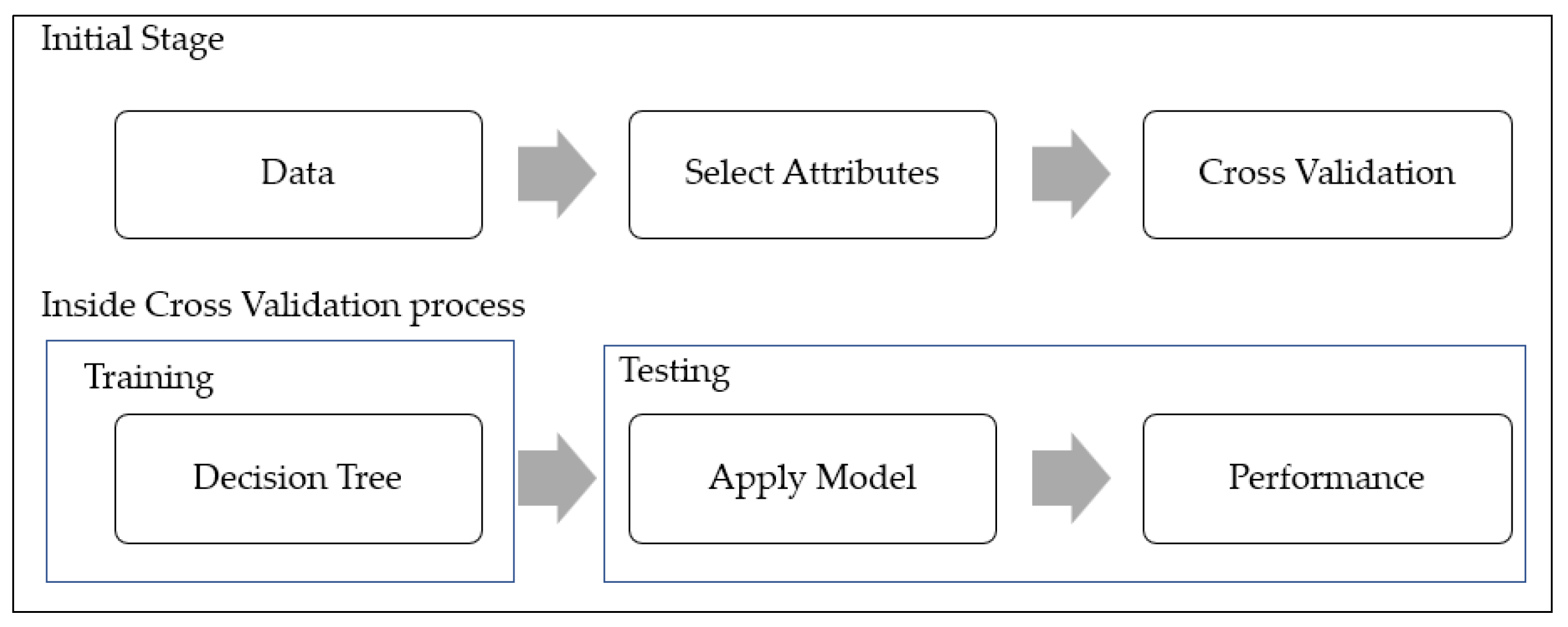
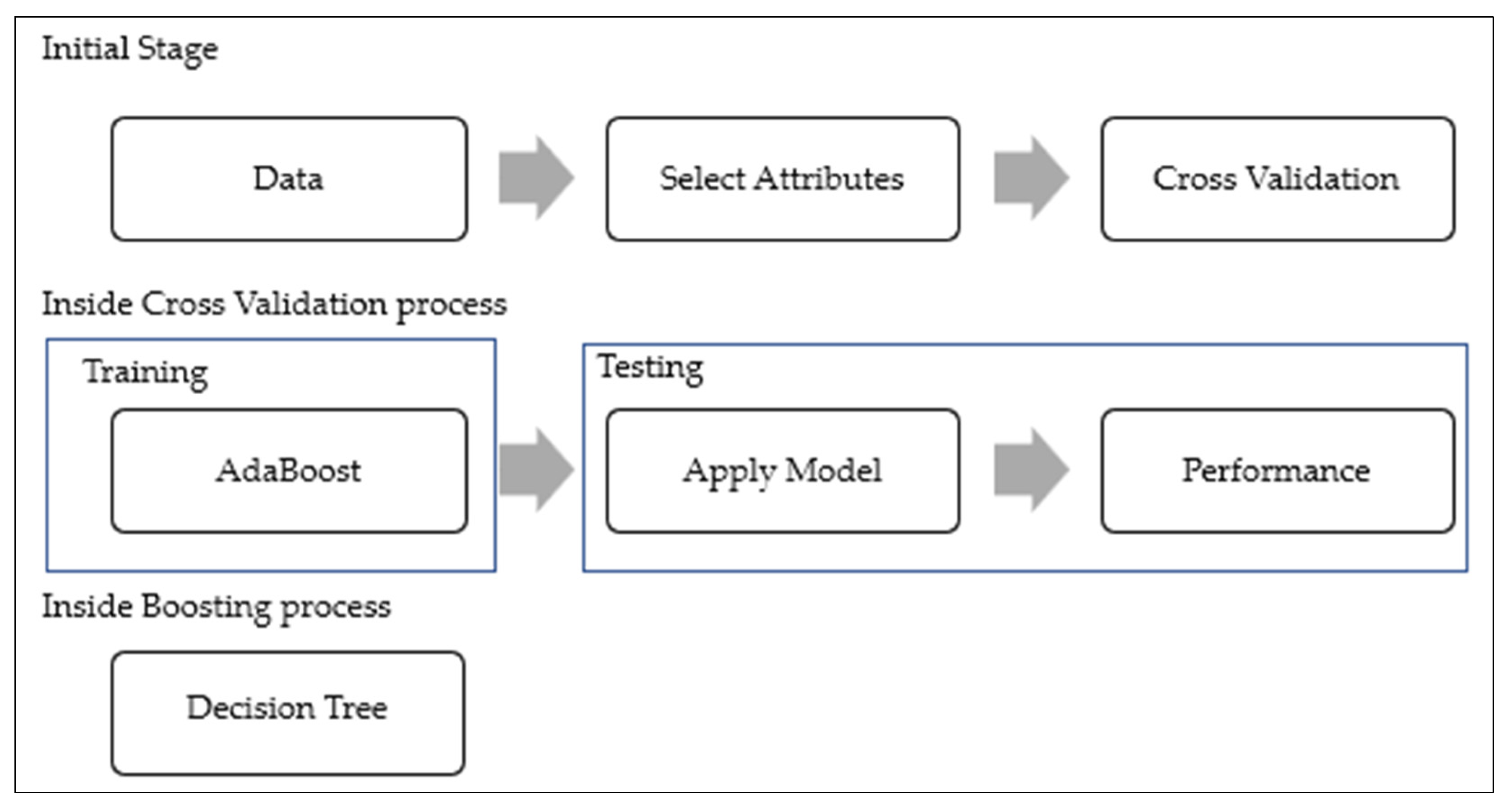
3. Materials and Method
4. Discussion
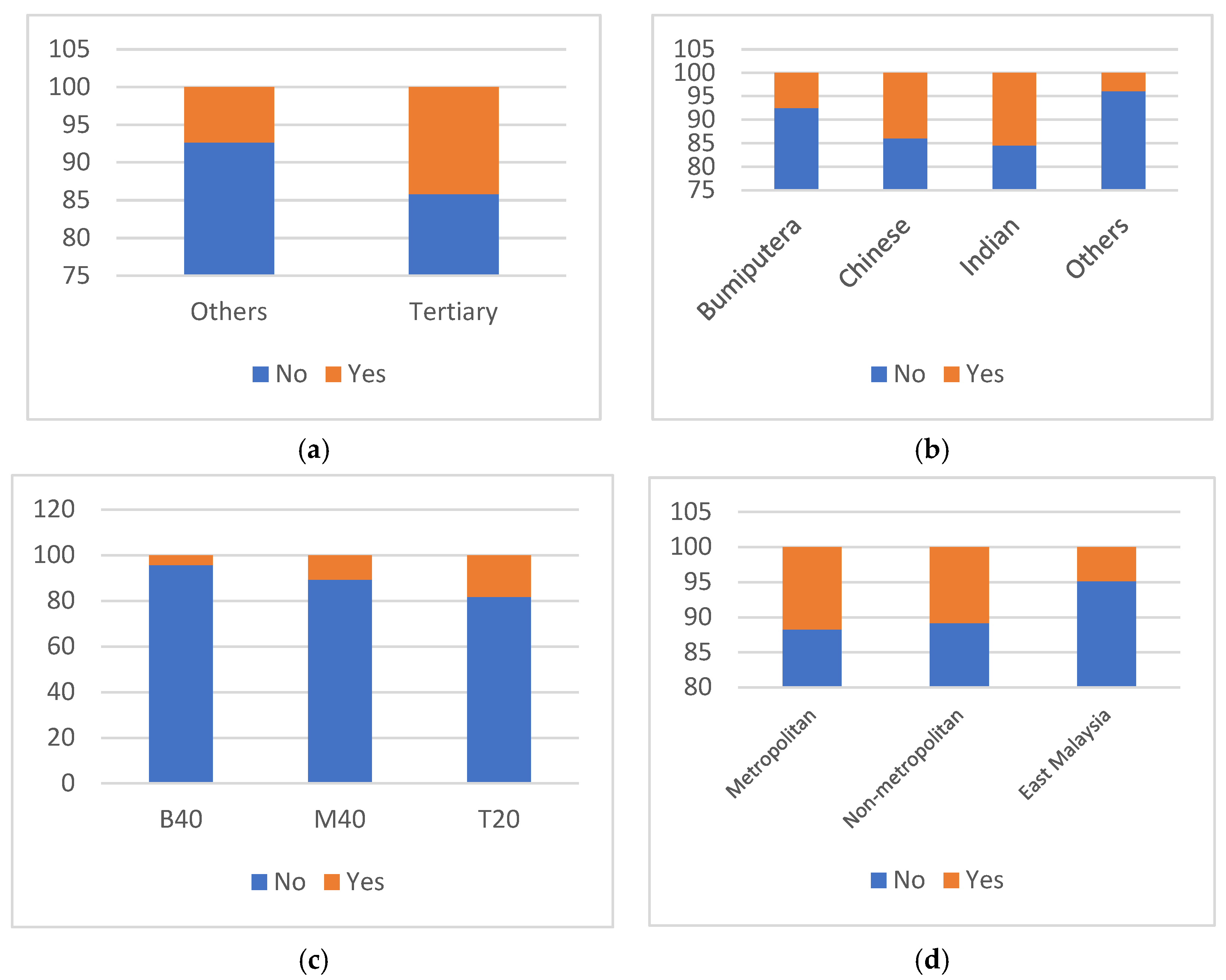
4.1. Descriptive Analysis
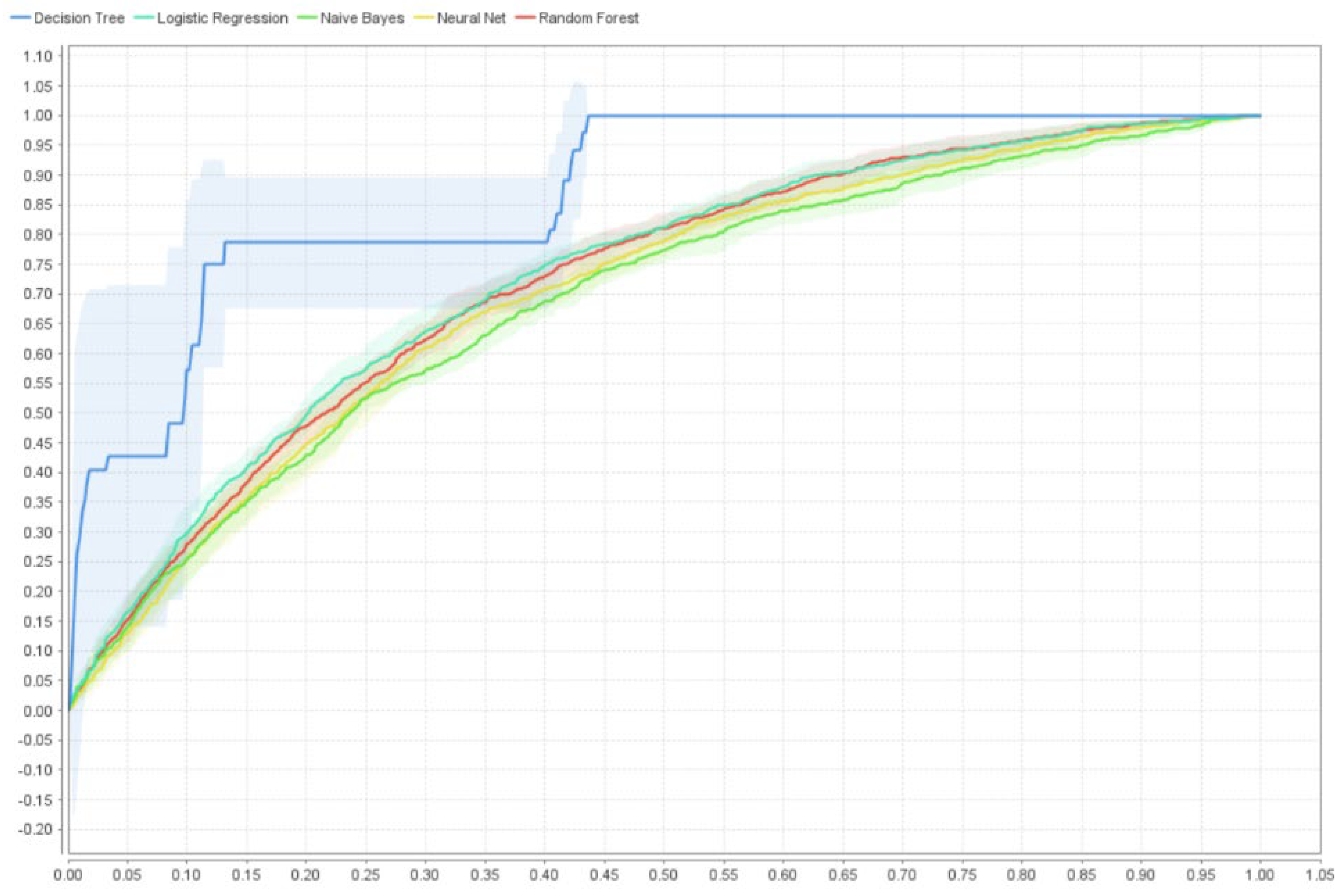
4.2. Best Model Comparison
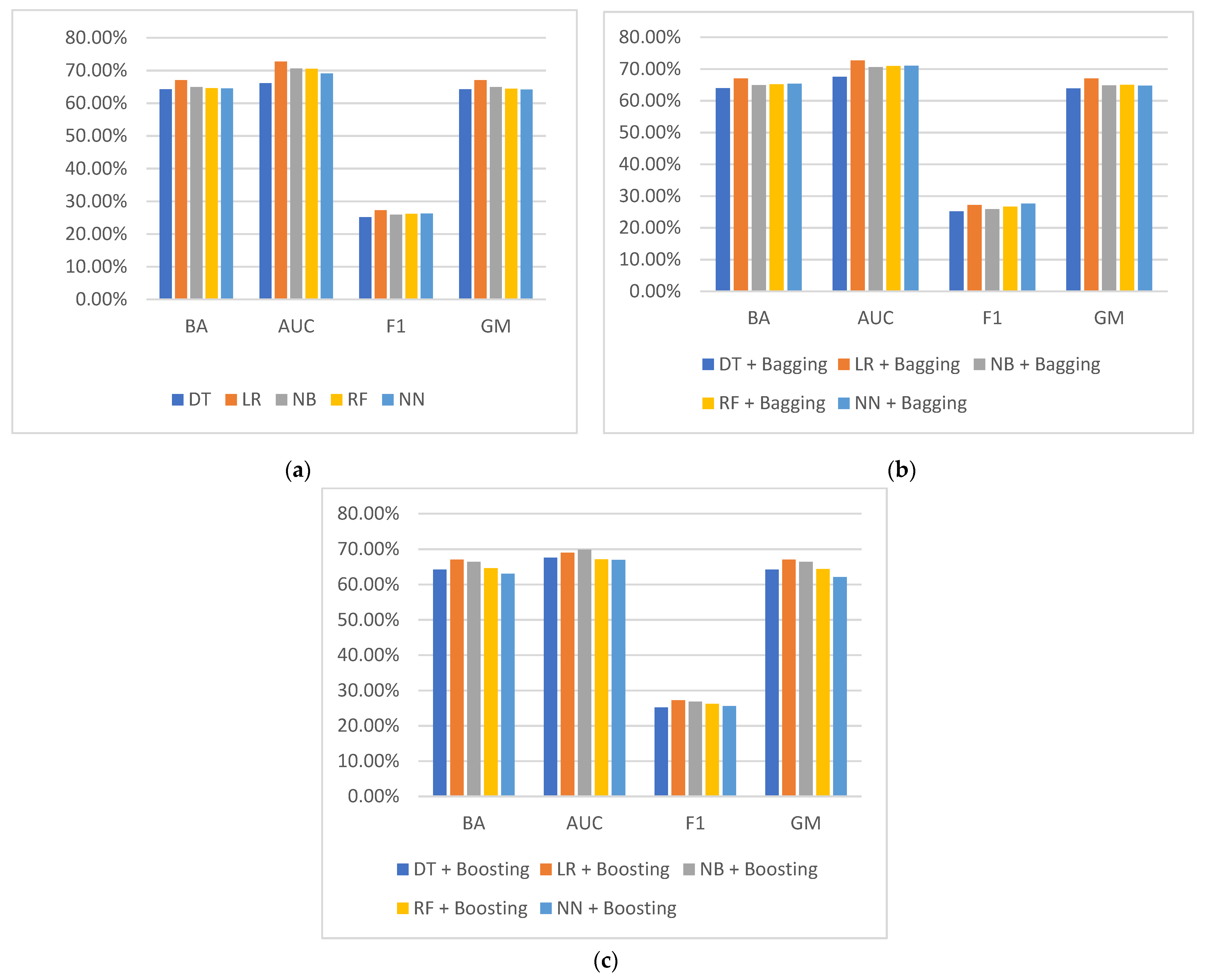
4.3. Model Scoring
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hiwase, V.A.; Agrawal, A.J. Review on application of data mining in life insurance. Int. J. Eng. Technol. 2018, 7, 159–162. [Google Scholar] [CrossRef]
- Emamgholipour, S.; Arab, M.; Mohajerzadeh, Z. Life insurance demand: Middle East and North Africa. Int. J. Soc. Econ. 2017, 44, 521–529. [Google Scholar] [CrossRef]
- Swiss Re Institute. Closing Asia’s Mortality Protection Gap. Report; Swiss Re Institute: Zurich, Switzerland, 2020. [Google Scholar]
- Descombes, J. Why Hasn’t COVID-19 Led to an Increase in Life Insurance Protection? Available online: https://www.swissre.com/institute/research/topics-and-risk-dialogues/health-and-longevity/covid-19-life-insurance.html (accessed on 7 September 2022).
- LIMRA and Life Happens. 2021 Insurance Barometer Study, LIMRA and Life Happens. COVID-19 Drives Interest in Life Insurance; LIMRA: Windsor, CT, USA, 2021. [Google Scholar]
- Bank Negara Malaysia. Monthly Highlights and Statistics; Report; Bank Negara Malaysia: Kuala Lumpur, Malaysia, 2020. [Google Scholar]
- Swiss Re Institute. Sigma No. 4/2022: World Insurance:Inflation Risks Frontand Centre; Swiss Re Institute: Zurich, Switzerland, 2022. [Google Scholar]
- Bhatia, R.; Bhat, A.K.; Tikoria, J. Life insurance purchase behaviour: A systematic review and directions for future research. Int. J. Consum. Stud. 2021, 45, 1149–1175. [Google Scholar] [CrossRef]
- Annamalah, S. Profiling and purchasing decision of life insurance policies among married couples in Malaysia. World Appl. Sci. J. 2013, 23, 296–304. [Google Scholar]
- Grabova, P.; Sharku, G. Drivers of life insurance consumption—An empirical analysis of Western Balkan countries. Econ. Ann. 2021, 66, 33–58. [Google Scholar] [CrossRef]
- Loke, Y.J.; Goh, Y.Y. Purchase Decision of Life Insurance Policies among Malaysians. Int. J. Soc. Sci. Humanit. 2013, 2, 415–420. [Google Scholar] [CrossRef]
- Tan, A.K.G.; Yen, S.T.; Hasan, A.R.; Muhamed, K. Demand for Life Insurance in Malaysia: An Ethnic Comparison Using Household Expenditure Survey Data. Asia-Pac. J. Risk Insur. 2014, 8, 179–204. [Google Scholar] [CrossRef]
- Giri, M. A Behavioral Study of Life Insurance Purchase Decisions. Ph.D. Thesis, Indian Institute of Technology Kanpur, Kanpur, India, 2018. [Google Scholar]
- Kabrt, T. Life Insurance Demand Analysis: Evidence from Visegrad Group Countries. East. Eur. Econ. 2022, 60, 50–78. [Google Scholar] [CrossRef]
- Segodi, M.P.; Sibindi, A.B. Determinants of Life Insurance Demand: Empirical Evidence from BRICS Countries. Risks 2022, 10, 73. [Google Scholar] [CrossRef]
- Shamsuddin, S.N.; Ismail, N.; Roslan, N.F. What We Know about Research on Life Insurance Lapse: A Bibliometric Analysis. Risks 2022, 10, 97. [Google Scholar] [CrossRef]
- Gramegna, A.; Giudici, P. Why to buy insurance? An explainable artificial intelligence approach. Risks 2020, 8, 137. [Google Scholar] [CrossRef]
- Azzone, M.; Barucci, E.; Giuffra Moncayo, G.; Marazzina, D. A machine learning model for lapse prediction in life insurance contracts. Expert Syst. Appl. 2022, 191, 116261. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, H. Research on the application of data mining technology in insurance informatization. In Proceedings of the 2009 9th International Conference on Hybrid Intelligent Systems, HIS 2009, Shenyang, China, 12–14 August 2009; Volume 3, pp. 202–205. [Google Scholar]
- Saidur Rahman, M.; Arefin, K.Z.; Masud, S.; Sultana, S.; Rahman, R.M. Analyzing Life Insurance Data with Different Classification Techniques for Customers’ Behavior Analysis. In Studies in Computational Intelligence; Springer Verlag: Berlin/Heidelberg, Germany, 2017; Volume 710, pp. 15–25. [Google Scholar]
- Abdul-Rahman, S.; Faiqah Kamal Arifin, N.; Hanafiah, M.; Mutalib, S. Customer Segmentation and Profiling for Life Insurance using K-Modes Clustering and Decision Tree Classifier. IJACSA Int. J. Adv. Comput. Sci. Appl. 2021, 12, 434–444. [Google Scholar] [CrossRef]
- Pereira, K.; Vinagre, J.; Alonso, A.N.; Coelho, F.; Carvalho, M. Privacy-Preserving Machine Learning in Life Insurance Risk Prediction. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Grenoble, France, 19–23 September 2022; Springer: Cham, Switzerland, 2023; Volume 1753, pp. 44–52. [Google Scholar]
- Rawat, S.; Rawat, A.; Kumar, D.; Sabitha, A.S. Application of machine learning and data visualization techniques for decision support in the insurance sector. Int. J. Inf. Manag. Data Insights 2021, 1, 100012. [Google Scholar] [CrossRef]
- Kaushik, K.; Bhardwaj, A.; Dwivedi, A.D.; Singh, R. Machine Learning-Based Regression Framework to Predict Health Insurance Premiums. Int. J. Environ. Res. Public Health 2022, 19, 7898. [Google Scholar] [CrossRef]
- Yap, C.T.; Khor, K.C. Utilising Sampling Methods to Improve the Prediction on Customers’ Buying Intention. In Proceedings of the 2022 International Conference on Decision Aid Sciences and Applications, DASA 2022, Chiangrai, Thailand, 23–25 March 2022; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022; pp. 352–356. [Google Scholar]
- Gonçalves, C.; Ferreira, D.; Neto, C.; Abelha, A.; Machado, J. Prediction of mental illness associated with unemployment using data mining. In Proceedings of the International Workshop on Healthcare Open Data, Intelligence and Interoperability (HODII), Madeira, Portugal, 2–5 November 2020; Elsevier B.V.: Amsterdam, The Netherlands, 2020; Volume 177, pp. 556–561. [Google Scholar]
- Tékouabou, S.C.K.; Gherghina, Ș.C.; Toulni, H.; Mata, P.N.; Martins, J.M. Towards Explainable Machine Learning for Bank Churn Prediction Using Data Balancing and Ensemble-Based Methods. Mathematics 2022, 10, 2379. [Google Scholar] [CrossRef]
- Díez-Pastor, J.F.; Rodríguez, J.J.; García-Osorio, C.; Kuncheva, L.I. Random Balance: Ensembles of variable priors classifiers for imbalanced data. Knowl. Based Syst. 2015, 85, 96–111. [Google Scholar] [CrossRef]
- Ramos-Pérez, I.; Arnaiz-González, Á.; Rodríguez, J.J.; García-Osorio, C. When is resampling beneficial for feature selection with imbalanced wide data? Expert Syst. Appl. 2022, 188, 116015. [Google Scholar] [CrossRef]
- Bauer, E.; Chan, P.; Stolfo, S.; Wolpert, D. An Empirical Comparison of Voting Classification Algorithms: Bagging, Boosting, and Variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Saleem, F.; Ullah, Z.; Fakieh, B.; Kateb, F. Intelligent decision support system for predicting student’s e-learning performance using ensemble machine learning. Mathematics 2021, 9, 2078. [Google Scholar] [CrossRef]
- Vafeiadis, T.; Diamantaras, K.I.; Sarigiannidis, G.; Chatzisavvas, K.C. A comparison of machine learning techniques for customer churn prediction. Simul. Model. Pract. Theory 2015, 55, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.; Sherry, X.; Jennifer, N.; Priestley, L. Improving Risk Modeling Via Feature Selection, Hyper-Parameter Adjusting, and Model Ensembling. Glob. J. Econ. Financ. 2019, 3, 30–47. [Google Scholar]
- Kumar, D.R.; Sree, B.C.U.; Veera, K.; Manoj Kumar, V. Predicting heart disease using machine learning techniques. Int. Res. J. Comput. Sci. 2019, 6, 149–153. [Google Scholar]
- El-Khamisy Mohamed, N.; El-Bhrawy, A.S.M. Artificial Neural Networks in Data Mining. IOSR J. Comput. Eng. 2016, 18, 55–59. [Google Scholar]
- Prajwala, T.R. A Comparative Study on Decision Tree and Random Forest Using R Tool. Int. J. Adv. Res. Comput. Commun. Eng. 2015, 4, 196–199. [Google Scholar]
- Lakshmi, K.V.; Kumari, N.S. Survey on Naive Bayes Algorithm. Int. J. Adv. Res. Sci. Eng. 2018, 7, 240–246. [Google Scholar]
- Ferreira, D.; Silva, S.; Abelha, A.; Machado, J. Recommendation system using autoencoders. Appl. Sci. 2020, 10, 5510. [Google Scholar] [CrossRef]
- Nazemi, A.; Rezazadeh, H.; Fabozzi, F.J.; Höchstötter, M. Deep learning for modeling the collection rate for third-party buyers. Int. J. Forecast. 2022, 38, 240–252. [Google Scholar] [CrossRef]
- Tékouabou, S.C.K.; Alaoui, E.A.A.; Chabbar, I.; Toulni, H.; Cherif, W.; Silkan, H. Optimizing the early glaucoma detection from visual fields by combining preprocessing techniques and ensemble classifier with selection strategies. Expert Syst. Appl. 2022, 189, 115975. [Google Scholar] [CrossRef]
- De Diego, I.M.; Redondo, A.R.; Fernández, R.R.; Navarro, J.; Moguerza, J.M. General Performance Score for classification problems. Appl. Intell. 2022, 52, 12049–12063. [Google Scholar] [CrossRef]
- Ibrahim, S.; Khairi, S.S.M. Predictive Data Mining Approaches for Diabetes Mellitus Type II Disease. Int. J. Glob. Optim. Its Appl. 2022, 1, 126–134. [Google Scholar] [CrossRef]
| Models | Advantages | Disadvantages |
|---|---|---|
| Decision Tree | ||
| Logistic Regression |
| |
| Naïve Bayes | ||
| Random Forest |
| |
| Artificial Neural Network |
|
| Attributes | Measurement Level | Category | Description | Frequency | Percentage (%) |
|---|---|---|---|---|---|
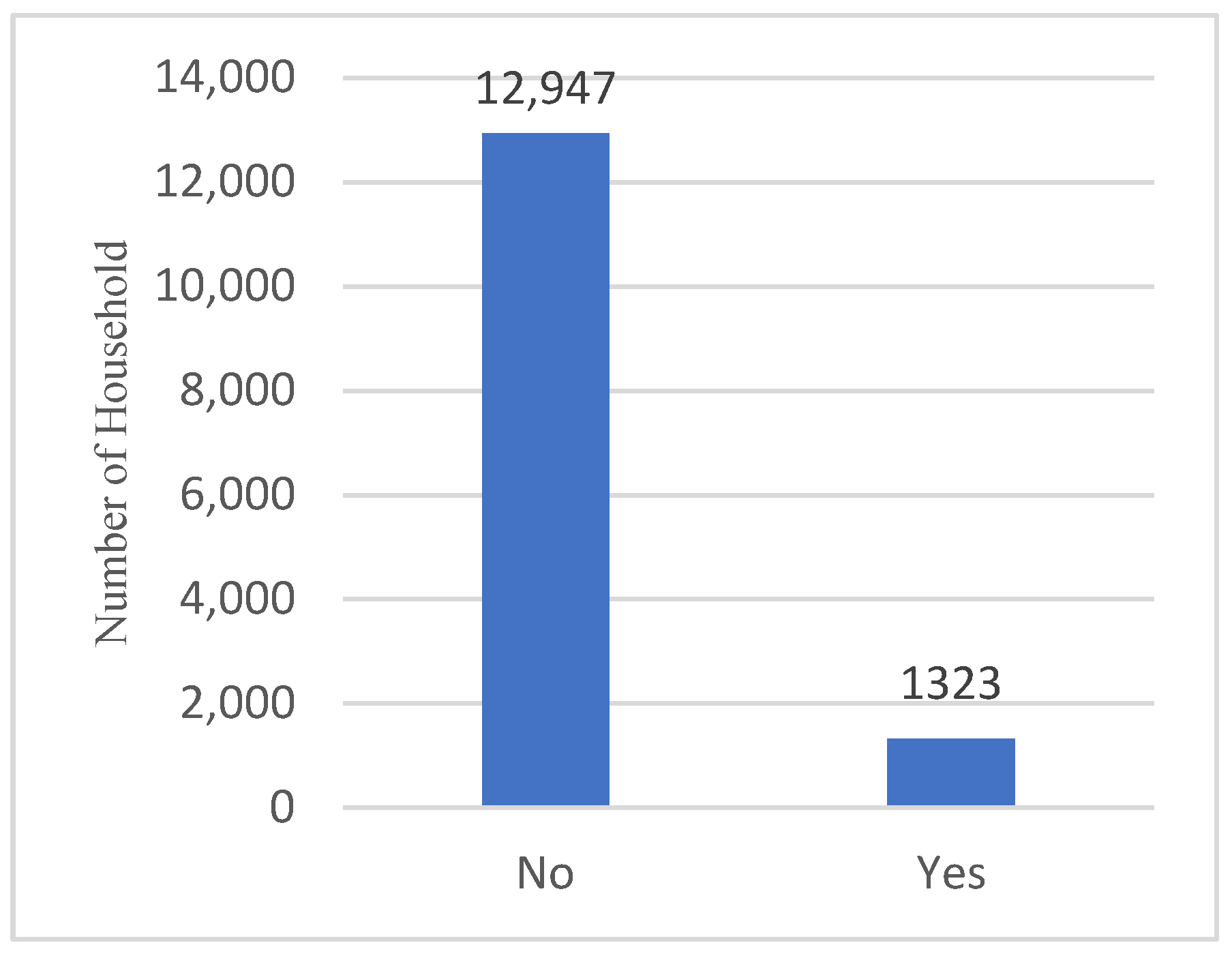
| Life Insurance Ownership | Binary | Yes | HH has purchased a life insurance policy | 12,947 | 90.73 |
| No | HH has not purchased a life insurance policy | 1323 | 9.27 | ||
| Gender | Binary | Male | HH is male | 11,856 | 83.08 |
| Female | HH is a female | 2414 | 16.92 | ||
| Age | Binary | 1 | Non-prime working age | 3408 | 23.88 |
| 2 | Prime working age (25–54) | 10,862 | 76.12 | ||
| Income category (IC) | Nominal | B40 | Household income is in the bottom 40% category * | 5904 | 41.37 |
| M40 | Household income is in the middle 40% category * | 5880 | 41.21 | ||
| T20 | Household income is in the top 20% category * | 2486 | 17.42 | ||
| Expenditure | Interval | - | Household expenditure per month in Ringgit Malaysia | - | - |
| Household Number (HN) | Interval | - | Number of family members in the household | - | - |
| Metropolitan Status (MS) | Nominal | Non-Metropolitan | Residing in the non-metropolitan West Malaysian | 6732 | 47.18 |
| East Malaysia | Residing in the East Malaysian | 4208 | 29.49 | ||
| Metropolitan | Residing in the metropolitan West Malaysian | 3330 | 23.34 | ||
| Strata | Binary | Urban | Residing in an urban area | 10,889 | 76.31 |
| Rural | Residing in a rural area | 3381 | 23.69 | ||
| Ethnicity | Nominal | Bumiputera | Bumiputera | 9609 | 67.34 |
| Chinese | Chinese | 3125 | 21.90 | ||
| Indian | Indian | 898 | 6.29 | ||
| Others | Others | 638 | 4.47 | ||
| Marital Status (MS) | Nominal | Married | Married | 10,738 | 75.25 |
| Others | Others | 3532 | 24.75 | ||
| Education Level (EL) | Nominal | Tertiary | HH’s highest level of education is a tertiary level | 10,259 | 71.89 |
| Others | HH’s highest level of education is other than tertiary | 4011 | 28.11 | ||
| Employment Status (ES) | Binary | Employed | HH is employed | 13,426 | 94.09 |
| Unemployed | HH is unemployed | 844 | 5.91 | ||
| Collar Status (CS) | Binary | White-collar | HH has white-collar occupations (e.g., legislators, senior officials, managers, professionals); | 8149 | 57.11 |
| Non-White collar | HH has a non-white-collar occupation | 6121 | 42.89 |
| Acronyms | Definitions |
|---|---|
| DT | Decision Tree |
| LR | Logistic Regression |
| NB | Naïve Bayes |
| RF | Random Forest |
| NN | Neural Network |
| k-NN | k-Nearest Neighbours |
| SMOTE | Synthetic Minority Oversampling Technique |
| TP | True Positive |
| TN | True Negative |
| FP | False Positive |
| FN | False Negative |
| ROC | Receiver Operating Characteristics |
| RUS | Random Under-Sampling |
| Symbol | Metric | Formula |
|---|---|---|
| ACC | Accuracy | (TP + TN)/(TP + TN + FP + FN) |
| BA | Balanced Accuracy | (TPR + TNR)/2 |
| GM | Geometric Mean | (TPR + TNR)1/2 |
| F1 | F1-score | 2 × (Recall × Precision)/(Recall + Precision) |
| AUC | Area Under the ROC Curve | Plotted with TPR against the FPR |
| Attribute | Missing | Mean | Standard Deviation | Minimum | Maximum | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Expenditure | 0 | 4187.442 | 2450.359 | 472.14 | 17978.06 | 1.642446 | 3.713083 |
| Number of Households | 0 | 3.668325 | 1.289895 | 1 | 5 | −0.53572 | −0.91988 |
| Model | No Sampling (Ratio 9:1) | RUS (Ratio 3:1) | RUS (Ratio 2:1) | RUS (Ratio 1:1) | SMOTE |
|---|---|---|---|---|---|
| DT | 89.44% | 86.09% | 81.13% | 66.90% | 65.21% |
| LR | 90.66% | 89.21% | 86.26% | 73.40% | 66.32% |
| NB | 86.13% | 81.18% | 78.37% | 71.16% | 66.70% |
| RF | 90.50% | 88.35% | 82.93% | 68.19% | 69.19% |
| NN | 90.50% | 85.96% | 79.60% | 68.40% | 69.75% |
| DT + Bagging | 89.49% | 86.59% | 81.42% | 67.34% | 66.38% |
| LR + Bagging | 90.65% | 89.26% | 86.21% | 73.57% | 66.36% |
| NB + Bagging | 86.06% | 81.21% | 78.38% | 71.17% | 66.67% |
| RF + Bagging | 90.64% | 88.82% | 84.37% | 69.60% | 69.57% |
| NN + Bagging | 90.59% | 87.43% | 82.21% | 68.56% | 72.45% |
| DT + Boosting | 89.44% | 86.09% | 81.13% | 66.90% | 65.21% |
| LR + Boosting | 90.66% | 89.21% | 86.26% | 73.40% | 66.32% |
| NB + Boosting | 88.85% | 84.27% | 79.13% | 71.66% | 66.29% |
| RF + Boosting | 90.50% | 88.35% | 82.92% | 68.19% | 69.19% |
| NN + Boosting | 90.24% | 84.82% | 79.21% | 67.30% | 71.75% |
| Model | No Sampling (Ratio 9:1) | RUS (Ratio 3:1) | RUS (Ratio 2:1) | RUS (Ratio 1:1) | SMOTE |
|---|---|---|---|---|---|
| DT | 50.79% | 53.15% | 57.02% | 61.81% | 64.24% |
| LR | 50.13% | 53.61% | 57.99% | 66.27% | 67.02% |
| NB | 57.00% | 60.14% | 61.81% | 64.66% | 64.96% |
| RF | 50.42% | 53.47% | 56.32% | 64.25% | 64.63% |
| NN | 50.31% | 54.81% | 60.46% | 64.13% | 64.47% |
| DT + Bagging | 50.78% | 52.98% | 56.95% | 62.66% | 63.94% |
| LR + Bagging | 50.13% | 53.77% | 57.86% | 66.19% | 66.97% |
| NB + Bagging | 57.00% | 60.19% | 61.93% | 64.64% | 64.90% |
| RF + Bagging | 50.36% | 52.55% | 56.68% | 64.89% | 65.21% |
| NN + Bagging | 50.13% | 53.75% | 59.15% | 64.96% | 65.31% |
| DT + Boosting | 50.79% | 53.15% | 57.02% | 61.81% | 64.24% |
| LR + Boosting | 50.13% | 53.61% | 57.99% | 66.27% | 67.02% |
| NB + Boosting | 52.15% | 57.19% | 61.56% | 65.38% | 66.39% |
| RF + Boosting | 50.42% | 53.47% | 56.32% | 64.25% | 64.63% |
| NN + Boosting | 50.45% | 56.04% | 59.19% | 63.55% | 63.06% |
| Model | No Sampling (Ratio 9:1) | RUS (Ratio 3:1) | RUS (Ratio 2:1) | RUS (Ratio 1:1) | SMOTE |
|---|---|---|---|---|---|
| DT | 0.672 | 0.660 | 0.640 | 0.621 | 0.661 |
| LR | 0.728 | 0.727 | 0.727 | 0.727 | 0.727 |
| NB | 0.708 | 0.708 | 0.708 | 0.707 | 0.706 |
| RF | 0.691 | 0.692 | 0.688 | 0.694 | 0.705 |
| NN | 0.704 | 0.698 | 0.686 | 0.683 | 0.691 |
| DT + Bagging | 0.678 | 0.673 | 0.672 | 0.662 | 0.675 |
| LR + Bagging | 0.728 | 0.727 | 0.727 | 0.727 | 0.727 |
| NB + Bagging | 0.708 | 0.708 | 0.708 | 0.707 | 0.706 |
| RF + Bagging | 0.699 | 0.704 | 0.705 | 0.710 | 0.709 |
| NN + Bagging | 0.723 | 0.714 | 0.713 | 0.704 | 0.710 |
| DT + Boosting | 0.510 | 0.548 | 0.619 | 0.667 | 0.676 |
| LR + Boosting | 0.693 | 0.662 | 0.660 | 0.674 | 0.690 |
| NB + Boosting | 0.668 | 0.684 | 0.678 | 0.701 | 0.699 |
| RF + Boosting | 0.506 | 0.550 | 0.599 | 0.682 | 0.671 |
| NN + Boosting | 0.681 | 0.672 | 0.668 | 0.674 | 0.670 |
| Model | No Sampling (Ratio 9:1) | RUS (Ratio 3:1) | RUS (Ratio 2:1) | RUS (Ratio 1:1) | SMOTE |
|---|---|---|---|---|---|
| DT | 0.0551 | 0.1447 | 0.2125 | 0.2370 | 0.2515 |
| LR | 0.0074 | 0.1432 | 0.2382 | 0.2863 | 0.2722 |
| NB | 0.2212 | 0.2525 | 0.2642 | 0.2672 | 0.2592 |
| RF | 0.0230 | 0.1450 | 0.2039 | 0.2573 | 0.2618 |
| NN | 0.0188 | 0.1785 | 0.2509 | 0.2567 | 0.2626 |
| DT + Bagging | 0.0541 | 0.1396 | 0.2116 | 0.2441 | 0.2515 |
| LR + Bagging | 0.0074 | 0.1473 | 0.2358 | 0.2865 | 0.2719 |
| NB + Bagging | 0.2210 | 0.2532 | 0.2635 | 0.2671 | 0.2588 |
| RF + Bagging | 0.0177 | 0.1177 | 0.2113 | 0.2650 | 0.2669 |
| NN + Bagging | 0.0089 | 0.1541 | 0.2426 | 0.2632 | 0.2759 |
| DT + Boosting | 0.0551 | 0.1447 | 0.2125 | 0.2370 | 0.2515 |
| LR + Boosting | 0.0074 | 0.1432 | 0.2382 | 0.2863 | 0.2722 |
| NB + Boosting | 0.1048 | 0.2157 | 0.2620 | 0.2747 | 0.2682 |
| RF + Boosting | 0.0230 | 0.1450 | 0.2038 | 0.2572 | 0.2618 |
| NN + Boosting | 0.0292 | 0.2005 | 0.2354 | 0.2507 | 0.2558 |
| Model | No Sampling (Ratio 9:1) | RUS (Ratio 3:1) | RUS (Ratio 2:1) | RUS (Ratio 1:1) | SMOTE |
|---|---|---|---|---|---|
| DT | 0.1809 | 0.3448 | 0.4874 | 0.6149 | 0.6423 |
| LR | 0.0616 | 0.3104 | 0.4645 | 0.6569 | 0.6701 |
| NB | 0.4439 | 0.5431 | 0.5837 | 0.6417 | 0.6492 |
| RF | 0.1098 | 0.3202 | 0.4588 | 0.6407 | 0.6438 |
| NN | 0.0988 | 0.3924 | 0.5570 | 0.6391 | 0.6414 |
| DT + Bagging | 0.1787 | 0.3323 | 0.4837 | 0.6240 | 0.6386 |
| LR + Bagging | 0.0616 | 0.3151 | 0.4621 | 0.6557 | 0.6697 |
| NB + Bagging | 0.4444 | 0.5438 | 0.5854 | 0.6413 | 0.6486 |
| RF + Bagging | 0.0953 | 0.2789 | 0.4534 | 0.6463 | 0.6499 |
| NN + Bagging | 0.0670 | 0.3433 | 0.5193 | 0.6481 | 0.6471 |
| DT + Boosting | 0.1809 | 0.3448 | 0.4874 | 0.6149 | 0.6423 |
| LR + Boosting | 0.0616 | 0.3104 | 0.4645 | 0.6569 | 0.6701 |
| NB + Boosting | 0.2627 | 0.4654 | 0.5765 | 0.6492 | 0.6639 |
| RF + Boosting | 0.1098 | 0.3202 | 0.4587 | 0.6406 | 0.6438 |
| NN + Boosting | 0.1257 | 0.4349 | 0.5384 | 0.6338 | 0.6214 |
| No | Y Status | Predicted: Y = No | Predicted: Y = Yes | Prediction for Y |
|---|---|---|---|---|
| 1 | Yes | 0.4988 | 0.5012 | Yes |
| 2 | Yes | 0.3004 | 0.6996 | Yes |
| 3 | Yes | 0.2971 | 0.7029 | Yes |
| 4 | No | 0.2691 | 0.7309 | Yes |
| 5 | No | 0.4774 | 0.5226 | Yes |
| 6 | No | 0.5804 | 0.4196 | No |
| 7 | No | 0.7665 | 0.2335 | No |
| 8 | No | 0.6339 | 0.3661 | No |
| 9 | No | 0.8418 | 0.1582 | No |
| 10 | No | 0.4208 | 0.5792 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamsuddin, S.N.; Ismail, N.; Nur-Firyal, R. Life Insurance Prediction and Its Sustainability Using Machine Learning Approach. Sustainability 2023, 15, 10737. https://doi.org/10.3390/su151310737
Shamsuddin SN, Ismail N, Nur-Firyal R. Life Insurance Prediction and Its Sustainability Using Machine Learning Approach. Sustainability. 2023; 15(13):10737. https://doi.org/10.3390/su151310737
Chicago/Turabian StyleShamsuddin, Siti Nurasyikin, Noriszura Ismail, and R. Nur-Firyal. 2023. "Life Insurance Prediction and Its Sustainability Using Machine Learning Approach" Sustainability 15, no. 13: 10737. https://doi.org/10.3390/su151310737
APA StyleShamsuddin, S. N., Ismail, N., & Nur-Firyal, R. (2023). Life Insurance Prediction and Its Sustainability Using Machine Learning Approach. Sustainability, 15(13), 10737. https://doi.org/10.3390/su151310737








