Integration of Superconducting Magnetic Energy Storage for Fast-Response Storage in a Hybrid Solar PV-Biogas with Pumped-Hydro Energy Storage Power Plant
Abstract
1. Introduction
1.1. Motivation and Incitement
1.2. Literature Review
1.3. Contribution and Organization of this Paper
- ✓
- For grid-connected hybrid solar PV–biogas systems, the optimal size is determined by considerating economic and reliability parameters.
- ✓
- A customized EWOA is introduced for determining the optimal sizing of grid-connected hybrid solar PV–biogas power plants.
- ✓
- A comprehensive examination is conducted of grid-connected hybrid solar PV–biogas applications, investigating the issue from a variety of perspectives, including the HESS’s size, rapid responses (i.e., SMES), and long-lasting (i.e., PHES) energy characteristics.
- ✓
- Comparisons between the EWOA and other metaheuristic optimization techniques for sizing energy sources and storage capacities, which consider the cost as well as reliability parameters, are carried out.
- ✓
- The hybrid system’s distinct instabilities can be reduced, and the load power demand can be leveled with the integration of PHES and SMES, both of which provide straightforward deployment and high effectiveness against weather variations and the inclusion or outage of RES.
- ✓
- The potential and requirements for implementing grid-connected hybrid solar PV/biogas with SMES-PHES, which are also interconnected hybrid renewable energy with hybrid energy storage, are highlighted in the Debre Markos distribution network.
2. Methodology
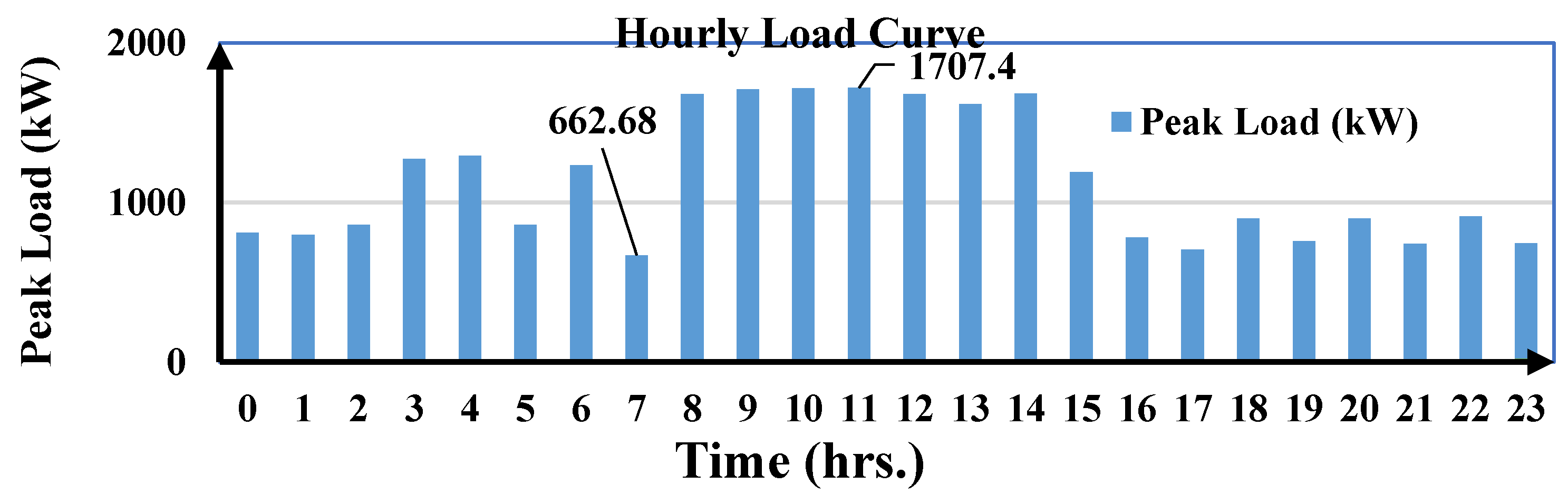
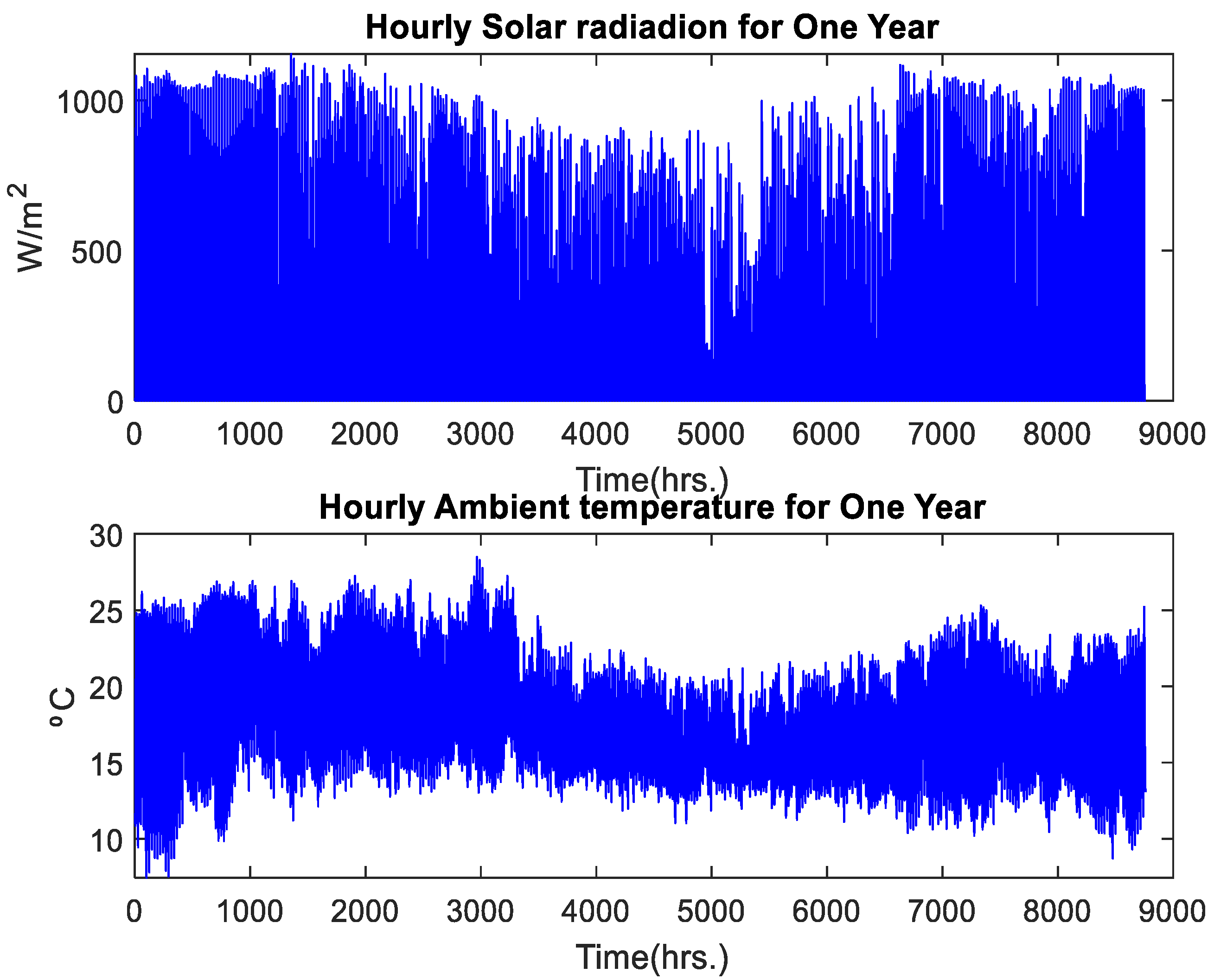
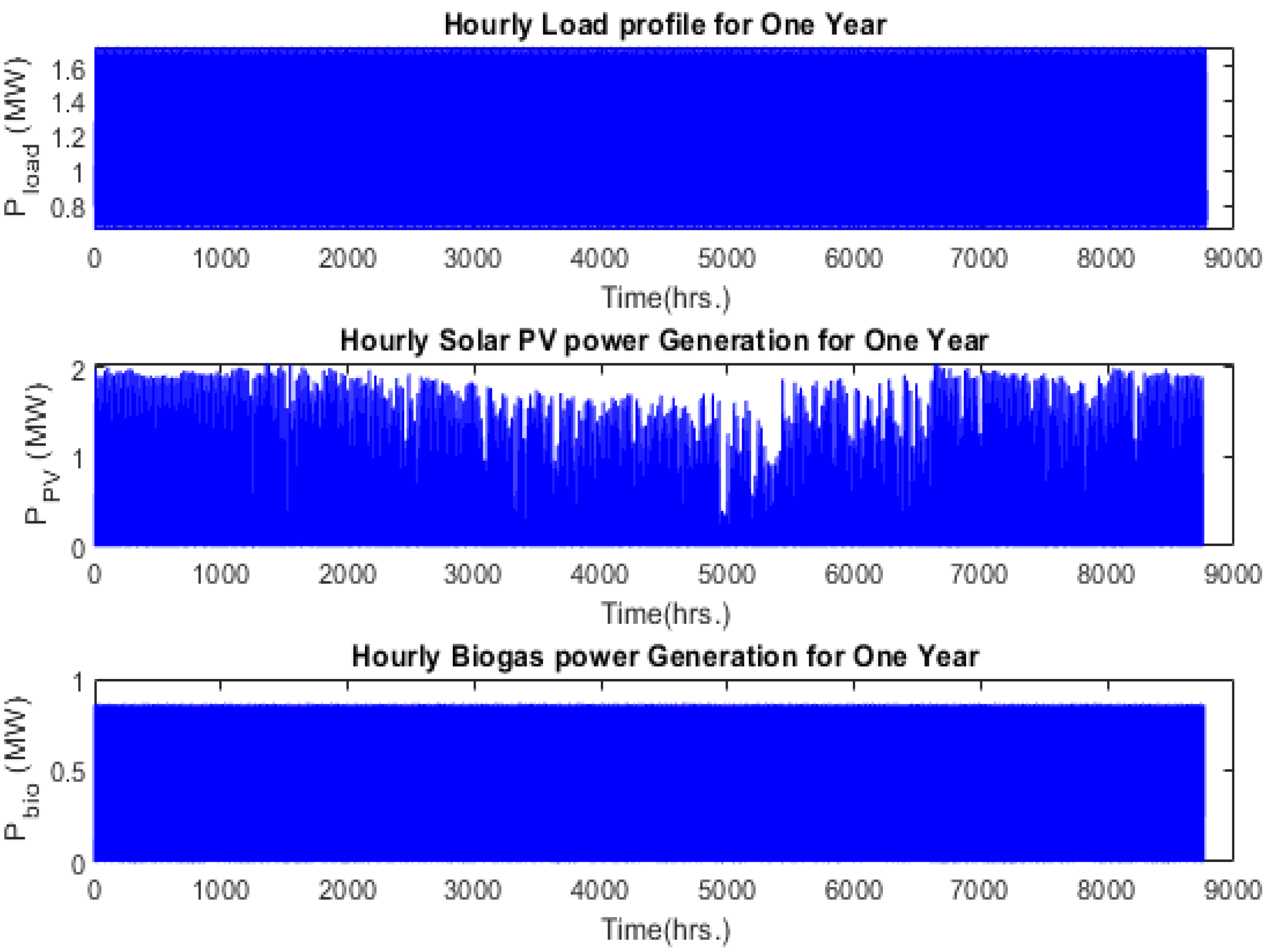
2.1. Load Assessment
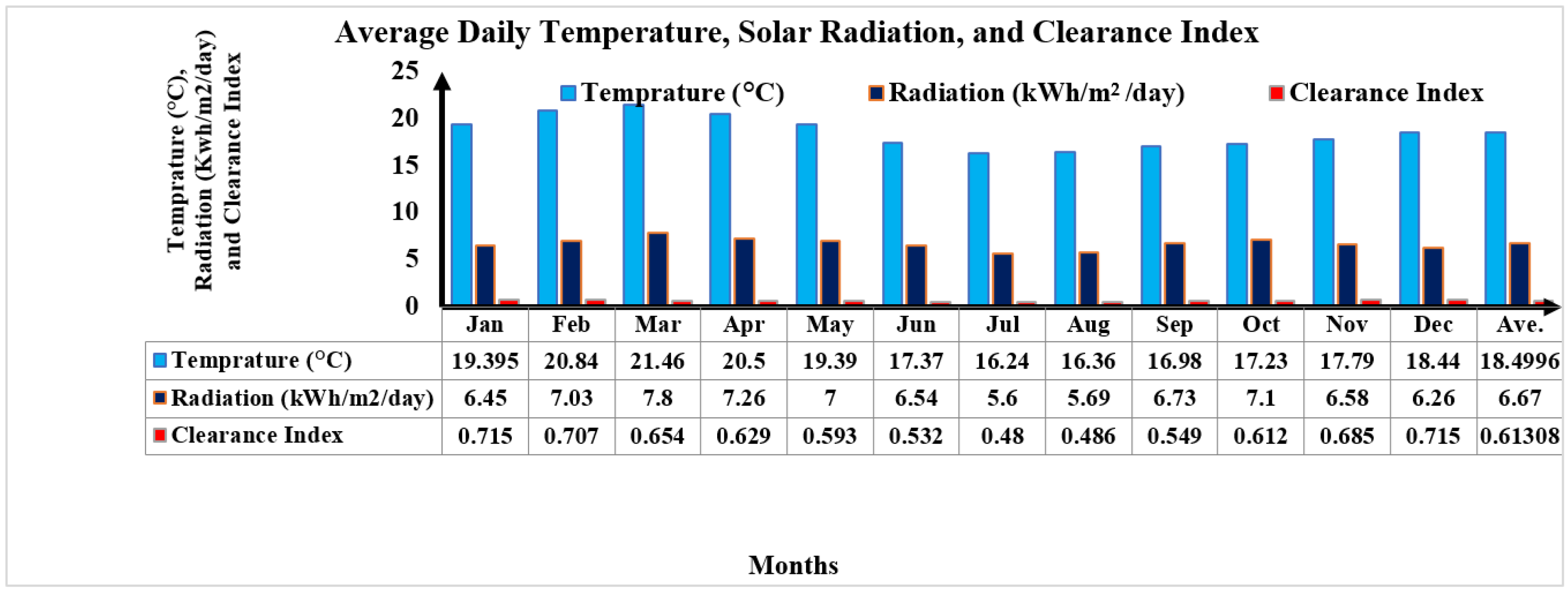
2.2. Renewable Energy Resource Assessment
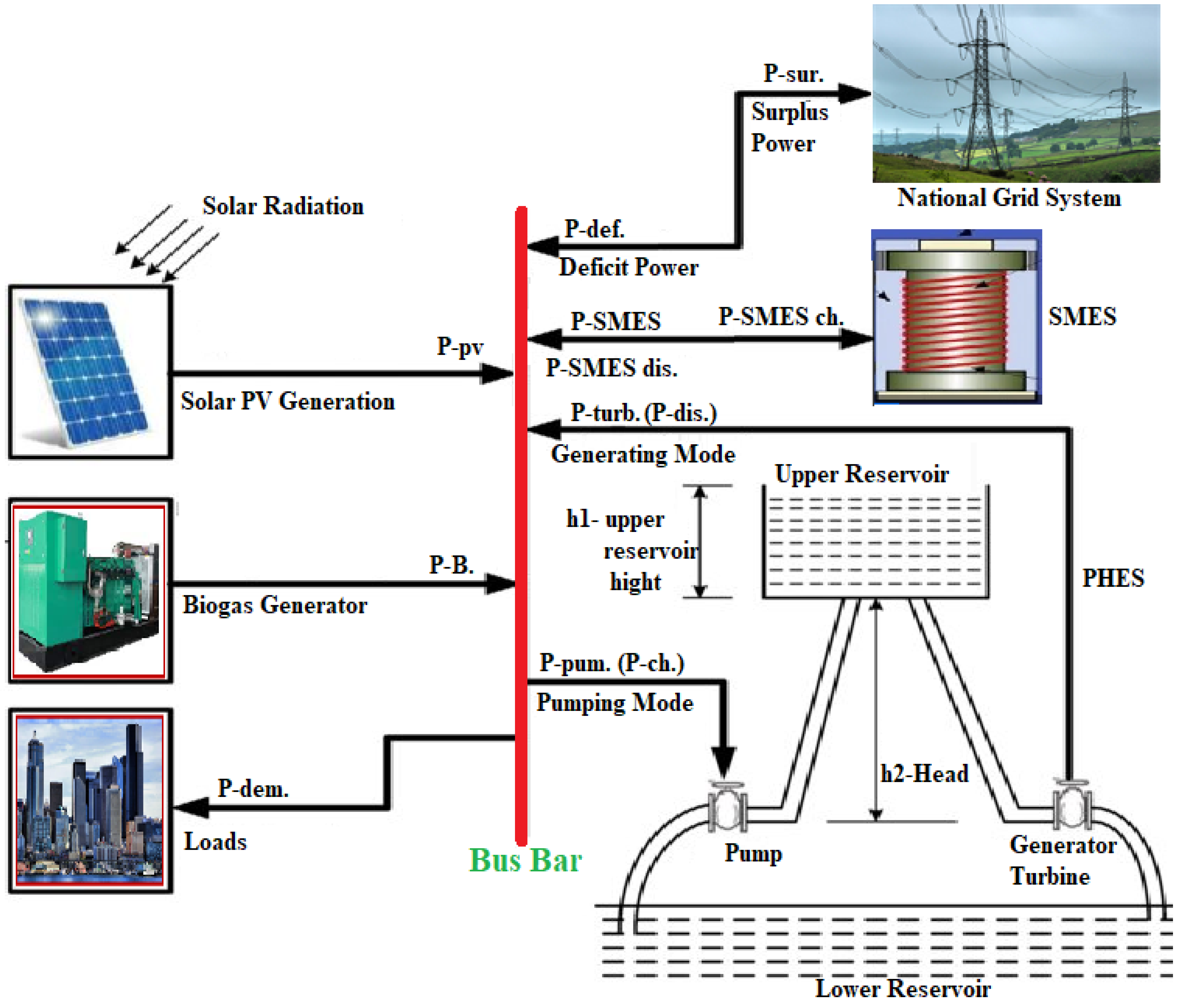
3. Proposed System Layout and Description
3.1. Mathematical Modeling of Hybrid Energy Sources
3.1.1. Solar PV Array Unit Modeling
3.1.2. Biogas Generator (BG) Unit Modeling
3.1.3. Hydraulic Pumped-Storage System Modeling
3.1.4. Superconducting Magnetic Energy Storage (SMES) System Modeling
- Charging Mode of Operation: This mode occurs when HRES power generation is higher than the load demand PL (i.e., PL − PHRES < 0 or PSMES Ex.(t) < 0).
- 2.
- Discharging Mode of Operation: This mode occurs when the load demand PL is higher than the HRES power generation (i.e., PL − PHRES > 0 or PSMES Ex.(t) > 0).
- 3.
- Standby Mode of Operation: This mode occurs when the load demand PL is equal to the HRES power generation (i.e., PL –PHRES = 0 or PSMES Ex.(t) = 0). The SMES system must run in standby mode to maintain the stored energy in the system when it is not necessary for it to exchange power with the primary DC-bus bar.
- where PSMES Ex.(t) is the exchanged power of SMES at period t, which is negative, positive, and equal to zero during charging mode, discharging mode, and standby (idle) mode, respectively; ηCha. and ηDis. are the efficiencies of charging and discharging modes, respectively; ΔP(t) is the difference between the output and load demand of HRES; PSMES,rated is the power rating of SMES; ESMES St.(t) is the energy storage capacity of SMES at period t; ESMES,min. and ESMES,max. are the minimum and maximum energy storage capacity limits of the SMES system, respectively; and Δt represents the time interval.
3.1.5. Modeling of Converter
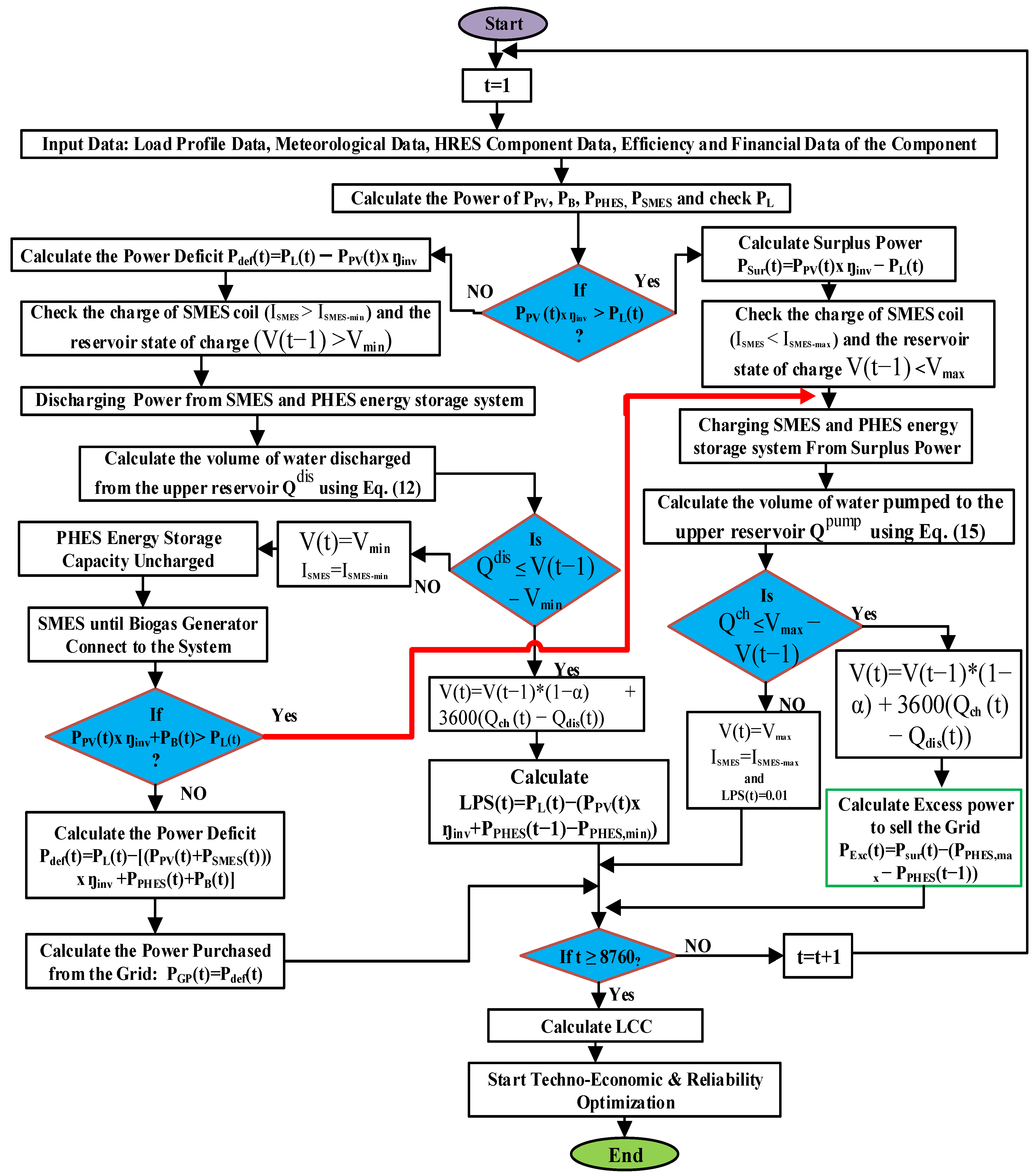
3.2. Operation and Energy Management Strategy
- The connected electric load requirement can be met by stored energy from the hybrid SMES-PHES system.
- If the energy in the storage units runs out, the connected national grid provides the required electric load demand.
4. Parameter Evaluation of the Optimization
4.1. Economic Evaluation
4.2. Reliability Evaluation
4.3. Formulation of Objective Function to Optimize the Problem
4.4. Constraints
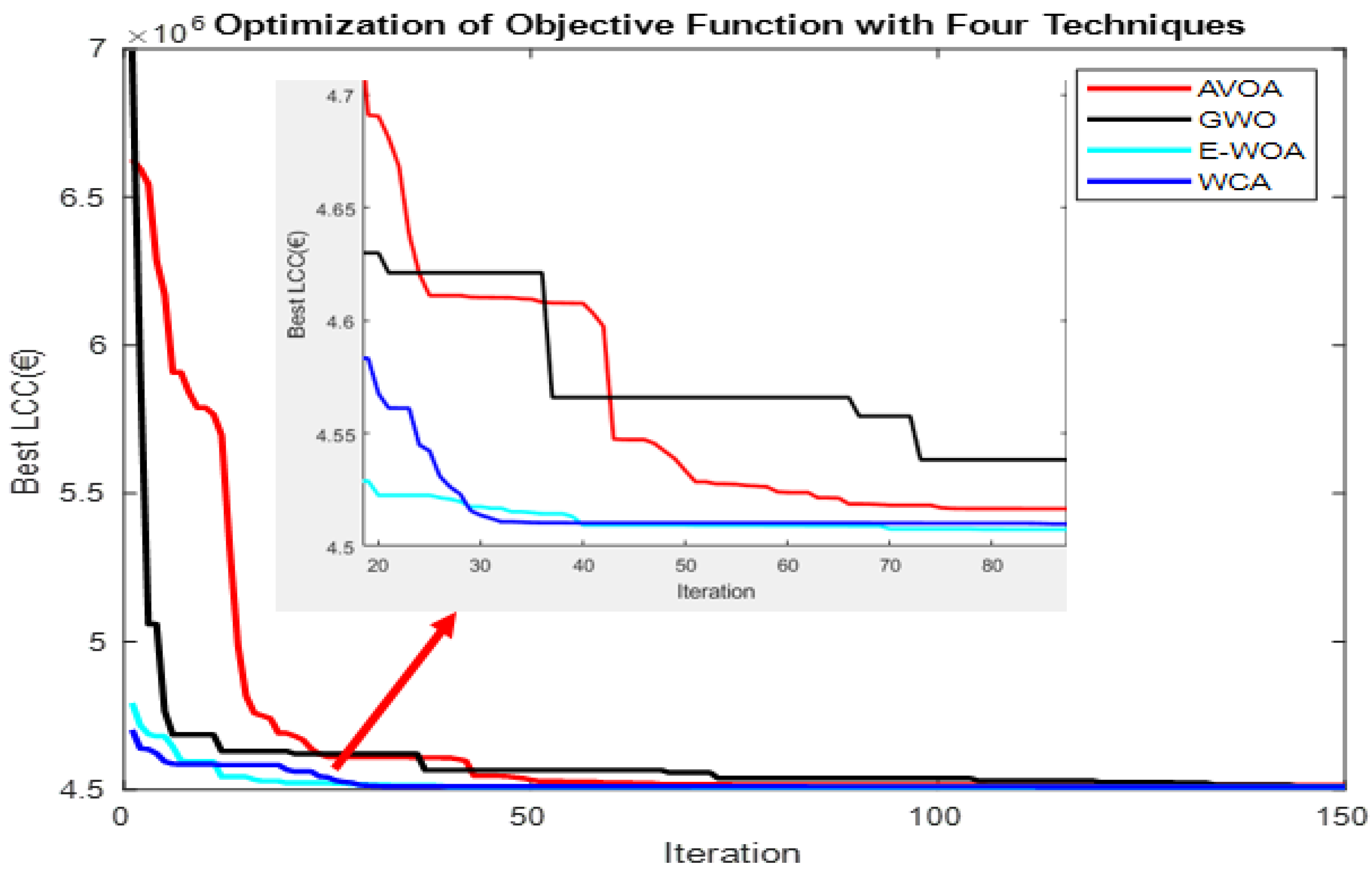
5. Optimization Technique
- a.
- Pooling mechanism: Using Equation (37), the member pools of a size matrix are generated, where is computed using Equation (39) to generate a random location near the best humpback whale , and is the worst solution found in the current iteration. In this equation, is a binary random vector, and is its inverse vector. The values of non-zero elements in are zero in , and the values of zero elements are equal to one. For variety, the pooling method uses a crossover operator to mix the worst and best solutions. When the pool is full, an existing pool member takes the place of the new member.
- b.
- Migrating search strategy: Using Equation (38), this search method randomly partitions a portion of the humpback whale to explore uncharted territory and improve the exploration process. The partitioned whale populations are also anticipated to diversify, which may lessen the likelihood of local whale trapping. Equation (39), where rand is a random number between 0 and 1, and and are the lower and upper limits of the problem, determines as a random point in the search space. Equation (40) is used to find the best humpback whale, , and is a random location nearby. In this case, and are the lower and upper limits of , respectively.
- c.
- Preferential selection search strategy: In the classical WOA, the prey search method can explore more effectively with the help of the preferred selection technique. This method is shown in Equation (42), where is the current location of the ith whale, and and are randomly chosen from the matrix. In iteration t, is defined using Equation (41), and is sampled using a Cauchy distribution with parameters. By dispersing the whales across the search space, a diverse range of solutions can be found. However, a larger step size is recommended for the preferential selection search method to improve the WOA’s ability to explore. In this method, the heavy-tailed Cauchy distribution is used because it has a higher chance of generating larger values.
- d.
- Enriched encircling prey search strategy: The WOA’s encircling prey method is enriched using Equation (42), where is computed using Equation (43) and is chosen at random from the matrix pool.
| Algorithm 1. The source code of the EWOA. |
| Input: Population size (N) and maximum iterations (ItrMax) |
| Output: The optimal solution |
| Begin |
| Distribute N wheels randomly in the future space using the equation: |
| Evaluate the fitness of the wheels using the equation: . |
| Set t = 1 |
| While |
| Randomly select a portion P of the population and compute using the migrating search strategy. |
| If i is not in P |
| Compute the probability rate and coefficient using the equation: |
| . |
| If |
| If |
| Compute using the enriched encircling prey strategy defined in the equation: |
| Else |
| Compute using the preferential selection strategy defined in the equation: |
| end if |
| Else |
| Compute using the spiral bubble-net attacking strategy defined in the equation: where |
| end if |
| Apply the following equations in order to map the continuous search space to the binary one: and |
| Update and evaluate the fitness of using the equation: |
| Update using the position with a lower fitness value from |
| end if |
| Update the global optimal solution |
| t = t + 1 |
| end while |
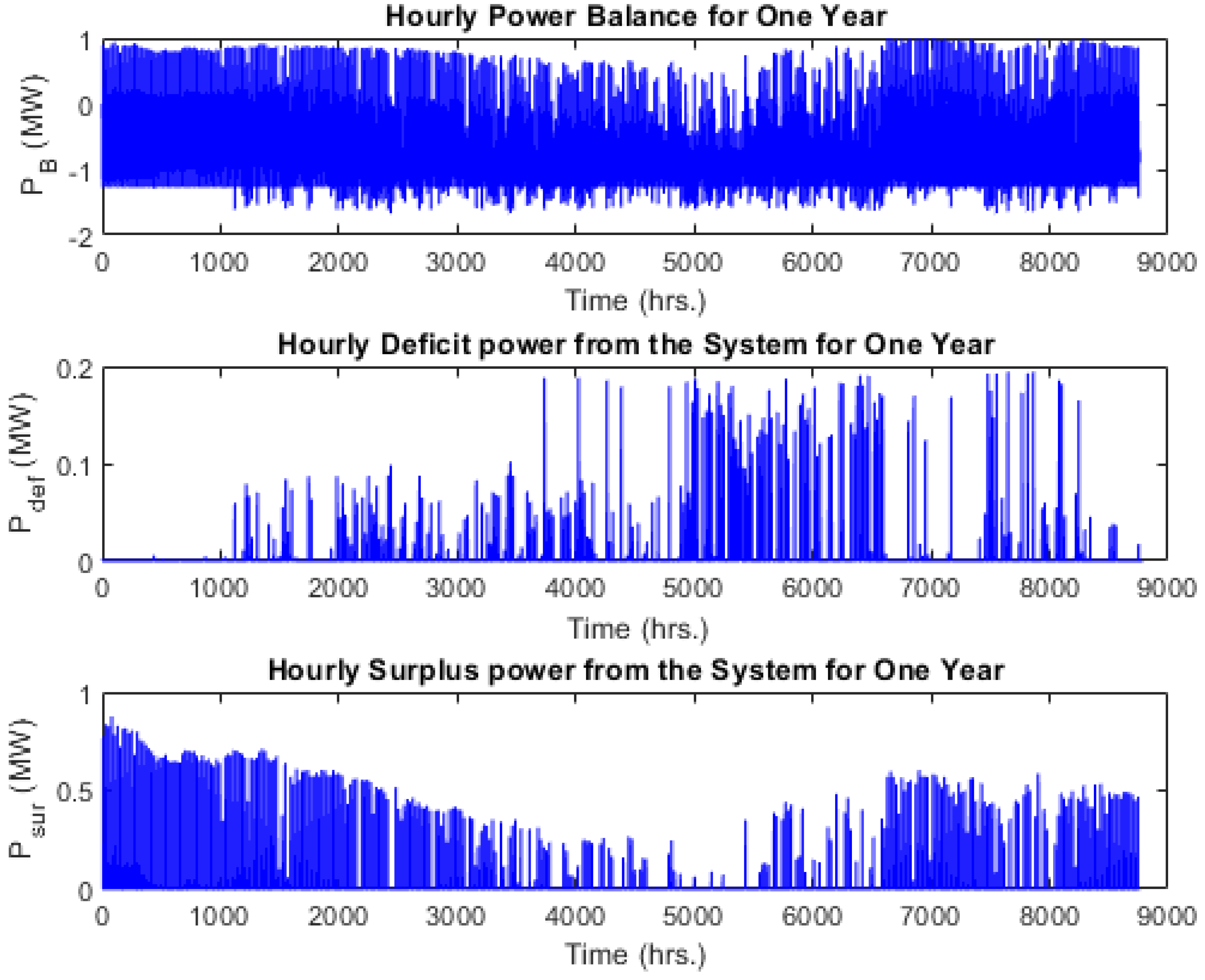
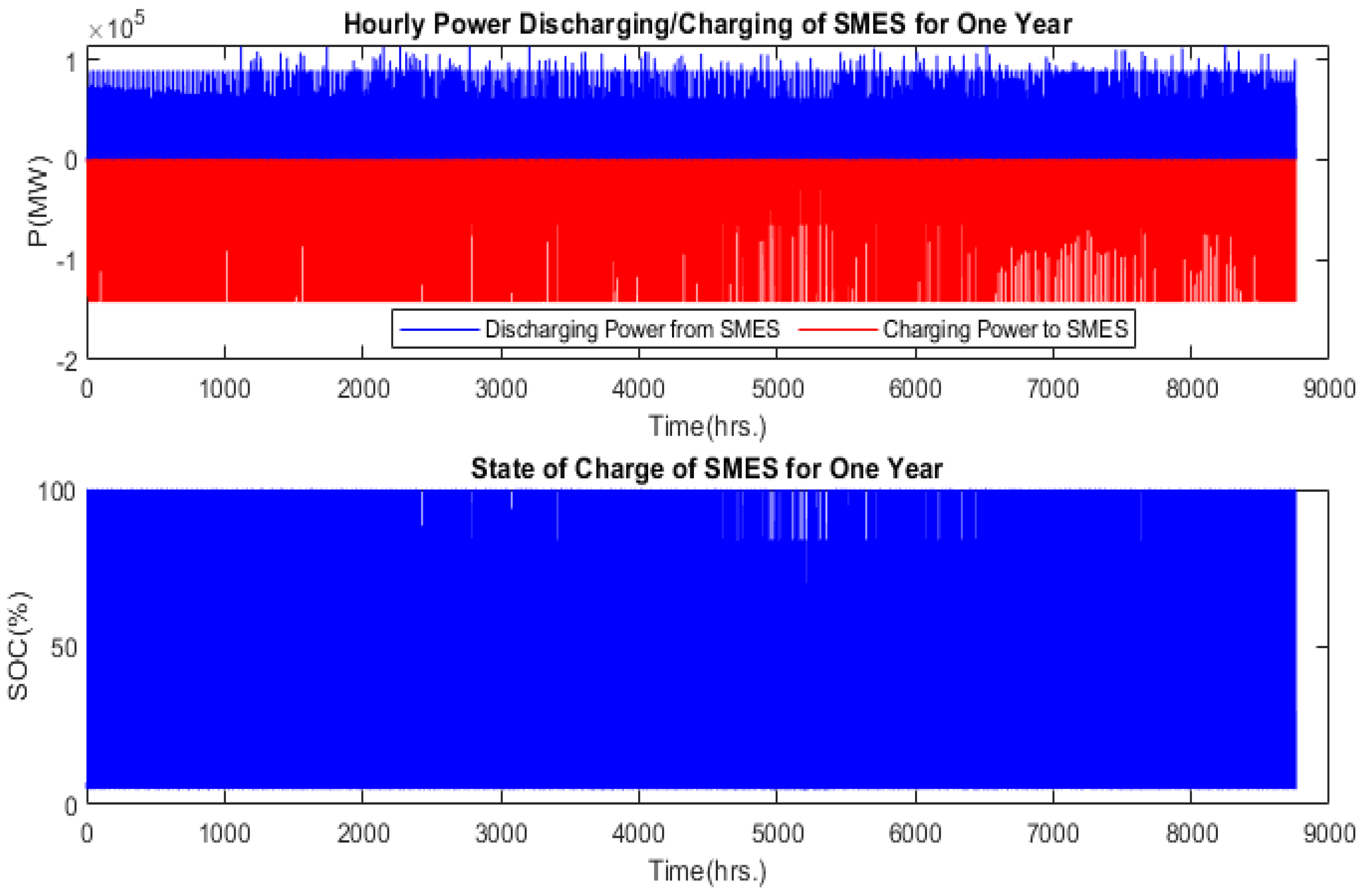
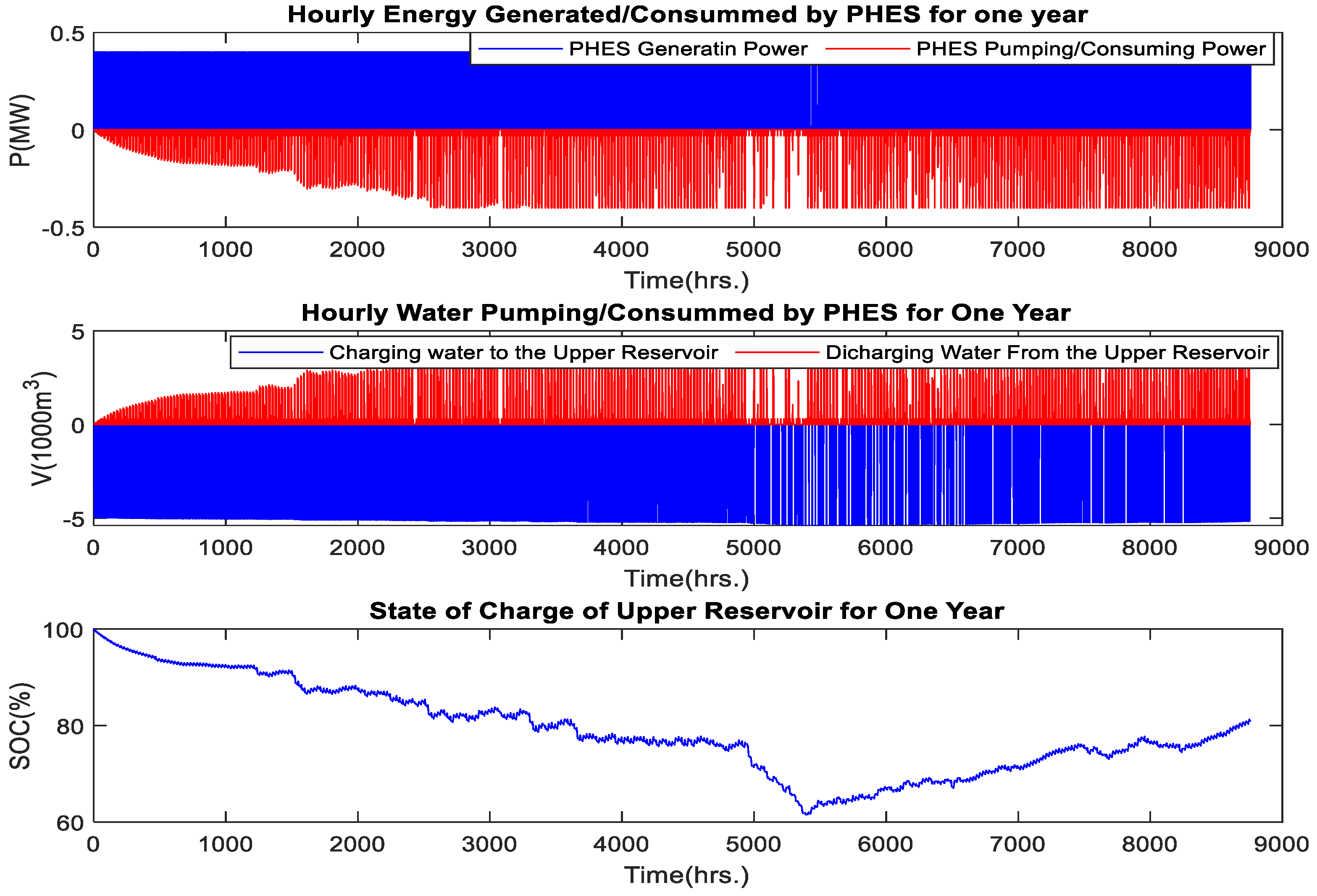
6. Results and Discussion
6.1. Results of Optimal Sizing of Hybrid Components
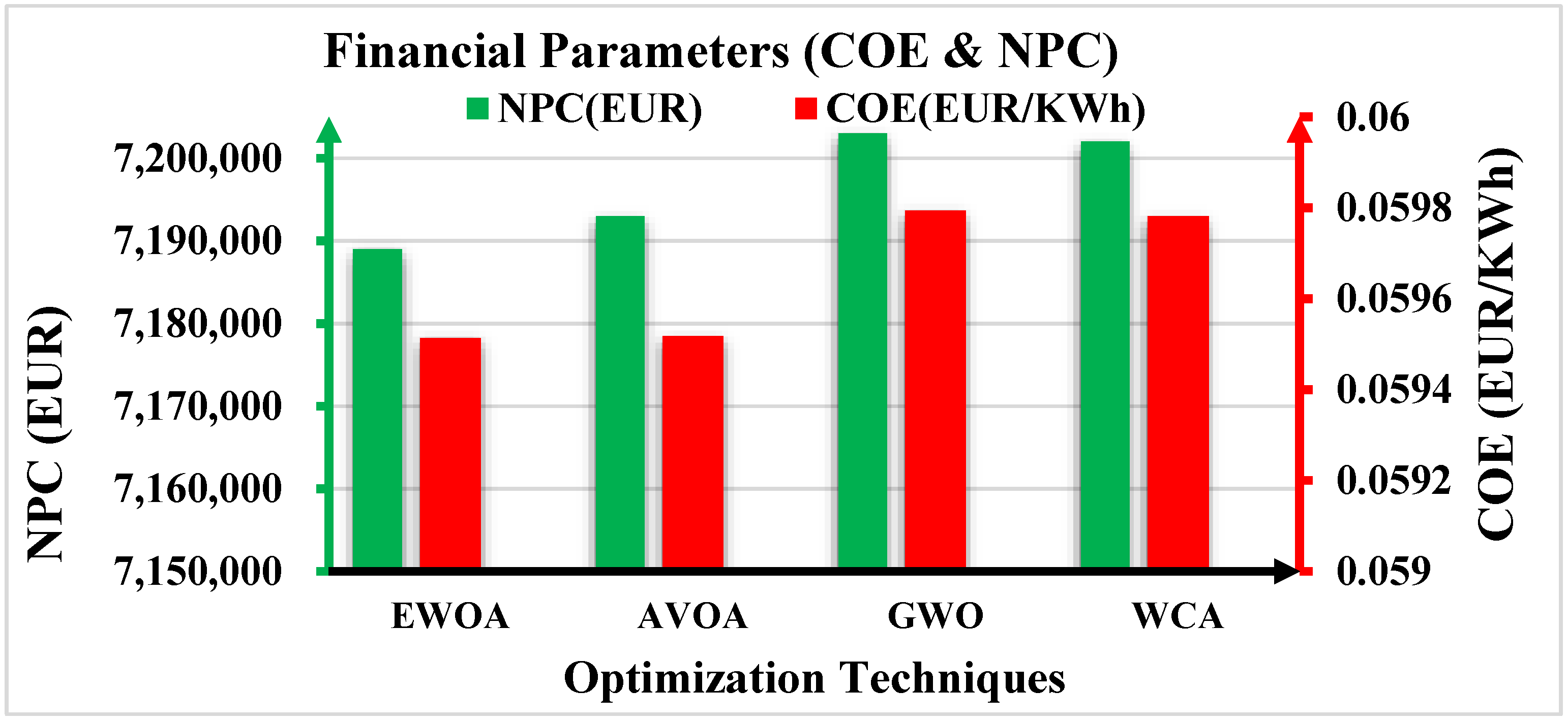
6.2. Results of Analysis of Financial and Reliability Parameters
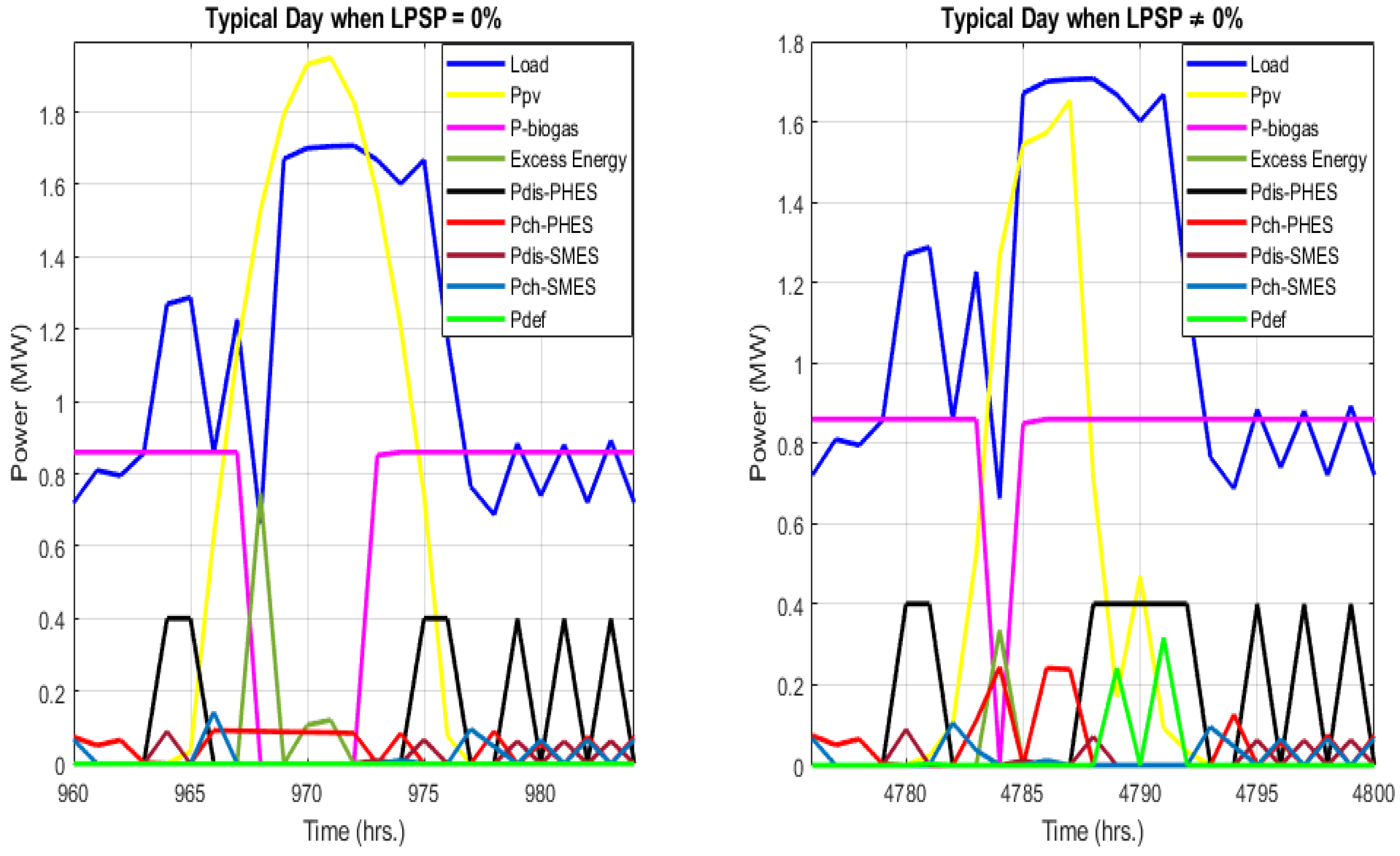
6.3. Discussion on the Application of the Optimal Solution
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, Q.; Wen, X.; Sun, Y.; Lei, X.; Wang, Z.; Qin, G. Evaluation of the risk and benefit of the complementary operation of the large wind-photovoltaic-hydropower system considering forecast uncertainty. Appl. Energy 2021, 285, 116442. [Google Scholar] [CrossRef]
- Zhong, J.; Bollen, M.; Rönnberg, S. Towards a 100% renewable energy electricity generation system in Sweden. Renew. Energy 2021, 171, 812–824. [Google Scholar] [CrossRef]
- Guzović, Z.; Duic, N.; Piacentino, A.; Markovska, N.; Mathiesen, B.V.; Lund, H. Recent advances in methods, policies and technologies at sustainable energy systems development. Energy 2022, 245, 123276. [Google Scholar] [CrossRef]
- Samour, A.; Baskaya, M.M.; Tursoy, T. The impact of financial development and FDI on renewable energy in the UAE: A path towards sustainable development. Sustainability 2022, 14, 1208. [Google Scholar] [CrossRef]
- Yoro, K.O.; Daramola, M.O. Chapter 1—CO2 emission sources, greenhouse gases, and the global warming effect. In Advances in Carbon Capture; Rahimpour, M.R., Farsi, M., Makarem, M.A., Eds.; Woodhead Publishing: Sawston, UK, 2020; pp. 3–28. [Google Scholar] [CrossRef]
- Du, Y.; Gao, T.; Rochelle, G.T.; Bhown, A.S. Zero- and negative-emissions fossil-fired power plants using CO2 capture by conventional aqueous amines. Int. J. Greenh. Gas Control 2021, 111, 103473. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Bidokhti, A.; Fakhrzad, M.-B.; Sadegheih, A.; Mehrjerdi, Y.Z. A new model for the use of renewable electricity to reduce carbon dioxide emissions. Energy 2022, 238, 121602. [Google Scholar] [CrossRef]
- Cho, H.H.; Strezov, V. A Comparative Review on the Environmental Impacts of Combustion-Based Electricity Generation Technologies. Energy Fuels 2020, 34, 10486–10502. [Google Scholar] [CrossRef]
- Child, M.; Kemfert, C.; Bogdanov, D.; Breyer, C. Flexible electricity generation, grid exchange and storage for the transition to a 100% renewable energy system in Europe. Renew. Energy 2019, 139, 80–101. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Hannan, M.A.; Jern, K.P.; Mansur, M.; Mahlia, T.M.I. Grid-connected renewable energy sources: Review of the recent integration requirements and control methods. J. Clean. Prod. 2020, 253, 119831. [Google Scholar] [CrossRef]
- Ayamolowo, O.J.; Manditereza, P.; Kusakana, K. Exploring the gaps in renewable energy integration to grid. Energy Rep. 2020, 6, 992–999. [Google Scholar] [CrossRef]
- Deng, X.; Lv, T. Power system planning with increasing variable renewable energy: A review of optimization models. J. Clean. Prod. 2020, 246, 118962. [Google Scholar] [CrossRef]
- Coester, A.; Hofkes, M.W.; Papyrakis, E. An optimal mix of conventional power systems in the presence of renewable energy: A new design for the German electricity market. Energy Policy 2018, 116, 312–322. [Google Scholar] [CrossRef]
- Adewumi, O.B.; Fotis, G.; Vita, V.; Nankoo, D.; Ekonomou, L. The Impact of Distributed Energy Storage on Distribution and Transmission Networks’ Power Quality. Appl. Sci. 2022, 12, 6466. [Google Scholar] [CrossRef]
- Shin, W.; Lee, C.; Chung, I.-Y.; Lim, J.; Youn, J.; Rhie, Y.; Hur, K.; Shim, J.W. Reserve replacement from governor to energy storage system on conventional generator for operating-cost reduction. Appl. Energy 2022, 324, 119697. [Google Scholar] [CrossRef]
- Choudhury, S. Flywheel energy storage systems: A critical review on technologies, applications, and future prospects. Int. Trans. Electr. Energy Syst. 2021, 31, e13024. [Google Scholar] [CrossRef]
- Kumar, G.B.; Palanisamy, K. Review of Energy Storage System for Microgrid. Microgrid Technol. 2021, 57–90. [Google Scholar] [CrossRef]
- Zyryanov, V.; Kiryanova, N.; Korotkov, I.; Nesterenko, G.; Prankevich, G.; Rudiuk, I. Analysis of energy storage systems application in the Russian and world electric power industry. In Proceedings of the 2020 Ural Smart Energy Conference (USEC), Ekaterinburg, Russia, 13–15 November 2020; pp. 106–109. [Google Scholar]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Matos, C.R.; Carneiro, J.F.; Silva, P.P. Overview of large-scale underground energy storage technologies for integration of renewable energies and criteria for reservoir identification. J. Energy Storage 2018, 21, 241–258. [Google Scholar] [CrossRef]
- Blakers, A.; Stocks, M.; Lu, B.; Cheng, C. A review of pumped hydro energy storage. Prog. Energy 2021, 3, 022003. [Google Scholar] [CrossRef]
- Olabi, A.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.A.; Alami, A.H. Compressed air energy storage systems: Components and operating parameters—A review. J. Energy Storage 2021, 34, 102000. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A.; Ramadan, M. Critical Review of Flywheel Energy Storage System. Energies 2021, 14, 2159. [Google Scholar] [CrossRef]
- Ali, M.; Sarker, M.R.; Saad, M.H.M.; Mohamed, R. Overview of Control System Topology of Flywheel Energy Storage System in Renewable Energy Application for Alternative Power Plant. Przegląd Elektrotechniczny 2022, 1, 147–155. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abbas, Q.; Al Makky, A.; Abdelkareem, M.A. Supercapacitors as next generation energy storage devices: Properties and applications. Energy 2022, 248, 123617. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Molina-Ibáñez, E.-L.; Rosales-Asensio, E.; López-Rey, Á. Technical approach for the inclusion of superconducting magnetic energy storage in a smart city. Energy 2018, 158, 1080–1091. [Google Scholar] [CrossRef]
- Jiao, Y.; Månsson, D. A Study of the Energy Exchange within a Hybrid Energy Storage System and a Comparison of the Capacities, Lifetimes, and Costs of Different Systems. Energies 2021, 14, 7045. [Google Scholar] [CrossRef]
- Hajiaghasi, S.; Salemnia, A.; Hamzeh, M. Hybrid energy storage system for microgrids applications: A review. J. Energy Storage 2019, 21, 543–570. [Google Scholar] [CrossRef]
- Tabart, Q.; Vechiu, I.; Etxeberria, A.; Bacha, S. Hybrid Energy Storage System Microgrids Integration for Power Quality Improvement Using Four-Leg Three-Level NPC Inverter and Second-Order Sliding Mode Control. IEEE Trans. Ind. Electron. 2017, 65, 424–435. [Google Scholar] [CrossRef]
- Geetha, A.; Subramani, C. A comprehensive review on energy management strategies of hybrid energy storage system for electric vehicles. Int. J. Energy Res. 2017, 41, 1817–1834. [Google Scholar] [CrossRef]
- Kasimalla, V.K.; Velisala, V. A review on energy allocation of fuel cell/battery/ultracapacitor for hybrid electric vehicles. Int. J. Energy Res. 2018, 42, 4263–4283. [Google Scholar] [CrossRef]
- Wieczorek, M.; Lewandowski, M. A mathematical representation of an energy management strategy for hybrid energy storage system in electric vehicle and real time optimization using a genetic algorithm. Appl. Energy 2017, 192, 222–233. [Google Scholar] [CrossRef]
- Hemmati, R.; Saboori, H. Emergence of hybrid energy storage systems in renewable energy and transport applications—A review. Renew. Sustain. Energy Rev. 2016, 65, 11–23. [Google Scholar] [CrossRef]
- Sutikno, T.; Arsadiando, W.; Wangsupphaphol, A.; Yudhana, A.; Facta, M. A review of recent advances on hybrid energy storage system for solar photovoltaics power generation. IEEE Access 2022, 10, 42346–42364. [Google Scholar] [CrossRef]
- Ramadan, H.S.; Alhelou, H.H.; Ahmed, A.A. Impartial near-optimal control and sizing for battery hybrid energy system balance via grey wolf optimizers: Lead acid and lithium-ion technologies. IET Renew. Power Gener. 2022, 1–14. [Google Scholar] [CrossRef]
- Tahir, Y.; Nadeem, M.F.; Ahmed, A.; Khan, I.A.; Qamar, F. A Review on Hybrid Energy Storage Systems in Microgrids. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Ibrahim, H.; Rezkallah, M.; Ilinca, A.; Ghandour, M. 10—Hybrid energy storage systems. In Hybrid Renewable Energy Systems and Microgrids; Kabalci, E., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 351–372. [Google Scholar] [CrossRef]
- Rohit, A.K.; Rangnekar, S. An overview of energy storage and its importance in Indian renewable energy sector: Part II–energy storage applications, benefits and market potential. J. Energy Storage 2017, 13, 447–456. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Yao, P.; Sun, Q.; Zhang, Z.; Zhang, M.; Yuan, W. A Novel use of the Hybrid Energy Storage System for Primary Frequency Control in a Microgrid. Energy Procedia 2016, 103, 82–87. [Google Scholar] [CrossRef]
- Li, J.; Xiong, R.; Yang, Q.; Liang, F.; Zhang, M.; Yuan, W. Design/test of a hybrid energy storage system for primary frequency control using a dynamic droop method in an isolated microgrid power system. Appl. Energy 2017, 201, 257–269. [Google Scholar] [CrossRef]
- Althubaiti, M.; Bernard, M.; Musilek, P. Fuzzy logic controller for hybrid renewable energy system with multiple types of storage. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Martín, I.S.; Ursua, A.; Sanchis, P. Integration of fuel cells and supercapacitors in electrical microgrids: Analysis, modelling and experimental validation. Int. J. Hydrogen Energy 2013, 38, 11655–11671. [Google Scholar] [CrossRef]
- Guney, M.S.; Tepe, Y. Classification and assessment of energy storage systems. Renew. Sustain. Energy Rev. 2017, 75, 1187–1197. [Google Scholar] [CrossRef]
- Arani, A.K.; Karami, H.; Gharehpetian, G.; Hejazi, M. Review of Flywheel Energy Storage Systems structures and applications in power systems and microgrids. Renew. Sustain. Energy Rev. 2017, 69, 9–18. [Google Scholar] [CrossRef]
- Inthamoussou, F.A.; Pegueroles-Queralt, J.; Bianchi, F.D. Control of a supercapacitor energy storage system for microgrid applications. IEEE Trans. Energy Convers. 2013, 28, 690–697. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Hussain, A.; Mansor, M.B.; Blaabjerg, F. Review of energy storage system technologies in microgrid applications: Issues and challenges. IEEE Access 2018, 6, 35143–35164. [Google Scholar] [CrossRef]
- Reza, M.S.; Rahman, N.; Wali, S.B.; Hannan, M.A.; Ker, P.J.; Rahman, S.A.; Muttaqi, K.M. Optimal Algorithms for Energy Storage Systems in Microgrid Applications: An Analytical Evaluation Towards Future Directions. IEEE Access 2022, 10, 10105–10123. [Google Scholar] [CrossRef]
- Elfeky, K.E.; Mohammed, A.G.; Wang, Q. Thermal Performance Evaluation of Combined Sensible-Latent Heat Storage Tank with a Different Storage Medium. Chem. Eng. Trans. 2022, 94, 1267–1272. [Google Scholar] [CrossRef]
- Li, G.; Lu, X.; Kim, J.Y.; Meinhardt, K.D.; Chang, H.J.; Canfield, N.L.; Sprenkle, V.L. Advanced intermediate temperature sodium–nickel chloride batteries with ultra-high energy density. Nat. Commun. 2016, 7, 10683. [Google Scholar] [CrossRef]
- Karimi-Rizvandi, A.; Sandjareh, M.B.; Nazari, M.H.; Ezati-Yaraziz, M. A Novel Frequency Control Scheme for Autonomous Microgrid Using Cooperative Application of Supercapacitor-Battery HESS, Photovoltaics, LED Lighting Loads and TCLs. IEEE Access 2021, 9, 57198–57214. [Google Scholar] [CrossRef]
- Song, Z.; Li, J.; Han, X.; Xu, L.; Lu, L.; Ouyang, M.; Hofmann, H. Multi-objective optimization of a semi-active battery/supercapacitor energy storage system for electric vehicles. Appl. Energy 2014, 135, 212–224. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, W.S.; Wong, M.D. Dynamic power allocation of battery-supercapacitor hybrid energy storage for standalone PV microgrid applications. Sustain. Energy Technol. Assess. 2017, 22, 55–64. [Google Scholar] [CrossRef]
- Yuan, Y.; Sun, C.; Li, M.; Choi, S.S.; Li, Q. Determination of optimal supercapacitor-lead-acid battery energy storage capacity for smoothing wind power using empirical mode decomposition and neural network. Electr. Power Syst. Res. 2015, 127, 323–331. [Google Scholar] [CrossRef]
- Chen, L.; Chen, H.; Li, Y.; Li, G.; Yang, J.; Liu, X.; Xu, Y.; Ren, L.; Tang, Y. SMES-Battery Energy Storage System for the Stabilization of a Photovoltaic-Based Microgrid. IEEE Trans. Appl. Supercond. 2018, 28, 1–7. [Google Scholar] [CrossRef]
- Cansiz, A.; Faydaci, C.; Qureshi, M.T.; Usta, O.; McGuiness, D.T. Integration of a SMES–Battery-Based Hybrid Energy Storage System into Microgrids. J. Supercond. Nov. Magn. 2018, 31, 1449–1457. [Google Scholar] [CrossRef]
- Ding, K.; Li, W.; Hu, P.; Hu, A.; Tao, Y.; Zhuang, J.; Lu, H. The Voltage Sag Mitigation Method Based on Hybrid SMES-BES Dynamic Voltage Restorer (DVR). In Proceedings of the 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019; pp. 545–549. [Google Scholar] [CrossRef]
- Abbassi, A.; Dami, M.A.; Jemli, M. Statistical characterization of capacity of Hybrid Energy Storage System (HESS) to assimilate the fast PV-Wind power generation fluctuations. In Proceedings of the 2017 International Conference on Advanced Systems and Electric Technologies (IC_ASET), Hammamet, Tunisia, 14–17 January 2017; pp. 467–472. [Google Scholar] [CrossRef]
- Ma, W.; Wang, W.; Wu, X.; Hu, R.; Tang, F.; Zhang, W.; Han, X.; Ding, L. Optimal Allocation of Hybrid Energy Storage Systems for Smoothing Photovoltaic Power Fluctuations Considering the Active Power Curtailment of Photovoltaic. IEEE Access 2019, 7, 74787–74799. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Development of hybrid battery–supercapacitor energy storage for remote area renewable energy systems. Appl. Energy 2015, 153, 56–62. [Google Scholar] [CrossRef]
- Wang, S.; Tang, Y.; Shi, J.; Gong, K.; Liu, Y.; Ren, L.; Li, J. Design and advanced control strategies of a hybrid energy storage system for the grid integration of wind power generations. IET Renew. Power Gener. 2015, 9, 89–98. [Google Scholar] [CrossRef]
- Lamsal, D.; Sreeram, V.; Mishra, Y.; Kumar, D. Output power smoothing control approaches for wind and photovoltaic generation systems: A review. Renew. Sustain. Energy Rev. 2019, 113, 109245. [Google Scholar] [CrossRef]
- Talal, M.; Kaddah, S.S.; Eladl, A.A. Impact of Energy Storage Devices on the Distribution System Stability with Distributed Generation. MEJ Mansoura Eng. J. 2020, 45, 1–10. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Robinson, F.; Liang, F.; Zhang, M.; Yuan, W. Design and test of a new droop control algorithm for a SMES/battery hybrid energy storage system. Energy 2017, 118, 1110–1122. [Google Scholar] [CrossRef]
- Yuan, X.; Song, C.; Platt, A.; Zhao, N.; Wang, H.; Li, H.; Fatih, K.; Jang, D. A review of all-vanadium redox flow battery durability: Degradation mechanisms and mitigation strategies. Int. J. Energy Res. 2019, 43, 6599–6638. [Google Scholar] [CrossRef]
- Shchurov, N.I.; Dedov, S.I.; Malozyomov, B.V.; Shtang, A.A.; Martyushev, N.V.; Klyuev, R.V.; Andriashin, S.N. Degradation of Lithium-Ion Batteries in an Electric Transport Complex. Energies 2021, 14, 8072. [Google Scholar] [CrossRef]
- Zdiri, M.A.; Guesmi, T.; Alshammari, B.M.; Alqunun, K.; Almalaq, A.; Ben Salem, F.; Abdallah, H.H.; Toumi, A. Design and Analysis of Sliding-Mode Artificial Neural Network Control Strategy for Hybrid PV-Battery-Supercapacitor System. Energies 2022, 15, 4099. [Google Scholar] [CrossRef]
- Babu, T.S.; Vasudevan, K.R.; Ramachandaramurthy, V.K.; Sani, S.B.; Chemud, S.; Lajim, R.M. A comprehensive review of hybrid energy storage systems: Converter topologies, control strategies and future prospects. IEEE Access 2020, 8, 148702–148721. [Google Scholar] [CrossRef]
- Faria, J.; Pombo, J.; Calado, M.d.R.; Mariano, S. Power Management Control Strategy Based on Artificial Neural Networks for Standalone PV Applications with a Hybrid Energy Storage System. Energies 2019, 12, 902. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Yang, Q.; Zhang, Z.; Yuan, W. SMES/Battery Hybrid Energy Storage System for Electric Buses. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Ciupageanu, D.; Pelosi, D. Integrating Hybrid Energy Storage System on a Wind Generator to enhance grid safety and stability: A Levelized Cost of Electricity analysis. J. Energy Storage 2021, 34, 102050. [Google Scholar] [CrossRef]
- Qi, M.; Liu, Y.; Landon, R.S.; Liu, Y.; Moon, I. Assessing and mitigating potential hazards of emerging grid-scale electrical energy storage systems. Process Saf. Environ. Prot. 2021, 149, 994–1016. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Cherubini, P.; Micangeli, A.; Pelosi, D.; Tacconelli, C. How Hybridization of Energy Storage Technologies Can Provide Additional Flexibility and Competitiveness to Microgrids in the Context of Developing Countries. Energies 2019, 12, 3138. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.C.; DE, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery Energy Storage System (BESS) and Battery Management System (BMS) for Grid-Scale Applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Ogunniyi, E.O.; Pienaar, H. Overview of battery energy storage system advancement for renewable (photovoltaic) energy applications. In Proceedings of the 2017 International Conference on the Domestic Use of Energy (DUE), Cape Town, South Africa, 4–5 April 2017; pp. 233–239. [Google Scholar]
- Alami, A.H.; Yasin, A.; Alrashid, R.; Alasad, S.; Aljaghoub, H.; Alabsi, G.; Alketbi, L.; Alkhzaimi, A.; Alteneji, A.; Shikhli, S. Experimental evaluation of compressed air energy storage as a potential replacement of electrochemical batteries. J. Energy Storage 2022, 54, 105263. [Google Scholar] [CrossRef]
- Ghadi, M.J.; Azizivahed, A.; Mishra, D.K.; Li, L.; Zhang, J.; Shafie-Khah, M.; Catalão, J.P. Application of small-scale compressed air energy storage in the daily operation of an active distribution system. Energy 2021, 231, 120961. [Google Scholar] [CrossRef]
- Yang, D.; Wang, M.; Yang, R.; Zheng, Y.; Pandzic, H. Optimal dispatching of an energy system with integrated compressed air energy storage and demand response. Energy 2021, 234, 121232. [Google Scholar] [CrossRef]
- Ali, M.H.; Wu, B.; Dougal, R.A. An Overview of SMES Applications in Power and Energy Systems. IEEE Trans. Sustain. Energy 2010, 1, 38–47. [Google Scholar] [CrossRef]
- Amaro, N.; Pina, J.M.; Martins, J.; Ceballos, J.M. Amaro, N.; Pina, J.M.; Martins, J.; Ceballos, J.M. A Study on Superconducting Coils for Superconducting Magnetic Energy Storage (SMES) Applications. In Technological Innovation for the Internet of Things; Springer: Berlin/Heidelberg, Germany, 2013; pp. 449–456. [Google Scholar] [CrossRef]
- Al Zaman, A.; Islam, M.; Maruf, H. Study on Conceptual Designs of Superconducting Coil for Energy Storage in SMES. East Eur. J. Phys. 2020, 111–120. [Google Scholar] [CrossRef]
- Moghadasi, A.H.; Heydari, H.; Farhadi, M. Pareto Optimality for the Design of SMES Solenoid Coils Verified by Magnetic Field Analysis. IEEE Trans. Appl. Supercond. 2010, 21, 13–20. [Google Scholar] [CrossRef]
- Li, J.; Gee, A.M.; Zhang, M.; Yuan, W. Analysis of battery lifetime extension in a SMES-battery hybrid energy storage system using a novel battery lifetime model. Energy 2015, 86, 175–185. [Google Scholar] [CrossRef]
- Mohamad, F.; Teh, J.; Lai, C.-M.; Chen, L.-R. Development of Energy Storage Systems for Power Network Reliability: A Review. Energies 2018, 11, 2278. [Google Scholar] [CrossRef]
- Hannan, M.; Faisal, M.; Ker, P.J.; Begum, R.; Dong, Z.; Zhang, C. Review of optimal methods and algorithms for sizing energy storage systems to achieve decarbonization in microgrid applications. Renew. Sustain. Energy Rev. 2020, 131, 110022. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Ren, L.; Xu, C.; Tang, Y.; Li, J.; Chen, L.; Jia, B. Research on the Application of Superconducting Magnetic Energy Storage in Microgrids for Smoothing Power Fluctuation Caused by Operation Mode Switching. IEEE Trans. Appl. Supercond. 2018, 28, 1–6. [Google Scholar] [CrossRef]
- Kularatna, N.; Jayananda, D. Supercapacitor-Based Long Time-Constant Circuits: A Unique Design Opportunity for New Power Electronic Circuit Topologies. IEEE Ind. Electron. Mag. 2020, 14, 40–56. [Google Scholar] [CrossRef]
- Ren, G.; Ma, G.; Cong, N. Review of electrical energy storage system for vehicular applications. Renew. Sustain. Energy Rev. 2015, 41, 225–236. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Feasibility study and economic analysis of pumped hydro storage and battery storage for a renewable energy powered island. Energy Convers. Manag. 2014, 79, 387–397. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Technical feasibility study on a standalone hybrid solar-wind system with pumped hydro storage for a remote island in Hong Kong. Renew. Energy 2014, 69, 7–15. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Optimal design of an autonomous solar–wind-pumped storage power supply system. Appl. Energy 2015, 160, 728–736. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Pumped storage-based standalone photovoltaic power generation system: Modeling and techno-economic optimization. Appl. Energy 2015, 137, 649–659. [Google Scholar] [CrossRef]
- Vijay, R.; Sowmya, R. Optimal sitting of PV-wind-energy storage system integrated micro grid using artificial bee colony optimization technique. Int. J. Innov. Res. Comput. Commun. Eng. 2017, 80, 9640–9652. [Google Scholar]
- Khosravi, M.; Afsharnia, S.; Farhangi, S. Optimal sizing and technology selection of hybrid energy storage system with novel dispatching power for wind power integration. Int. J. Electr. Power Energy Syst. 2021, 127, 106660. [Google Scholar] [CrossRef]
- Zhou, T.; Sun, W. Optimization of Battery–Supercapacitor Hybrid Energy Storage Station in Wind/Solar Generation System. IEEE Trans. Sustain. Energy 2014, 5, 408–415. [Google Scholar] [CrossRef]
- Hailu, A.; Mezgebu, C. Design and simulation of standalone hybrid (solar/biomass) electricity generation system for a rural village in Ethiopia. Int. J. Sci. Eng. Res. 2017, 8, 1570–1574. [Google Scholar]
- Kefalew, T.; Lami, M. Biogas and bio-fertilizer production potential of abattoir waste: Implication in sustainable waste management in Shashemene City, Ethiopia. Heliyon 2021, 7, e08293. [Google Scholar] [CrossRef]
- Leung, D.Y.C.; Wang, J. An overview on biogas generation from anaerobic digestion of food waste. Int. J. Green Energy 2016, 13, 119–131. [Google Scholar] [CrossRef]
- Anand, P.; Rizwan, M.; Bath, S.K. Sizing of renewable energy based hybrid system for rural electrification using grey wolf optimisation approach. IET Energy Syst. Integr. 2019, 1, 158–172. [Google Scholar] [CrossRef]
- Yaghoubi, M.; Eslami, M.; Noroozi, M.; Mohammadi, H.; Kamari, O.; Palani, S. Modified Salp Swarm Optimization for Parameter Estimation of Solar PV Models. IEEE Access 2022, 10, 110181–110194. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; El-ajmi, S.I.; Sultan, H.M.; Hassan, Y.B. Modified farmland fertility optimization algorithm for optimal design of a grid-connected hybrid renewable energy system with fuel cell storage: Case study of Ataka, Egypt. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 119–132. [Google Scholar] [CrossRef]
- Heydari, A.; Askarzadeh, A. Optimization of a biomass-based photovoltaic power plant for an off-grid application subject to loss of power supply probability concept. Appl. Energy 2016, 165, 601–611. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Molina, M.G.; Mercado, P.E.; Watanabe, E.H. Improved Superconducting Magnetic Energy Storage (SMES) Controller for High-Power Utility Applications. IEEE Trans. Energy Convers. 2011, 26, 444–456. [Google Scholar] [CrossRef]
- Alhamali, A.; Farrag, M.E.; Bevan, G.; Hepburn, D.M. Review of Energy Storage Systems in electric grid and their potential in distribution networks. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 546–551. [Google Scholar] [CrossRef]
- Worku, M.Y. Recent Advances in Energy Storage Systems for Renewable Source Grid Integration: A Comprehensive Review. Sustainability 2022, 14, 5985. [Google Scholar] [CrossRef]
- Pappachen, A.; Fathima, A.P. Critical research areas on load frequency control issues in a deregulated power system: A state-of-the-art-of-review. Renew. Sustain. Energy Rev. 2017, 72, 163–177. [Google Scholar] [CrossRef]
- Mir, A.S.; Senroy, N. Adaptive Model Predictive Control Scheme for Application of SMES for Load Frequency Control. IEEE Trans. Power Syst. 2017, 1. [Google Scholar] [CrossRef]
- Shayeghi, H.; Shayanfar, H.; Jalili, A. Load frequency control strategies: A state-of-the-art survey for the researcher. Energy Convers. Manag. 2009, 50, 344–353. [Google Scholar] [CrossRef]
- Deng, J.; Shi, J.; Liu, Y.; Tang, Y. Application of a hybrid energy storage system in the fast charging station of electric vehicles. IET Gener. Transm. Distrib. 2016, 10, 1092–1097. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, Y.; Agnihotri, G. Design of an autonomous renewable hybrid power system. Int. J. Renew. Energy Technol. 2011, 2, 86. [Google Scholar] [CrossRef]
- Salman, U.T.; Al-Ismail, F.S.; Khalid, M. Optimal Sizing of Battery Energy Storage for Grid-Connected and Isolated Wind-Penetrated Microgrid. IEEE Access 2020, 8, 91129–91138. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Ganapathy, V.G.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Zhou, T.; Francois, B. Energy Management and Power Control of a Hybrid Active Wind Generator for Distributed Power Generation and Grid Integration. IEEE Trans. Ind. Electron. 2011, 58, 95–104. [Google Scholar] [CrossRef]
- Ramli, M.A.; Bouchekara, H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- El-Sattar, H.A.; Sultan, H.M.; Kamel, S.; Menesy, A.S.; Rahmann, C. Optimal Design of Hybrid Stand-alone Microgrids Using Tunicate Swarm Algorithm. In Proceedings of the 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Online, 22–26 March 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Abu-Rumman, A.K.; Muslih, I.; Barghash, M.A. Life Cycle Costing of PV Generation System. J. Appl. Res. Ind. Eng. 2017, 4, 252–258. [Google Scholar] [CrossRef]
- Munuswamy, S.; Nakamura, K.; Katta, A. Comparing the cost of electricity sourced from a fuel cell-based renewable energy system and the national grid to electrify a rural health centre in India: A case study. Renew. Energy 2011, 36, 2978–2983. [Google Scholar] [CrossRef]
- Diaf, S.; Notton, G.; Belhamel, M.; Haddadi, M.; Louche, A. Design and techno-economical optimization for hybrid PV/wind system under various meteorological conditions. Appl. Energy 2008, 85, 968–987. [Google Scholar] [CrossRef]
- Al-Sefri, A.K.; Al-Shaalan, A.M. Availability, Performance and Reliability Evaluation for PV Distributed Generation. World J. Eng. Technol. 2019, 07, 429–454. [Google Scholar] [CrossRef]
- Upadhyay, S.; Sharma, M. Development of hybrid energy system with cycle charging strategy using particle swarm optimization for a remote area in India. Renew. Energy 2015, 77, 586–598. [Google Scholar] [CrossRef]
- Sultan, H.M.; Kuznetsov, O.N.; Menesy, A.S.; Kamel, S. Optimal Configuration of a Grid-Connected Hybrid PV/Wind/Hydro-Pumped Storage Power System Based on a Novel Optimization Algorithm. In Proceedings of the 2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 12–14 March 2020; pp. 1–7. [Google Scholar]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S. Stochastic Performance Assessment and Sizing for a Hybrid Power System of Solar/Wind/Energy Storage. IEEE Trans. Sustain. Energy 2013, 5, 363–371. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Safder, U.; Nguyen, X.N.; Yoo, C. Multi-objective decision-making and optimal sizing of a hybrid renewable energy system to meet the dynamic energy demands of a wastewater treatment plant. Energy 2019, 191, 116570. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Mirjalili, S. Enhanced whale optimization algorithm for medical feature selection: A COVID-19 case study. Comput. Biol. Med. 2022, 148, 105858. [Google Scholar] [CrossRef]
- Suhartini, S.; Lestari, Y.P.; Nurika, I. Estimation of methane and electricity potential from canteen food waste. IOP Conf. Series: Earth Environ. Sci. 2019, 230, 012075. [Google Scholar] [CrossRef]
- Loyyal Website. (December 2021). Luminous Solar…—Google Scholar. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Loyyal+Website.+%282021%2C+December%29.+Luminous+Solar+Panel+380Watt+%2F+24Volt+Mono+Perc+%5BCommercial%5D.+Luminous+Solar+Panel+380Watt+%2F+24Volt+Mono+Perc.+https%3A%2F%2Floyyal.in%2Fproduct-details%2Fluminous-solar-panel380watt-24volt-mono-perc+%28Accessed+2022-06-17%29&btnG= (accessed on 22 December 2022).
- Salama, H.S.; Vokony, I. Voltage and Frequency Control of Balanced/Unbalanced Distribution System Using the SMES System in the Presence of Wind Energy. Electricity 2021, 2, 205–224. [Google Scholar] [CrossRef]
- Jackson, N.D.; Gunda, T.; Gayoso, N.; Desai, J.; Walker, A. Operations, maintenance, and cost considerations for PV+Storage in the United States. United States: N. p., 2022. Web. Available online: https://www.osti.gov/biblio/1899420 (accessed on 24 April 2023).
- Mongird, K.; Viswanathan, V.V.; Balducci, P.J.; Alam, J.E.; Fotedar, V.; Koritarov, V.S.; Hadjerioua, B. Energy Storage Technology and Cost Characterization Report; Pacific Northwest National Lab.: Richland, WA, USA, 2019. [Google Scholar] [CrossRef]
- Schröder, A.; Kunz, F.; Meiss, J.; Mendelevitch, R.; Von Hirschhausen, C. Current and Prospective Costs of Electricity Generation until 2050; DIW Data Documentation; DIW Berlin, German Institute for Economic Research: Berlin, Germany, 2013. [Google Scholar]
- Solar Inverter Costs and How to Choose the Right One. Understand Solar. 23 February 2017. Available online: https://understandsolar.com/solar-inverter-costs/ (accessed on 24 November 2022).
- Bhattacharjee, S.; Acharya, S. PV–wind hybrid power option for a low wind topography. Energy Convers. Manag. 2015, 89, 942–954. [Google Scholar] [CrossRef]
- Li, C.; Zhang, L.; Qiu, F.; Fu, R. Optimization and enviro-economic assessment of hybrid sustainable energy systems: The case study of a photovoltaic/biogas/diesel/battery system in Xuzhou, China. Energy Strat. Rev. 2022, 41, 100852. [Google Scholar] [CrossRef]
- Mwakitalima, I.J.; Rizwan, M.; Kumar, N. Integrating Solar Photovoltaic Power Source and Biogas Energy-Based System for Increasing Access to Electricity in Rural Areas of Tanzania. Int. J. Photoenergy 2023, 2023, e7950699. [Google Scholar] [CrossRef]

| Solar panel | [128] |
| Max power | 380 Wp |
| Length x width | 1.976 × 0.991 m |
| Efficiency | 19.41% |
| Temperature coefficient | 0.41% |
| Initial cost | 145.845 EUR/kW |
| O and M cost | 1% |
| Life span | 25 Years |
| SMES | [129] |
| Energy, ESMES | 1 MJ |
| Inductance, LSMES | 0.5 H |
| Current, ISMES | 1 KA |
| Voltage, Vdc-link | 2 KV |
| Capacitance, Cdc-link | 0.01 F |
| PHES | [130,131] |
| Overall efficiency | 77% |
| Cost of power conversion | 165–740 EUR/kW |
| Fixed O and M cost | 8.5 EUR/kW |
| Variable O and M cost | 0.8 EUR/MWh |
| Life Span | 30 years |
| Biogas generator | [132] |
| Initial Cost | 1342.5 EUR/kW |
| Fixed O and M cost | 71.65 EUR/kW |
| Variable O and M cost | 20.7 EUR/MWh |
| Inverter | [133,134] |
| Model | UnderstandSolar |
| Initial cost | 172 EUR/kW |
| O and M cost | 1% |
| Efficiency | 95% |
| Economic parameters | |
| Real discount rate | 12% |
| Lifetime of the project | 25 Years |
| Technique | Type of Renewable Energy Resource | ||||
|---|---|---|---|---|---|
| No. of PV Panels | PHES Capacity (KW) | Reservoir Capacity (m3) | Capacity of Biogas (KW) | SMES Capacity (KWh) | |
| EWOA | 5495.44 | 400.67 | 26,798.14 | 860.29 | 142.28 |
| AVOA | 2928.58 | 346.97 | 25,296.88 | 999.94 | 142.28 |
| GWOA | 2964.31 | 349.86 | 24,975.71 | 997.63 | 142.28 |
| WCA | 5117.57 | 396.92 | 27,597.56 | 869.33 | 142.28 |
| Techniques | Financial Parameters | Reliability Parameters | ||||
|---|---|---|---|---|---|---|
| LCC (EUR) | COE (EUR/kWh) | NPC (EUR) | LOLP (%) | EENS (KW) | IR | |
| EWOA | 4.507 × 106 | 0.059513 | 7.189 × 106 | 3.804 | 1.124 × 105 | 0.990066 |
| AVOA | 4.515 × 106 | 0.059517 | 7.193 × 106 | 4.533 | 1.176 × 105 | 0.990001 |
| GWOA | 4.511 × 106 | 0.059794 | 7.203 × 106 | 3.884 | 1.166 × 105 | 0.990003 |
| WCA | 4.509 × 106 | 0.059781 | 7.202 × 106 | 4.043 | 1.184 × 105 | 0.990066 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agajie, T.F.; Fopah-Lele, A.; Ali, A.; Amoussou, I.; Khan, B.; Elsisi, M.; Nsanyuy, W.B.; Mahela, O.P.; Álvarez, R.M.; Tanyi, E. Integration of Superconducting Magnetic Energy Storage for Fast-Response Storage in a Hybrid Solar PV-Biogas with Pumped-Hydro Energy Storage Power Plant. Sustainability 2023, 15, 10736. https://doi.org/10.3390/su151310736
Agajie TF, Fopah-Lele A, Ali A, Amoussou I, Khan B, Elsisi M, Nsanyuy WB, Mahela OP, Álvarez RM, Tanyi E. Integration of Superconducting Magnetic Energy Storage for Fast-Response Storage in a Hybrid Solar PV-Biogas with Pumped-Hydro Energy Storage Power Plant. Sustainability. 2023; 15(13):10736. https://doi.org/10.3390/su151310736
Chicago/Turabian StyleAgajie, Takele Ferede, Armand Fopah-Lele, Ahmed Ali, Isaac Amoussou, Baseem Khan, Mahmoud Elsisi, Wirnkar Basil Nsanyuy, Om Prakash Mahela, Roberto Marcelo Álvarez, and Emmanuel Tanyi. 2023. "Integration of Superconducting Magnetic Energy Storage for Fast-Response Storage in a Hybrid Solar PV-Biogas with Pumped-Hydro Energy Storage Power Plant" Sustainability 15, no. 13: 10736. https://doi.org/10.3390/su151310736
APA StyleAgajie, T. F., Fopah-Lele, A., Ali, A., Amoussou, I., Khan, B., Elsisi, M., Nsanyuy, W. B., Mahela, O. P., Álvarez, R. M., & Tanyi, E. (2023). Integration of Superconducting Magnetic Energy Storage for Fast-Response Storage in a Hybrid Solar PV-Biogas with Pumped-Hydro Energy Storage Power Plant. Sustainability, 15(13), 10736. https://doi.org/10.3390/su151310736










