Water Inflow Amount Prediction for Karst Tunnel with Steady Seepage Conditions
Abstract
:1. Introduction
2. Stable Seepage Field Distribution Model of Karst Water-Rich Tunnel
2.1. Basic Assumptions
- (1)
- The surrounding rock of the tunnel is a homogeneous continuous medium.
- (2)
- The water head around the tunnel is equal to H1, and the groundwater level line is constant, which is H2.
- (3)
- The volume of groundwater is incompressible and accords with Darcy’s seepage law.
- (4)
- To simplify the calculation, the seepage field distribution of the tunnel is solved by conformal mapping and a circular island steady well flow model [27].
2.2. Establishment and Solution of Tunnel Steady Seepage Field Distribution Model
3. Engineering Example Analysis
3.1. Project Overview
3.2. Prediction and Evaluation of Tunnel Inflow Calculation
- (1)
- Water balance method
- (2)
- Underground runoff modulus method
3.3. Discussion on Calculation Methods for Tunnel Inflow
3.4. Field Application Analysis of Water Inflow Prediction
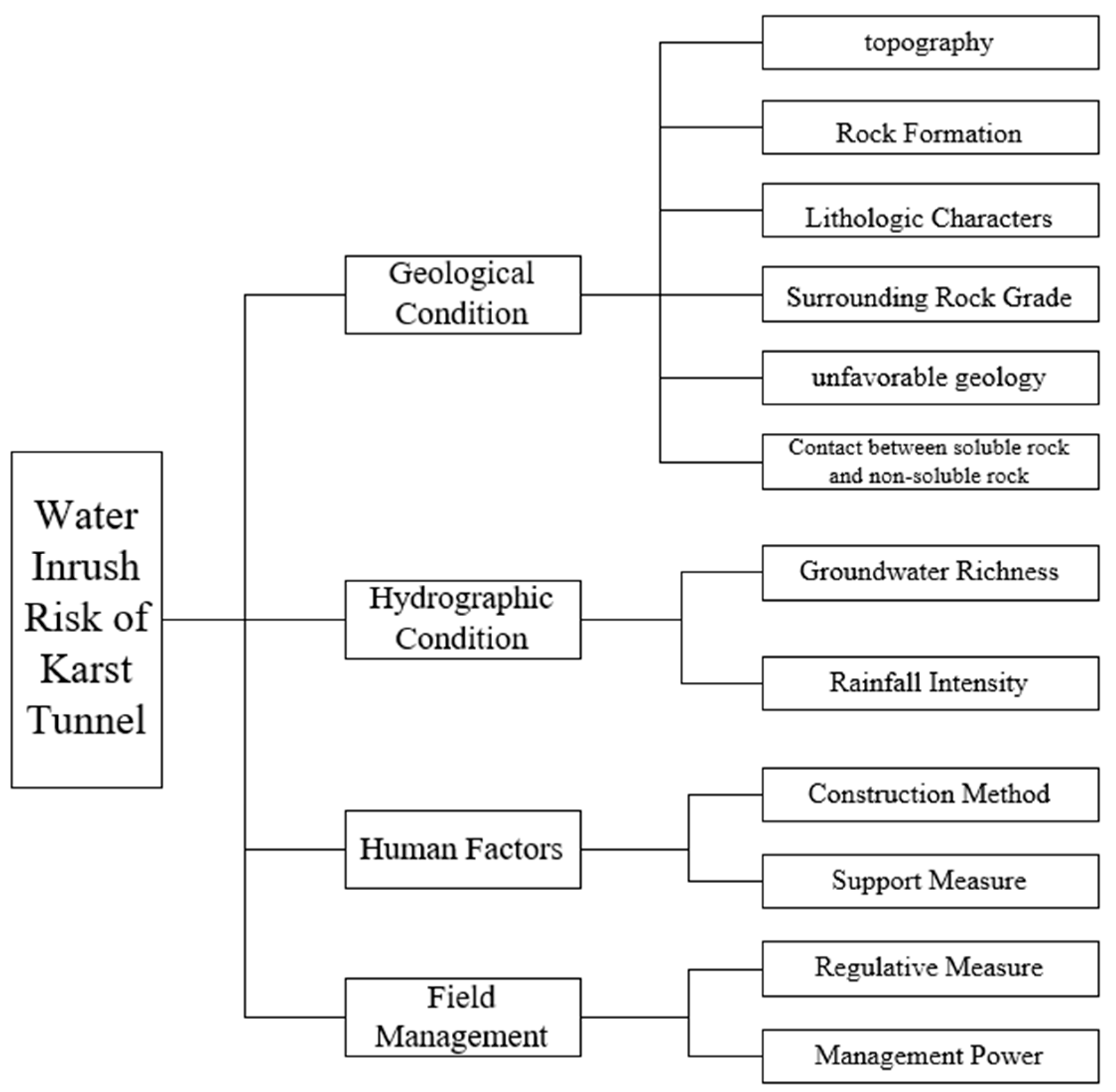
4. Prediction of Water Inrush Risk in Karst Tunnels
4.1. SVR Model
4.2. Prediction of Water Inrush Risk in Tunnels Based on the SVR Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, Q.H. Urban sustainable development and underground space development benefits. Undergr. Space 1998, 18, 69–74. [Google Scholar]
- Shi, W.; Li, J.H.; Wang, W.; Wang, C.M. Analysis of the impact of underground space on the groundwater environment and its controlling factors. Chin. J. Undergr. Space Eng. 2022, 18, 893–902+909. [Google Scholar]
- Lei, S.X.; Shen, Y.J.; Xiao, Q.H.; Xi, J.M.; Gu, L.J. Status quo and future development concept of urban underground space development and utilization. Chin. J. Undergr. Space Eng. 2019, 15, 965–979. [Google Scholar]
- Xie, H.P.; Gao, M.Z.; Zhang, R.; Xu, H.; Wang, Y.; Deng, J. Concept and key technologies of underground ecological city and deep ecology circle strategy. Chin. J. Rock Mech. Eng. 2017, 36, 1301–1313. [Google Scholar]
- Editorial Department of China Journal of Highway. Overview of academic research on China’s tunnel engineering in 2022. China J. Highw. 2022, 35, 1–40. [Google Scholar]
- Shen, Y.; Zhong, H.W.; Li, L.; Zheng, H.B.; Shi, L.; Li, X.J. Data fusion analysis method and case study of tunnel engineering based on iS3 platform. China Civ. Eng. J. 2022, 55, 103–109+148. [Google Scholar]
- Li, Z.R. Application status and analysis of building information modeling technology in tunnel engineering. J. Disaster Prev. Mitig. Eng. 2023, 43, 192. [Google Scholar]
- Gao, P. Retrospect of tunnel and underground engineering hotspots in 2018. Sci. Technol. Rev. 2019, 37, 186–195. [Google Scholar]
- Fu, H.L.; An, P.T.; Wu, Y.M.; Cheng, G.W. Analysis of sudden water in tunnel considering drainage system. J. Railw. Sci. Eng. 2022, 19, 3335–3342. [Google Scholar]
- Fu, H.L.; An, P.T.; Cheng, G.W.; Li, J.; Chen, L.; Yu, X.H. Study on the influence of the spatial position relationship between fault and parallel tunnel on the water influx. J. Railw. Sci. Eng. 2022, 19, 1032–1040. [Google Scholar]
- Shi, B.B. Calculation software development and application of water influx in Yueling tunnel. J. Railw. Eng. Soc. 2018, 12, 41–45. [Google Scholar]
- Zhou, W.Y.; Yang, Y.Y. Damage and fracture model of jointed rock mass and its validation. Chin. J. Rock Mech. Eng. 1991, 9, 43–54. [Google Scholar]
- Huang, T. Study on the coupled effect of seepage-stress-temperature of fractured rock mass. Chin. J. Rock Mech. Eng. 2002, 21, 77–82. [Google Scholar]
- Pei, X.H. Study on the Reasonable Permeability of Water-Permeable Lining in Unpressurized Tunnel. Master’s Theses, Northwest A&F University, Xi’an, China, 2013. [Google Scholar]
- Ren, S.L. Analysis of the evolution of seepage flow and the influence of parameters in the excavation of a four-line seafront tunnel. J. Railw. Sci. Eng. 2022, 19, 1985–1996. [Google Scholar]
- Zheng, L.; Chen, Z.Q.; He, C.; Ma, C.C.; Duan, C.R. Seepage field distribution and water inflow laws of tunnels in water-rich regions. J. Mt. Sci. 2022, 19, 591–605. [Google Scholar]
- Zheng, L.; He, C.; Chen, Z.Q.; Yang, S.; Ding, J.; Pen, Y. Study of seepage field distribution and its influence on urban tunnels in water-rich regions. Bull. Eng. Geol. Environ. 2019, 78, 4035–4045. [Google Scholar]
- Liu, G.Y. Analysis and comparison of water influx prediction methods in Yanshan tunnel. Railw. Constr. 2021, 61, 67–70. [Google Scholar]
- Zhou, W.J. Research on water influx prediction technology of Guanshan tunnel on Tianping line. Mod. Tunneling Technol. 2021, 58, 22–30. [Google Scholar]
- Wang, L.F.; Tang, N.; Mo, Q.; Ren, Q.Y. Prediction of water influx in tunnels in water-rich mountainous areas considering the effect of water-permeable interlayer. Sci. Technol. Eng. 2020, 20, 13865–13871. [Google Scholar]
- Shi, S.; Guo, W.; Li, S.; Xie, X.; Li, X.; Zhao, R.; Xue, Y.; Lu, J. Prediction of tunnel water inflow based on stochastic deterministic three-dimensional fracture network. Tunn. Undergr. Space Technol. 2023, 135, 104997. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, Z.; Huang, T.; Peng, D. A Dynamic Modeling Approach to Predict Water Inflow during Karst Tunnel Excavation. Water 2022, 14, 2380. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Noori, K.; Khishe, M.; Ibrahim, H.H.; Ali, H.F.H.; Abdulhamid, S.N. Presenting the best prediction model of water inflow into drill and blast tunnels among several machine learning techniques. Autom. Constr. 2021, 127, 103719. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, M.; Zhang, D.; Huang, H.; Zhang, F. Quantification of water inflow in rock tunnel faces via convolutional neural network approach. Autom. Constr. 2021, 123, 103526. [Google Scholar] [CrossRef]
- Chen, X. Study of the prediction method of water yield of the Liupan, mountain tunnel. Railw. Constr. Technol. 2020, 10, 37–41. [Google Scholar]
- Liu, X. Predicting tunnel groundwater inflow by geological investigation using horizontal directional drilling technology. Adv. Civ. Eng. 2022, 2022, 6578331. [Google Scholar] [CrossRef]
- Chen, C.; Lin, M. Groundwater Dynamics; Geological Publishing House: Beijing, China, 2011. [Google Scholar]
- Li, Z.J.; Lei, X.H.; Liao, W.H.; Yang, Q.; Cai, S.; Wang, X.; Wang, C.; Wang, J. Lake inflow simulation using the coupled water balance method and Xin’anjiang Model in an ungauged stream of Chaohu Lake Basin, China. Front. Earth Sci. 2021, 9, 615692. [Google Scholar] [CrossRef]
- Du, Y.; Zhu, H.; Li, M. Risk Assessment of Tunnel Mud and Water Inrush Based on AHP-Ideal Point Method. J. Highw. Transp. Res. Dev. 2022, 39, 100–107. [Google Scholar]
- Xu, Z.; Deng, H.; Lu, P.; Peng, L.T.; Wan, K.; Lei, P.B. Preliminary Exploration of Risk Assessment System for Water Inrush and Mud Inrush in Tunnel Karst Section. Water Resour. Hydropower Eng. 2018, 49, 127–134. [Google Scholar]
- China Railway Corporation. TB10017-2021 Code for Hydrological Survey and Design of Railway Engineering; China Railway Press: Beijing, China, 2021. [Google Scholar]
- Zi, X.Y. Study on risk assessment of water inrush disaster in tunnel in fault fracture zone. Highway 2021, 66, 410–416. [Google Scholar]
- Liang, Z.; Li, Y.; Hu, Y.; Li, B.; Wang, J. A data-driven SVR model for long-term runoff prediction and uncertainty analysis based on the Bayesian framework. Theor. Appl. Climatol. 2018, 133, 137–149. [Google Scholar] [CrossRef]









| Partition | Topography | Rock Formation | Lithological Characters | Karst Feature | Surrounding Rock Grade |
|---|---|---|---|---|---|
| Three springs | Surface dissolution depressions, karst lakes, stone buds, ditches, and sinkholes. Mainly karst caves and underground rivers. | 37~42° | Mainly limestone, dolomite, and carbonate rock. | Karst development, karst depression, funnel, falling water cave, karst lake, and karst pipeline development. | Ⅳ |
| The mouth | The surface is characterized by a small gully on the ‘mouth’, which is slow up and steep down. | 55° | Mainly dolomite limestone. | Karst is developed, and the surface is a karst trough. | Ⅲ |
| Long Beach | Mainly for ‘Shangwan’ and ‘Maiyincao’ depressions. | 60° | Mainly carbonate, dolomite. | Karst depressions, funnels, and sinkholes. | Ⅳ |
| Exit | Mainly steep slope short ditch, karst depression, and funnel with no development. | 58° | Mainly limestone, dolomite. | Karst is more developed, and individual sinkholes are distributed on the surface. | Ⅳ |
| Partition | Mileage | λ | Area (km2) | Groundwater Recharge (m3/d) |
|---|---|---|---|---|
| Sanquan | K5+030–K5+850 | 0.35 | 1.04 | 1121.13 |
| Kouzi | K5+850–K6+600 | 0.15 | 0.50 | 231.00 |
| Changtan | K6+600–K7+050 | 0.65 | 1.94 | 3883.92 |
| Export | K7+050–K8+476 | 0.33 | 1.01 | 1026.58 |
| Partition | Mileage | M (L/(s·km2)) | Area (km2) | Groundwater Recharge (m3/d) |
|---|---|---|---|---|
| Sanquan | K5+030–K5+850 | 10.60 | 1.04 | 952.47 |
| Kouzi | K5+850–K6+600 | 3.10 | 0.50 | 133.92 |
| Changtan | K6+600–K7+050 | 33.50 | 1.94 | 5615.14 |
| Export | K7+050–K8+476 | 23.30 | 1.01 | 2033.25 |
| Partition | Water Balance Method (m3/d) | Underground Runoff Modulus Method (m3/d) | Actual Water Inflow (m3/d) | Accuracy (%) | |
|---|---|---|---|---|---|
| Sanquan | 1121.13 | 952.47 | 1053 | 93.53 | 90.45 |
| Kouzi | 231.00 | 133.92 | 151 | 47.02 | 88.69 |
| Changtan | 3883.92 | 5615.14 | 4926 | 78.85 | 86.01 |
| Classification | Ⅰ | Ⅱ | Ⅲ | Ⅳ |
|---|---|---|---|---|
| Topography (valuation) | Weak karst development 75–100 | Less karst development 50–75 | Obvious karst development 25–50 | Extremely strong karst development 0–25 |
| Rock formation (dip angle/°) | 0–5° | 5–10° | 10–25° | >25° |
| Karst feature (valuation) | soluble rock <10% 75–100 | Interbedded pure carbonates, interbedded impure carbonates 50–75 | Homogeneous impure limestone, homogeneous impure carbonate 25–50 | Homogeneous pure limestone, homogeneous pure dolomite, homogeneous pure carbonate 0–25 |
| Surrounding rock grade | Ⅰ, Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 75–100 | 50–75 | 25–50 | 0–25 | |
| Unfavorable geology (valuation) | Fissure 66.6–100 | Fault 33.3–66.6 | Karst cavity 0–33.3 | |
| Contact between a soluble rock and non-soluble rock (valuation) | Weakly in favor of karst development 75–100 | In favor of karst development | Moderately in favor of karst development | Strongly in favor of karst development |
| 50–75 | 25–50 | 0–25 | ||
| Groundwater richness (valuation) | Drying up 66.6–100 | Water-rich 33.3–66.6 | High-pressure and water-rich 0–33.3 | |
| Rainfall intensity (valuation) | No rainfall | Moderate rain | Heavy rain | Rainstorm |
| 75–100 | 50–75 | 25–50 | 0–25 | |
| Construction method (valuation) | Reasonable 75–100 | Seems reasonable 50–75 | Illogicality 25–50 | Extremely illogicality 0–25 |
| Support measure (valuation) | Reasonable 75–100 | Seems reasonable 50–75 | Illogicality 25–50 | Extremely illogicality 0–25 |
| Regulative measure (valuation) | Reasonable 75–100 | Seems reasonable 50–75 | Illogicality 25–50 | Extremely illogicality 0–25 |
| Management power (valuation) | Reasonable 75–100 | Seems reasonable 50–75 | Illogicality 25–50 | Extremely illogicality 0–25 |
| Risk Level | Ⅰ | Ⅱ | Ⅲ | Ⅳ |
|---|---|---|---|---|
| Water inflow (m3/d) | >3000 | 600–3000 | 300–600 | <300 |
| Sanquan | Kouzi | Changtan | Export | |
|---|---|---|---|---|
| SVR predict level | 1.816 | 3.827 | 1.091 | 2.292 |
| BP predict level | 1.399 | 3.534 | 0.825 | 2.535 |
| Actual level | 2 | 4 | 1 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, M.; Feng, D.; Wang, J. Water Inflow Amount Prediction for Karst Tunnel with Steady Seepage Conditions. Sustainability 2023, 15, 10638. https://doi.org/10.3390/su151310638
Zhang X, Wang M, Feng D, Wang J. Water Inflow Amount Prediction for Karst Tunnel with Steady Seepage Conditions. Sustainability. 2023; 15(13):10638. https://doi.org/10.3390/su151310638
Chicago/Turabian StyleZhang, Xianmeng, Minghao Wang, Dan Feng, and Jingchun Wang. 2023. "Water Inflow Amount Prediction for Karst Tunnel with Steady Seepage Conditions" Sustainability 15, no. 13: 10638. https://doi.org/10.3390/su151310638
APA StyleZhang, X., Wang, M., Feng, D., & Wang, J. (2023). Water Inflow Amount Prediction for Karst Tunnel with Steady Seepage Conditions. Sustainability, 15(13), 10638. https://doi.org/10.3390/su151310638








