Abstract
China proposes to construct green mines as one of the significant means to elevate the green degree of mining industry and protect the mining environment. This paper constructs six evaluation indicators, namely mine environment, Resource development mode, Comprehensive utilization of resources, Energy conservation and emission reduction, Technological innovation and digital mining, Enterprise management and corporate image, to reflect green degree of mining firms. An improved multiattribute evaluation method (MAEM) is proposed based on hesitant fuzzy TOPSIS and kernel method. A case study of green mining firms in Panxi, southwestern China is provided to demonstrate the application of the proposed model. According to the research in this paper, it is more appropriate to expand the data in accordance with the optimistic criteria. The results also show that the improved hesitant fuzzy TOPSIS is a better method in the evaluation of green degree. Through the results of this paper, a reasonable and scientific method is introduced for the evaluation of the green degree of mining firms, and it can be promoted to the evaluation of the mineral resource development efficiency.
1. Introduction
Mineral resources provide a large number of indispensable and basic materials for the development of human society. The development of the mining industry also brings problems such as ecological environment perturbation, land damage, water pollution and shortages, and mining geological impacts [1,2,3,4]. Mining industries around the world are plagued by environmental problems associated with the extraction and utilization of mineral resources, as well as economic problems caused by resource depletion [5,6]. Western countries have established legislation to regulate and improve the development and production processes of enterprises to achieve sustainable development. The exploitation of mineral resources has caused many environmental issues, and the estimated cost of environmental damage due to illegal mining activity is too low [7,8]. The Chinese government has put forward the concept of the green mine (Planning of National Mineral resources, 2008–2015), clearly requiring the development of the green mining industry and determining the strategic goal of basically establishing the pattern of the green mine by 2020. The “Planning of National Mineral Resources (2015–2020)” document proposed that more than 50 demonstration areas for green mining should be built in China. The National Green Mine Construction Plan of nine major mining industries was issued and formally implemented by the Ministry of Land and Resources in October 2018. When companies in the process of building green mine practice, some enterprises have achieved good results, but scientifically evaluating the green degree of mining firms are important tasks in the future.
At present, the two most important issues in the evaluation of green mine construction level are the construction of the index system and the selection of the evaluation model [9,10,11]. The reasonability and scientificity of an evaluation index systems has a direct impact on the objectivity and accuracy of the evaluation results of green mines [10]. In the existing studies, scholars have often constructed different evaluation index systems from different research objects and according to different theories. The evaluation index system of different minerals is often different. The evaluation indices for phosphorus mining [12] cover mining effectiveness, R&D, cleaner production, corporate management, environmental equity, and social benefits. The basic circumstances, standardized management, resource utilization, energy conservation and emission reduction, technical innovation, environmental protection and land reclamation, corporate culture, and community harmony are all included in the evaluation index system for coal mines [9]. For salt mines, the evaluation index system contains the utilization of resources and energy, modernization of mining and beneficiation, nonpolluting production of mines, standardized management of mines, safety of production of mines and indicators for ecological environment reconstruction [13]. Based on the Driver-Pressure-State-Impact-Response model, Chen et al. created an evaluation index system with 20 indications [2]. Based on an analysis of the existing research results, the evaluation indicators are different because of the different evaluation objects and starting points. However, the exploration and use of mineral resources, advances in science and technology, the ecology around mines, and other factors are often taken into account. Moreover, most of the qualitative indicators are obtained by the expert scoring method, which has a certain level of subjectivity. The evaluation method of green degree involves multiple indicators, which include linguistic variables, exact values and interval values. In the multiattribute problem, evaluation techniques including the fuzzy comprehensive evaluation, the analytic hierarchy process, and data envelopment analysis are well known and often used.
In the constructed green mine evaluation index system, the importance of each index is different. The methods to determine the importance of evaluation indicators are subjective assignment method and objective assignment method. In view of the characteristics of both quantitative and qualitative indicators, the weight of each indicator is determined by an analytic hierarchy process, and the green degree evaluation is carried out by using a multilevel fuzzy pattern recognition model [13,14]. From the perspective of inputs and outputs, the mine can be regarded as a system, and the construction of a green mine is evaluated by using data envelopment analysis (DEA) [15]. In view of the fuzziness of some index values, the methods of interval fuzzy sets and fuzzy entropy have also been applied in the evaluation of green mines [9].
In the evaluation of complex systems, there are often ambiguous uncertainties due to various attributes, such as management, environment, and resources [16]. How to address the uncertainty of complex system evaluation or decision-making has always been a focus of widespread concern. Zadeh’s fuzzy set theory (FST) has been an effective method to solve this kind of evaluation problem since 1965. In this theory, the fuzzy uncertainty is described by the membership degree of an element belonging to a set. Since FST was put forward, it has developed very rapidly, and many extended forms have appeared successively, such as the intuitionistic fuzzy set [17,18], interval fuzzy set [19,20], 2-type fuzzy set [21], fuzzy multiple set [22] and hesitant fuzzy set [23]. In the multiattribute evaluation of complex systems, when determining the membership degree of an attribute belonging to a set, the evaluator is often hesitant or uncertain, resulting in an inconsistency of the evaluation results, which makes it difficult for decision makers to make a choice between different opinions. The introduction of the hesitant fuzzy set (HFS) allows the membership degree of each attribute to have multiple possible values, which makes the evaluation results of each evaluation object unique and facilitates decision makers in making judgments and decisions.
Under the attention and research of many scholars, the theory of the HFS has been constantly improved, and its application field has been constantly broadened. The research on HFS theory mainly focuses on the integration operator [24,25,26], algorithm [23,27], and the hesitant fuzzy information’s distance, similarity, correlation and entropy [24,27]. The HFS has been applied in various fields, such as decision analysis [28] and clustering analysis [29].
Among the multiattribute decision making (MADM) methods, TOPSIS is a widely used method [1]. The basic idea of TOPSIS is to rank the schemes by calculating the distance between the schemes to be evaluated and the ideal ones to determine the best scheme. In this method, the attribute values are exact values, while a large number of attribute values of decision-making problems appear as linguistic variables and interval values. An effective way to solve this contradiction is the fuzzy set and its expanded form. Thus, fuzzy TOPSIS [30,31,32,33] and hesitant fuzzy TOPSIS [34,35] have been produced.
The concept of green mining is to comprehensively improve the mining industry to make it safe, efficient and environmentally sustainable [1]. The green degree evaluation is a complex system involving resources, technology, environment, management and other types of variables. Because some indicators have fuzzy characteristics, evaluators often cannot give the exact value of indicators. Then, when the evaluator needs to determine if an index belongs to a certain membership degree of a set, he/she is often hesitant or uncertain. The experts who study green mines may themselves come from different fields, so their background knowledge is different, different experts give different evaluation values for the same green mine evaluation index, and they may not be able to agree on a single value. The above two reasons can lead to evaluators’ inconsistent evaluation results on the level of green mine construction in the same area, and it is difficult to choose between different evaluation results. When HFS theory is applied to the evaluation of the green mine construction level, the evaluation value of different experts can be expressed by a hesitant fuzzy number, which helps to reduce the complexity of decision making. Aiming at the actual situation of green degree evaluation, this paper proposed the improved hesitant fuzzy TOPSIS, and evaluates the green degree of a vanadium-titanium magnetite firms in the Panxi area of China.
To bridge the above research gaps, this paper aims to Evaluate green degree of mining firms of China. The evaluation model based hesitant fuzzy TOPSIS and kernel method is proposed. The following is a summary of this paper’s significant contributions:
- (1)
- Constructing an evaluation indicator system of green degree from six aspects.
- (2)
- This paper integrates the hesitant fuzzy and kernel method to propose improved hesitant fuzzy TOPSIS.
- (3)
- This paper evaluates green degree of a vanadium titanomagnetite mine in the Panxi, which provide implication for other related researches.
The remainder of this paper unfolds as follows: Section 2 introduces the Hesitant fuzzy TOPSIS, and proposes improved hesitant fuzzy TOPSIS to evaluate green degree. Study area and data is investigated in Section 3. Section 4 applies the proposed improved hesitant fuzzy TOPSIS to evaluate green degree of a vanadium titanomagnetite mine in Panxi, China, and some comparative and sensitivity analyses are provided. Section 5 ends the paper with some concluding remarks.
2. Method
2.1. Evaluation Index System
The construction of index system is one of the main tasks in the evaluation of green degree. This paper is based on norms issued by the former Ministry of Land and Resources and synthesizes the contributions of domestic scholars to construct an evaluation index system from three aspects: technology economy, enterprise management and mine environment. The specific evaluation indicators are shown in Figure 1.
- (1)
- Mining environment
It is required that the development planning and functional zoning of mining is reasonable and that the greening of a mining area is realized in an all-round manner so that the waste generated in the production process is entirely disposed of and the management of every link in the mining production and transportation process is standardized and orderly.
- (2)
- Resource development mode
Mines should reasonably select mining and beneficiation processes according to their own resource endowment and ecological environment characteristics. They should actively carry out technological innovation and improve technological processes; to limit environmental damage and assure the prompt restoration of the damaged environment, businesses should coordinate resource development and usage with local environmental protection, resource protection, and urban and rural construction.
- (3)
- Comprehensive utilization of resources
The comprehensive usage of resources by mines must always be improved, and nonrenewable mineral resources must be protected.
They should strengthen the exploration, development and utilization of the associated resources and make full use of the available resources under the existing technological and economic conditions. They should consider the scientific utilization of solid waste and wastewater to improve the efficiency of enterprises, protect the environment and develop a circular economy.
- (4)
- Energy conservation and emission reduction
Mines should adopt new technologies, new processes, new equipment and new materials to control and reduce energy consumption per unit production and reduce the discharge of “the three wastes”: solid waste, waste water and waste gas.
- (5)
- Technological innovation and digital mine
As the main body of innovation, enterprises should establish technological research and development teams to implement key technologies in enterprise production and constantly improve the technological and production efficiency of enterprises. An intelligent mine and production automation system is constructed by using computers and intelligent control technology to improve the automation level of mine production and realize centralized control and information linkages across the whole production process.
- (6)
- Enterprise management and corporate image
Mines should establish sound rules and work mechanisms for resource management, ecological environment protection and safety in production. Enterprises have core values that reflect people orientation, innovative learning and green development and possess a corporate culture that conforms to the characteristics of the enterprise and promotes the realization of the strategic objectives of enterprise development. They develop the concepts of coconstruction, benefit sharing and common development between mines and local governments in order to improve the quality of people’s lives in mining areas.
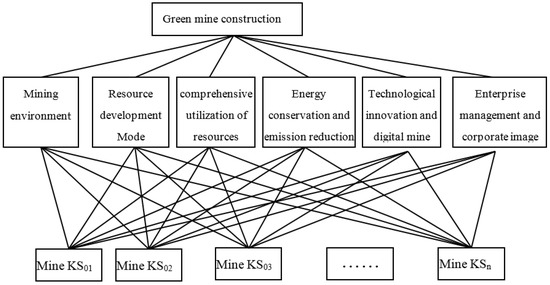
Figure 1.
Evaluation index system of green mines.
2.2. Hesitant Fuzzy TOPSIS
Considering a multiattribute decision making (MADM) problem, is scheme set, is a mining firm to be evaluated and is the index set. A hesitant fuzzy set (HFS) on X is [24]: where is possible membership degree of the element to the set A. So the membership degree can be expressed by a hesitant fuzzy element (HFE) , and the hesitant fuzzy decision matrix H of A on X is:
The TOPSIS methodology determines the best scheme by calculating the proximity between the schemes to be evaluated and the ideal scheme. This technique is easy to use, flexible and widely used. In this method, one of the keys is to determine the positive ideal solution (PIS) and the negative ideal solution (NIS). In the case of HFSs, PIS can be extended to a hesitant PIS (S+) and a hesitant NIS (S−) [34].
Let denote the distance between PIS and scheme, let denote the distance between NIS and scheme. Where m is the number of indicators, are the largest values in . The relative closeness Ci between PIS and scheme is calculated as follows:
The distance between the schemes is obtained by extending the Hamming distance, Euclidean distance and Hausdorff distance in a hesitant fuzzy environment [36]. Let be the weight of the indicator and be the number of elements in the hesitant fuzzy number . and are expressed as follows:
- (1)
- The hesitant normalized Hamming distance (HNHD):
- (2)
- The hesitant normalized Euclidean distance (HNED):
- (3)
- The hesitant normalized Hamming-Hausdorff distance (HNHH)
In the case of HFSs, the weight of each evaluation index can be reduced to an optimization problem [34].
where dij is the distance between the hesitant fuzzy elements. The distance is obtained by extending the Hamming distance (HNHD, Formula (7)), Euclidean distance(HNED, Formula (8)) in a hesitant fuzzy environment [36].
2.3. Improved Hesitant Fuzzy TOPSIS
Kernel method is one of the research hotspots in machine learning field, which is widely used in classification, face recognition, comprehensive evaluation. Kernel methods transform an input X into a higher dimensional space F so that the nonlinear problems can be solved linearly. Euclidean distance is not robust, and the distance measurement derived from Gaussian kernel induction is robust. Considering the advantages of it, kernel distance is introduced into hesitant fuzzy.
It is not necessary to know the specific form of nonlinear transformation, and the main process is transformed into selecting the kernel function representing nonlinear transformation. Therefore, Kernel function is very important for evaluation results. Let be a set of d-dimensional vocters. A positive definite of kernel function can be expressed as . The kernel function are often used as follows:
- (1)
- Polynomial kernel:
- (2)
- Gaussian RBF kernel:where d is the degree of polynomial, is the parameter that controls the width of RBF.
If the kernel function is Gaussian RBF kernel, the distance between and can be calculated by following formulas:
Assume numbers of the value of each hesitant fuzzy element are same in hesitant fuzzy set, and according to the descending order. The evaluation value of each unit with different attributes is regarded as a vector. If the kernel function is Gaussian RBF kernel, the hesitant fuzzy kernel distance(HFKD) can be defined as follows.
It is easy to prove HFKD meet three properties of the distance [34]:
- (i)
- ;
- (ii)
- if and only if ;
- (iii)
- .
After determining the hesitant fuzzy kernel distance and the hesitant fuzzy PIS and NIS, the improved hesitant fuzzy TOPSIS is used to evaluate the green degree of the mining firms.
Step 1: According to the evaluation index set, the index value is obtained, and standardization is carried out by expanding the HFE based on the criterion of optimism or pessimism.
Step 2: Determine the hesitant fuzzy PIS and NIS based on Equations (1) and (2).
Step 3: Calculate the distance from each mine to the hesitant PIS based on Equation (13) and the hesitant NIS based on Equation (14).
Step 4: The relative closeness of each scheme is calculated based on Equation (3).
Step 5: Evaluate the construction level of green mines. According to the relative closeness calculated in step (4), the scheme is sorted.
3. Study Area and Data
3.1. Study Area
Vanadium-titanium magnetite is a symbiotic mineral resource formed by elements such as iron, vanadium and titanium and accompanied by a variety of rare and precious metals [25]. Vanadium and titanium magnetite ores have large reserves and wide distribution in the world, and are distributed mainly in Russia, the United States, South Africa, Norway, Canada, China and other countries. The Panxi region is the largest vanadium-titanium magnetite metallogenic belt in China. The Panxi area is located in Southwest China and has an area of 6000 km2. The Panxi area is located in the Hengduan Mountains and belongs to the transition zone from the Qinghai-Tibet Plateau and Yunnan-Guizhou Plateau to the Sichuan Basin [37].
The Panxi area is a highly concentrated metallogenic belt of vanadium-titanium magnetite deposits in China. It is one of the most important producing areas of similar deposits in the world [38]. The Panzhihua mining area, Hongge mining area, Baima mining area and Taihe mining area in Panxi constitute super large deposits. The thickness of the ore body is ranges from tens of meters to 200 m, extending from hundreds of meters to more than several kilometers. The proven reserves of vanadium-titanium magnetite in the Panxi area are 9.396 billion tons. Among them, the reserves of vanadium are 23.48 million tons in V2O5 and 870 million tons in titanium, accounting for approximately one-fifth of all the iron ore resources of various kinds in China. It is one of the most well-known and comprehensively utilized mineral resources in China [39].
Panxi, has made remarkable achievements in the development and comprehensive utilization of vanadium-titanium magnetite resources after more than 40 years of development. Especially in recent years, the development momentum has been strong and has entered a rapid development stage. The level of comprehensive utilization of mineral resources have been remarkably improved in Panxi, which has become the area with the best developed vanadium and titanium industry, the highest level of development and utilization of vanadium and titanium resources and the broadest development prospects in China.
In the past 10 years, the construction level of green mines in Panxi region has been greatly improved, and a total of 7 were carried out to the national green mine list, mainly involving iron ore, copper ore, lead-zinc ore, gold ore coal mine, etc., among which 7 were iron ore mines. In order to increase the comparability of green mine construction level evaluation results, this study selects mining enterprises of the same mine type, i.e., 10 vanadium-titanium magnetite mines, and constructs the measurement object set A = {KS01, KS02, …, KS10}.
3.2. Data Sources and Analysis
The indicators value are obtained by inviting three experts to give evaluation values based on the relevant resources. The experts give evaluation values based on field research, mineral resource planning of study area (2016–2020), and Green Mine Construction Specification for Metallurgical Industry issued by the Ministry of Natural Resources of China in 2018 (DZ/T 0319-2018). The collected evaluation values of each mine given by experts for each index can be regarded as a hesitant fuzzy element (HFE) (Table 1).

Table 1.
Hesitant fuzzy evaluation matrix.
4. Results and Discussion
In this section, we introduce the comparative analysis and discussion in terms of two aspects: Comparative analysis Extension of Hesitant Fuzzy Data, The Influence of Distance on the Evaluation Results, Validation of the proposed method.
4.1. Comparative Analysis Extension of Hesitant Fuzzy Data
In Table 1, the number of values in different HFEs is different. Different types of decision makers tend to take different ways to extend the HFE. Conservative decision makers may obtain a hesitant fuzzy decision matrix by adding the minimum value to the HFEs (Table 2); radical decision makers may obtain a decision matrix by adding the maximum value to the HFEs (Table 3). For instance, two possible values of mine KS04 evaluation index X1 {0.9, 0.7} should be extended to {0.9, 0.9, 0.7} according to the optimism criterion and {0.9, 0.9, 0.7} according to the pessimism criterion [40].

Table 2.
Hesitation fuzzy evaluation value matrix of the pessimistic criterion.

Table 3.
Hesitation fuzzy evaluation value matrix of the optimistic criterion.
To analyze the impact of the two extension methods on the evaluation results, the evaluation results based on improved hesitant fuzzy TOPSIS are shown in Table 4 and Figure 2. As shown in Table 4, the hesitant fuzzy data are expanded according to the pessimistic criterion and the optimistic criterion, and the evaluation results of each mining firm are consistent. 80% of all mines have the same ranking and 20% of all the mines have an inconsistent ranking. Under the optimistic criterion, mine KS02 ranks second, and it ranks third under the pessimistic criterion. Mine KS10 has a similar situation.

Table 4.
The evaluation results of different criteria.
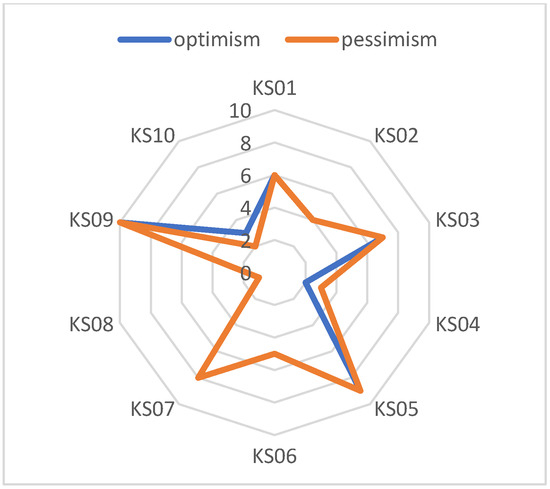
Figure 2.
The Radar Chart of evaluation results of different criteria.
4.2. Validation of the Proposed Method
The distance measure is important in the study of hesitant fuzzy set theory. By calculating the distance, it is convenient to compare the similarity and difference between different schemes. To consider the influence of the different distance measures in evaluating the green degree of mining firms, the hesitant fuzzy TOPSIS and improved hesitant fuzzy TOPSIS are used to calculate the closeness of mining firms, and then the green degree of mining firms is ranked according to the degree of closeness.
According to the optimization model, the weights of each evaluation index under different extension modes can be obtained in Figure 3. The weight of the X6 evaluation index is the largest of all six evaluation indexes under different extension modes. In fact, optimization model is based on the maximum deviation method (MDM) because the attribute value of the X6 evaluation index has a large deviation and is given a larger weight.
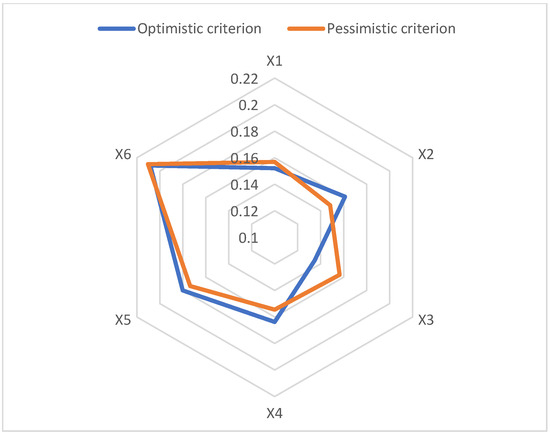
Figure 3.
The Radar Chart of Weight of each evaluation index for different criteria.
Using the hesitant fuzzy TOPSIS method based on HNHD and HNED, the ranking of mining firms are shown in columns 2, 3, 4, 5 of Table 5. The improved hesitant fuzzy TOPSIS based on HFKD are used to calculate the closeness of mining firms, and then rank the green degree of mining firms according to the relative closeness degree in columns 6, 7 of Table 5.

Table 5.
Evaluation results of different distance measures.
From columns 2 to 7 in Table 5, it can be seen that when using the HNHD, HNED and HFKD, the evaluation results of each mining firms are almost consistent according to the principles of pessimism and optimism. 50% of all mining firms have the same ranking, including KS03, KS05, KS07, KS08 and KS09.
The results (Figure 4) according to the principles of optimism are shown as follows:
HNHD:
HNED:
HFKD:
The results (Figure 5) according to the principles of pessimism are expressing as follows:
HNHD:
HNED:
HFKD:
According to the above results, when HNHD, HNED, HNKD is used to evaluate the green level of mines, no matter it is based on optimistic criterion or pessimistic criterion, KS04, KS08, KS10 rank first three, KS07, KS05, KS09 rank last three; when using HNHD, HNED, The optimization model should be used to solve the weights in advance, the improved hesitant fuzzy TOPSIS is based on HNKD, no need to calculate weight, and greatly reduce the complexity of computation.
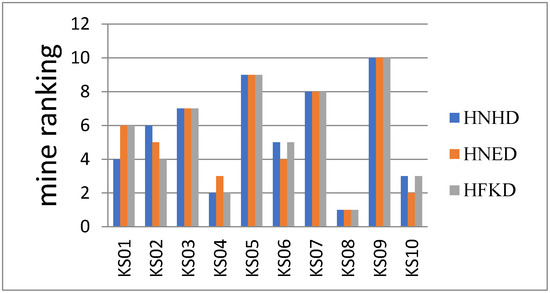
Figure 4.
Mine ranking under the optimistic principle.
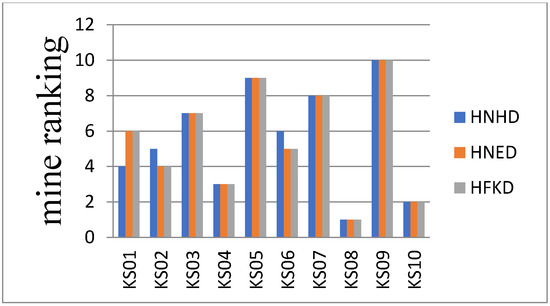
Figure 5.
Mine ranking under the pessimistic principle.
5. Conclusions and Policy Implications
5.1. Conclusions
In view of the fact that some of the indicators have fuzzy characteristics and the evaluators are often hesitant or uncertain, this paper proposes a improved evaluation method for mining firms based on hesitant fuzzy TOPSIS and kernel method. The indexes of the green degree include the resource development mode, comprehensive utilization of resources, energy savings and emission reduction, innovation and digital mining, and enterprise management and corporate image. We consider the extension of the hesitant fuzzy set. According to the optimistic and pessimistic criteria, the HFSs are expanded, and the influences of different expansion modes on the evaluation results of green degree are compared. The results show that on the basis of different principles, the evaluation results of green mine construction have little or no impact. In practical work, either of the two criteria can be chosen freely by the evaluators. Considering the progress of technology and technology and the increasing attention of producers to the development of the green mining industry, it is appropriate to expand hesitant fuzzy data by using the optimistic criterion. The HNHD, HNED and HFKD distances are appropriate for the distance measure when evaluating the level of green mine. Although the evaluation results of different distance measure are basically the same, the improved hesitant fuzzy TOPSIS is based on HNKD, no need to calculate weight, and greatly reduce the complexity of computation. Through the results of this study, a reasonable and scientific method is introduced to evaluate the level of green mine construction. Furthermore, the evaluation model proposed in this study can be extended to other areas in China, such as the green development level of manufacturing industry.
In addition, to the contribution mentioned above, our study had some limitations that are worth attention. In the evaluation of green mines, we have constructed a single-layer evaluation index system and only used it for vanadium and titanium magnetite mines, but did not construct a more detailed multi-layer index system. Therefore, in future research, we can try to construct a multi-layer evaluation index system and give more examples of other mine types.
5.2. Policy Implications
Discussing the technical system of evaluation and green degree of mining firms degree in Southwest China will not only explore the green mining development of Southeast China, but also propose several policy implications based on our empirical conclusions.
First, increasing the proportion of large and medium-sized mines. In order to increase it, the government should push forward the rectification and integration of mining industry, and strictly control small, scattered, disorderly and polluted mines, them improve green scale benefit.
Second, improving the innovation ability of green technology. Natural resources management department should encourage mining firms to increase investment, strengthen technological innovation and technology introduction, Improve the comprehensive utilization of resources, Reduce energy consumption and carbon emissions.
Third, comprehensively promote the construction of green mines. Through policy guidance and supportive policies for land, taxation, financing, etc, the government proceed green mines construction from point to whole, then promote the development of green mining industry.
Finally, Natural resources management department Establish and improve the mine environment restoration fun system that should be standardized management, unified responsibilities and rights, and convenient use, and urge mining firms to implement the responsibility of eco-geological environment restoration. The government may give policy to protect the eco-geological from a systematic point of view, and propose some key measures to control of soil and water loss, Vegetation restoration, Land reclamation, Ecological function restoration in mining area.
Author Contributions
D.L.: Conceptualization, Methodology, Validation, Data curation, Methodology; S.H.: Software, Validation, Data curation, Writing—original draft; H.W.: Data curation, Supervision, Writing—review & editing; L.C.: Software, Validation and Data curation; J.L.: Software, Validation and Data curation. All authors have read and agreed to the published version of the manuscript.
Funding
This work is Supported by Natural Science Foundation of Sichuan Province (Grant no. 2022NSFSC0510), Geomathematics Key Laboratory of Sichuan Province (Grant to no. scsxdz2021yb01), Sichuan Mineral Resources Research Center (Grant no. SCKCZY2022-YB009).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, G.; Zhang, Q.; Hu, Y. Dust removal effect of negatively-pressured spraying collector for advancing support in fully mechanized coal mining face: Numerical simulation and engineering application. Tunn. Undergr. Space Technol. 2020, 95, 103149. [Google Scholar] [CrossRef]
- Chen, J.; Jiskani, I.M.; Jinliang, C.; Yan, H. Evaluation and future framework of green mine construction in China based on the DPSIR model. Sustain. Environ. Res. 2020, 30, 13. [Google Scholar] [CrossRef]
- Liu, Q.; Qiu, Z.; Li, M.; Shang, J.; Niu, W. Evaluation and empirical research on green mine construction in coal industry based on the AHP-SPA model. Resour. Policy 2023, 82, 103503. [Google Scholar] [CrossRef]
- Luo, D.; Huang, J.; Wu, H.; Cheng, L.; Huo, Z. Measuring green development index and coupling coordination of mining industry: An empirical analysis based on panel data in China. J. Clean. Prod. 2023, 401, 136764. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, H.; Xiong, Z. Game theory attack pricing for mining pools in blockchain-based IoT. Digit. Commun. Netw. 2022; in press. [Google Scholar] [CrossRef]
- Bai, T.; Liu, Y.Y.; Muhammad, I. Mixed nitrogen form addition facilitates the growth adaptation of legume plant to heavy metal contamination in degraded mining areas. Glob. Ecol. Conserv. 2020, 24, e01387. [Google Scholar] [CrossRef]
- Huang, X.; Li, X.; Hu, K. Status and Achievement of the Green Mine in China. Int. Proc. Chem. Biol. Environ. Eng. 2012, 36, 21–25. [Google Scholar] [CrossRef]
- Shen, L.; Kong, H.; Wang, J. The Status and Achievements of Green Mines and Mining Ethics in China. J. Resour. Ecol. 2016, 7, 317–322. [Google Scholar]
- Jing, P.X.; Lu, M.Y.; Gong, W.C. Evaluation of underground coal mining green mine based on interval-valued intuitionistic fuzzy entropy and contingency theory. China Min. Mag. 2016, 25, 59–75. [Google Scholar] [CrossRef]
- Zhang, W.L.; Lu, Z.X. Principles and ideas on the construction of comprehensive evaluation system of green mine construc-tion. China Min. Mag. 2017, 26, 134–137. [Google Scholar] [CrossRef]
- Wang, R.; Feng, Y. Evaluation research on green degree of equipment manufacturing industry based on improved particle swarm optimization algorithm. Chaos Solitons Fractals 2020, 131, 109502. [Google Scholar] [CrossRef]
- Shang, D.; Yin, G.; Li, X.; Li, Y.; Jiang, C.; Kang, X.; Liu, C.; Zhang, C. Analysis for Green Mine (phosphate) performance of China: An evaluation index system. Resour. Policy 2015, 46, 71–84. [Google Scholar] [CrossRef]
- Huang, J.J.; Song, Y.F.; Wang, Y.J. Study on the main evaluation in Jintan salt green mines to create indexes. China Min. Mag. 2010, 19, 79–85. [Google Scholar] [CrossRef]
- Song, X.F.; Wen, B. Research into the quatitative evaluation of the mine construction. China Min. Mag. 2014, 23, 54–61. [Google Scholar] [CrossRef]
- Wang, W.S.; Zou, J.L. Efficiency evaluation and optimization of green mining construction in coal enterprises based on DEA. China Coal. 2013, 39, 119–121. [Google Scholar] [CrossRef]
- Luo, S.; He, S.Y. Understanding gender difference in perceptions toward transit services across space and time: A social media mining approach. Transp. Policy 2021, 111, 63–73. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Bustince, H.; Barrenechea, E.; Pagola, M.; Fernandez, J. Interval-valued fuzzy sets constructed from matrices: Application to edge detection. Fuzzy Sets Syst. 2009, 160, 1819–1840. [Google Scholar] [CrossRef]
- Deschrijver, G. A representation of t-norms in interval-valued L-fuzzy set theory. Fuzzy Sets Syst. 2008, 159, 1597–1618. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Systems of linear fuzzy constraints. Fuzzy Sets Syst. 1980, 3, 37–48. [Google Scholar] [CrossRef]
- Yager, R.R. An Introduction to Fuzzy Set Theory. Adv. Hum. Factors Ergon. 1986, 6, 29–39. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z.; Chen, N. Induced aggregation under confidence levels. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2011, 19, 201–227. [Google Scholar] [CrossRef]
- Yu, D.J.; Wu, Y.Y.; Zhou, W. Generalized Hesitant Fuzzy Bonferroni Mean and Its Application in Multi-Criteria Group Decision Making. J. Inf. Comput. Sci. 2012, 9, 267–274. [Google Scholar]
- Wei, G. Hesitant fuzzy prioritized operators and their application to multiple attribute decision making. Knowl.-Based Syst. 2012, 31, 176–182. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.; Xia, M. Interval-valued hesitant preference relations and their applications to group decision making. Knowl.-Based Syst. 2013, 37, 528–540. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, X.; Li, X. Wireless Sensor Network nodes correlation method in coal mine tunnel based on Bayesian decision. Measurement 2013, 46, 2335–2340. [Google Scholar] [CrossRef]
- Boran, F.E.; Genç, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Chen, C.-T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, W.; Chang, W. An improved TOPSIS with weighted hesitant vague information. Chaos Solitons Fractals 2016, 89, 47–53. [Google Scholar] [CrossRef]
- Mahmood, M.; Salih, B.; Zaidan, A.A. Survey on fuzzy TOPSIS state-of-the-art between 2007 and 2017. Comput. Oper. Res. 2019, 104, 207–227. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, X. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl.-Based Syst. 2013, 52, 53–64. [Google Scholar] [CrossRef]
- Sun, Y.X.; Wu, S.; Hou, H.L. Enlightenment on construction of green mine in Zhejiang province. China Min. Mag. 2018, 27, 46–48. [Google Scholar] [CrossRef]
- Tong, X.; Yu, L. MADM based on distance and correlation coefficient measures with decision-maker preferences under a hesitant fuzzy environment. Soft Comput. 2016, 20, 4449–4461. [Google Scholar] [CrossRef]
- Munteanu, M.; Yao, Y.; Wilson, A.H.; Chunnett, G.; Luo, Y.; He, H.; Cioacă, M.; Wen, M. Panxi region (South-West China): Tectonics, magmatism and metallogenesis. A review. Tectonophysics 2013, 608, 51–71. [Google Scholar] [CrossRef]
- Hou, T.; Zhang, Z.; Encarnacion, J.; Santosh, M. Petrogenesis and metallogenesis of the Taihe gabbroic intrusion associated with Fe–Ti-oxide ores in the Panxi district, Emeishan Large Igneous Province, southwest China. Ore Geol. Rev. 2012, 49, 109–127. [Google Scholar] [CrossRef]
- Yang, S.G. Sustainable Development and Comprehensive Utilization of the Vandium and Titanium in Panxi Region. Met. Mine 2002, 7, 31–34. [Google Scholar]
- Luo, D.J.; Wu, H.; He, S.; Li, J.B.; Pu, H.; Wang, Y. Multiattribute Evaluation Method for Green Mines Based on Hesitant Fuzzy TOPSIS. Multipurp. Util. Miner. Resour. 2021, 4, 41–49. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).