Abstract
In China, the majority of mountainous regions are characterized by complex topography and a delicate, sensitive geological environment. These areas, which exhibit insufficient infrastructure and widespread irrational human engineering activities, are often susceptible to geological hazards such as slope instability and soil mass movements. These geological hazards pose substantial threats to human lives and property, hindering the progress of mountainous areas. Therefore, conducting research on evaluating the vulnerability of slope rock and soil mass movement geological hazards (hereinafter referred to as geological hazards) is of utmost importance for hazard prevention, emergency management, and economic advancement in these regions. This study focuses on Xuanwei City and selects eight factors for evaluation, including elevation, gradient, slope aspect, normalized vegetation index, stratigraphic lithology, distance from faults, distance from rivers, and distance from roads. These factors are chosen based on a comprehensive analysis of the spatial and temporal distribution of geological hazards and hazard incubation conditions. Two paired models, the deterministic coefficient model + logistic regression model (CF+LR) and the information quantity model + logistic regression model (I+LR), were employed to assess the study area quantitatively. The performance of these models was assessed by employing receiver operating characteristic (ROC) curves and calculating the corresponding area under curve (AUC) values. The results indicate that: (1) The AUC values for the coupled CF+LR and I+LR models are 0.799 and 0.772, respectively. These results indicate that both models provide an objective and reliable assessment of the vulnerability to geological hazards, specifically slope rock and soil mass movements, in the study area. (2) Based on the CF+LR model calculations, the geological hazard susceptibility of Xuanwei City can be categorized into four zones: extremely high susceptibility (6.09%), high susceptibility (31.08%), medium susceptibility (32.26%), and low susceptibility (30.57%). (3) The CF+LR model more accurately represents the evaluation results and offers a strong reference value.
1. Introduction
Assessing the susceptibility of geological hazards is crucial in evaluating the risk they pose. This refers to the likelihood of geological hazards occurring due to various internal factors, such as topography, geomorphology, stratigraphic lithology, and geological structure, in combination with external factors, such as extreme rainfall and earthquakes. Precise forecasting and categorization of geological hazard vulnerability play a pivotal role in promoting regional economic growth, safeguarding the welfare of individuals, and fostering high-quality development. The exploration of geohazard susceptibility assessment commenced in the 1960s, transitioning from initial qualitative evaluation methods to quantitative approaches. With the advent of the 21st century, the proliferation of 3S technology alongside advancements in mathematical and statistical theories has facilitated an upsurge in studies adopting quantitative evaluation techniques. Wang Q et al. [1] applied the information quantity method to assess and delineate geological hazard vulnerability in Wen County, Sun et al. [2] integrated the Dempster–Shafer evidence theory to evaluate geohazard susceptibility along the northern route of the Sichuan–Tibet highway, and Kohno et al. [3] employed the AHP-GIS method to examine earthquake-induced slope damage. Nevertheless, relying solely on quantitative evaluation methods can lead to the issue of mutual interference among evaluation factors. When there is a significant correlation between these factors, it can compromise the performance of the evaluation model, resulting in assessment results that may not meet the desired expectations. To overcome this, the logistic regression model has been used to test independence and diagnose covariance between evaluation factors, eliminating highly correlated factors and more objectively and scientifically determining weights of evaluation factors.
Due to the constraints associated with employing single evaluation methods and recognizing the advantages offered by logistic regression models, a growing number of researchers have been proficiently combining these two approaches to evaluate the vulnerability of geological hazards in their respective study regions. After conducting field investigations and tests, the results have been found to be consistent with on-site conditions, and the evaluation model demonstrates greater performance. Riegel et al. [4] utilized a geographic information system (GIS) and logistic regression model to investigate landslide susceptibility in Novo Hamburgo, with the model effectively determining landslide occurrence probability and exhibiting strong predictive capabilities. Devkota et al. [5] employed GIS-based certainty factors, an entropy index, and logistic regression models to evaluate landslide susceptibility, focusing on the Mugling–Narayanghat road section in the Nepal Himalayas; their results indicated that the model demonstrated high performance. Fan et al. [6] assessed geological hazard vulnerability in Wenchuan County using an information quantity–logistic regression model and compared the evaluation performance of the information quantity model, logistic regression model, and coupled model simultaneously. Luo et al. [7] applied the CF-Logistic model to evaluate landslide susceptibility in the Jiuzhaigou scenic area, with their findings revealing that the coupled evaluation model had higher performance than the single evaluation model and that its zoning results were highly reliable. The focus of this study is Xuanwei City, where the vulnerability of geological hazards in the area is assessed using a combination of the information quantity model, deterministic coefficient model, and logistic model. The evaluation involves a comprehensive and unbiased analysis of the spatial and temporal distribution patterns, as well as the current hazard conditions associated with geological hazards in the region. Eight factors of influence were carefully chosen, including elevation, slope, slope aspect, normalized difference vegetation index (NDVI), stratigraphic lithology, distance from faults, distance from rivers, and distance from roads. By comparing various geological hazard susceptibility evaluation models, results, and performance within the same study area, this research explores a coupled quantitative evaluation model with high precision and reliability. This model serves as a reference for assessing geological hazard susceptibility in the study area and potentially in other county-level regions. It offers a scientific basis for hazard prevention and mitigation, development planning, and the selection of suitable locations for major projects in Xuanwei.
2. Overview of the Study Area
Xuanwei City, situated in Qujing City within Yunnan Province, is located in the northeastern part of Yunnan Province (Figure 1; the grid and vector data of the study area are derived from the geospatial data cloud [https://www.gscloud.cn/ (accessed on 13 April 2023)] and are processed by the ArcGIS platform). Its geographical coordinates range from 103°35′30″ E to 104°40′50″ E longitude and 25°53′30″ N to 26°44′50″ N latitude. Xuanwei City is strategically located at the interprovincial junction of Yunnan and Guizhou, often referred to as the gateway to Yunnan Province. It shares its eastern borders with Panxian and Shuicheng in Guizhou Province, while being separated from Huize County to the west. Xuanwei City shares its southern border with Fuyuan County and Zhanyi County, while its northern boundary is adjacent to Weining in Guizhou Province. The city is situated at a high altitude, characterized by a cool climate, notable diurnal temperature variations, and relatively low rainfall. These environmental conditions make the region suitable for the cultivation of cold-resistant and drought-tolerant crops. Geographically, Xuanwei City is positioned on the outskirts of the Yunnan Plateau, classifying it as a mountainous alpine area. It is a transition slope to the Guizhou Plateau, with the terrain generally higher in the northwest and lower in the southeast. The highest peak in the area is the main peak of East Mountain which has an elevation of 2868 m, and the lowest point is the Lakeng Iron Cable Bridge of the Beipan River, with an elevation of 920 m.
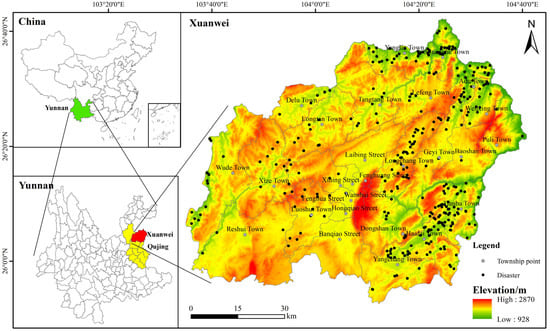
Figure 1.
Overview of the study area.
The primary rivers in the region are part of the upper reaches of the Beipan River within the Pearl River system, originating from the northwestern foothills of MaXiong Mountain in Xuanwei City. The area features two major tributaries: the GeXiang River, which flows through Xuanwei City, and the Kedu River, which flows through Kedu. The region’s main landforms encompass three types: basin, tectonic erosion and denudation, and karst. The stratigraphic lithology in the area is complex, with the most extensive exposures being the Xuanwei Formation and Emeishan Basalt Formation of the Diametrion System. Next in sequence are the tuffs of the Qixia Maokou Formation, which also belong to the Diametrion System. The third area consists of Carboniferous and Devonian carbonates. The rock masses throughout the study area exhibit varying degrees of hardness, with generally poor rock quality, low weathering resistance, poor mechanical properties, and suboptimal engineering geological characteristics. The area has a temperate monsoon climate with three-dimensional climatic characteristics, with higher temperatures in the basin and river valley and lower temperatures in the mountainous areas. The annual precipitation ranges from 623 to 1348 mm, with an average of 940 mm and concentrated rainfall from May to October. The study area has experienced a total of 254 landslide disasters, which constitute one of the region’s primary types of geological disasters. Among these, there were 229 soil landslides, 20 stone landslides, and 5 rock landslides. It is evident that soil landslides dominate the landslide occurrences in the study area, accounting for 90% of the total. The peak period of landslide hazards mainly occurs from June to October, coinciding with the region’s rainy season. Heavy rainfall serves as the primary triggering factor for geological hazards. Xuanwei City exhibits a high vegetation coverage rate; however, its distribution is uneven. Forest resources are mainly concentrated in sparsely populated areas such as Wenxing Township, Yangliu Town, and Puli Township, where geological hazards that occur are relatively less frequent. In mountainous towns and villages, the scarcity of available land and high population density contribute to prevalent deforestation and land reclamation practices. These activities result in soil erosion and elevate the risk of landslides, debris flows, and collapses. Generally, areas with lower vegetation coverage are more susceptible to severe geological hazards. A detailed investigation report conducted in 2015 at a scale of 1:50,000 revealed that Xuanwei City recorded a total of 485 geological disasters related to slope rock and soil mass movements. During the rainy season, the number of potential geological hazard hotspots triggered by rainfall continues to rise, posing a significant threat to the safety of local residents and their properties and hampering economic development. In 2018, a landslide in Yangliu Town, Xuanwei City resulted in one fatality and varying degrees of damage to over 200 houses. The region’s population, transportation infrastructure, and buildings are the primary vulnerable elements to geological disasters, as their occurrence entails substantial losses. As the second-largest city in Qujing, Xuanwei City has witnessed a growing contribution to the local economy. The industrial sector, serving as an economic pillar, has spurred rapid regional development. In summary, the vulnerability assessment of slope rock and soil mass movement geological hazards is of paramount importance in Xuanwei City due to the significant threat posed by these hazards.
3. Research Methods
3.1. Certainty Factors Methods (CF)
The certainty factor (CF) model is a bivariate statistical analysis probability function that can be used to assess the sensitivity of geohazard occurrence for each causative factor. The model assumes that future geohazard events will occur under the same working conditions as past geohazard events. The calculation formula for the model is:
where ‘’ represents the conditional probability of a geological hazard occurring in the evaluation factor classification level ‘a’. It is typically calculated as the ratio of the number of geological hazard points in level ‘a’ to the ratio of the area of the study area occupied by level ‘a’. ‘’ represents the prior probability of the event occurring in all data. It is expressed as the ratio of the number of geohazard sites in the whole study area to the area of the whole study area.
The CF model assigns values within the range of −1 to 1, with a positive value closer to 1 indicating a higher predictability of geohazard occurrence. This signifies that the specific influence factor contributes significantly to the susceptibility of geohazards [8]. A negative value nearing −1 implies a lower level of certainty regarding the occurrence of geohazards, indicating a reduced likelihood of geological hazards under the influence of the specific factor. When the result approaches zero, it indicates that the impact of this factor on geohazard susceptibility cannot be definitively determined [9].
3.2. Information Methods (I)
Information methods for geological hazard susceptibility assessment are based on information theory. The methods were first applied to landslide prediction by Yan Guozhen and later expanded to include other geological hazards [10]. The underlying logic of these methods is to convert the measured values of impact factors reflecting the occurrence of geological hazards into informative values that serve as quantitative indicators for vulnerability zoning. The information value of each evaluation factor is calculated by combining the geological hazard point data with the raster layer of each evaluation factor in the study area. The information quantity values of each layer are combined using the raster calculator within the ArcGIS platform to derive the evaluation result of geological hazard susceptibility for the study area. A higher information value indicates a greater susceptibility to geological hazards, and it is calculated using the formula:
where ‘I(,H)’ represents the information value provided by the evaluation factor ‘’ concerning the occurrence of geohazards, which reflects the likelihood of geohazards. A larger I value indicates a higher probability of occurrence. ‘S’ denotes the total area of the evaluation unit within the study area, ‘’ is the area of the cell occupied by the evaluation factor ‘’ in the study area, ‘N’ refers to the total number of geological hazard units in the study area, and ‘’ represents the number of geohazard units containing the evaluation factor ‘’ in the study area.
3.3. Logistic Regression Model (LR)
The logistic model is a commonly employed statistical analysis model for binomial dependent variables. It is used to describe the relationship between the occurrence of a geological hazard, where 0 represents no geological hazard and 1 represents occurrence, and it has multiple independent variables (,…) [11]. In the logistic model, the independent variable is the CF value (or information value) for each evaluation factor grading index. This value can be continuous or discrete and does not need to satisfy a normal frequency distribution [7]. The functional expression of the model is:
Formula (3) describes the logistic model: ‘P’ represents the probability of geohazard occurrence, ranging from 0 to 1, where 0 indicates that a geohazard cannot occur, while 1 indicates that it will occur. ‘n’ represents the number of evaluation factors, ‘’ is the logistic regression coefficient, and ‘’ represents the deterministic coefficient value (or information value) for each evaluation factor.
3.4. Certainty Factors–Logistic Regression Model (CF+LR)
The CF values obtained from Equation (1) for various levels of each evaluation factor are used as independent variables in the CF-LR model. These CF values are employed as input for the binary logistic regression analysis model in the SPSS 25.0 software, facilitating the calculation of logistic regression coefficients for each evaluation factor. To determine the weights of the evaluation factors, factors with high covariance are eliminated [12]. By substituting the obtained values from the logistic regression analysis into Equation (3) using the corresponding deterministic coefficient values, the susceptibility evaluation results of the CF-LR model can be obtained.
3.5. Informativeness–Logistic Regression Model (I+LR)
Similarly, Equation (2) enables the calculation of informativeness values for various levels of each evaluation factor. These computed informativeness values serve as the independent variables for the I-LR model. Using SPSS 25.0 software, each factor’s information value is substituted, and logistic regression analysis is conducted to obtain logistic regression coefficients. After conducting a correlation analysis of the evaluation factors, those exhibiting high correlation are excluded from further consideration. The aforementioned procedure is then repeated to determine the weights assigned to each remaining evaluation factor. By integrating the information quantity values with the logistic regression coefficients through Equation (3), the I-LR model for geohazard susceptibility evaluation can be successfully implemented.
4. Susceptibility Evaluation
4.1. Selection and Grading of the Evaluation Factor
The selection of evaluation factors and models represents two critical steps in assessing the susceptibility of slope rock and soil mass movement geological hazards. These steps directly impact the scientific accuracy and feasibility of the evaluation results [13]. When choosing factors for evaluating the susceptibility of slope rock and soil mass movement geological hazards, it is important to consider field survey information and select appropriate evaluation factors accordingly [14]. Informed by prior research and the field investigation data from the study area, this paper primarily examines the natural influencing factors, such as geological conditions and geographical environment in the study area, and selects elevation, slope, aspect, NDVI, stratigraphic lithology, distance from faults, distance from rivers, and distance from roads as evaluation indices for geological hazard susceptibility. Taking into account the spatial and temporal evolution characteristics and hazard-causing mechanisms of geological hazards, the classification results are depicted in Figure 2.
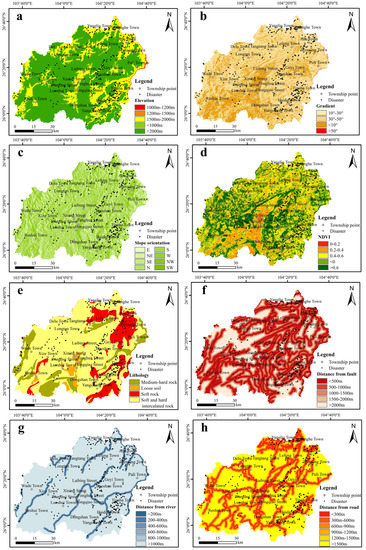
Figure 2.
Evaluation factors grading chart. (a) is the grading map of the evaluation factor ‘Elevation’; (b) is the grading map of the evaluation factor ‘Gradient’; (c) is the grading map of the evaluation factor ‘Slope orientation’; (d) is the grading map of the evaluation factor ‘NDVI’; (e) is the grading map of the evaluation factor ‘Lithology’; (f) is the grading map of the evaluation factor ‘The proximity to faults’; (g) is the grading map of the evaluation factor ‘Distance from rivers’; (h) is the grading map of the evaluation factor ‘Distance from roads’.
- (1)
- Elevation: Elevation represents the macroscopic landform within a specific area. Numerous research findings indicate that geological hazard occurrence and elevation distribution exhibit significant regional patterns [15]. Simultaneously, elevation largely determines the movement potential energy of the hazard body. As the elevation increases, the dynamic potential energy accumulated post-sliding also increases, leading to a greater impact on the hazard-prone area and more significant losses as a result. Considering the spatial distribution characteristics of geological hazard points and elevation in the study area, elevation is divided into five grades: <1000 m, 1000 m–1200 m, 1200 m–1500 m, 1500 m–2000 m, and >2000 m (Figure 2a).
- (2)
- Gradient: In the study area, the slope magnitude is intimately connected to the extent of geological hazards. The displacement and impact force of the hazard body largely depends on the slope size. Moreover, the slope factor significantly controls the formation mechanism of geological hazards and the critical point of anti-slipping for the sliding body. The slope of the study area is divided into four grades: <10°, 10°–30°, 30°–50°, and >50° (Figure 2b).
- (3)
- Slope orientation: When vegetation coverage is equal, the sunny slope exhibits ample water and heat, leading to the saturation of internal water within the rock mass. This saturation, coupled with water infiltration, results in lower initiation conditions for geological hazards, increasing the likelihood of their occurrence [16]. Utilizing the surface analysis function of ArcGIS 10.2 software, the slope aspect information of the study area was extracted from the DEM data, and it was divided into north, northeast, east, southeast, south, southwest, west, and northwest (Figure 2c).
- (4)
- Normalized difference vegetation index (NDVI): Vegetation serves the functions of slope protection, stabilization, and soil conservation, which contribute to slope stability [17]. In general, areas characterized by high vegetation coverage tend to experience less severe development of geological hazards. The robust root systems of vegetation exert substantial tension on the slope, effectively anchoring it and increasing its resistance to the formation of sliding zones caused by the infiltration of rainwater. In this study, the normalized vegetation index in the study area is divided into five categories: <0, 0–0.2, 0.2–0.4, 0.4–0.6, and >0.6 (Figure 2d).
- (5)
- Lithology: Lithology reflects the physical and chemical properties of the minerals that compose the rock mass. During the evaluation of geological hazard susceptibility, the chemical properties primarily manifest through the chemical reactions occurring between minerals within the rock mass and other factors such as water, atmospheric rainfall, fertilizers, and so on. These reactions lead to a reduction in the original strength of the rock mass. The physical properties are more evident in the structure, mechanical properties, and engineering geological properties of the mineral itself. The lithology of the study area is divided into four categories: loose soil, soft rock, soft and hard interbedded rock, and medium hard rock (Figure 2e).
- (6)
- The proximity to faults: Geological hazards tend to transpire in regions with active fault structures, and a close correlation exists between the two. Specifically, in the intersecting zones of regional fault structures, the rock tends to be more fragmented, creating a structural environment conducive to the formation and progression of geological hazards [18]. Based on the 1:50,000 geological map of the study area, fault belt information is extracted using the ArcGIS platform, and a 500 m interval buffer zone is established. The study area’s distance from faults is divided into five categories: <500 m, 500 m–1000 m, 1000 m–1500 m, 1500 m–2000 m, and >2000 m (Figure 2f).
- (7)
- Distance from rivers: Rivers alter surface morphology and constitute a major cause of geological hazards. Rivers exert an erosive effect on the slopes on both sides. Under the cyclic erosion of hydrodynamics, slopes can easily form an empty face, causing the gravity of the upper rock mass to exceed the critical tension it can withstand and thus triggering geological hazards. Based on the distribution characteristics of the water system and geological hazards in the study area, the distance from rivers is divided into six grades: <200 m, 200 m–400 m, 400 m–600 m, 600 m–800 m, 800 m–1000 m, and >1000 m (Figure 2g).
- (8)
- Distance from roads: Roads represent the impact of human engineering activities on rock and soil. During the construction of essential projects, excavating mountains and cutting slopes are inevitable processes. Consequently, the occurrence of vibrations and disturbances can create voids within rock and soil masses, facilitating water infiltration and altering their natural stress state. This modification subsequently reduces cohesion and internal friction angle of these masses. As a result, the sliding body is more prone to surpass the equilibrium state. Based on the vector data of the main roads in the study area, this paper establishes a buffer zone with 300 m as a segment in ArcGIS 10.2 software and divides the distance from roads into six categories of 1500 m (Figure 2h).
4.2. Evaluation Model
(1) Calculation of CF and I value
The evaluation factor layers were transformed into grid layers and reclassified according to their respective classifications. The number of hazard points and the area of each classification were then counted to determine the CF and I values for each evaluation factor level using Equations (1) and (2), as presented in Table 1. The CF and I values not only demonstrate the relative significance of different grades within the same evaluation factor but also show the contribution rate of each evaluation index in geological hazards.

Table 1.
Calculation results for information value and CF value across various evaluation factor classification levels.
The CF value characterizes the certainty of geological hazards objectively and fairly. The closer the CF value is to 1, the higher the probability of geological hazards. Based on the results in Table 1, it can be concluded that areas with elevations of <1000 m and 1000 m–1200 m have the lowest certainty of geological hazards, and geological hazards are less likely to occur. A gradient exceeding 50° is associated with a high certainty coefficient, indicating a substantial likelihood of geological hazards. Nevertheless, the precise influence of the northeast, east, and south directions on the occurrence of geological hazards cannot be accurately determined, whereas the certainty regarding geological hazards in the southwest and west is relatively low. Furthermore, areas with denser vegetation demonstrate lower susceptibility to geological hazards. The occurrence of geological hazards is more prominent in proximity to fault zones, with the number of geological hazard occurrences decreasing as the distance from the fault zone increases. Additionally, soft rock mass areas are more prone to experiencing geological hazards. The CF value is highest within the range of 200 m–400 m from the water system, indicating a higher likelihood of geological hazards in this particular environment. The influence of distance from the road on geological hazards is inversely proportional to some extent, suggesting that greater distance from roads is associated with lower susceptibility to hazards. However, it is important to note that the general slope and hazard distribution pattern observed in this study differs from previous research. The discrepancy can be attributed to several factors, including the inadequate accuracy of geological hazard record data, errors in the information extracted through the ArcGIS multi-value extraction to point tool during operation, and the presence of high-quality vegetation growth in landforms with slopes ranging between 30° and 50°. The robust vegetation growth positively contributes to slope reinforcement and protection, thereby reducing the likelihood of geological hazards. When the slope is >50°, the vegetation is sparse, which weakens the ability of the surface cover to fix itself, and the tensile stress of the landslide is increased, making geological hazards more likely to occur.
The degree of influence of evaluation factors on the susceptibility of slope rock and soil mass movement geological hazards is reflected by the information quantity of observed values of geological hazards in the study area. The larger the information variable of evaluation factors, the more prone to geological hazards under the action of this factor. Based on the analysis of the calculation results of the information value, it can be concluded that geological hazards often occur in the 1500 m–2000 m altitude range, and when the slope is >50°, the information value is the largest, indicating a high probability of hazards. The northwest slope is prone to geological hazards due to the influence of the natural environment (climate, sunshine, precipitation, etc.). Vegetation coverage is negatively correlated with the probability of geological hazards. Soft rock masses serve as the foundation and material source for developing geological hazards. The impact of faults, rivers, and roads on geological hazards demonstrates a certain degree of correlation. Within a specific distance, these three evaluation factors contribute to the promotion of geological hazard occurrences.
(2) Weight calculation
The logistic regression analysis was conducted using the SPSS 25.0 software. A total of 660 sample points were selected, consisting of 330 points representing geological hazards and 330 points representing non-geological hazards. The occurrence of geological hazards was treated as the dependent variable, with a value of 1 indicating occurrence and 0 indicating non-occurrence. The independent variables were the CF, and I values corresponding to each classification level of the evaluation factors. The logistic regression coefficient (β) value and significance (Sig.) value were obtained through binary logistic regression analysis in SPSS 25.0 software (Table 2), using a stepwise backward calculation method based on the partial likelihood ratio test results to eliminate variables [19]. Typically, if the Sig. value is greater than 0.05, it suggests that there is collinearity between the evaluation factor and other evaluation factors, necessitating collinearity diagnosis. In the collinearity diagnosis table (Table 3), a larger conditional index implies more significant collinearity with other evaluation factors. It is generally considered that multi-collinearity exists when the conditional index exceeds 10 [20], requiring a comprehensive assessment of the intrinsic relationship between the evaluation factor and other predisposing factors for hazards and the elimination of highly correlated evaluation factors. This process is repeated until all Sig. values of the evaluation factors are less than 0.05 (Table 4), indicating that the model is reasonable and accurate, with the corresponding β value representing the weight of the evaluation factor. In the CF model (Table 2), the significance values of distance from the road, distance from the fault, slope direction, and distance from the river were all greater than 0.05, indicating their collinearity with other factors. The collinearity diagnosis results showed that the variance ratio of the seventh dimension from the road distance and the ninth dimension from the river distance were significantly larger. Consequently, the distance factor from the river was excluded from the analysis as roads and other human engineering activities in the study area primarily align with the river. Moreover, the aspect factor was disregarded due to its limited influence on the susceptibility of geological hazards in the study area. This decision was made considering the significant correlation observed between most geological hazards in the study area and the fault zone factor. In the information model (Table 2), the significance values of the distance from the river and slope factor exceeded 0.05, indicating significant collinearity effects with other evaluation factors. These two factors were eliminated, and the remaining factors were used as independent variables for binary logistic regression analysis.

Table 2.
Results of logistic regression analysis without removing covariate causative factors.

Table 3.
The results of evaluation factor covariance diagnosis.

Table 4.
Results of logistic regression analysis excluding covariate causative factors.
(3) CF-Logistic model
A functional relationship was established between the CF value and the β value obtained from logistic regression analysis. The model formula can be expressed as:
The formula above presents the probability of geological hazards, with a value range of [0~1]. ~ represent the evaluation factors: NDVI, distance from the road, distance from the fault, elevation, slope, and CF value of lithology.
(4) I-Logistic model
A model was developed based on the information value and the β value obtained from logistic regression analysis. The formula for the model is as follows:
In the above formula, is the probability of geological hazards, and the value range is [0~1]. ~ represent the evaluation indexes: NDVI, distance from the road, distance from the fault, elevation, gradient, and information value of lithology.
4.3. Evaluation Results and Verification
The weight and CF value of the CF-Logistic model were applied using Formula (4), and grid weighting superposition was performed utilizing the map algebra function on the ArcGIS platform. This process led to the final outcomes of susceptibility evaluation for the study area. Subsequently, the natural breakpoint method was employed to classify the evaluation results into four categories: extremely high-prone area, high-prone area, medium-prone area, and low-prone area. This categorization helps generate the geological hazard susceptibility zoning map for Xuanwei City based on the CF-Logistic model (Figure 3a). Similarly, the evaluation factor weight and information value of the CF-I model were utilized. The process was repeated using Formula (5) to produce the susceptibility zoning map for the study area based on the I-Logistic model (Figure 3b).
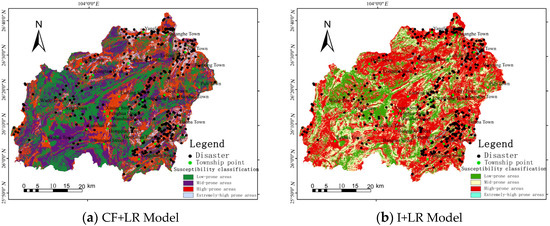
Figure 3.
Geological hazard susceptibility zoning map of the study area.
Through the comparison and analysis of the slope rock and soil mass movement geological hazard susceptibility zoning maps obtained from the two evaluation models (Figure 3a,b) and the statistical table presenting the area and number of hazard points for both models (Table 5), it is possible to ascertain the reasonability of the evaluation results from the two models. This comparison also facilitates an assessment of whether the models accurately and impartially depict the true susceptibility of slope rock and soil mass movement geological hazards in Xuanwei City. Table 5 reveals a notable contrast in the distribution of hazard points between the extremely high-prone and high-prone areas for both the CF-Logistic and I-Logistic models. A thorough analysis of the field survey data in the study area reveals that slope considerably impacts geological hazards in the extremely high-prone area. Alongside the analysis of the slope factor classification map (Figure 2b), it is concluded that when the slope ranges between 30° and 50°, the region’s geological hazards are extremely high-prone. Due to the high correlation between the slope factor and other evaluation factors, the I-Logistic model differs from the CF-Logistic model in the susceptibility evaluation of geological hazards in Xuanwei City, as it lacks the key evaluation factor of slope. Upon comparing Figure 3a,b, it becomes evident that the CF-Logistic model and the I-Logistic model exhibit similar spatial distributions of high-risk areas for geological hazards in the study area. However, discrepancies arise in the partitioned area of the I-Logistic model. The high susceptibility area is characterized by sunnier slopes, resulting in significant physical and chemical impacts, reduced vegetation coverage, elevated surface runoff coefficients, and intensified erosion. These factors have created favorable conditions for geological hazards. However, the CF-Logistic model does not consider aspect as an evaluation parameter; therefore, its final evaluation outcomes differ from those of the I-Logistic model.

Table 5.
Statistical table of the results of geological hazard susceptibility zoning in Xuanwei City.
The ROC curve is a prevalent method for verifying the accuracy of geological hazard-prone areas. The ROC curve provides a clear, intuitive, and accurate visualization of the relationship between the specificity and sensitivity of the evaluation model, effectively demonstrating its excellent test performance. As a result, it has been extensively employed in geological hazard susceptibility evaluations [21]. The AUC value of the ROC curve, representing the area under the curve, serves as a criterion for measuring the model’s performance. Its value range is [0.5~1], with a value closer to 1 indicating a more convex curve toward the upper left, which signifies higher model performance. In this study, the ArcGIS platform was employed to generate 99 new non-hazard point samples (30% of the non-hazard points) in the medium- and low-prone areas, according to the two models. The purpose of selecting non-hazard points in this manner was to prevent the misclassification of potential hazard points as non-hazard points, which could introduce errors to the model’s evaluation performance. Simultaneously, 99 hazard point samples were randomly chosen from the susceptibility zoning maps of the two models, resulting in a total of 198 sample points used for testing in this experiment. The normalized comprehensive information values of the two models were assigned to the respective test samples using the ArcGIS multi-value extraction to point function. The test sample data, carrying the information content, were then imported into SPSS 25.0 software to evaluate the performance of the model. As shown in Figure 4, the AUC value for the CF-Logistic model is 0.799, while the AUC value for the I-Logistic model is 0.772. These findings indicate that the CF-Logistic evaluation model demonstrates superior performance and yields more reasonable evaluation results. Therefore, it is better suited for assessing the susceptibility of geological hazards in Xuanwei City. The existing geological hazards in the study area are used to verify the performance of the CF-Logistic model. It is found that the model can well predict the susceptibility of geological hazards in Xuanwei City, and can be used as a scientific reference for hazard prevention and early warning, major project site selection, and land space planning in Xuanwei City (Figure 5).
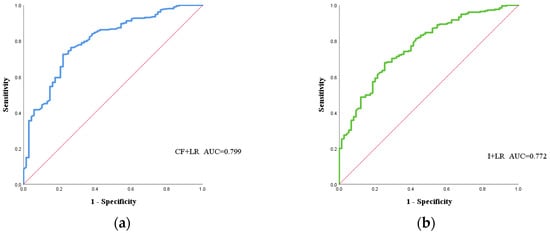
Figure 4.
ROC curve of each mode. (a) is the ROC curve of the ‘CF+LR’ model; (b) is the ROC curve of the ‘I+LR’ model. The red line indicates the reference line. The blue line represents the ROC curve of the ‘ CF+LR’ model. The green line represents the ROC curve of the ‘I+LR’ model.
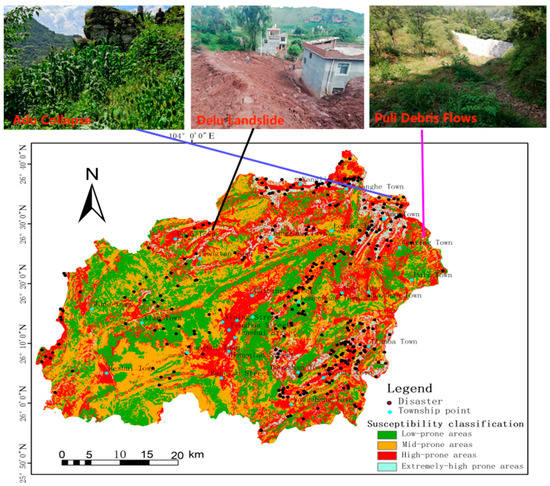
Figure 5.
Verification of field hazards.
5. Conclusions
- (1)
- This study concentrated on evaluating the susceptibility of slope rock and soil mass movement geological hazards in Xuanwei City. After examining the spatial distribution and development environment characteristics of existing geological hazards in the region, elevation, slope, aspect, NDVI, stratigraphic lithology, distance from faults, distance from rivers, and distance from roads were chosen as evaluation factors. The CF-Logistic evaluation model and I-Logistic evaluation model were employed to divide geological hazard susceptibility in Xuanwei City using the ArcGIS platform.
- (2)
- Based on the two coupling models, it was determined that NDVI, elevation, and distance from faults have a significant influence on geological hazard susceptibility in the study area. Particularly, when NDVI < 0, when the altitude ranges between 1500 and 2000 m, and when the distance from the fault is less than 500 m, the CF value, I value, and logistic regression coefficients of the three factors are relatively large. This implies that there is a high likelihood of slope rock and soil mass movement geological hazards occurring under these conditions. Therefore, areas with such environmental characteristics should be prioritized for significant attention and mitigation measures.
- (3)
- The areas with extremely high susceptibility to slope rock and soil mass movement geological hazards are primarily concentrated along road networks and densely populated regions. These areas exhibit a well-developed geological structure characterized by fragmented rock and significant influence from fault zones. High-prone areas are primarily situated near rivers and fault zones, featuring diverse terrains. Medium-prone areas are notably affected by recent tectonic movements, encompass a relatively well-developed surface water system, and possess complex geological environmental conditions. Low-prone areas are mainly distributed in the central, northeastern, and southwestern regions of Xuanwei City. The slope of these areas is mostly between 5° and 10°, hydrogeological conditions are relatively simple, and the hazard environment is not complicated.
- (4)
- The partition results of the two models are roughly similar in spatial distribution, and differences in the partition area arise due to slight variations in evaluation factors among different models. Overall, the evaluation results of the two models align with the distribution of existing geological hazards in the study area and offer valuable reference for geological hazard risk assessments, hazard prevention, and emergency work. The AUC values of the CF + Logistic model and the I + Logistic model are 0.799 and 0.772, respectively, indicating that both models meet the requirements for objective and scientific evaluations of geological hazards in Xuanwei City. The CF + Logistic model demonstrates higher evaluation performance.
- (5)
- The distribution of hazardous rock mass in the study area is extensive, and engineering treatment would require considerable economic investment. Currently, the most effective measures for prevention and control involve extensive observation and preparedness, coupled with enhanced rainfall monitoring and regulations on large-scale excavation to mitigate the impact of collapse hazards. Landslide hazards profoundly impact the safety of lives and property in the study area, and the collective relocation of affected communities presents both challenges and feasibility. Based on the findings of the susceptibility zoning for slope rock and soil mass movement geological hazards, it is crucial to implement suitable engineering control measures that are tailored to the local conditions. These measures aim to effectively manage areas that are susceptible to landslides. This includes formulating clear prevention and control policies for geological hazards during flood seasons, thereby reducing their impact on landslide hazards. Debris flow hazards mainly occur in deep valleys with steep terrain, fragmented rock, and heavy rainfall, causing severe damage to affected bodies. Planting trees in debris flow formation areas can help reduce soil erosion and control from the roots, employing blocking engineering measures in circulation areas can obstruct debris flow, and constructing sedimentation fields or drainage ditches in accumulation areas can prevent debris flow from impacting villages or blocking rivers.
6. Discussion and Prospect
6.1. Discussion
China is among the countries with the most severe global geological hazards, constituting a fundamental national condition. Conducting comprehensive surveys of hazard risks in countries and regions is an inevitable necessity and a requirement for high-quality economic and social development. The selection of evaluation methods, evaluation factors, and weight determination are critical components of the entire evaluation process. In the past, qualitative evaluation methods contained numerous subjective factors, and future-developed quantitative evaluation methods lacked thorough research on the correlation of evaluation factors. These considerations can impact the precision of the evaluation outcomes. The proposed approach of combining a single quantitative method with a logistic regression model addresses both the issue of high collinearity among factors in a single evaluation method and the limitation of the logistic regression model in quantifying the classification level of evaluation factors. By employing this approach, the evaluation results are rendered scientifically robust and trustworthy. In a study conducted by Wang et al. [22], the CF-LR model was utilized to assess the susceptibility of geological hazards in Chenggu County. The results revealed that the coupled evaluation model exhibited higher prediction accuracy compared to the single evaluation model. Similarly, Tu et al. [23] employed the CF-LR model to evaluate the susceptibility of geological hazards in Yanhe County. They found that the single evaluation method did not account for variations in the influence of evaluation factors on hazard susceptibility. To address this, the coupled LR method expressed the complex non-linear relationship between evaluation factors through linear regression, considering the weight of each factor to enhance prediction accuracy. In another study by Zhang et al. [24], the CF-LR model was combined to evaluate the susceptibility of geological hazards in Huangzhong County. The results demonstrated that the coupled model could effectively quantify complex multi-factor data within the same range and resolve collinearity issues between factors. In this study, the CF-LR model was applied to assess the susceptibility of geological hazards in Xuanwei City using a similar approach to the aforementioned literature. Comparative analysis of the evaluation results reveals that the coupled model adeptly combines the strengths of a single model, comprehensively considers the weight of each evaluation factor, and enhances the reliability of the results. Moreover, the coupled model can reflect the significance of each evaluation factor, enabling targeted measures for hazard prevention and control. The findings collectively indicate that the coupled model is well-suited for evaluating regional geological hazard susceptibility, providing valuable information and guidance for decision-makers to formulate effective strategies and measures for disaster prevention and mitigation. This contributes to a better understanding and management of geological disaster risks, leading to reduced losses and the safeguarding of lives and property. In this study, the following questions merit in-depth analysis: (1) In the CF-Logistic model, whether the inclusion of the highly correlated factor of distance from the road will directly impact the evaluation results. (2) The two models in this study reveal a high degree of collinearity between the river and other evaluation indicators. As the river serves as an external force transforming surface morphology, it is scientifically reasonable to eliminate this factor.
6.2. Prospect
Changes in location affect geological conditions, such as topography, geological structure, and stratigraphic lithology, which in turn influence the hazard mechanism of a region. Therefore, the evaluation model used for each region differs because of its unique characteristics. The accuracy of this evaluation model primarily depends on the quality, correlation, reliability, and representativeness of the input evaluation factor data. The selection of appropriate evaluation factors and models depends on the hazard-causing conditions of geological hazards in a region which can lead to more accurate prediction results that meet ideal requirements. In our forthcoming research, our objective is to investigate a series of quantitative evaluation models for assessing the susceptibility of slope rock and soil mass movement geological hazards. Through the utilization of machine learning algorithms, the model can autonomously and objectively select evaluation factors, minimizing the subjective influence of human factors on the model and accurately determining their weighting. This evaluation model is scientifically grounded, universally applicable, and can be applied to diverse hazard-prone areas characterized by similar hazard-prone characteristics in human habitation environments. It ensures a rigorous and impartial assessment process.
Author Contributions
All authors contributed to the study conception and design. Material preparation and data collection and analysis were performed by S.T., L.L., D.D., Y.S. and J.L. The first draft of the manuscript was written by S.Z. and all authors commented on previous versions of the manuscript. All authors read and approved the final version. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Science and Technology Innovation Team Program of Yunnan Province Education Department (Grant NO. CY22624109); the Graduate Tutor Team Program of Yunnan Province Education Department (Grant NO. CY22622205); the First Class University Program of Yunnan University (Grant NO. CY22624108).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The DEM and NDVI data are openly available in the geospatial data cloud platform at https://www.gscloud.cn/ (accessed on 12 May 2023). The disaster sites and geological data are from the Yunnan Provincial Bureau of Nonferrous Geology. They can be obtained from author Shaohan Zhang upon reasonable request. Water system and road data can be obtained from the National Catalogue Service for Geographic Information at https://www.webmap.cn/ (accessed on 12 May 2023).
Acknowledgments
Heartful thanks for the data provided by the 317 teams of Yunnan Provincial Bureau of Nonferrous Geology and thank you to all the teachers who worked hard on this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Q.; Guo, Y.; Li, W.; He, J.; Wu, Z. Predictive modeling of landslide hazards in Wen County, northwestern China based on information value, weights-of-evidence, and certainty factor. Geomat. Nat. Hazards Risk 2019, 10, 820–835. [Google Scholar] [CrossRef]
- Sun, Y.; Ge, Y.; Chen, X.; Zeng, L.; Liang, X. Risk assessment of debris flow along the northern line of the Sichuan-Tibet highway. Geomat. Nat. Hazards Risk 2023, 14, 2195531. [Google Scholar] [CrossRef]
- Kohno, M.; Higuchi, Y.; Ono, Y. Evaluating earthquake-induced widespread slope failure hazards using an AHP-GIS combination. Nat. Hazards 2023, 116, 1485–1512. [Google Scholar] [CrossRef]
- Riegel, R.P.; Alves, D.D.; Schmidt, B.C.; de Oliveira, G.G.; Haetinger, C.; Osório, D.M.M.; Rodrigues, M.A.S.; de Quevedo, D.M. Assessment of susceptibility to landslides through geographic information systems and the logistic regression model. Nat. Hazards 2020, 103, 497–511. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Fan, Z.; Gou, X.; Qin, M.; Fan, Q.; Yu, J.; Zhao, J. Information and logistic regression models based coupl-Ing analysis for susceptibility of geological hazards. J. Eng. Geol. 2018, 26, 340–347. [Google Scholar] [CrossRef]
- Luo, L.; Pei, X.; Huang, R.; Pei, Z.; Zhu, L. Landslide susceptibility assessment in Jiuzhaigou scenic area with GIS based on certainty factor and Logistic regression model. J. Eng. Geol. 2021, 29, 526–535. [Google Scholar] [CrossRef]
- Lin, W.; Yin, K.; Wang, N.; Xu, Y.; Guo, Z.; Li, Y. Landslide hazard assessment of rainfall-induced landslide based on the CF-SINMAP model: A case study from Wuling Mountain in Hunan Province, China. Nat. Hazards 2021, 106, 679–700. [Google Scholar] [CrossRef]
- Li, Y.; Mei, H.; Ren, X.; Hu, X.; Li, M. Geological Disaster Susceptibility Evaluation Based on Certainty Factor and Support Vector Machine. J. Geo-Inf. Sci. 2018, 12, 1701–1703. [Google Scholar] [CrossRef]
- Huang, R.; Xu, X.; Tang, C. Geoenvironmental Assessment and Geohazard Management; Science Press: Beijing, China, 2008. [Google Scholar]
- Xing, X.; Wu, C.; Li, J.; Li, X.; Zhang, L.; He, R. Susceptibility assessment for rainfall-induced landslides using a revised logistic regression method. Nat. Hazards 2021, 106, 97–117. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Moradi, H.R.; Aghda Fatemi, S.M. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances. Nat. Hazards 2013, 69, 749–779. [Google Scholar] [CrossRef]
- Zhao, X.; Tan, S.; Li, Y. Dongchuan district based on slope unit and combined empowerment method geological hazard risk evaluation. J. Yunnan Univ. Nat. Sci. Ed. 2021, 43, 299–300. [Google Scholar] [CrossRef]
- He, P.; Tong, L.; Guo, Z.; Liu, C.; Tu, J.; Wang, S.; Xu, J. Evaluation research on the landslide disaster liability in Zhada region of Tibet. Sci. Technol. Eng. 2016, 16, 193–200. [Google Scholar] [CrossRef]
- Tian, C.S.; Liu, X.L.; Wang, J. Geohazard susceptibility assessment based on CF model and Logistic Regression models in Guangdong. Hydrogeol. Eng. Geol. 2016, 43, 154–170. [Google Scholar] [CrossRef]
- Chen, L.; Li, L.; Wu, F.; Xu, Y. Evaluation of the geological hazard vulnerability in the Beiliu City based on GIS and information value model. Earth Environ. 2020, 48, 471–479. [Google Scholar] [CrossRef]
- Dong, L. Evaluation of Ecosystem Service Value and Its Driving Force Analysis Based on Landscape Pattern: Taking Chengdu Plain and Longmen Mountain Transition Zone as an Example. Ph.D. Thesis, Sichuan Normal University, Chengdu, China, 2017. [Google Scholar]
- Wang, Z.W.; Li, D.Y.; Wang, X.G. Zonation of landslide hazards based on weights of evidence model. Chin. J. Geotech. Eng. 2007, 29, 1268–1273. [Google Scholar]
- Wang, C.M.; Huang, J.; Li, Q.; Zhang, S. Evaluation of geological hazard vulnerability in Lyuliang City in Shanxi Province based on coupling of information content model and Logistic regression model. Water Resour. Hydropower Eng. 2019, 50, 132–138. [Google Scholar] [CrossRef]
- Zhang, X.D.; Liu, X.N.; Zhao, Z.P.; Wu, W.Z.; Liu, H.Y.; Zhang, Y.; Gao, Y.L. Comparative Study of Geological Hazards Susceptibility Assessment: Constraints from the Information Value + Logistic Regression Model and the CF +Logistic Regression Model. Geoscience 2018, 32, 608–609. [Google Scholar] [CrossRef]
- Du, Q.; Fan, W.; Li, K. Geohazard susceptibility assessment by using binary logical regression and information value model. J. Catastr. 2017, 32, 220–226. [Google Scholar]
- Wang, X.; Shi, Y.; Chen, H. Evaluation of geological hazard susceptibility based on certainty factorscoupling logistic regression. Bull. Surv. Mapp. 2022, 11, 112–117. [Google Scholar] [CrossRef]
- Tu, S.Y.; Zhang, Z.Y.; Fu, H.L.; Xu, S.G.; Deng, M.G.; He, L.C.; Liu, J.Y. Geological hazard susceptibility evaluation based onCF and CF-LR model. Chin. J. Geol. Hazard Control 2022, 2, 97–102. [Google Scholar] [CrossRef]
- Zhang, X.B.; Zhou, P.; Zhang, K.; Zhang, X.; Liu, B.S.; Deng, H. Evaluation method of geological hazard susceptibility: A case study on GIS and CF-Logistic regression model in Huangzhong, Oinghai. Sediment. Geol. Tethyan Geol. 2021, 2, 1–9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).