Fault-Tolerant Control Strategy for Hall Sensors in BLDC Motor Drive for Electric Vehicle Applications
Abstract
1. Introduction
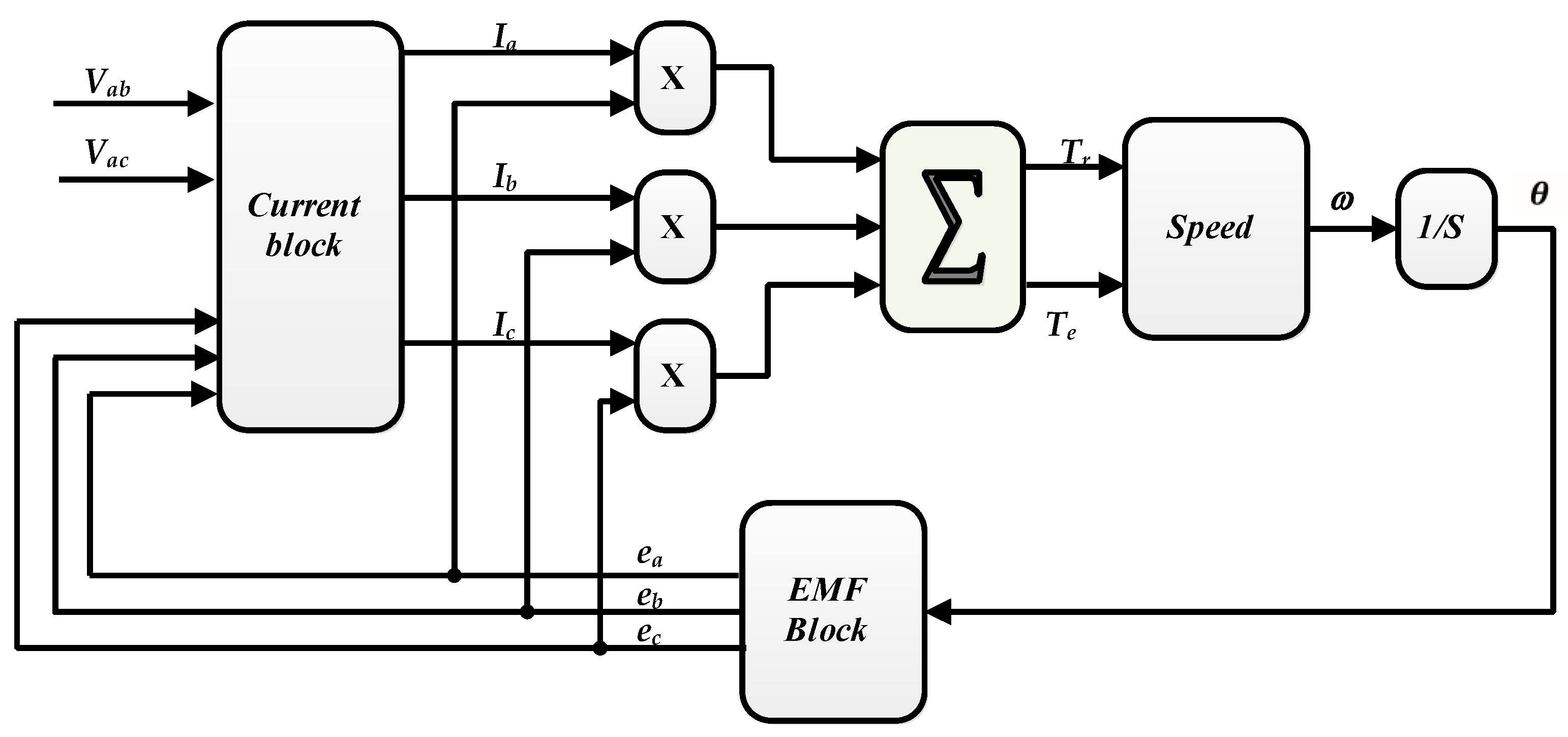
2. Electrical Traction System Design and Mathematical Model
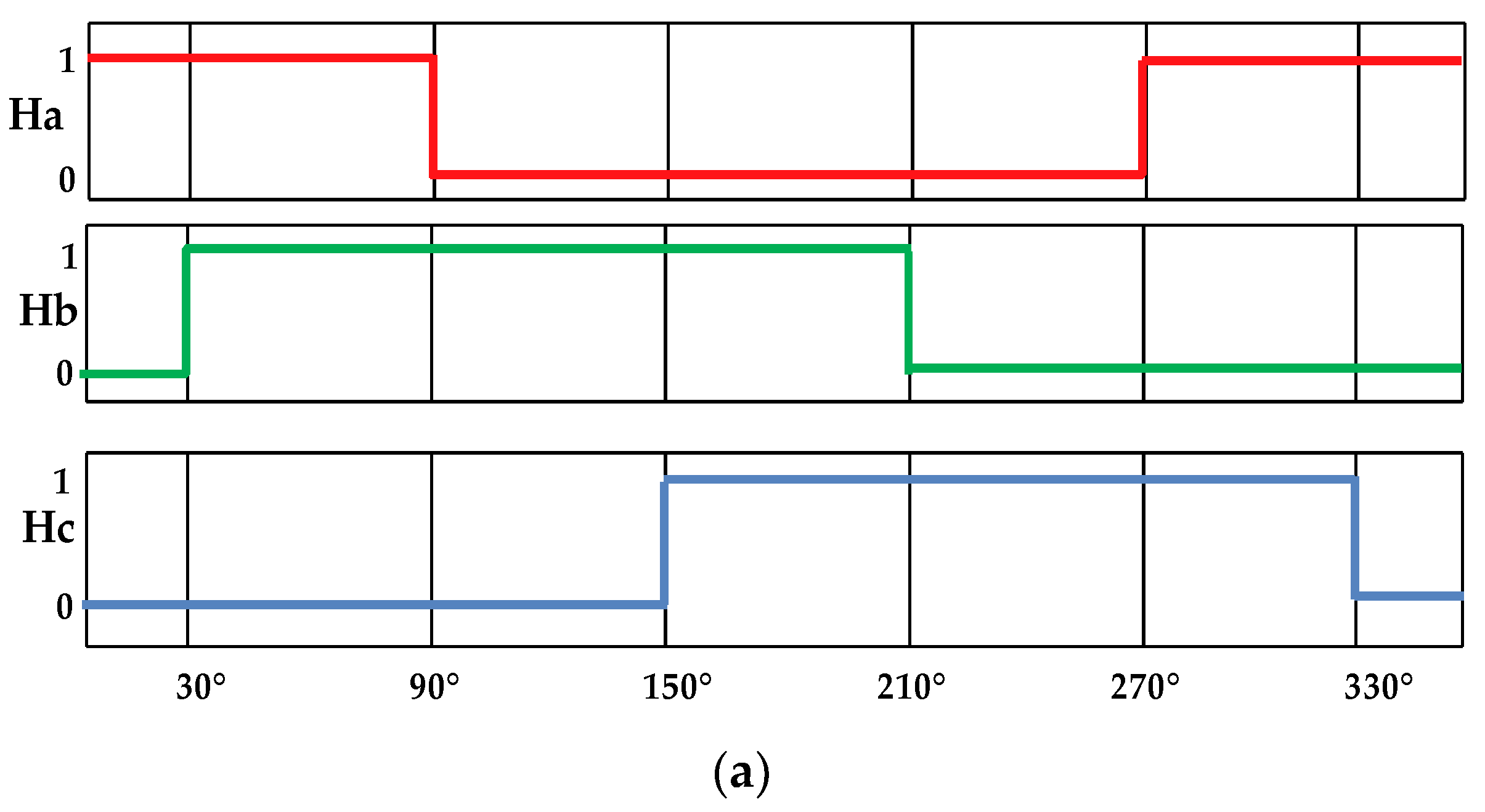
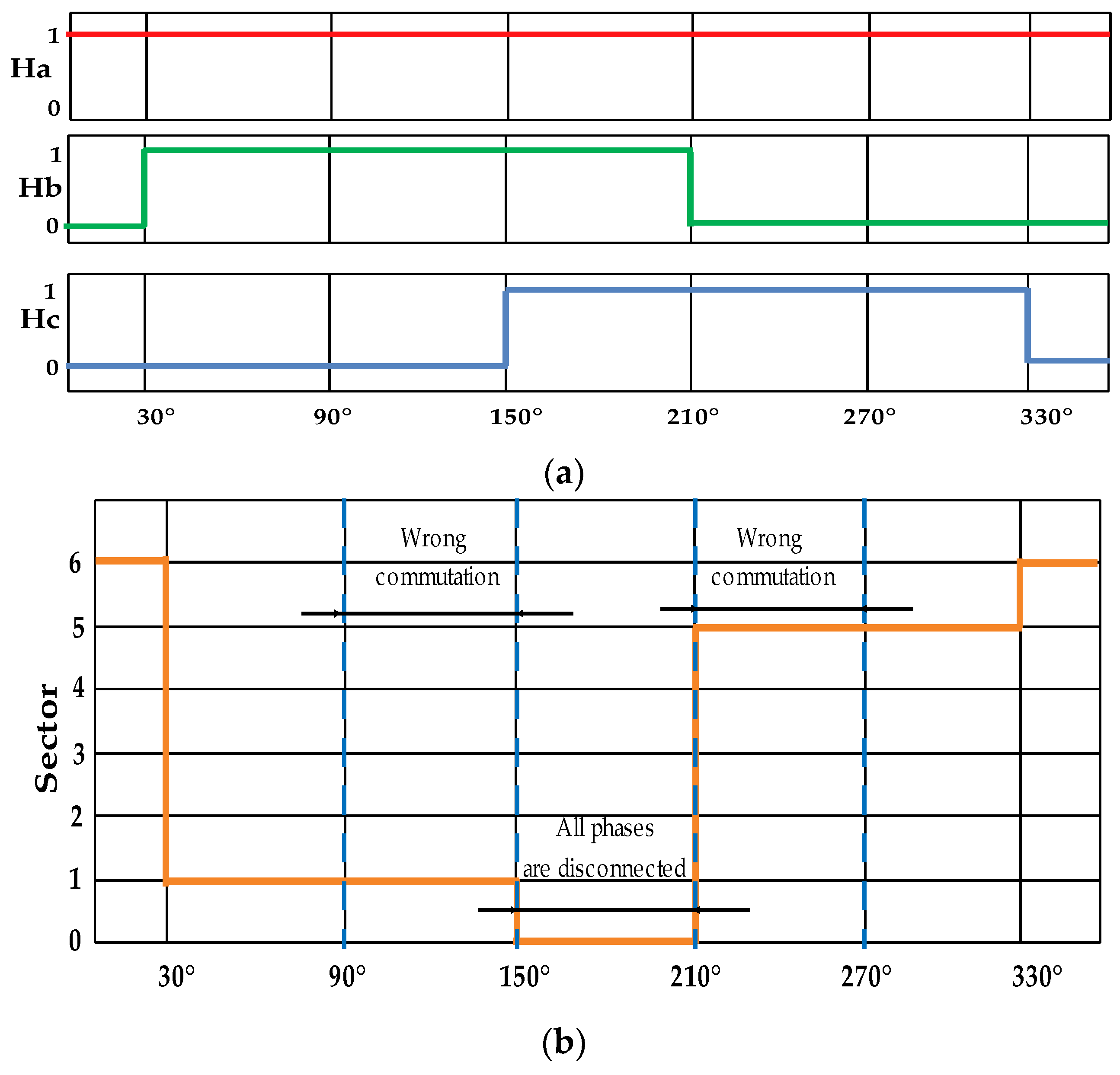
3. Ideal Hall Signal and Hall Sensor (HS) Fault Types
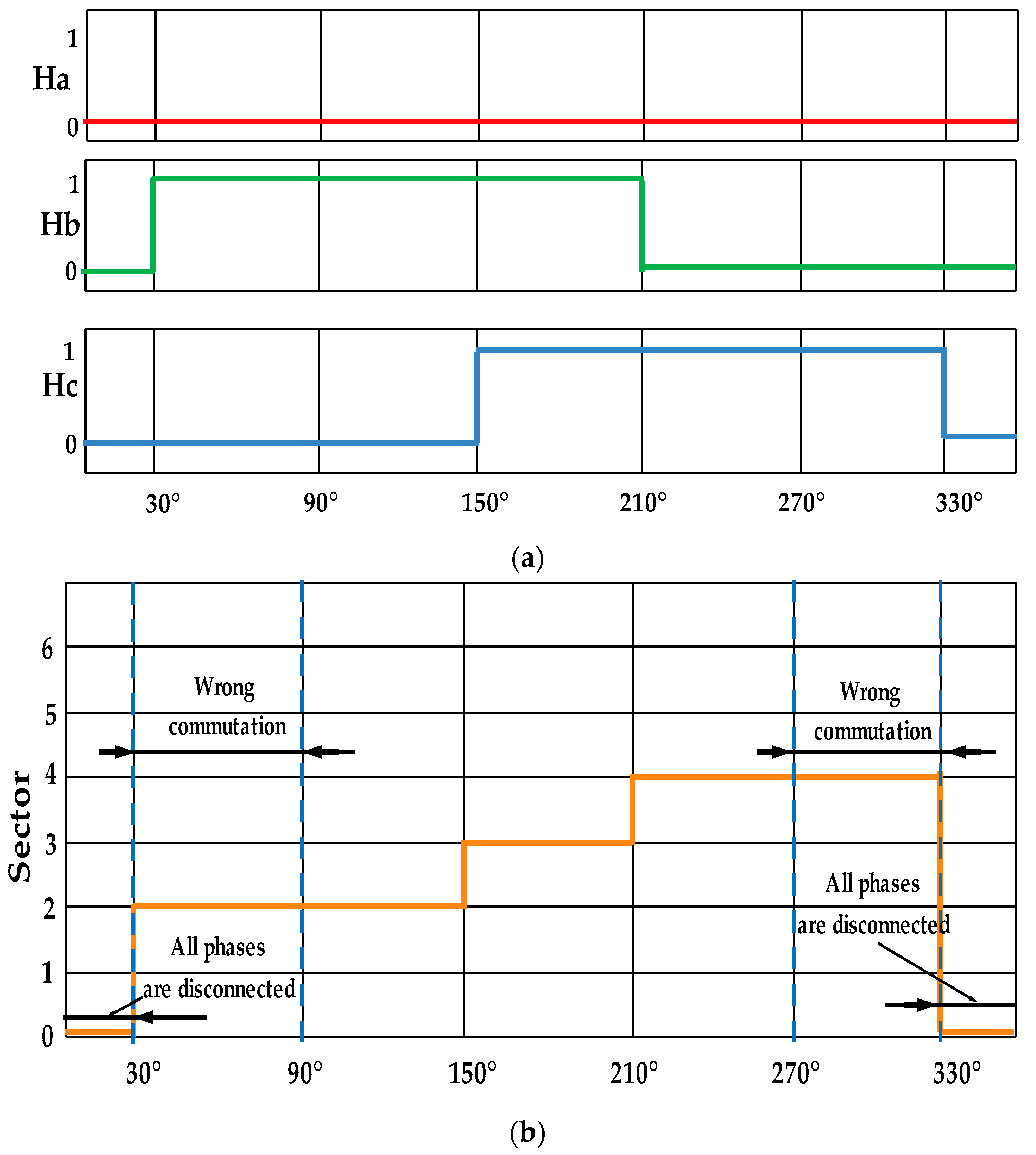
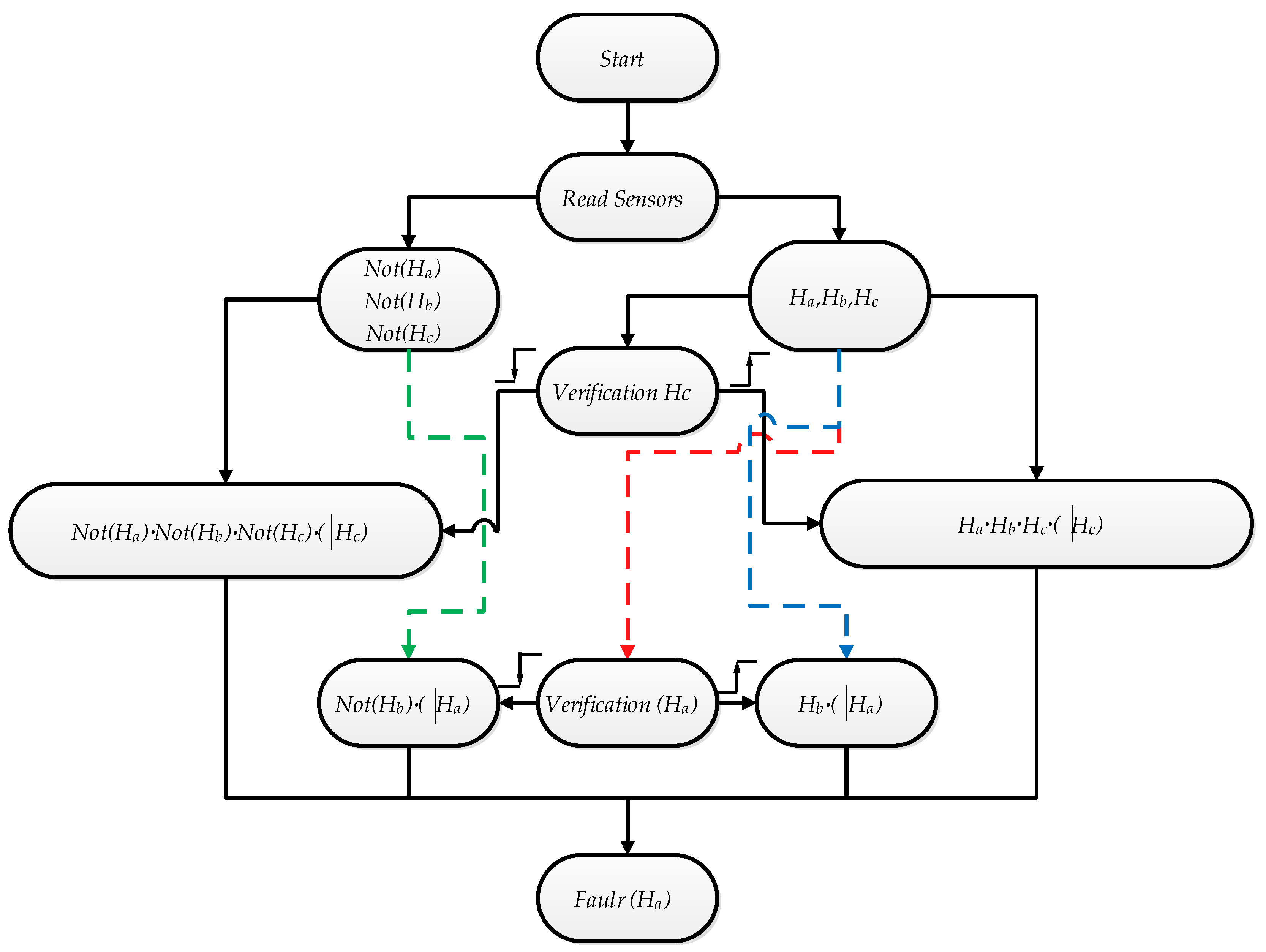
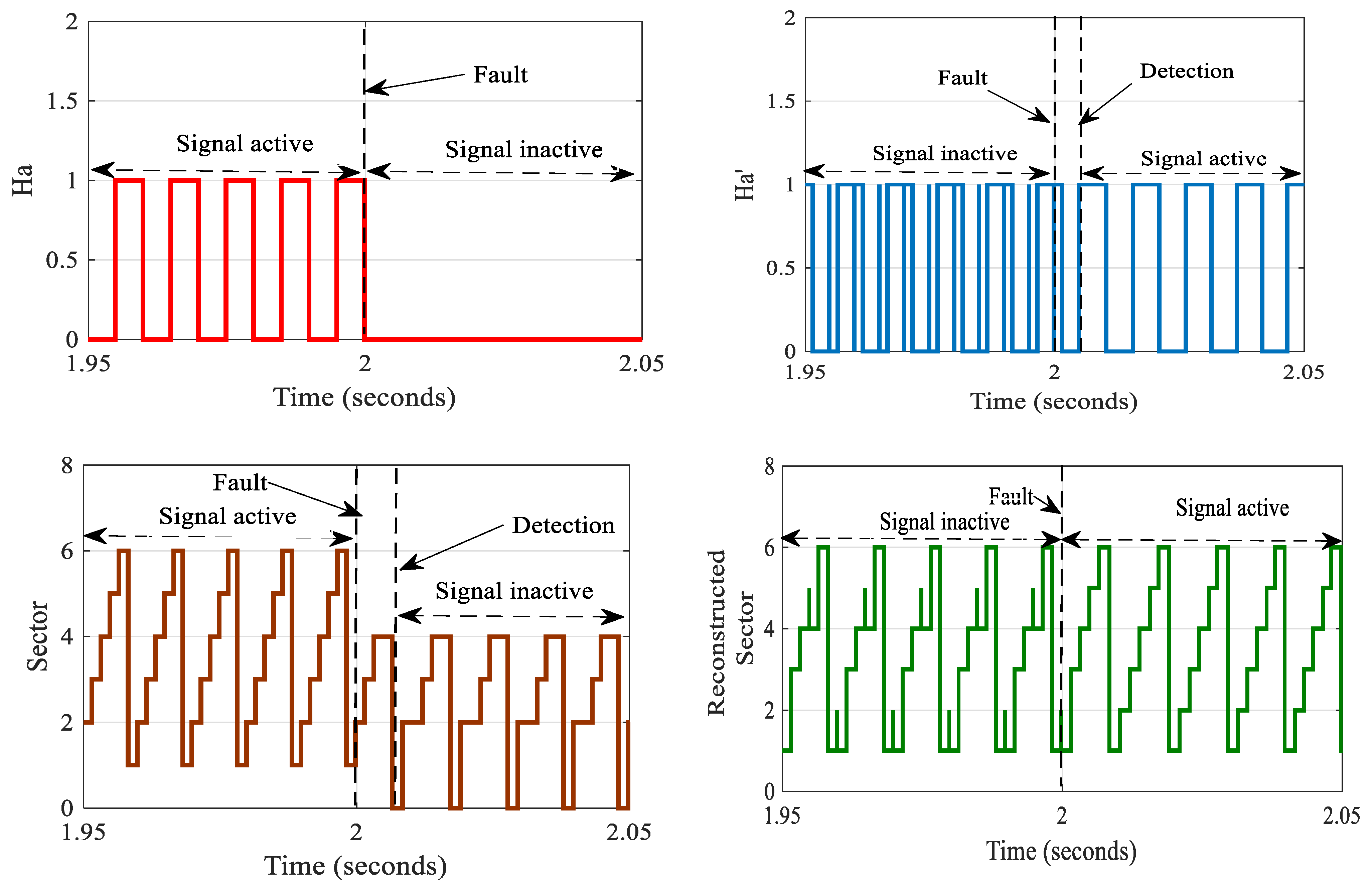
3.1. Fault Detection
3.2. Proposed Fault Diagnosis Method
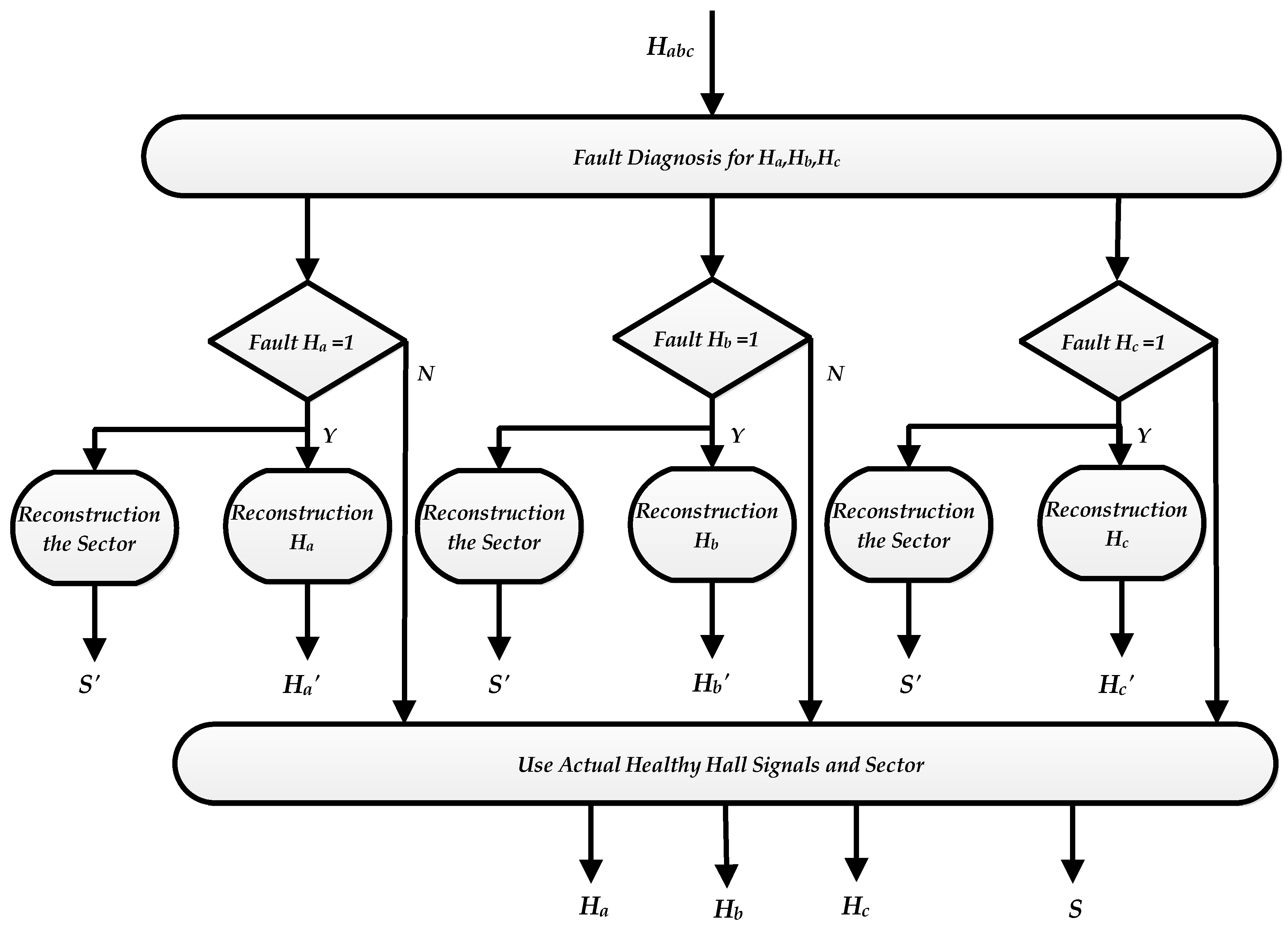
3.3. Signal Reconstruction
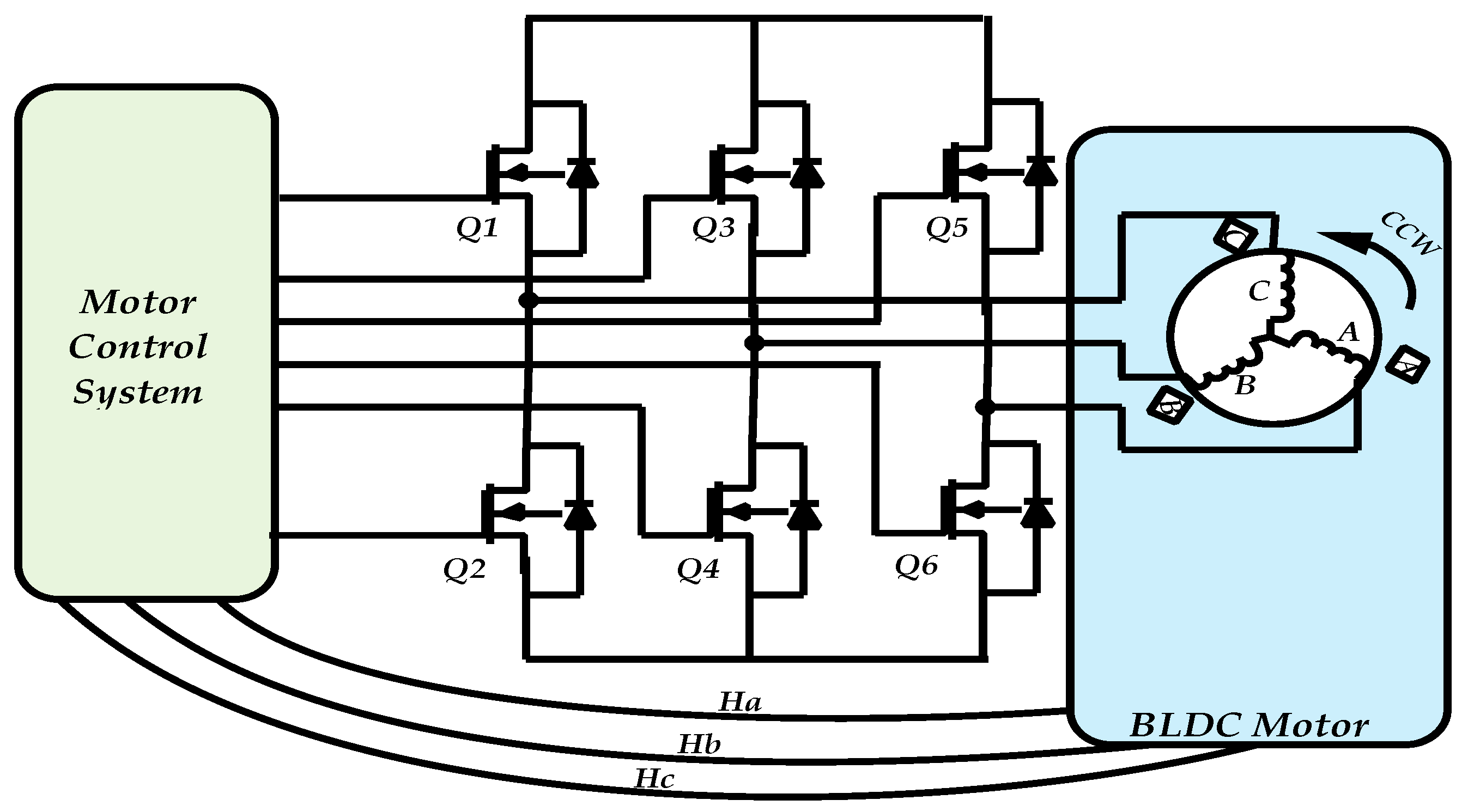
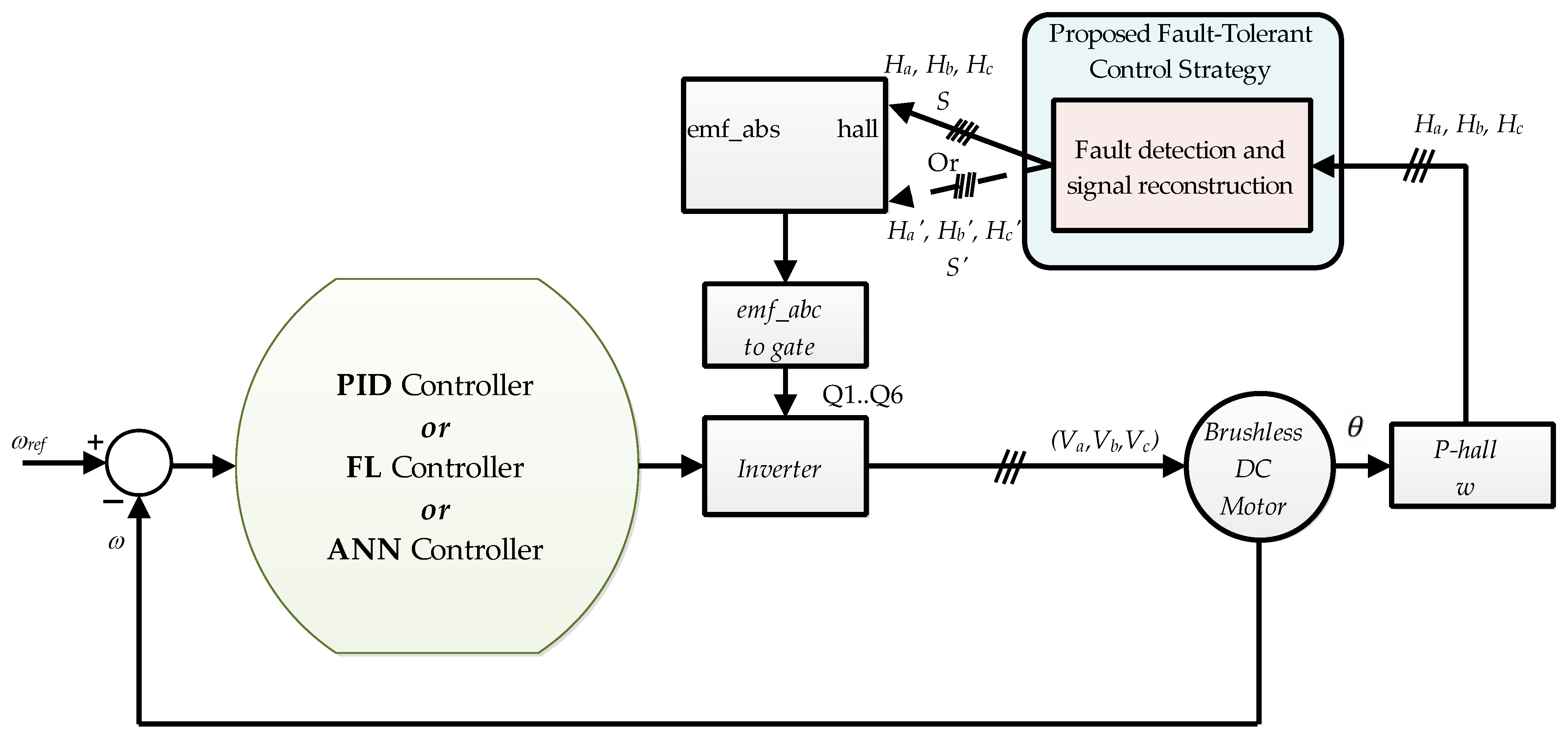
4. BLDC Motor Control Architecture
4.1. Proportional–Integral–Derivative Controller (PID)
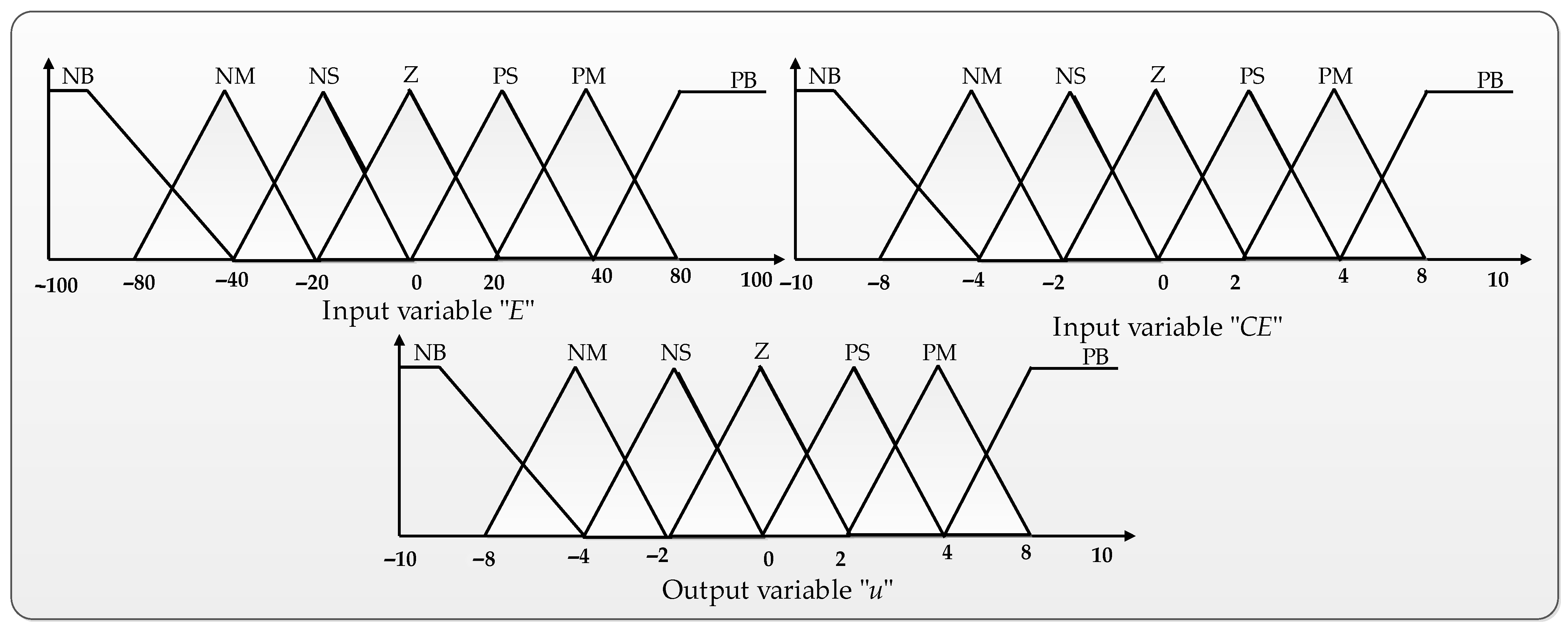
4.2. Fuzzy Logic Controller
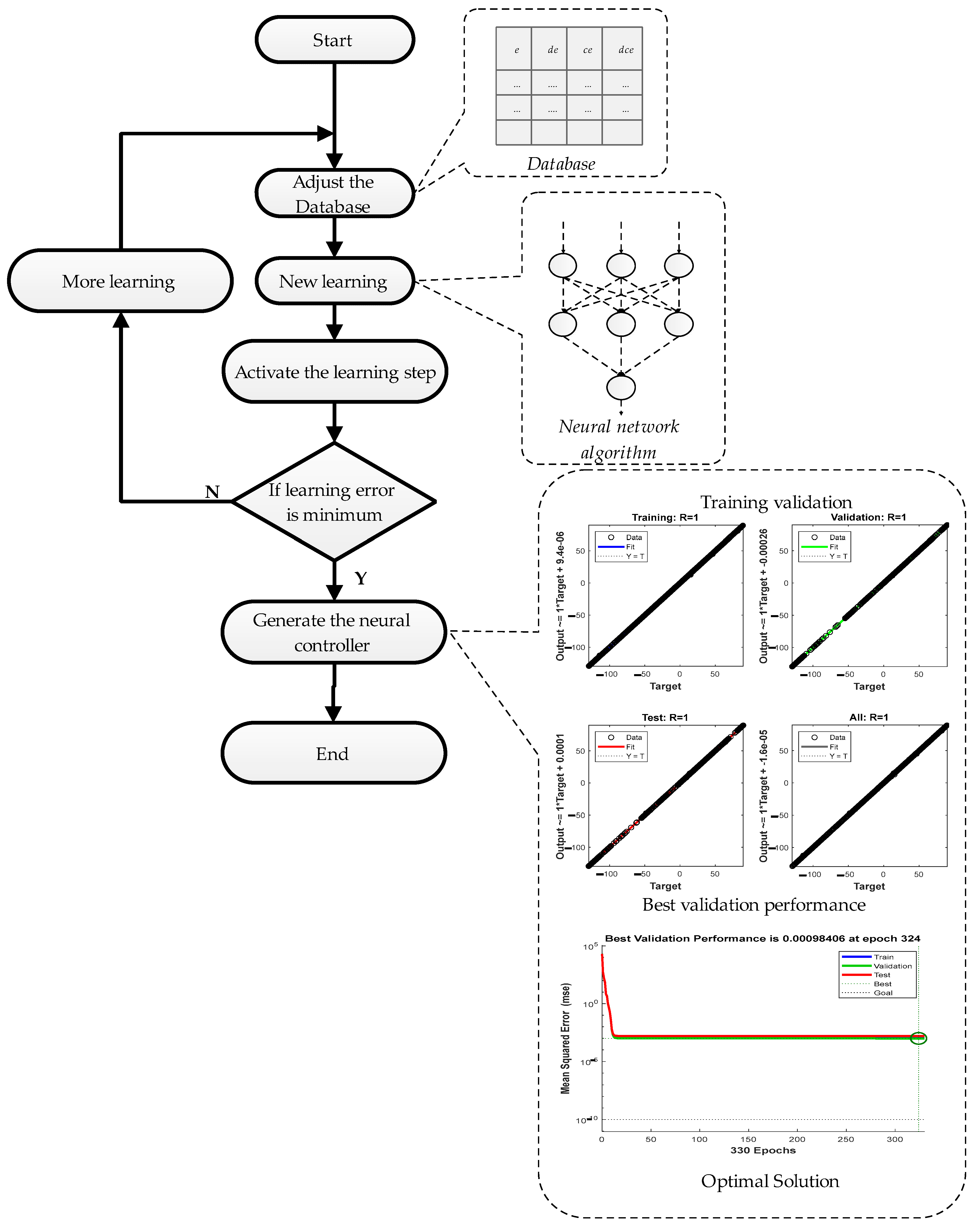
4.3. Neural Network Controller
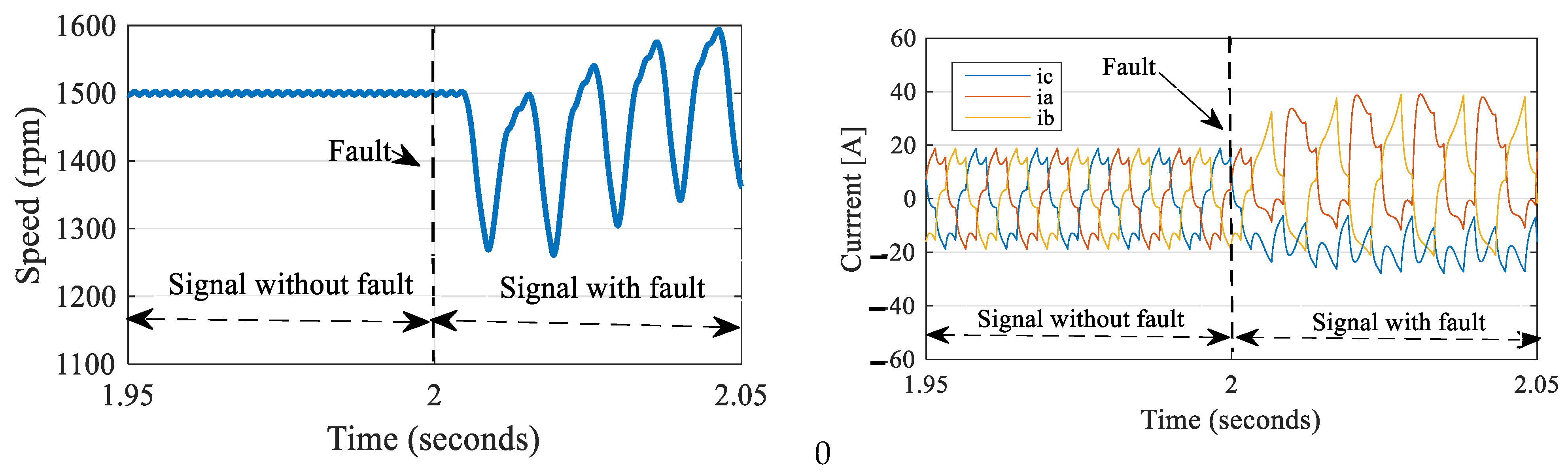
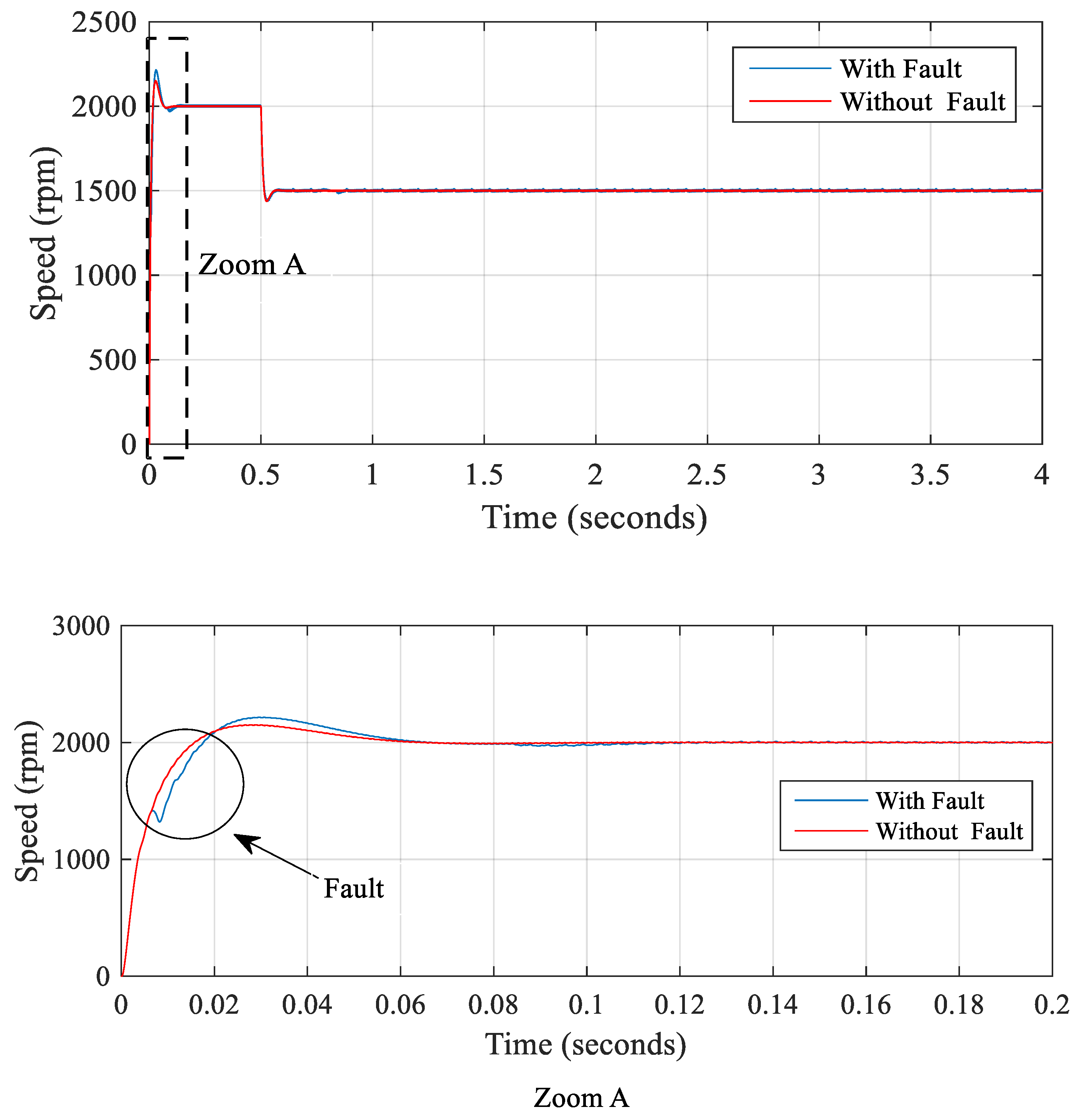
5. Discussion of Simulation Results
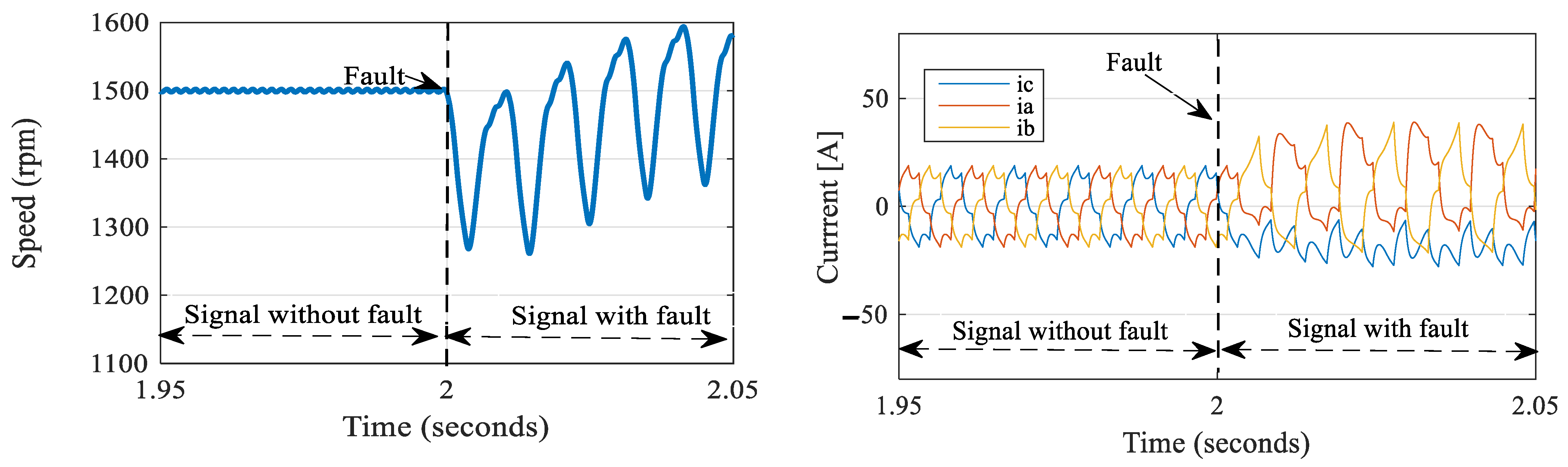
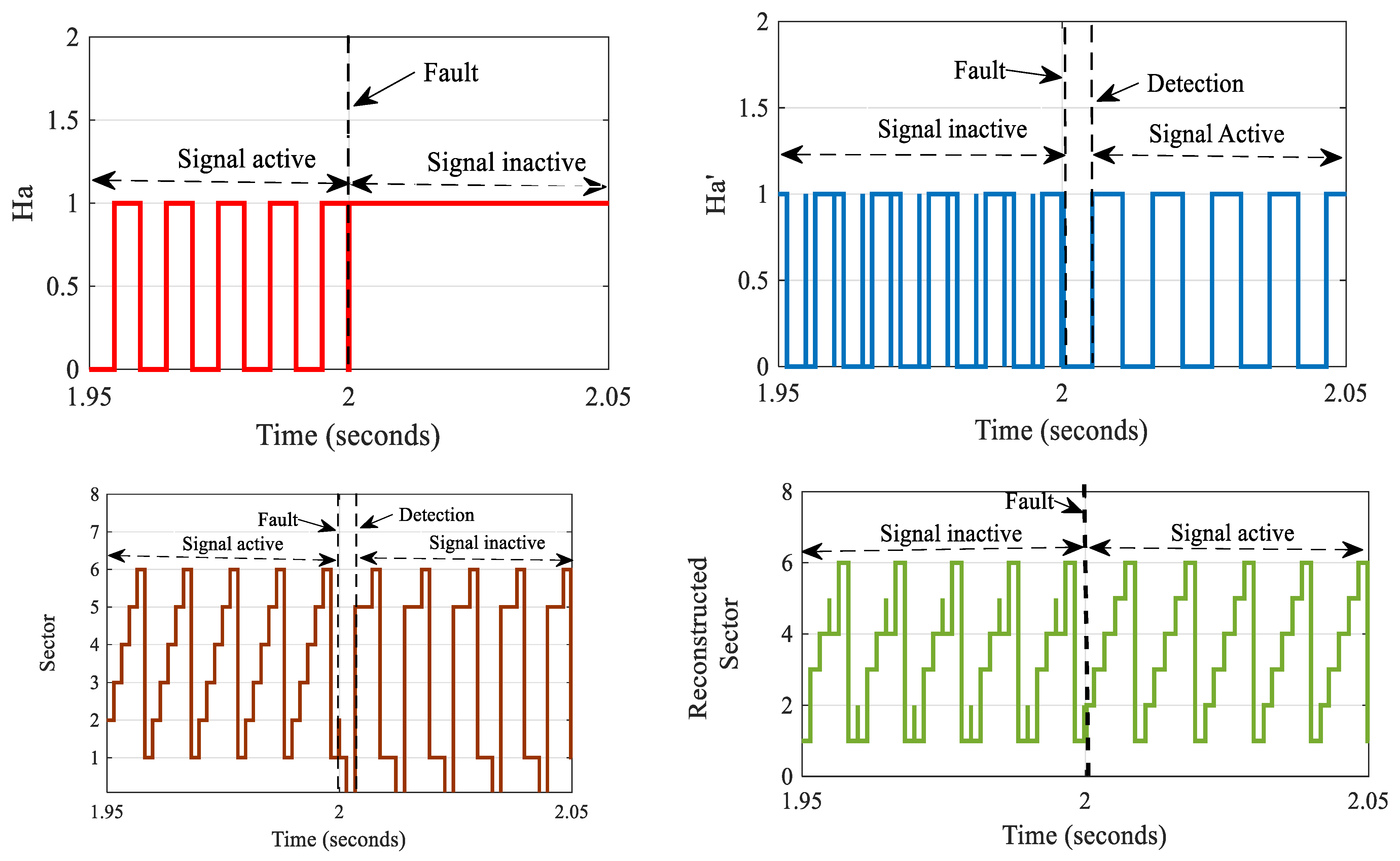
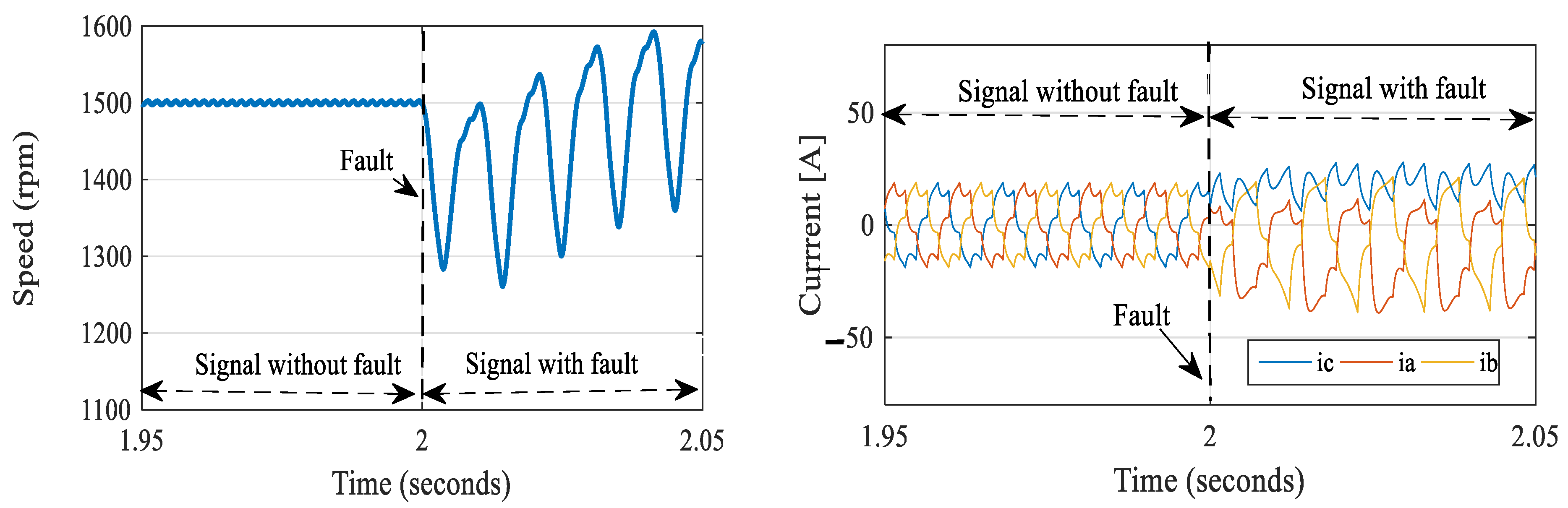
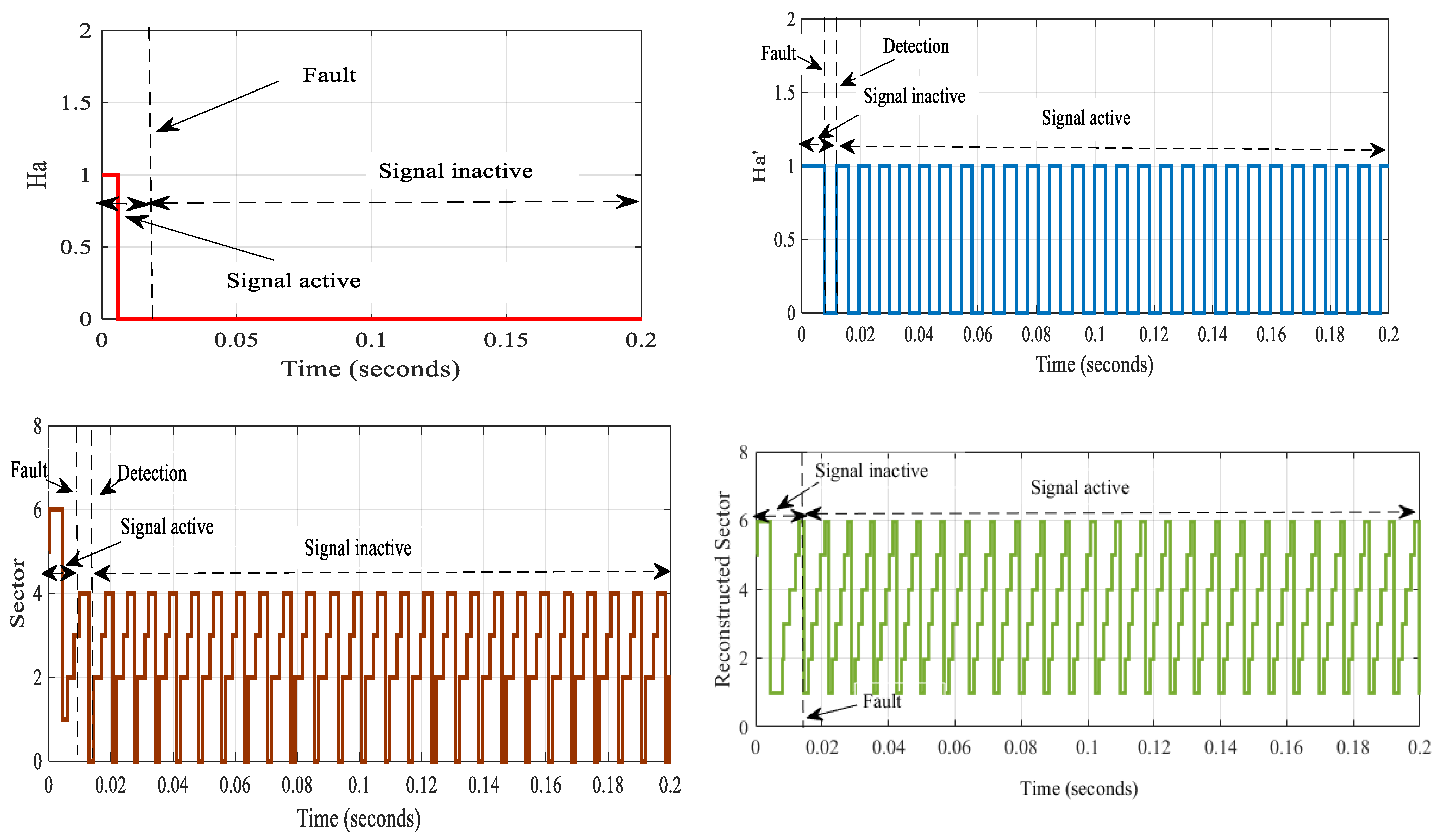
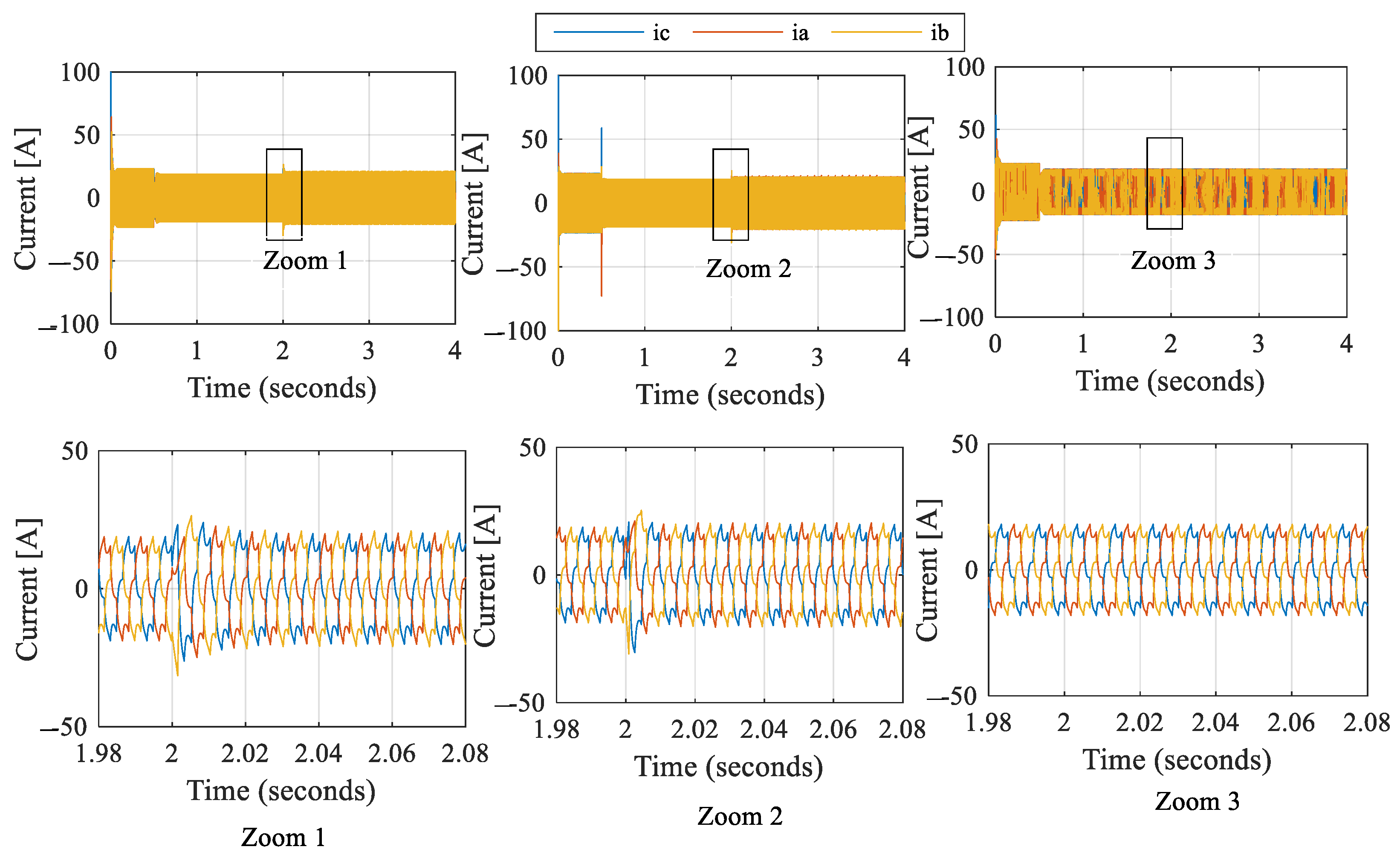
5.1. Signal Faults and Reconstructed Sector
- A.
- Case 1: In a Steady State:
- B.
- Case 2: In the Transient State:
5.2. Efficiency for the Proposed Speed Control with Fault-Tolerant Control
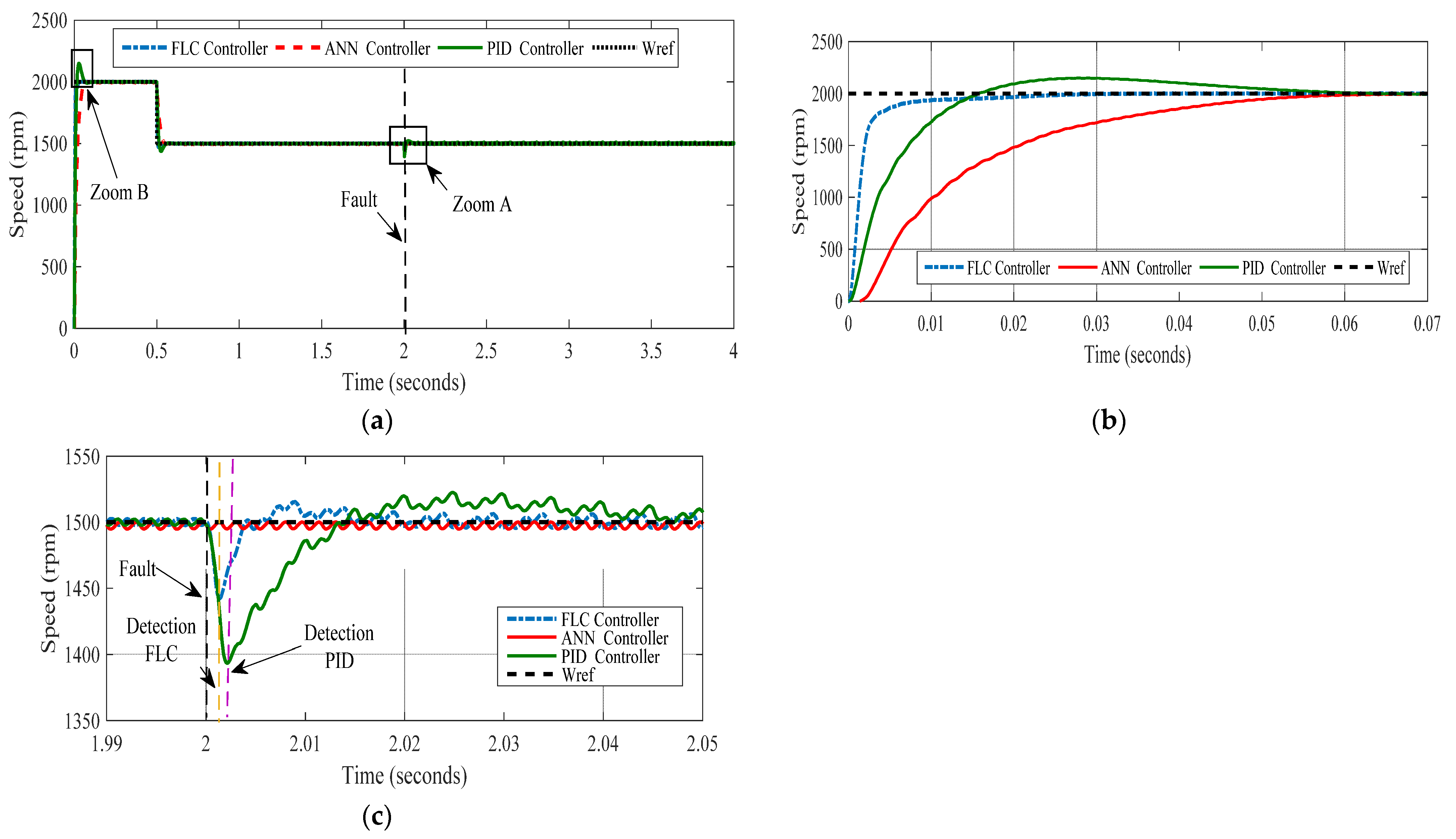
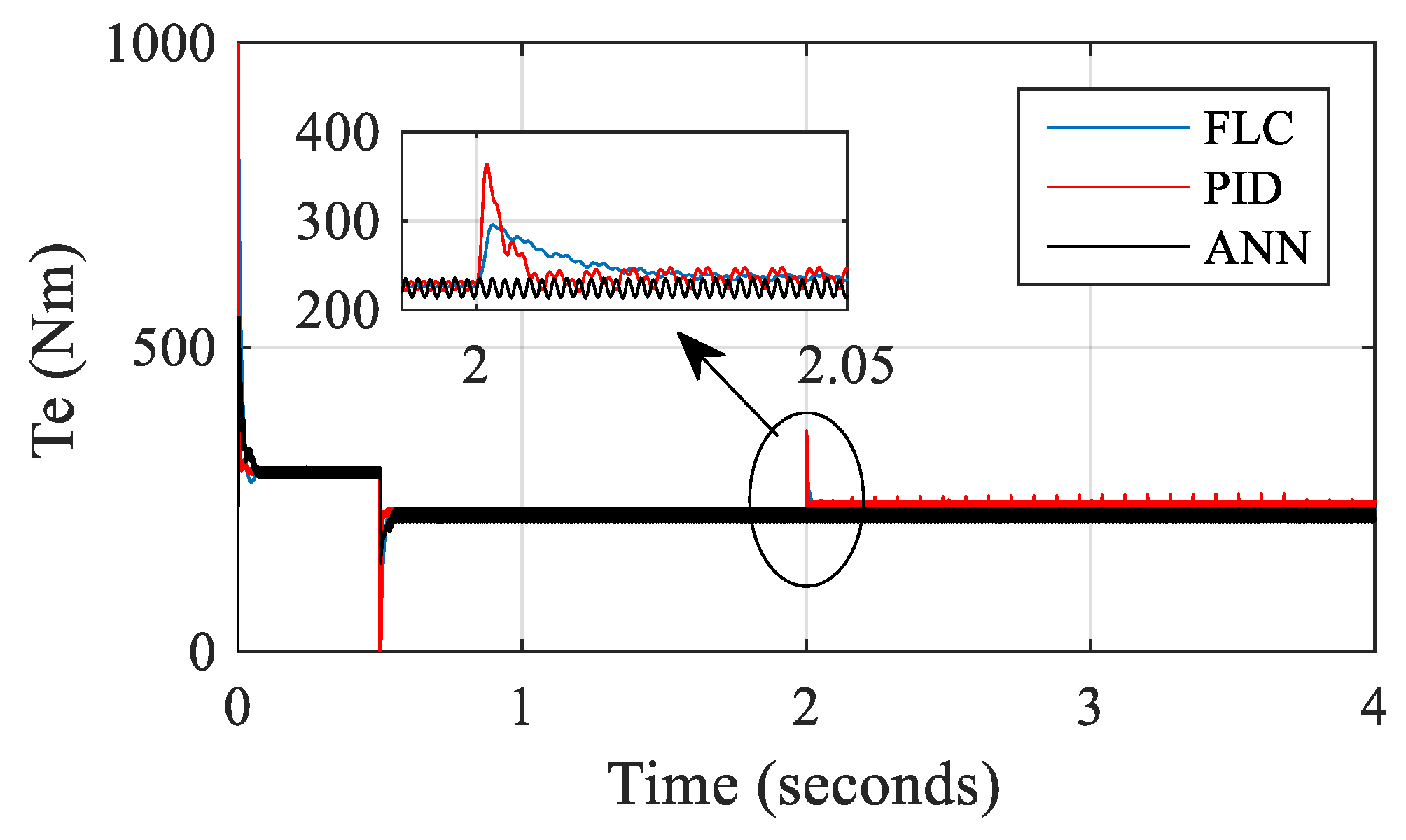
5.3. Comparison of Different Control Strategies
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| Abbreviations | |
| EVs | Electric vehicles |
| BLDCM | Brushless DC motor |
| BLDC | Brushless DC |
| EMF | Electromotive force |
| PMSM | Permanent magnet synchronous motor |
| PID | Proportional–integral–derivative controller |
| FLC | Fuzzy logic control |
| ANN | Neural network control |
| FTC | Fault-tolerant control |
| List of symbols | |
| Kp, Ki, Kd | Proportional, integral, and derivative gains |
| Va,Vb,Vc | Phase voltages a,b,c |
| ia,ib,ic | Phase currents a,b,c |
| ω | Rotor speed |
| J | Moment of inertia |
| Q1–Q6 | Switching states |
| ke | Coefficient of the electromotive force |
| L | Inductance |
| B | Coefficient of friction |
| Functions depending on rotor position | |
| Te | Electromagnetic torque |
| Tr | Load torque |
| S | Sector |
| S’ | Reconstruction sector |
References
- Primiceri, P.; Visconti, P.; Melpignano, A.; Colleoni, G.; Vilei, A. Hardware and software solution developed in arm MBED environment for driving and controlling DC brushless motors based on ST X-Nucleo development boards. Int. J. Smart Sens. Intell. Syst. 2016, 9, 1534–1562. [Google Scholar] [CrossRef]
- Singh, K.V.; Bansal, H.O.; Singh, D. A comprehensive review on hybrid electric vehicles: Architectures and components. J. Mod. Transp. 2019, 27, 77–107. [Google Scholar] [CrossRef]
- Eldho Aliasand, A.; Josh, F.T. Selection of Motor foran Electric Vehicle: A Review. Mater. Today Proc. 2020, 24, 1804–1815. [Google Scholar] [CrossRef]
- Yildirim, M.; Polat, M.; Kurum, H. A survey on comparison of electric motor types and drives used for electric vehicles. In Proceedings of the 16th International Power Electronics and Motion Control Conference and Exposition, Antalya, Turkey, 21–24 September 2014; pp. 218–223. [Google Scholar] [CrossRef]
- Baba, M.A.; Naoui, M.; Cherkaoui, M. Modeling and Simulation of a BLDC Motor Speed Control in Electric Vehicles. Int. Conf. Digit. Technol. Appl. 2023, 1, 883–895. [Google Scholar] [CrossRef]
- Goswami, R.; Joshi, D. Performance Review of Fuzzy Logic Based Controllers Employed in Brushless DC Motor. Procedia Comput. Sci. 2018, 132, 623–631. [Google Scholar] [CrossRef]
- Kristiyono, R. Wiyono Autotuning fuzzy PID controller for speed control of BLDC motor. J. Robot. Control 2021, 2, 400–407. [Google Scholar] [CrossRef]
- Ramírez-Cárdenas, O.-D.; Trujillo-Romero, F. Sensorless Speed Tracking of a Brushless DC Motor Using a Neural Network. Math. Comput. Appl. 2020, 25, 57. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, L. The Brushless DC motor control system Based on neural network fuzzy PID control of power electronics technology. Optik 2022, 271, 169879. [Google Scholar] [CrossRef]
- Gamazo-Real, J.C.; Vázquez-Sánchez, E.; Gómez-Gil, J. Position and speed control of brushless dc motors using sensorless techniques and application trends. Sensors 2010, 10, 6901–6947. [Google Scholar] [CrossRef]
- Vanchinathan, K.; Valluvan, K.T.R.; Gnanavel, C.; Gokul, C.; Renold, R.A. An improved incipient whale optimization algorithm based robust fault detection and diagnosis for sensorless brushless DC motor drive under external disturbances. Int. Trans. Electr. Energy Syst. 2021, 31, e13251. [Google Scholar] [CrossRef]
- Naoui, M.; Flah, A.; Sbita, L.; Ben Hamed, M.; Azar, A.T. Intelligent Control System for Hybrid Electric Vehicle with Autonomous Charging. In Artificial Intelligence for Robotics and Autonomous Systems Applications; Azar, A.T., Koubaa, A., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 405–437. ISBN 978-3-031-28715-2. [Google Scholar]
- Mousmi, A.; Abbou, A.; El Houm, Y. Binary Diagnosis of Hall Effect Sensors in Brushless DC Motor Drives. IEEE Trans. Power Electron. 2020, 35, 3859–3868. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, M. Fast Fault Diagnosis Method for Hall Sensors in Brushless DC Motor Drives. IEEE Trans. Power Electron. 2019, 34, 2585–2596. [Google Scholar] [CrossRef]
- Ebadpour, M.; Amiri, N.; Jatskevich, J. Fast Fault-Tolerant Control for Improved Dynamic Performance of Hall-Sensor-Controlled Brushless DC Motor Drives. IEEE Trans. Power Electron. 2021, 36, 14051–14061. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, W.; Yang, J. Fault diagnosis of low-cost hall-effect sensors used in controlling permanent magnet synchronous motor. In Proceedings of the 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2017; pp. 2–6. [Google Scholar]
- Gayatri Sarman, K.V.S.H.; Madhu, T.; Mallikharjuna Prasad, A. Fault diagnosis of BLDC drive using advanced adaptive network-based fuzzy inference system. Soft Comput. 2021, 25, 12759–12774. [Google Scholar] [CrossRef]
- Shifat, T.A.; Hur, J.W. EEMD assisted supervised learning for the fault diagnosis of BLDC motor using vibration signal. J. Mech. Sci. Technol. 2020, 34, 3981–3990. [Google Scholar] [CrossRef]
- Kumar, P.H.; Somasekhar, V.T. An Enhanced Fault-Tolerant and Autoreconfigurable BLDC Motor Drive for Electric Vehicle Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 4, 368–380. [Google Scholar] [CrossRef]
- Mohamed, N.; Aymen, F.; Mouna, B.H.; Lassaad, S. Modeling and simulation of vector control for a Permanent Magnet Synchronous Motor in electric vehicle. In Proceedings of the 4th International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Alkhobar, Saudi Arabia, 6–8 December 2021; pp. 1–5. [Google Scholar]
- Obed, A.A.; Kadhim, A.K. Speed and Current Limiting Control Strategies for BLDC Motor Drive System: A Comparative Study. Int. J. Adv. Eng. Res. Sci. 2018, 5, 119–130. [Google Scholar] [CrossRef]
- Mondal, S.; Mitra, A.; Chattopadhyay, M. Mathematical modeling and simulation of Brushless DC motor with ideal Back EMF for a precision speed control. In Proceedings of the IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 5–7 March 2015; pp. 15–19. [Google Scholar] [CrossRef]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D. Brushless dc Motor Drives. In Analysis of Electric Machinery and Drive Systemsl; Wiley-IEEE Press: Piscataway, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Tibor, B.; Fedak, V.; Ďurovský, F. Modeling and simulation of the BLDC motor in MATLAB GUI. In Proceedings of the IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1403–1407. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Y.; Lin, H.; Riaz, S.; Elahi, H. Real-time fault diagnosis and fault-tolerant control strategy for hall sensors in permanent magnet brushless dc motor drives. Electronics 2021, 10, 1268. [Google Scholar] [CrossRef]
- Dong, L.; Jatskevich, J.; Huang, Y.; Chapariha, M.; Liu, J. Fault diagnosis and signal reconstruction of hall sensors in brushless permanent magnet motor drives. IEEE Trans. Energy Convers. 2016, 31, 118–131. [Google Scholar] [CrossRef]
- Aqil, M.; Hur, J. A Direct Redundancy Approach to Fault-Tolerant Control of BLDC Motor with a Damaged Hall-Effect Sensor. IEEE Trans. Power Electron. 2020, 35, 1732–1741. [Google Scholar] [CrossRef]
- Tashakori, A.; Ektesabi, M. Position sensors fault tolerant control system in BLDC motors. Eng. Lett. 2014, 22, 39–46. [Google Scholar]
- Aqil, M.; Hur, J. Multiple sensor fault detection algorithm for fault tolerant control of bldc motor. Electronics 2021, 10, 1038. [Google Scholar] [CrossRef]
- Dong, L.; Huang, Y.; Jatskevich, J.; Liu, J. Improved Fault-Tolerant Control for Brushless Permanent Magnet Motor Drives with Defective Hall Sensors. IEEE Trans. Energy Convers. 2016, 31, 789–799. [Google Scholar] [CrossRef]
- Magistrale, L. Sensorless Brushless DC Motors: Development and comparison of different fault tolerant control algorithms. 2018; 2005, (Doctoral dissertation, Politecnico di Torino). [Google Scholar]
- Mousa, M.E.; Ebrahim, M.A.; Hassan, M.A.M. Stabilizing and Swinging-Up the Inverted Pendulum Using PI and PID Controllers Based on Reduced Linear Quadratic Regulator Tuned by PSO. Int. J. Syst. Dyn. Appl. 2015, 4, 52–69. [Google Scholar] [CrossRef]
- Sushita, K. Performance of BLDC motor with PI, PID and Fuzzy controller and its Comparative Analysis. Eur. J. Mol. Clin. Med. 2021, 25, 219–228. [Google Scholar]
- Singh, G.; Kour, V.; Singh, L. Design and Performance Analysis of PID Controller for Automatic Generation Control of an Autonomous Power System. Int. J. Eng. Res. Technol. 2020, 7, 2520–2524. [Google Scholar]
- Kilic, E.; Yilmaz, S.; Ozcalik, H.R.; Sit, S. A comparative analysis of FLC and ANFIS controller for vector controlled induction motor drive. In Proceedings of the Intl Aegean Conference on Electrical Machines & Power Electronics (ACEMP), 2015 Intl Conference on Optimization of Electrical & Electronic Equipment (OPTIM) & 2015 Intl Symposium on Advanced Electromechanical Motion Systems (ELECTROMOTION), Side, Turkey, 2–4 September 2015; pp. 102–106. [Google Scholar] [CrossRef]
- Mishra, S.; Anurag, M.; Tomer, S. Speed Control of PMSM Drives by Using Neural Network Controller. Adv. Electron. Electr. 2014, 4, 353–360. [Google Scholar]
- Huang, C.; Lei, F.; Han, X.; Zhang, Z. Determination of modeling parameters for a brushless DC motor that satisfies the power performance of an electric vehicle. Meas. Control 2019, 52, 765–774. [Google Scholar] [CrossRef]



| Ha | Hb | Hc | |
|---|---|---|---|
| 1 | 0 | 0 | |
| 1 | 1 | 0 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 0 | 0 | 1 | |
| 1 | 0 | 1 | |
| 1 | 0 | 0 |
| Ha | Hb | Hc | Sector | Active Switches | Stator Magnetic Axis |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | Q3 Q6 | V2 |
| 0 | 1 | 0 | 2 | Q3 Q2 | V3 |
| 0 | 1 | 1 | 3 | Q5 Q2 | V4 |
| 0 | 0 | 1 | 4 | Q5 Q4 | V5 |
| 1 | 0 | 1 | 5 | Q1 Q4 | V6 |
| 1 | 0 | 0 | 6 | Q1 S6 | V1 |
| Ha = 0 | |||||
| Ha | Hb | Hc | Sector | Active Switches | Stator Magnetic Axis |
| 0 | 1 | 0 | 2 | Q3 Q2 | V3 |
| 0 | 1 | 0 | |||
| 0 | 1 | 1 | 3 | Q5 Q2 | V4 |
| 0 | 0 | 1 | 4 | Q5 Q4 | V5 |
| 0 | 0 | 1 | |||
| 0 | 0 | 0 | 0 | No | 0 |
| Ha = 1 | |||||
| Ha | Hb | Hc | Sector | Active Switches | Stator Magnetic Axis |
| 1 | 1 | 0 | 1 | Q3 Q6 | V2 |
| 1 | 1 | 0 | |||
| 1 | 1 | 1 | 0 | No one | 0 |
| 1 | 0 | 1 | 5 | Q1 Q4 | V6 |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 6 | Q1 Q6 | V1 |
| Ha = 0 | |||
| Cases | Failure Sector | Sector Switches From | |
| Case 1 | 6 in (from 0° to 30°) | From 6 to 0 | |
| Case 2 | 1 in (30–90°) | From 1 to 2 | |
| Case 3 | 5 in (270–330°) | From 5 to 6 | |
| Case 4 | 6 in (from 330° to 360°) | From 6 to 0 | |
| Ha = 1 | |||
| Cases | Failure Sector | Sector Switches from | |
| Case 5 | 2 in (from 90° to 150°) | From 2 to 1 | |
| Case 6 | 3 in (150–210°) | From 3 to 0 | |
| Case 7 | 4 in (210–270°) | From 4 to 5 | |
| E/CE | NB | NM | NS | Z | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| NB | NB | NB | NB | NB | NM | NS | Z |
| NM | NB | NB | NB | NM | NS | Z | PS |
| NS | NB | NB | NM | NS | Z | PS | PM |
| Z | NB | NM | NS | Z | PS | PM | PB |
| PS | NM | NS | Z | PS | PM | PB | PB |
| PM | NS | Z | PS | PM | PB | PB | PB |
| PB | Z | PS | PM | PB | PB | PB | PB |
| Parameter | Value |
|---|---|
| Input elements | 3 |
| Output element | 1 |
| Training | 70% |
| Validation | 15% |
| Testing | 15% |
| Number of Hidden Neurons | 10 |
| Training Algorithm | Levenberg–Marquardt |
| Epochs | 5000 |
| Parameter | Value |
|---|---|
| Base velocity | 2300 (r/min) |
| Stator inductance | 58.9 µH |
| Supply voltage | 400 v |
| Maximum power (kW) | 90 |
| Magnet excitation flux | 0.0030225 wb |
| Number of pairs of poles | 4 |
| e.m.f. constant (ke) | 0.18 |
| Moment of inertia of rotating parts (j) | 0.0000528 n.m.s2 |
| Stator resistance | 0.025 ω |
| Controller Type | Control System Parameters | ||||
|---|---|---|---|---|---|
| Settling Time (s) | Peak Overshoot | Steady Stat Error | Numbers of Oscillations | Response Time When a Signal Fault | |
| PID controller | 0.07 | Low | 0.6 | 1 | Medium |
| FLC controller | 0.02 | Nil | Very low | Nil | Low |
| ANN controller | 0.06 | Nil | Very low | Nil | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed Baba, M.; Naoui, M.; Cherkaoui, M. Fault-Tolerant Control Strategy for Hall Sensors in BLDC Motor Drive for Electric Vehicle Applications. Sustainability 2023, 15, 10430. https://doi.org/10.3390/su151310430
Ahmed Baba M, Naoui M, Cherkaoui M. Fault-Tolerant Control Strategy for Hall Sensors in BLDC Motor Drive for Electric Vehicle Applications. Sustainability. 2023; 15(13):10430. https://doi.org/10.3390/su151310430
Chicago/Turabian StyleAhmed Baba, Mariem, Mohamed Naoui, and Mohamed Cherkaoui. 2023. "Fault-Tolerant Control Strategy for Hall Sensors in BLDC Motor Drive for Electric Vehicle Applications" Sustainability 15, no. 13: 10430. https://doi.org/10.3390/su151310430
APA StyleAhmed Baba, M., Naoui, M., & Cherkaoui, M. (2023). Fault-Tolerant Control Strategy for Hall Sensors in BLDC Motor Drive for Electric Vehicle Applications. Sustainability, 15(13), 10430. https://doi.org/10.3390/su151310430








