Site Index Curves for Abies borisii-regis Mattf. and Fagus sylvatica L. Mixed Stands in Central Greece
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.3. Fitted Site Index Models
3. Results
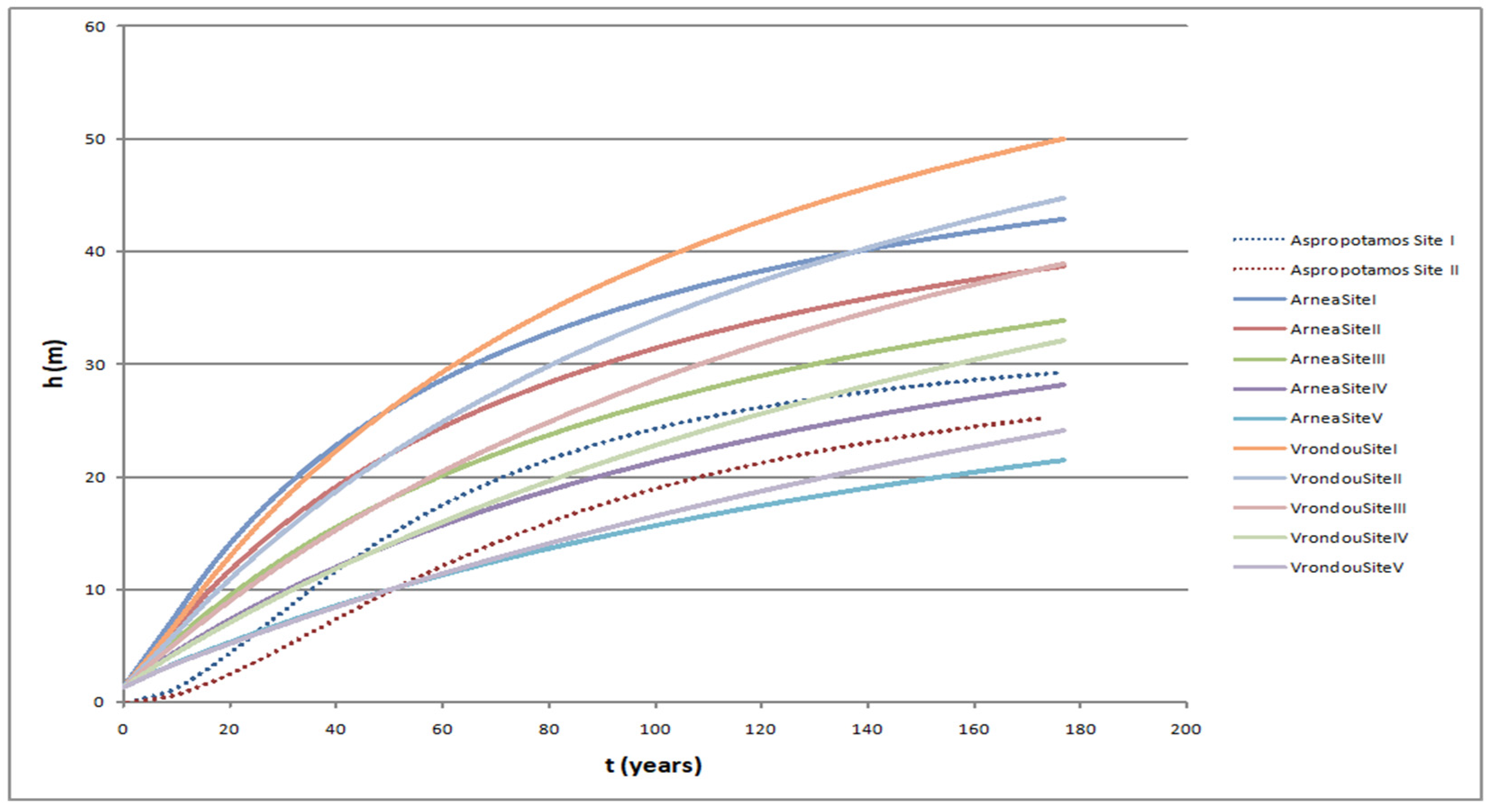
3.1. A. borisii-regis Site Index Curves
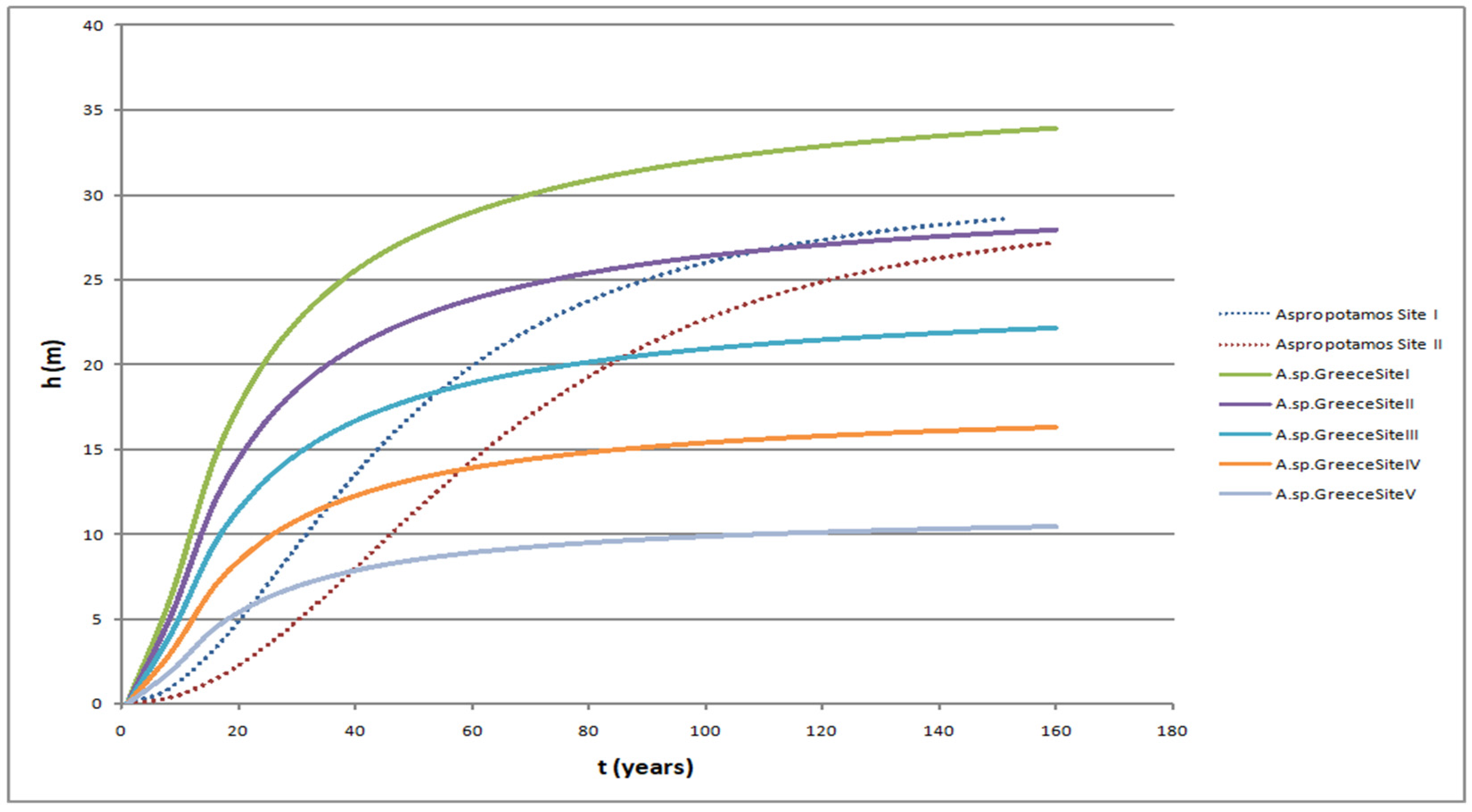
3.2. F. sylvatica Site Index Curves
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ministry of Agriculture. Results of the First National Forest Inventory; Publication of Department of Forest Mapping: Athens, Greece, 2021. (In Greek) [Google Scholar]
- Korakis, G. Forest Botany; Hellenic Academic Libraries Link: Athens, Greece, 2015. (In Greek) [Google Scholar]
- Bella, E.; Liepelt, S.; Parducci, L.; Drouzas, A. Genetic insights into the hybrid origin of Abies × borisii-regis Mattf. Plant Syst. Evol. 2015, 301, 749–759. [Google Scholar] [CrossRef]
- Milios, E.; Pipinis, E.; Smiris, P.; Aslanidou, M. The influence of overhead shade on the shade mortality of Abies borisii-regis Mattf. seedlings and saplings in the central Rhodope mountains of north-eastern Greece. Plant Biosyst. 2008, 142, 219–227. [Google Scholar] [CrossRef]
- Milios, E.; Papalexandris, C. Height growth of sprouts emerged from small stumps and seed origin saplings under shade, in low elevation Fagus sylvatica L. s.l. stands in Greece. Dendrobiology 2019, 82, 1–7. [Google Scholar] [CrossRef]
- Clutter, J.; Fortson, J.; Pienaar, V.; Brister, G.; Bailey, R. Timber Management—A Quantitative Approach; John Wiley and Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Weiskittel, A.; Hann, D.; Kershaw, J.; Vanclay, J. Forest Growth and Yield Modeling; Wiley-Blackwell: Chichester, UK, 2011. [Google Scholar]
- Burkhart, H.; Tomé, M. Modeling Forest Trees and Stands; Springer: New York, NY, USA, 2012. [Google Scholar]
- Sharma, R.; Brunner, A.; Eid, T. Site index prediction from site and climate variables for Norway spruce and Scots pine in Norway. Scand. J. For. Res. 2012, 27, 619–636. [Google Scholar] [CrossRef]
- Avery, T.; Bukhart, H. Forest Measurements; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface lidar remote sensing of basal area and biomass in deciduous forests of eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res. 1998, 28, 1016–1031. [Google Scholar] [CrossRef]
- Means, J.E.; Acker, S.A.; Harding, D.J.; Blair, J.B.; Lefsky, M.A.; Cohen, W.B.; Harmon, M.E.; McKee, W.A. Use of large-footprint scanning airborne lidar to estimate forest stand characteristics in the western Cascades of Oregon. Remote Sens. Environ. 1999, 67, 298–308. [Google Scholar] [CrossRef]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ. 1988, 24, 247–267. [Google Scholar] [CrossRef]
- Næsset, E.; Bjerknes, K.O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner data. Remote Sens. Environ. 2001, 78, 328–340. [Google Scholar] [CrossRef]
- Magnussen, S.; Eggermont, P.; LaRiccia, V.N. Recovering tree heights from airborne laser scanner data. For. Sci. 1999, 45, 407–422. [Google Scholar]
- Næsset, E.; Økland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Nelson, R.; Oderwald, R.; Gregoire, G. Separating the ground and airborne laser sampling phases to estimate tropical forest basal area, volume, and biomass. Remote Sens. Environ. 1997, 60, 311–326. [Google Scholar] [CrossRef]
- Nelson, R. Modeling forest canopy heights: The effects of canopy shape. Remote Sens. Environ. 1997, 60, 327–334. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Maltamo, M.; Bollandsås, O.M.; Næsset, E.; Gobakken, T.; Packalén, P. Different plot selection strategies for field training data in ALS-assisted forest inventory. Forestry 2010, 84, 23–31. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Kotivuori, E.; Korhonen, L.; Packalen, P. Nationwide airborne laser scanning based models for volume, biomass and dominant height in Finland. Silva Fenn. 2016, 50, 1567. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: The Nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Packalén, P.; Hyyppä, J. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79, 217–229. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res. 2010, 129, 1131–1142. [Google Scholar] [CrossRef]
- Saukkola, A.; Melkas, T.; Riekki, K.; Sirparanta, S.; Peuhkurinen, J.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Predicting forest inventory attributes using airborne laser scanning, aerial imagery, and harvester data. Remote Sens. 2019, 11, 797. [Google Scholar] [CrossRef]
- Poulianidis, P. Study of Protection and Management of the Public Forest of Aspopotamos Period 2017–2026; Forest service of Kalambaka: Kalambaka, Greece, 2019. (In Greek) [Google Scholar]
- Rinn, F. Time Series Analysis and Presentation Software (TSAP-Win). User Reference (Version 0.55); RinnTech: Heidelberg, Germany, 2005. [Google Scholar]
- Newberry, J. A note on Carmean’s estimate of height from stem analysis data. For. Sci. 1991, 37, 368–369. [Google Scholar]
- Magnussen, S.; Penner, M. Recovering time trends in dominant height from stem analysis. Can. J. For. Res. 1996, 26, 9–22. [Google Scholar] [CrossRef]
- Aldenderfer, M.; Blashfield, K. Cluster Analysis; Sage Publications: Newbury Park, CA, USA, 1984. [Google Scholar]
- IBM SPSS Statistics for Windows, Version 21; IBM Corp.: Armonk, NY, USA, 2021.
- Kitikidou, K. Forestbiometrical Models for SPSS. 2008. Available online: http://spsstools.net/ru/documents/56/kitikidou.doc (accessed on 12 January 2020).
- Stajić, B.; Obradović, S.; Baković, Z.; Kazimirović, M.; Janjatović, Ž. Polymorphic site index curves for beech (Fagus sylvatica L.) in Central and Eastern Serbia. Šumarski List 2021, 145, 31–41. [Google Scholar] [CrossRef]
- Gatzojannis, S. Ertragstafeln für Buchenbestände in Griechenland. Allg. Forst-u. J.-Ztg. 1998, 12, 219–224. [Google Scholar]
- Gatzojannis, S. Yield tables for beech stands in the forest A. Brontou Serres Prefecture, N. Greece. For. Res. 1999, 12, 91–104. (In Greek) [Google Scholar]
- Apatsides, L.; Skouteri, A.; Albanis, K. Site index estimation based on soil and physiography characteristics in the fir (Abies sp.) distribution zone. For. Res. 2008, 21, 29–40. (In Greek) [Google Scholar]
- Gatzojannis, S. Site-index model for Abies chephalonica in the mount Taygetos forest in Greece. Scand. J. For. Res. 2000, 15, 326–333. [Google Scholar] [CrossRef]
- Milios, E.; Petrou, P.; Pytharidis, K.; Christou, A.; Eliades, N. Assessment of how natural stand structure for narrow endemic Cedrus brevifolia Henry supports silvicultural treatments for its sustainable management. South-East Eur. For. 2021, 12, 21–34. [Google Scholar] [CrossRef]
- Dais, G.; Kitikidou, K.; Milios, E. Volume equations for Abies borisii-regis and Fagus sylvatica in central Greece. Ann. Silvic. Res. 2022, 47, 24–29. [Google Scholar]
- Tourist Market of Chamber of Trikala. Available online: http://www.meteorabooking.gr/trikala/tourism/articles/article.jsp;jsessionid=71719D5C9ED92DC97AAF19D3FE25AF90?context=1504&categoryid=17386 (accessed on 12 January 2020).



| A. borisii-regis | F. sylvatica | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Min | Max | N of Trees | Mean | Standard Deviation | Min | Max | N of Trees | ||
| Whole sample | Age (years) | 99.48 | 31.62 | 53.00 | 160.00 | 23 | 116.07 | 40.33 | 60.00 | 177.00 | 29 |
| Height (m) | 26.26 | 3.53 | 20.32 | 33.27 | 23 | 24.81 | 3.62 | 17.81 | 32.42 | 29 | |
| Site I | Age (years) | 85.25 | 22.76 | 53.00 | 151.00 | 16 | 104.00 | 39.31 | 60.00 | 177.00 | 19 |
| Height (m) | 25.79 | 3.61 | 20.32 | 33.27 | 16 | 24.77 | 4.06 | 17.81 | 32.42 | 19 | |
| Site II | Age (years) | 132.00 | 24.42 | 104.00 | 160.00 | 7 | 139.00 | 32.82 | 90.00 | 173.00 | 10 |
| Height (m) | 27.33 | 3.35 | 22.59 | 31.65 | 7 | 24.89 | 2.81 | 18.73 | 28.77 | 10 | |
| Model No | Model | Site Quality I | Site Quality II | ||||
|---|---|---|---|---|---|---|---|
| R2 (Optimum Value: 1) | SEE (Optimum Value: Min) | RMSE (Optimum Value: Min) | R2 (Optimum Value: 1) | SEE (Optimum Value: Min) | RMSE (Optimum Value: Min) | ||
| 1 | H = b0 + b1t + b2t2 + b3t3 | 0.92 | 2.50 | 2.68 | 0.95 | 2.02 | 2.34 |
| 2 | H = b0 + b1t + b2t2 | 0.92 | 2.51 | 1.50 | 0.95 | 2.07 | 1.01 |
| 3 | H = b0 + b1t + b2t3 | 0.85 | 3.39 | 1.98 | 0.92 | 2.65 | 1.27 |
| 4 | H = b1t + b2t2 | 0.87 | 3.15 | 20.52 | 0.92 | 2.65 | 30.43 |
| 5 | H = b0 + b1 + b2t | 0.89 | 2.91 | 7.74 | 0.93 | 2.49 | 7.39 |
| 6 | H = b0 + b1 + b2t + b3t2 | 0.89 | 2.91 | 8.99 | 0.92 | 2.51 | 8.32 |
| 7 | H = b0 + b1 + b2t | 0.88 | 2.97 | 1.73 | 0.93 | 2.44 | 1.17 |
| 8 | H = b0 + b1 + b2 + b3t | 0.87 | 3.11 | 3.37 | 0.90 | 2.83 | 4.57 |
| 9 | H = b0 + b1t + b2 | 0.85 | 3.34 | 1.95 | 0.92 | 2.64 | 1.27 |
| 10 | H = b0 + b1 + b2 | 0.48 | 6.23 | 3.63 | 0.42 | 6.93 | 3.33 |
| 11 | H = b0 + b1 | 0.22 | 7.64 | 4.46 | 0.18 | 8.24 | 3.96 |
| 12 | H = b0 + b1 | 0.07 | 8.37 | 4.89 | 0.04 | 8.91 | 4.28 |
| 13 | H = b0 + b1t + b2lnt | 0.87 | 3.11 | 1.81 | 0.92 | 2.53 | 1.21 |
| 14 | H = b0 + b1lnt | 0.77 | 4.17 | 2.43 | 0.78 | 4.25 | 2.04 |
| 15 | H = b0 + b1lnt + b2(lnt)2 | 0.77 | 4.17 | 10.55 | 0.78 | 4.25 | 12.47 |
| 16 | lnH = b0 + b1lnt | 0.83 | 3.56 | 2.27 | 0.89 | 3.03 | 1.57 |
| 17 | lnH = b0 + b1lnt + b2(lnt)2 | 0.84 | 3.42 | 2.32 | 0.93 | 2.45 | 4.93 |
| 18 | lnH = b0 + b1lnt + b2(lnt)3 | 0.83 | 3.57 | 2.32 | 0.91 | 2.67 | 3.36 |
| 19 | lnH = b0 + b1 | 0.58 | 5.63 | 4.37 | 0.55 | 6.11 | 4.11 |
| 20 | lnH = b0 + b1 + b2 | 0.81 | 3.74 | 2.97 | 0.83 | 3.81 | 2.88 |
| 21 | lnH = b0 + b1 + b2t | 0.89 | 2.92 | 7.97 | 0.93 | 2.42 | 7.34 |
| 22 | lnH = b0 + b1 + b2t | 0.92 | 2.42 | 1.46 | 0.94 | 2.18 | 1.09 |
| 23 | lnH = b0 + b1 | 0.87 | 3.08 | 2.76 | 0.91 | 2.77 | 2.58 |
| 24 | lnH = b0 + b1t + b2 | 0.64 | 5.17 | 3.98 | 0.74 | 4.65 | 2.95 |
| 25 | lnH = b1lnt + b2(lnt)2 | 0.88 | 3.05 | 7.20 | 0.83 | 3.78 | 7.59 |
| 26 | lnH = b0 + b1 + b2 + b3 | 0.78 | 4.09 | 6.05 | 0.78 | 4.32 | 6.32 |
| 27 | 0.90 | 2.69 | 1.63 | 0.94 | 2.28 | 1.16 | |
| 28 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 29 | 0.91 | 2.55 | 2.17 | N/A | N/A | N/A | |
| 30 | 0.92 | 2.38 | 1.40 | 0.96 | 1.80 | 0.87 | |
| 31 | 0.00 | 8.66 | 214.47 | 0.00 | 9.10 | 285.04 | |
| 32 | 0.92 | 2.52 | 1.48 | 0.95 | 2.00 | 0.97 | |
| 33 | 0.92 | 2.45 | 1.44 | 0.96 | 1.81 | 0.87 | |
| 34 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 35 | 0.92 | 2.45 | 1.44 | 0.96 | 1.81 | 0.87 | |
| 36 | 0.91 | 2.60 | 1.52 | 0.95 | 2.13 | 1.05 | |
| 37 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 38 | 0.03 | 8.54 | 4.98 | 0.02 | 9.03 | 4.33 | |
| 39 | 0.67 | 5.01 | 3.00 | 0.79 | 4.19 | 2.09 | |
| 40 | 0.30 | 7.24 | 9.44 | 0.25 | 7.88 | 8.21 | |
| 41 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 42 | N/A | N/A | N/A | N/A | N/A | N/A | |
| Model No | Model | Site Quality I | Site Quality II | ||||
|---|---|---|---|---|---|---|---|
| R2 (Optimum Value: 1) | SEE (Optimum Value: Min) | RMSE (Optimum Value: Min) | R2 (Optimum Value: 1) | SEE (Optimum Value: Min) | RMSE (Optimum Value: Min) | ||
| 1 | H = b0 + b1t + b2t2 + b3t3 | 0.95 | 1.97 | 2.57 | 0.92 | 2.24 | 2.89 |
| 2 | H = b0 + b1t + b2t2 | 0.95 | 2.02 | 2.03 | 0.89 | 2.70 | 2.52 |
| 3 | H = b0 + b1t + b2t3 | 0.88 | 3.05 | 2.14 | 0.90 | 2.56 | 1.51 |
| 4 | H = b1t + b2t2 | 0.91 | 2.71 | 33.97 | 0.90 | 2.56 | 42.07 |
| 5 | H = b0 + b1 + b2t | 0.93 | 2.27 | 9.36 | 0.91 | 2.41 | 7.89 |
| 6 | H = b0 + b1 + b2t + b3t2 | 0.93 | 2.26 | 11.08 | 0.91 | 2.43 | 8.83 |
| 7 | H = b0 + b1 + b2t | 0.93 | 2.35 | 1.65 | 0.91 | 2.37 | 1.40 |
| 8 | H = b0 + b1 + b2 + b3t | 0.92 | 2.46 | 3.07 | 0.89 | 2.68 | 4.74 |
| 9 | H = b0 + b1t + b2 | 0.89 | 2.95 | 2.07 | 0.90 | 2.55 | 1.50 |
| 10 | H = b0 + b1 + b2 | 0.48 | 6.35 | 4.46 | 0.41 | 6.19 | 3.64 |
| 11 | H = b0 + b1 | 0.22 | 7.79 | 5.47 | 0.18 | 7.31 | 4.31 |
| 12 | H = b0 + b1 | 0.06 | 8.54 | 6.00 | 0.04 | 7.89 | 4.65 |
| 13 | H = b0 + b1t + b2lnt | 0.92 | 2.55 | 1.79 | 0.91 | 2.44 | 1.43 |
| 14 | H = b0 + b1lnt | 0.82 | 3.71 | 2.61 | 0.78 | 3.83 | 2.25 |
| 15 | H = b0 + b1lnt + b2(lnt)2 | 0.82 | 3.71 | 13.16 | 0.78 | 3.83 | 13.18 |
| 16 | lnH = b0 + b1lnt | 0.88 | 3.09 | 2.64 | 0.89 | 2.67 | 1.67 |
| 17 | lnH = b0 + b1lnt + b2(lnt)2 | 0.86 | 3.30 | 5.17 | 0.91 | 2.47 | 3.41 |
| 18 | lnH = b0 + b1lnt + b2(lnt)3 | 0.85 | 3.40 | 6.85 | 0.90 | 2.58 | 2.00 |
| 19 | lnH = b0 + b1 | 0.59 | 5.65 | 5.32 | 0.53 | 5.55 | 4.35 |
| 20 | lnH = b0 + b1 + b2 | 0.84 | 3.57 | 3.54 | 0.78 | 3.76 | 3.12 |
| 21 | lnH = b0 + b1 + b2t | 0.93 | 2.30 | 9.77 | 0.91 | 2.37 | 7.87 |
| 22 | lnH = b0 + b1 + b2t | 0.95 | 1.88 | 1.33 | 0.93 | 2.19 | 1.32 |
| 23 | lnH = b0 + b1 | 0.92 | 2.53 | 3.04 | 0.88 | 2.82 | 2.73 |
| 24 | lnH = b0 + b1t + b2 | 0.80 | 3.90 | 3.06 | 0.78 | 3.76 | 2.94 |
| 25 | lnH = b1lnt + b2(lnt)2 | 0.93 | 2.34 | 8.49 | 0.85 | 3.15 | 8.00 |
| 26 | lnH = b0 + b1 + b2 + b3 | 0.80 | 3.92 | 7.22 | 0.74 | 4.13 | 6.56 |
| 27 | 0.95 | 2.03 | 1.49 | 0.92 | 2.28 | 1.58 | |
| 28 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 29 | 0.96 | 1.76 | 1.27 | 0.93 | 2.18 | 1.54 | |
| 30 | 0.96 | 1.75 | 1.24 | 0.93 | 2.11 | 1.24 | |
| 31 | 0.58 | 5.70 | 21.83 | 0.64 | 4.81 | 15.58 | |
| 32 | 0.96 | 1.85 | 1.30 | 0.93 | 2.14 | 1.26 | |
| 33 | 0.96 | 1.81 | 1.30 | 0.93 | 2.13 | 1.26 | |
| 34 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 35 | 0.96 | 1.81 | 1.30 | 0.93 | 2.13 | 1.26 | |
| 36 | 0.95 | 1.93 | 1.38 | 0.93 | 2.20 | 1.37 | |
| 37 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 38 | 0.03 | 8.69 | 6.11 | 0.02 | 8.00 | 4.71 | |
| 39 | 0.74 | 4.49 | 3.31 | 0.79 | 3.72 | 2.24 | |
| 40 | 0.30 | 7.39 | 11.95 | 0.25 | 7.00 | 9.11 | |
| 41 | N/A | N/A | N/A | N/A | N/A | N/A | |
| 42 | N/A | N/A | N/A | N/A | N/A | N/A | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dais, G.; Kitikidou, K.; Milios, E. Site Index Curves for Abies borisii-regis Mattf. and Fagus sylvatica L. Mixed Stands in Central Greece. Sustainability 2023, 15, 10349. https://doi.org/10.3390/su151310349
Dais G, Kitikidou K, Milios E. Site Index Curves for Abies borisii-regis Mattf. and Fagus sylvatica L. Mixed Stands in Central Greece. Sustainability. 2023; 15(13):10349. https://doi.org/10.3390/su151310349
Chicago/Turabian StyleDais, Georgios, Kyriaki Kitikidou, and Elias Milios. 2023. "Site Index Curves for Abies borisii-regis Mattf. and Fagus sylvatica L. Mixed Stands in Central Greece" Sustainability 15, no. 13: 10349. https://doi.org/10.3390/su151310349
APA StyleDais, G., Kitikidou, K., & Milios, E. (2023). Site Index Curves for Abies borisii-regis Mattf. and Fagus sylvatica L. Mixed Stands in Central Greece. Sustainability, 15(13), 10349. https://doi.org/10.3390/su151310349







