Photovoltaic Power Prediction Using Analytical Models and Homer-Pro: Investigation of Results Reliability
Abstract
1. Introduction
2. Materials and Methods
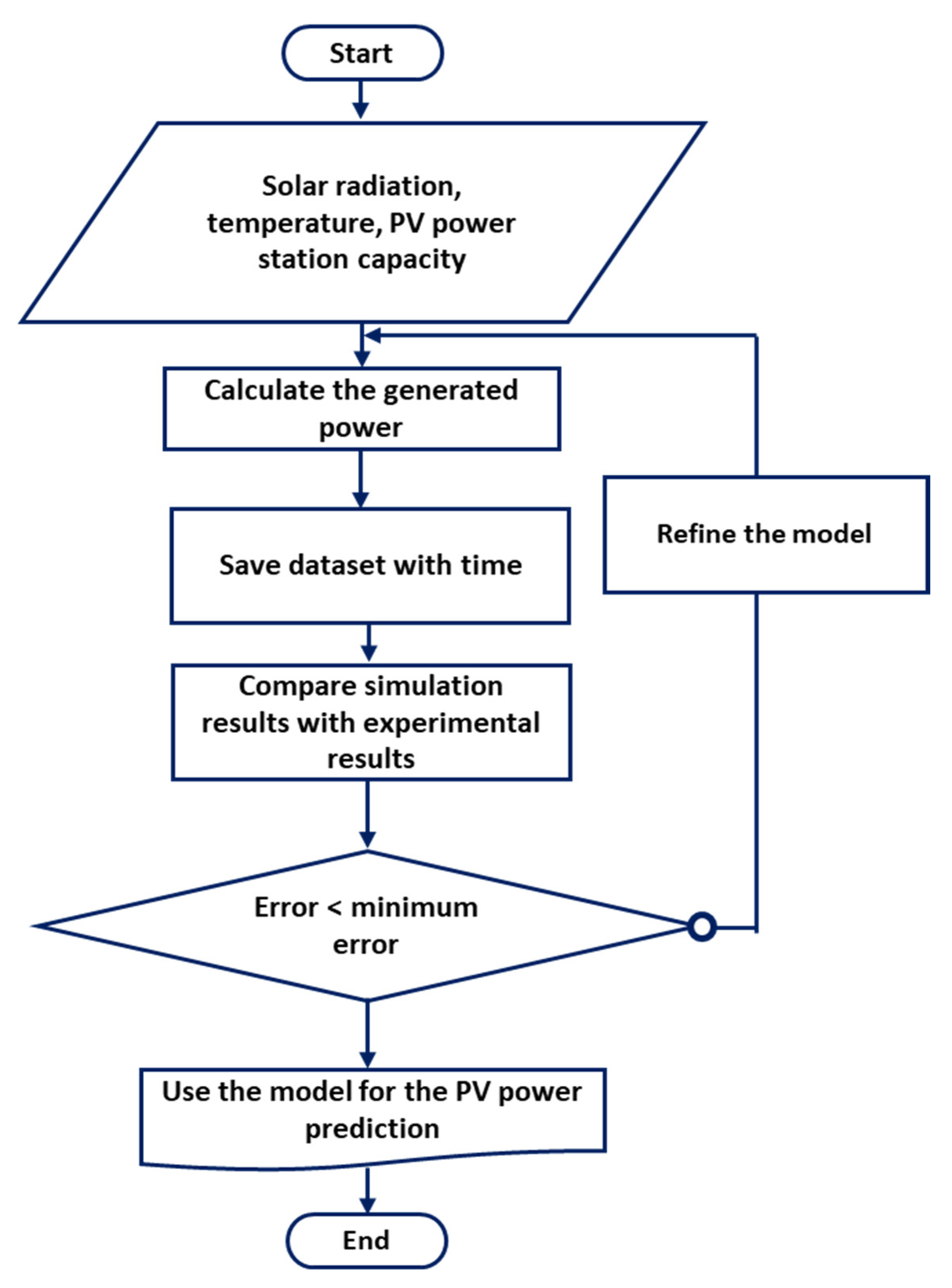
2.1. Analytical Model
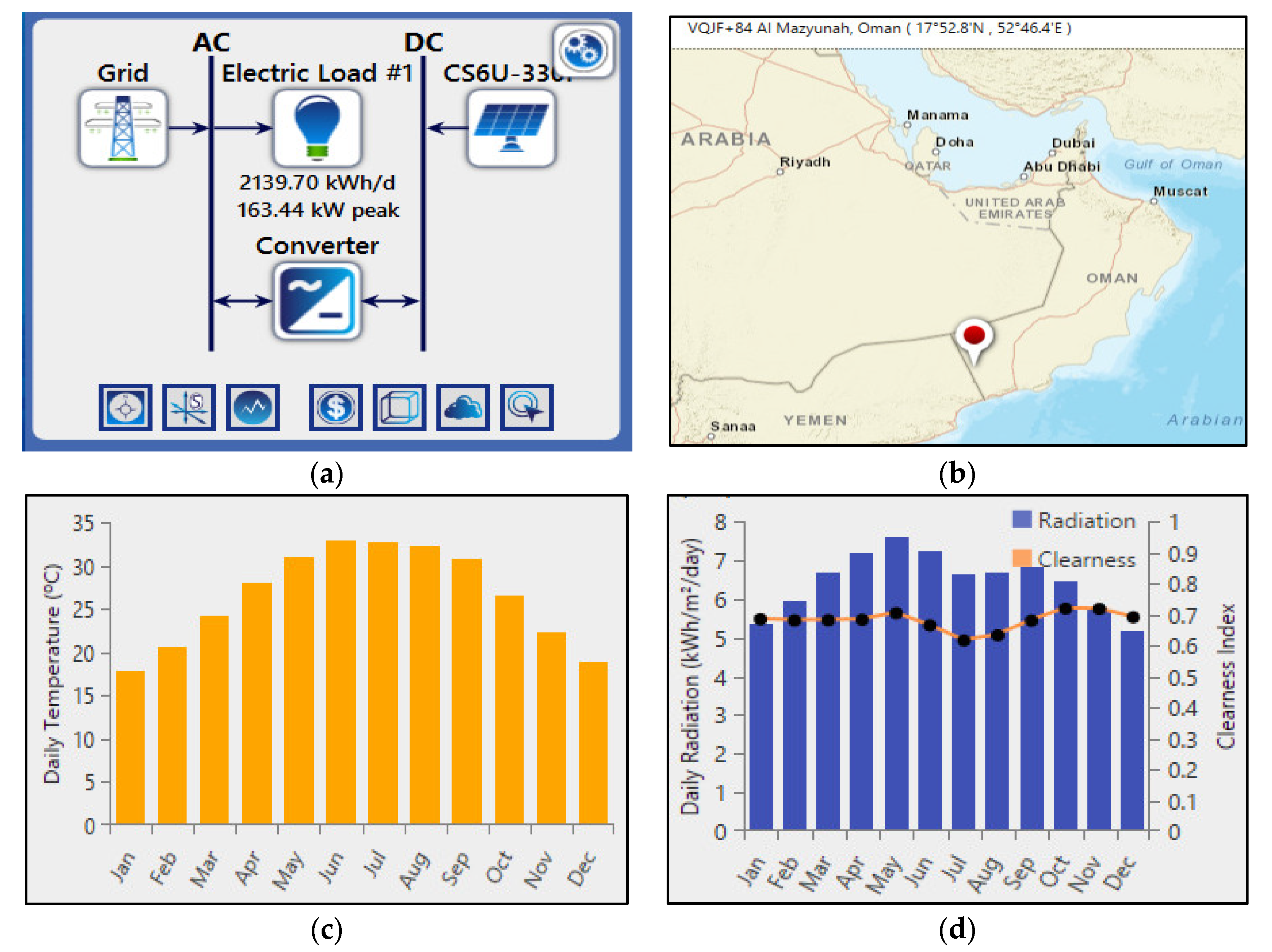
2.2. Homer-Pro Model
2.3. Experiments
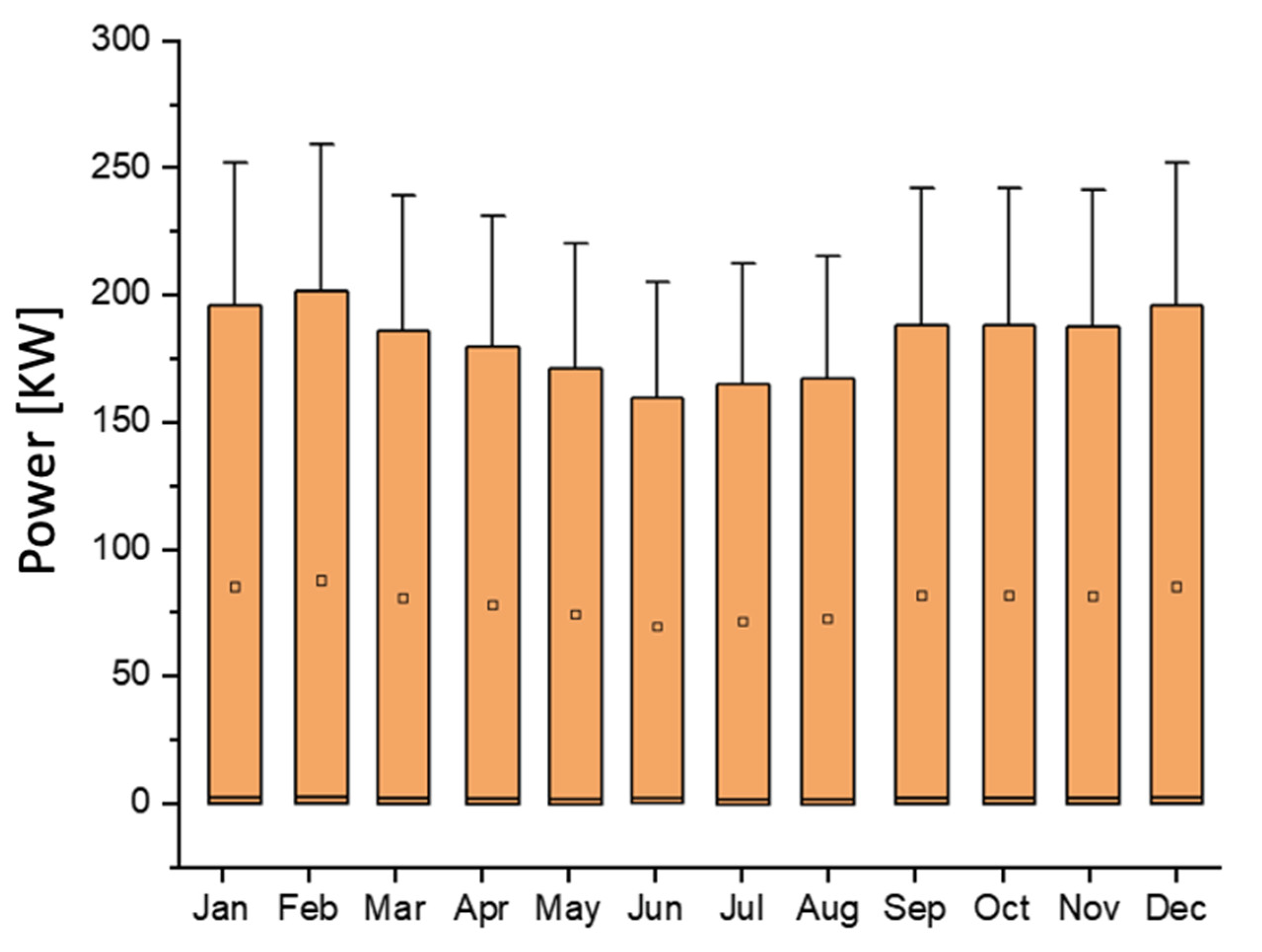
3. Results
3.1. Analytical Model Results
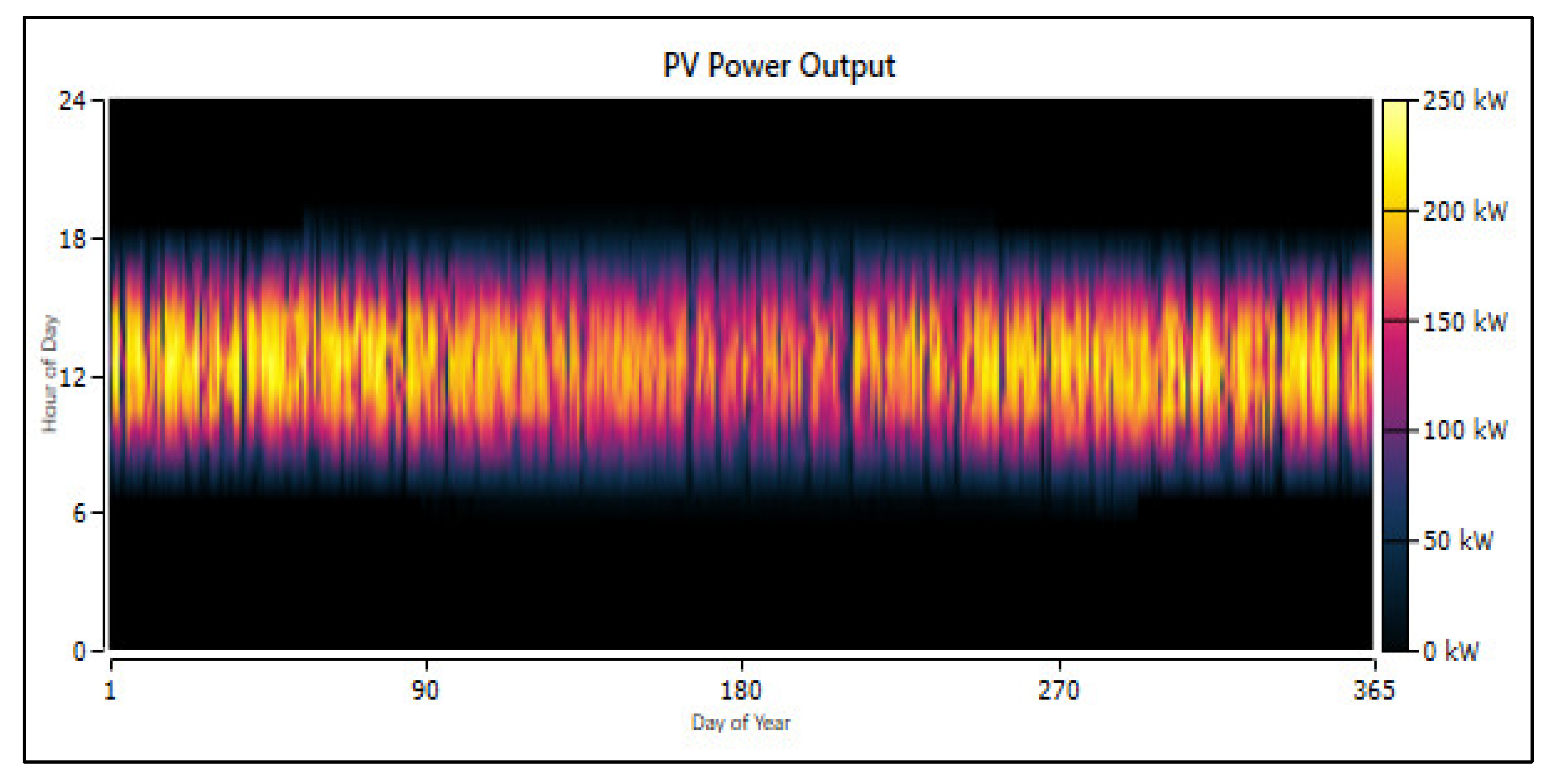
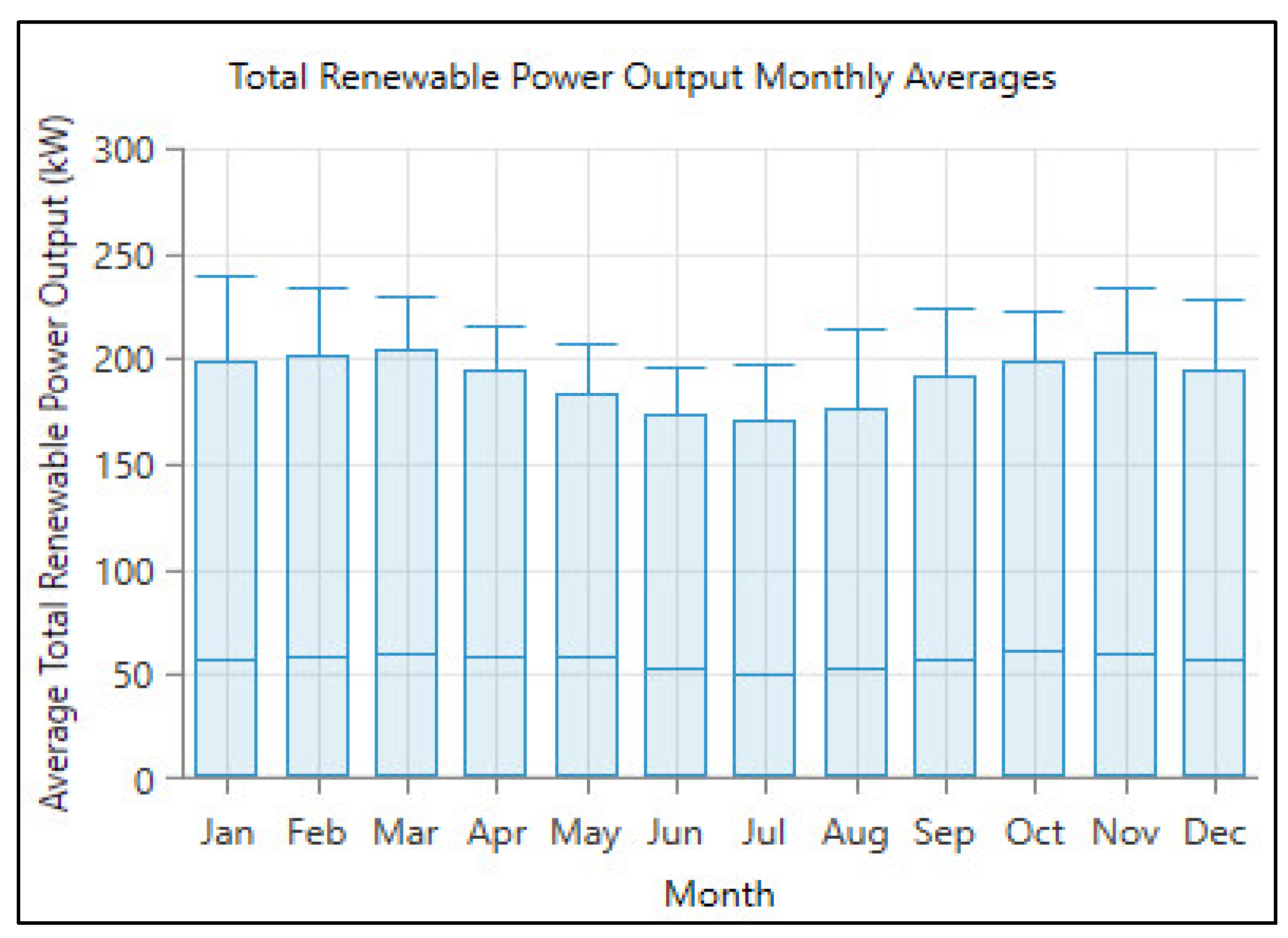
3.2. Homer-Pro Model Results
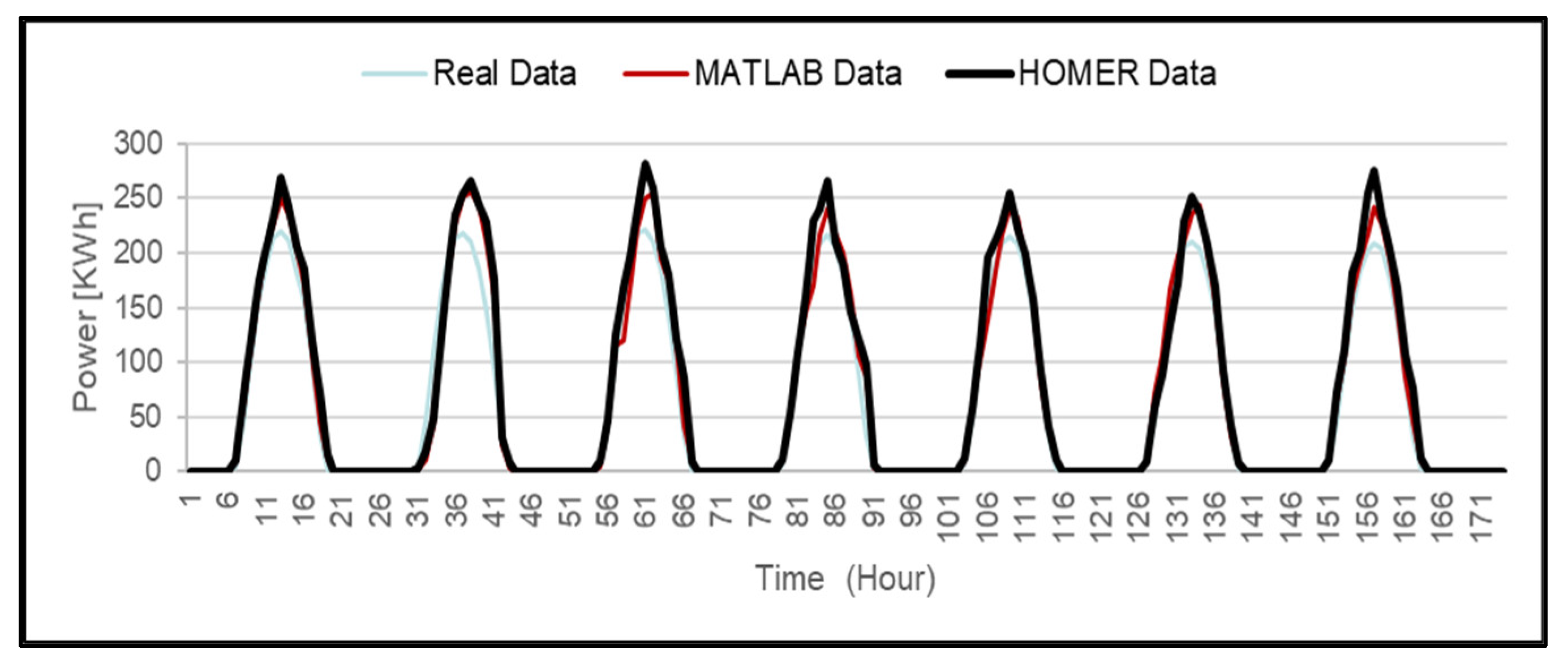
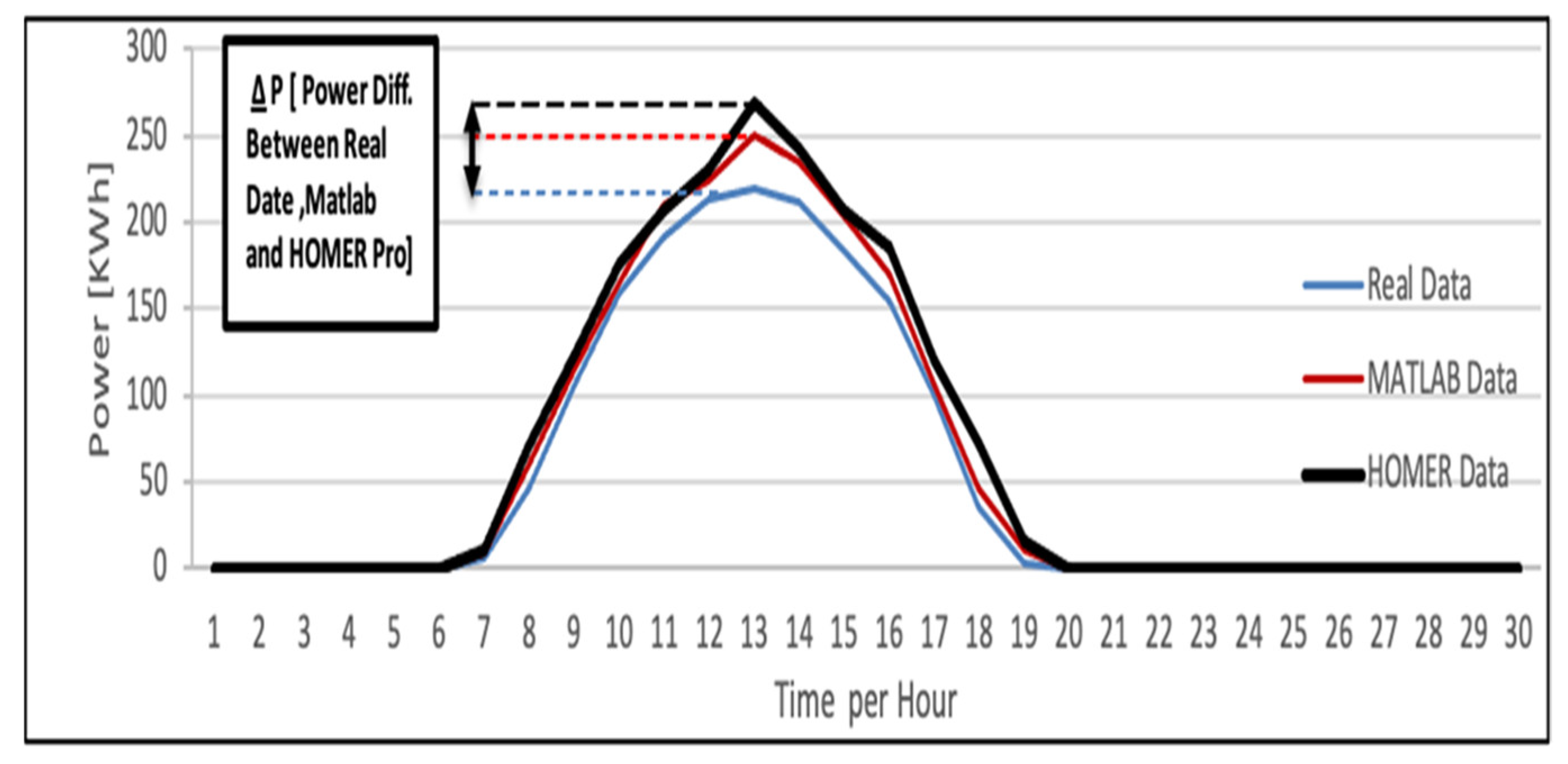
3.3. Experimental and Recorded Real Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kazem, H.A. Renewable energy in Oman: Status and future prospects. Renew. Sustain. Energy Rev. 2011, 15, 3465–3469. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Y.; Wang, Q.; Lv, J.; Wen, J.; Chen, X.; Kang, C.; Cheng, S.; McElroy, M.B. Pathway toward carbon-neutral electrical systems in China by mid-century with negative CO2 abatement costs informed by high-resolution modeling. Joule 2021, 5, 2715–2741. [Google Scholar] [CrossRef]
- Rahman, M.M.; Khan, I.; Field, D.L.; Techato, K.; Alameh, K. Powering agriculture: Present status, future potential, and challenges of renewable energy applications. Renew. Energy 2022, 188, 731–749. [Google Scholar] [CrossRef]
- Obaideen, K.; Olabi, A.G.; Al Swailmeen, Y.; Shehata, N.; Abdelkareem, M.A.; Alami, A.H.; Rodriguez, C.; Sayed, E.T. Solar Energy: Applications, Trends Analysis, Bibliometric Analysis and Research Contribution to Sustainable Development Goals (SDGs). Sustainability 2023, 15, 1418. [Google Scholar] [CrossRef]
- Mukisa, N.; Zamora, R.; Lie, T.T. Energy Business Initiatives for Grid-Connected Solar Photovoltaic Systems: An Overview. Sustainability 2022, 14, 15060. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D.; Huang, C.; Zhang, H.; Dai, N.; Song, Y.; Chen, H. Artificial intelligence in sustainable energy industry: Status Quo, challenges and opportunities. J. Clean. Prod. 2021, 289, 125834. [Google Scholar] [CrossRef]
- O’Shaughnessy, E.; Cruce, J.R.; Xu, K. Too much of a good thing? Global trends in the curtailment of solar PV. Sol. Energy 2020, 208, 1068–1077. [Google Scholar] [CrossRef]
- You, M.; Wang, Q.; Sun, H.; Castro, I.; Jiang, J. Digital twins based day-ahead integrated energy system scheduling under load and renewable energy uncertainties. Appl. Energy 2022, 305, 117899. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Ghalandari, M.; Maleki, A.; Haghighi, A.; Shadloo, M.S.; Nazari, M.A.; Tlili, I. Applications of nanofluids containing carbon nanotubes in solar energy systems: A review. J. Mol. Liq. 2020, 313, 113476. [Google Scholar] [CrossRef]
- Barhoumi, E.M.; Belgacem, I.B.; Khiareddine, A.; Zghaibeh, M.; Tlili, I. A Neural Network-Based Four Phases Interleaved Boost Converter for Fuel Cell System Applications. Energies 2018, 11, 3423. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. One-shot battery degradation trajectory prediction with deep learning. J. Power Sources 2021, 506, 230024. [Google Scholar] [CrossRef]
- Ridha, H.M.; Gomes, C.; Hizam, H.; Ahmadipour, M.; Heidari, A.A.; Chen, H. Multi-objective optimization and multi-criteria decision-making methods for optimal design of standalone photovoltaic system: A comprehensive review. Renew. Sustain. Energy Rev. 2021, 135, 110202. [Google Scholar] [CrossRef]
- Rejeb, O.; Shittu, S.; Ghenai, C.; Li, G.; Zhao, X.; Bettayeb, M. Optimization and performance analysis of a solar concentrated photovoltaic-thermoelectric (CPV-TE) hybrid system. Renew. Energy 2020, 152, 1342–1353. [Google Scholar] [CrossRef]
- Sailor, D.J.; Anand, J.; King, R.R. Photovoltaics in the built environment: A critical review. Energy Build. 2021, 253, 111479. [Google Scholar] [CrossRef]
- Conceição, R.; González-Aguilar, J.; Merrouni, A.A.; Romero, M. Soiling effect in solar energy conversion systems: A review. Renew. Sustain. Energy Rev. 2022, 162, 112434. [Google Scholar] [CrossRef]
- Alzoubi, A. Machine Learning for Intelligent Energy Consumption in Smart Homes. Int. J. Comput. Inf. Manuf. 2022, 2, 62–75. [Google Scholar] [CrossRef]
- Okonkwo, P.C.; Barhoumi, E.M.; Emori, W.; Shammas, M.I.; Uzoma, P.C.; Mohamed, A.M.A.; Abdullah, A.M. Economic evaluation of hybrid electrical systems for rural electrification: A case study of a rural community in Nigeria. Int. J. Green Energy 2022, 19, 1059–1071. [Google Scholar] [CrossRef]
- Barhoumi, E.M.; Okonkwo, P.C.; Zghaibeh, M.; Belgacem, I.B.; Farhani, S.; Bacha, F. Optimization of PV-Grid Connected System Based Hydrogen Refueling Station. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; pp. 1603–1607. [Google Scholar] [CrossRef]
- Al-Karaghouli, A.; Kazmerski, L.L. Optimization and life-cycle cost of health clinic PV system for a rural area in southern Iraq using HOMER software. Sol. Energy 2010, 84, 710–714. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, A.; Khemariya, M. Homer Optimization Based Solar PV; Wind Energy and Diesel Generator Based Hybrid System. Int. J. Soft Comput. Eng. 2013, 3, 199–204. [Google Scholar]
- Garni, H.A.; Awasthi, A. Techno-economic feasibility analysis of a solar PV grid-connected system with different tracking using HOMER software. In Proceedings of the 2017 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 14–17 August 2017; pp. 217–222. [Google Scholar] [CrossRef]
- Cebecauer, T.; Suri, M. Typical Meteorological Year Data: SolarGIS Approach. Energy Procedia 2015, 69, 1958–1969. [Google Scholar] [CrossRef]
- Tarigan, E.; Djuwari; Purba, L. Assessment of PV Power Generation for Household in Surabaya Using SolarGIS–pvPlanner Simulation. Energy Procedia 2014, 47, 85–93. [Google Scholar] [CrossRef]
- Jamil, I.; Zhao, J.; Zhang, L.; Jamil, R.; Rafique, S.F. Evaluation of Energy Production and Energy Yield Assessment Based on Feasibility, Design, and Execution of 3 × 50 MW Grid-Connected Solar PV Pilot Project in Nooriabad. Int. J. Photoenergy 2017, 2017, 6429581. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Y.; Meng, F.; Liu, Z. Experimental Investigation of the Shading and Mismatch Effects on the Performance of Bifacial Photovoltaic Modules. IEEE J. Photovolt. 2020, 10, 296–305. [Google Scholar] [CrossRef]
- Akram, N.; Khan, L.; Agha, S.; Hafeez, K. Global Maximum Power Point Tracking of Partially Shaded PV System Using Advanced Optimization Techniques. Energies 2022, 15, 4055. [Google Scholar] [CrossRef]
- Singh, A.; Baredar, P.; Gupta, B. Techno-economic feasibility analysis of hydrogen fuel cell and solar photovoltaic hybrid renewable energy system for academic research building. Energy Convers. Manag. 2017, 145, 398–414. [Google Scholar] [CrossRef]
- Alizadeh, H.; Nazari, M.A.; Ghasempour, R.; Shafii, M.B.; Akbarzadeh, A. Numerical analysis of photovoltaic solar panel cooling by a flat plate closed-loop pulsating heat pipe. Sol. Energy 2020, 206, 455–463. [Google Scholar] [CrossRef]
- Okedu, K.E.; Uhunmwangho, R. Optimization of Renewable Energy Efficiency using HOMER. Int. J. Renew. Energy Res. 2014, 4, 421–427. [Google Scholar]


| Parameter | Symbol | Value |
|---|---|---|
| Photocurrent | Iph | 8 A |
| Saturation current | I0 | 2.5 × 10−10 A |
| Series resistance | Rs | 0.5 Ω |
| Diode ideality factor | a | 1.3 |
| Thermal voltage | VT | 25.85 mV |
| Nominal output power | P0 | 250 kW |
| Reference temperature | T0 | 25 °C |
| Reference solar radiation | G0 | 1000 W/m2 |
| Temperature coefficient | α | 0.5%/°C |
| Time | T.PV. Surface [°C] | Solar Radiation [W/m2] | Generated Power Recorded Data [kWh] | Generated Power MatalbModel [kWh] | Generated Power Homer Model [kWh] |
|---|---|---|---|---|---|
| 4 a.m. | 21.45 | 0 | 0 | 0 | 0 |
| 5 a.m. | 20.66 | 0 | 0 | 0 | 0 |
| 6 a.m. | 20.81 | 21.02 | 5.23 | 8.6566 | 10.998 |
| 7 a.m. | 26.52 | 208.27 | 45.65 | 59.91 | 70.12675 |
| 8 a.m. | 34.84 | 478.58 | 106.15 | 114.97 | 122.89457 |
| 9 a.m. | 46.21 | 722.03 | 158.4 | 165.593 | 175.3129 |
| 10 a.m. | 57.02 | 906.68 | 191.68 | 209.593 | 207.4723 |
| 11 a.m. | 59.19 | 1017.42 | 213.13 | 223.656 | 230.1718 |
| 12 p.m. | 59.42 | 1049.62 | 219.18 | 250.07 | 269.4676 |
| 1 p.m. | 57.93 | 998.62 | 212.3 | 235.285 | 242.39704 |
| 2 p.m. | 52.86 | 869.34 | 183.43 | 204.334 | 207.10436 |
| 3 p.m. | 49.23 | 661.32 | 154.28 | 170.5987 | 185.45966 |
| 4 p.m. | 43.04 | 398.08 | 100.1 | 106.9301 | 120.33 |
| 5 p.m. | 36.9 | 145.6 | 35.2 | 45.533 | 72.467 |
| 6 p.m. | 32.39 | 4 | 2.2 | 10.466 | 15.222 |
| 7 p.m. | 30.7 | 0 | 0 | 0 | 0 |
| 8 p.m. | 30.06 | 0 | 0 | 0 | 0 |
| 9 p.m. | 29.52 | 0 | 0 | 0 | 0 |
| 10 p.m. | 28.25 | 0 | 0 | 0 | 0 |
| Experimental Results | Analytical Model | % Error | Homer | % Error | |
|---|---|---|---|---|---|
| Hourly average produced power | 46 kWh | 48.6 kWh | 5.65 | 49.2 kWh | 6.96 |
| Daily average produced power | 1090 kWh | 1120 kWh | 2.75 | 1154 kWh | 5.87 |
| Monthly average produced power | 36.5 MWh | 38 MWh | 4.11 | 39 MWh | 6.85 |
| Monthly maximum produced power | 37 MWh | 39.8 MWh | 7.57 | 40.3 MWh | 8.92 |
| Monthly minimum produced power | 33.5 MWh | 34 MWh | 1.49 | 35 MWh | 4.48 |
| Yearly produced power | 411,252 kWh | 430,100 kWh | 4.62 | 444,320 kWh | 8.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhousni, F.K.; Alnaimi, F.B.I.; Okonkwo, P.C.; Ben Belgacem, I.; Mohamed, H.; Barhoumi, E.M. Photovoltaic Power Prediction Using Analytical Models and Homer-Pro: Investigation of Results Reliability. Sustainability 2023, 15, 8904. https://doi.org/10.3390/su15118904
Alhousni FK, Alnaimi FBI, Okonkwo PC, Ben Belgacem I, Mohamed H, Barhoumi EM. Photovoltaic Power Prediction Using Analytical Models and Homer-Pro: Investigation of Results Reliability. Sustainability. 2023; 15(11):8904. https://doi.org/10.3390/su15118904
Chicago/Turabian StyleAlhousni, Fadhil Khadoum, Firas Basim Ismail Alnaimi, Paul C. Okonkwo, Ikram Ben Belgacem, Hassan Mohamed, and El Manaa Barhoumi. 2023. "Photovoltaic Power Prediction Using Analytical Models and Homer-Pro: Investigation of Results Reliability" Sustainability 15, no. 11: 8904. https://doi.org/10.3390/su15118904
APA StyleAlhousni, F. K., Alnaimi, F. B. I., Okonkwo, P. C., Ben Belgacem, I., Mohamed, H., & Barhoumi, E. M. (2023). Photovoltaic Power Prediction Using Analytical Models and Homer-Pro: Investigation of Results Reliability. Sustainability, 15(11), 8904. https://doi.org/10.3390/su15118904







