Deep-Reinforcement-Learning-Based Active Disturbance Rejection Control for Lateral Path Following of Parafoil System
Abstract
1. Introduction
- A new guidance law for the lateral path-following control of the parafoil system is proposed.
- Based on the guidance law, an LADRC controller is designed to overcome the influence of unknown disturbances during parafoil flight.
- The DQN algorithm of RL is applied to obtain the real-time parameters of the controller based on the parafoil flight states.
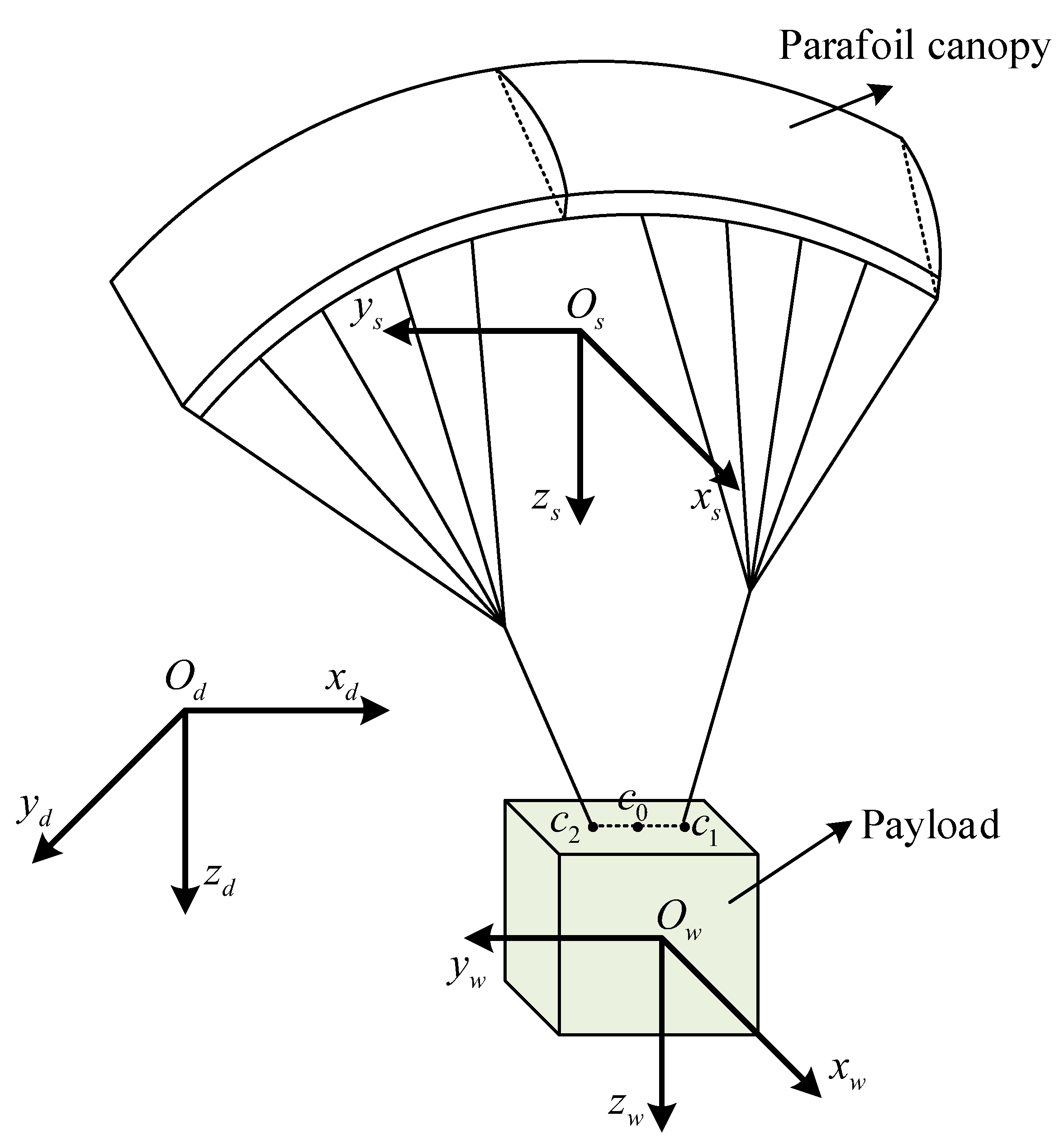
2. Dynamic Model of Parafoil System
- The mass center of the parafoil canopy coincides with the aerodynamic pressure center but does not coincide with the gravity center.
- The lift of the payload is ignored and only the aerodynamic drag is considered.
- The elastic deformation of the connecting ropes is ignored.
2.1. Motion Equation of Payload
2.2. Motion Equation of Parafoil Canopy
2.3. Constraints of Velocity and Angular Velocity
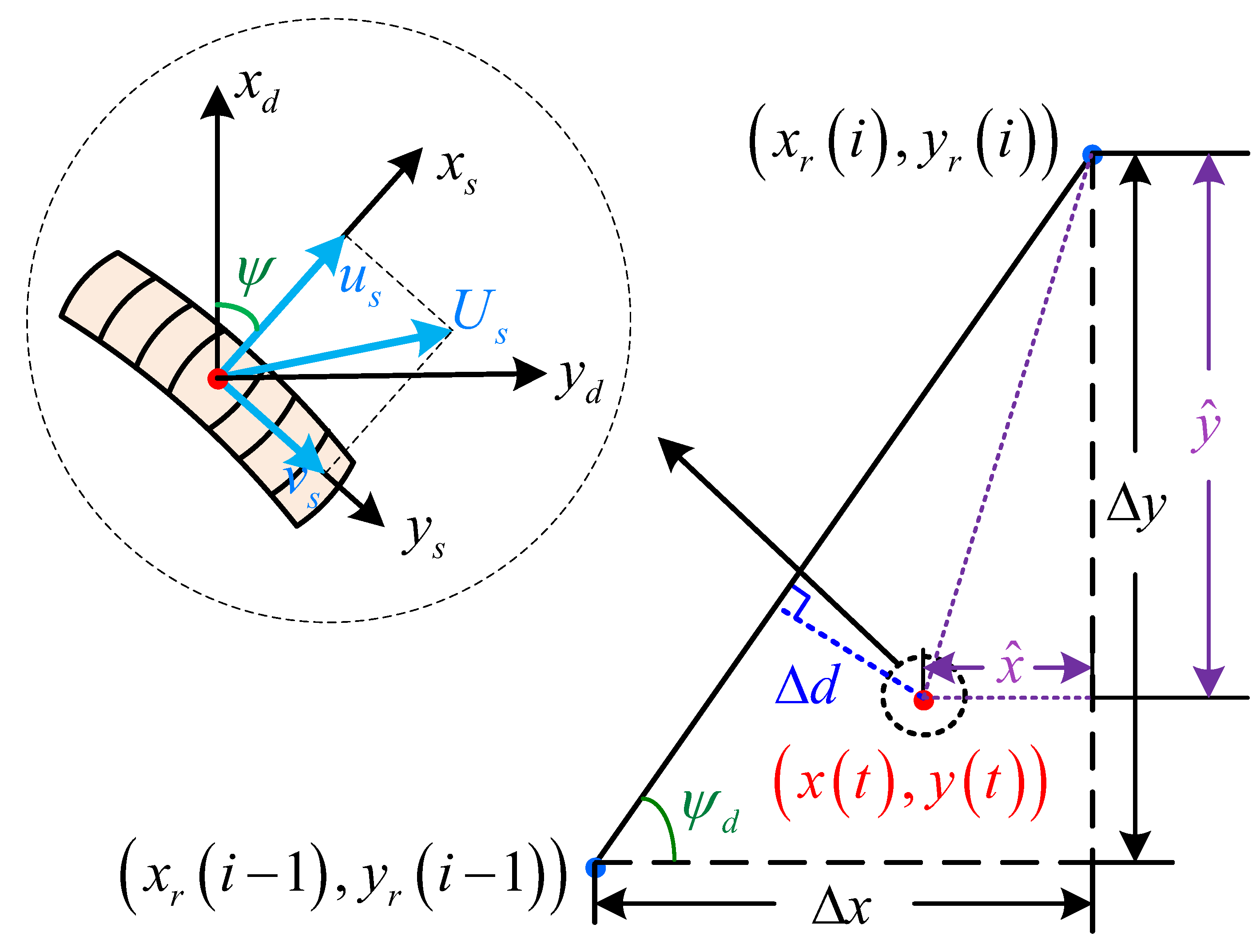
3. Linear Active Disturbance Rejection Controller (LADRC)-Based Path-Following Control
3.1. Guidance Law
- (a)
- . In this case, .
- (b)
- . In this case, . Then, , and thus, .
- (c)
- . In this case, . Then, , and thus, .
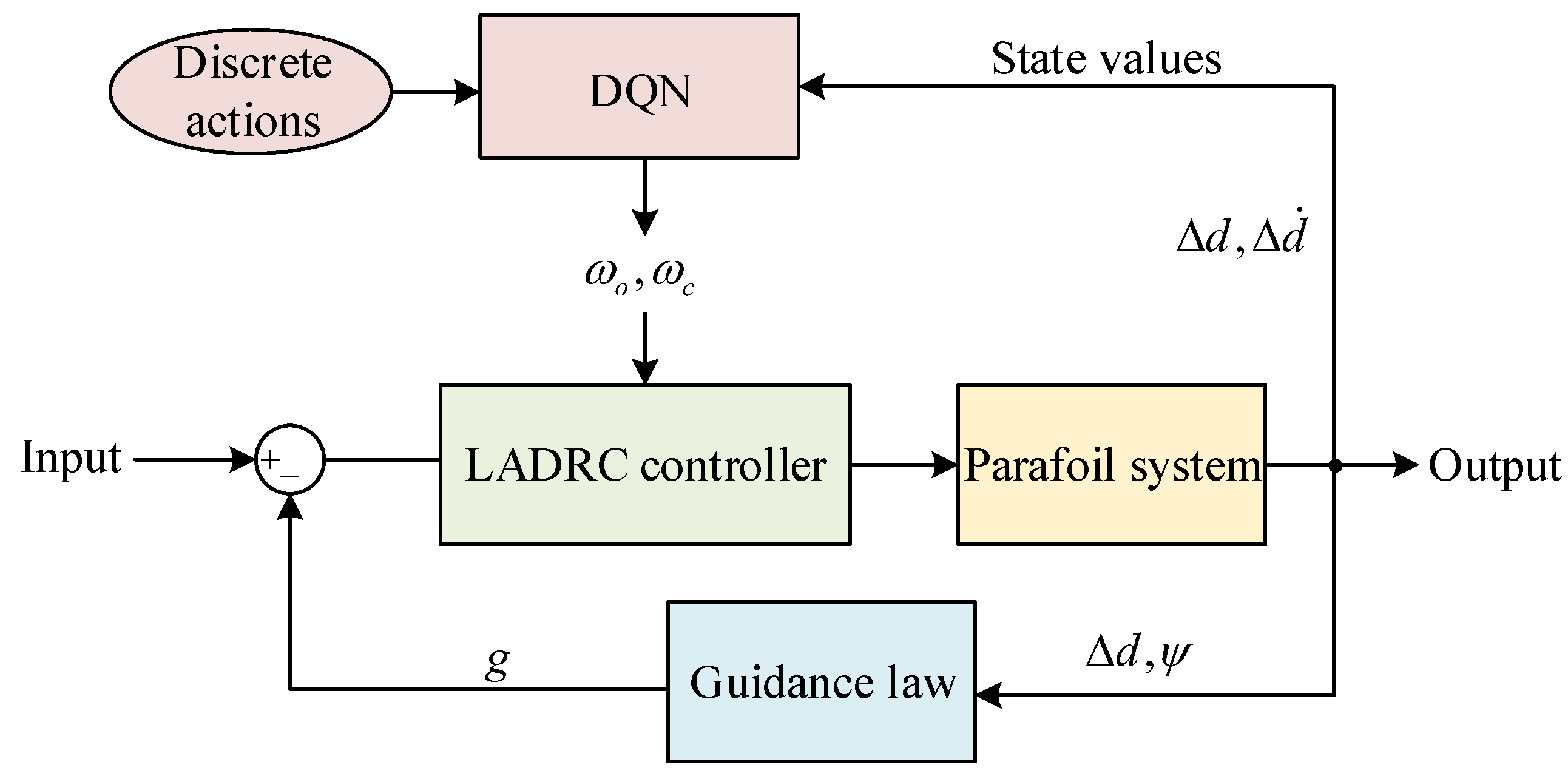
3.2. Design of LADRC
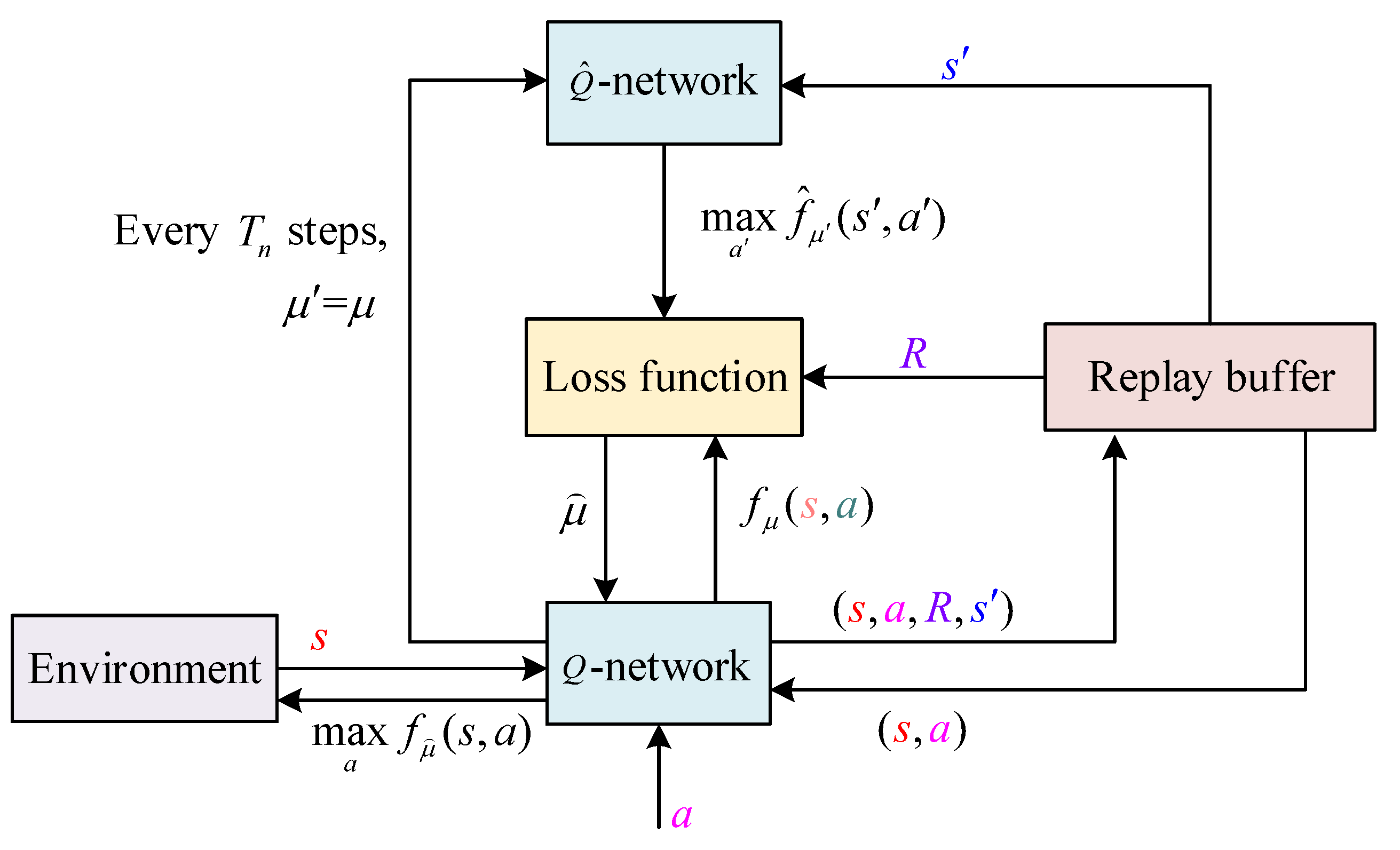
4. Deep Q-Network (DQN)-Optimized LADRC
4.1. Basics of DQN
4.2. Design of Agent Based on Parafoil System
| Algorithm 1: DQN algorithm. |
|
5. Simulation and Analysis
5.1. Environment Setting
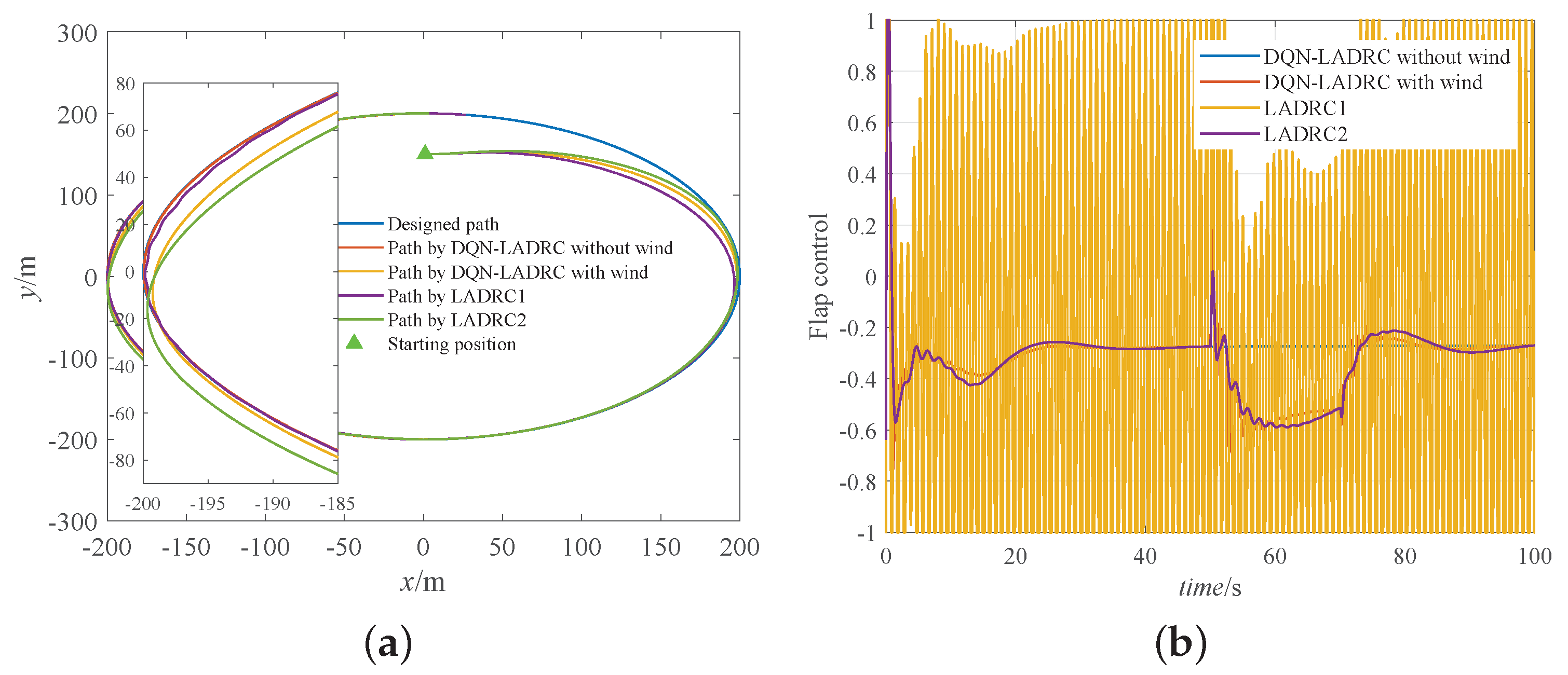
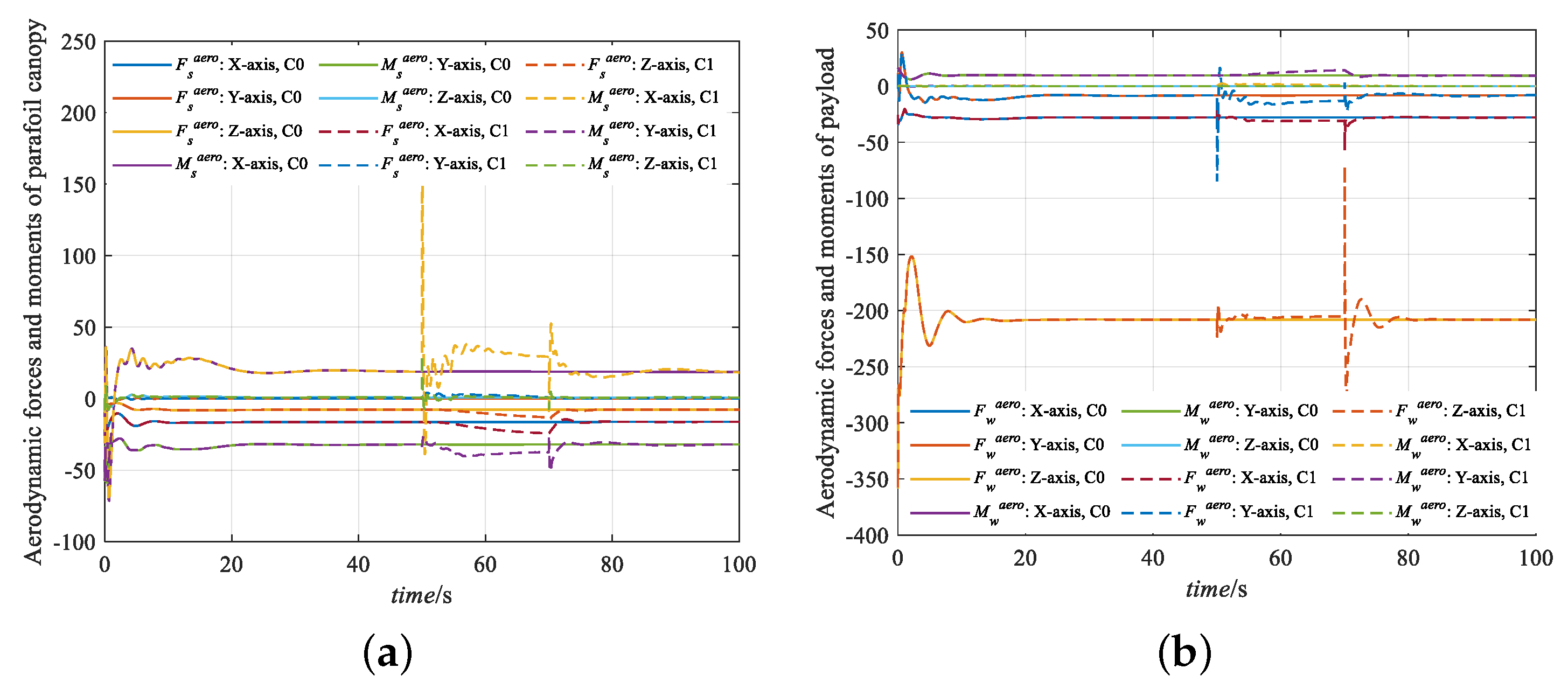
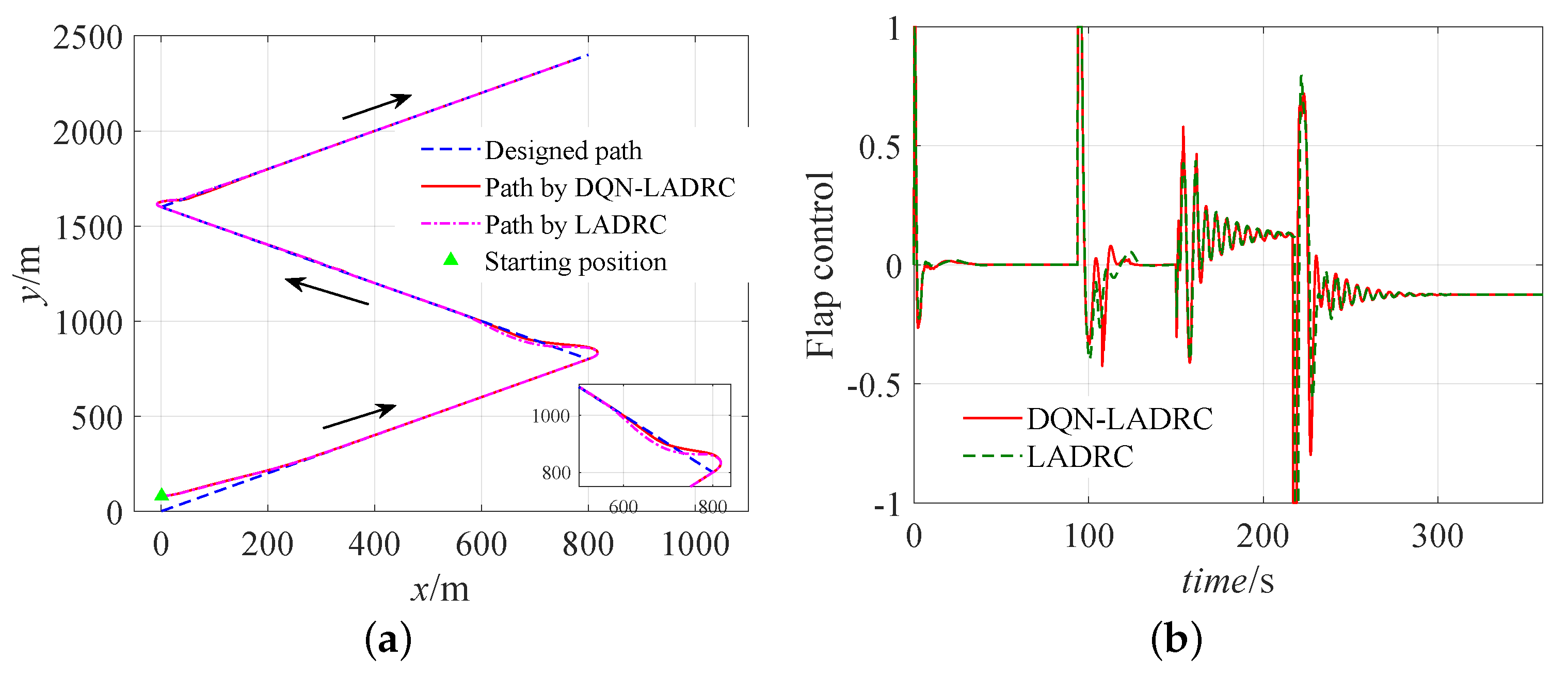
5.2. Performance Study of DQN-LADRC under Wind Disturbances
5.2.1. Circular Path Following
5.2.2. Straight Path Following
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, H.; Sun, Q.; Liu, X.; Liu, J. Fluid–structure interaction-based aerodynamic modeling for flight dynamics simulation of parafoil system. Nonlinear Dyn. 2021, 104, 3445–3466. [Google Scholar] [CrossRef]
- Guo, Y.; Yan, J.; Wu, C.; Xiao, B. Modeling and practical fixed-time attitude tracking control of a paraglider recovery system. ISA Trans. 2022, 128, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Slegers, N.; Costello, M. Model predictive control of a parafoil and payload system. J. Guid. Control Dyn. 2005, 28, 816–821. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Z.; Fu, Y. Dynamics analysis and simulation of six DOF parafoil system. Clust. Comput. 2018, 22, 12669–12680. [Google Scholar] [CrossRef]
- Zhu, E.; Sun, Q.; Tan, P.; Chen, Z. Modeling of powered parafoil based on Kirchhoff motion equation. Nonlinear Dyn. 2014, 79, 617–629. [Google Scholar] [CrossRef]
- Tan, P.; Sun, M.; Sun, Q.; Chen, Z. Dynamic modeling and experimental verification of powered parafoil with two suspending points. IEEE Access 2020, 8, 12955–12966. [Google Scholar] [CrossRef]
- Prakash, O. NDI based generic heading tracking control law for parafoil/payload system. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020. [Google Scholar] [CrossRef]
- Tao, J.; Dehmer, M.; Xie, G.; Zhou, Q. A generalized predictive control-based path following method for parafoil systems in wind environment. IEEE Access 2019, 7, 42586–42595. [Google Scholar] [CrossRef]
- Zhao, L.; He, W.; Lv, F. Model-free adaptive control for parafoil systems based on the iterative feedback tuning method. IEEE Access 2021, 9, 35900–35914. [Google Scholar] [CrossRef]
- Guo, Y.; Yan, J.; Wu, C.; Wu, X.; Chen, M.; Xing, X. Autonomous homing design and following for parafoil/rocket system with high-altitude. J. Intell. Robot. Syst. 2021, 101, 73. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Yao, M.; Chen, Q.; Guo, R.; Sun, T.; Jiang, T.; Zhao, Z. 6-DOF modeling and 3D trajectory tracking control of a powered parafoil system. IEEE Access 2020, 8, 151087–151105. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.; Sun, H.; Chen, Z.; Dehmer, M.; Sun, M. Dynamic modeling and trajectory tracking control of parafoil system in wind environment. IEEE ASME Trans. Mechatron. 2017, 22, 2736–2745. [Google Scholar] [CrossRef]
- Tao, J.; Liang, W.; Sun, Q.; Tan, P.; Luo, S.; Chen, Z.; He, Y. Modeling and control of a powered parafoil in wind and rain environments. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1642–1659. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2019, 56, 900–906. [Google Scholar] [CrossRef]
- Han, J. Auto-disturbance-rejection controller and its applications. Contr. Decis. 1998, 13, 19–23. [Google Scholar]
- Gao, Z. On the foundation of active disturbance rejection control. Control. Theory Appl. 2013, 30, 1498–1510. [Google Scholar]
- Chen, Z.; Wang, Y.; Sun, M.; Sun, Q. Convergence and stability analysis of active disturbance rejection control for first-order nonlinear dynamic systems. Trans. Inst. Meas. Control 2019, 41, 2064–2076. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Sun, M.; Sun, Q. On the stability and convergence rate analysis for the nonlinear uncertain systems based upon active disturbance rejection control. Int. J. Robust Nonlinear Control 2020, 30, 5728–5750. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Z.; Huang, Z.; Sun, M. Active disturbance rejection controller for multi-area interconnected power system based on reinforcement learning. Neurocomputing 2021, 425, 149–159. [Google Scholar] [CrossRef]
- Zheng, Y.; Tao, J.; Sun, H.; Sun, Q. An intelligent course keeping active disturbance rejection controller based on Double Deep Q-network for towing system of unpowered cylindrical drilling platform. Int. J. Robust Nonlinear Control 2021, 31, 8463–8480. [Google Scholar] [CrossRef]
- Tao, J.; Du, L.; Dehmer, M.; Wen, Y. Path following control for towing system of cylindrical drilling platform in presence of disturbances and uncertainties. ISA Trans. 2019, 95, 185–193. [Google Scholar] [CrossRef]
- Zeng, D.; Yu, Z.; Xiong, L.; Fu, Z.; Li, Z. HFO-LADRC lateral motion controller for autonomous road sweeper. Sensors 2020, 20, 2274. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Luo, G.; Duan, X. Adaptive LADRC-based disturbance rejection method for electromechanical servo system. IEEE Trans. Ind. Appl. 2020, 56, 876–889. [Google Scholar] [CrossRef]
- Li, R.; Li, T.; Bu, R.; Zheng, Q.; Chen, C.L. Active disturbance rejection with sliding mode control-based course and path following for underactuated ships. Math. Probl. Eng. 2013, 2013, 743716-1–743716-9. [Google Scholar] [CrossRef]
- Zhao, P.; Nagamune, R. Switching linear parameter-varying control with improved local performance and optimized switching surfaces. Int. J. Robust Nonlinear Control 2018, 28, 3403–3421. [Google Scholar] [CrossRef]
- Li, Y.; Jia, M.; Han, X. Towards a comprehensive optimization of engine efficiency and emissions by coupling artificial neural network (ANN) with genetic algorithm (GA). Energy 2021, 225, 120331. [Google Scholar] [CrossRef]
- Ho, S.; Shu, L. Optimizing fuzzy neural networks for tuning PID controllers using an orthogonal simulated annealing algorithm OSA. IEEE Trans. Fuzzy Syst. 2006, 14, 421–434. [Google Scholar] [CrossRef]
- Sun, C.; Liu, M.; Liu, C.A.; Feng, X.; Wu, H. An industrial quadrotor UAV control method based on fuzzy adaptive linear active disturbance rejection control. Electronics 2021, 10, 376. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Zhao, Y.; Qi, X.; Ma, Y.; Li, Z.; Malekian, R.; Sotelo, M.A. Path following optimization for an underactuated USV using smoothly-convergent deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1–13. [Google Scholar] [CrossRef]
- Xue, W.; Huang, Y. Performance analysis of active disturbance rejection tracking control for a 513 class of uncertain LTI systems. ISA Trans. 2015, 58, 133–154. [Google Scholar] [CrossRef]
- Sun, Q.; Yu, L.; Zheng, Y.; Tao, J.; Sun, H.; Sun, M.; Dehmer, M.; Chen, Z. Trajectory tracking control of powered parafoil system based on sliding mode control in a complex environment. Aerosp. Sci. Technol. 2022, 122, 107406. [Google Scholar] [CrossRef]





| Parameter Description | Value |
|---|---|
| Wing span | 4.5 m |
| Mean aerodynamic chord | 1.3 m |
| Mass of parafoil | 1.7 kg |
| Mass of payload | 20 kg |
| Wing area | 6.5 |
| Rope length | 3 m |
| Parameter Description | Value |
|---|---|
| Simulation sample step | 0.02 s |
| Number of iterations | 300 |
| Learning rate of Q-network | |
| Discount factor | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Tao, J.; Sun, Q.; Sun, H.; Chen, Z.; Sun, M.; Duan, F. Deep-Reinforcement-Learning-Based Active Disturbance Rejection Control for Lateral Path Following of Parafoil System. Sustainability 2023, 15, 435. https://doi.org/10.3390/su15010435
Zheng Y, Tao J, Sun Q, Sun H, Chen Z, Sun M, Duan F. Deep-Reinforcement-Learning-Based Active Disturbance Rejection Control for Lateral Path Following of Parafoil System. Sustainability. 2023; 15(1):435. https://doi.org/10.3390/su15010435
Chicago/Turabian StyleZheng, Yuemin, Jin Tao, Qinglin Sun, Hao Sun, Zengqiang Chen, Mingwei Sun, and Feng Duan. 2023. "Deep-Reinforcement-Learning-Based Active Disturbance Rejection Control for Lateral Path Following of Parafoil System" Sustainability 15, no. 1: 435. https://doi.org/10.3390/su15010435
APA StyleZheng, Y., Tao, J., Sun, Q., Sun, H., Chen, Z., Sun, M., & Duan, F. (2023). Deep-Reinforcement-Learning-Based Active Disturbance Rejection Control for Lateral Path Following of Parafoil System. Sustainability, 15(1), 435. https://doi.org/10.3390/su15010435










