1. Introduction
Hydrometry, which is the knowledge of assessing volumetric or hefty flow under pressure in open canals, is important for managing water resources. Various methods have been employed to measure flow in open channels, including pressure differences, hydraulic structures (flumes and weirs), velocity-area and tracer dilution [
1,
2,
3]. Among these, gates and weirs are most widely used for flow measurement and discharge control in open canals [
4,
5]. The shape of the critical section and the upstream potential energy are the most effective parameters to determine the flow discharge in the crucial section (Dayev et al., 2021; Alkhatib and Gogus, 2014) [
6,
7]. Broad-crested weirs (BCW) can be used as dam channels and often as a dam. The BCW is a specially shaped weir (weir with a broad crest) designed to fit complex channel cross-sections [
8]. The control section can also be shaped according to the range of variation of the discharge and head. Furthermore, the BCW, especially when the upstream side is inclined, can easily transmit the floating elements and sediment better than the sharp-crested weir [
7]. Various investigations conducted on broad-crested weirs reported that the combined weir gate could adjust the upstream water level, flow control, and discharge measurement to meet agricultural needs [
9,
10,
11,
12,
13]. According to Sakaruya and Kokpinar [
14], the topmost benefit of a combined weir gate is the minimization and prevention of upstream sediment accumulation, which enhances the structure’s efficiency.
Several studies have been conducted to investigate the combined sharp-crested weir and gate [
14,
15,
16,
17,
18]. Negm et al. [
15] studied unrestricted flow over sharp-crested weirs and underneath gates. They investigated the effect of the geometrical and hydraulic parameters on the structures and reported that the rate of upstream water depth to gate opening (
H/
d) had major effects on the discharge. Ferro [
19] presented discharge equations for a simple broad-crested-weir gate using incomplete self-similarity theory and dimensional analysis. Alhamid [
16] investigated various combinations of weir-like gate proportions for both unrestricted and inundated flow and developed a discharge equation considering the effective parameters.
Soft computing approaches such as artificial intelligence (AI)-based models and multivariate analysis are widely employed in hydrology nowadays for decision-making [
20,
21,
22,
23,
24,
25,
26,
27,
28,
29]. The AI models have helped in the reduction in operation costs and time for decision-making rather than assessment through experimentation [
30,
31]. These techniques efficiently use the parameters and their backgrounds for problem estimation instead of merely resolving the prime equations [
32,
33]. Therefore, they can be used directly for resolving problems despite the many parameters and their interactions which create ambiguity and complexity in finding the solutions [
25]. Discharge coefficient prediction using AI models has been successfully tested for triangular-labyrinth side weirs [
34,
35,
36,
37,
38,
39], semi-elliptical side weirs [
40], trapezoidal-labyrinth side weirs [
41,
42,
43,
44,
45,
46], rectangular side weirs [
47,
48,
49,
50,
51,
52,
53], and other types of weirs and gates [
54,
55,
56,
57,
58,
59]. However, the literature suggests that despite several existing acceptable techniques for estimating the discharge coefficient of hydraulic structures, the flow passing over a rectangular compound broad-crested-weir gate has not been considered using these techniques.
The main purpose of the present study was to develop new simple methods to predict this combined structure discharge coefficient (Cdt). The validated computational fluid dynamics (CFD) model was used to achieve this goal for a combined structure. This study proposed random forest (RF), M5P, support vector machine (SVM), genetic programming (GP), multilinear regression (MLR) and multimode artificial neural networks (ANN) to predict the Cdt in the compound BCW gate. All the effective parameters were changed to make different combinations of this structure. The BCW gate can be used as a flood control reservoir and a measuring device for minimizing the sediments and preventing their accumulation. An accurate prediction of the Cdt in the compound BCW gate could significantly improve its operational management and, thus, water resources management.
2. Theoretical Background
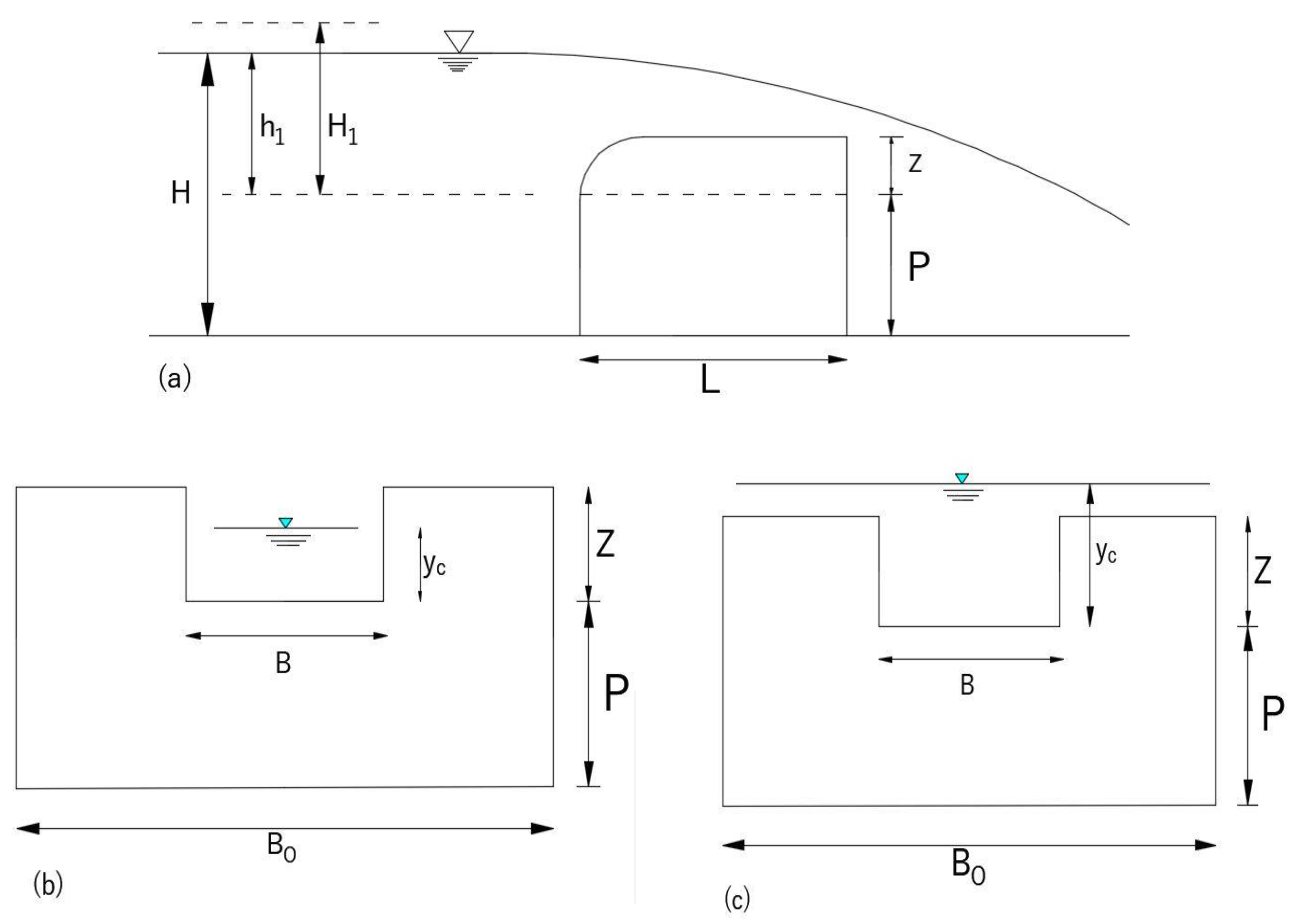
Figure 1a shows a rectangular, compound broad-crested weir. According to the upstream hydraulic head, there can be two cases. First, if the passage of the outlet discharge is only through the central weir (
h1 <
Z) (
Figure 1b), the broad-crested weir performs like a basic weir, and there will be no flow over the compound section.
In this case, the critical depth (
yc) will be lower than the central weir height (
Z) and weir discharge (
Qw) though the broad-crested weir can be as follows [
60,
61];
where
where
Cdw denotes the weir discharge coefficient,
Cv denotes the weir velocity coefficient. Furthermore,
h1,
g,
B and
H1 are the water height above the central weir, acceleration gravity, central weir width and head overall energy at the weir head assessment section, respectively.
In another case, the water height above the central weir (
h1) surpasses the central weir height (
Z), and the weir acts as a compound weir (
Figure 1c). Furthermore, the critical flow depth (
yc) will be greater than the central weir height (
Z). In this case, the BCW discharge (
Qw) is obtained by Equation (4) [
5,
61]:
Similarly, the equation of discharge pertaining to gates (
Qg) can be obtained by utilizing the equation of energy, as below [
62]:
where
Cdg is the gate discharge coefficient and
d,
b and
H are the gate opening height, gate breadth and level of upstream water, respectively. The investigation of the compound BCW and gate collectively for the two mentioned cases of compound BCW are elaborated below.
2.1. Case 1
As mentioned above, when the passage of outlet discharge is only via the central weir, the complex BCW performs as a basic weir. Thus, the combined structure (
Figure 2b) discharge (
Qt) is the sum of Equation (1) and Equation (7) and can be written as Equation (8). The discharge coefficient for the combined compound BCW gate (
Cdt) can be presented by Equation (9):
2.2. Case 2
When the passage of outlet discharge is through the compound section, the complex BCW can pass more water. Therefore, the discharge equation is different. In this case, the discharge related to the compound BCW gate (
Qt) (
Figure 2c) is the sum of Equation (4) and Equation (7):
2.3. Governing Equations and Numerical Method
A three-dimensional CFD code was used to simulate a combined BCW–gate. The FLOW 3D code uses the finite volume scheme to resolve Reynolds-averaged Navier–Stokes (RANS) [
63]. The Navier–Stokes equations are known as the equations of motion in fluid velocity mechanisms (
u,
v,
w) in the three synchronous directions with some additional terms:
where
Gx-z,
fx-z and
bx-z denote body accelerations, viscous accelerations and flow losses in porous media, respectively. Furthermore,
Ax,
Ay and
Az refer to the cross-sectional extent of the flow;
ρ denotes the density of water, indicates the fractional volume open to flow in fractional area/volume obstacle representation (FAVOR), R
SOR denotes the source term,
p denotes the pressure, and the concluding terms constitute the inclusion of mass at a source signified by a geometry component. The term
Uw = (
uw, uw,
ww) is the velocity of the source component, and the term
Us = (
us,
vs,
ws) is the velocity at the surface of the source relative to the source itself.
R in Equation (12) is the coefficient that depends on the choice of coordination system.
The volume of fluid (VOF) and FAVOR are the volume-fraction techniques employed for the condition of the depicting cell in the water surface and determination of the geometry, respectively [
64]. Using this method, the CFD code enables us to ignore the surrounding air and its effect on the flowing water and create a sharp boundary between the air and water without the existence of fine interlocks [
65,
66,
67]:
Hirt and Sicilian [
68] formulated the FAVOR method which is used to ascertain the level of the solid body inside an individual cell. In addition, this method can also determine the volume of cells unoccupied by a solid body. The CFD code used presents six turbulence models, including
k−
w,
k−
ε,
RNG (the design is devised on
Re normalization groups with the equation of stress), one equation model, large-eddy simulation (
LES) and the Prandtl mixing-length model [
69].
3. Methods
The current investigation aimed to simulate a combined compound rectangular broad-crested-weir gate using FLOW-3D software. In order to do this, validation of numerical code was carried out using experimental results. The literature review indicated that the compound BCW-gate structure has not been studied before. Therefore, the experimental results of a single compound broad-crested weir by Salmasi et al., [
12] were used for the calibration of CFD code. Salmasi et al. [
12] experimentally studied a single broad-crested weir and estimated its properties, as given in
Table 1. To achieve the actual BCW, an attempt was made to deduce the relationship 0.1 <
h1/
L ≤ 0.35 (where
h1 and
L refer to the hydraulic head on the weir’s central section and the compound weir’s length, respectively) to establish the physical and arithmetic design [
70]. The flow separation was decreased by rounding with a radius of 0.065 m at the weir entrance to develop physical and numerical models of the weir [
5].
Figure 3 shows the geometry of the experimental study conducted by Salmasi et al., [
12].
To select a turbulence model with high accuracy based on the experimental results, the
K–ω and
RNG models’ outcomes were compared with those of the experimental measurements. Then, the most accurate model was used for the study. Instantaneous Navier–Stokes equations employing renormalization group theory were used to extract the
RNG model [
71]. For dissipation of the turbulent kinetic energy, the
RNG two equations model uses an additional term in the transport equations [
72]. The
RNG equations appear as follows:
where
K denotes kinetic energy,
ε stands for rate of kinetic energy dissipation,
denotes effective viscosity,
GK and
Gb stand for the generation of turbulent kinetic energy arising because of average velocity gradients and buoyancy, separately,
YM is the fluctuating dilation in compressible turbulence,
Sε and
SK are the source terms set by the user,
and
are inverse effective Prandtl numbers for the turbulent kinetic energy and its dissipation, and
,
and
are constants. Furthermore, the
refers to the main difference between the numerical models used.
CFD code uses the standard
k–w model. This empirical-based model was presented by Wilcox [
73]. Because of its formulation, it is used for better computation of shear flow spreading the low Reynolds number’s effect and compressibility. Furthermore, transport equations are used in the
k–w model for estimating turbulent kinetic energy (
k) and its dissipation rate (
w).
where
is generation of
ω,
is dissipation of ω due to turbulence,
is dissipation of
k due to turbulence,
and
are the Prandtl number of turbulent (here they are constant; equal to 2),
is the source term set by the user and
is viscosity of turbulence.
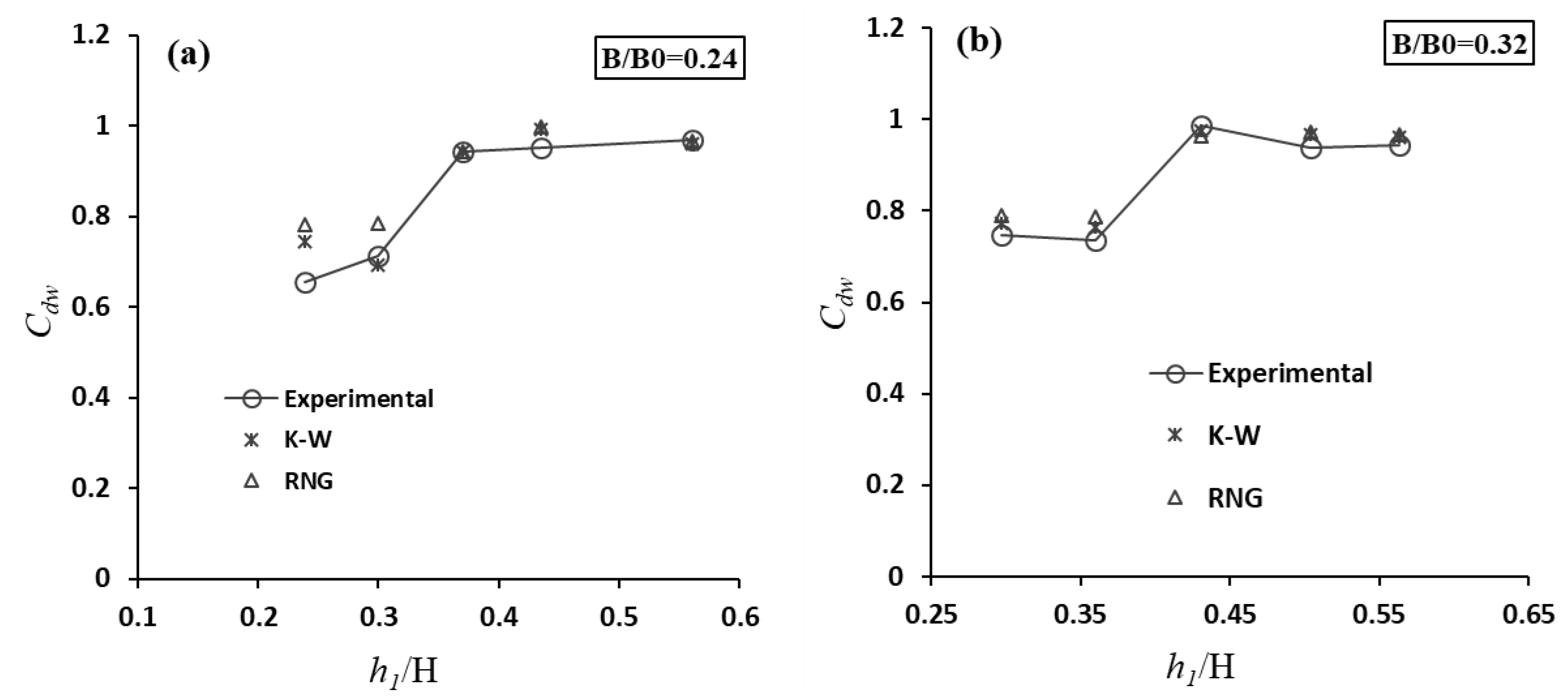
Figure 4 shows the results of
RNG and
k−
w models in estimating
Cdw.
Figure 4 shows that both models provide acceptable results in estimating
Cdw and can be used to simulate a combined compound BCW gate. The root mean square (RMSE) values were 0.2685 for
k-w against 0.3122 for
RNG, when the
k-w model was used for the simulation of the combined compound BCW-gate structure by CFD code.
The studied parameters were combined structure width, length and height (
B0,
L,
P +
Z), central weir height and width (
Z and
B) and gate opening height and width (
d and
b). For upstream water level (
H), different values were considered and two types of compound weir performance (simple weir and compound weir (
Figure 2) were studied. Considering the mentioned parameters, the results are presented using dimensionless parameters. The structure’s total section width (
B0), the height of the structure (
Z +
P) and combined structure length (
L) were considered as 0.25, 0.25 and 0.4, respectively.
Table 2 shows the studied dimensionless parameters and values.
Using these parameters, 61 numerical models were simulated using CFD code. For the arithmetic simulation, a grid of 1,200,000 elements was employed. After altering the mesh size and selecting the optimal size, the number of elements was selected. Specified pressure with specified water level and outflow was selected as X
min and X
max boundary conditions. Y
min, Y
max and Z
min were selected as boundary conditions. Furthermore, the symmetry was the Z
max boundary condition.
Figure 5 shows one of the used models and its boundary conditions.
A constancy criterion such as the Courant number was used for temporal stage calculation. Both convergence criteria and stability were used to control the time step during the iterations. Flow kinetic energy monitoring was also used to survey the steady state condition. After calibration of CFD code with experimental results, k-w model was used to simulate the combined compound BCW gate. Combined structure discharge coefficients (Cdt) were generated using the simulation results for the two mentioned cases. Using the generated Cdt values, six soft computing-based models, including RF, M5P, SVM, GP, MLP and multimode ANN, were used to predict Cdt. The mentioned dimensionless parameters were the inputs of the soft computing models.
3.1. Soft Computing Models and Artificial Intelligence Techniques
3.1.1. M5P Model
M5P is a simple tree group technique for solving nonlinear and complex issues. This novel tree technique was introduced by Quinlan [
74] for forecasting complex phenomena encompassing a huge quantity of datasets and variables. M5 tree is a piecewise simple model and takes a halfway situation between the linear and nonlinear designs [
75]. Pruning is additionally associated with this technique to avoid overfitting. The separating technique is used at each node to accomplish higher information with minor deviation inside the subset down to the individual branch. This design has three significant advances: growth of tree, trimming and smoothing. Jothiprakash and Kote [
76] explored the impact of trimming and smoothing and reported the favorable circumstances of unpruned and unsmoothed in hydrological studies. The tree model is created by unravelling the measures responsible for yielding standard deviation of the range class values to the nodes. In this strategy, linear connections are created at each node. Generally, it creates an excellent tree structure with a larger extent of precision.
3.1.2. Random Forest (RF)
RF, pioneered by Breiman [
77], is widely used for resolving intricate engineering issues due to its flexibility. It employs a massive number of trees. The root nodes receive more diverse bootstrap (known as bagging) samples than the original data set. The assigned subset of the estimator parameters is unravelled randomly at the individual node. RF is simple, less training sensitive, yet meticulous in prediction [
78]. Only two user-defined parameters: the number of trees grown (k) and the number of input parameters (m), are required. The formulation of this method employs a trial and error process. WEKA 3.9 software was used in this study for implementing RF.
3.1.3. Gaussian Process (GP)
GP is a set of random variables in which some variables have a multivariable Gaussian distribution. The chief objective of GP is to develop systems that can predict variables based on historical data. The uniqueness of GP lies in its specification through its mean and covariance function. It can be updated whenever new observational information is available [
79]. GP depends on probability, which makes estimating input data easier and provides accuracy for probable variances. The statistical significance of the prediction is raised broadly by the estimated variances. GP can have vast dimensionality and produce data using the random domain of subset ranges. Choosing a suitable covariance function and its parameters is important because the main role of the GP belongs to the covariance function underlying the geometric structure of the training samples. The hyper-parameters (mean and covariance functions) must be determined from the data to improve accuracy [
80,
81,
82].
3.1.4. Support Vector Machine (SVM)
SVM, a prevailing method in data mining, is a supervised-learning technique for solving regression and classification problems. It relies on the structural risk minimization principle [
83,
84,
85]. SVM has been effectively used for linear and complex problems in various engineering and medical fields over the last few decades. Inadequate adjustment of user-defined constraints in SVM may result in overfitting and underfitting. To ascertain the best fit model, numerous trials were carried out to fix the user-defined parameters.
3.1.5. Multiple Linear Regression (MLR)
MLR employs the least square technique. The following is the equation of the MLR model:
where
R stands for dependent variable and
x1,
x2,…
, xn stand for independent variables. MLR was developed in this study using XLSTAT software.
3.1.6. Artificial Neural Networks (ANN)
The main benefit of ANN is its simplicity and ability to approximate any input/output [
12]. The significant disadvantage of ANN techniques is that it shows information regarding the weight matrix that is currently beyond the discerning ability of human beings. In this way, normally, they are considered black box models. In addition, the ANN approach is aimed at finding user-defined parameters, such as the number of latent layers and neurons in latent layers, by trial and error, which is very time-consuming. The detailed theory about ANN occurs in Haykin [
86]. Furthermore, the network is constrained by components, for example, learning rate, momentum, neuron numbers in layers and the number of hidden layers. Many trials were performed to find the best-fit model. The ANN was developed using the WEKA software.
Figure 6 depicts the general structure of ANN with input, middle and output layers.
4. Application of the Methods
The prediction performance of the models was evaluated using the coefficient of correlation (CC), mean absolute error (MAE), root mean square error (RMSE), Nash–Sutcliffe model efficiency coefficient (Nash) and scattering index (SI) values, as defined below.
where
is observed values,
is predicted values,
is average observed values and
n is the number of observations. If the values of CC and Nash Sutcliffe model efficiency are near 1, then the model is the best performing (if CC, Nash = 1, then the model is ideal). The lower values of MAE, RMSE and SI reflect the model’s suitability for prediction (if error is zero, then the model is ideal).
A total of 61 observations were used in this study for model development and validation. The models were constructed using 41 observations, whereas the remaining 20 observations were used for the testing. These groups were used for model development and validation.
Table 3 summarizes the descriptive statistics of the training and testing phases, including maximum, minimum, standard deviation, mean, Kurtosis and skewness. The input data set consisted of
d/
p,
b/
B0,
z/
p,
B/
B0 and
h1/
H whereas the
Cdt of the BCW gate was considered output.
5. Results and Discussion
The models were developed with training data and checked for accuracy on testing data. WeKA 3.9 software was used for this purpose. The optimum values of user-defined parameters of the models are shown in
Table 4.
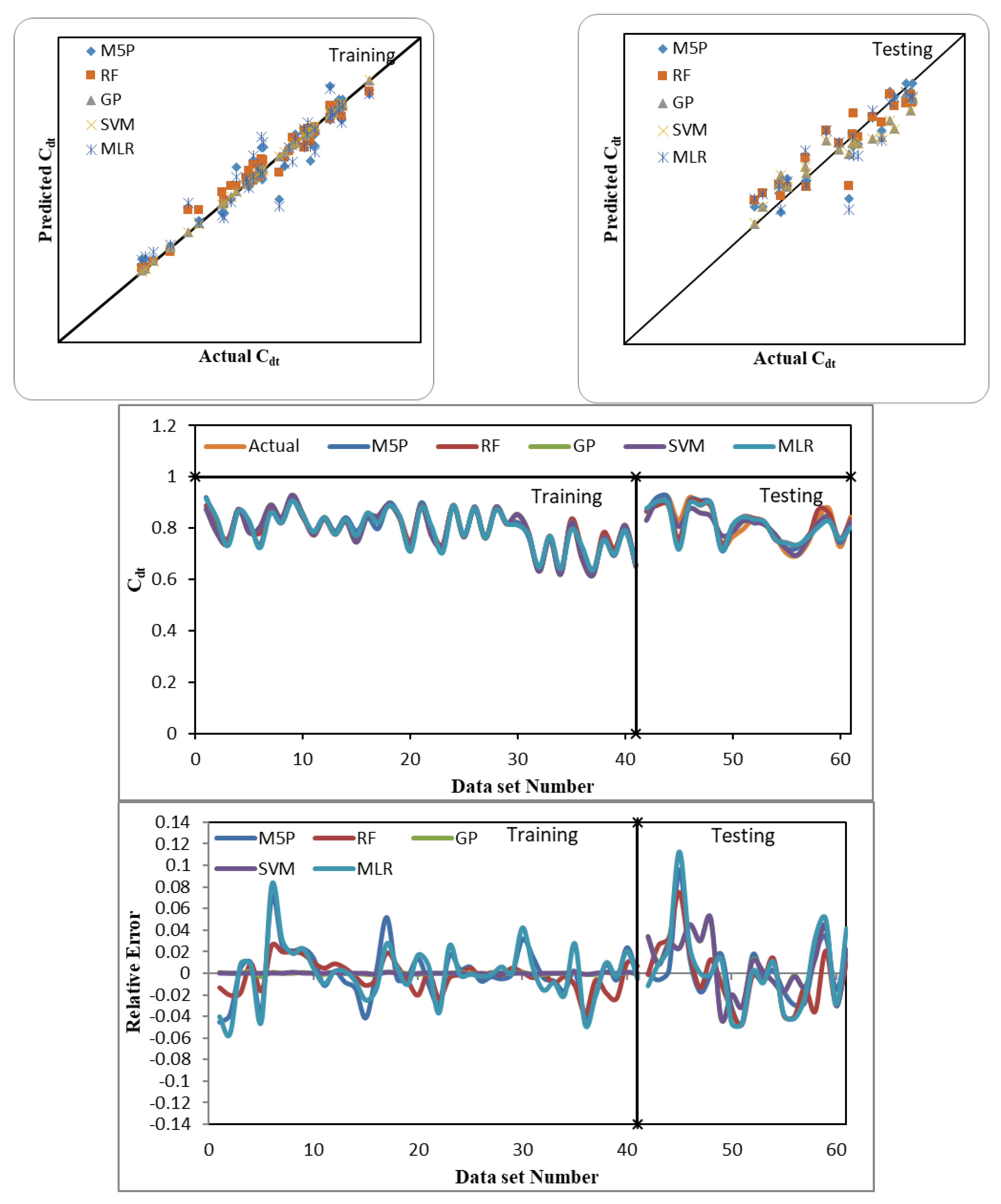
Figure 7 also depicts their performance during the two stages. The predicted
Cdt of the BCW gate using soft computing approaches are presented against the modeled (real) values in the figure to show their performance based on the best fit line (y = x).
Table 5 also shows that the SVM model outperformed the other models in predicting the
Cdt with CC of 0.9585, NSE of 0.8562, MAE of 0.0237, RMSE of 0.0276 and SI of 0.0337 during testing. The SVM reduced the RMSE of M5P, RF, GP and MLR by 32, 7.1, 0.4 and 27%, respectively. However, the difference between GP and SVM was minor.
Figure 7 shows that the SVM-estimated
Cdt during training and testing was the closest to the best-fit line relative to other models. It confirmed the better performance of SVM compared to the other models. The outcomes of single-factor ANOVA presented in
Table 6 show insignificant differences between theactual and predicted values for the different models.
Table 5 and
Figure 7 also show that the GP model’s performance was comparable to the SVM model and surpassed the M5P, RF and MLR models with a CC of 0.9581, NSE of 0.8557, MAE of 0.0239, RMSE of 0.0277 and SI of 0.0338 at the testing stage. The RF model’s performance surpassed the M5P and MLR models with a CC of 0.9187, NSE of 0.8339, MAE of 0.0240, RMSE of 0.0297 and SI of 0.0363 at the testing stage. The least-square technique was used for developing the MLR equation. The final form of the MLR model is listed in Equation (24). The performance of the MLR model was the worst of all the models with the lowest CC (0.8549) and NSE (0.7280), and the highest MAE (0.0284), RMSE (0.0380) and SI (0.0464).
5.1. Sensitivity Investigation
A sensitivity study was carried out to ascertain the effect of the independent variable on the dependent variable. This is very important in preparing AI models since they are more sensitive to inputs than empirical methods. Therefore, finding the influencing input variables in developing AI models is highly significant. Many methods have been employed for sensitivity studies. In this investigation, the best-performing model (SVM) was selected for the sensitivity study by eliminating one input parameter from the input combination each time. The performance assessed in the absence of one of the inputs of each model is shown in
Table 7. The results suggest that
h1/
H is the most influencing parameter in predicting the
Cdt of BCW gate, followed by d/p,
b/
B0,
B/
B0 and z/p.
5.2. Results of Multimode ANN Model
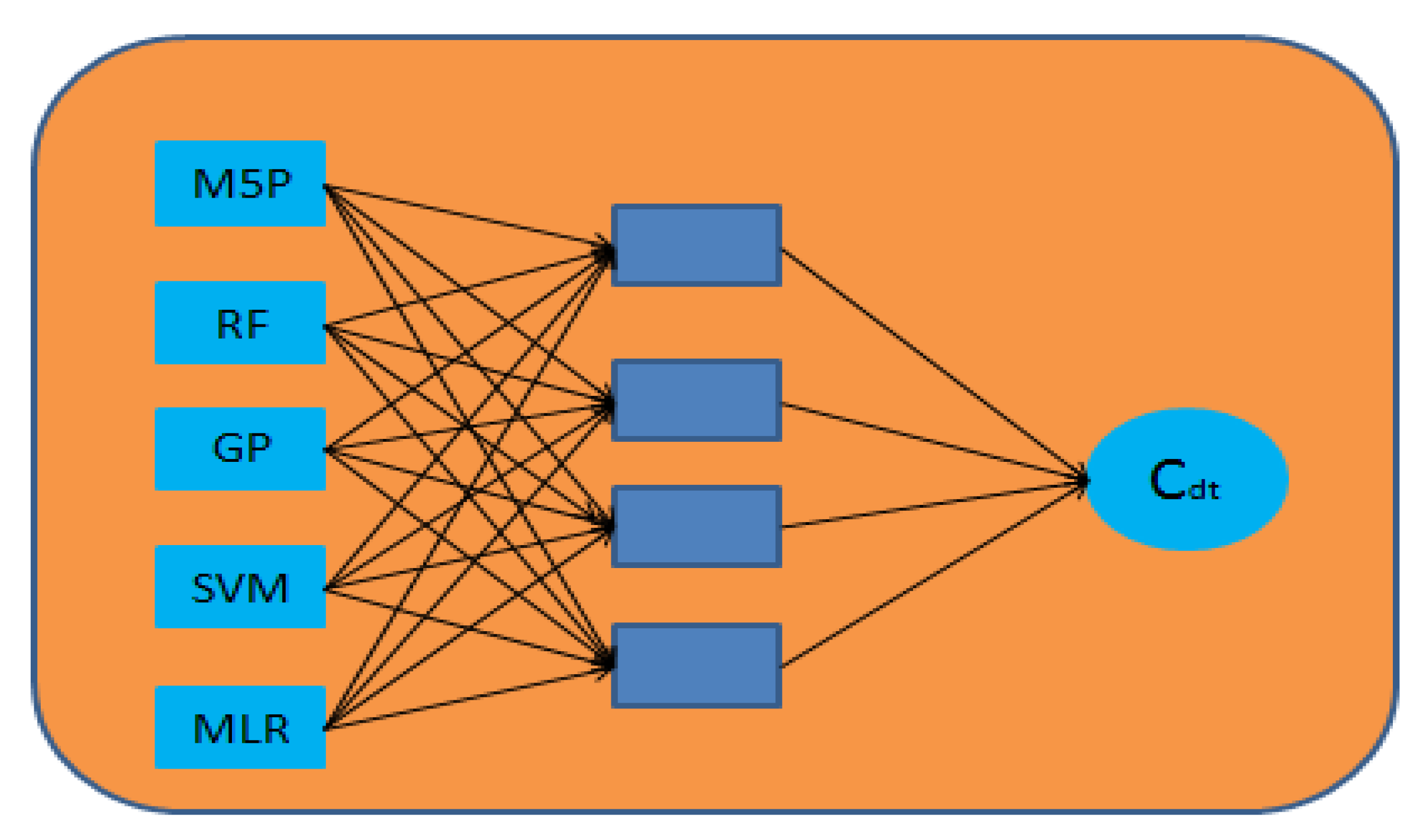
A new multimode ANN model was developed using RF, M5P, GP, SVM, and MLR predicted values. In this novel model, the RF, M5P, GP, SVM and MLR predicted values were used as inputs and the
Cdt values were the output. The multimode ANN model was developed using a hit-and-miss process.
Figure 8 indicates the structure of the novel multimode model in which five neurons in the input layer and four neurons in the latent layer were selected for predicting
Cdt of BCW gate.
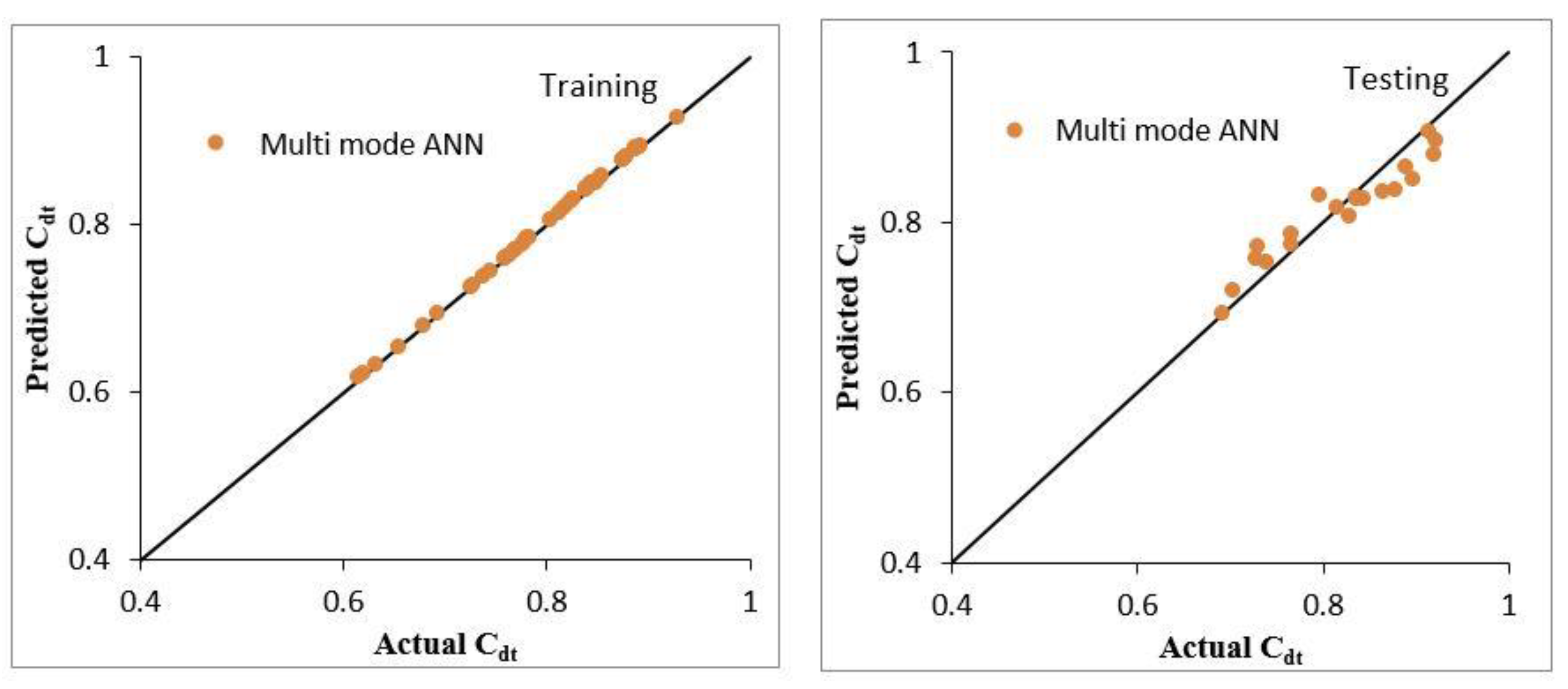
Figure 9 shows the observed and estimated
Cdt using novel multimode ANN models during the training and testing stages. The novel multimode ANN estimated
Cdt with CC = 0.9998 and 0.9618, RMSE of 0.0016 and 0.0258, MAE of 0.0013 and 0.0217, NSE as 0.9996 and 0.8746 and SI of 0.0020 and 0.0315 during training and testing, respectively. Overall, the performance of the novel multimode ANN was better than the RF, M5P, GP, SVM and MLR models in predicting
Cdt of BCW gate. Comparison with
Table 5 revealed that the novel multimode ANN reduced the RMSE of M5P, RF, GP, SVM and MLR by 37, 13, 6.9, 6.5 and 32%, respectively.
The entire error distribution was plotted using a box plot to evaluate the outcomes (
Figure 10). The positive and negative error values indicated the under- and over-prediction tendencies of the models.
Table 8 lists the distribution of the overall error. The minimum errors, first quartile, median, third quartile and maximum error are also provided in
Table 8 and plotted in
Figure 10 for all implemented models. The lower quartile value in the multimode ANN model was −0.0118, which was lower than the other considered models.
Figure 10 and
Table 8 indicated that the maximum and minimum errors predicted by the multimode ANN model were −0.0400 and 0.0470, respectively, which verify the capability of this model in predicting the
Cdt of a BCW gate.
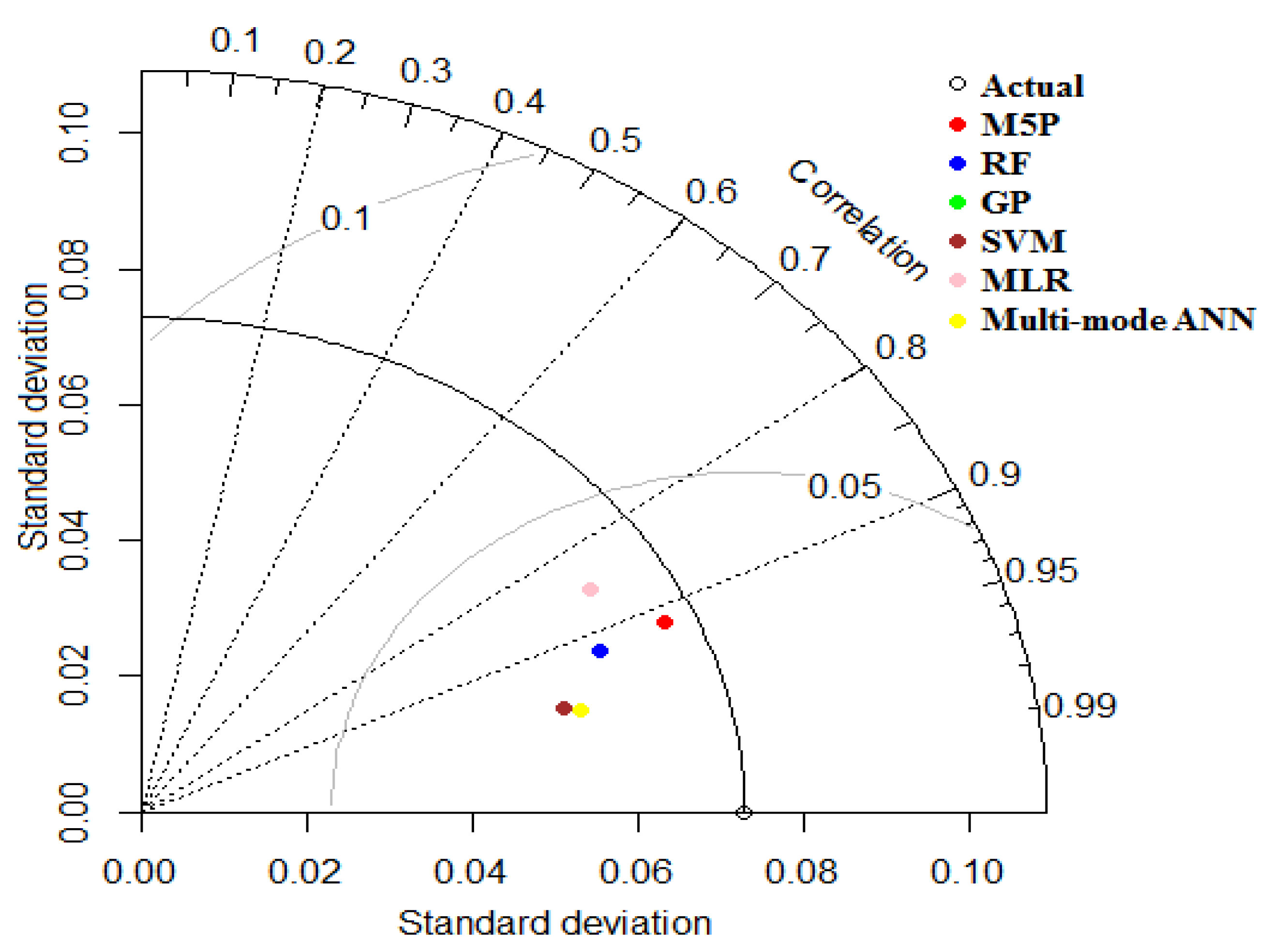
Taylor’s diagram [
87] in
Figure 11 shows the performance of all the developed models in predicting
Cdt. Three statistical parameters involving RMSE, CC and standard deviation were used to evaluate the applied models’ accuracy in the Taylor diagram.
Figure 11 indicates that the multimode ANN model attained a higher CC with minimal RMSE. The Taylor diagram also confirmed that the performance of the multimode ANN model surpassed the other applied models.
6. Conclusions
Broad-crested weirs are widely used as flood control reservoirs and as measuring structures. Upstream sediment accumulation reduces the performance of broad-crested weirs and similar structures. The combined weir-gate devices can minimize sediment and prevent upstream accumulation [
88]. The current study determined the discharge coefficient (
Cdt) of a combined compound rectangular broad-crested weir (BCW) gate. For this purpose, the experimental results of a simple broad-crested weir were employed for the code’s calibration, and the
k-w model was selected for numerical simulation. The effective parameters of the combined structure were changed for a comprehensive investigation. The studied dimensionless parameters were:
b/
Bo,
d/
P,
B/
Bo,
Z/
P and
h1/
H. A total of 61 compound BCW gates were numerically simulated using different values of the dimensionless parameters. Finally, the results of the calibrated CFD code were used to develop models for the prediction of a compound BCW-gate
Cdt. Six data-driven algorithms, including M5P tree, RF, Gaussian process, SVM, MLR and multimode ANN, were used.
The results showed better performance from the SVM model than the RF, M5P, GP and MLR models, in terms of CC, NSE, MAE, RMSE and SI. The sensitivity investigation indicated h1/H as the most effective parameter, followed by d/p, b/B0, B/B0 and z/p, in predicting Cdt using SVM. The novel multimode ANN model outperformed all other models. It reduced the RMSE by 37, 13, 6.9, 6.5 and 32% of the M5P, RF, GP, SVM and MLR, respectively. The Taylor diagram and box plot also confirmed the novel multimode ANN model as the most suitable model in predicting the Cdt of a BCW gate with minimum errors and maximum correlation.