Sustainability of an Open-Loop GWHP System in an Italian Alpine Valley
Abstract
1. Introduction
2. Study Area
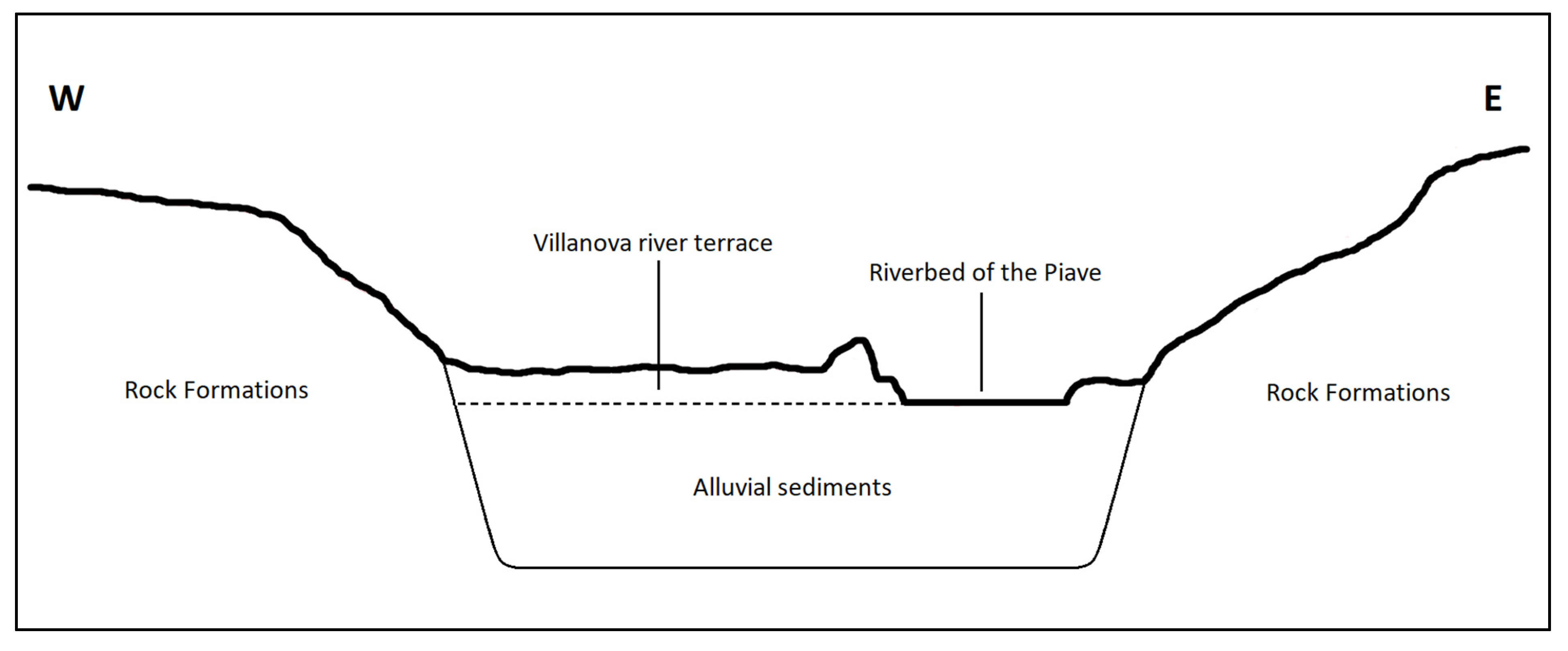
2.1. Geological and Hydrogeological Settings
- the rock formations, with a low hydraulic conductivity, that can be considered an aquiclude;
- the alluvial deposits, hosting a phreatic or unconfined aquifer, consist mainly of pebbles, gravel and sand; the hydraulic conductivity of the aquifer (K), calculated by pumping tests, ranges from 2.7 × 10−2 to 1.0 × 10−3 m/s.
2.2. Geothermal Plants
3. Material and Methods
3.1. Hydrogeological and Thermal Characterization
3.1.1. Thermal Logs
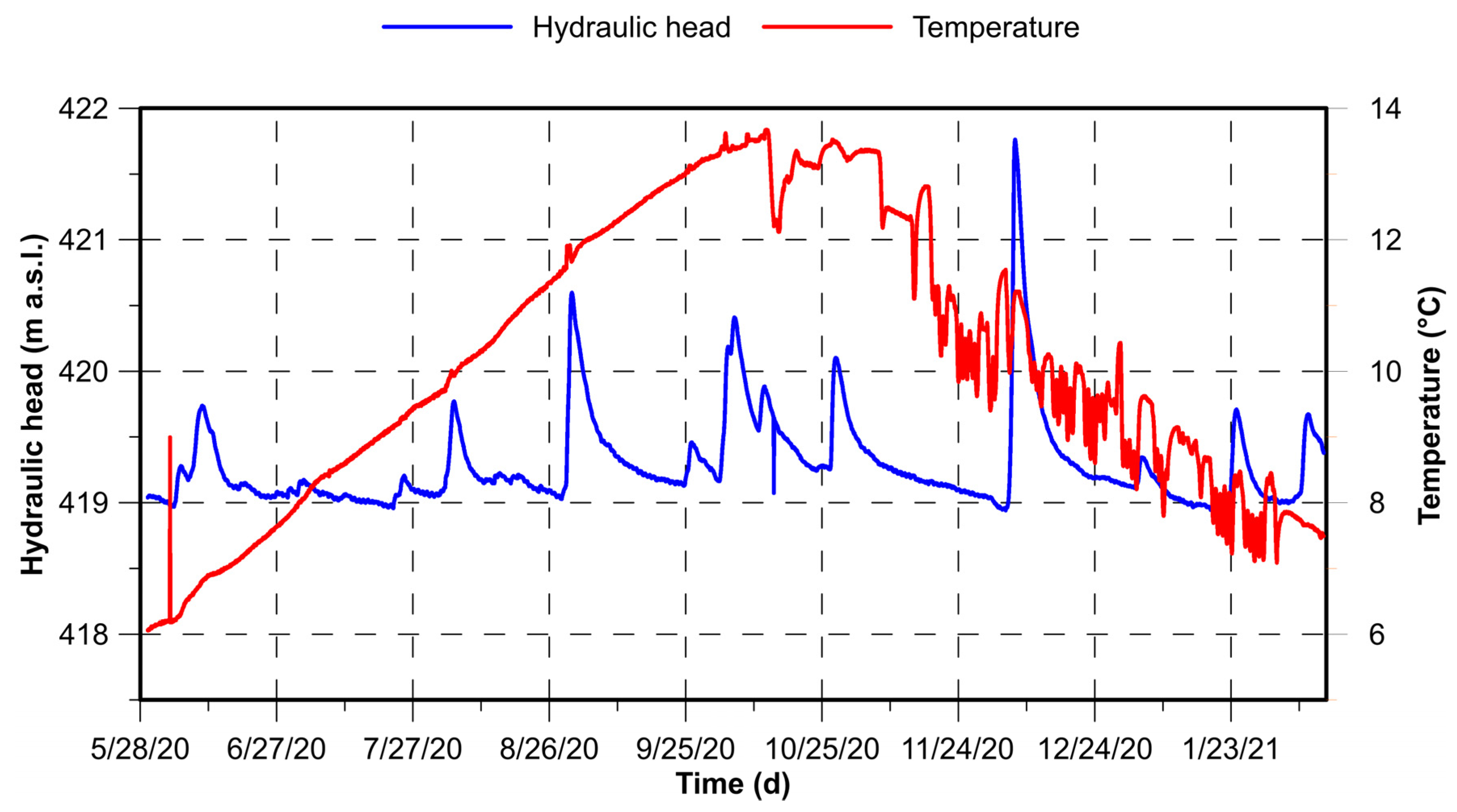
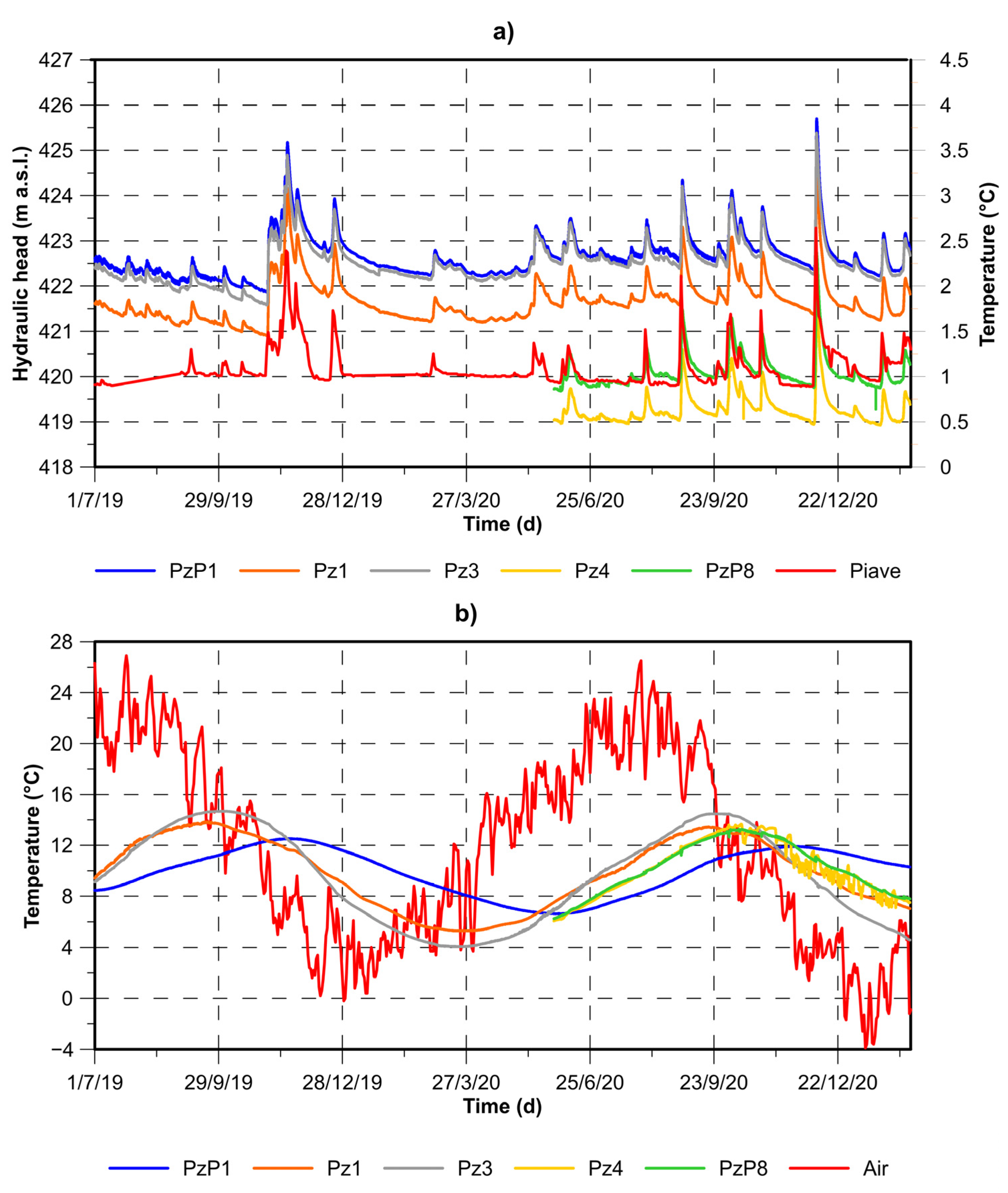
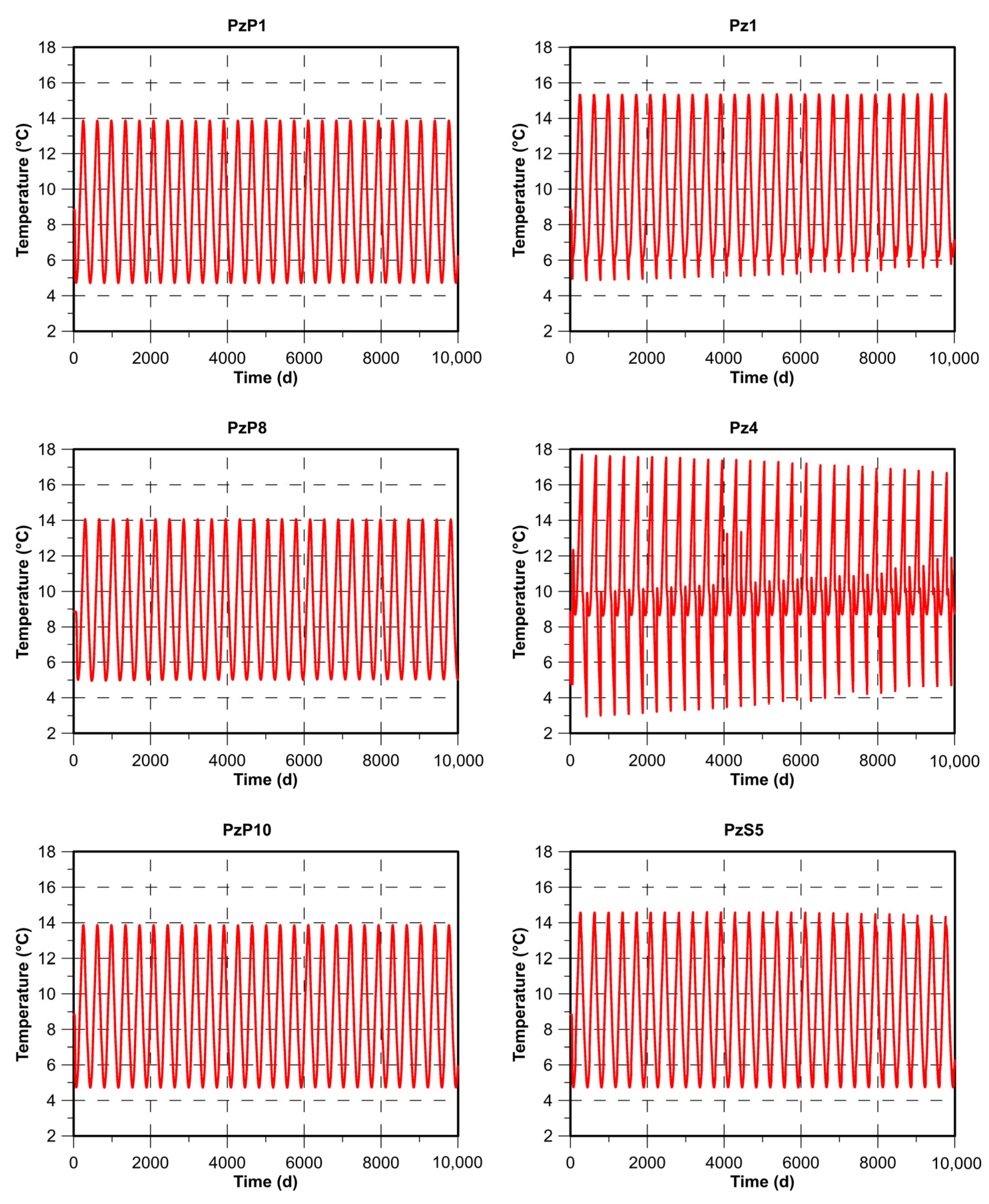
3.1.2. Continuous Monitoring
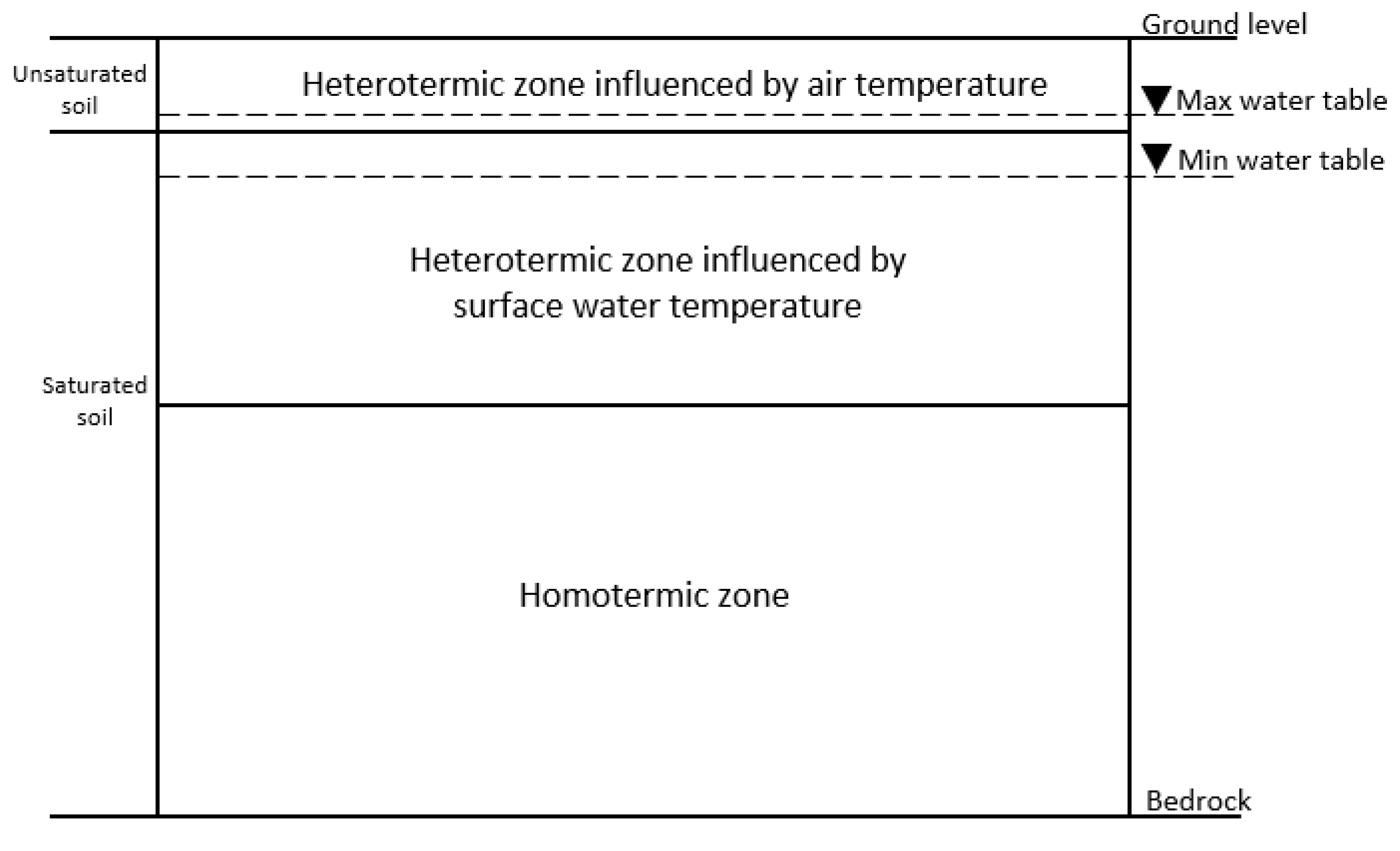
3.1.3. Hydrogeological and Thermal Conceptual Model
3.2. Numerical Modeling
- Normalized root mean square (nRMS), with a calibration target ≤ 0.1;
- Nash–Sutcliffe efficiency (NSE), with a calibration target > 0.5;
- RMSE–observation standard deviation ratio (RSR), with a calibration target ≤ 0.7.
3.2.1. Discretization
3.2.2. Parameterization
3.2.3. Initial and Boundary Conditions
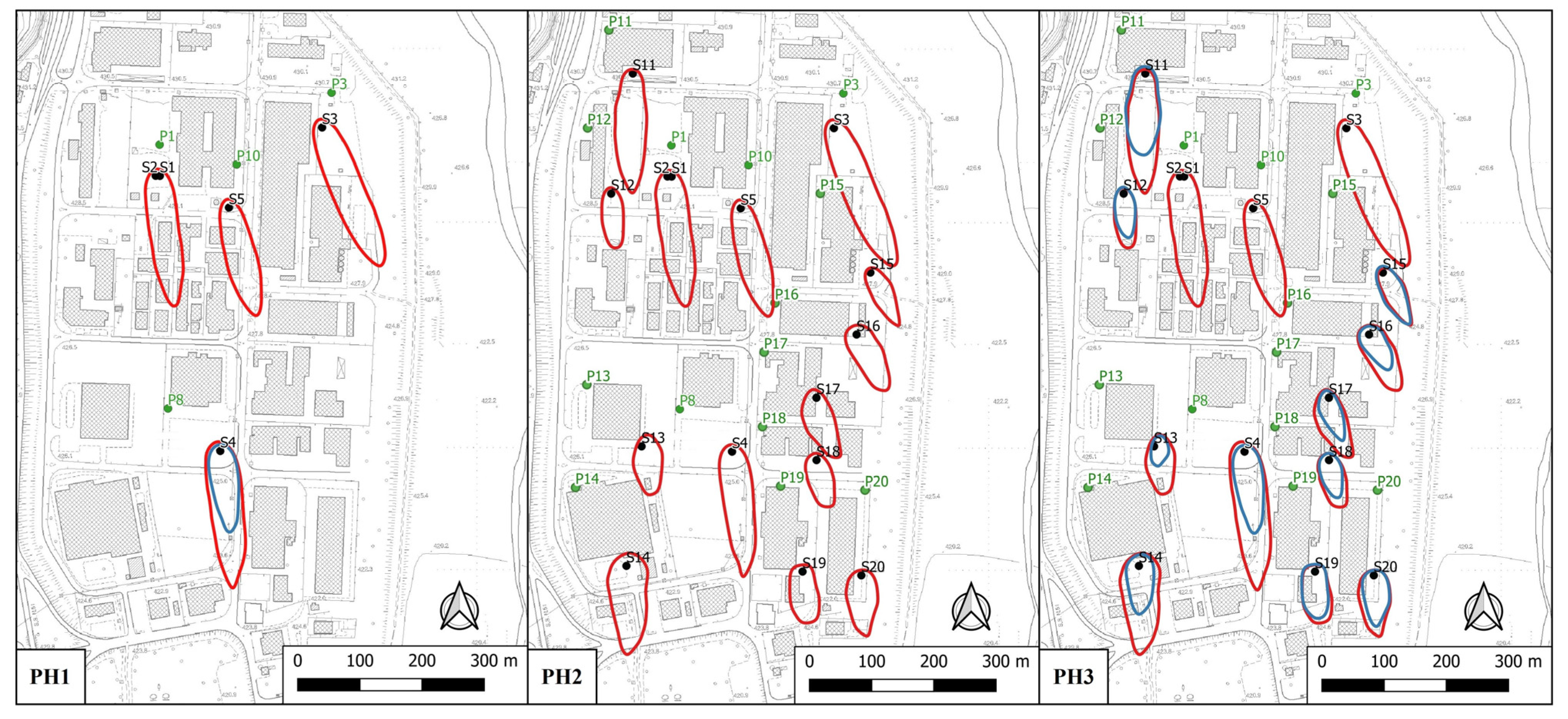
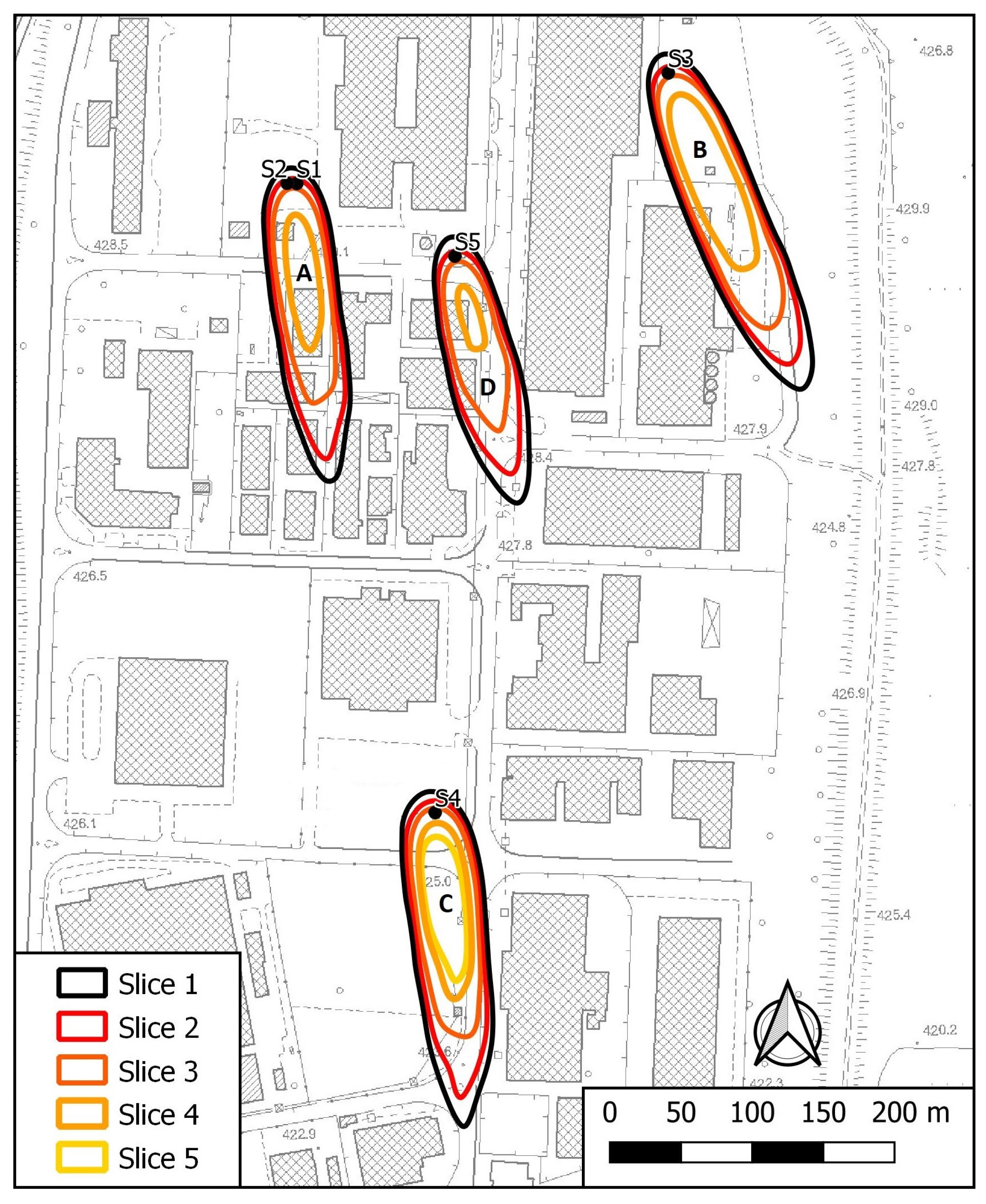
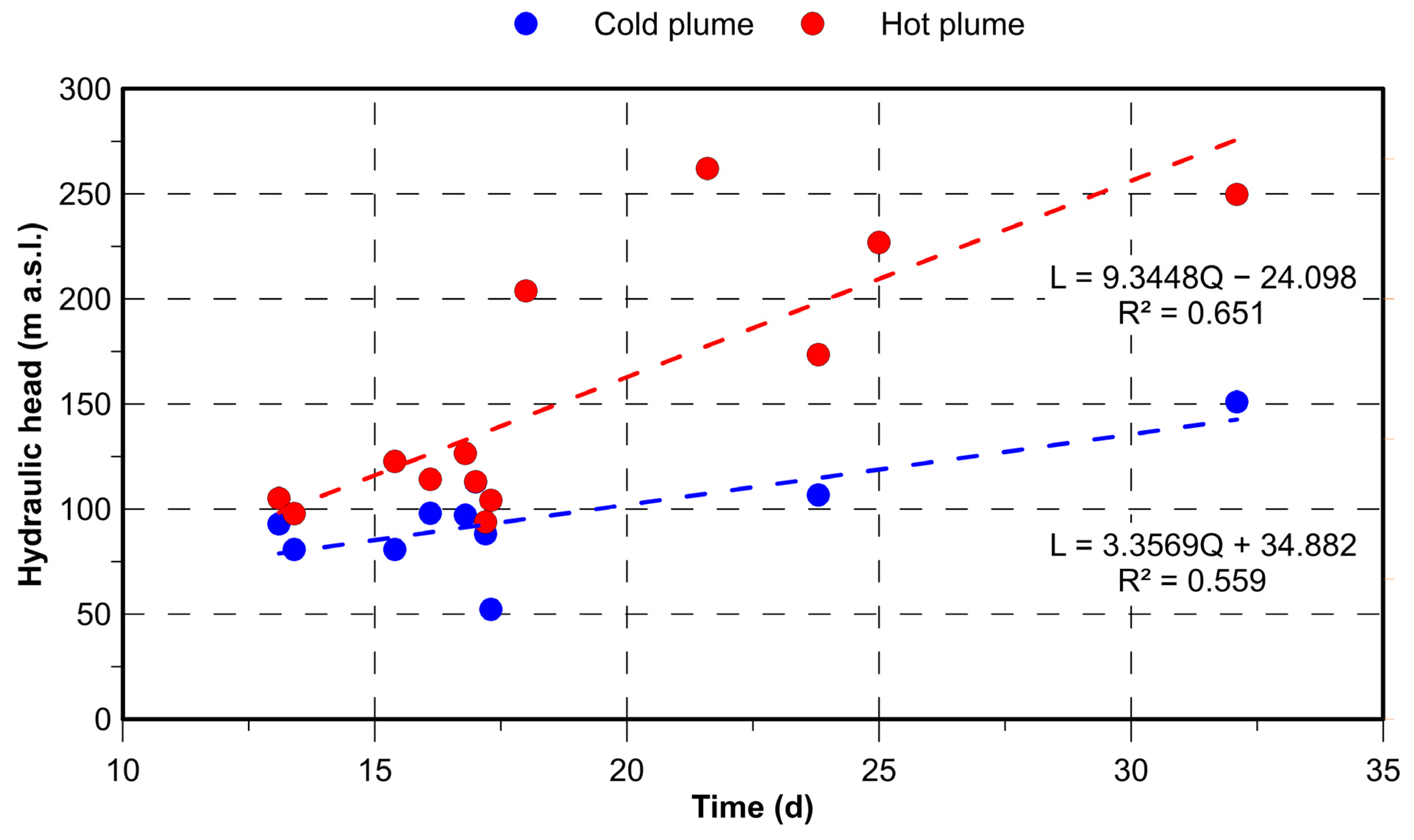
4. Results and Discussion
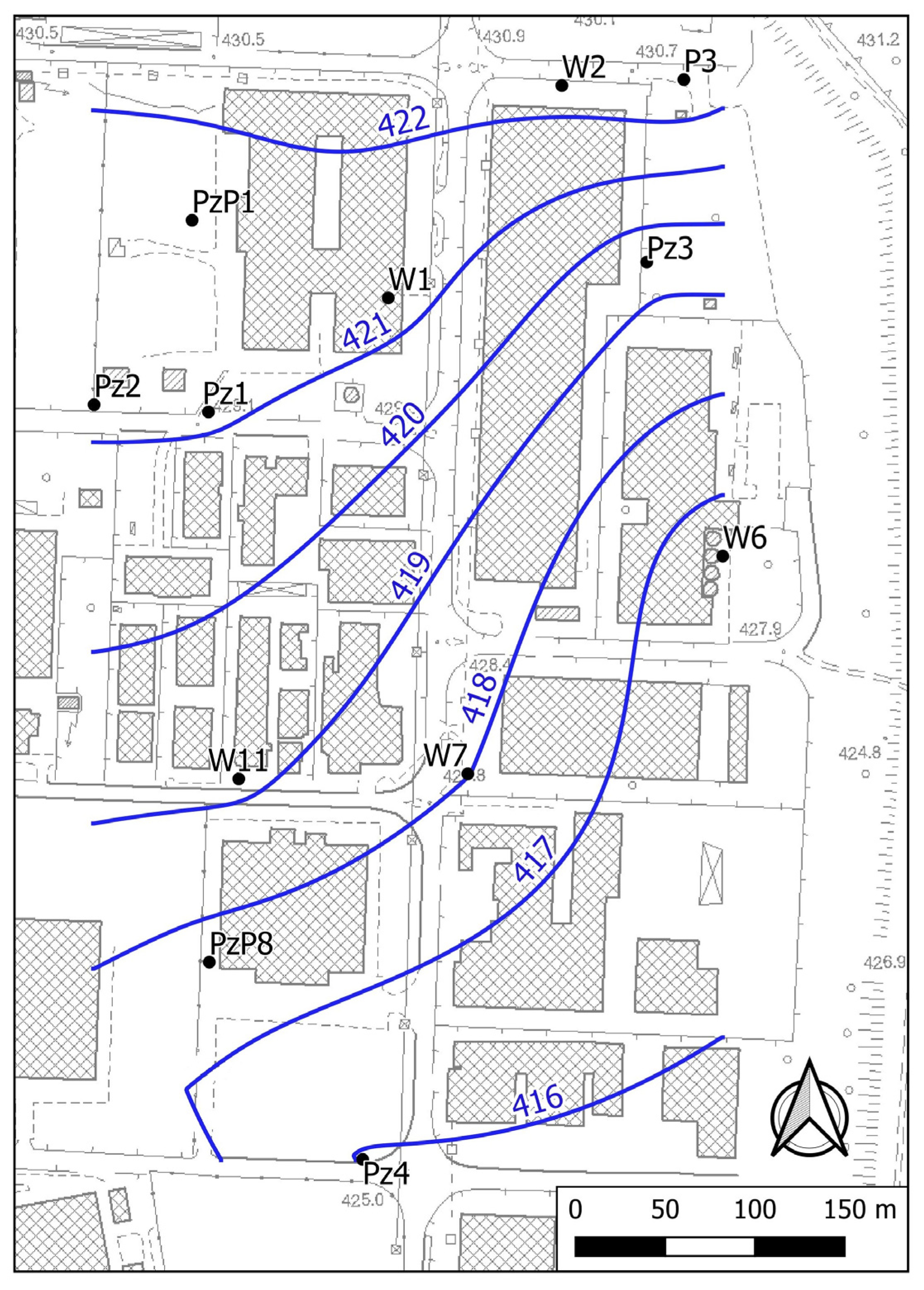
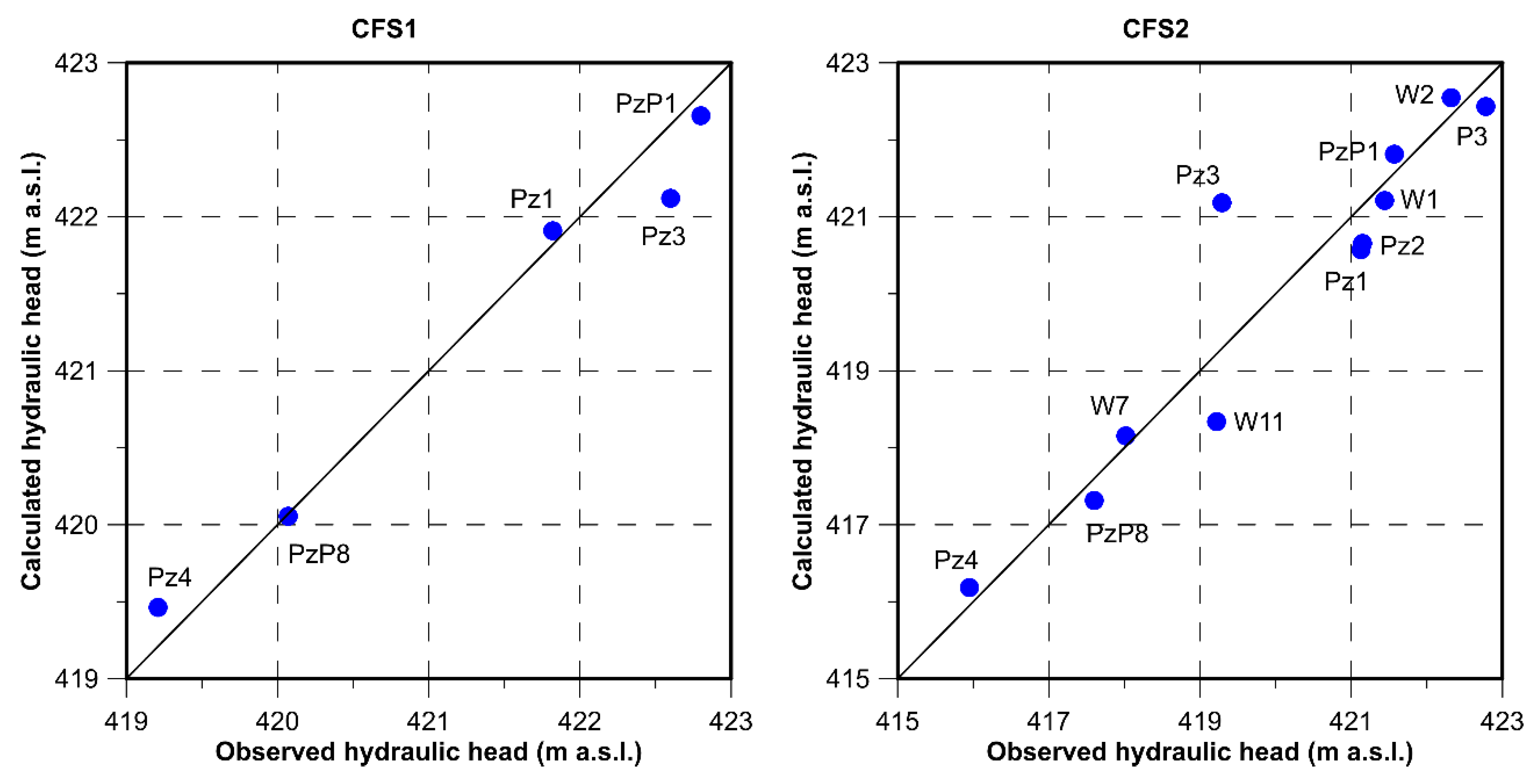
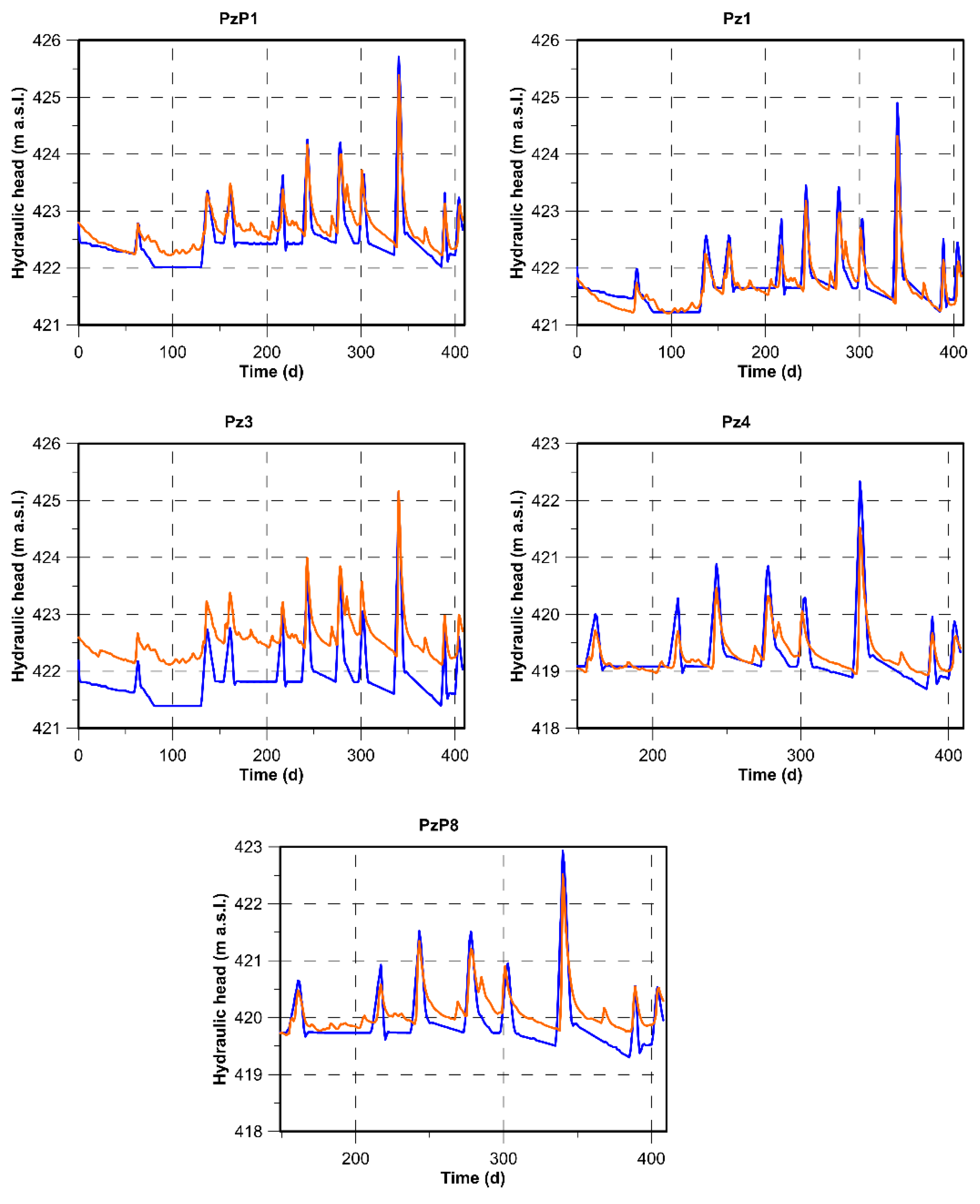
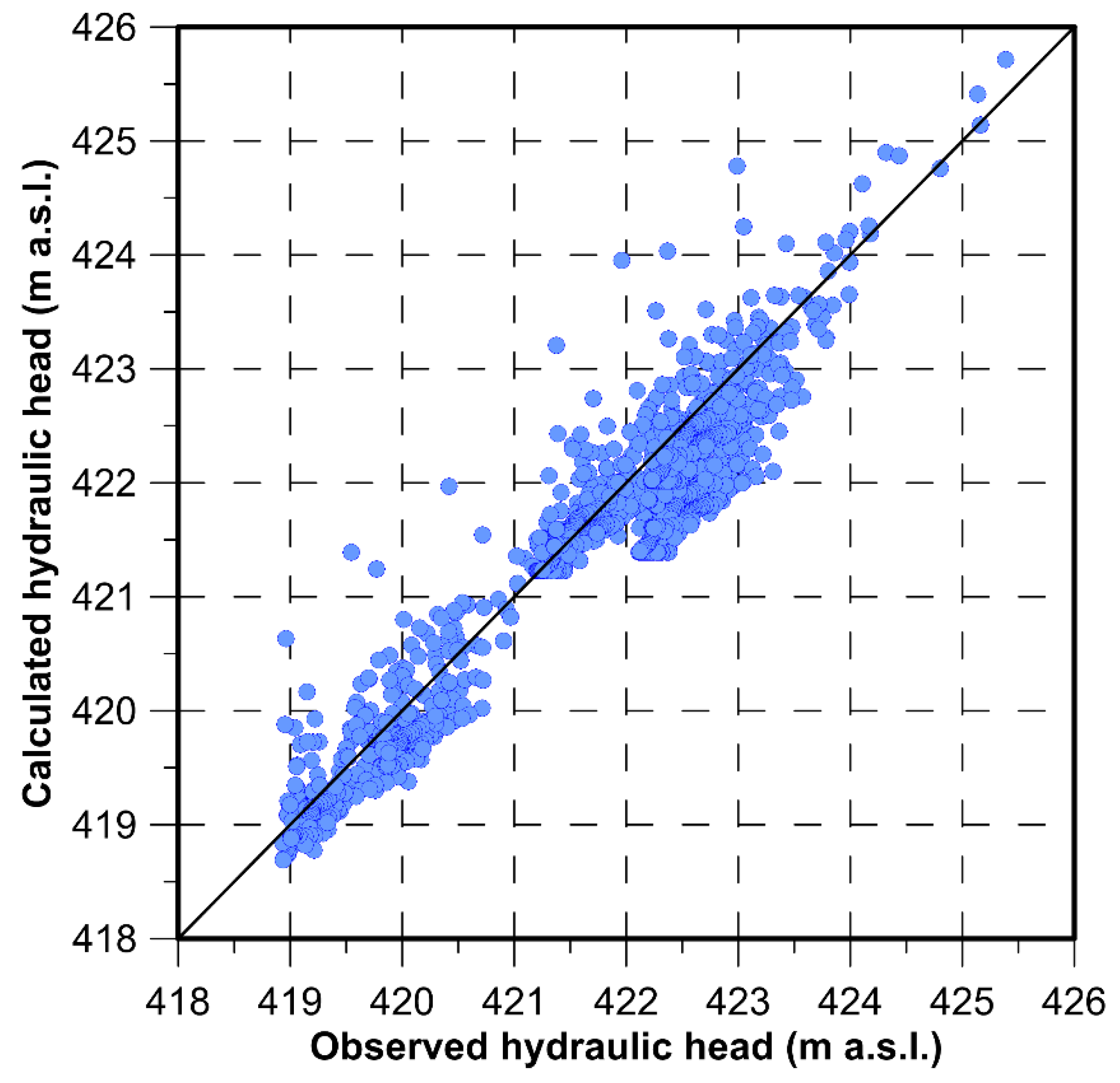
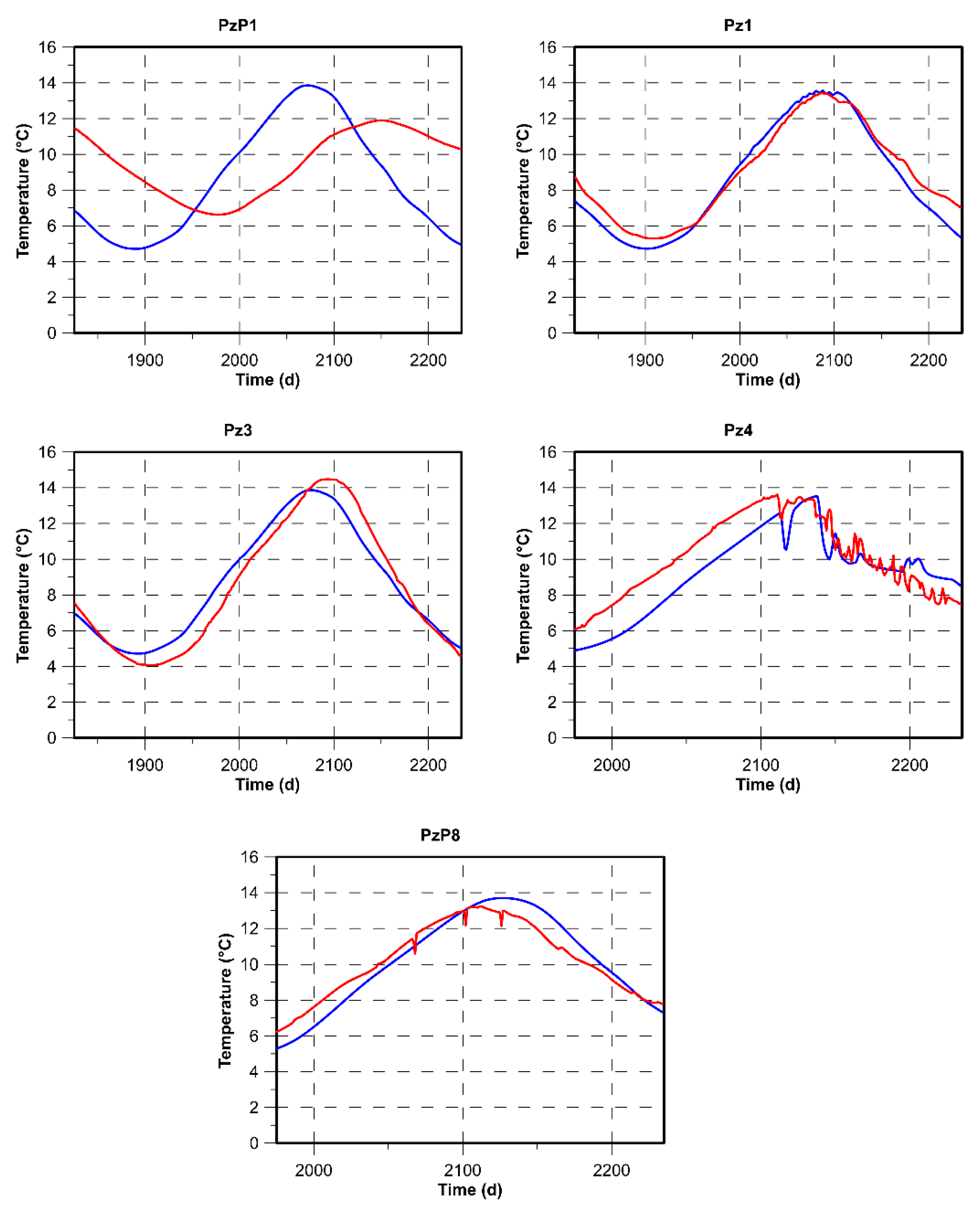
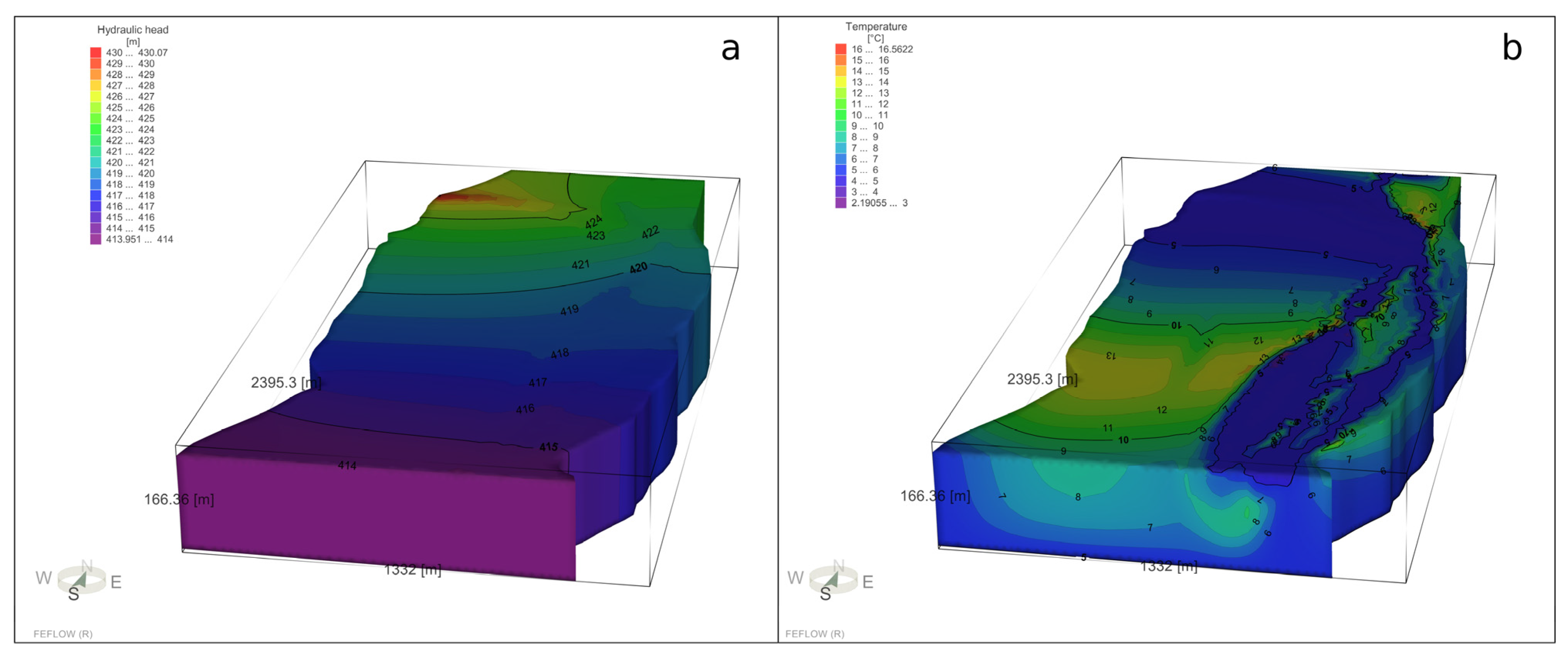
4.1. Calibration Simulation
4.2. Predictive Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. (Eds.) Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2007: The Physical Science Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; p. 996. [Google Scholar]
- Solomon, S.; Plattner, G.K.; Knutti, R.; Friedlingstein, P. Irreversible climate change due to carbon dioxide emissions. PNAS 2008, 106, 1704–1709. [Google Scholar] [CrossRef] [PubMed]
- Leung, D.Y.C.; Caramanna, G.; Maroto-Valer, M.M. An overview of current status of carbon dioxide capture and storage technologies. Renew. Sustain. Energy Rev. 2014, 39, 426–443. [Google Scholar]
- Goldstein, B.; Hiriart, G.; Bertani, R.; Bromley, C.; Gutiérrez-Negrín, L.; Huenges, E.; Muraoka, H.; Ragnarsson, A.; Tester, J.; Zui, V. Geothermal Energy; IPCC Special Report on Renewable Energy Sources and Climate Change Mitigation; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Seyboth, K., Matschoss, P., Kadner, S., Zwickel, T., Eickemeier, P., Hansen, G., Schlömer, S., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011. [Google Scholar]
- Lund, J.W.; Freeston, D.H.; Boyd, T.L. Direct utilization of geothermal energy 2010 worldwide review. Geothermics 2011, 40, 159–180. [Google Scholar] [CrossRef]
- Lund, J.W.; Huttrer, G.W.; Toth, A.N. Characteristics and trends in geothermal development and use, 1995 to 2020. Geothermics 2022, 105, 102522. [Google Scholar] [CrossRef]
- Banks, D. An Introduction to Thermogeology: Ground Source Heating and Cooling, 2nd ed.; Wiley-Blackwell: Chichester, UK, 2012; p. 517. [Google Scholar]
- Lo Russo, S.; Boffa, C.; Civita, M.V. Low-enthalpy geothermal energy: An opportunity to meet increasing energy needs and reduce CO2 and atmospheric pollutant emissions in Piemonte, Italy. Geothermics 2009, 38, 254–262. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. General review of ground-source heat pump systems for heating and cooling of buildings. Energy Build. 2014, 70, 441–454. [Google Scholar] [CrossRef]
- Aresti, L.; Christodoulides, P.; Florides, G.A. An investigation on the environmental impact of various Ground Heat Exchangers configurations. Renew. Energy 2021, 171, 592–605. [Google Scholar] [CrossRef]
- European Commission. Directive 2000/60/EC of the European Parliament and of the Council Establishing a Framework for the Community Action in the Field of Water Policy; Official Journal of the European Union: Luxembourg, Luxembourg, 2000. [Google Scholar]
- Perego, R.; Guandalini, R.; Fumagalli, L.; Aghib, F.S.; De Biase, L.; Bonomi, T. Sustainability evaluation of a medium scale GSHP system in a layered alluvial setting using 3D modeling suite. Geothermics 2016, 59, 14–26. [Google Scholar] [CrossRef]
- Abesser, C. Open-loop ground source heat pumps and the groundwater systems: A literature review of current applications, regulations and problems. Br. Geol. Surv. Open Rep. 2007, OR/10/045, 31. [Google Scholar]
- Banks, D. Thermogeological assessment of open-loop well-doublet schemes: A review and synthesis of analytical approaches. Hydrogeol. J. 2009, 17, 1149–1155. [Google Scholar] [CrossRef]
- Milnes, E.; Perrochet, P. Assessing the impact of thermal feedback and recycling in open-loop groundwater heat pump (GWHP) systems: A complementary design tool. Hydrogeol. J. 2013, 21, 505–514. [Google Scholar]
- Ferguson, G.; Woodbury, A.D. Subsurface heat flow in an urban environment. J. Geophys. Res. 2004, 109, B02402. [Google Scholar] [CrossRef]
- Perego, R.; Pera, S.; Boaga, J.; Bulgheroni, M.; Dalla Santa, G.; Galgaro, A. Thermal modeling of a Swiss urban aquifer and implications for geothermal heat pump systems. Hydrogeol. J. 2021, 29, 2187–2210. [Google Scholar] [CrossRef]
- Epting, J.; Händel, F.; Huggenberger, P. Thermal management of an unconsolidated shallow urban groundwater body. Hydrol. Earth Syst. Sci. 2013, 17, 1851–1869. [Google Scholar] [CrossRef]
- Choi, W.; Ooka, R.; Nam, Y. Impact of long-term operation of ground-source heat pump on subsurface thermal state in urban area. Sustain. Cities Soc. 2018, 38, 429–439. [Google Scholar] [CrossRef]
- Perego, R.; Dalla Santa, G.; Galgaro, A.; Pera, S. Intensive thermal exploitation from closed and open shallow geothermal systems at urban scale: Unmanaged conflicts and potential synergies. Geothermics 2022, 103, 102417. [Google Scholar] [CrossRef]
- Torresan, F.; Piccinini, L.; Cacace, M.; Pola, M.; Zampieri, D.; Fabbri, P. Numerical modeling as a tool for evaluating the renewability of geothermal resources: The case study of the Euganean Geothermal System (NE Italy). Environ. Geochem. Health 2022, 44, 2135–2162. [Google Scholar]
- Abesser, C.; Lewis, M.A.; Marchant, A.P.; Hulbert, A.G. Mapping suitability for open-loop ground source heat pump systems: A screening tool for England and Wales, UK. Q. J. Eng. Geol. Hydrogeol. 2014, 47, 373–380. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, S.; Zhou, W.; LaMoreaux, J. Hydrogeology and design of groundwater heat pump systems. Environ. Earth Sci. 2015, 73, 3683–3695. [Google Scholar] [CrossRef]
- Chahoud, A.; Gelati, L.; Palumbo, A.; Patrizi, G.; Pellegrino, I.; Zaccanti, G. Groundwater flow model management and case studies in Emilia-Romagna (Italy). Acque Sotter. Ital. J. Groundw. 2013, AS04019, 59–73. [Google Scholar] [CrossRef][Green Version]
- Dendys, M.; Tomaszewska, B.; Pajak, L. Numerical modelling in research on geothermal systems. Bull. Geogr. Phys. Geogr. Ser. 2015, 9, 39–44. [Google Scholar] [CrossRef]
- Vaccaro, M.; Conti, P. Numerical simulation of geothermal resources: A critical overlook. In Proceedings of the European Geothermal Conference, Pisa, Italy, 3–7 June 2013. Paper HS1-26. [Google Scholar]
- Diersch, H.J.G. FEFLOW—Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: Berlin/Heidelberg, Germany, 2014; p. 996. [Google Scholar]
- Halilovic, S.; Böttcher, F.; Kramer, S.C.; Piggott, M.D.; Zosseder, K.; Hamacher, T. Well layout optimization for groundwater heat pump systems using the adjoint approach. Energy Convers. Manag. 2022, 268, 116033. [Google Scholar] [CrossRef]
- Masetti, D.; Bianchin, G. Geologia del Gruppo della Schiara (Dolomiti Bellunesi)—Suo inquadramento nella evoluzione giurassica del margine orientale della Piattaforma di Trento. Mem. Di Sci. Geol. 1987, 39, 187–212. [Google Scholar]
- Carton, A.; Bondesan, A.; Fontana, A.; Meneghel, M.; Miola, A.; Mozzi, P.; Primon, S.; Surian, N. Geomorphological evolution and sediment transfer in the Piave River system (northeastern Italy) since the Last Glacial Maximum. Géomorphologie Relief Process. Environ. 2009, 15, 155–174. [Google Scholar] [CrossRef]
- Fontana, A.; Mozzi, P.; Marchetti, M. Alluvial fans and megafans along the southern side of the Alps. Sediment. Geol. 2014, 301, 150–171. [Google Scholar] [CrossRef]
- Pellegrini, G.B.; Zambrano, R. Il corso del Piave a Ponte nelle Alpi nel Quaternario. Studi Trentini Di Sci. Nat. 1979, 56, 69–100. [Google Scholar]
- Badino, G. Geothermal flux and phreatic speleogenesis in gypsum, halite and quartzite rocks. Int. J. Speleol. 2018, 47, 1–11. [Google Scholar] [CrossRef]
- Kitanidis, P.K. Introduction to Geostatistics: Applications to Hydrogeology; Cambridge University Press: Cambridge, UK, 1997; p. 249. [Google Scholar]
- Fabbri, P.; Trevisani, S. A geostatistical simulation approach to a pollution case in the Northeastern Italy. Math. Geol. 2005, 37, 569–586. [Google Scholar] [CrossRef]
- Trefry, M.G.; Muffels, C. FEFLOW: A Finite-Element Ground Water Flow and Transport Modeling Tool. Ground Water 2007, 45, 525–528. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Anderson, M.P.; Woessner, W.W. Applied Groundwater Modeling—Simulation of Flow and Advective Transport, 1st ed.; Academic Press: San Diego, CA, USA, 1992; p. 381. [Google Scholar]
- Doherty, J. Calibration and Uncertainty Analysis for Complex Environmental Models; Watermark Numerical Computing: Brisbane, Australia, 2015; p. 237. ISBN 978-0-9943786-0-6. [Google Scholar]
- Verlag des Vereins Deutscher Ingenieure. Thermal Use of the Underground: Fundamentals, Approvals, Environmental Aspects; VDI 4640 Part 1; Verlag des Vereins Deutscher Ingenieure: Düsseldorf, Germany, 2000. [Google Scholar]
- Casasso, A.; Sethi, R. Modelling thermal recycling occurring in groundwater heat pumps (GWHPs). Renew. Energy 2015, 77, 86–93. [Google Scholar] [CrossRef]
- Park, D.K.; Kaown, D.; Lee, K.K. Development of a simulation-optimization model for sustainable operation of groundwater heat pump system. Renew. Energy 2020, 145, 585–595. [Google Scholar] [CrossRef]
- Park, D.K.; Lee, E.; Kaown, D.; Lee, S.S.; Lee, K.K. Determination of optimal well locations and pumping/injection rates for groundwater heat pump system. Geothermics 2021, 92, 102050. [Google Scholar] [CrossRef]
- Krčmář, D.; Marschalko, M.; Yilmaz, I.; Malík, P.; Černák, R.; Švasta, J.; Kullman, E.; Rusnáková, D.; Popielarczyk, D.; Yang, S. Mapping the low-enthalpy geothermal potential of Quaternary alluvial aquifers in Slovakia. Bull. Eng. Geol. Environ. 2020, 79, 1225–1238. [Google Scholar] [CrossRef]
- Previati, A.; Crosta, G.B. Regional-scale assessment of the thermal potential in a shallow alluvial aquifer system in the Po plain (northern Italy). Geothermics 2021, 90, 101999. [Google Scholar] [CrossRef]
- Garcìa-Gil, A.; Vázquez-Suñe, E.; Garrido Schneider, E.; Sánchez-Navarro, J.A.; Mateo-Lázaro, J. The thermal consequences of river-level variations in an urban groundwater body highly affected by groundwater heat pumps. Sci. Total Environ. 2014, 485, 575–587. [Google Scholar] [CrossRef]
- Garcìa-Gil, A.; Mejías Moreno, M.; Garrido Schneider, E.; Marazuela, M.A.; Abesser, C.; Lázaro, J.M.; Sánchez Navarro, J.A. Nested Shallow Geothermal Systems. Sustainability 2020, 12, 5152. [Google Scholar] [CrossRef]
- Permanda, R.; Ohtani, T. Thermal Impact by Open-Loop Geothermal Heat Pump Systems in Two Different Local Underground Conditions on the Alluvial Fan of the Nagara River, Gifu City, Central Japan. Energies 2022, 15, 6816. [Google Scholar] [CrossRef]
- Bates, B.C.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J.P. Climate Change and Water; Technical Paper of the Intergovernmental Panel on Climate Change; IPCC Secretariat: Geneva, Switzerland, 2008; p. 210. [Google Scholar]
- Poulin, A.; Brissette, F.; Leconte, R.; Arsenault, R.; Malo, J.S. Uncertainty of hydrological modelling in climate change impact studies in a Canadian, snow-dominated river basin. J. Hydrol. 2011, 409, 626–636. [Google Scholar]
- Sonnenborg, T.O.; Seifert, D.; Refsgaard, J.C. Climate model uncertainty versus conceptual geological uncertainty in hydrological modeling. Hydrol. Earth Syst. Sci. 2015, 19, 3891–3901. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Teng, J.; Vaze, J.; Post, D.A.; Perraud, J.M.; Kirono, D.G.C.; Viney, N.R. Estimating climate change impact on runoff across southeast Australia: Method, results, and implications of the modeling method. Water Resour. Res. 2009, 45, W10414. [Google Scholar] [CrossRef]
- Vaze, J.; Post, D.A.; Chiew, F.H.S.; Perraud, J.M.; Viney, N.R.; Teng, J. Climate non-stationarity—Validity of calibrated rainfall-runoff models for use in climate change studies. J. Hydrol. 2010, 394, 447–457. [Google Scholar] [CrossRef]
- Jang, S.; Hamm, S.Y.; Yoon, H.; Kim, G.-B.; Park, J.H.; Kim, M. Predicting long-term change of groundwater level with regional climate model in South Korea. Geosci. J. 2015, 19, 503–513. [Google Scholar] [CrossRef]
- Achieng, K.O.; Zhu, J. Estimation of groundwater recharge using multiple climate models in Bayesian frameworks. J. Water Clim. Chang. 2021, 12, 3865. [Google Scholar] [CrossRef]
- Kelleher, C.; Wagener, T.; Gooseff, M.; McGlynn, B.; McGuire, K.; Marshall, L. Investigating controls on the thermal sensitivity of Pennsylvania streams. Hydrol. Process. 2012, 26, 771–785. [Google Scholar] [CrossRef]
- Jackson, F.L.; Fryer, R.J.; Hannah, D.M.; Millar, C.P.; Malcolm, I.A. A spatio-temporal statistical model of maximum daily river temperatures to inform the management of Scotland’s Atlantic salmon rivers under climate change. Sci. Total Environ. 2018, 612, 1543–1558. [Google Scholar] [CrossRef] [PubMed]

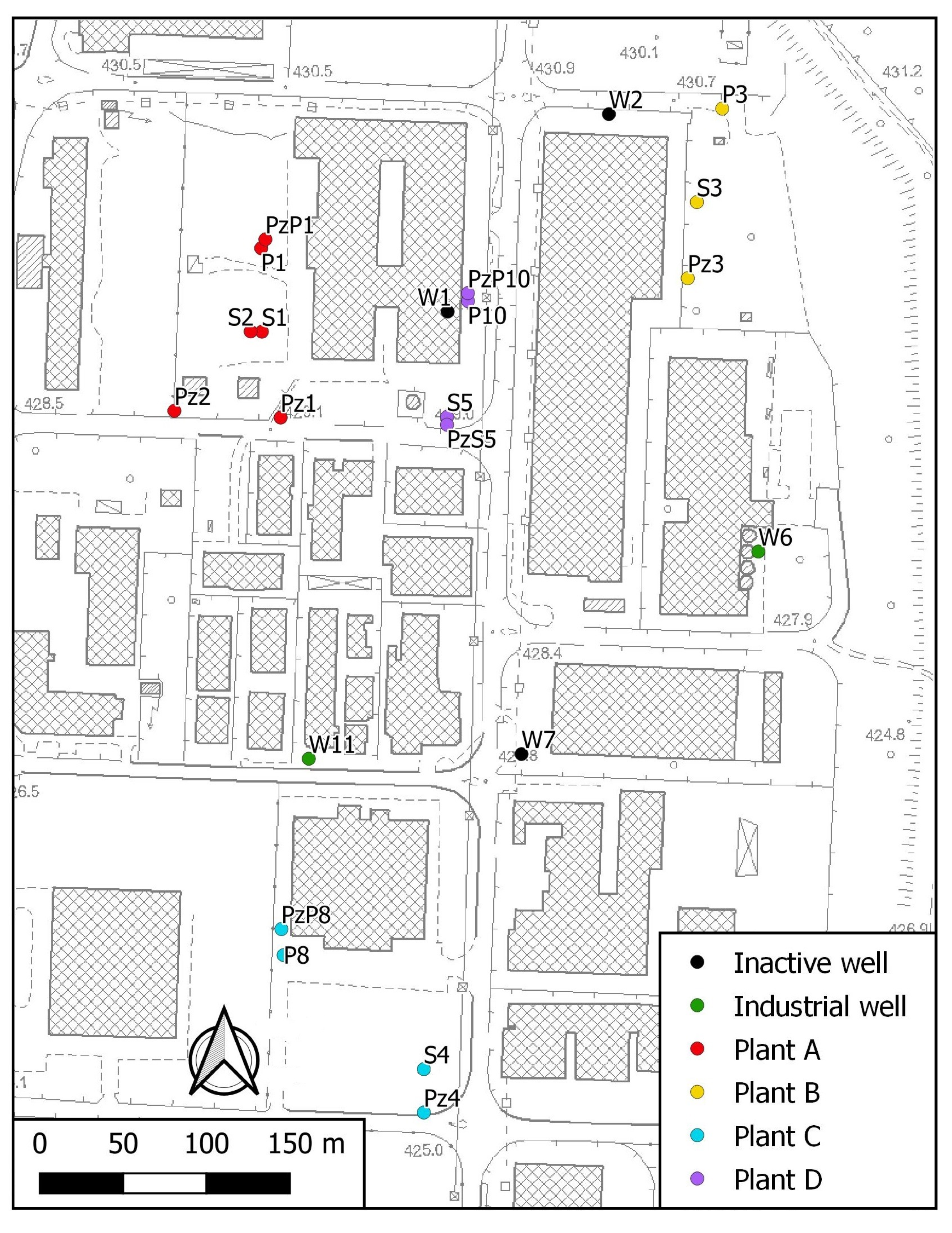


| Name | Plant | Type | Depth (m) | Depth of filter (m) | Altitude (m a.s.l.) | Diameter (mm) |
|---|---|---|---|---|---|---|
| PzP1 | A | UPZ | 20.30 | 3–20.30 | 429.35 | 101.6 |
| P1 | A | EW | 42 | 6–12/18–20/32–34/40–42 | 429.26 | 230 |
| S1 | A | IW | 2.8 | - | 429.12 | 2000 |
| S2 | A | IW | 2.8 | - | 429.09 | 2000 |
| Pz1 | A | DPZ | 15.45 | 3–15.45 | 429.17 | 101.6 |
| Pz2 | A | DPZ | 14.70 | 3–14.70 | 428.91 | 101.6 |
| P3 | B | EW | 27 | 12–27 | 430.65 | 400 |
| S3 | B | IW | 2.8 | - | 427.31 | 2000 |
| Pz3 | B | DPZ | 15.20 | 3–15.20 | 426.33 | 101.6 |
| PzP8 | C | UPZ | 30 | 3–30 | 425.66 | 101.6 |
| P8 | C | EW | 30 | 20–30 | 425.53 | 177 |
| S4 | C | IW | 3 | - | 425.14 | 2000 |
| Pz4 | C | DPZ | 30 | 3–30 | 425.04 | 101.6 |
| P10 | D | EW | 30 | 15–27 | 429.90 | 168.3 |
| PzP10 | D | UPZ | 20 | 0–20 | 429.95 | 76.2 |
| S5 | D | IW | 3 | - | 429.18 | 2000 |
| PzS5 | D | DPZ | 20 | 0–20 | 429.12 | 76.2 |
| Plant | Regime | Period of Activity | Extraction Rate (L/s) |
|---|---|---|---|
| A | Cooling | 1 March–31 October | 25.0 |
| B | Cooling | 15 April–15 October | 21.6 |
| C | Cooling | 1 March–31 October | 32.1 |
| Heating | 1 November–28 February | 38.8 | |
| D | Cooling | 1 May–30 September | 18.0 |
| ID | Start | End | Depth (m) |
|---|---|---|---|
| P1 | 20 June 2012 | 28 December 2017 | 17.00 |
| PzP1 | 12 April 2017 | 12 February 2021 | 17.25 |
| Pz1 | 07August 2012 | 12 February 2021 | 13.70 |
| S1 | 20 June 2012 | 12 February 2021 | 2.80 |
| P3 | 19 March 2014 | 12 February 2021 | 21.00 |
| Pz3 | 19 March 2014 | 12 February 2021 | 13.80 |
| S3 | 19 March 2014 | 12 February 2021 | 2.80 |
| PzP8 | 29 May 2020 | 12 February 2021 | 20.35 |
| Pz4 | 29 May 2020 | 12 February 2021 | 15.45 |
| S4 | 29 May 2020 | 12 February 2021 | 3.00 |
| ID | Hmin (m a.s.l.) | Hmax (m a.s.l.) | Hmean (m a.s.l.) | Tmin (°C) | Tmax (°C) | Tmean (°C) |
|---|---|---|---|---|---|---|
| PzP1 | 421.86 | 425.70 | 422.65 | 6.6 | 12.5 | 9.9 |
| Pz1 | 420.90 | 424.64 | 421.66 | 5.3 | 13.8 | 9.9 |
| Pz3 | 421.58 | 425.38 | 422.50 | 4.1 | 14.7 | 9.7 |
| Pz4 | 418.92 | 421.76 | 419.29 | 6.1 | 13.7 | 10.2 |
| PzP8 | 419.27 | 422.75 | 420.11 | 6.2 | 13.3 | 10.3 |
| ID | Objective | Type | Temporal Discretization | Simulation Time |
|---|---|---|---|---|
| CFS1 | Calibration | Flow | Steady-state | 1 Januray 2020 |
| CFS2 | Calibration | Flow | Steady-state | 29 March 2021 |
| CFS3 | Calibration | Flow | Steady-state | 21 April 2021 |
| CFS4 | Calibration | Flow | Steady-state | 20 May 2021 |
| CFS5 | Calibration | Flow | Steady-state | 15 June2021 |
| CFS6 | Calibration | Flow | Steady-state | 13 July 2021 |
| CFT | Calibration | Flow | Transient-state | 1 January 2020–12 Februray 2021 |
| CHT | Calibration | Flow and heat | Transient-state | 1 January 2020–12 Februray 2021 |
| PH1 | Predictive | Flow and heat | Transient-state | 1 January 2020–1 January 2050 |
| PH2 | Predictive | Flow and heat | Transient-state | 1 January 2020–1 January 2050 |
| PH3 | Predictive | Flow and heat | Transient-state | 1 January 2020–1 January 2050 |
| Parameter | Value | |
|---|---|---|
| Flow | K (m/s) | 1.0 × 10−3 |
| Sy (-) | 0.2 | |
| Ss (1/m) | 1.0 × 10−4 | |
| ITr (1/d) | 108 | |
| OTr (1/d) | 108 | |
| Heat | ne (-) | 0.2 |
| Cvw (MJ·m−3·K−1) | 4.2 | |
| Cvs (MJ·m−3·K−1) | 2.4 | |
| λw (W·m−1·K−1) | 0.65 | |
| λs (W·m−1·K−1) | 1.8 | |
| acs (-) | 1 | |
| αL (m) | 5 | |
| αT (m) | 0.5 |
| Parameters | Calibrated Values | |
|---|---|---|
| Flow | K (m/s) | 1.0 × 10−2 |
| Sy (-) | 0.35 | |
| Ss (1/m) | 4.5 × 10−5 | |
| ITr (1/d) | 13,172.4 | |
| OTr (1/d) | 13,172.4 | |
| Heat | ne (-) | 0.35 |
| Cvw (MJ·m−3·K−1) | 4.2 | |
| Cvs (MJ·m−3·K−1) | 2.4 | |
| λw (W·m−1·K−1) | 0.65 | |
| λs ( W·m−1·K−1) | 1.8 | |
| acs (-) | 1.0 | |
| αL (m) | 5.0 | |
| αT (m) | 0.5 |
| Simulation | Parameter | N. Targets | nRMS | NSE | RSR |
|---|---|---|---|---|---|
| CFS1 | H | 4 | 0.04 | 0.99 | 0.11 |
| CFS2 | H | 10 | 0.06 | 0.96 | 0.19 |
| CFS3 | H | 7 | 0.05 | 0.97 | 0.16 |
| CFS4 | H | 7 | 0.04 | 0.98 | 0.13 |
| CFS5 | H | 7 | 0.07 | 0.96 | 0.21 |
| CFS6 | H | 7 | 0.05 | 0.98 | 0.15 |
| CFT | H | 5 | 0.07 | 0.90 | 0.32 |
| CHT | H-T | 5 | 0.09 | 0.89 | 0.33 |
| Plant | Regime | Plume Area (m2) |
|---|---|---|
| A | Cooling | 8976.87 |
| B | Cooling | 11,402.16 |
| C | Cooling | 10,306.17 |
| Heating | 5061.06 | |
| D | Cooling | 7562.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappellari, D.; Piccinini, L.; Pontin, A.; Fabbri, P. Sustainability of an Open-Loop GWHP System in an Italian Alpine Valley. Sustainability 2023, 15, 270. https://doi.org/10.3390/su15010270
Cappellari D, Piccinini L, Pontin A, Fabbri P. Sustainability of an Open-Loop GWHP System in an Italian Alpine Valley. Sustainability. 2023; 15(1):270. https://doi.org/10.3390/su15010270
Chicago/Turabian StyleCappellari, Davide, Leonardo Piccinini, Alessandro Pontin, and Paolo Fabbri. 2023. "Sustainability of an Open-Loop GWHP System in an Italian Alpine Valley" Sustainability 15, no. 1: 270. https://doi.org/10.3390/su15010270
APA StyleCappellari, D., Piccinini, L., Pontin, A., & Fabbri, P. (2023). Sustainability of an Open-Loop GWHP System in an Italian Alpine Valley. Sustainability, 15(1), 270. https://doi.org/10.3390/su15010270







