A Novel Linguistic Interval-Valued Pythagorean Fuzzy Multi-Attribute Group Decision-Making for Sustainable Building Materials Selection
Abstract
1. Introduction
2. Preliminaries
2.1. The Linguistic Interval-Valued Pythagorean Fuzzy Sets
- (1)
- If , then ;
- (2)
- if , then
- If , then ;
- If , then .
- (1)
- (2)
- (3)
- ;
- (4)
- .
2.2. The Extended Power Average and Extended Power Geometric Operators
- (1)
- ;
- (2)
- ;
- (3)
- , if .
3. New Operations for LIVPFNs Based on ATT
3.1. The Concept of ATT
- Property I: , and for all ;
- Property II: , for all x and y;
- Property III: , for all x, y and z;
- Property IV: if and , then ;
- Property I: , and for all x;
- Property II: , for all x and y;
- Property III: , for all x, y and z;
- Property IV: if and , then ;
- Property I: if has the property of monotonic decreasing, such that and with the limit conditions: and , then we can use the function to generate a T-norm.
- Property II: if has the property of monotonic decreasing, such that and with the limit conditions: and , then we can use the function to generate a T-conorm.
3.2. New Operations for LIVPFNs Based on ATT
- (1)
- (2)
- (3)
- ;
- (4)
- .
- (1)
- (2)
- (3)
- (4)
- (1)
- (2)
- (3)
- (4)
- (1)
- (2)
- (3)
- (4)
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
- ;
- (6)
- .
4. Novel Aggregation Operators for LIVPFNS and Their Properties
4.1. The Linguistic Interval-Valued Pythagorean Fuzzy Archimedean Extended Power Average Operator
- (1)
- ;
- (2)
- ;
- (3)
- , if .
4.2. The Linguistic Interval-Valued Pythagorean Fuzzy Archimedean Extended Power Weighted Average Operator
4.3. The Linguistic Interval-Valued Pythagorean Fuzzy Archimedean Extended Power Geometric Operator
4.4. The Linguistic Interval-Valued Pythagorean Fuzzy Archimedean Extended Power Weighted Geometric Operator
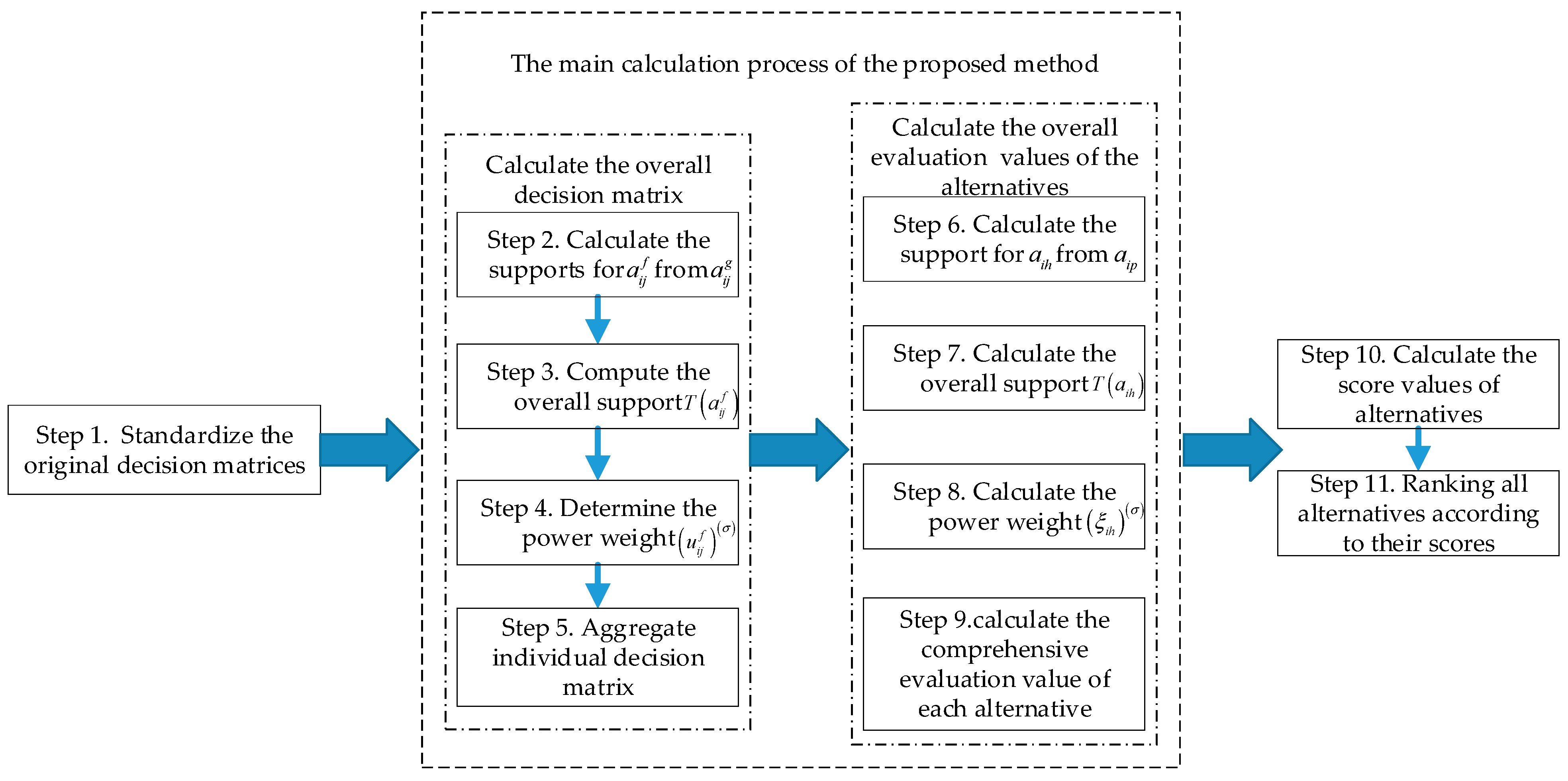
5. A Novel MAGDM Method under LIVPFSs
6. An Application of the New MAGDM Method in SBMS in Cement Industry
6.1. The Process of Determining the Most Suitable Supplementary Material
6.2. Analysis of the Influence of the Parameters
6.2.1. The Impact of Different Operational Rules on the Final Decision Results
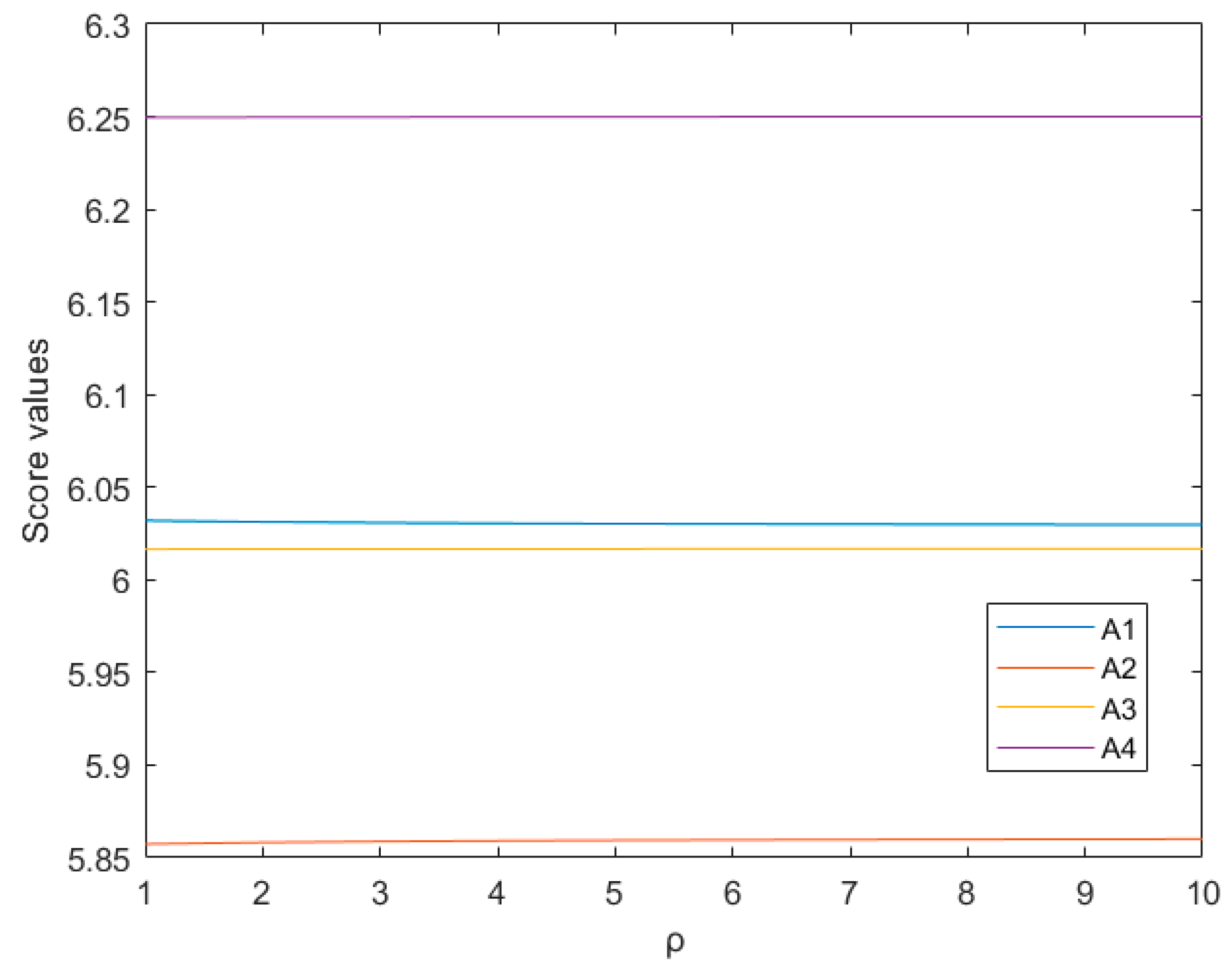
6.2.2. The Impact of the Parameter on the Final Decision Results
6.3. Comparative Analysis
6.3.1. Compare with Garg’s [28] Method
6.3.2. Compare with Garg and Kumar’s [39] Method
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akadiri, P.O.; Olomolaiye, P.O.; Chinyio, E.A. Multi-criteria evaluation model for the selection of sustainable materials for building projects. Autom. Constr. 2013, 30, 113–125. [Google Scholar] [CrossRef]
- Mahmoudkelaye, S.; Azari, K.T.; Pourvaziri, M.; Asadian, E. Sustainable material selection for building enclosure through ANP method. Case Stud. Constr. Mater. 2018, 9, e00200. [Google Scholar] [CrossRef]
- Roy, J.; Das, S.; Kar, S.; Pamucar, D. An extension of the CODAS approach using interval-valued intuitionistic fuzzy set for sustainable material selection in construction projects with incomplete weight information. Symmetry 2019, 11, 393. [Google Scholar] [CrossRef]
- Meng, F.Y.; Dong, B.H. Linguistic intuitionistic fuzzy PROMETHEE method based on similarity measure for the selection of sustainable building materials. J. Ambient Intel. Hum. Comp. 2022, 13, 4415–4435. [Google Scholar] [CrossRef]
- Chen, Z.S.; Martinez, L.; Chang, J.P.; Wang, X.J.; Xiong, S.H.; Chin, K.S. Sustainable building material selection: A QFD-and ELECTRE III-embedded hybrid MCGDM approach with consensus building. Eng. Appl. Artif. Intel. 2019, 85, 783–807. [Google Scholar] [CrossRef]
- Khoshnava, S.M.; Rostami, R.; Valipour, A.; Ismail, M.; Rahmat, A.R. Rank of green building material criteria based on the three pillars of sustainability using the hybrid multi criteria decision making method. J. Clean. Prod. 2018, 173, 82–99. [Google Scholar] [CrossRef]
- Ahmed, M.; Qureshi, M.N.; Mallick, J.; Ben Kahla, N. Selection of sustainable supplementary concrete materials using OSM-AHP-TOPSIS approach. Adv. Mater. Sci. Eng. 2019, 2019, 2850480. [Google Scholar] [CrossRef]
- Chen, Z.S.; Yang, L.L.; Chin, K.S.; Yang, Y.; Pedrycz, W.; Chang, J.P.; Martínez, L.; Skibniewski, M.J. Sustainable building material selection: An integrated multi-criteria large group decision making framework. Appl. Soft Comput. 2021, 113, 107903. [Google Scholar] [CrossRef]
- Siksnelyte-Butkiene, I.; Streimikiene, D.; Balezentis, T.; Skulskis, V. A systematic literature review of multi-criteria decision-making methods for sustainable selection of insulation materials in buildings. Sustainability 2021, 13, 737. [Google Scholar] [CrossRef]
- Mukherjee, I.; Singh, U.K.; Chakma, S. Evaluation of groundwater quality for irrigation water supply using multi-criteria decision-making techniques and GIS in an agroeconomic tract of Lower Ganga basin, India. J. Environ. Manag. 2022, 309, 114691. [Google Scholar] [CrossRef]
- Sajjad, M.; Sałabun, W.; Faizi, S.; Ismail, M.; Watrobski, J. Statistical and analytical approach of multi-criteria group decision-making based on the correlation coefficient under intuitionistic 2-tuple fuzzy linguistic environment. Expert Syst. Appl. 2022, 193, 116341. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zhang, X.Y.; Wang, W.J.; Li, Z. Multi-criteria probabilistic dual hesitant fuzzy group decision making for supply chain finance credit risk assessments. Expert Syst. 2022, 39, e13015. [Google Scholar] [CrossRef]
- Haseena, S.; Saroja, S.; Revathi, T. A fuzzy approach for multi criteria decision making in diet plan ranking system using cuckoo optimization. Neural Comput. Appl. 2022, 34, 13625–13638. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J.J.; Long, Q.Q.; Wang, J.Q.; Goh, M. Extended picture fuzzy MULTIMOORA method based on prospect theory for medical institution selection. Cogn. Comput. 2022, 14, 1446–1463. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Zhang, H. Linguistic intuitionistic fuzzy sets and application in MAGDM. J. Appl. Math. 2014, 2014, 432092. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Sarkar, B.; Biswas, A. Linguistic Einstein aggregation operator-based TOPSIS for multicriteria group decision making in linguistic Pythagorean fuzzy environment. Int. J. Intell. Syst. 2021, 36, 2825–2864. [Google Scholar] [CrossRef]
- Lin, M.W.; Wei, J.C.; Xu, Z.S.; Chen, R.Q. Multiattribute group decision-making based on linguistic Pythagorean fuzzy interaction partitioned Bonferroni mean aggregation operators. Complexity 2018, 2018, 9531064. [Google Scholar] [CrossRef]
- Lin, M.W.; Huang, C.; Xu, Z.S. TOPSIS method based on correlation coefficient and entropy measure for linguistic Pythagorean fuzzy sets and its application to multiple attribute decision making. Complexity 2019, 2019, 6967390. [Google Scholar] [CrossRef]
- Ping, Y.J.; Liu, R.; Wang, Z.L.; Liu, H.C. New approach for quality function deployment with an extended alternative queuing method under linguistic Pythagorean fuzzy environment. Eur. J. Ind. Eng. 2022, 16, 349–370. [Google Scholar] [CrossRef]
- Han, Q.; Li, W.M.; Lu, Y.L.; Zheng, M.F.; Quan, W.; Song, Y.F. TOPSIS method based on novel entropy and distance measure for linguistic Pythagorean fuzzy sets with their application in multiple attribute decision making. IEEE Access 2019, 8, 14401–14412. [Google Scholar] [CrossRef]
- Liu, H.C.; Quan, M.Y.; Li, Z.W.; Wang, Z.L. A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment. Inf. Sci. 2019, 486, 254–270. [Google Scholar] [CrossRef]
- Mu, Z.M.; Zeng, S.Z.; Wang, P.Y. Novel approach to multi-attribute group decision-making based on interval-valued Pythagorean fuzzy power Maclaurin symmetric mean operator. Comput. Ind. Eng. 2021, 155, 107049. [Google Scholar] [CrossRef]
- Garg, H. Linguistic interval-valued Pythagorean fuzzy sets and their application to multiple attribute group decision-making process. Cogn. Comput. 2020, 12, 1313–1337. [Google Scholar] [CrossRef]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Wang, L.; Garg, H. Algorithm for multiple attribute decision-making with interactive Archimedean norm operations under Pythagorean fuzzy uncertainty. Int. J. Comput. Intell. Syst. 2021, 14, 503–527. [Google Scholar] [CrossRef]
- Qin, Y.C.; Qi, Q.F.; Shi, P.Z.; Scott, P.J.; Jiang, X.Q. Linguistic interval-valued intuitionistic fuzzy Archimedean prioritised aggregation operators for multi-criteria decision making. J. Intell. Fuzzy Syst. 2020, 38, 4643–4666. [Google Scholar] [CrossRef]
- Yager, R.R. The power average operator. IEEE Trans. Syst. Man Cybern.-Part A 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Power geometric operators and their use in group decision making. IEEE Trans. Fuzzy Syst. 2009, 18, 94–105. [Google Scholar]
- Xu, Z.S. Approaches to multiple attribute group decision making based on intuitionistic fuzzy power aggregation operators. Knowl.-Based Syst. 2011, 24, 749–760. [Google Scholar] [CrossRef]
- He, Y.D.; He, Z.; Wang, G.D.; Chen, H.Y. Hesitant fuzzy power Bonferroni means and their application to multiple attribute decision making. IEEE Trans. Fuzzy Syst. 2014, 23, 1655–1668. [Google Scholar] [CrossRef]
- Xiong, S.H.; Chen, Z.S.; Chang, J.P.; Chin, K.S. On extended power average operators for decision-making: A case study in emergency response plan selection of civil aviation. Comput. Ind. Eng. 2019, 130, 258–271. [Google Scholar] [CrossRef]
- Li, L.; Ji, C.; Wang, J. A novel multi-attribute group decision-making method based on q-rung dual hesitant fuzzy information and extended power average operators. Cogn. Comput. 2021, 13, 1345–1362. [Google Scholar] [CrossRef]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic; Prenticehall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Meng, F.Y.; Tang, J.; Fujita, H. Linguistic intuitionistic fuzzy preference relations and their application to multi-criteria decision making. Inf. Fusion 2019, 46, 77–90. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. Linguistic interval-valued Atanassov intuitionistic fuzzy sets and their applications to group decision making problems. IEEE Trans. Fuzzy. Syst. 2019, 27, 2302–2311. [Google Scholar] [CrossRef]
- Pei, F.; He, Y.W.; Yan, A.; Zhou, M.; Chen, Y.W.; Wu, J. A consensus model for intuitionistic fuzzy group decision-making problems based on the construction and propagation of trust/distrust relationships in social networks. Int. J. Fuzzy Syst. 2020, 22, 2664–2679. [Google Scholar] [CrossRef]
- Chen, H.P. Hesitant fuzzy multi-attribute group decision making method based on weighted power operators in social network and their application. J. Intell. Fuzzy Syst. 2021, 40, 9383–9401. [Google Scholar] [CrossRef]
- Liu, Y.; Diao, W.X.; Yang, J.; Yi, J.H. A visual social network group consensus approach with minimum adjustment based on Pythagorean fuzzy set. Iran. J. Fuzzy Syst. 2021, 18, 167–183. [Google Scholar]
- Ren, R.X.; Tang, M.; Liao, H.C. Managing minority opinions in micro-grid planning by a social network analysis-based large scale group decision making method with hesitant fuzzy linguistic information. Knowl.-Based Syst. 2020, 189, 105060. [Google Scholar] [CrossRef]
- Li, Y.H.; Kou, G.; Li, G.X.; Peng, Y. Consensus reaching process in large-scale group decision making based on bounded confidence and social network. Eur. J. Oper. Res. 2022, 303, 790–802. [Google Scholar] [CrossRef]
- Gai, T.T.; Cao, M.S.; Chiclana, F.; Wu, J.; Laing, C.Y.; Herrera-Viedma, E. A decentralized feedback mechanism with compromise behavior for large-scale group consensus reaching process with application in smart logistics supplier selection. Expert Syst. Appl. 2022, 204, 117547. [Google Scholar] [CrossRef]
- Zha, Q.B.; Cai, J.F.; Gu, J.P.; Liu, G.W. Information learning-driven consensus reaching process in group decision-making with bounded rationality and imperfect information: China’s urban renewal negotiation. Appl. Intell. 2022. [Google Scholar] [CrossRef]
- Li, Z.L.; Zhang, Z.; Yu, W.Y. Consensus reaching with consistency control in group decision making with incomplete hesitant fuzzy linguistic preference relations. Comput. Ind. Eng. 2022, 170, 108311. [Google Scholar] [CrossRef]
- Zha, Q.B.; Dong, Y.C.; Chiclana, F.; Herrera-Viedma, E. Consensus reaching in multiple attribute group decision making: A multi-stage optimization feedback mechanism with individual bounded confidences. IEEE Trans. Fuzzy Syst. 2022, 30, 3333–3346. [Google Scholar] [CrossRef]
| Name | Additive Generators | T-Norm | T-Conorm |
|---|---|---|---|
| Algebraic T-norm and T-conorm ( and ) | |||
| Einstein T-norm and T-conorm ( and ) | |||
| Hamacher T-norm and T-conorm ( and ) | |||
| Frank T-norm and T-conorm ( and ) | |||
| Dombi T-norm and T-conorm ( and ) |
| Operations | Parameters | Ranking Order | |
|---|---|---|---|
| Algebraic | None | ||
| Einstein | None | ||
| Hamacher | |||
| Frank | |||
| Dombi |
| Decision-Making Methods | Ranking Order | |
|---|---|---|
| Garg’s [28] method based on the LIVPFWA operator | ||
| Our proposed method based on the LIVPFAEPWA |
| Decision-Making Methods | Ranking Order | |
|---|---|---|
| Garg and Kumar’s [39] method based on a LIVAIFWA operator | ||
| Our proposed method based on the LIVPFAEPWA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Yang, G. A Novel Linguistic Interval-Valued Pythagorean Fuzzy Multi-Attribute Group Decision-Making for Sustainable Building Materials Selection. Sustainability 2023, 15, 106. https://doi.org/10.3390/su15010106
Zhou Y, Yang G. A Novel Linguistic Interval-Valued Pythagorean Fuzzy Multi-Attribute Group Decision-Making for Sustainable Building Materials Selection. Sustainability. 2023; 15(1):106. https://doi.org/10.3390/su15010106
Chicago/Turabian StyleZhou, Yang, and Guangmin Yang. 2023. "A Novel Linguistic Interval-Valued Pythagorean Fuzzy Multi-Attribute Group Decision-Making for Sustainable Building Materials Selection" Sustainability 15, no. 1: 106. https://doi.org/10.3390/su15010106
APA StyleZhou, Y., & Yang, G. (2023). A Novel Linguistic Interval-Valued Pythagorean Fuzzy Multi-Attribute Group Decision-Making for Sustainable Building Materials Selection. Sustainability, 15(1), 106. https://doi.org/10.3390/su15010106






