Fuzzy Demand Vehicle Routing Problem with Soft Time Windows
Abstract
:1. Introduction
2. Problem Description
3. Constructing a Fuzzy Chance-Constrained Programming Model
Sign Convention
4. Designing an Algorithm for Solving the Model
4.1. Random Simulation Operator
4.2. Coding
4.3. Neighborhood Search Algorithm
4.4. Fitness Function
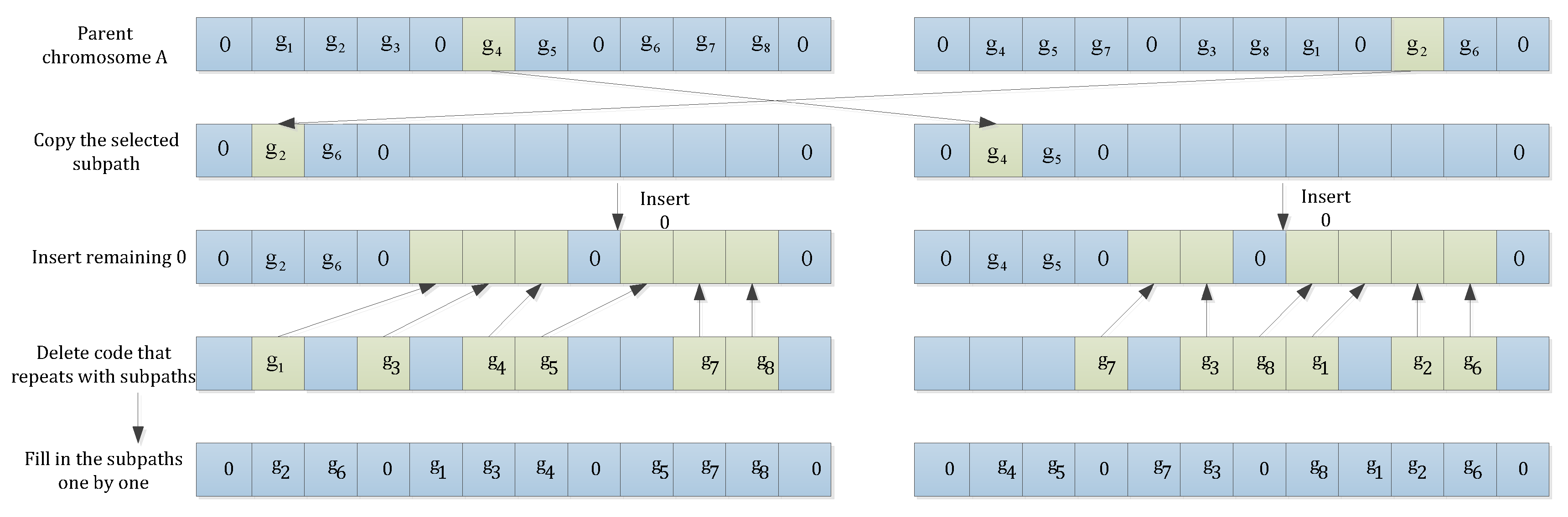
4.5. Selection, Crossover, and Mutation Operators
4.6. Termination Conditions
5. Simulation Experiment and Result Analysis
5.1. Description of Instance and Experimental Environment
5.2. Experiment in a Sample Instance
5.3. Comparative Analysis of Algorithms
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Li, B. Multi-objective tabu search algorithm for vehicle routing problem with fuzzy due-time. Comput. Integr. Manuf. Syst. 2011, 17, 858–866. [Google Scholar]
- Hoogeboom, M.; Dullaert, W.; Lai, D.; Vigo, D. Efficient neighborhood evaluations for the vehicle routing problem with multiple time windows. Transp. Sci. 2020, 54, 400–416. [Google Scholar] [CrossRef]
- Kuo, R.J.; Wibowo, B.S.; Zulvia, F.E. Application of a fuzzy ant colony system to solve the dynamic vehicle routing problem with uncertain service time. Appl. Math. Model. 2016, 40, 9990–10001. [Google Scholar] [CrossRef]
- Nadizadeh, A.; Hosseini, N.H. Solving the dynamic capacitated location-routing problem with fuzzy demands by hybrid heuristic algorithm. Eur. J. Oper. Res. 2014, 238, 458–470. [Google Scholar] [CrossRef]
- Li, Y.; Fan, H.M.; Zhang, X.N.; Yang, X. Two-phase variable neighborhood tabu search for the capacitated vehicle routing problem with fuzzy demand. Syst. Eng. Theory Pract. 2018, 38, 522–531. [Google Scholar]
- Zhang, X.N.; Fan, H.M. Optimization for multi-trip vehicle routing problem with fuzzy demands considering time window preference. Comput. Integr. Manuf. Syst. 2018, 10, 2461–2477. [Google Scholar]
- Lei, H.; Laporte, G.; Guo, B. The capacitated vehicle routing problem with stochastic demands and time windows. Comput. Oper. Res. 2011, 38, 1775–1783. [Google Scholar] [CrossRef]
- Ferreira, H.S.; Bogue, E.T.; Noronha, T.F. Variable neighborhood search for vehicle routing problem with multiple time windows. Electron. Notes Discret. Math. 2018, 66, 207–214. [Google Scholar] [CrossRef]
- Qi, M.Y.; Zhang, J.J.; Ren, L. Vehicle routing algorithm based on spatiotemporal clustering. Comput. Sci. 2014, 41, 218–222. [Google Scholar]
- Amiri-Aref, M.; Javadian, N.; Tavakkoli-Moghaddam, R.; Baboli, A.; Shiripour, S. The center location-dependent relocation problem with a probabilistic line barrier. Appl. Soft Comput. 2013, 13, 3380–3391. [Google Scholar] [CrossRef]
- Alizadeh, M.; Mahdavi, I.; Mahdavi-Amiri, N.; Shiripour, S. A capacitated location-allocation problem with stochastic demands using sub-sources: An empirical study. Appl. Soft Comput. 2015, 34, 551–571. [Google Scholar] [CrossRef]
- Shiripour, S.; Mahdavi-Amiri, N. Optimal distribution of the injured in a multi-type transportation network with damage-dependent travel times: Two metaheuristic approaches. Socio Econ. Plan. Sci. 2018, 68, 100660. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Wang, S. Multi-depot open vehicle routing problem with time windows based on carbon trading. Int. J. Environ. Res. Public Health 2018, 15, 2025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Y.; Lv, L.; Hu, F.; Han, Q. A heuristic solution method for multi-depot vehicle routing-based waste collection problems. Appl. Sci. 2020, 10, 2403. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhou, C.Y. A three-stage saving-based heuristic for vehicle routing problem with time windows and stochastic travel timesa. Discret. Dyn. Nat. Soc. 2016, 2016, 7841297. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Shiripour, S.; Mahdavi-Amiri, N.; Mahdavi, I. Optimal location-multi-allocation-routing in capacitated transportation networks under population-dependent travel times. Int. J. Comput. Integr. Manuf. 2015, 29, 652–676. [Google Scholar] [CrossRef]
- Shiripour, S.; Mahdavi-Amiri, N.; Mahdavi, I. A transportation network model with intelligent probabilistic travel times and two hybrid algorithms. Transp. Lett. 2017, 9, 90–122. [Google Scholar] [CrossRef]




| Step 1. Randomly generate all customer demand data, which represent the fuzzy demand, as follows: (1) Generate a number γ randomly according to the customer fuzzy demand and calculate its membership degree λ. (2) Randomly generate a number ξ in the range [0, 1]. (3) If λ < ξ, then γ is the customer demand; otherwise, repeat the above steps. (4) Repeat steps 1–3 until all customer demands are generated. |
| Step 2. Calculate the additional cost under the condition of customer demand. |
| Step 3. Repeat steps 1 and 2 N times. |
| Step 4. Take the average value of N simulations as the penalty cost. |
| No. | x | y | Demand | No. | x | y | Demand |
|---|---|---|---|---|---|---|---|
| 1 | 38 | 46 | ----- | 16 | 36 | 48 | 5 |
| 2 | 59 | 46 | 16 | 17 | 45 | 36 | 16 |
| 3 | 96 | 42 | 18 | 18 | 73 | 57 | 7 |
| 4 | 47 | 61 | 1 | 19 | 10 | 91 | 4 |
| 5 | 26 | 15 | 13 | 20 | 98 | 51 | 22 |
| 6 | 66 | 6 | 8 | 21 | 92 | 62 | 7 |
| 7 | 96 | 23 | 23 | 22 | 43 | 43 | 23 |
| 8 | 37 | 25 | 7 | 23 | 53 | 25 | 16 |
| 9 | 68 | 92 | 27 | 24 | 78 | 65 | 2 |
| 10 | 78 | 84 | 1 | 25 | 72 | 79 | 2 |
| 11 | 82 | 28 | 3 | 26 | 37 | 88 | 9 |
| 12 | 93 | 90 | 6 | 27 | 16 | 73 | 2 |
| 13 | 74 | 42 | 24 | 28 | 75 | 96 | 12 |
| 14 | 60 | 20 | 19 | 29 | 11 | 66 | 1 |
| 15 | 78 | 58 | 2 | 30 | 9 | 49 | 9 |
| A | Route Cost | Time Cost | Penalty Cost | Total Cost |
|---|---|---|---|---|
| 0.1 | 3165.33 | 89.75 | 255.45 | 4351.15 |
| 0.2 | 3246.54 | 90.61 | 257.63 | 4339.37 |
| 0.3 | 3209.71 | 88.98 | 256.92 | 4277.83 |
| 0.4 | 3193.26 | 89.25 | 258.77 | 4196.46 |
| 0.5 | 3006.09 | 88.64 | 260.55 | 4138.41 |
| 0.6 | 3227.15 | 89.79 | 257.39 | 4375.34 |
| 0.7 | 3421.48 | 90.53 | 260.93 | 4299.71 |
| 0.8 | 3568.9 | 91.62 | 265.47 | 4239.53 |
| 0.9 | 3504.11 | 92.88 | 278.36 | 4447.68 |
| 1 | 3732.27 | 93.58 | 279.49 | 4585.27 |
| e.g., | With Soft Time Windows | Without Soft Time Windows | ||||
|---|---|---|---|---|---|---|
| k | Time Cost | Total Cost | k | Time Cost | Total Cost | |
| C101 | 3 | 90.75 | 4277.01 | 3 | 73.35 | 4369.54 |
| C102 | 3 | 88.61 | 4283.68 | 3 | 72.64 | 4354.27 |
| C103 | 2 | 90.98 | 4159.93 | 2 | 77.58 | 4342.85 |
| C104 | 4 | 87.25 | 4319.72 | 2 | 78.52 | 4521.33 |
| C105 | 2 | 91.64 | 4124.55 | 3 | 68.63 | 4238.76 |
| C106 | 3 | 88.79 | 4305.72 | 3 | 73.22 | 4395.04 |
| C107 | 3 | 88.53 | 4211.4 | 2 | 77.83 | 4321.78 |
| C108 | 2 | 90.62 | 4199.23 | 2 | 76.42 | 4253.69 |
| C109 | 3 | 89.88 | 4189.87 | 3 | 72.98 | 4283.47 |
| C201 | 3 | 90.58 | 4423.27 | 3 | 73.57 | 4498.06 |
| e.g., | Optimal | Dual Population Genetic Algorithm | Genetic Simulated Annealing Algorithm | SA-GA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| k | Total Cost | k | Total Cost | Gap (%) | k | Total Cost | Gap (%) | k | Total Cost | Gap (%) | |
| C101 | 3 | 4279.16 | 2 | 4380.68 | 2.41 | 3 | 4332.15 | 1.21 | 3 | 4279.16 | 0 |
| C102 | 3 | 4146.58 | 3 | 4200.95 | 1.22 | 2 | 4146.58 | 0 | 3 | 4159.93 | 0.23 |
| C103 | 2 | 4397.38 | 3 | 4431.01 | 0.78 | 3 | 4421.06 | 0.55 | 2 | 4397.38 | 0 |
| C104 | 3 | 4428.58 | 3 | 4428.58 | 0 | 3 | 4521.13 | 2.09 | 2 | 4435.04 | 0.13 |
| C105 | 2 | 4138.29 | 3 | 4188.96 | 1.25 | 2 | 4231.57 | 2.25 | 2 | 4138.29 | 0 |
| C106 | 3 | 4438.54 | 3 | 4487.92 | 1.13 | 3 | 4438.54 | 0 | 2 | 4455.34 | 0.36 |
| C107 | 2 | 4199.23 | 2 | 4276.13 | 1.84 | 3 | 4243.11 | 1.04 | 2 | 4199.23 | 0 |
| C108 | 3 | 4189.86 | 3 | 4198.17 | 0.24 | 3 | 4288.55 | 2.37 | 3 | 4189.86 | 0 |
| C109 | 3 | 4423.26 | 3 | 4538.06 | 2.61 | 3 | 4526.23 | 2.3 | 3 | 4423.26 | 0 |
| C201 | 3 | 4685.27 | 3 | 4761.73 | 1.65 | 3 | 4695.19 | 0.3 | 3 | 4685.27 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Wang, W.; Wu, Q. Fuzzy Demand Vehicle Routing Problem with Soft Time Windows. Sustainability 2022, 14, 5658. https://doi.org/10.3390/su14095658
Yang T, Wang W, Wu Q. Fuzzy Demand Vehicle Routing Problem with Soft Time Windows. Sustainability. 2022; 14(9):5658. https://doi.org/10.3390/su14095658
Chicago/Turabian StyleYang, Tao, Weixin Wang, and Qiqi Wu. 2022. "Fuzzy Demand Vehicle Routing Problem with Soft Time Windows" Sustainability 14, no. 9: 5658. https://doi.org/10.3390/su14095658
APA StyleYang, T., Wang, W., & Wu, Q. (2022). Fuzzy Demand Vehicle Routing Problem with Soft Time Windows. Sustainability, 14(9), 5658. https://doi.org/10.3390/su14095658






