Long-Term Freezing Temperatures Frequency Change Effect on Wind Energy Gain (Eurasia and North America, 1950–2019)
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
2.2. Annual Freezing Frequency Temperature at 100 m
2.3. Annual FTF Mean Data and Decadal Trends
2.4. AEP Loss Approximation
2.5. AEP Gain
3. Results
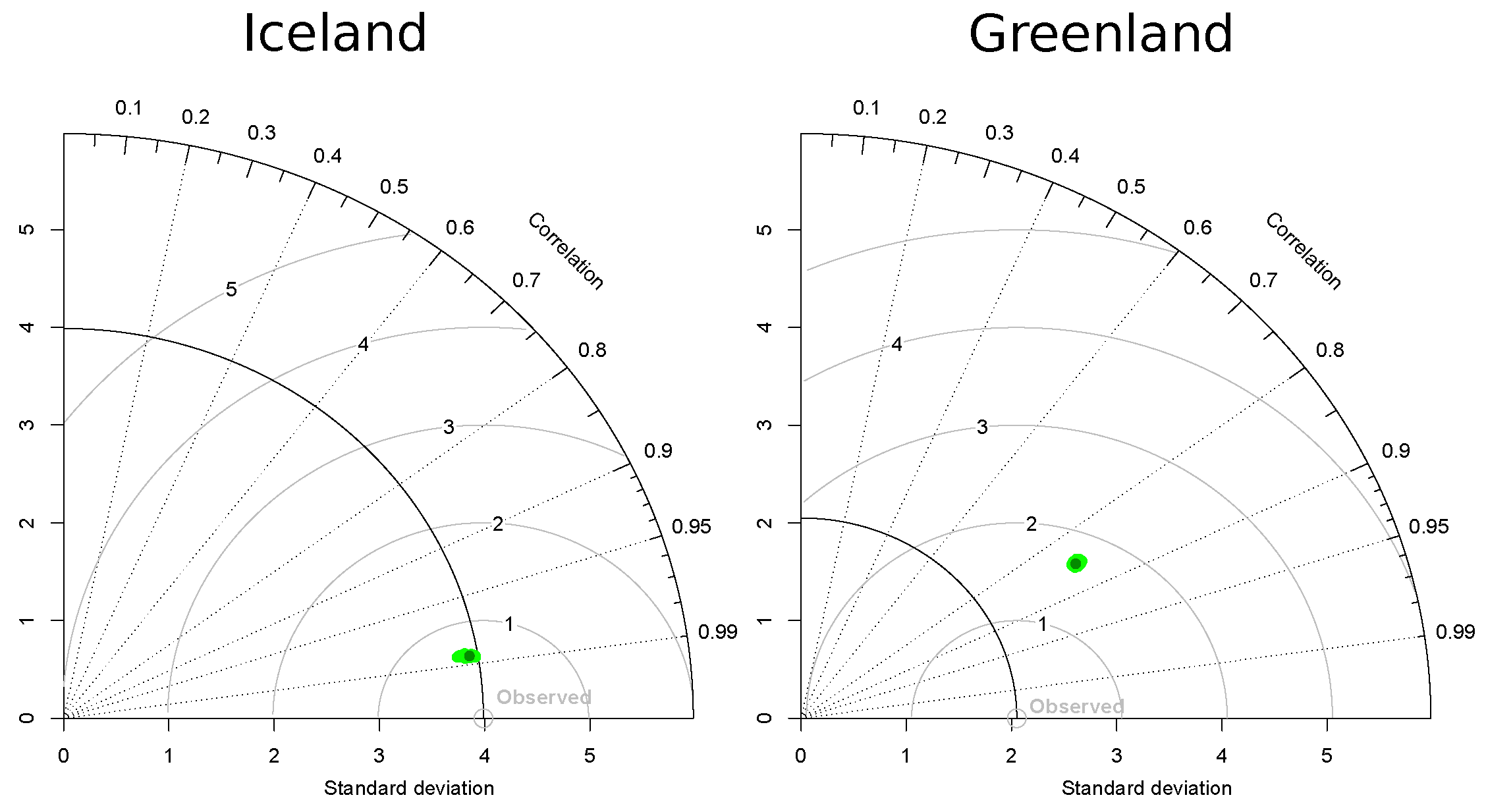
3.1. ERA5 Validation on Two Buoys
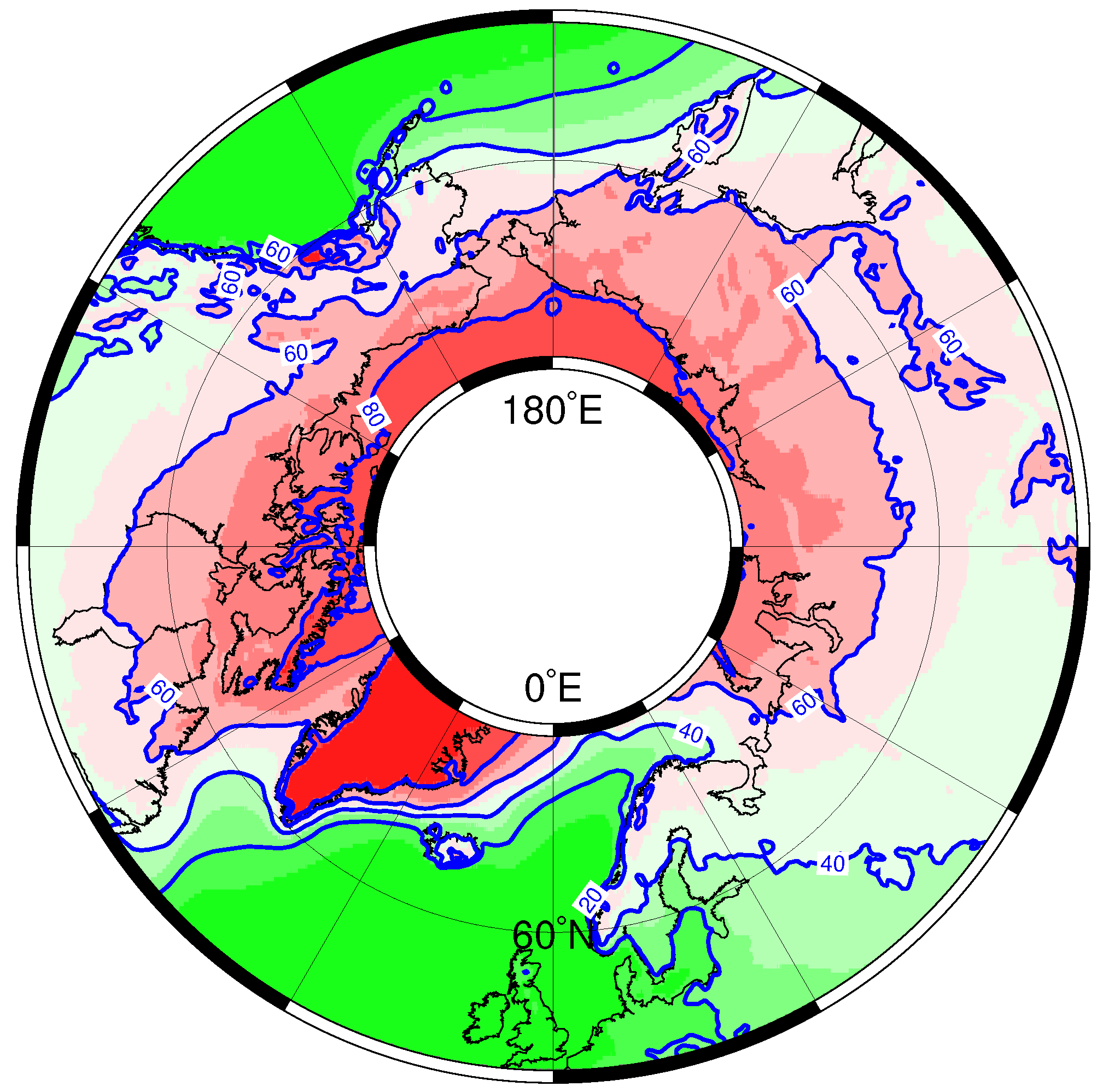
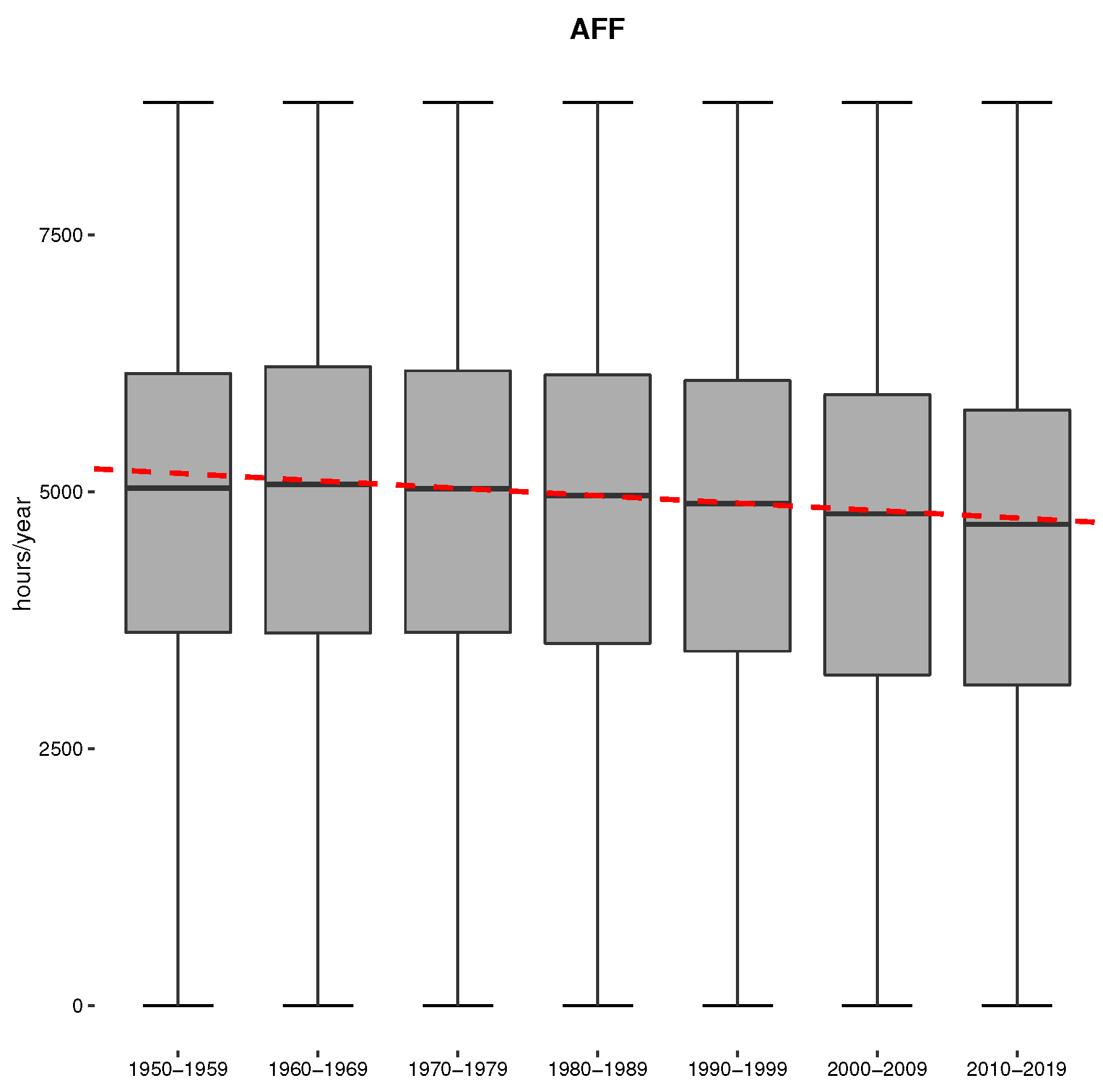
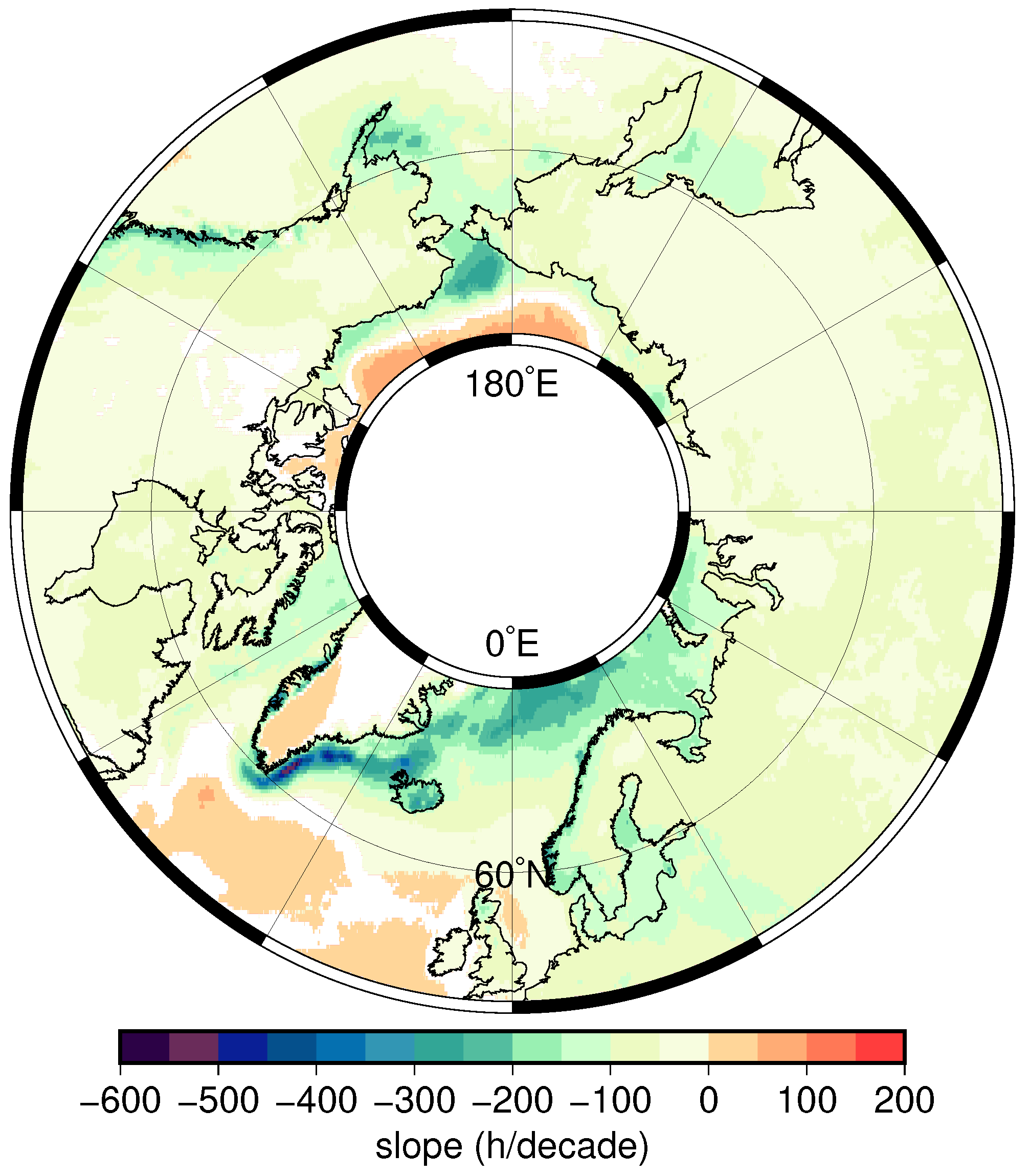
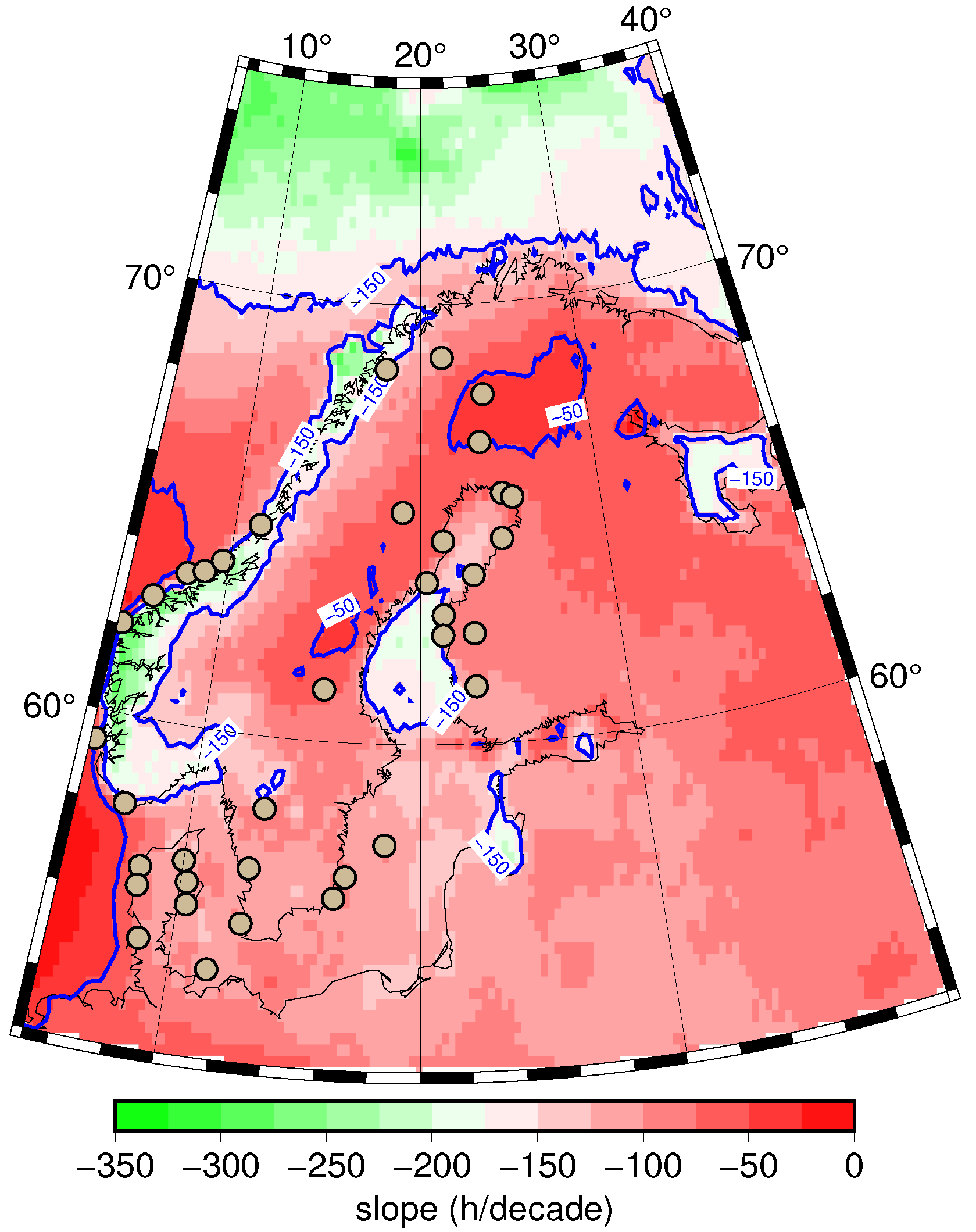
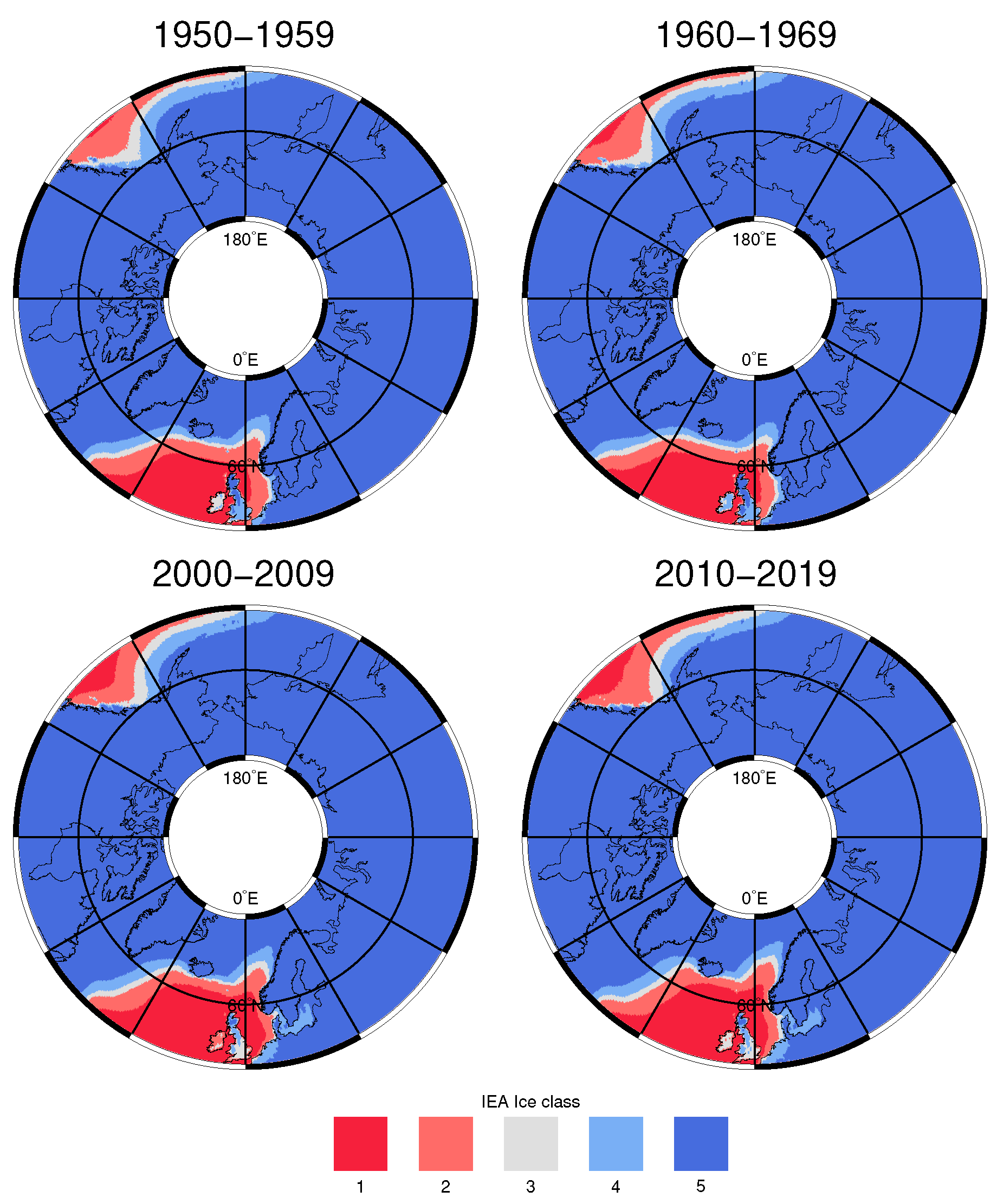
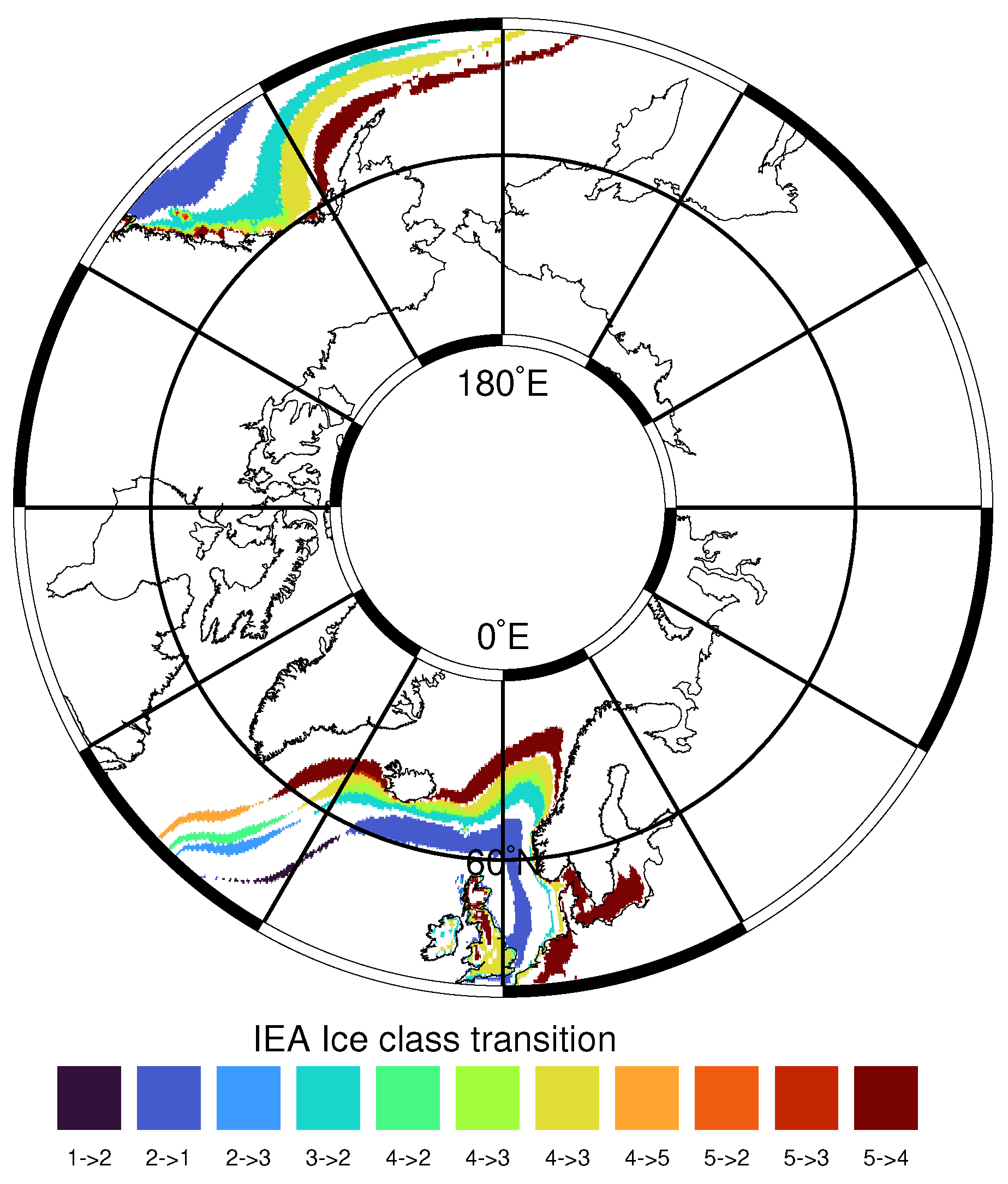
3.2. Annual FTF Mean Data and Decadal Trends
3.3. AEP Losses Approximation and Gain
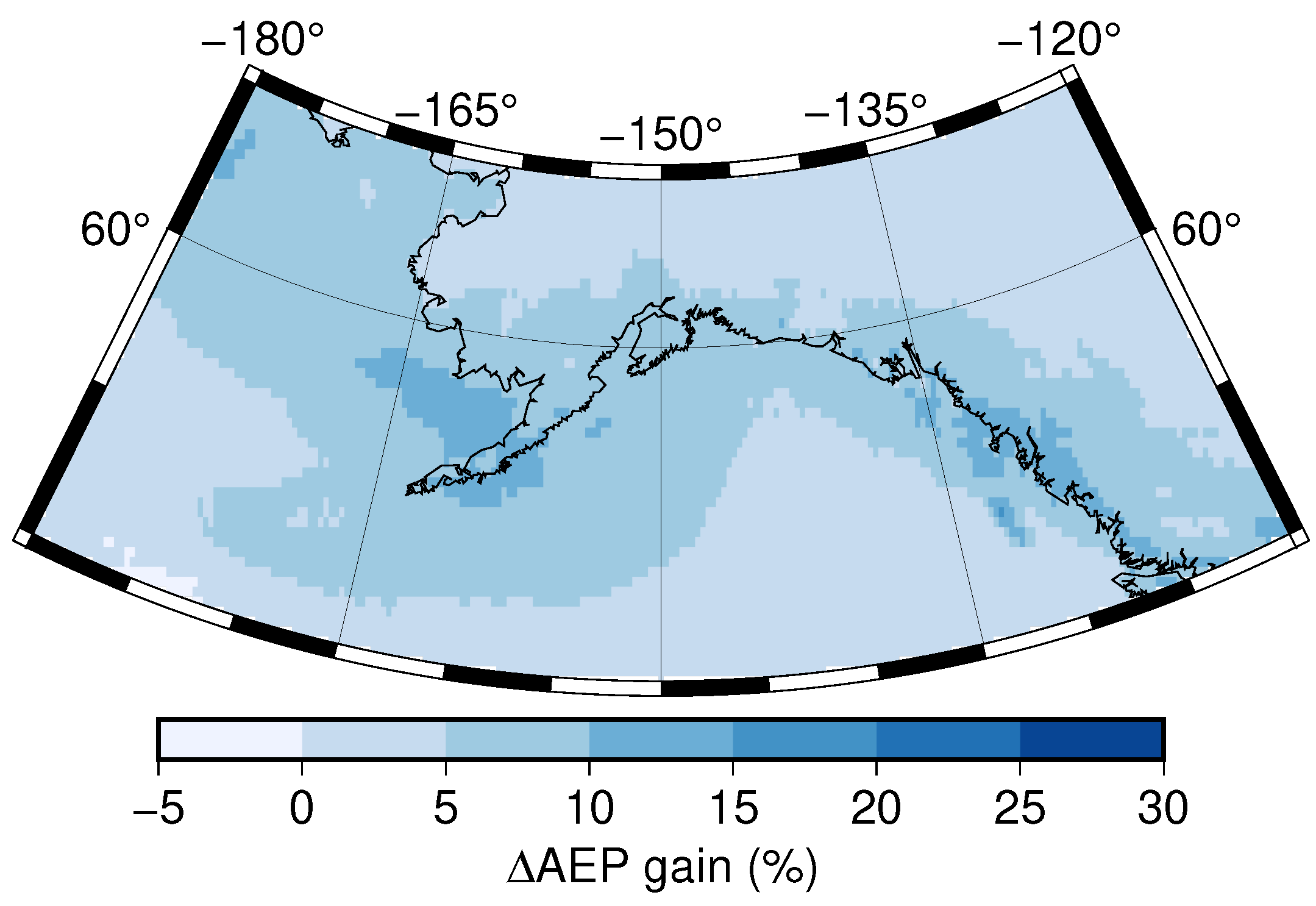
3.3.1. AEP Gain in Gulf of Alaska
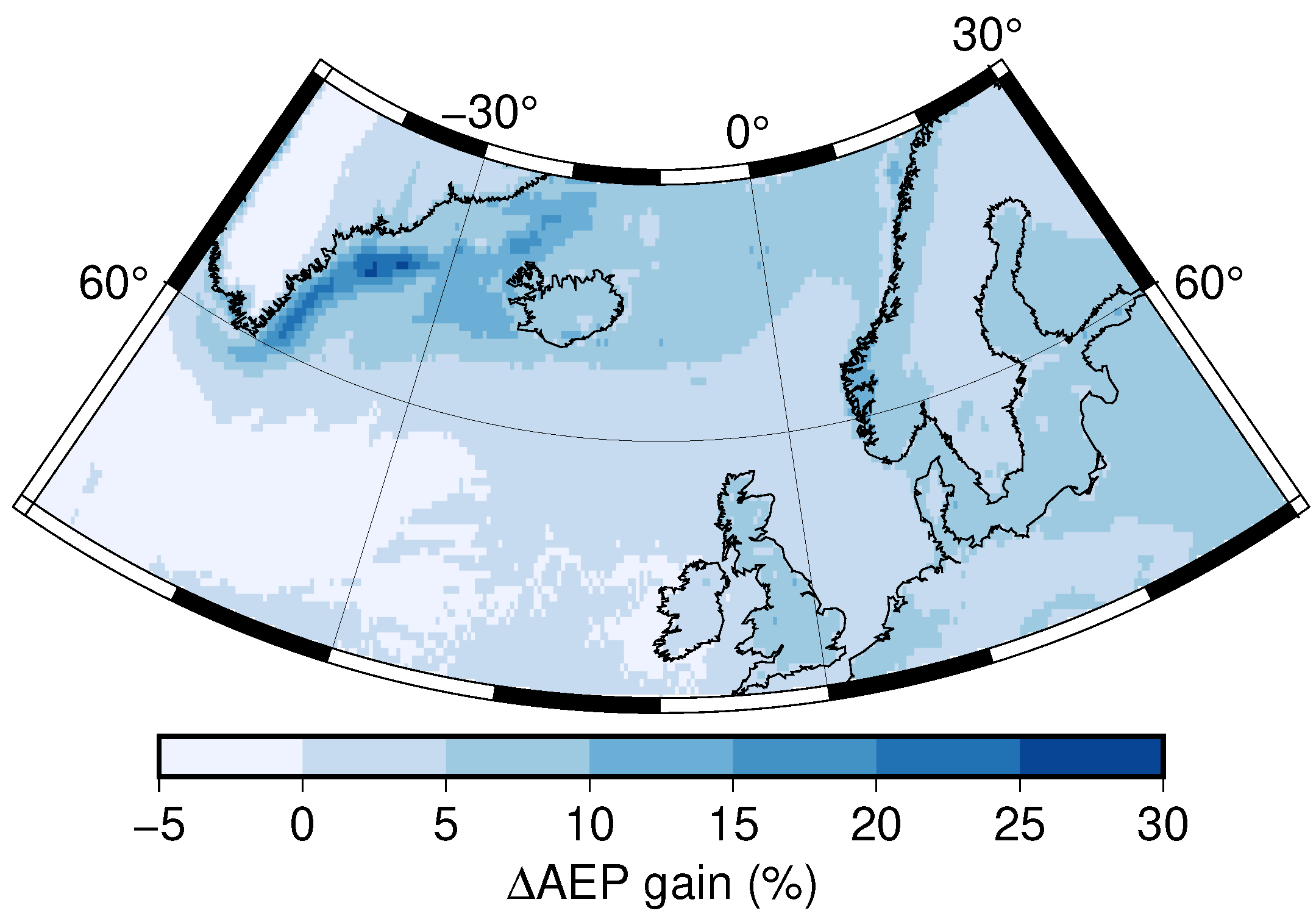
3.3.2. AEP Gain in Northern Europe
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEP | Annual Energy Production |
| FTF | Freezing Frequency Temperature |
| IEA | International Energy Agency |
| IPCC | Intergovernmental Panel on Climate Change |
| NOAA | National Oceanic and Atmospheric Administration |
| NREL | National Renewable Energies Laboratory |
| RCP | Representative Concentration Pathways |
| SSP | Shared Socioeconomic Pathways |
| GHG | Greenhouse Gas |
References
- Association, W.W.E. Worldwide Wind Capacity Reaches 744 Gigawatts—An Unprecedented 93 Gigawatts added in 2020. 2021. Available online: https://wwindea.org/worldwide-wind-capacity-reaches-744-gigawatts/ (accessed on 18 June 2021).
- Battisti, L. Wind Turbines in Cold Climates: Icing Impacts and Mitigation Systems; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Bredesen, R.E.; Vindteknikk, K.; Jordaens, P.J.; Owi-lab, S.; Khadiri-Yazami, B.Z.; Klintström, R.; Krenn, S.A.; Verein, E.; Lehtomäki, A.V.; Ronsten, G.; et al. Expert Group Study on Recommended Practices 13. Wind Energy Projects in Cold Climates 2. Edition; International Energy Agency: France, Paris, 2017.
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey; Elsevier: Amsterdam, The Netherlands, 2006; Volume 92. [Google Scholar]
- Lamraoui, F.; Fortin, G.; Benoit, R.; Perron, J.; Masson, C. Atmospheric icing impact on wind turbine production. Cold Reg. Sci. Technol. 2014, 100, 36–49. [Google Scholar] [CrossRef]
- Ulazia, A.; Gonzalez-Roji, S.J.; Ibarra-Berastegi, G.; Carreno-Madinabeitia, S.; Saenz, J.; Nafarrate, A. Seasonal Air Density Variations over The East of Scotland and The Consequences for Offshore Wind Energy. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 261–265. [Google Scholar]
- Ulazia, A.; Sáenz, J.; Ibarra-Berastegi, G.; González-Rojí, S.J.; Carreno-Madinabeitia, S. Global estimations of wind energy potential considering seasonal air density changes. Energy 2019, 187, 115938. [Google Scholar] [CrossRef]
- Ulazia, A.; Ibarra-Berastegi, G.; Sáenz, J.; Carreno-Madinabeitia, S.; González-Rojí, S.J. Seasonal correction of offshore wind energy potential due to air density: Case of the Iberian Peninsula. Sustainability 2019, 11, 3648. [Google Scholar] [CrossRef] [Green Version]
- Ulazia, A.; Nafarrate, A.; Ibarra-Berastegi, G.; Sáenz, J.; Carreno-Madinabeitia, S. The consequences of air density variations over northeastern Scotland for offshore wind energy potential. Energies 2019, 12, 2635. [Google Scholar] [CrossRef] [Green Version]
- Barber, S.; Wang, Y.; Jafari, S.; Chokani, N.; Abhari, R.S. The impact of ice formation on wind turbine performance and aerodynamics. J. Sol. Energy Eng. Trans. ASME 2011, 133, 011007. [Google Scholar] [CrossRef]
- Gao, L.; Hu, H.; Sharma, A.; Ward, T.; Hu, S.; Wang, X. Experimental Investigations on Wind Turbine Icing Physics and Anti-/de-Icing Technology. Available online: https://dr.lib.iastate.edu/entities/publication/7e1f84ec-2724-471d-88b2-89614a4d5039 (accessed on 1 April 2022).
- Nygaard, B.E.K.; Kristjánsson, J.E.; Makkonen, L. Prediction of in-cloud icing conditions at ground level using the WRF model. J. Appl. Meteorol. Climatol. 2011, 50, 2445–2459. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J.; Schmitz, S. Scaled ice accretion experiments on a rotating wind turbine blade. J. Wind Eng. Ind. Aerodyn. 2012, 109, 55–67. [Google Scholar] [CrossRef]
- Villalpando, F.; Reggio, M.; Ilinca, A. Prediction of ice accretion and anti-icing heating power on wind turbine blades using standard commercial software. Energy 2016, 114, 1041–1052. [Google Scholar] [CrossRef]
- Gao, L.; Liu, Y.; Hu, H. An experimental investigation on the dynamic glaze ice accretion process over a wind turbine airfoil surface. Int. J. Heat Mass Transf. 2020, 149, 119120. [Google Scholar] [CrossRef]
- Li, Y.; Tagawa, K.; Feng, F.; Li, Q.; He, Q. A wind tunnel experimental study of icing on wind turbine blade airfoil. Energy Convers. Manag. 2014, 85, 591–595. [Google Scholar] [CrossRef]
- Pena, D.; Hoarau, Y.; Laurendeau, E. A single step ice accretion model using Level-Set method. J. Fluids Struct. 2016, 65, 278–294. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Tao, T.; Liu, Y.; Hu, H. A field study of ice accretion and its effects on the power production of utility-scale wind turbines. Renew. Energy 2021, 167, 917–928. [Google Scholar] [CrossRef]
- Gao, L.; Dasari, T.; Hong, J. Wind farm icing loss forecast pertinent to winter extremes. Sustain. Energy Technol. Assess. 2022, 50, 101872. [Google Scholar] [CrossRef]
- Zalhaf, A.S.; Elboshy, B.; Kotb, K.M.; Han, Y.; Almaliki, A.H.; Aly, R.M.; Elkadeem, M. A High-Resolution Wind Farms Suitability Mapping Using GIS and Fuzzy AHP Approach: A National-Level Case Study in Sudan. Sustainability 2021, 14, 358. [Google Scholar] [CrossRef]
- Zhongming, Z.; Linong, L.; Xiaona, Y.; Wangqiang, Z.; Wei, L. AR6 Synthesis Report: Climate Change 2022; The Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2022.
- Lindsey, R.; Dahlman, L. Climate Change: Global Temperature. Climate. gov. Available online: https://www.climate.gov/news-features/understanding-climate/climate-change-global-temperature (accessed on 1 April 2022).
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term climate change: Projections, commitments and irreversibility. In Climate Change 2013-The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 1029–1136. [Google Scholar]
- Yan, W.X.; Zhao, J.F.; Li, J.P.; Wang, Y.X. Assessment of Seasonal Variability of Extreme Temperature in Mainland China under Climate Change. Sustainability 2021, 13, 12462. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hersbach, H. The ERA5 Atmospheric Reanalysis. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2016; Volume 2016, p. NG33D–01. [Google Scholar]
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef] [Green Version]
- Soukissian, T.H.; Karathanasi, F.E.; Zaragkas, D.K. Exploiting offshore wind and solar resources in the Mediterranean using ERA5 reanalysis data. Energy Convers. Manag. 2021, 237, 114092. [Google Scholar] [CrossRef]
- ERA5: Data Documentation. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation#ERA5:datadocumentation-Observations,year={} (accessed on 1 April 2022).
- Petersen, G.N. Meteorological buoy measurements in the Iceland Sea, 2007–2009. Earth Syst. Sci. Data 2017, 9, 779–789. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- American Meteorological Society. Glossary of Meteorology. Available online: https://glossary.ametsoc.org/wiki/Welcome (accessed on 1 April 2022).
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis; Koninalijke Nederlandse Akademie van Weinenschatpen: Amsterdam, The Netherlands, 1950; pp. 386–392. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Tian, T.S. WILCOX, RR (2010) Fundamentals of Modern Statistical Methods: Substantially Improving Power and Accuracy. 2011. Available online: https://link.springer.com/book/10.1007/978-1-4757-3522-2 (accessed on 1 April 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Komsta, L. CRA—Package Mblm. Available online: https://cran.r-project.org/web/packages/mblm/index.html (accessed on 1 April 2022).
- Cattin, R. IEA R&D Wind Task 19 «Wind Energy in Cold Climates» on Behalf of IEA RD&D Wind Task 19: «Wind Energy in Cold Climates» Validation of the IEA Task 19 Ice Classification; International Energy Agency (IEA): Paris, France, 2016.
- Carrière, J.M.; Alquier, S.; Le Bot, C.; Moulin, E. Statistical verification of forecast icing risk indices. Meteorol. Appl. 1997, 4, 115–130. [Google Scholar] [CrossRef]
- Wang, C.; Graham, R.M.; Wang, K.; Gerland, S.; Granskog, M.A. Comparison of ERA5 and ERA-Interim near-surface air temperature, snowfall and precipitation over Arctic sea ice: Effects on sea ice thermodynamics and evolution. Cryosphere 2019, 13, 1661–1679. [Google Scholar] [CrossRef] [Green Version]
- Tetzner, D.; Thomas, E.; Allen, C. A Validation of ERA5 Reanalysis Data in the Southern Antarctic Peninsula—Ellsworth Land Region, and Its Implications for Ice Core Studies. Geosciences 2019, 9, 289. [Google Scholar] [CrossRef] [Green Version]
- Wind Energy Database. Available online: https://www.thewindpower.net/index.php (accessed on 1 April 2022).
- Doubrawa Moreira, P.; Scott, G.N.; Musial, W.D.; Kilcher, L.F.; Draxl, C.; Lantz, E.J. Offshore Wind Energy Resource Assessment for Alaska; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018.
- Musial, W.; Heimiller, D.; Beiter, P.; Scott, G.; Draxl, C. Offshore Wind Energy Resource Assessment for the United States; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2016.
- Dong, C.; Huang, G.G.; Cheng, G. Offshore wind can power Canada. Energy 2021, 236, 121422. [Google Scholar] [CrossRef]
- Rusu, E. An evaluation of the wind energy dynamics in the Baltic Sea, past and future projections. Renew. Energy 2020, 160, 350–362. [Google Scholar] [CrossRef]
- Schillings, C.; Wanderer, T.; Cameron, L.; van der Wal, J.T.; Jacquemin, J.; Veum, K. A decision support system for assessing offshore wind energy potential in the North Sea. Energy Policy 2012, 49, 541–551. [Google Scholar] [CrossRef] [Green Version]
- Meier, K. Hydrogen production with sea water electrolysis using Norwegian offshore wind energy potentials: Techno-economic assessment for an offshore-based hydrogen production approach with state-of-the-art technology. Int. J. Energy Environ. Eng. 2014, 5, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Aizpurua-Etxezarreta, M.; Carreno-Madinabeitia, S.; Ulazia, A.; Sáenz, J.; Saenz-Aguirre, A. Ice Class Categorization Transition from 1950–1959 to 2010–2019 in High Latitudes. 2022. Available online: https://zenodo.org/record/6502404#.YnLWe-hBxPY (accessed on 1 April 2022).
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Miao, C.; Duan, Q.; Shen, C.; Wu, Y. The Performance of CMIP6 Versus CMIP5 in Simulating Temperature Extremes Over the Global Land Surface. J. Geophys. Res. Atmos. 2020, 125, e2020JD033031. [Google Scholar] [CrossRef]
- Watts, D.; Oses, N.; Pérez, R. Assessment of wind energy potential in Chile: A project-based regional wind supply function approach. Renew. Energy 2016, 96, 738–755. [Google Scholar] [CrossRef]
- Mattar, C.; Cabello-Españon, F.; Alonso-de Linaje, N.G. Towards a Future Scenario for Offshore Wind Energy in Chile: Breaking the Paradigm. Sustainability 2021, 13, 7013. [Google Scholar] [CrossRef]
- Labriola, C. Wind Energy in Argentina: Actuality and Prospects. In The Age of Wind Energy; Springer: Berlin/Heidelberg, Germany, 2020; pp. 147–173. [Google Scholar]
- Kelly, G. History and potential of renewable energy development in New Zealand. Renew. Sustain. Energy Rev. 2011, 15, 2501–2509. [Google Scholar] [CrossRef] [Green Version]
| IEA Ice Class | Meteorological Icing | AEP Loss Due to Icing |
|---|---|---|
| % of Year | % | |
| 1 | 0–0.5 | 0–0.5 |
| 2 | 0.5–3 | 0.5–5 |
| 3 | 3–5 | 3–12 |
| 4 | 5–10 | 10–25 |
| 5 | >10 | >20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aizpurua-Etxezarreta, M.; Carreno-Madinabeitia, S.; Ulazia, A.; Sáenz, J.; Saenz-Aguirre, A. Long-Term Freezing Temperatures Frequency Change Effect on Wind Energy Gain (Eurasia and North America, 1950–2019). Sustainability 2022, 14, 5630. https://doi.org/10.3390/su14095630
Aizpurua-Etxezarreta M, Carreno-Madinabeitia S, Ulazia A, Sáenz J, Saenz-Aguirre A. Long-Term Freezing Temperatures Frequency Change Effect on Wind Energy Gain (Eurasia and North America, 1950–2019). Sustainability. 2022; 14(9):5630. https://doi.org/10.3390/su14095630
Chicago/Turabian StyleAizpurua-Etxezarreta, Maddi, Sheila Carreno-Madinabeitia, Alain Ulazia, Jon Sáenz, and Aitor Saenz-Aguirre. 2022. "Long-Term Freezing Temperatures Frequency Change Effect on Wind Energy Gain (Eurasia and North America, 1950–2019)" Sustainability 14, no. 9: 5630. https://doi.org/10.3390/su14095630
APA StyleAizpurua-Etxezarreta, M., Carreno-Madinabeitia, S., Ulazia, A., Sáenz, J., & Saenz-Aguirre, A. (2022). Long-Term Freezing Temperatures Frequency Change Effect on Wind Energy Gain (Eurasia and North America, 1950–2019). Sustainability, 14(9), 5630. https://doi.org/10.3390/su14095630






