Analyzing and Mitigating the Impacts of Integrating Fast-Charging Stations on the Power Quality in Electric Power Distribution Systems
Abstract
:1. Introduction
1.1. Background
1.2. Previous Work
1.3. Research Gaps
- None of the reported works have quantified the impact of FCS on the voltage quality such as voltage variation, voltage unbalance, and voltage fluctuation and light flicker, to mitigate that impact.
- Most of the relevant works assume the output power of the FCS is constant without justification and do not consider the power variation over time when the EV SOC is increased.
- Most of the previous works have quantified the impact of the FCS on an hourly basis. Vehicles with small battery capacities that take a couple of minutes to recharge may not be considered, which indicates that the impact may not be quantified properly.
1.4. Contribution
- Development and modification of the test system to encompass fast-charging stations, commercial loads, and residential houses. Different scenarios were applied to quantify and mitigate the impact of the FCSs.
- Proposal of a probabilistic models for two methods of charging: when the power pro-file of FCS is estimated and when the power profile of FCS is real.
- Two voltage magnitude variations, namely undervoltage and overvoltage, as well as voltage unbalance and voltage fluctuation, are analyzed to quantify the impact of fast-charging stations.
- Introducing and comparing different mitigation technologies and selecting the best mitigation devices based on defined criteria, to improve the voltage quality.
2. Power Quality Problems of Integrating FCS
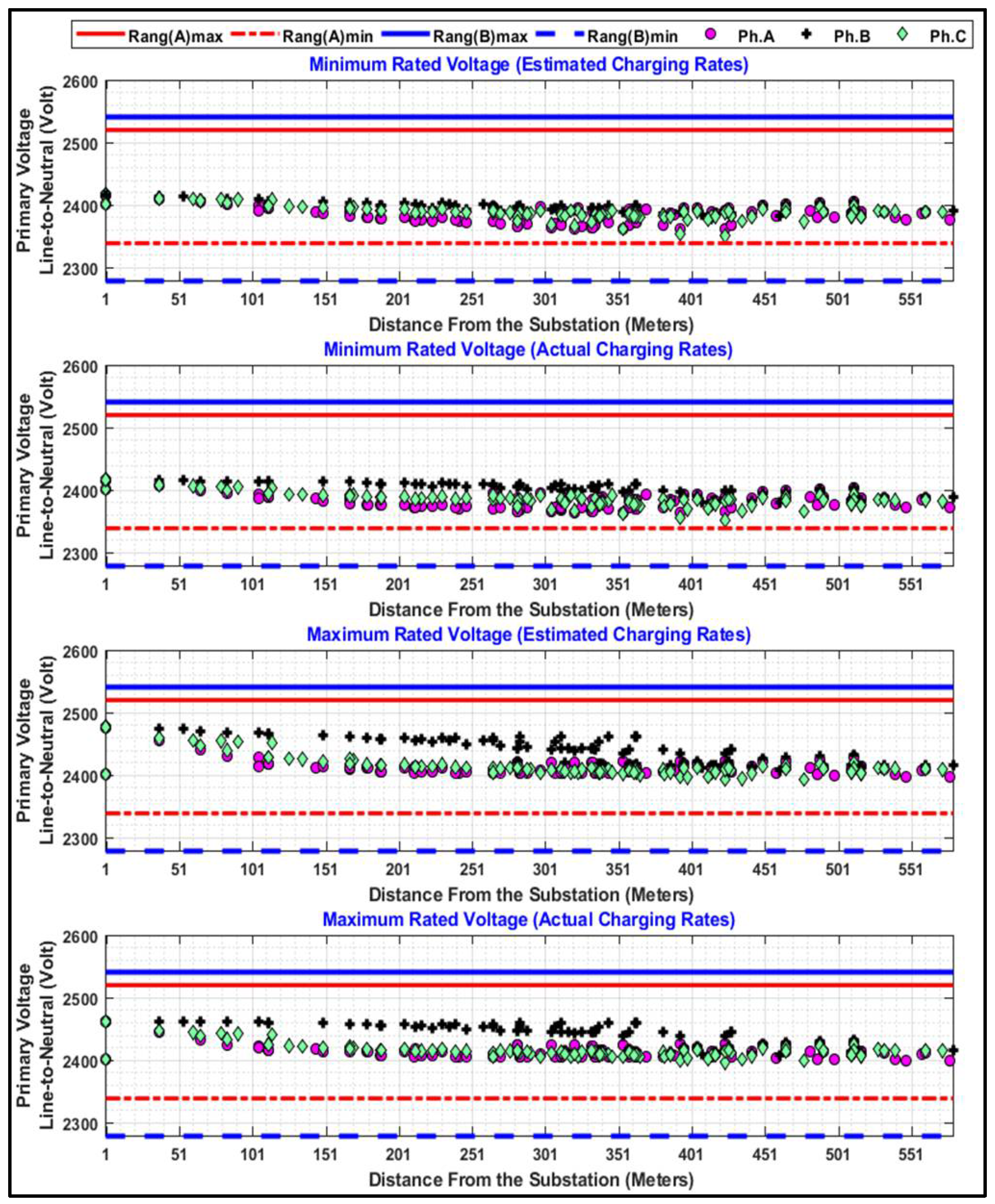
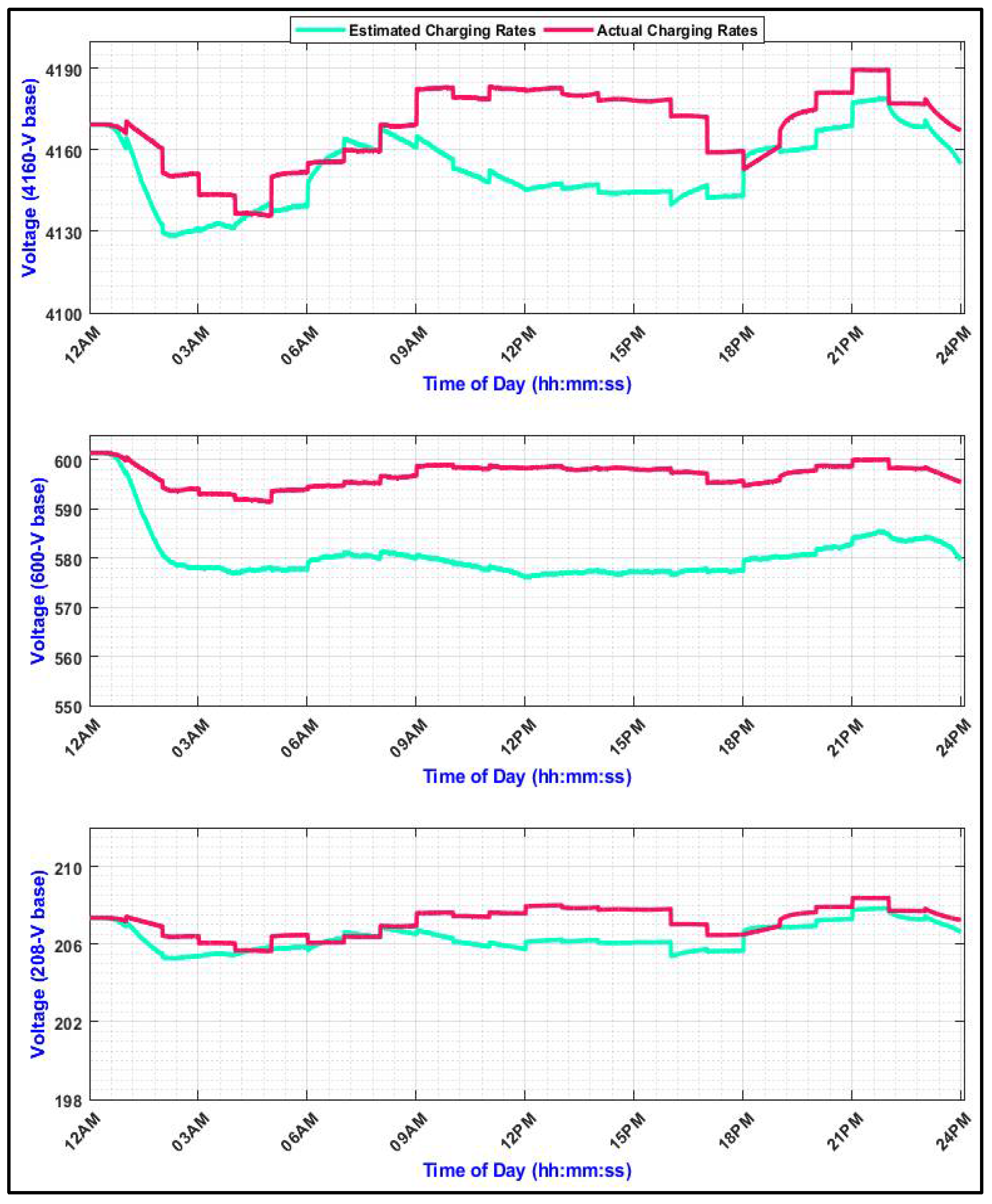
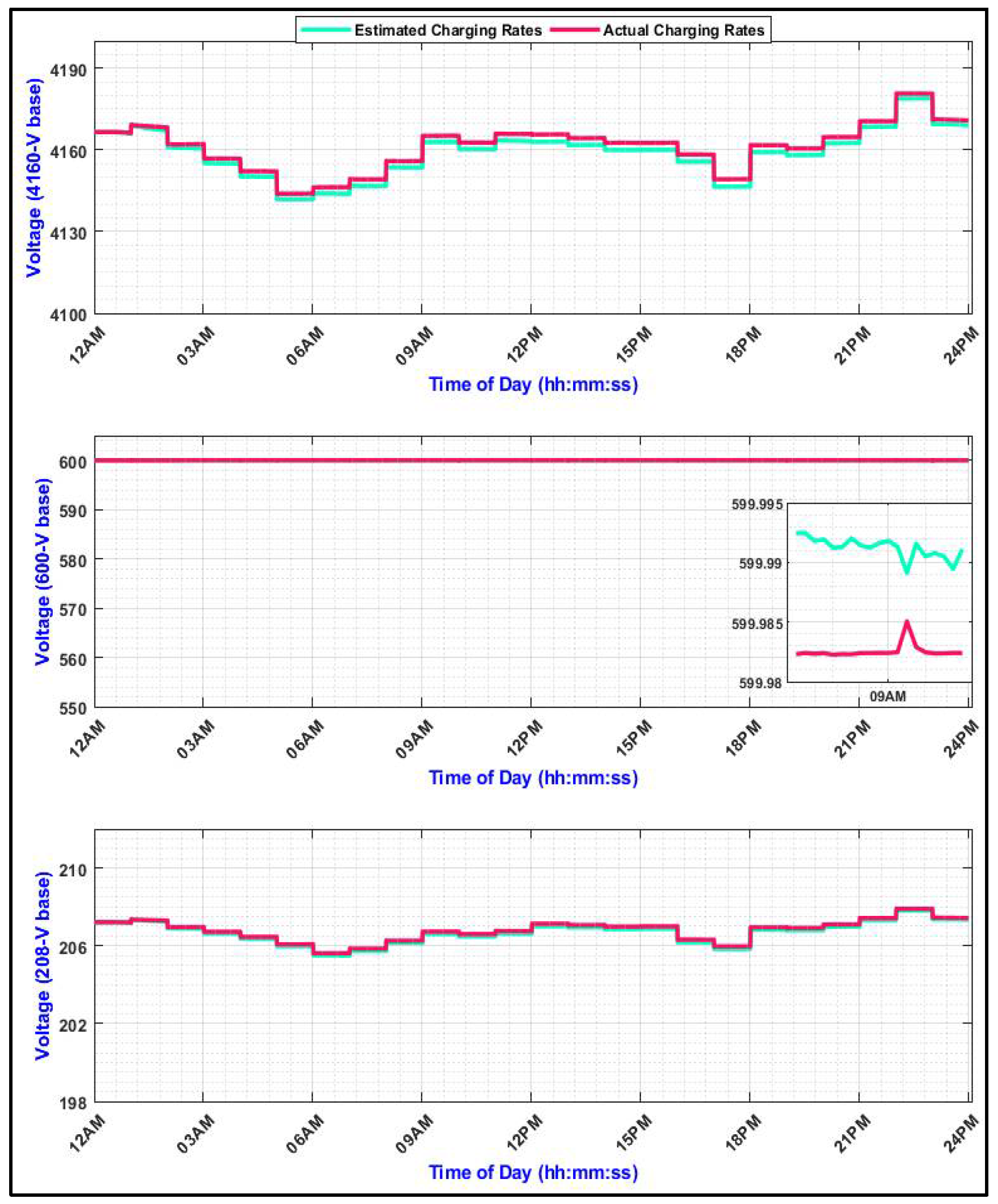
2.1. Voltage Magnitude Variations
2.2. Voltage Unbalance
2.3. Voltage Fluctuation and Light Flicker
3. Power Quality Mitigation
3.1. Comparison of Voltage Fluctuation Technologies
| the per unit cost of the Unified Power Quality Conditioner, (USD/kVAr) | |
| the per unit cost of the Distribution Static Compensator, (USD/kVAr) | |
| the per unit cost of the Thyristor Switched Capacitor, (USD/kVAr) | |
| the per unit cost of the Fixed Capacitors/Thyristor Controlled Reactors, (USD/kVAr) | |
| the per unit cost of the Dynamic Voltage Restorer, (USD/kVAr) | |
| the per unit cost of the Fixed Series Capacitor, (USD/kVAr) | |
| the operating range of the Unified Power Quality Conditioner, MVAr | |
| the operating range of the Distribution Static Compensator, MVAr | |
| the operating range of the Thyristor Switched Capacitor, MVAr | |
| the operating range of the Fixed Capacitors/Thyristor Controlled Reactors, MVAr | |
| the operating range of the Dynamic Voltage Restorer, MVAr | |
| the operating range of the Fixed Series Capacitor, MVAr |
3.2. Comparison of Costs of Flicker Mitigation Technologies
3.3. Comparison of Advantages and Disadvantages of Mitigation Technologies
3.4. Technology Selection
- Overload capability;
- Losses;
- Response time;
- Reactive power range;
- Investment costs;
- Control interaction;
- Special requirements (i.e., protection devices; special connection; customization);
- Efficiency during low/high loading;
- Single-phase control;
- Energization.
4. Probabilistic Load Charging Modelling
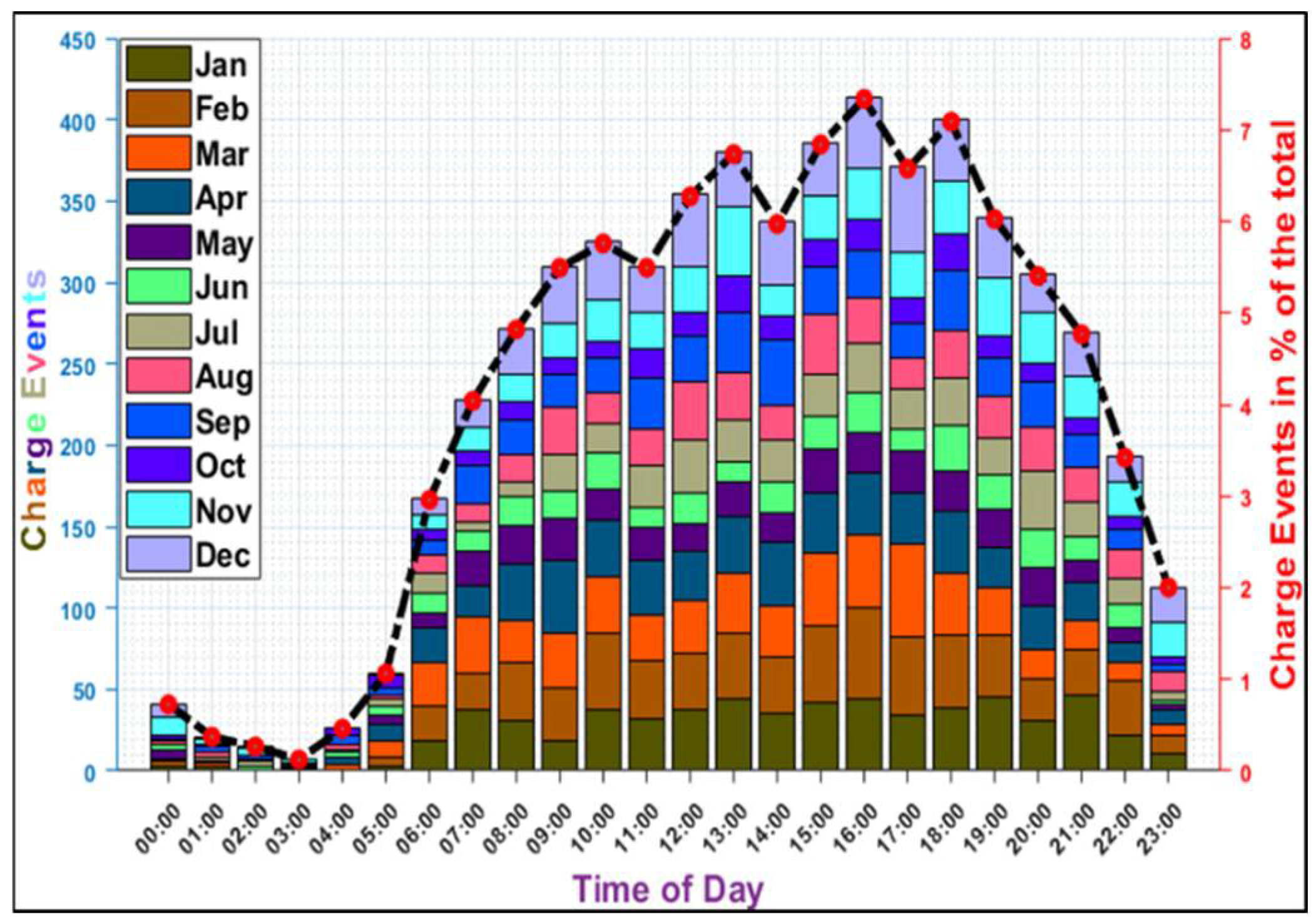
4.1. Commercial Load Profiles
4.2. Residential Load Profiles
4.3. Type Selction of Electric Vehicles
4.4. Type Selction of Electric Vehicles
4.5. Markov Chain Monte Carlo Approach
4.6. Rated Power of FCSs
5. Results and Discussion
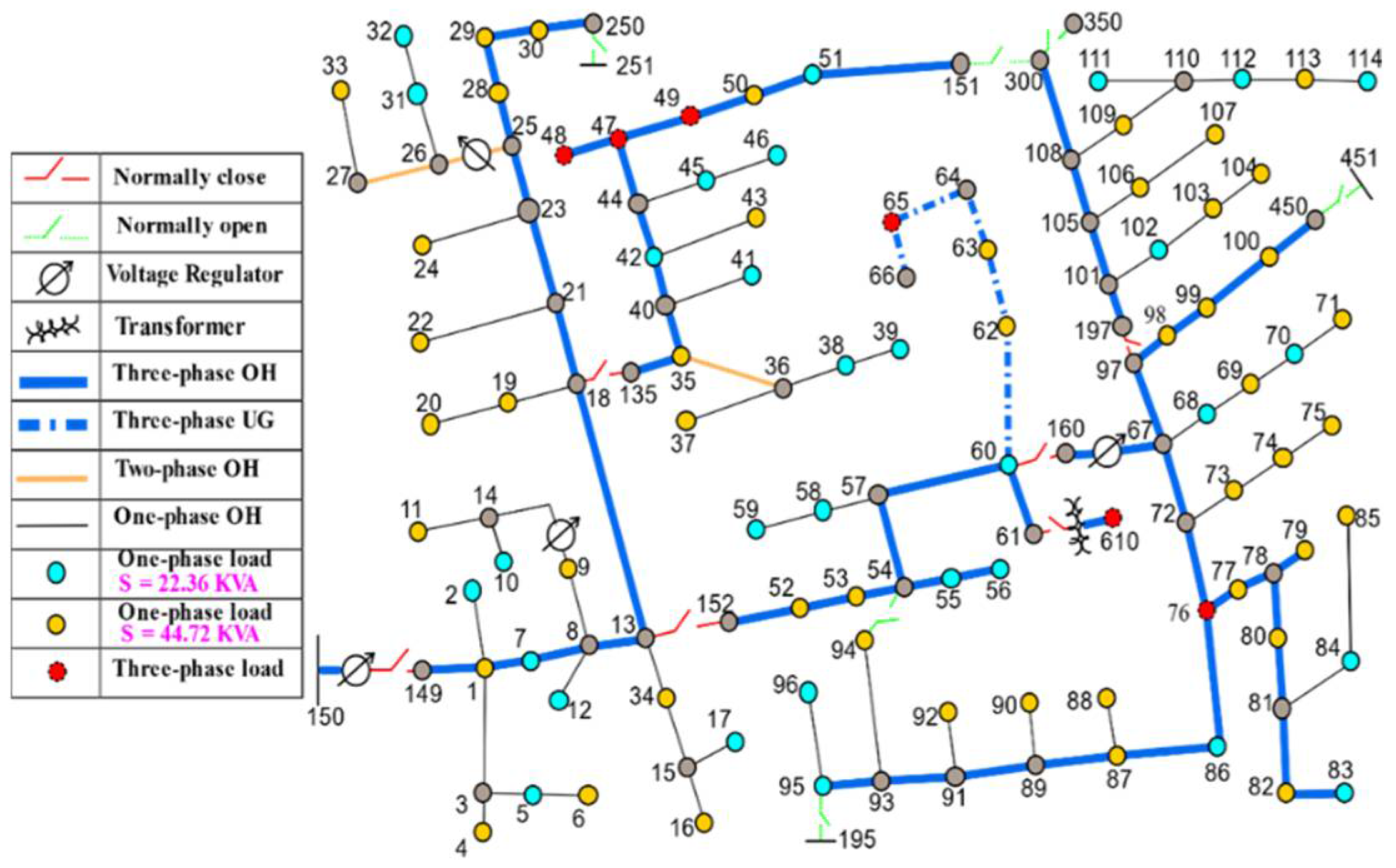
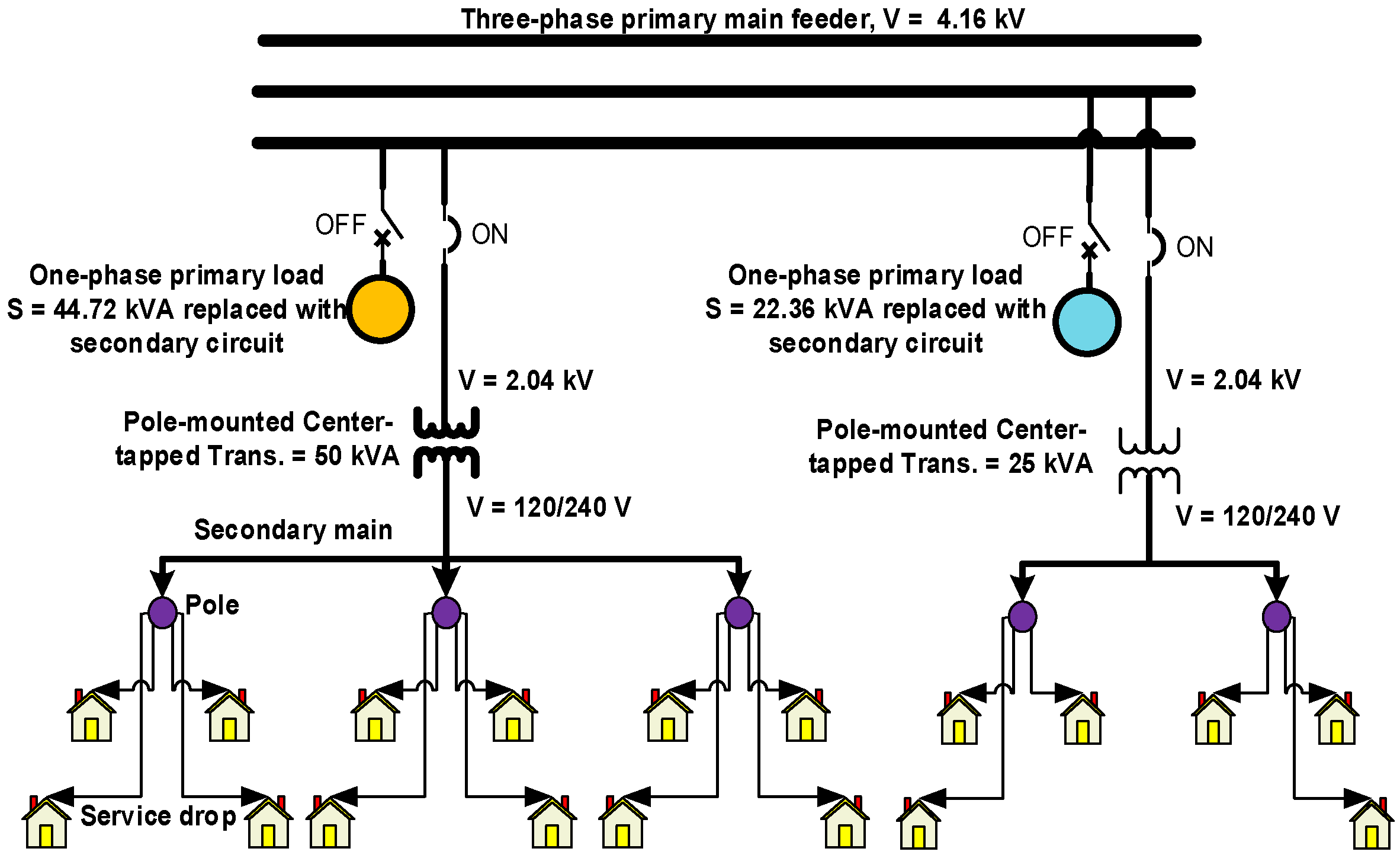
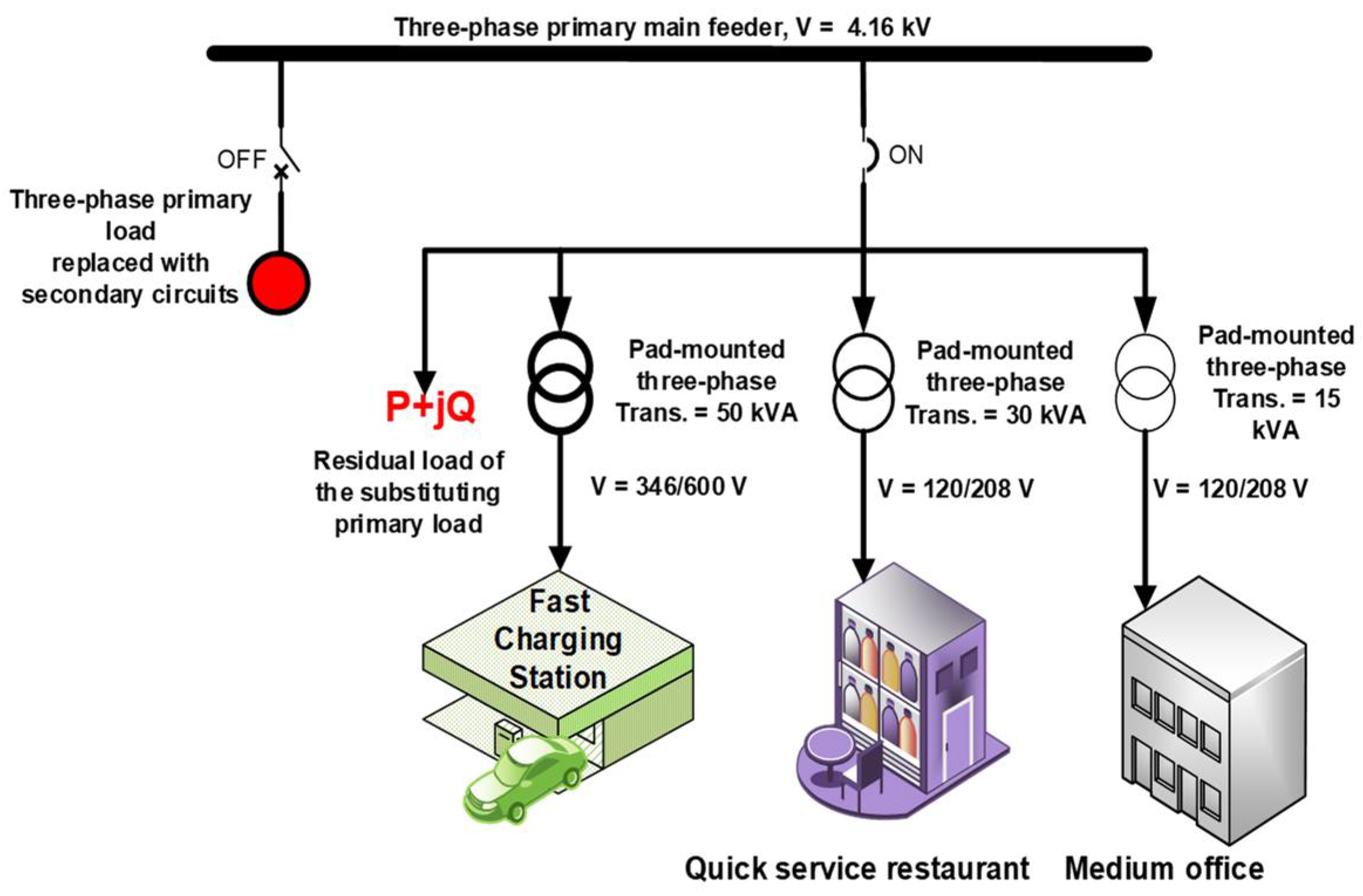
5.1. Test System Description and Modification
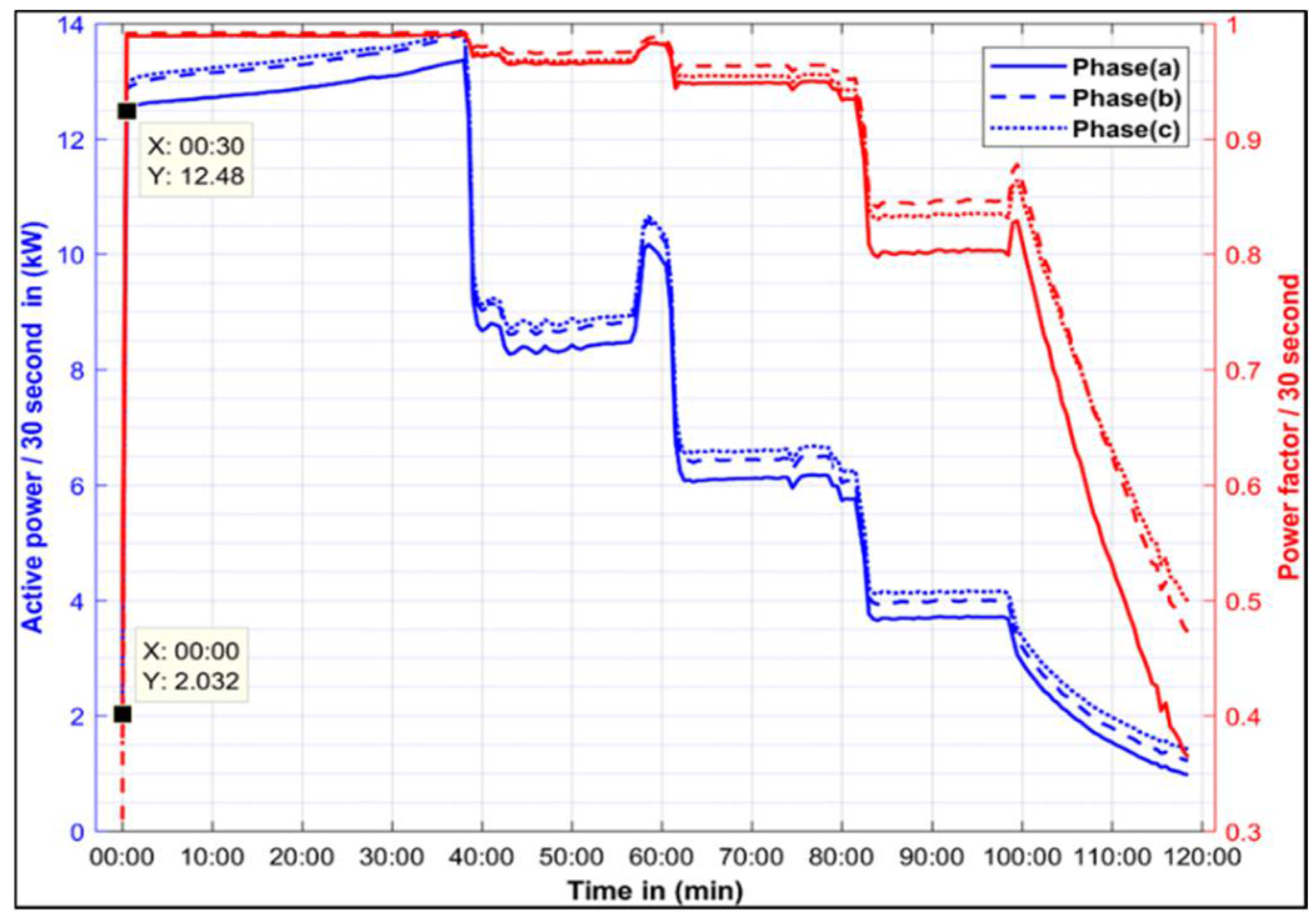
5.2. Voltage Quality Assessment Results and Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melhorn, C.; McGranaghan, M. Interpretation and analysis of power quality measurements. IEEE Trans. Ind. Appl. 1995, 31, 1363–1370. [Google Scholar] [CrossRef]
- PDini, P.; Saponara, S. Electro-Thermal Model-Based Design of Bidirectional On-Board Chargers in Hybrid and Full Electric Vehicles. Electronics 2021, 11, 112. [Google Scholar] [CrossRef]
- Alshareef, S.M.; Morsi, W.G. Impact of fast charging stations on the voltage flicker in the electric power distribution systems. In Proceedings of the 2017 IEEE Electrical Power and Energy Conference (EPEC), Saskatoon, SK, Canada, 22–25 October 2017. [Google Scholar] [CrossRef]
- Pazouki, S.; Mohsenzadeh, A.; Haghifam, M.-R. The effect of aggregated plug-in electric vehicles penetrations in charging stations on electric distribution netwroks reliability. In Proceedings of the 2014 Smart Grid Conference (SGC), Tehran, Iran, 9–10 December 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Benedetti, D.; Agnelli, J.; Gagliardi, A.; Dini, P.; Saponara, S. Design of an Off-Grid Photovoltaic Carport for a Full Electric Vehicle Recharging. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Febriwijaya, Y.H.; Purwadi, A.; Rizqiawan, A.; Heryana, N. A study on the impacts of DC Fast Charging Stations on power distribution system. In Proceedings of the 2014 International Conference on Electrical Engineering and Computer Science (ICEECS), Kuta, Bali, Indonesia, 24–25 November 2014; pp. 136–140. [Google Scholar] [CrossRef]
- Mauri, G.; Valsecchi, A. Fast charging stations for electric vehicle: The impact on the mv distribution grids of the milan metropolitan area. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 1055–1059. [Google Scholar] [CrossRef]
- Pinto, R.J.C.; Pombo, J.; Calado, M.R.A.; Mariano, S.J.S. An electric vehicle charging station: Monitoring and analysis of power quality. In Proceedings of the 2015 9th International Conference on Compatibility and Power Electronics (CPE), Costa da Caparica, Portugal, 24–26 June 2015; pp. 37–42. [Google Scholar] [CrossRef]
- Bosovic, A.; Music, M.; Sadovic, S. Analysis of the impacts of plug-in electric vehicle charging on the part of a real medium voltage distribution network. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Li, Q.; Tao, S.; Xiao, X.; Wen, J. Monitoring and analysis of power quality in electric vehicle charging stations. In Proceedings of the 2013 1st International Future Energy Electronics Conference (IFEEC), Tainan, Taiwan, 24–16 November 2013; pp. 277–282. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Cavone, G.; Dotoli, M. Distributed control of electric vehicle fleets considering grid congestion and battery degradation. Internet Technol. Lett. 2020, 3, e161. [Google Scholar] [CrossRef] [Green Version]
- Khan, W.; Ahmad, F.; Alam, M.S. Fast EV charging station integration with grid ensuring optimal and quality power exchange. Eng. Sci. Technol. Int. J. 2019, 22, 143–152. [Google Scholar] [CrossRef]
- Pea-Da, B.; Dechanupaprittha, S. Impact of fast charging station to voltage profile in distribution system. In Proceedings of the 2014 International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 19–21 March 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Malik, F.H.; Lehtonen, M. Analysis of power network loading due to fast charging of Electric Vehicles on highways. In Proceedings of the 2016 Electric Power Quality and Supply Reliability (PQ), Tallinn, Estonia, 29–31 August 2016; pp. 101–106. [Google Scholar] [CrossRef]
- Pawelek, R.; Kelm, P.; Wasiak, I. Experimental analysis of DC electric vehicles charging station operation and its impact on the supplying grid. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Pea-Da, B.; Dechanupaprittha, S. Impact analysis of fast charging to voltage profile in PEA distribution system by Monte Carlo simulation. In Proceedings of the 2015 7th International Conference on Information Technology and Electrical Engineering (ICITEE), Chiang Mai, Thailand, 29–30 October 2015; pp. 204–208. [Google Scholar] [CrossRef]
- Chan, C.-M.; Liou, H.-R.; Lu, C.-N. Operation of distribution feeders with electric vehicle charging loads. In Proceedings of the 2012 IEEE 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012; pp. 695–700. [Google Scholar] [CrossRef]
- Gjelaj, M.; Traeholt, C.; Hashemi, S.; Andersen, P.B. Optimal design of DC fast-charging stations for EVs in low voltage grids. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 684–689. [Google Scholar] [CrossRef] [Green Version]
- Celli, G.; Soma, G.G.; Pilo, F.; Lacu, F.; Mocci, S.; Natale, N. Aggregated electric vehicles load profiles with fast charging stations. In Proceedings of the 2014 Power Systems Computation Conference, Wrocław, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Salapic, V.; Grzanic, M.; Capuder, T. Optimal sizing of battery storage units integrated into fast charging EV stations. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Iyer, V.M.; Gulur, S.; Gohil, G.; Bhattacharya, S. Extreme fast charging station architecture for electric vehicles with partial power processing. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 659–665. [Google Scholar] [CrossRef]
- Pothinun, T.; Premrudeepreechacharn, S. Power Quality Impact of Charging Station on MV Distribution Networks: A Case Study in PEA Electrical Power System. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- ANSI C84-1; American National Standard for Electric Power Systems and Equipment-Voltage Ratings (60 Hertz). National Electrical Manufacturers Association: Rosslyn, VI, USA, 2016.
- Pennsylvania Power & Light. Voltage Fluctuation and Lamp Flicker Establishment Of Guidelines; PPl: Lehigh Valley, PE, USA, 1994. [Google Scholar]
- Wilkins, A.; Veitch, J.; Lehman, B. LED lighting flicker and potential health concerns: IEEE standard PAR1789 update. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 171–178. [Google Scholar] [CrossRef]
- 1789-2015; IEEE Recommended Practices for Modulating Current in High-Brightness LEDs for Mitigating Health Risks to Viewers. IEEE: New York, NY, USA, 2015. [CrossRef]
- May, C.; Collins, E.R. An investigation of the response of incandescent lamps and compact fluorescent lamps to voltage fluctuations. In Proceedings of the 14th International Conference on Harmonics and Quality of Power-ICHQP 2010, Bergamo, Italy, 26–29 September 2010; pp. 1–8. [Google Scholar] [CrossRef]
- 1453-2011; IEEE Recommended Practice—Adoption of IEC 61000-4-15:2010, Electromagnetic Compatibility (EMC)—Testing and Measurement Techniques—Flickermeter—Functional and Design Specifications. IEEE: New York, NY, USA, 2011. [CrossRef]
- Marei, M.I.; El-Saadany, E.F.; Salama, M.M. Envelope tracking techniques for FlickerMitigation and Voltage regulation. IEEE Trans. Power Deliv. 2004, 19, 1854–1861. [Google Scholar] [CrossRef]
- Hock, R.T.; De Novaes, Y.R.; Batschauer, A.L. A Voltage Regulator for Power Quality Improvement in Low-Voltage Distribution Grids. IEEE Trans. Power Electron. 2018, 33, 2050–2060. [Google Scholar] [CrossRef]
- Molina, M.G.; Mercado, P.E. Control Design and Simulation of DSTATCOM with Energy Storage for Power Quality Improvements. In Proceedings of the 2006 IEEE/PES Transmission & Distribution Conference and Exposition: Latin America, Caracas, Venezuela, 15–18 August 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Molina, M.G.; Mercado, P.E. Dynamic modeling and control design of DSTATCOM with ultra-capacitor energy storage for power quality improvements. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America, Bogota, Colombia, 13–15 August 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Electric Power Research Institute (EPRI). Guidebook on Custom Power Devices. 2000. Available online: https://www.epri.com/research/products/000000000001000340 (accessed on 4 January 2020).
- Mathur, R.M.; Varma, R. Thyristor-Based FACTS Controllers for Electrical Transmission Systems; Wiley-IEEE Press: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Taher, S.A.; Afsari, S.A. Optimal Location and Sizing of UPQC in Distribution Networks Using Differential Evolution Algorithm. Math. Probl. Eng. 2012, 2012, 838629. [Google Scholar] [CrossRef]
- Marjani, S.R.; Talavat, V.; Galvani, S. Optimal allocation of D-STATCOM and reconfiguration in radial distribution network using MOPSO algorithm in TOPSIS framework. Int. Trans. Electr. Energ. Syst. 2019, 29, e2723. [Google Scholar] [CrossRef]
- Saravanan, M.; Slochanal, S.M.R.; Venkatesh, P.; Abraham, J.P.S. Application of particle swarm optimization technique for optimal location of FACTS devices considering cost of installation and system loadability. Electr. Power Syst. Res. 2007, 77, 276–283. [Google Scholar] [CrossRef]
- Moghadasi, A.; Sarwat, A.; Guerrero, J. A comprehensive review of low-voltage-ride-through methods for fixed-speed wind power generators. Renew. Sustain. Energy Rev. 2016, 55, 823–839. [Google Scholar] [CrossRef] [Green Version]
- Hosseinpour, M.; Yazdian, A.; Hohamadian, M.; Kazempour, J. Desing and simulation of UPQC to improve power quality and transfer wind energy to grid. J. Appl. Sci. 2008, 8, 3770–3782. [Google Scholar] [CrossRef]
- Somsai, K.; Kulworawanichpong, T. Cost Estimation for Reactive Power Compensation in Distribution Power System by Using D-STATCOM. Available online: http://www.i-asem.org/publication_conf/anbre13/M3D.4.ER655_1199F.pdf (accessed on 7 January 2020).
- Milanovic, J.; Zhang, Y. Global Minimization of Financial Losses Due to Voltage Sags With FACTS Based Devices. IEEE Trans. Power Deliv. 2010, 25, 298–306. [Google Scholar] [CrossRef]
- McGranaghan, M.; Roettger, B. Economic Evaluation of Power Quality. IEEE Power Eng. Rev. 2002, 22, 8–12. [Google Scholar] [CrossRef]
- Arrillaga, J.; Liu, Y.H.; Watson, N.R. Flexible Power Transmission; John Wiley & Sons, Ltd.: Chichester, UK, 2007. [Google Scholar] [CrossRef]
- Sumper, A.; Baggini, A. (Eds.) Electrical Energy Efficiency: Technologies and Applications; John Wiley & Sons, Ltd.: Chichester, UK, 2012. [Google Scholar] [CrossRef]
- Vedam, R.S.; Sarma, M.S. Power Quality: Var Compensation in Power Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Kusko, A.; Thompson, M.T. Power Quality in Electrical Systems; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Habur, K.; O’Leary, D. FACTS-Flexible Alternating Current Transmission Systems: For Cost Effective and Reliable Transmission of Electrical Energy. Siemens-World Bank Doc. Draft Rep. Erlangen 2004. [Google Scholar]
- Nielsen, J.; Blaabjerg, F. A Detailed Comparison of System Topologies for Dynamic Voltage Restorers. IEEE Trans. Ind. Appl. 2005, 41, 1272–1280. [Google Scholar] [CrossRef]
- Alshareef, S.M.; Morsi, W.G. Probabilistic Models for Residential and Commercial Loads with High Time Resolution. In Proceedings of the 2019 IEEE Electrical Power and Energy Conference (EPEC), Montréal, QU, Canada, 16–18 October 2019; pp. 1–6. [Google Scholar]
- Alshareef, S.M.; Morsi, W.G. Probabilistic commercial load profiles at different climate zones. In Proceedings of the2017 IEEE Electrical Power and Energy Conference (EPEC), Saskatoon, SK, Canada, 22–25 October 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Deru, M.; Field, K.; Studer, D.; Benne, K.; Griffith, B.; Torcellini, P.; Liu, B.; Halverson, M.; Winiarski, D.; Rosenberg, M.; et al. US Department of Energy Commercial Reference Building Models of the National Building Stock; NREL: Golden, CO, USA, 2011.
- Klippenstein, M. Plug-in Electric Car Sales in Canada, May 2018: Rewriting records. Green Car Rep. 2018. [Google Scholar]
- Gjelaj, M.; Traeholt, C.; Hashemi, S.; Andersen, P.B. DC Fast-charging stations for EVs controlled by a local battery storage in low voltage grids. In Proceedings of the PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Energy Efficiency Requirements for Houses in British Columbia (Lower Mainland and Southern Vancouver Island). Available online: https://www.bchousing.org/research-centre/library/residential-design-construction/ig-energy-efficiency-houses-climate-zone-4-lowermainland&sortType=sortByDate (accessed on 20 December 2018).
- evCloud|FleetCarma. Available online: https://www.fleetcarma.com/evCloud (accessed on 19 December 2018).
- Alshareef, S.M.; Morsi, W.G. Probabilistic Modeling of Plug-in Electric Vehicles Charging from Fast Charging Stations. In Proceedings of the 2019 IEEE Electrical Power and Energy Conference (EPEC), Montréal, QU, Canada, 16–18 October 2019; pp. 1–6. [Google Scholar]
- Brooks, S.; Gelman, A.; Jones, G.; Meng, X.-L. Handbook of Markov Chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Genovese, A.; Ortenzi, F.; Villante, C. On the energy efficiency of quick DC vehicle battery charging. World Electr. Veh. J. 2015, 7, 570–576. [Google Scholar] [CrossRef] [Green Version]
- IEEE PES AMPS DSAS Test Feeder Working Group. Resources|PES Test Feeder. Available online: http://sites.ieee.org/pes-testfeeders/resources/ (accessed on 11 March 2019).
- Bishops, J. Profiles on Residential Power Consumption: Phase I Final Report. Fire Protection Research Foundation, Quincy, MA. 2010. Available online: https://library.nfpa.org/GeniePLUS/GeniePLUS/Portal/Public.aspx?lang=en-US (accessed on 16 March 2019).
- Electric Vehicles Sales Update Q3 2018, Canada. FleetCarma, 6 November 2018. Available online: https://www.fleetcarma.com/electric-vehicles-sales-update-q3-2018-canada/ (accessed on 3 May 2019).

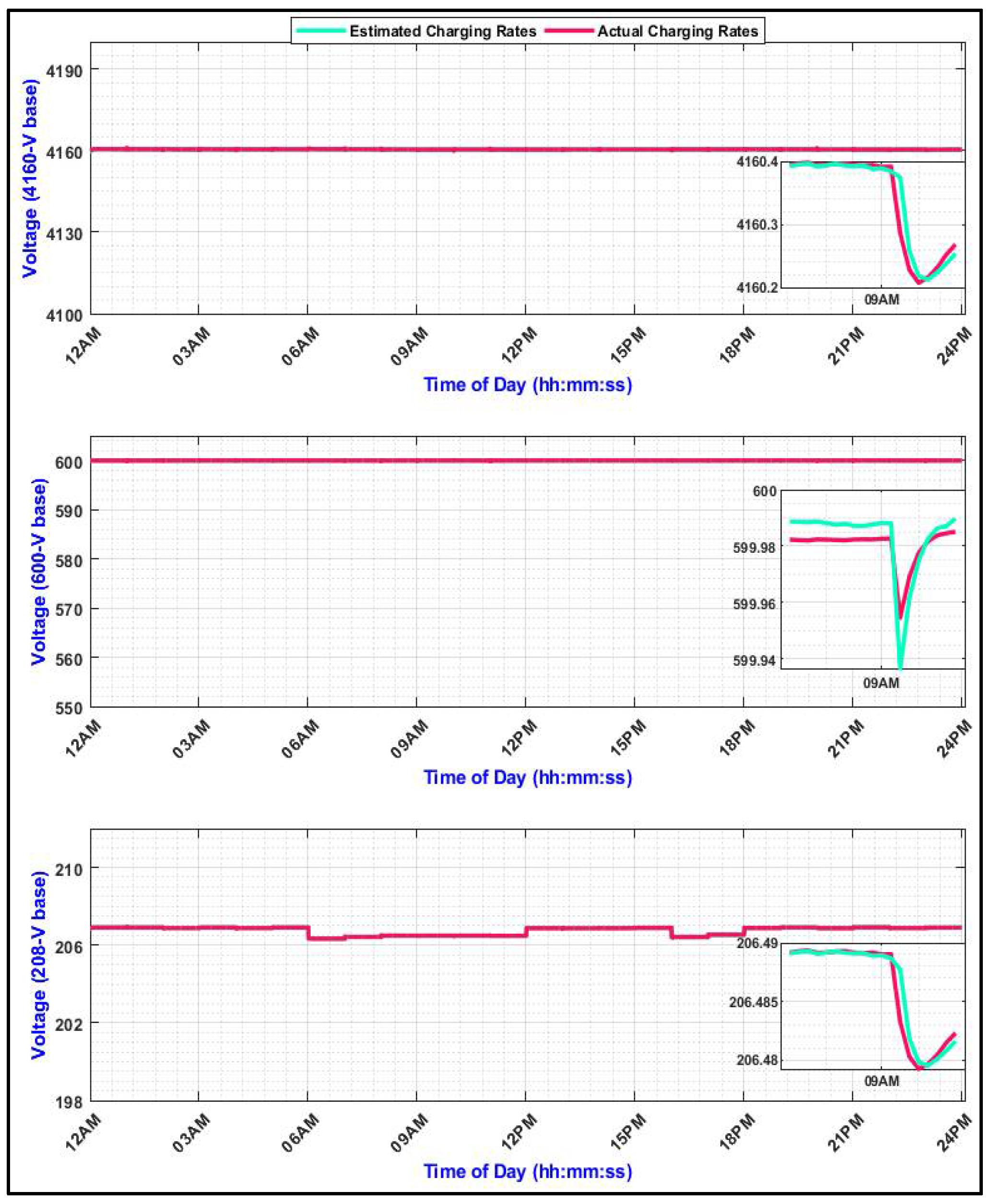

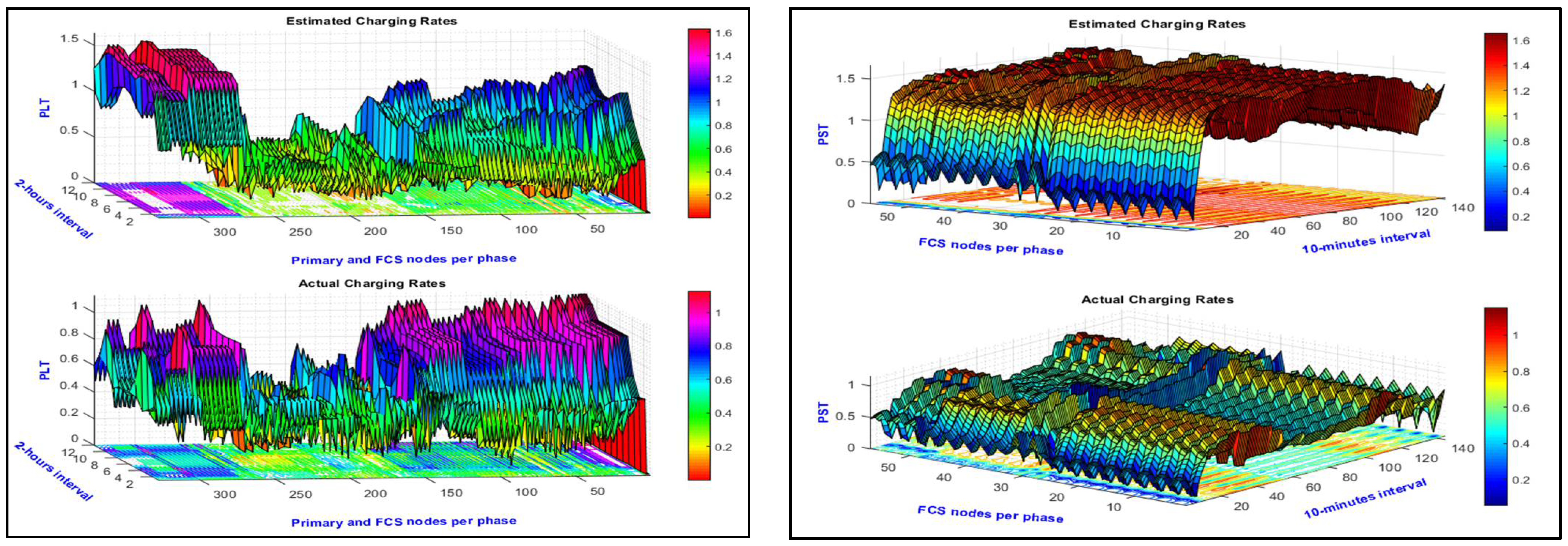
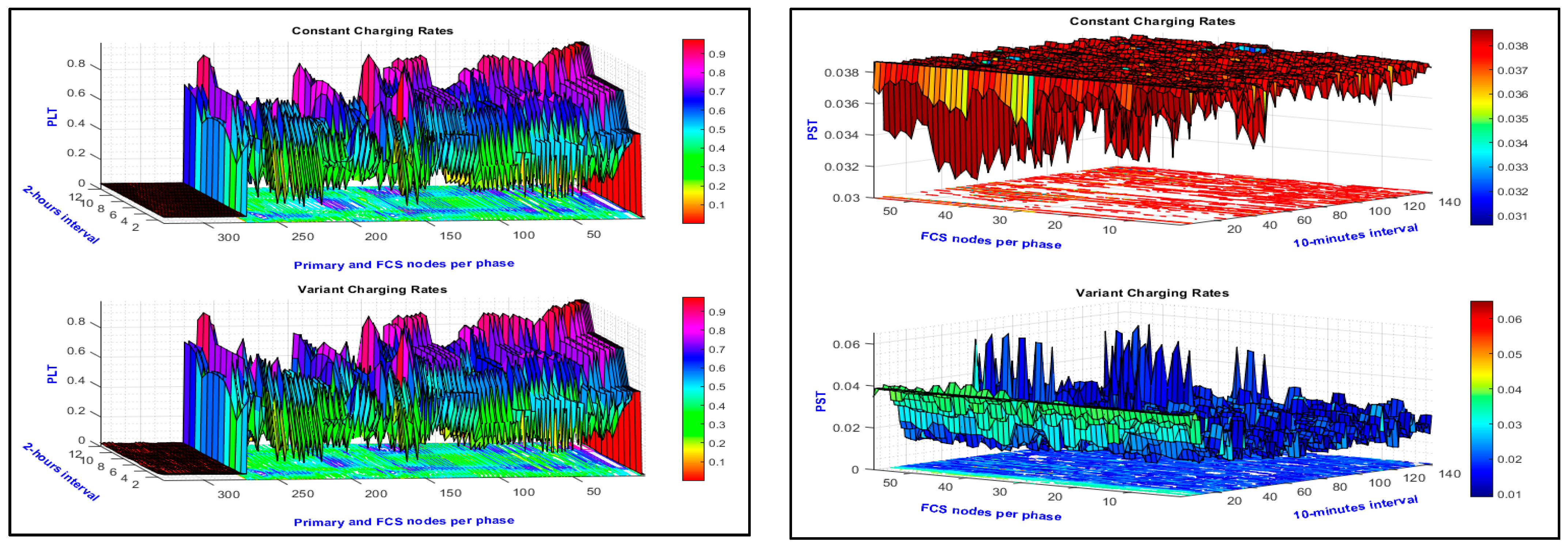
| Mitigation Device | % of the First Cost | The Source |
|---|---|---|
| 10 | [39] | |
| 5 | [40] | |
| 10 | [41] | |
| 10 | [41] | |
| 5 | [42] | |
| 1 | [43] |
| Mitigation Techniques | ||||||
|---|---|---|---|---|---|---|
| Parameters | UPQC | DSTATCOM | TSC | FC-TCR | DVR | FSC |
| , (years) | 20 | 20 | 20 | 20 | 20 | 20 |
| , (%) | 6 | 6 | 6 | 6 | 6 | 6 |
| , (%) | 10 | 5 | 10 | 10 | 5 | 1 |
| , (MVAr) | 2 | 2 | 2 | 2 | 2 | 2 |
| , (USD/kVAr) | 187.66 | 79.55 | 126.8 | 126.8 | 153.3 | 89.97 |
| 375,320 | 159,100 | 253,600 | 253,600 | 306,600 | 179,940 | |
| 0.0872 | 0.0872 | 0.0872 | 0.0872 | 0.0872 | 0.0872 | |
| 0.0272 | 0.0272 | 0.0272 | 0.0272 | 0.0272 | 0.0272 | |
| 32,728 | 13,874 | 22,114 | 22,114 | 26,735 | 15,691 | |
| 3,272 | 694 | 2,211 | 2,211 | 1,337 | 157 | |
| 36,000 | 14,568 | 24,325 | 24,325 | 28,072 | 15,848 | |
| I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|
| FSC | FC/TCR | TSC | DSTACOM | DVR | UPQC | |
| Steady state Characteristic | Self-regulation | Controller easily adjustable | Controller easily adjustable | Controller easily adjustable | Controller easily adjustable | Controller easily adjustable |
| Control range | Capacitive | generation and absorption | Capacitive | Both generation and absorption | Both generation and absorption | Both generation and absorption. |
| Harmonic content | Negligible | Requires filters | Negligible | Small low order. Large: high order | Small; depends on the hardware | Small low order; eliminated by a shunt filter |
| Losses | Negligible | Low at full generation. High at full absorption | High at full output. Low at zero var output | High at full output. Low at zero var output | Low | Low |
| Overload capability | Limited to capacitor rating | Limited to capacitor rating | Limited to capacitor rating | Limited to rating of shunt compensator | Up to 150% for 30 s | Up to 150% |
| Response time in the system | 0–0.05 s | 0.02–0.06 s | 0.02–0.06 s | 0.01–0.02 s | 0.01–0.02 s | 0.01–0.02 s |
| Maintenance requirements | Moderate | Moderate as for electronic indoor equipment | Moderate | Moderate | Moderate | Moderate |
| Response to rapidly fluctuating load | Inherently fast | Less rapid than I | Slower than II | Faster than III | Faster than III | Faster than III |
| Voltage control under line outage | Requires metal varistor for protection | Require switched capacitors to support voltage | Require switched capacitors to support voltage | Require switched capacitors to support voltage | Require energy storage to provide power | Require a DC capacitor to support voltage |
| Behavior following system fault | Cannot tolerate fault current; automatic switch required | Auxiliary controls used to damp load swings | Auxiliary controls used to damp load swings | Auxiliary controls used to damp load swings | Auxiliary controls used against overcurrent | Series converter utilized to improve system stability |
| Mitigation Techniques | Advantages | Disadvantages |
|---|---|---|
| TSC |
|
|
| FC/TCR |
|
|
| Dynamic Voltage Restorer |
|
|
| DSTATCOMs |
|
|
| Series capacitors |
|
|
| UPQC |
|
|
| Mitigating Techniques | ||||||
|---|---|---|---|---|---|---|
| FSC | FC/TCR | TSC | DSTATCOMs | DVR | UPQC | |
| Overload capability | Limited | Limited | Limited | Limited | Good | Good |
| Losses | small | Moderate | Small | Small | Small | Small |
| Response Time | Very fast | fast | fast | fast | Very fast | Very fast |
| Reactive power range | Capacitive | Capacitive inductive | Capacitive | Capacitive inductive | Capacitive inductive | Capacitive inductive |
| Capital costs | Good | High | High | Good | Very high | Very high |
| Maintenance costs | Very good | Good | Good | Good | Very high | Very high |
| Control interaction | Limited | Good | Good | Good | Good | Good |
| Special requirements | Overvoltage resonance | Harmonic | Resonance | Short-circuit | Short-circuit | Short-circuit |
| Efficiency during low/high loading | Good | Good | Good | Good | Good | Limited |
| Single-Phase control | Yes | Yes | Yes | Yes | Yes | Yes |
| Energization | Fast and direct | Fast w/control | Fast w/control | Fast w/control | Fast w/control | Fast w/control |
| Given Weight | |||
|---|---|---|---|
| + | − | + + | − − |
| Cheap | High | Very fast | Very high |
| Fast | Slow | Fast and direct | Very slow |
| Fast w/control | Short-circuit | Very good | |
| Capacitive | Moderate | ||
| Yes | Limited | ||
| Good | Resonance | ||
| Small | Harmonic | ||
| Inductive | |||
| Overvoltage | |||
| No | |||
| Mitigation Techniques | ||||||
|---|---|---|---|---|---|---|
| FSC | FC/TCR | TSC | DSTATCOMs | DVR | UPQC | |
| Overload capability | − | − | − | − | + | + |
| Losses | + | − | + | + | + | + |
| Response Time | + + | + | + | + | + + | + + |
| Reactive power range | + | + + | + | + + | + + | + + |
| Cost per kVAr | + | − | − | + | − − | − − |
| Maintenance Cost | + + | − − | − − | + | + | − − |
| Control interaction | − | + | + | + | + | + |
| Single-Phase control | + | + | + | + | + | + |
| Special requirements | − − | − | − | − | − | − |
| low/high loading Eff. | + | + | + | + | + | − |
| Energization | + + | + | + | + | + | + |
| Sum (-) | −4 | −6 | −5 | −2 | −3 | −6 |
| Sum (+) | 11 | 7 | 7 | 10 | 11 | 9 |
| Sum (total) | 7 | 1 | 2 | 8 | 8 | 3 |
| Location | Number of FCSs | Number of Ports |
|---|---|---|
| Node 47 | 2 | 2 |
| Node 48 | 5 | 5 |
| Node 49 | 2 | 2 |
| Node 65 | 2 | 2 |
| Node 76 | 5 | 5 |
| Node 610 | 3 | 3 |
| Scenarios | Charging Methods | Maximum VU (%) | Time (hh:mm:ss) |
|---|---|---|---|
| First | Estimated charging rates | 2.079 | 19:03 |
| Actual charging rates | 1.965 | 19:01 | |
| Second | Estimated charging rates | 1.609 | 19:02:30 |
| Actual charging rates | 1.558 | 19:01 | |
| Third | Estimated charging rates | 0.948 | 19:01 |
| Actual charging rates | 0.930 | 19:01 |
| Statistics | First Scenario FCS Only | Second Scenario FCS and D-STATCOMs in Secondary Nodes | Third Scenario FCS and D-STATCOMs in Primary–Secondary Nodes | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ph. A | Ph. B | Ph. C | Ph. A | Ph. B | Ph. C | Ph. A | Ph. B | Ph. C | |||
| Estimated Charging Rates | PLT | Minimum | 0.801 | 0.801 | 0.012 | 0.801 | 0.801 | 0.012 | 0.012 | 0.012 | 0.012 |
| Average | 1.034 | 1.226 | 0.236 | 0.884 | 0.872 | 0.284 | 0.196 | 0.236 | 0.284 | ||
| 95% | 1.272 | 1.503 | 0.612 | 0.977 | 0.965 | 0.720 | 0.485 | 0.612 | 0.720 | ||
| Maximum | 1.383 | 1.637 | 0.648 | 0.977 | 0.977 | 0.737 | 0.610 | 0.648 | 0.737 | ||
| Location | Node 49 | Node 51 | Node 1 | Node 28 | Node 150 | Node 1 | Node 150 | Node 1 | Node 1 | ||
| PST | Minimum | 1.000 | 1.000 | 0.007 | 0.003 | 0.003 | 0.010 | 0.007 | 0.007 | 0.010 | |
| Average | 1.149 | 1.320 | 0.235 | 0371 | 0.456 | 0.282 | 0.194 | 0.235 | 0.282 | ||
| 95% | 1.321 | 1.539 | 0.613 | 0.784 | 0.942 | 0.721 | 0.486 | 0.613 | 0.721 | ||
| Maximum | 1.434 | 1.682 | 0.652 | 0.977 | 0.978 | 0.741 | 0.671 | 0.652 | 0.741 | ||
| Location | Node 48 | Node 51 | Node 53 | Node 150 | Node 150 | Node 53 | Node 150 | Node 53 | Node 53 | ||
| Actual Charging Rates | PLT | Minimum | 0.800 | 0.802 | 0.011 | 0.901 | 0.802 | 0.011 | 0.011 | 0.011 | 0.011 |
| Average | 0.934 | 0.898 | 0.234 | 0.952 | 0.876 | 0.291 | 0.192 | 0.234 | 0.291 | ||
| 95% | 1.086 | 1.097 | 0.609 | 0.977 | 0.969 | 0.719 | 0.479 | 0.609 | 0.719 | ||
| Maximum | 1.123 | 1.123 | 0.639 | 0.977 | 0.977 | 0.733 | 0.609 | 0.639 | 0.733 | ||
| Location | Node 150 | Node 150 | Node 1 | Node 150 | Node 150 | Node 1 | Node 150 | Node 1 | Node 1 | ||
| PST | Minimum | 1.000 | 1.003 | 0.007 | 0.001 | 0.001 | 0.010 | 0.006 | 0.007 | 0.010 | |
| Average | 1.072 | 1.082 | 0.232 | 0.362 | 0.423 | 0.289 | 0.190 | 0.232 | 0.289 | ||
| 95% | 1.123 | 1.131 | 0.610 | 0.783 | 0.944 | 0.720 | 0.479 | 0.610 | 0.720 | ||
| Maximum | 1.123 | 1.157 | 0.643 | 0.977 | 0.977 | 0.738 | 0.671 | 0.643 | 0.738 | ||
| Location | Node 150 | Node 51 | Node 54 | Node 150 | Node 150 | Node 53 | Node 150 | Node 54 | Node 53 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshareef, S.M. Analyzing and Mitigating the Impacts of Integrating Fast-Charging Stations on the Power Quality in Electric Power Distribution Systems. Sustainability 2022, 14, 5595. https://doi.org/10.3390/su14095595
Alshareef SM. Analyzing and Mitigating the Impacts of Integrating Fast-Charging Stations on the Power Quality in Electric Power Distribution Systems. Sustainability. 2022; 14(9):5595. https://doi.org/10.3390/su14095595
Chicago/Turabian StyleAlshareef, Sami M. 2022. "Analyzing and Mitigating the Impacts of Integrating Fast-Charging Stations on the Power Quality in Electric Power Distribution Systems" Sustainability 14, no. 9: 5595. https://doi.org/10.3390/su14095595
APA StyleAlshareef, S. M. (2022). Analyzing and Mitigating the Impacts of Integrating Fast-Charging Stations on the Power Quality in Electric Power Distribution Systems. Sustainability, 14(9), 5595. https://doi.org/10.3390/su14095595






