A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use?
Abstract
:1. Introduction
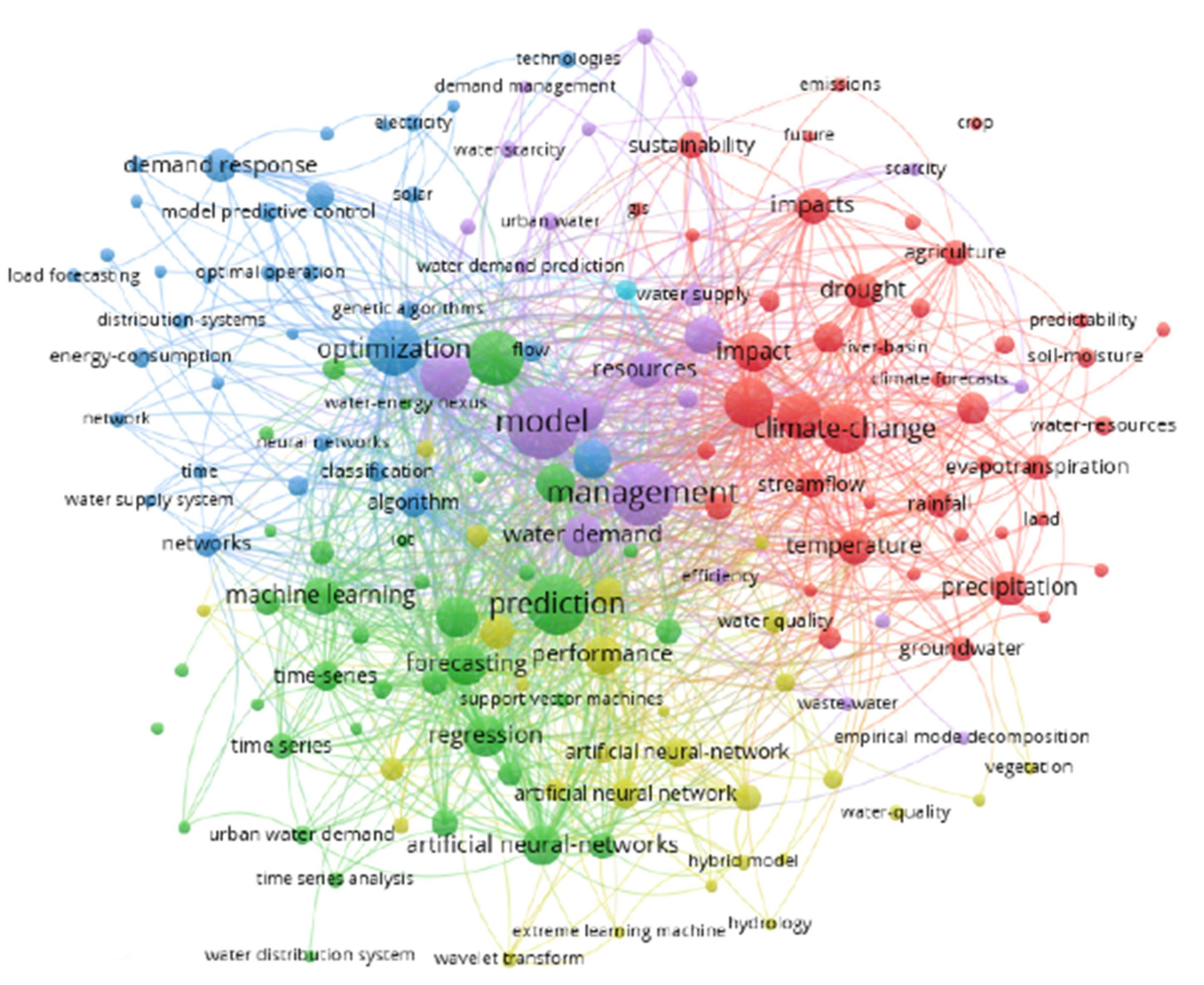
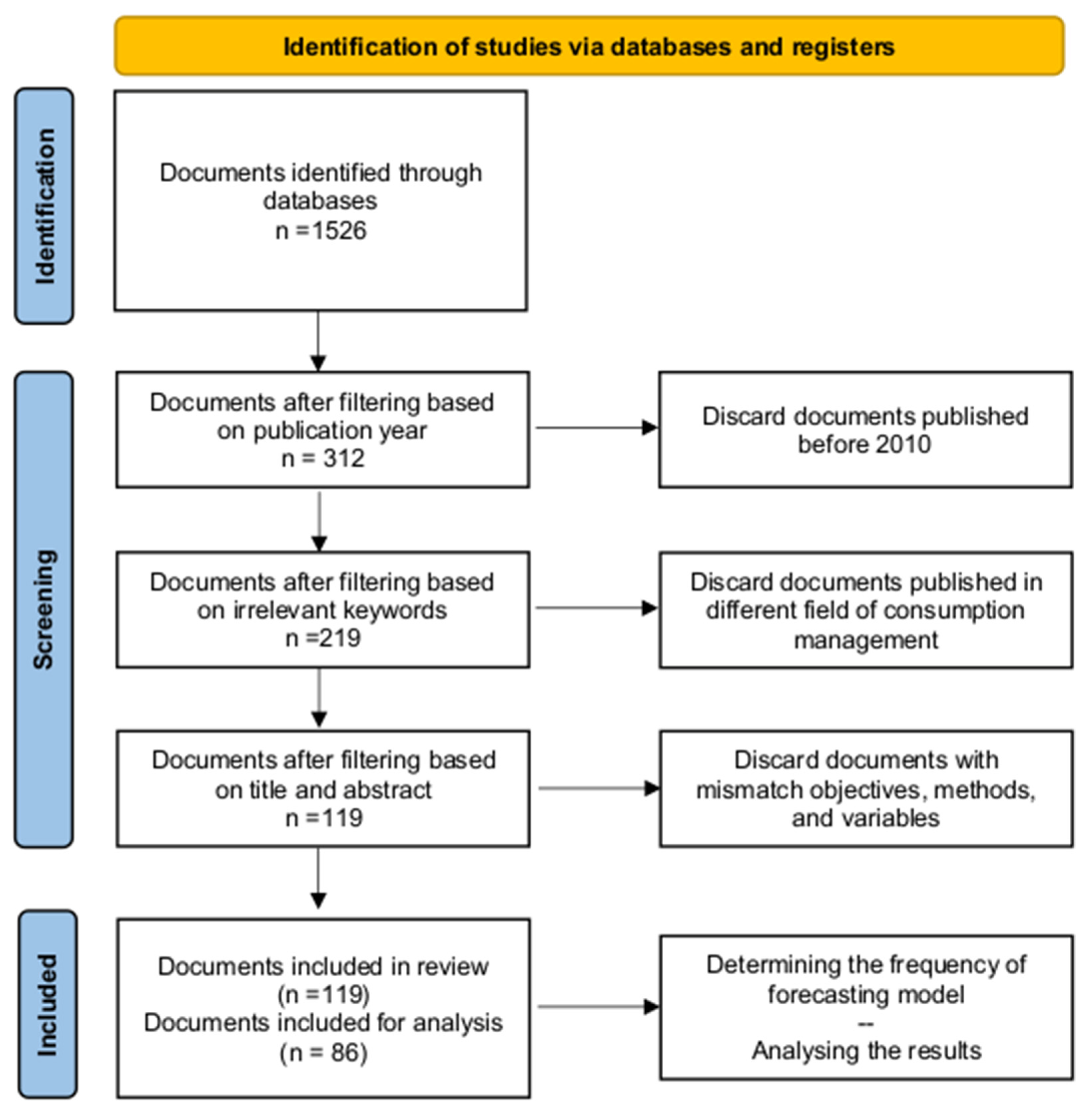
2. Systematic Literature Review: Methodology
3. Predictive Methods and Validation
3.1. Impact of Exogenous Factors in Water Demand Models
- Climatic or weather conditions (e.g., temperature, humidity, and precipitation): There is almost an evident correlation between weather and water use, and often this is co-founded to customer behaviour and a general seasonality effect on outdoor activity. However, the exposure to severe weather periods will also have a significant impact on the water demand. Climatic variables are among the most used, along with historical past water consumption, and they have been considered in many studies. For example, Brentan et al. [15] examined the correlation between weather factors with water demand and showed that three factors, temperature, relative humidity, and hour of the day, are the most relevant variables for forecasting water demand. Moreover, Hu et al. [16] used temperatures, dew point, humidity, wind speed, and atmospheric pressure as input variables in the water demand forecasting model.
- Economic inputs (e.g., water price, billing, and income): One of the reasons why economic factors, such as price, can be naturally considered for water demand forecasting is due to the fact that a higher price may lead to lower consumption [14]. In some studies, these factors have been considered too. For example, de Maria André and Carvalho [17] showed that some factors, including water price and household income, have a positive effect on water demand, since an increase in these variables will increase water demand.
- Social-demographic situation (e.g., population, household size, and occupants’ ages) and other household properties (e.g., house type and property value): In this regard, Hussien et al. [18] investigated the effect of social-demographic factors, such as the number of children, adult male members, adult female members, and elderly household occupation, as well as some physical property factors, such as household size, household type, the total built-up area of all floors, garden area per household, number of rooms, and number of floors, on per capita water consumption. Additionally, Bennett et al. [19] has introduced the number of adults, children, and teenagers in a household as independent variables for a model based on neural networks.
- Geographical factors (e.g., urban density, and type of location): In the literature, geographical factors have been shown to have an impact on forecasting water demand, and they should be considered further for efficient water supply planning and management [20]. One of the main examples including geographical factors for water demand forecasting is the work of Bao and Chen [21]. They used spatial econometric models to analyse the influencing factors in water consumption efficiency and found that urbanisation level is one of the most important covariables affecting water consumption among the socio-economic and eco-environmental indicators. Among the more relevant works that include GFs in the methodology development for water demand forecasting, Benítez et al. [22] considered the type of location, including the city centre site, the production site (industrial), and the residential site (suburb) to develop predictive models for water demand.
- Technological factors (e.g., smart meters, sensors, and data loggers): Smart meters are the most widely used technological factor among the others. Hence, they have been included in multiple research endeavours on water demand forecasting models. In these studies, users’ consumption information is collected hourly or even instantaneously through such smart meters and used as consumption input data in the forecasting models [13,23]. Other technology factors, such as high-efficiency fixtures and appliances [24] or alarming display monitors [25], have been shown to also have an impact on water consumption. However, such factors have rarely been used in water demand forecasting models.
- Calendar variables (weekdays, weekends, holidays, and special events): Although calendar information is inherently present in other factors, such as weather, socio-demographic, and geographic factors, it is a good practice to specifically consider its effect on water demand models. Calendar variables can be considered as information at a finer granularity than other related factors, having the potential to increase the accuracy of any predictive method. Among the studies that have specifically considered calendar factors, we highlight the works of Pesantez et al. [13]; Benítez et al. [22]; Antunes et al. [12]; Hu et al. [16]; Brentan et al. [15]; Liu et al. [26]; and Herrera et al. [9].
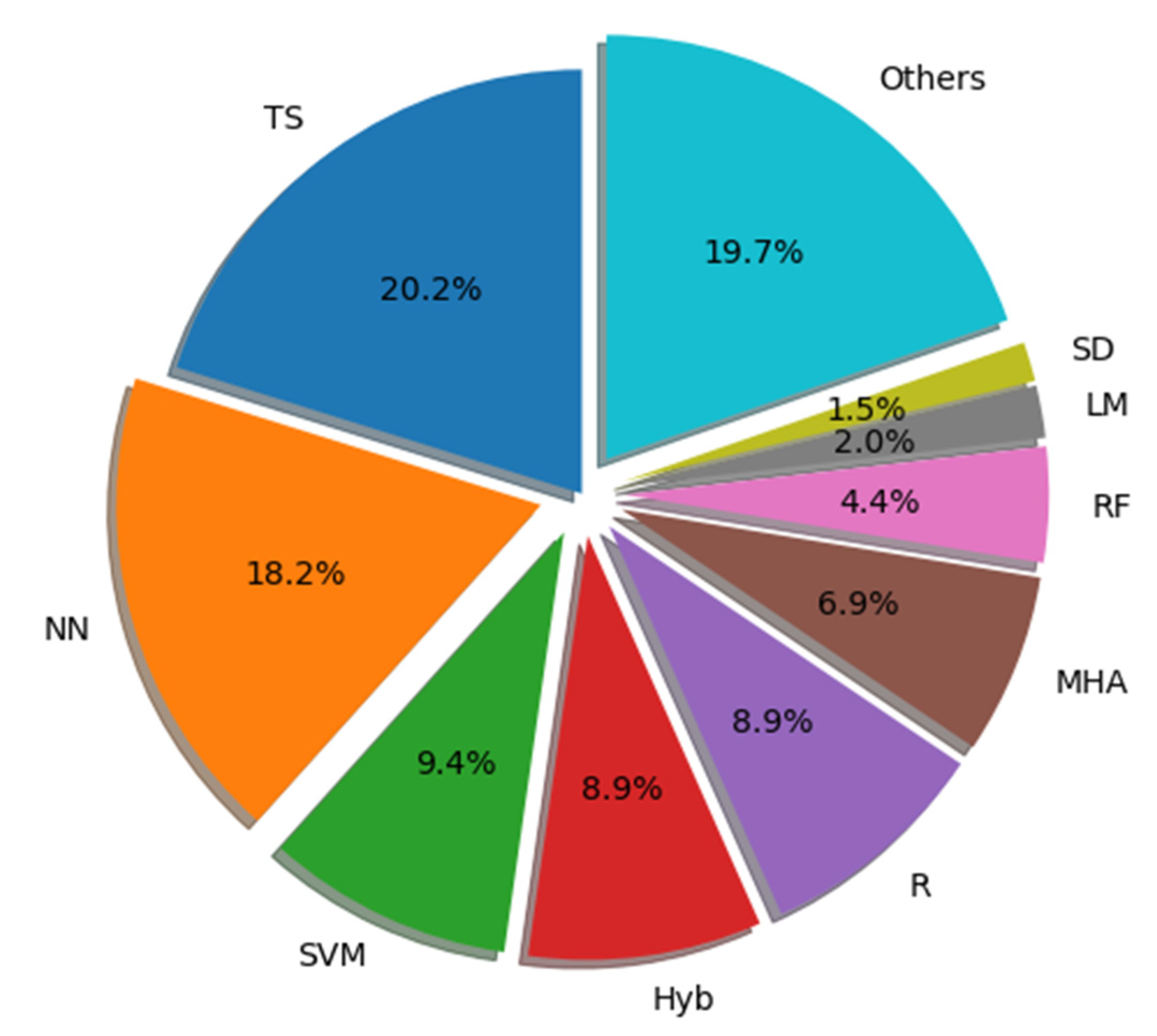
3.2. Predictive Methods for Forecasting Urban Water Demand
3.2.1. Artificial Neural Networks
3.2.2. Support Vector Machines
3.2.3. Traditional Time Series Analysis
3.2.4. Metaheuristic Algorithms
3.2.5. Regression
3.2.6. Hybrid Methods
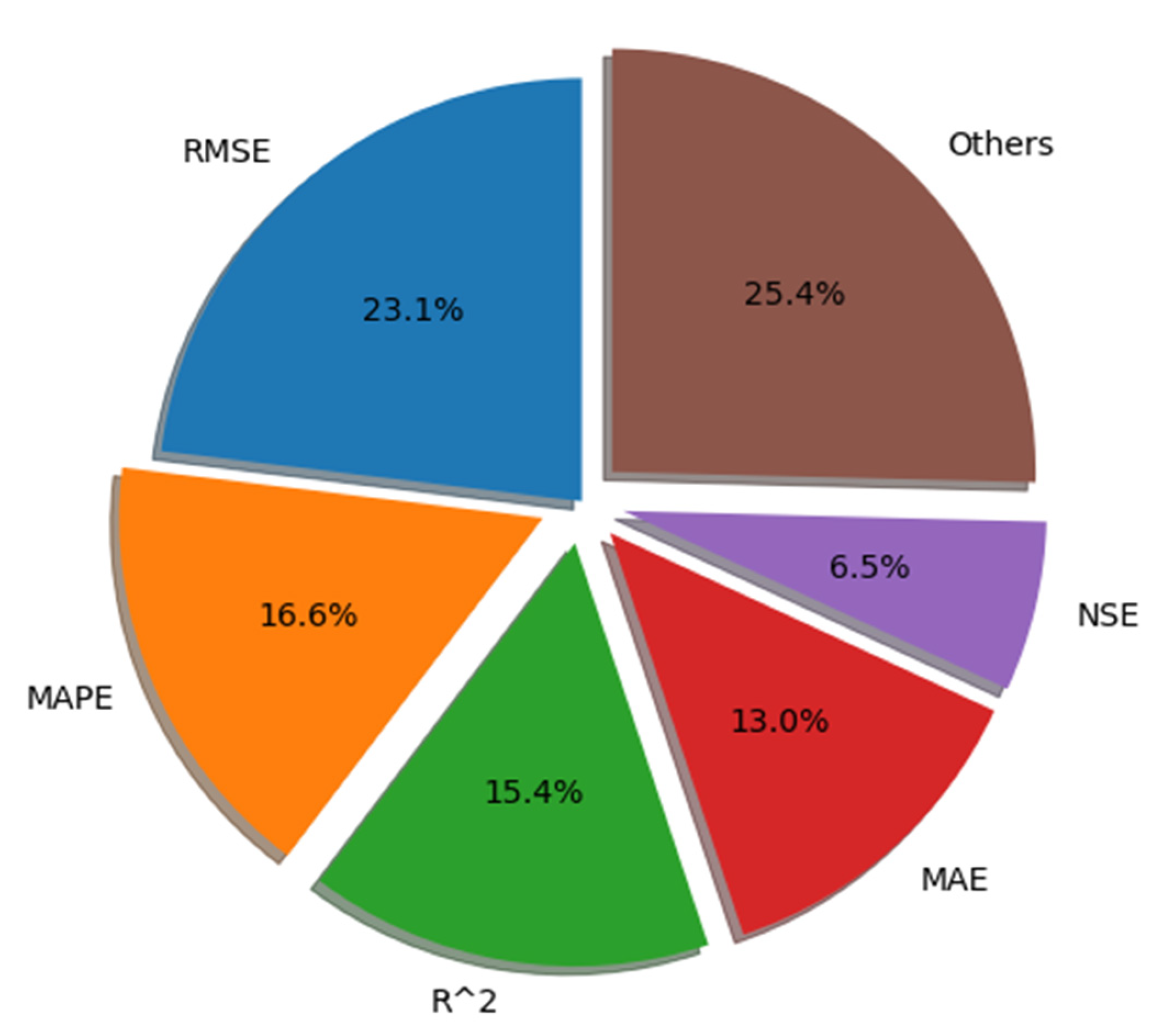
3.3. Model Validation
3.4. Peaks of Water Demand
4. Future Directions for Short-Term Water Demand Forecasting
4.1. Upcoming Challenges for Water Demand Forecasting
4.2. So, What Method Should I Use?
- Identification of the temporal scope and (exogenous) factors of influence at each particular use case.
- Objective of the analysis: average vs. peak demand and anomaly detection vs. future prediction.
- Technology available: Requirement of near-real-time models. Solutions for multidimensional data streams.
4.3. Recommended Software: R, Python, Julia
- The R environment for statistical computing is a free software platform used for statistics and data mining [110]. R is widely used for time-series analysis and forecasting; such is the case of the development of predictive models for water demand. The R community is active in providing programming support and in the number and up-to-date quality of the so-called R packages, which are software libraries developed to run specific methods and data analysis. Among them, they highlight the package “neuralnet” to work with ANN [111], “e1071” to work with SVR [112], or “randomForest” to work with RF [113]. An additional advantage of R working with water demand comes thanks to matching data analyses to the Epanet-toolkit R packages “epanetReader” [114] and “epanet2toolkit” [115].
- Python is an interpreted, general-purpose programming language that can provide a multiplatform solution for scientific computing [116]. This is thanks to Python libraries such as “pandas” and “numpy” for data manipulation and basic analysis and “scikit-learn” [117] for machine and statistical learning software development (including functions to work with ANN, SVR, RF, and many more). Python also has the backup of a huge community supporting up-to-date libraries, creating an ideal framework for research and software development. Importantly, there is a Python library to run the Epanet toolkit called “Epanettools” and a library called “WNTR” that is an Epanet-compatible Python library for the simulation and analysis of water distribution systems resilience, developed by the Sandia National Laboratories and the US Environmental Protection Agency (EPA) [118].
- Julia is a high-level programming language that naturally supports concurrent, parallel, and distributed computing [119]. This means that, although Julia is a general-purpose language, it was originally designed for machine learning and statistical programming. Julia is a quite new language, and it is still far from the popularity of R or Python. However, there is foreseen a brilliant future for Julia given its properties of speed, using just-in-time compilers making it as fast as low-level compiled languages such as C. In addition, Julia can be executed in R, Latex, Python, and C, while Julia can also wrap R and Python code, thanks to the libraries “RCall” and “PyCall”, respectively.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Mean Squared Error | MSE | Comparing with benchmark | B |
| Root Mean Squared Error | RMSE | Lagrange multipliers tests | LM |
| Relative Root Mean Square Error | RRMSE | Moran-I test | MI |
| Normalized Root Mean Square Error | NRMSE | Normal Mean Square Error | NMSE |
| Mean Absolute Percentage Error | MAPE | Pearson coefficient | r |
| Mean Absolute Error | MAE | Percentage deviation in peak | Pdv |
| Coefficient of Determination | R2 | Persistence Index | PI |
| Correlation coefficient | CC | Fraction Out of Bounds | FOB |
| Nash–Sutcliffe coefficient | NSE | Mean Bias Error | MBE |
| Relative Error | RE | Mean absolute scaled error | MASE |
| Absolute Relative Error | ARE | Standard Error Prediction | SEP |
| Average Absolute Relative Error | AARE | Variance accounted for | VAF |
| Average Absolute Error | AAE | Akaike’s Information Criterion | AICc |
| Maximal Root Error | MaxRE | Standard Deviation | SDe |
| Standard deviation of the absolute relative error | SDARE | Accuracy | Ac |
| Mean Absolute Relative Error | MARE | Gini coefficient | GINI |
| Mean Relative Error | MRE | Theil’s coefficients | UI & UII |
| Efficiency Index | E | Average prediction interval width | AWPI |
| Threshold statistic | Ts | Average empirical coverage rate | ECPI |
| Descriptive accuracy metrics and formal statistical tests | ST | Negatively-oriented interval score | NOIS |
References
- Leitão, J.; Simões, N.; Sá Marques, J.A.; Gil, P.; Ribeiro, B.; Cardoso, A. Detecting urban water consumption patterns: A time-series clustering approach. Water Supply 2019, 19, 2323–2329. [Google Scholar] [CrossRef]
- Vijai, P.; Sivakumar, P.B. Performance comparison of techniques for water demand forecasting. Procedia Comput. Sci. 2018, 143, 258–266. [Google Scholar] [CrossRef]
- Tiwari, M.; Adamowski, J.; Adamowski, K. Water demand forecasting using extreme learning machines. J. Water Land Dev. 2016, 28, 37–52. [Google Scholar] [CrossRef] [Green Version]
- Koohbanani, H.; Barati, R.; Yazdani, M.; Sakhdari, S.; Jomemanzari, R. Groundwater recharge by selection of suitable sites for underground dams using a GIS-based fuzzy approach in semi-arid regions. In Progress in River Engineering & Hydraulic Structures; International Energy and Environment Foundation: Najaf, Iraq, 2018; pp. 11–32. [Google Scholar]
- Alvisi, S.; Franchini, M.; Marinelli, A. A short-term, pattern-based model for water-demand forecasting. J. Hydroinform. 2007, 9, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Bougadis, J.; Adamowski, K.; Diduch, R. Short-term municipal water demand forecasting. Hydrol. Process. Int. J. 2005, 19, 137–148. [Google Scholar] [CrossRef]
- Jain, A.; Varshney, A.K.; Joshi, U.C. Short-term water demand forecast modelling at IIT Kanpur using artificial neural networks. Water Resour. Manag. 2001, 15, 299–321. [Google Scholar] [CrossRef]
- Kim, S.; Koo, J.; Kim, H.; Choi, Y. Optimization of pumping schedule based on forecasting the hourly water demand in Seoul. Water Sci. Technol. Water Supply 2007, 7, 85–93. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- de Souza Groppo, G.; Costa, M.A.; Libânio, M. Predicting water demand: A review of the methods employed and future possibilities. Water Supply 2019, 19, 2179–2198. [Google Scholar] [CrossRef]
- Kozłowski, E.; Kowalska, B.; Kowalski, D.; Mazurkiewicz, D. Water demand forecasting by trend and harmonic analysis. Arch. Civ. Mech. Eng. 2018, 18, 140–148. [Google Scholar] [CrossRef]
- Antunes, A.; Andrade-Campos, A.; Sardinha-Lourenço, A.; Oliveira, M. Short-term water demand forecasting using machine learning techniques. J. Hydroinform. 2018, 20, 1343–1366. [Google Scholar] [CrossRef] [Green Version]
- Pesantez, J.E.; Berglund, E.Z.; Kaza, N. Smart meters data for modeling and forecasting water demand at the user-level. Environ. Model. Softw. 2020, 125, 104633. [Google Scholar] [CrossRef]
- Bich-Ngoc, N.; Teller, J. A review of residential water consumption determinants. In Proceedings of the International Conference on Computational Science and Its Applications, Melbourne, VIC, Australia, 2–5 July 2018; pp. 685–696. [Google Scholar]
- Brentan, B.M.; Luvizotto, E., Jr.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Hybrid regression model for near real-time urban water demand forecasting. J. Comput. Appl. Math. 2017, 309, 532–541. [Google Scholar] [CrossRef]
- Hu, P.; Tong, J.; Wang, J.; Yang, Y.; de Oliveira Turci, L. A hybrid model based on CNN and Bi-LSTM for urban water demand prediction. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1088–1094. [Google Scholar]
- André, D.D.M.; Carvalho, J.R. Spatial determinants of urban residential water demand in Fortaleza, Brazil. Water Resour. Manag. 2014, 28, 2401–2414. [Google Scholar] [CrossRef]
- Hussien, W.A.; Memon, F.A.; Savic, D.A. Assessing and modelling the influence of household characteristics on per capita water consumption. Water Resour. Manag. 2016, 30, 2931–2955. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.; Stewart, R.A.; Beal, C.D. ANN-based residential water end-use demand forecasting model. Expert Syst. Appl. 2013, 40, 1014–1023. [Google Scholar] [CrossRef] [Green Version]
- Franczyk, J.; Chang, H. Spatial analysis of water use in Oregon, USA, 1985–2005. Water Resour. Manag. 2009, 23, 755–774. [Google Scholar] [CrossRef]
- Bao, C.; Chen, X. Spatial econometric analysis on influencing factors of water consumption efficiency in urbanizing China. J. Geogr. Sci. 2017, 27, 1450–1462. [Google Scholar] [CrossRef] [Green Version]
- Benítez, R.; Ortiz-Caraballo, C.; Preciado, J.C.; Conejero, J.M.; Figueroa, F.S.; Rubio-Largo, A. A short-term data based water consumption prediction approach. Energies 2019, 12, 2359. [Google Scholar] [CrossRef] [Green Version]
- Candelieri, A. Clustering and support vector regression for water demand forecasting and anomaly detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Willis, R.M.; Stewart, R.A.; Giurco, D.P.; Talebpour, M.R.; Mousavinejad, A. End use water consumption in households: Impact of socio-demographic factors and efficient devices. J. Clean. Prod. 2013, 60, 107–115. [Google Scholar] [CrossRef] [Green Version]
- Willis, R.M.; Stewart, R.A.; Panuwatwanich, K.; Jones, S.; Kyriakides, A. Alarming visual display monitors affecting shower end use water and energy conservation in Australian residential households. Resour. Conserv. Recycl. 2010, 54, 1117–1127. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-Q.; Cheng, W.-P.; Zhang, T.-Q. Principal factor analysis for forecasting diurnal water-demand pattern using combined rough-set and fuzzy-clustering technique. J. Water Resour. Plan. Manag. 2013, 139, 23–33. [Google Scholar] [CrossRef]
- Vonk, E.; Cirkel, D.G.; Blokker, M. Estimating peak daily water demand under different climate change and vacation scenarios. Water 2019, 11, 1874. [Google Scholar] [CrossRef] [Green Version]
- Abu-Bakar, H.; Williams, L.; Hallett, S.H. Quantifying the impact of the COVID-19 lockdown on household water consumption patterns in England. NPJ Clean Water 2021, 4, 1–9. [Google Scholar] [CrossRef]
- Shirkoohi, M.G.; Doghri, M.; Duchesne, S. Short-term water demand predictions coupling an artificial neural network model and a genetic algorithm. Water Supply 2021, 21, 2374–2386. [Google Scholar] [CrossRef]
- Koo, K.-M.; Han, K.-H.; Jun, K.-S.; Lee, G.; Kim, J.-S.; Yum, K.-T. Performance assessment for short-term water demand forecasting models on distinctive water uses in Korea. Sustainability 2021, 13, 6056. [Google Scholar] [CrossRef]
- Pandey, P.; Bokde, N.D.; Dongre, S.; Gupta, R. Hybrid models for water demand forecasting. J. Water Resour. Plan. Manag. 2021, 147, 04020106. [Google Scholar] [CrossRef]
- Rezaali, M.; Quilty, J.; Karimi, A. Probabilistic urban water demand forecasting using wavelet-based machine learning models. J. Hydrol. 2021, 600, 126358. [Google Scholar] [CrossRef]
- Du, B.; Zhou, Q.; Guo, J.; Guo, S.; Wang, L. Deep learning with long short-term memory neural networks combining wavelet transform and principal component analysis for daily urban water demand forecasting. Expert Syst. Appl. 2021, 171, 114571. [Google Scholar] [CrossRef]
- Hu, S.; Gao, J.; Zhong, D.; Deng, L.; Ou, C.; Xin, P. An innovative hourly water demand forecasting preprocessing framework with local outlier correction and adaptive decomposition techniques. Water 2021, 13, 582. [Google Scholar] [CrossRef]
- Al-Ghamdi, A.-B.; Kamel, S.; Khayyat, M. Evaluation of artificial neural networks performance using various normalization methods for water demand forecasting. In Proceedings of the 2021 National Computing Colleges Conference (NCCC), Taif, Saudi Arabia, 27–28 March 2021; pp. 1–6. [Google Scholar]
- Salloom, T.; Kaynak, O.; He, W. A novel deep neural network architecture for real-time water demand forecasting. J. Hydrol. 2021, 599, 126353. [Google Scholar] [CrossRef]
- Bata, M.H.; Carriveau, R.; Ting, D.S.-K. Short-term water demand forecasting using hybrid supervised and unsupervised machine learning model. Smart Water 2020, 5, 1–18. [Google Scholar] [CrossRef]
- Xenochristou, M.; Hutton, C.; Hofman, J.; Kapelan, Z. Water demand forecasting accuracy and influencing factors at different spatial scales using a gradient boosting machine. Water Resour. Res. 2020, 56, e2019WR026304. [Google Scholar] [CrossRef]
- Yousefi, P.; Courtice, G.; Naser, G.; Mohammadi, H. Nonlinear dynamic modeling of urban water consumption using chaotic approach (Case study: City of Kelowna). Water 2020, 12, 753. [Google Scholar] [CrossRef] [Green Version]
- Pacchin, E.; Gagliardi, F.; Alvisi, S.; Franchini, M. A comparison of short-term water demand forecasting models. Water Resour. Manag. 2019, 33, 1481–1497. [Google Scholar] [CrossRef]
- Villarin, M.C.; Rodriguez-Galiano, V.F. Machine learning for modeling water demand. J. Water Resour. Plan. Manag. 2019, 145, 04019017. [Google Scholar] [CrossRef]
- Perea, R.G.; Poyato, E.C.; Montesinos, P.; Díaz, J.A.R. Optimisation of water demand forecasting by artificial intelligence with short data sets. Biosyst. Eng. 2019, 177, 59–66. [Google Scholar] [CrossRef]
- Maruyama, Y.; Yamamoto, H. A study of statistical forecasting method concerning water demand. Procedia Manuf. 2019, 39, 1801–1808. [Google Scholar] [CrossRef]
- Gharabaghi, S.; Stahl, E.; Bonakdari, H. Integrated nonlinear daily water demand forecast model (Case study: City of Guelph, Canada). J. Hydrol. 2019, 579, 124182. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Mousavi-Mirkalaei, P. Extended linear and non-linear auto-regressive models for forecasting the urban water consumption of a fast-growing city in an arid region. Sustain. Cities Soc. 2019, 48, 101585. [Google Scholar] [CrossRef]
- Candelieri, A.; Giordani, I.; Archetti, F.; Barkalov, K.; Meyerov, I.; Polovinkin, A.; Sysoyev, A.; Zolotykh, N. Tuning hyperparameters of a SVM-based water demand forecasting system through parallel global optimization. Comput. Oper. Res. 2019, 106, 202–209. [Google Scholar] [CrossRef]
- Brentan, B.M.; Meirelles, G.L.; Manzi, D.; Luvizotto, E. Water demand time series generation for distribution network modeling and water demand forecasting. Urban Water J. 2018, 15, 150–158. [Google Scholar] [CrossRef]
- Sardinha-Lourenço, A.; Andrade-Campos, A.; Antunes, A.; Oliveira, M. Increased performance in the short-term water demand forecasting through the use of a parallel adaptive weighting strategy. J. Hydrol. 2018, 558, 392–404. [Google Scholar] [CrossRef]
- Shabani, S.; Candelieri, A.; Archetti, F.; Naser, G. Gene expression programming coupled with unsupervised learning: A two-stage learning process in multi-scale, short-term water demand forecasts. Water 2018, 10, 142. [Google Scholar] [CrossRef] [Green Version]
- Pacchin, E.; Alvisi, S.; Franchini, M. A short-term water demand forecasting model using a moving window on previously observed data. Water 2017, 9, 172. [Google Scholar] [CrossRef]
- Oliveira, P.J.; Steffen, J.L.; Cheung, P. Parameter estimation of seasonal ARIMA models for water demand forecasting using the Harmony Search Algorithm. Procedia Eng. 2017, 186, 177–185. [Google Scholar] [CrossRef]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A probabilistic short-term water demand forecasting model based on the Markov Chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Arandia, E.; Ba, A.; Eck, B.; McKenna, S. Tailoring seasonal time series models to forecast short-term water demand. J. Water Resour. Plan. Manag. 2016, 142, 04015067. [Google Scholar] [CrossRef] [Green Version]
- Walker, D.; Creaco, E.; Vamvakeridou-Lyroudia, L.; Farmani, R.; Kapelan, Z.; Savić, D. Forecasting domestic water consumption from smart meter readings using statistical methods and artificial neural networks. Procedia Eng. 2015, 119, 1419–1428. [Google Scholar] [CrossRef] [Green Version]
- Candelieri, A.; Soldi, D.; Archetti, F. Short-term forecasting of hourly water consumption by using automatic metering readers data. Procedia Eng. 2015, 119, 844–853. [Google Scholar] [CrossRef]
- Hutton, C.J.; Kapelan, Z. A probabilistic methodology for quantifying, diagnosing and reducing model structural and predictive errors in short term water demand forecasting. Environ. Model. Softw. 2015, 66, 87–97. [Google Scholar] [CrossRef]
- Al-Zahrani, M.A.; Abo-Monasar, A. Urban residential water demand prediction based on artificial neural networks and time series models. Water Resour. Manag. 2015, 29, 3651–3662. [Google Scholar] [CrossRef]
- Vijayalaksmi, D.; Babu, K.J. Water supply system demand forecasting using adaptive neuro-fuzzy inference system. Aquat. Procedia 2015, 4, 950–956. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J.F. Medium-term urban water demand forecasting with limited data using an ensemble wavelet–bootstrap machine-learning approach. J. Water Resour. Plan. Manag. 2015, 141, 04014053. [Google Scholar] [CrossRef] [Green Version]
- Bakker, M.; Van Duist, H.; Van Schagen, K.; Vreeburg, J.; Rietveld, L. Improving the performance of water demand forecasting models by using weather input. Procedia Eng. 2014, 70, 93–102. [Google Scholar] [CrossRef] [Green Version]
- Romano, M.; Kapelan, Z. Adaptive water demand forecasting for near real-time management of smart water distribution systems. Environ. Model. Softw. 2014, 60, 265–276. [Google Scholar] [CrossRef] [Green Version]
- Okeya, I.; Kapelan, Z.; Hutton, C.; Naga, D. Online modelling of water distribution system using data assimilation. Procedia Eng. 2014, 70, 1261–1270. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Wang, P.; Li, C.; Xie, J.; Wang, Y. A multi-scale relevance vector regression approach for daily urban water demand forecasting. J. Hydrol. 2014, 517, 236–245. [Google Scholar] [CrossRef]
- Candelieri, A.; Archetti, F. Identifying typical urban water demand patterns for a reliable short-term forecasting—The icewater project approach. Procedia Eng. 2014, 89, 1004–1012. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Boccelli, D. Demand forecasting for water distribution systems. Procedia Eng. 2014, 70, 339–342. [Google Scholar] [CrossRef] [Green Version]
- Alvisi, S.; Franchini, M. Assessment of the predictive uncertainty within the framework of water demand forecasting by using the model conditional processor. Procedia Eng. 2014, 89, 893–900. [Google Scholar] [CrossRef] [Green Version]
- Sampathirao, A.K.; Grosso, J.M.; Sopasakis, P.; Ocampo-Martinez, C.; Bemporad, A.; Puig, V. Water demand forecasting for the optimal operation of large-scale drinking water networks: The Barcelona case study. IFAC Proc. Vol. 2014, 47, 10457–10462. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Islam, M.Z.; Hafeez, M. Evaluating the performance of several data mining methods for predicting irrigation water requirement. In Proceedings of the Tenth Australasian Data Mining Conference, Darlinghurst, Australia, 5–7 December 2012; Volume 134, pp. 199–207. [Google Scholar]
- Adamowski, J.; Chan, H.F.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48, W01528. [Google Scholar] [CrossRef]
- Azadeh, A.; Neshat, N.; Hamidipour, H. Hybrid fuzzy regression—Artificial neural network for improvement of short-term water consumption estimation and forecasting in uncertain and complex environments: Case of a large metropolitan city. J. Water Resour. Plan. Manag. 2012, 138, 71–75. [Google Scholar] [CrossRef]
- Odan, F.K.; Reis, L.F.R. Hybrid water demand forecasting model associating artificial neural network with Fourier series. J. Water Resour. Plan. Manag. 2012, 138, 245–256. [Google Scholar] [CrossRef] [Green Version]
- Herrera, M.; García-Díaz, J.C.; Izquierdo, J.; Pérez-García, R. Municipal water demand forecasting: Tools for intervention time series. Stoch. Anal. Appl. 2011, 29, 998–1007. [Google Scholar] [CrossRef]
- Adamowski, J.; Karapataki, C. Comparison of multivariate regression and artificial neural networks for peak urban water-demand forecasting: Evaluation of different ANN learning algorithms. J. Hydrol. Eng. 2010, 15, 729–743. [Google Scholar] [CrossRef] [Green Version]
- Caiado, J. Performance of combined double seasonal univariate time series models for forecasting water demand. J. Hydrol. Eng. 2010, 15, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.Y.; Yan, X. Applying genetic programming approaches to short-term water demand forecast for district water system. In Water Distribution Systems Analysis 2010; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1498–1506. [Google Scholar]
- Shuang, Q.; Zhao, R.T. Water demand prediction using machine learning methods: A case study of the Beijing–Tianjin–Hebei region in China. Water 2021, 13, 310. [Google Scholar] [CrossRef]
- Ristow, D.C.; Henning, E.; Kalbusch, A.; Petersen, C.E. Models for forecasting water demand using time series analysis: A case study in Southern Brazil. J. Water Sanit. Hyg. Dev. 2021, 11, 231–240. [Google Scholar] [CrossRef]
- Karamaziotis, P.I.; Raptis, A.; Nikolopoulos, K.; Litsiou, K.; Assimakopoulos, V. An empirical investigation of water consumption forecasting methods. Int. J. Forecast. 2020, 36, 588–606. [Google Scholar] [CrossRef]
- Sanchez, G.M.; Terando, A.; Smith, J.W.; García, A.M.; Wagner, C.R.; Meentemeyer, R.K. Forecasting water demand across a rapidly urbanizing region. Sci. Total Environ. 2020, 730, 139050. [Google Scholar] [CrossRef]
- Guo, W.; Liu, T.; Dai, F.; Xu, P. An improved whale optimization algorithm for forecasting water resources demand. Appl. Soft Comput. 2020, 86, 105925. [Google Scholar] [CrossRef]
- Rasifaghihi, N.; Li, S.; Haghighat, F. Forecast of urban water consumption under the impact of climate change. Sustain. Cities Soc. 2020, 52, 101848. [Google Scholar] [CrossRef]
- Duerr, I.; Merrill, H.R.; Wang, C.; Bai, R.; Boyer, M.; Dukes, M.D.; Bliznyuk, N. Forecasting urban household water demand with statistical and machine learning methods using large space-time data: A comparative study. Environ. Model. Softw. 2018, 102, 29–38. [Google Scholar] [CrossRef]
- Sharvelle, S.; Dozier, A.; Arabi, M.; Reichel, B. A geospatially-enabled web tool for urban water demand forecasting and assessment of alternative urban water management strategies. Environ. Model. Softw. 2017, 97, 213–228. [Google Scholar] [CrossRef]
- Haque, M.M.; de Souza, A.; Rahman, A. Water demand modelling using independent component regression technique. Water Resour. Manag. 2017, 31, 299–312. [Google Scholar] [CrossRef]
- Shabani, S.; Yousefi, P.; Naser, G. Support vector machines in urban water demand forecasting using phase space reconstruction. Procedia Eng. 2017, 186, 537–543. [Google Scholar] [CrossRef]
- Yousefi, P.; Shabani, S.; Mohammadi, H.; Naser, G. Gene expression programing in long term water demand forecasts using wavelet decomposition. Procedia Eng. 2017, 186, 544–550. [Google Scholar] [CrossRef]
- Nassery, H.R.; Adinehvand, R.; Salavitabar, A.; Barati, R. Water management using system dynamics modeling in semi-arid regions. Civ. Eng. J. 2017, 3, 766–778. [Google Scholar] [CrossRef] [Green Version]
- Altunkaynak, A.; Nigussie, T.A. Monthly water consumption prediction using season algorithm and wavelet transform-based models. J. Water Resour. Plan. Manag. 2017, 143, 04017011. [Google Scholar] [CrossRef]
- Vani, G. Estimation of urban water demand using system dynamics modeling for madurai city. Int. J. Res. Eng. Technol. 2017, 6, 106–113. [Google Scholar]
- Fullerton, T.M., Jr.; Ceballos, A.; Walke, A.G. Short-term forecasting analysis for municipal water demand. J. Am. Water Work. Assoc. 2016, 108, E27–E38. [Google Scholar] [CrossRef]
- Peña-Guzmán, C.; Melgarejo, J.; Prats, D. Forecasting water demand in residential, commercial, and industrial zones in Bogotá, Colombia, using least-squares support vector machines. Math. Probl. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Shabani, S.; Yousefi, P.; Adamowski, J.; Naser, G.; Rahman, I. Intelligent soft computing models in water demand forecasting. In Water Stress in Plants; IntechOpen: London, UK, 2016; pp. 99–117. [Google Scholar]
- Shabri, A.; Samsudin, R.; Teknologi, U. Empirical mode decomposition—Least squares support vector machine based for water demand forecasting. Int. J. Adv. Soft Comput. Its Appl. 2015, 7, 38–53. [Google Scholar]
- Kofinas, D.; Mellios, N.; Papageorgiou, E.; Laspidou, C. Urban water demand forecasting for the island of Skiathos. Procedia Eng. 2014, 89, 1023–1030. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.N.; Guo, H.; Li, Y.; Liu, J.L. The application of system dynamics model of city water demand forecasting. Appl. Mech. Mater. 2014, 535, 440–445. [Google Scholar] [CrossRef]
- Almutaz, I.; Ajbar, A.; Khalid, Y.; Ali, E. A probabilistic forecast of water demand for a tourist and desalination dependent city: Case of Mecca, Saudi Arabia. Desalination 2012, 294, 53–59. [Google Scholar] [CrossRef]
- Nasseri, M.; Moeini, A.; Tabesh, M. Forecasting monthly urban water demand using extended Kalman filter and genetic programming. Expert Syst. Appl. 2011, 38, 7387–7395. [Google Scholar] [CrossRef]
- Qi, C.; Chang, N.-B. System dynamics modeling for municipal water demand estimation in an urban region under uncertain economic impacts. J. Environ. Manag. 2011, 92, 1628–1641. [Google Scholar] [CrossRef]
- Firat, M.; Turan, M.E.; Yurdusev, M.A. Comparative analysis of neural network techniques for predicting water consumption time series. J. Hydrol. 2010, 384, 46–51. [Google Scholar] [CrossRef]
- Varahrami, V. Application of genetic algorithm to neural network forecasting of short-term water demand. In Proceedings of the International Conference on Applied Economics—ICOAE, Athens, Greece, 26–28 August 2010. [Google Scholar]
- Mohamed, M.M.; Al-Mualla, A.A. Water demand forecasting in Umm Al-Quwain using the constant rate model. Desalination 2010, 259, 161–168. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A.; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Environ. Monit. Assess. 2017, 189, 1–13. [Google Scholar] [CrossRef]
- Herrera, M.; Izquierdo, J.; Pérez-Garćıa, R.; Ayala-Cabrera, D. On-line learning of predictive kernel models for urban water demand in a smart city. Procedia Eng. 2014, 70, 791–799. [Google Scholar] [CrossRef]
- Herrera, M.; Guglielmetti, A.; Xiao, M.; Coelho, R.F. Metamodel-assisted optimization based on multiple kernel regression for mixed variables. Struct. Multidiscip. Optim. 2014, 49, 979–991. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Roberson, J.A. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Oyebode, O.; Babatunde, D.E.; Monyei, C.G.; Babatunde, O.M. Water demand modelling using evolutionary computation techniques: Integrating water equity and justice for realization of the sustainable development goals. Heliyon 2019, 5, e02796. [Google Scholar] [CrossRef] [Green Version]
- Bi, W.; Maier, H.R.; Dandy, G.C. Impact of starting position and searching mechanism on the evolutionary algorithm convergence rate. J. Water Resour. Plan. Manag. 2016, 142, 04016026. [Google Scholar] [CrossRef]
- Davino, C.; Furno, M.; Vistocco, D. Quantile Regression: Theory and Applications; John Wiley & Sons: Chichester, UK, 2013; Volume 988. [Google Scholar]
- Beal, C.D.; Stewart, R.A. Identifying residential water end uses underpinning peak day and peak hour demand. J. Water Resour. Plan. Manag. 2014, 140, 04014008. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Fritsch, S.; Guenther, F.; Suling, M.; Mueller, S. Package ‘Neuralnet’. Training of Neural Networks, R Package Version; R Foundation for Statistical Computing: Vienna, Austria, 2019; p. 1. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.-C.; Lin, C.-C.; Meyer, M.D. Package ‘e1071’. R J. 2019, 1–66. [Google Scholar]
- Breiman, L. Breiman and Cutler’s Random Forests for Classification and Regression, R package version; R Foundation for Statistical Computing: Vienna, Austria, 2012; p. 2. [Google Scholar]
- Eck, B.J. An R package for reading EPANET files. Environ. Model. Softw. 2016, 84, 149–154. [Google Scholar] [CrossRef]
- Arandia, E.; Eck, B.J. An R package for EPANET simulations. Environ. Model. Softw. 2018, 107, 59–63. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Klise, K.A.; Hart, D.; Moriarty, D.M.; Bynum, M.L.; Murray, R.; Burkhardt, J.; Haxton, T. Water Network Tool for Resilience (WNTR) User Manual; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2017. [Google Scholar]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef] [Green Version]
| Journal Name | References | Publisher | Impact Factor (5 year) | Best Quartile |
|---|---|---|---|---|
| Procedia Engineering | [12] | Elsevier | - | - |
| Water Resources Planning and Mgmt. | [11] | ASCE | 3.563 | Q2 |
| Water | [8] | MDPI | 3.229 | Q2 |
| Environmental Modelling & Software | [7] | Elsevier | 6.036 | Q1 |
| Hydrology | [6] | Elsevier | 6.033 | Q1 |
| Water Resources Management | [4] | Springer | 3.868 | Q2 |
| Water Supply | [3] | IWA Publishing | 1.152 | Q4 |
| Water Resources Research | [2] | Wiley | 6.006 | Q1 |
| Desalination | [2] | Elsevier | 9.189 | Q1 |
| Sustainable Cities and Society | [2] | Elsevier | 7.308 | Q1 |
| Authors (Year) | Study Area | Measures of Accuracy | Time Periods | Methods | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hourly and Less | Daily | Weekly | Monthly | TS | NN | R / RF | Hyb | SVM | MHA | LM | SD | Others | |||
| Shirkouhi et al. [29] | Canada | RRMSE, MAPE, and NSE | * | * | * | * | * | ||||||||
| Koo et al. [30] | Korea | RMSE, NRMSE, NSE, r, and Residual | * | * | * | * | |||||||||
| Pandey et al. [31] | Spain and India | RMSE, MAE, and MAPE | * | * | * | * | * | ||||||||
| Rezaali et al. [32] | Iran | RMSE, r, NSE, MAE, and MARE | * | * | * | * | * | ||||||||
| Du et al. [33] | China | MAPE, MAPE of peaks, r, and explain variance score (EVS) | * | * | |||||||||||
| Hu et al. [34] | China | MAE, RMSE, NSE, and r | * | * | * | ||||||||||
| Al-Ghamdi [35] | Saudi Arabian | RMSE | * | * | |||||||||||
| Salloom et al. [36] | China | MAPE | * | * | |||||||||||
| Pesantez et al. [13] | United States | RMSE | * | * | * | * | * | ||||||||
| Bata et al. [37] | Canada | MAPE and NRMSE | * | * | * | * | * | ||||||||
| Xenochristou et al. [38] | UK | MAPE, MSE, and R2 | * | * | |||||||||||
| Yousefi et al. [39] | Canada | CC, RMSE, and MAE | * | * | * | * | * | ||||||||
| Pacchin et al. [40] | Italy | MAE and RMSE | * | * | * | ||||||||||
| Villarin and Rodriguez-Galiano [41] | Spain | R2 and RMSE | * | * | |||||||||||
| Perea et al. [42] | Spain | SEP and R2 | * | * | * | * | * | ||||||||
| Maruyama and Yamamoto [43] | Japan | ARE | * | * | * | ||||||||||
| Gharabaghi et al. [44] | Canada | MAPE, R2, VAF, AICc, and UI & UII | * | * | * | * | |||||||||
| Banihabib and Mousavi-Mirkalaei [45] | Iran | RMSE, MARE, MaxRE, MBE, and R2 | * | * | * | ||||||||||
| Benítez et al. [22] | Spain | MAPE, RMSE, and FOB | * | * | * | ||||||||||
| Candelieri et al. [46] | Italy | MAPE | * | * | * | * | |||||||||
| Hu et al. [16] | Not mentioned | MAE and MAPE | * | * | * | * | |||||||||
| Kozłowski et al. [11] | Poland | R2 | * | * | |||||||||||
| Antunes et al. [12] | Portugal | RMSE and NSE | * | * | * | * | * | ||||||||
| Vijai and Sivakumar [2] | EU | RMSE, R2, MSE, and MAE | * | * | * | * | * | * | |||||||
| Brentan et al. [47] | Brazil | SDe | * | * | * | ||||||||||
| Sardinha-Lourenço et al. [48] | Portugal | R2 and MAPE | * | * | * | ||||||||||
| Shabani et al. [49] | Canada | MAE, RMSE, R2, and MAPE | * | * | * | * | |||||||||
| Pacchin et al. [50] | Italy | RMSE and MAE | * | * | |||||||||||
| Oliveira et al. [51] | Brazil | MAPE and RMSE | * | * | * | * | |||||||||
| Gagliardi et al. [52] | UK | NSE | * | * | * | ||||||||||
| Brentan et al. [15] | Brazil | RMSE, MAE, and R2 | * | * | * | * | |||||||||
| Candelieri [23] | Italy | MAPE | * | * | * | ||||||||||
| Tiwari et al. [3] | Canada | R2, RMSE, Pdv, MAE, and PI | * | * | * | ||||||||||
| Arandia et al. [53] | Ireland | RMSE, NRMSE, and MAPE | * | * | * | ||||||||||
| Walker et al. [54] | Greece | CC and Sde | * | * | * | * | |||||||||
| Candelieri et al. [55] | Italy | MAPE | * | * | * | ||||||||||
| Hutton and Kapelan [56] | UK | MAPE | * | * | |||||||||||
| Al-Zahrani and Abo-Monasar [57] | Saudi Arabia | MAPE and R2 | * | * | * | ||||||||||
| Vijayalaksmi and Babu [58] | India | RMSE, MAPE, and CC | * | * | |||||||||||
| Tiwari and Adamowski [59] | Canada | R2, RMSE, Pdv, MAE, and PI | * | * | * | * | * | ||||||||
| Bakker et al. [60] | Netherlands | RE, MAPE, and R2 | * | * | * | * | |||||||||
| Romano and Kapelan [61] | UK | MAPE and MSE | * | * | * | ||||||||||
| Okeya et al. [62] | UK | MAE | * | * | * | ||||||||||
| Bai et al. [63] | China | NRMSE, CC, and MAPE | * | * | * | * | |||||||||
| Candelieri and Archetti [64] | Italy | MAPE | * | * | * | ||||||||||
| Chen and Boccelli [65] | Not mentioned | AARE | * | * | |||||||||||
| Alvisi and Franchini [66] | Italy | NSE and RMSE | * | * | * | * | |||||||||
| Sampathirao et al. [67] | Spain | Average PMSE24, Average PRMSE24, and Number of Parameters | * | * | * | * | * | * | |||||||
| Bennett et al. [19] | Australia | R2, ARE, AAE, RMSE, Mann–Whitney, Wilcoxon (MW), and p-value | * | * | |||||||||||
| Liu et al. [26] | China | AARE | * | * | |||||||||||
| Khan et al. [68] | Australia | Ac | * | * | * | * | |||||||||
| Adamowski et al. [69] | Canada | R2, RMSE, RRMSE, and E | * | * | * | * | * | ||||||||
| Azadeh et al. [70] | Iran | MAPE | * | * | * | * | |||||||||
| Odan and Reis [71] | Brazil | MAE and r | * | * | * | ||||||||||
| Herrera et al. [72] | Spain | RMSE and MAE | * | * | * | * | |||||||||
| Herrera et al. [9] | Spain | RMSE and MAE | * | * | * | * | * | ||||||||
| Adamowski and Karapataki [73] | Cyprus | R2, RMSE, AARE, and MaxARE | * | * | * | ||||||||||
| Caiado [74] | Spain | MSE | * | * | |||||||||||
| Wu and Yan [75] | United Kingdom | MSE, RMSE, MRE, and MaxRE | * | * | |||||||||||
| Authors (Year) | Study Area | Measures of Accuracy | Time Periods | Methods | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monthly | Quarterly | Yearly | TS | ANN | R/RF | Hyb | SVM | MHA | LM | SD | Others | |||
| Shuang and Zhao [76] | China | MSE–MAE-R2 | * | * | * | * | ||||||||
| Ristow et al. [77] | Brazil | MAPE | * | * | ||||||||||
| Karamaziotis et al. [78] | Greece | MAE, MASE, RMSE, and MAPE | * | * | ||||||||||
| Sanchez et al. [79] | United States | ST | * | * | * | |||||||||
| Guo et al. [80] | China | B, RE, and MRE | * | * | ||||||||||
| Rasifaghihi et al. [81] | Canada | Silhouette coefficient | * | * | * | * | ||||||||
| Duerr et al. [82] | United States | RMSE, GINI, AWPI, ECPI, and NOIS | * | * | * | * | ||||||||
| Sharvelle et al. [83] | United States | MRE, bias fraction (BIAS), and NSE | * | * | ||||||||||
| Haque et al. [84] | Brazil | R2, RMSE, MARE, and NSE | * | * | ||||||||||
| Shabani et al. [85] | Canada | R2 and RMSE | * | * | ||||||||||
| Yousefi et al. [86] | Canada | R2, RMSE, and MAE | * | * | ||||||||||
| Nassery et al. [87] | Iran | ME, MAE, MAPE, and RMSE | * | * | * | |||||||||
| Altunkaynak and Nigussie [88] | Turkey | RMSE and NSE | * | * | * | * | ||||||||
| Vani [89] | India | - | * | * | ||||||||||
| Fullerton Jr et al. [90] | United States | B and ST | * | * | ||||||||||
| Peña-Guzmán et al. [91] | Colombia | RMSE, AARE, and R2 | * | * | * | |||||||||
| Shabani et al. [92] | Canada | R2, MAE, RMSE, and NSE | * | * | * | |||||||||
| Shabri et al. [93] | Malaysia | RMSE, MAE, and CC | * | * | * | |||||||||
| Kofinas et al. [94] | Greece | R2, MAPE, RMSE, and MAE | * | * | * | * | ||||||||
| de Maria André and Carvalho [17] | Brazil | LM, Moran-I test, and R2 | * | * | * | * | ||||||||
| Yang et al. [95] | Not mentioned | - | * | * | ||||||||||
| Almutaz et al. [96] | Saudi Arabia | SDe | * | * | ||||||||||
| Nasseri et al. [97] | Iran | B, NMSE, and R2 | * | * | * | * | * | |||||||
| Qi and Chang [98] | United States | Compared with Real-world water demand data | * | * | ||||||||||
| Firat et al. [99] | Turkey | AARE, NRMSE, and Ts | * | * | * | |||||||||
| Varahrami [100] | Iran | RMSE, MAE, and MAPE | * | * | * | * | ||||||||
| Mohamed and Al-Mualla [101] | Emirates | AARE, ARE, and SDARE | * | * | * | |||||||||
| Method | Data Requirements | Accuracy | Interpretability | Efficiency | Adaptability |
|---|---|---|---|---|---|
| ANN-like | High | High | Low | Low | Medium |
| SVR-like | High | High | Medium | Low | Medium |
| ARIMA(X) | Low | Low | High | High | Low |
| Metaheuristics | High | Medium | Low | Low | Low |
| Regression | Low | Medium | High | High | Low |
| Hybrid | High | High | Medium | Medium | High |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niknam, A.; Zare, H.K.; Hosseininasab, H.; Mostafaeipour, A.; Herrera, M. A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use? Sustainability 2022, 14, 5412. https://doi.org/10.3390/su14095412
Niknam A, Zare HK, Hosseininasab H, Mostafaeipour A, Herrera M. A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use? Sustainability. 2022; 14(9):5412. https://doi.org/10.3390/su14095412
Chicago/Turabian StyleNiknam, Azar, Hasan Khademi Zare, Hassan Hosseininasab, Ali Mostafaeipour, and Manuel Herrera. 2022. "A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use?" Sustainability 14, no. 9: 5412. https://doi.org/10.3390/su14095412
APA StyleNiknam, A., Zare, H. K., Hosseininasab, H., Mostafaeipour, A., & Herrera, M. (2022). A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use? Sustainability, 14(9), 5412. https://doi.org/10.3390/su14095412








