Shear Strength Estimation of Reinforced Concrete Deep Beams Using a Novel Hybrid Metaheuristic Optimized SVR Models
Abstract
:1. Introduction
2. Background of Variables Impacts the Shear Strength of RC Deep Beams
3. Material and Data Collection
4. Methods and Development Models
4.1. Support Vector Regression
4.2. Optimization Methods
4.2.1. PSO
- First, it initializes the particle of the swarm, then defines the maximum number of iterations, and finally defines the cost function.
- After defining the cost function, it evaluates the swarm in order to identify the global and local best.
- Lastly, it calculates the velocity of each particle and then updates its position using the following equations:
4.2.2. HHO
4.2.3. AVOA
4.3. Models’ Development and Accuracy Assessment
4.4. Sensitivity Analysis
5. Results and Discussion
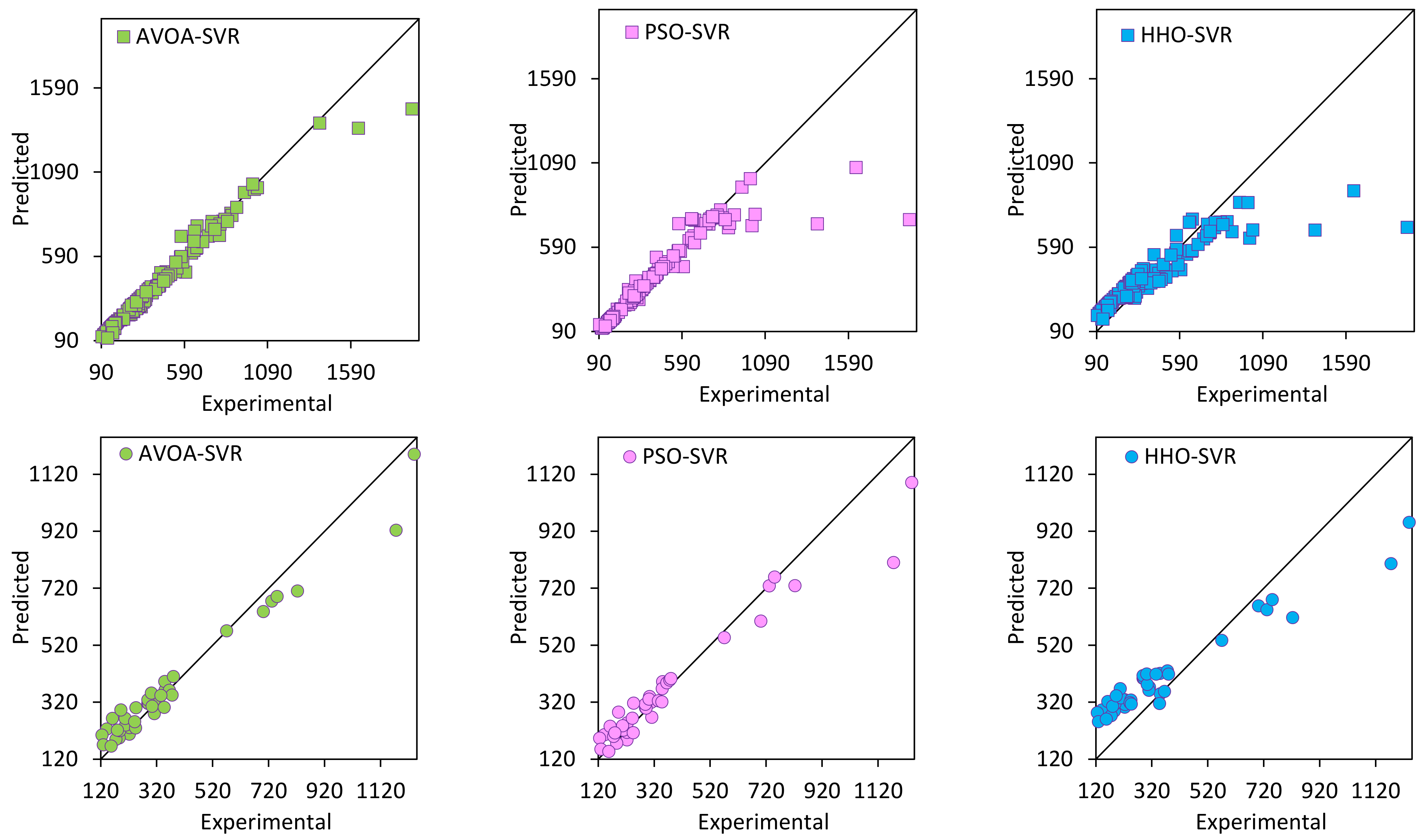
5.1. All Variables Impact on Vu Estimation
5.2. Selected Variables Impact on Vu Estimation
5.3. Comparison with Previous Studies and Codes
5.4. Sensitivity Analysis of Input Variables
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, Y.; Kim, S.; Kim, S. FEM Analysis of RC Deep Beam Depending on Shear-Span Ratio. Archit. Res. 2017, 19, 117–124. [Google Scholar]
- Gandomi, A.; Alavi, A.; Shadmehri, D.M.; Sahab, M. An empirical model for shear capacity of RC deep beams using genetic-simulated annealing. Arch. Civ. Mech. Eng. 2013, 13, 354–369. [Google Scholar] [CrossRef]
- Chou, J.-S.; Ngo, N.-T.; Pham, A.-D. Shear Strength Prediction in Reinforced Concrete Deep Beams Using Nature-Inspired Metaheuristic Support Vector Regression. J. Comput. Civ. Eng. 2016, 30, 04015002. [Google Scholar] [CrossRef]
- Liu, J. Kinematics-Based Modelling of Deep Transfer Girders in Reinforced Concrete Frame Structures. Ph.D. Thesis, Liege University, Liege, Belgium, 2019. [Google Scholar]
- Hwang, W.-Y.L.S.; Lee, H. Shear Strength Prediction for Deep Beams. ACI Struct. J. 2000, 97, 367–376. [Google Scholar] [CrossRef]
- Yavuz, G. Shear strength estimation of RC deep beams using the ANN and strut-and-tie approaches. Struct. Eng. Mech. 2016, 57, 657–680. [Google Scholar] [CrossRef]
- Nguyen, T.-A.; Ly, H.-B.; Mai, H.-V.T.; Tran, V.Q. On the Training Algorithms for Artificial Neural Network in Predicting the Shear Strength of Deep Beams. Complexity 2021, 2021, 5548988. [Google Scholar] [CrossRef]
- Russo, G.; Venir, R.; Pauletta, M. Reinforced Concrete Deep Beams-Shear Strength Model and Design Formula. ACI Struct. J. 2005, 102, 429–437. [Google Scholar]
- Dang, T.D.; Tran, D.T.; Nguyen-Minh, L.; Nassif, A.Y. Shear resistant capacity of steel fibres reinforced concrete deep beams: An experimental investigation and a new prediction model. Structures 2021, 33, 2284–2300. [Google Scholar] [CrossRef]
- ACI. Building Code Requirement for Structural Concrete and Commentary; ACI: Detroit, MI, USA, 2011; p. ACI-318. [Google Scholar]
- Ben Chaabene, W.; Nehdi, M.L. Novel soft computing hybrid model for predicting shear strength and failure mode of SFRC beams with superior accuracy. Compos. Part C Open Access 2020, 3, 100070. [Google Scholar] [CrossRef]
- Keshtegar, B.; Nehdi, M.L.; Kolahchi, R.; Trung, N.-T.; Bagheri, M. Novel hybrid machine leaning model for predicting shear strength of reinforced concrete shear walls. Eng. Comput. 2021, 0123456789. [Google Scholar] [CrossRef]
- Al-Musawi, A.; Alwanas, A.A.H.; Salih, S.; Ali, Z.; Tran, M.T.; Yaseen, Z.M. Shear strength of SFRCB without stirrups simulation: Implementation of hybrid artificial intelligence model. Eng. Comput. 2018, 36, 1–11. [Google Scholar] [CrossRef]
- Ning, C.; Li, B. Analytical probabilistic model for shear strength prediction of reinforced concrete beams without shear reinforcement. Adv. Struct. Eng. 2017, 21, 171–184. [Google Scholar] [CrossRef]
- Naderpour, H.; Nagai, K. Shear strength estimation of reinforced concrete beam–column sub-assemblages using multiple soft computing techniques. Struct. Des. Tall Spéc. Build. 2020, 29, 1–15. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Cao, M.-T. Evolutionary multivariate adaptive regression splines for estimating shear strength in reinforced-concrete deep beams. Eng. Appl. Artif. Intell. 2014, 28, 86–96. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Dafinescu, V. Review of Metaheuristics Inspired from the Animal Kingdom. Mathematics 2021, 9, 2335. [Google Scholar] [CrossRef]
- Bagal, H.A.; Soltanabad, Y.N.; Dadjuo, M.; Wakil, K.; Zare, M.; Mohammed, A.S. SOFC model parameter identification by means of Modified African Vulture Optimization algorithm. Energy Rep. 2021, 7, 7251–7260. [Google Scholar] [CrossRef]
- Sharafati, A.; Haghbin, M.; Aldlemy, M.S.; Mussa, M.H.; Al Zand, A.W.; Ali, M.; Bhagat, S.K.; Al-Ansari, N.; Yaseen, Z.M. Development of Advanced Computer Aid Model for Shear Strength of Concrete Slender Beam Prediction. Appl. Sci. 2020, 10, 3811. [Google Scholar] [CrossRef]
- Parsa, P.; Naderpour, H. Shear strength estimation of reinforced concrete walls using support vector regression improved by Teaching–learning-based optimization, Particle Swarm optimization, and Harris Hawks Optimization algorithms. J. Build. Eng. 2021, 44, 102593. [Google Scholar] [CrossRef]
- Tosee, S.V.R.; Faridmehr, I.; Bedon, C.; Sadowski, Ł.; Aalimahmoody, N.; Nikoo, M.; Nowobilski, T. Metaheuristic Prediction of the Compressive Strength of Environmentally Friendly Concrete Modified with Eggshell Powder Using the Hybrid ANN-SFL Optimization Algorithm. Materials 2021, 14, 6172. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Support vector regression based shear strength modelling of deep beams. Comput. Struct. 2011, 89, 1430–1439. [Google Scholar] [CrossRef]
- Zhang, D.; Shahin, M.; Yang, Y.; Liu, H.; Chang, L. Effect of microbially induced calcite precipitation treatment on the bonding properties of steel fiber in ultra-high performance concrete. J. Build. Eng. 2022, 50, 104132. [Google Scholar] [CrossRef]
- Chen, B.; Zhou, J.; Zhang, D.; Su, J.; Nuti, C.; Sennah, K. Experimental study on shear performances of ultra-high performance concrete deep beams. Structures 2022, 39, 310–322. [Google Scholar] [CrossRef]
- Smith, K.N.; Vantsiotis, A.S. Shear Strength of Deep Beams. J. Am. Concr. Inst. 1982, 79, 201–213. [Google Scholar] [CrossRef]
- Ahmed, A.K.E.-S. Concrete Contribution to the Shear Resistance of FRP-Reinforced Concrete Beams. Ph.D. Thesis, University of Sherbrooke, Sherbrooke, QC, Canada, 2006. [Google Scholar]
- Oh, J.-K.; Shin, S.-W. Shear Strength of Reinforced High-Strength Concrete Deep Beams. ACI Struct. J. 2001, 98, 164–173. [Google Scholar] [CrossRef]
- El-Zoughiby, M.E. Z-Shaped Load Path: A Unifying Approach to Developing Strut-and-Tie Models. ACI Struct. J. 2021, 118, 35–48. [Google Scholar] [CrossRef]
- Jin-Keun, K.; Yon-Dong, P. Shear strength of reinforced high strength concrete beam without web reinforcement. Mag. Concr. Res. 1994, 46, 7–16. [Google Scholar] [CrossRef]
- Londhe, R. Shear strength analysis and prediction of reinforced concrete transfer beams in high-rise buildings. Struct. Eng. Mech. 2011, 37, 39–59. [Google Scholar] [CrossRef] [Green Version]
- Mau, S.T.; Hsu, T. Formula for the Shear Strength of Deep Beams. ACI Struct. J. 1989, 86, 516–523. [Google Scholar] [CrossRef]
- Ashour, A.; Alvarez, L.; Toropov, V. Empirical modelling of shear strength of RC deep beams by genetic programming. Comput. Struct. 2003, 81, 331–338. [Google Scholar] [CrossRef]
- Mozumder, R.A.; Roy, B.; Laskar, A.I. Support Vector Regression Approach to Predict the Strength of FRP Confined Concrete. Arab. J. Sci. Eng. 2016, 42, 1129–1146. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Yaseen, Z.M.; Tran, M.T.; Kim, S.; Bakhshpoori, T.; Deo, R. Shear strength prediction of steel fiber reinforced concrete beam using hybrid intelligence models: A new approach. Eng. Struct. 2018, 177, 244–255. [Google Scholar] [CrossRef]
- Yap, C.W.; Li, Z.; Chen, Y. Quantitative structure–pharmacokinetic relationships for drug clearance by using statistical learning methods. J. Mol. Graph. Model. 2006, 24, 383–395. [Google Scholar] [CrossRef]
- Du, K.; Liu, M.; Zhou, J.; Khandelwal, M. Investigating the Slurry Fluidity and Strength Characteristics of Cemented Backfill and Strength Prediction Models by Developing Hybrid GA-SVR and PSO-SVR. Min. Met. Explor. 2022, 39, 433–452. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.; Yin, J.; Li, T.; Han, M. Simulation of mechanical behavior of carbonate gravel with hybrid PSO–SVR algorithm. Mar. Georesour. Geotechnol. 2022, 1–14. [Google Scholar] [CrossRef]
- Ortúzar, J. Future transportation: Sustainability, complexity and individualization of choices. Commun. Transp. Res. 2021, 1, 100010. [Google Scholar] [CrossRef]
- Mohammed, A.; Kurda, R.; Armaghani, D.J.; Hasanipanah, M. Prediction of Compressive Strength of Concrete Modified with Fly Ash: Applications of Neuro-Swarm and Neuro-Imperialism Models. Comput. Concr. 2021, 27, 489–512. [Google Scholar]
- Shahbazian, A.; Rabiefar, H.; Aminnejad, B. Shear Strength Determination in RC Beams Using ANN Trained with Tabu Search Training Algorithm. Adv. Civ. Eng. 2021, 2021, 1639214. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Yang, H.-C.; Zhang, S.-B.; Deng, K.-Z.; DU, P.-J. Research into a Feature Selection Method for Hyperspectral Imagery Using PSO and SVM. J. China Univ. Min. Technol. 2007, 17, 473–478. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Arashpour, M.; Behnood, A. Predicting the compressive strength of green concretes using Harris hawks optimization-based data-driven methods. Constr. Build. Mater. 2021, 318, 125944. [Google Scholar] [CrossRef]
- Wei, W.; Li, X.; Liu, J.; Zhou, Y.; Li, L.; Zhou, J. Performance Evaluation of Hybrid WOA-SVR and HHO-SVR Models with Various Kernels to Predict Factor of Safety for Circular Failure Slope. Appl. Sci. 2021, 11, 1922. [Google Scholar] [CrossRef]
- Zhang, H.; Nguyen, H.; Bui, X.-N.; Pradhan, B.; Asteris, P.G.; Costache, R.; Aryal, J. A generalized artificial intelligence model for estimating the friction angle of clays in evaluating slope stability using a deep neural network and Harris Hawks optimization algorithm. Eng. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Sammen, S.; Ghorbani, M.; Malik, A.; Tikhamarine, Y.; AmirRahmani, M.; Al-Ansari, N.; Chau, K.-W. Enhanced Artificial Neural Network with Harris Hawks Optimization for Predicting Scour Depth Downstream of Ski-Jump Spillway. Appl. Sci. 2020, 10, 5160. [Google Scholar] [CrossRef]
- Ji, X.; Liang, S.Y. Model-based sensitivity analysis of machining-induced residual stress under minimum quantity lubrication. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 231, 1528–1541. [Google Scholar] [CrossRef]
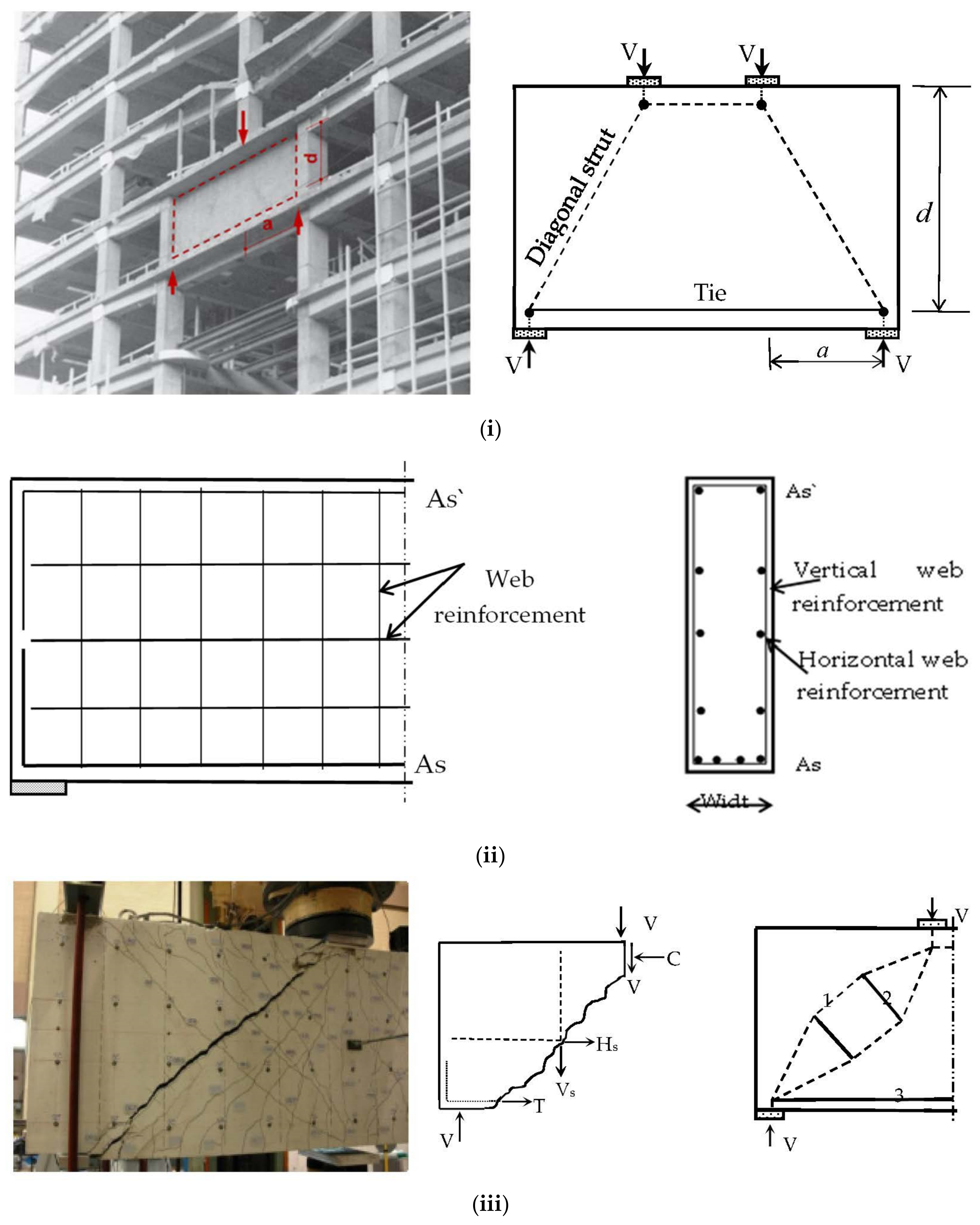







| Ref. | Equation | Explanation |
|---|---|---|
| ACI [10] | is the angle between the stirrups and the beam longitudinal axis | |
| Russo [8] | ||
| Liu [4] | is the shear resisted at the critical loading zone, represents the contribution of aggregate interlock, is the shear resisted by web reinforcement and is the dowel action in the main longitudinal bars. |
| Variable | Equation (R2) | Variable | Equation (R2) | Variable | Equation (R2) |
|---|---|---|---|---|---|
| a/d | y = 358.43x−0.803 (0.26) | b | y = 117.38 × 100.0052x (0.21) | Ag | y = 476.32x−0.164 (0.03) |
| ρ | y = 65.95ln(x) + 345.74 (0.01) | d | y = 0.7899x + 35.304 (0.35) | Std | y = 165.06 × 100.0731x (0.05) |
| y = 396ln(x) − 2024.7 (0.16) | h | y = 0.6985x + 32.425 (0.33) | Bd | y = 524.3x−0.262 (0.03) | |
| y = 495.94ln(x) − 1234.7 (0.39) | a | y = 259.88 × 100.0003x (0.015) | where: y represents the Vu x represents input variables R2 is the coefficient of determination | ||
| ρv | y = 325.96 × 10−0.159x (0.01) | Lp | y = 169.42 × 100.0054x (0.15) | ||
| y = 0.2678x + 344.21 (0.06) | Sp | y = 169.42 × 100.0054x (0.15) | |||
| y = 19.734x0.4588 (0.07) | V/P | y = 199.58x + 199.66 (0.010) | |||
| y = −371.18x + 429.11 (0.10) | # bars | y = 483.29ln(x) − 199.43 (0.37) | |||
| Variable | RA | M | SD | KU | SK | Variable | RA | M | SD | KU | SK |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a/d | 1.93 | 1.28 | 0.46 | −0.03 | 0.38 | b (mm) | 200.00 | 188.18 | 66.50 | −0.94 | 0.28 |
| (%) | 3.50 | 2.00 | 0.82 | 0.16 | 0.65 | d (mm) | 1374.00 | 443.74 | 212.19 | 11.52 | 3.14 |
| (MPa) | 502.00 | 459.71 | 147.09 | 0.50 | 1.26 | h (mm) | 1550.00 | 505.91 | 235.73 | 12.91 | 3.32 |
| (MPa) | 66.10 | 28.33 | 13.75 | 7.04 | 2.64 | a (mm) | 1600.00 | 543.97 | 242.31 | 2.87 | 1.09 |
| (%) | 1.25 | 0.29 | 0.32 | 0.69 | 1.10 | Lp (mm) | 210.00 | 113.11 | 45.63 | 3.05 | 2.04 |
| (mm) | 330.00 | 155.33 | 80.63 | 0.54 | 1.07 | Sp (mm) | 210.00 | 113.11 | 45.63 | 3.05 | 2.04 |
| (MPa) | 791.00 | 430.68 | 171.05 | 6.12 | 2.55 | V/P | 0.50 | 0.93 | 0.16 | 2.96 | −2.18 |
| (%) | 0.91 | 0.12 | 0.24 | 3.58 | 2.15 | #bars | 10.00 | 3.61 | 1.70 | 10.50 | 2.95 |
| Vu (kN) | 1869.00 | 385.80 | 285.02 | 6.25 | 2.09 | Ag (mm) | 22.00 | 14.20 | 5.67 | 0.53 | 1.29 |
| Std (mm) | 12.70 | 8.67 | 2.42 | −0.38 | −0.11 | ||||||
| Bd (mm) | 6.20 | 7.66 | 2.08 | −0.74 | −0.65 |
| Metaheuristic Algorithm | Parameters | Value |
|---|---|---|
| AVOA | Population | 5 |
| Iteration | 15 | |
| P1 | 0.9 | |
| P2 | 0.3 | |
| P3 | 0.6 | |
| Alpha | 0.8 | |
| Beta | 0.2 | |
| Gamma | 2.5 | |
| Range of C | [103, 10−3] | |
| Range of ε | [103, 10−3] | |
| Range of γ | [103, 10−3] | |
| PSO | Population | 5 |
| Iteration | 15 | |
| C1 | 1 | |
| C2 | 2 | |
| Range of C | [103, 10−3] | |
| Range of ε | [103, 10−3] | |
| Range of γ | [103, 10−3] | |
| HHO | Population | 5 |
| Iteration | 15 | |
| N | 3 | |
| Range of C | [103, 10−3] | |
| Range of ε | [103, 10−3] | |
| Range of γ | [103, 10−3] |
| Training | R2 | VAF | VIF | PI | RMSE | MAE | MBE | PE |
| AVOA-SVR | 0.984 | 97.330 | 64.510 | −30.241 | 32.198 | 24.377 | −0.047 | 1.723 |
| PSO-SVR | 0.813 | 78.261 | 5.358 | −89.973 | 91.568 | 31.605 | 26.960 | 4.899 |
| HHO-SVR | 0.818 | 66.278 | 5.500 | −62.003 | 63.483 | 105.885 | −6.032 | 3.397 |
| Testing | R2 | VAF | VIF | PI | RMSE | MAE | MBE | PE |
| AVOA-SVR | 0.756 | 67.921 | 4.102 | −76.076 | 77.505 | 101.702 | −13.001 | 6.949 |
| PSO-SVR | 0.630 | 52.981 | 2.706 | −75.687 | 76.837 | 106.357 | 17.850 | 6.889 |
| HHO-SVR | 0.715 | 45.786 | 3.514 | −46.690 | 47.856 | 162.579 | −56.320 | 4.290 |
| Model | M | Maximum | Minimum | SD | COV |
|---|---|---|---|---|---|
| Liu [4] | 1.10 | 1.54 | 0.65 | 0.15 | 0.13 |
| Russo [8] | 1.00 | 1.63 | 0.48 | 0.19 | 0.19 |
| ACI [10] | 0.59 | 2.06 | 0.09 | 0.41 | 0.69 |
| AVOA-SVR | 0.95 | 1.87 | 0.34 | 0.16 | 0.17 |
| Training | R2 | VAF | VIF | PI | RMSE | MAE | MBE | PE |
| AVOA-SVR | 0.974 | 96.726 | 39.202 | −40.095 | 42.036 | 26.728 | −0.360 | 2.249 |
| PSO-SVR | 0.834 | 81.625 | 6.042 | −90.753 | 92.402 | 32.755 | 18.958 | 4.944 |
| HHO-SVR | 0.816 | 71.805 | 5.427 | −72.442 | 73.975 | 92.860 | −7.926 | 3.958 |
| Testing | R2 | VAF | VIF | PI | RMSE | MAE | MBE | PE |
| AVOA-SVR | 0.970 | 94.460 | 33.512 | −35.876 | 37.790 | 43.168 | −7.149 | 3.388 |
| PSO-SVR | 0.950 | 91.774 | 20.118 | −45.091 | 46.958 | 44.085 | 0.475 | 4.210 |
| HHO-SVR | 0.948 | 79.860 | 19.147 | −33.841 | 35.586 | 106.952 | −50.633 | 3.190 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaloop, M.R.; Roy, B.; Chaurasia, K.; Kim, S.-M.; Jang, H.-M.; Hu, J.-W.; Abdelwahed, B.S. Shear Strength Estimation of Reinforced Concrete Deep Beams Using a Novel Hybrid Metaheuristic Optimized SVR Models. Sustainability 2022, 14, 5238. https://doi.org/10.3390/su14095238
Kaloop MR, Roy B, Chaurasia K, Kim S-M, Jang H-M, Hu J-W, Abdelwahed BS. Shear Strength Estimation of Reinforced Concrete Deep Beams Using a Novel Hybrid Metaheuristic Optimized SVR Models. Sustainability. 2022; 14(9):5238. https://doi.org/10.3390/su14095238
Chicago/Turabian StyleKaloop, Mosbeh R., Bishwajit Roy, Kuldeep Chaurasia, Sean-Mi Kim, Hee-Myung Jang, Jong-Wan Hu, and Basem S. Abdelwahed. 2022. "Shear Strength Estimation of Reinforced Concrete Deep Beams Using a Novel Hybrid Metaheuristic Optimized SVR Models" Sustainability 14, no. 9: 5238. https://doi.org/10.3390/su14095238
APA StyleKaloop, M. R., Roy, B., Chaurasia, K., Kim, S.-M., Jang, H.-M., Hu, J.-W., & Abdelwahed, B. S. (2022). Shear Strength Estimation of Reinforced Concrete Deep Beams Using a Novel Hybrid Metaheuristic Optimized SVR Models. Sustainability, 14(9), 5238. https://doi.org/10.3390/su14095238








