Train Operational Plan Optimization for Urban Rail Transit Lines Considering Circulation Balance
Abstract
:1. Introduction
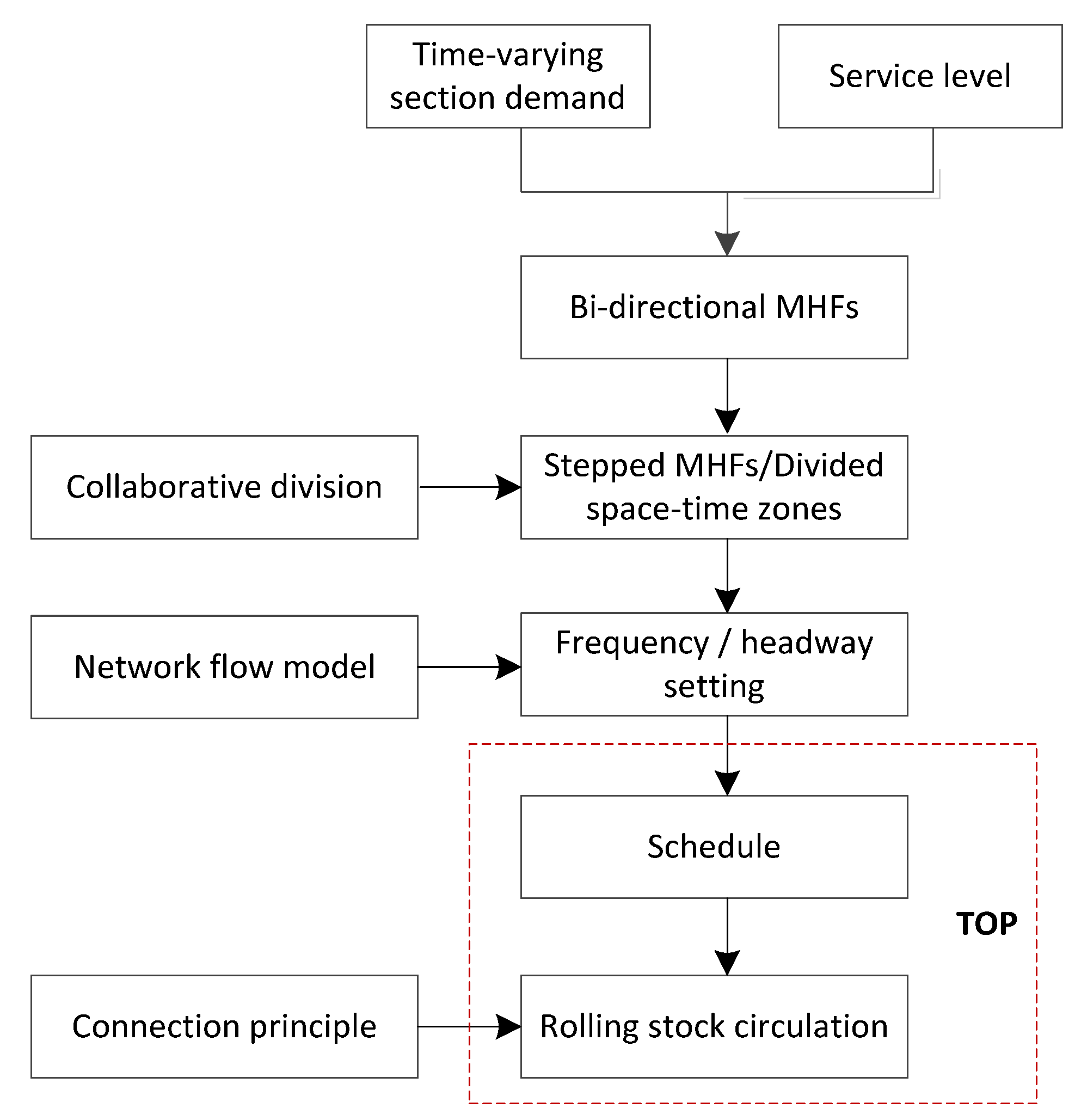
- Based on the time-varying section demand and predetermined service level, we collaboratively construct the bi-directional stepped MHFs to connect the two directions by sequences and obtain the space-time zones of trips departing in each divided interval.
- Using the division and stepped MHFs, we construct the trip flow circulation network to describe the relaxed circulation process of bi-directional trips, which is formulated by an integer linear programming (ILP) model to minimize the overall operation cost and obtain the optimized frequencies in each divided interval.
- The TOP is solved by a two-stage approach to sequentially obtain the schedule and rolling stock circulations at terminals based on the optimized frequencies and the corresponding stepped headways.
- The proposed approach is evaluated by an URT line in Shenzhen, China. Combined with the comparison with the practical TOP and the existing approach, the performance of the solved solution is measured in terms of service level, operation cost, as well as the efficiency of circulation and utilization. The impacts of involved circulation balance strategies on TOP optimization are further investigated.
2. Problem Statement
2.1. Maximum Headway Function
- During off-peak hours
- 2.
- During peak hours
2.2. Circulation Imbalance in TOP Optimization
3. Collaborative Construction of Bi-Directional Stepped Maximum Headway Function
| Algorithm 1: Division of connection sequences from down direction |
| Input Bi-directional MHFs , the operation period and the error threshold |
| Output and the corresponding stepped MHFs |
| Begin |
| ; |
| while |
| ; |
| ; |
| while do |
| ; |
| ; |
| end while |
| ; |
| Obtain by Equations (4)–(8); |
| while do |
| ; |
| ; |
| while do |
| ; |
| ; |
| end while |
| ; |
| Obtain by Equations (4)–(8); |
| end while |
| end while |
| End |
4. Network Flow Model Formulation for Circulation Process
4.1. Construction of Trip Flow Circulation Network
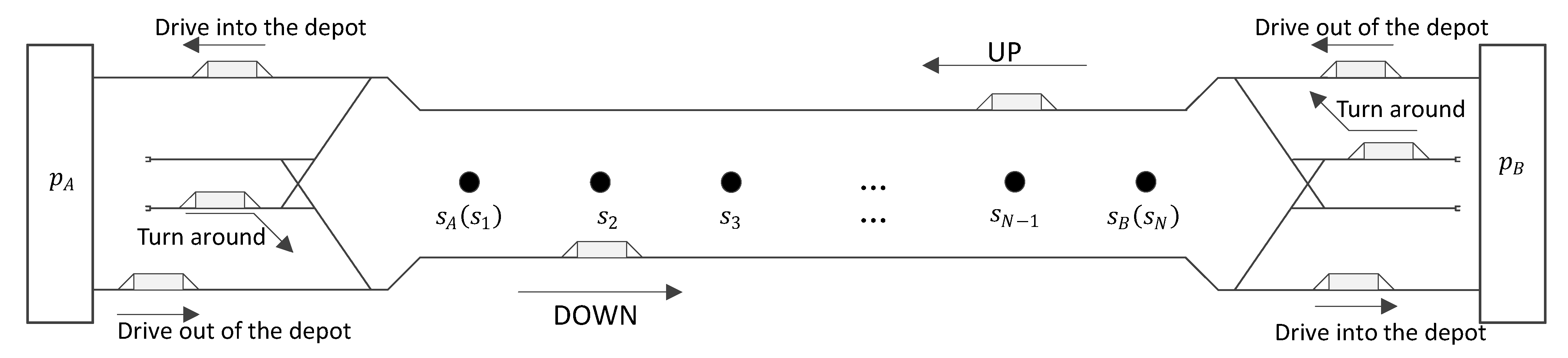
- Space-time nodes represent the divided bi-directional intervals with specific time lengths. Down-direction space-time nodes are denoted by and up-direction space-time nodes are denoted by , where are respectively the numbers of divided intervals from the two directions.
- Source nodes represent the two terminal depots . Because trips all depart from depots and would return depots after one day’s operation, the source nodes are also sink nodes in this network.
- Out-depot arcs represent the process that new rolling stocks drive out of depots to execute trips, denoted by and without capacity constraint or cost.
- Transmission arcs represent bi-directional trips’ running process between the two terminals, i.e., the connection sequences. The bi-directional transmission arcs and sets are denoted by and , which are determined by the specific incidence relationship in connection sequences. Since each divided interval has a specific stepped MHF, the flow lower bound of a transmission arc or is the frequency with the corresponding stepped MHF, while the flow upper bound of a transmission arc or is the frequency with the minimum headway . The cost factor of a transmission arc is , indicating the cost of executing a running trip.
- Waiting arcs, denoted by or , connect each two neighbor space-time nodes in the same direction and involve the waiting and connection process of trips at terminal stations and depots. In fact, waiting arcs only mean a relaxed circulation process because they cannot indicate specific connections between bi-directional trips or the corresponding connection locations. Thus, waiting arcs also have no capacity constraint or cost.
- In-depot arcs represent the process that trips return the depots after one day’s operation, denoted by and . The number of used rolling stocks from either depot cannot exceed the storage capacity of a depot . The cost factor of an in-depot arc is , indicating the operation cost of one used rolling stock.
4.2. Network Flow Model Formulation
5. Solution Method
5.1. Schedule Generation
5.2. Calculation of Rolling Stock Circulation
- (1)
- if , then ,;
- (2)
- .
| Algorithm 2: Solving procedure of rolling stock circulation at |
| Input Down-direction departure time , up-direction arrival time |
| Output Rolling stock circulation at |
|
|
|
|
6. Case Study
6.1. Input Data Setting
6.2. Performance Discussion
6.2.1. Headway Distribution of the Solved TOP
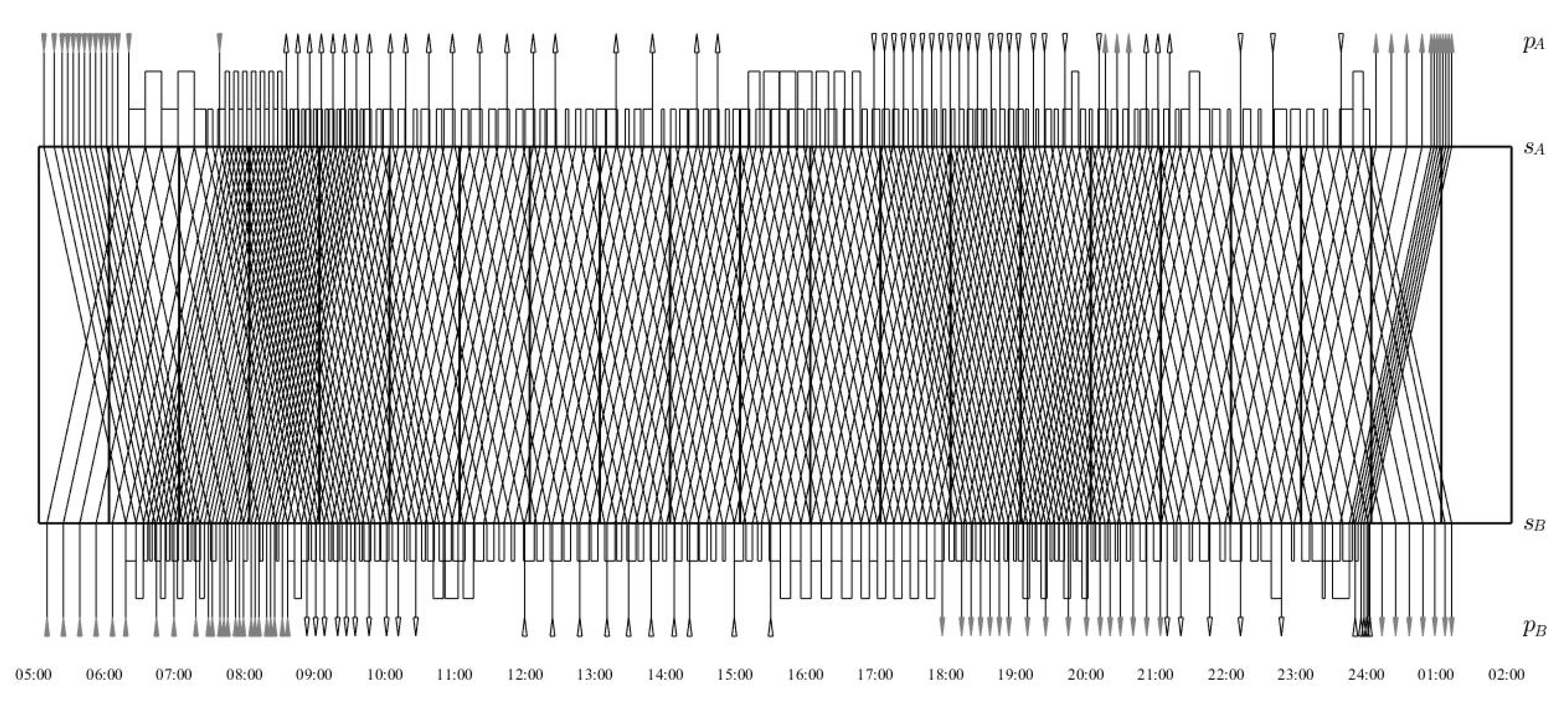
6.2.2. Rolling Stock Circulation of the Solved TOP
6.2.3. Comparison between the Practical TOP and the Solved TOP
6.2.4. Comparison between the Proposed Approach and the Existing Approach
6.3. Impact of Circulation Balance Strategies on TOP Optimization
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, S.; Yang, H.; Wu, Y. An integrated approach of train scheduling and rolling stock circulation with skip-stopping pattern for urban rail transit lines. Transp. Res. Part C Emerg. Technol. 2021, 128, 103170. [Google Scholar] [CrossRef]
- Shi, F.; Zhao, S.; Zhou, Z.; Wang, P.; Bell, M. Optimizing train operational plan in an urban rail corridor based on the maximum headway function. Transp. Res. Part C Emerg. Technol. 2017, 74, 51–80. [Google Scholar] [CrossRef]
- Wang, Y.; D’Ariano, A.; Yin, J.; Meng, L.; Tang, T. Passenger demand oriented train scheduling and rolling stock circulation planning for an urban rail transit line. Transp. Res. Part B Methodol. 2018, 118, 193–227. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, H.; Zhao, S.; Shang, P. Mitigating unfairness in urban rail transit operation: A mixed-integer linear programming approach. Transp. Res. Part B Methodol. 2021, 149, 418–442. [Google Scholar] [CrossRef]
- Ceder, A. Bus timetables with even passenger loads as opposed to even headways. Transp. Res. Rec. 2001, 1760, 3–9. [Google Scholar] [CrossRef]
- Ceder, A. Public-transport automated timetables using even headway and even passenger load concepts. In Proceedings of the 32nd Australasian Transport Research Forum, Auckland, New Zealand, 29 Semptember–1 October 2009. [Google Scholar]
- Guihaire, V.; Hao, J.-K. Transit network design and scheduling: A global review. Transp. Res. Part A Policy Pract. 2008, 42, 1251–1273. [Google Scholar] [CrossRef] [Green Version]
- Liebchen, C. The first optimized railway timetable in practice. Transp. Sci. 2008, 42, 420–435. [Google Scholar] [CrossRef]
- Kroon, L.; Maróti, G.; Helmrich, M.R.; Vromans, M.; Dekker, R. Stochastic improvement of cyclic railway timetables. Transp. Res. Part B Methodol. 2006, 42, 553–570. [Google Scholar] [CrossRef] [Green Version]
- Niu, H.; Zhou, X. Optimizing urban rail timetable under time-dependent demand and oversaturated conditions. Transp. Res. Part C Emerg. Technol. 2013, 36, 212–230. [Google Scholar] [CrossRef]
- Barrena, E.; Canca, D.; Coelho, L.C.; Laporte, G. Exact Formulations and Algorithm for the Train Timetabling Problem with Dynamic Demand. Comput. Oper. Res. 2014, 44, 66–74. [Google Scholar] [CrossRef]
- Barrena, E.; Canca, D.; Coelho, L.C.; Laporte, G. Single-line rail rapid transit timetabling under dynamic passenger demand. Transp. Res. Part B Methodol. 2014, 70, 134–150. [Google Scholar] [CrossRef]
- Sun, L.; Jin, J.G.; Lee, D.; Axhausen, K.W.; Erath, A. Demand-driven timetable design for metro services. Transp. Res. Part C Emerg. Technol. 2014, 46, 284–299. [Google Scholar] [CrossRef]
- Li, X.; Lo, H.K. Energy minimization in dynamic train scheduling and control for metro rail operations. Transp. Res. Part B Methodol. 2014, 70, 269–284. [Google Scholar] [CrossRef]
- Niu, H.; Zhou, X.; Gao, R. Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns: Nonlinear integer programming models with linear constraints. Transp. Res. Part B Methodol. 2015, 76, 117–135. [Google Scholar] [CrossRef]
- Hassannayebi, E.; Zegordi, S.H.; Yaghini, M. Train timetabling for an urban rail transit line using a Lagrangian relaxation approach. Appl. Math. Model. 2016, 40, 9892–9913. [Google Scholar] [CrossRef]
- Yin, J.; Yang, L.; Tang, T.; Gao, Z.; Ran, B. Dynamic passenger demand oriented metro train scheduling with energy-efficiency and waiting time minimization: Mixed-integer linear programming approaches. Transp. Res. Part B Methodol. 2017, 97 (Suppl. C), 182–213. [Google Scholar] [CrossRef]
- Zhang, T.; Li, D.; Qiao, Y. Comprehensive optimization of urban rail transit timetable by minimizing total travel times under time-dependent passenger demand and congested conditions. Appl. Math. Model. 2018, 58, 421–446. [Google Scholar] [CrossRef]
- Shang, P.; Li, R.; Liu, Z.; Xian, K.; Guo, J. Timetable synchronization and optimization considering time-dependent passenger demand in an urban subway network. Transp. Res. Rec. 2018, 2672, 243–254. [Google Scholar] [CrossRef]
- Shi, J.; Yang, L.; Yang, J.; Gao, Z. Service-oriented train timetabling with collaborative passenger flow control on an oversaturated metro line: An integer linear optimization approach. Transp. Res. Part B Methodol. 2018, 110, 26–59. [Google Scholar] [CrossRef]
- Freyss, M.; Giesen, R.; Muñoz, J. Continuous approximation for skip-stop operation in rail transit. Transp. Res. Part C Emerg. Technol. 2013, 36, 419–433. [Google Scholar] [CrossRef]
- Jamili, A.; Pourseyed-Aghaee, M. Robust stop-skipping patterns in urban rail operations under traffic alteration situation. Transp. Res. Part C Emerg. Technol. 2015, 61, 63–74. [Google Scholar] [CrossRef]
- Abdelhafiez, E.; Salama, M.; Shalaby, M. Minimizing passenger travel time in URT system adopting skip-stop strategy. J. Rail Transp. Plan. Manag. 2017, 7, 277–290. [Google Scholar] [CrossRef]
- Yang, S.; Wu, J.; Yang, X.; Liao, F.; Ding, D.; Wei, Y. Analysis of energy consumption reduction in metro systems using rolling stop-skipping patterns. Comput. Ind. Eng. 2019, 127, 129–142. [Google Scholar] [CrossRef]
- Yang, A.; Wang, B.; Huang, J.; Li, C. Service replanning in urban rail transit networks: Cross-line express trains for reducing the number of passenger transfers and travel time. Transp. Res. Part C Emerg. Technol. 2020, 115, 102629. [Google Scholar] [CrossRef]
- Gkiotsalitis, K. Periodic stop skipping: NP-hardness and computational limitations. In Proceedings of the 99th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 12–16 January 2020. [Google Scholar]
- Wang, Y.; De Schutter, B.; van den Boom, T.; Ning, B.; Tang, T. Efficient bi-level approach for urban rail transit operation with stop-skipping. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2658–2670. [Google Scholar] [CrossRef]
- Yang, L.; Qi, J.; Li, S.; Gao, Y. Collaborative optimization for train scheduling and train stop planning on high-speed railways. Omega 2016, 64, 57–76. [Google Scholar] [CrossRef]
- Yue, Y.; Wang, S.; Zhou, L.; Tong, L.; Saat, M. Optimizing train stopping patterns and schedules for high-speed rail corridors. Transp. Res. Part C Emerg. Technol. 2016, 63, 126–146. [Google Scholar] [CrossRef]
- Cacchiani, V.; Qi, J.; Yang, L. Robust optimization models for integrated train stop planning and timetabling with passenger demand uncertainty. Transp. Res. Part B Methodol. 2020, 136, 1–29. [Google Scholar] [CrossRef]
- Zhou, X.; Zhong, M. Single-track train timetabling with guaranteed optimality: Branch and bound algorithms with enhanced lower bounds. Transp. Res. Part B Methodol. 2007, 41, 320–341. [Google Scholar] [CrossRef]
- Cadarso, L.; Marín, Á. Robust routing of rapid transit rolling stock. Public Transp. 2010, 2, 51–68. [Google Scholar] [CrossRef]
- Cadarso, L.; Marín, Á. Robust rolling stock in rapid transit networks. Comput. Oper. Res. 2011, 38, 1131–1142. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liao, Z.; Tang, T.; Ning, B. Train scheduling and circulation planning in urban rail transit lines. Control Eng. Pract. 2017, 61, 112–123. [Google Scholar] [CrossRef]
- Cadarso, L.; Marín, Á. Integration of timetable planning and rolling stock in rapid transit networks. Ann. Oper. Res. 2012, 199, 113–135. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Tang, T.; Ning, B.; Meng, L. Integrated optimization of regular train schedule and train circulation plan for urban rail transit lines. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 83–104. [Google Scholar] [CrossRef]
- Yue, Y.; Han, J.; Wang, S.; Liu, X. Integrated train timetabling and rolling stock scheduling model based on time-dependent demand for urban rail transit. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 856–873. [Google Scholar] [CrossRef]
- Mo, P.; Yang, L.; D’Ariano, A.; Yin, J.; Yao, Y.; Gao, Z. Energy-efficient train scheduling and rolling stock circulation planning in a metro line: A linear programming approach. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3621–3633. [Google Scholar] [CrossRef]
- Yin, Y.; Li, D.; Běsinovic, N.; Cao, Z. Hybrid demand-driven and cyclic timetabling considering rolling stock circulation for a bidirectional railway line. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 164–187. [Google Scholar] [CrossRef]
- Yang, L.; Yao, Y.; Shi, H.; Shang, P. Dynamic passenger demand-oriented train scheduling optimization considering flexible short-turning strategy. J. Oper. Res. Soc. 2021, 72, 1707–1725. [Google Scholar] [CrossRef]
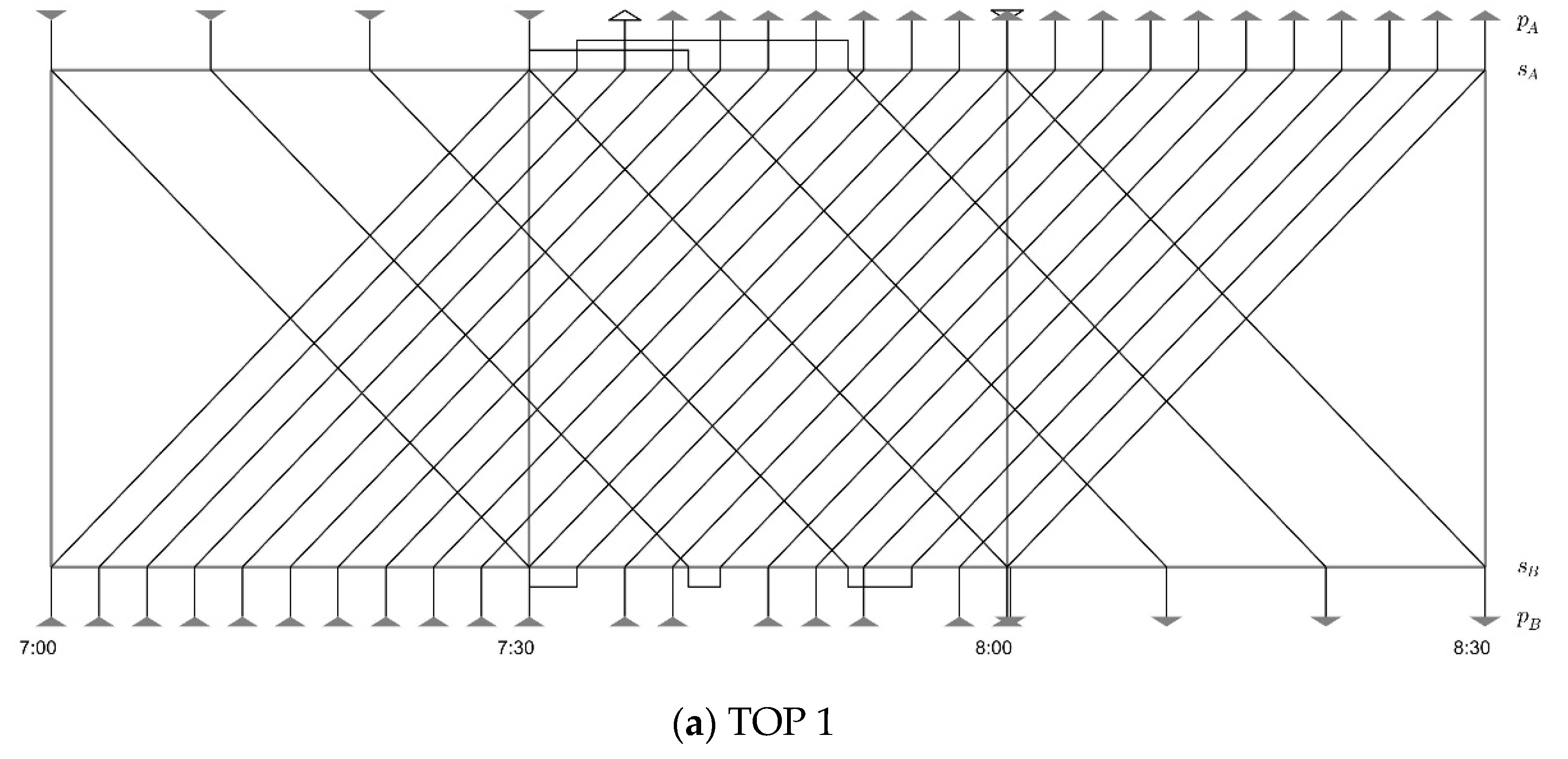
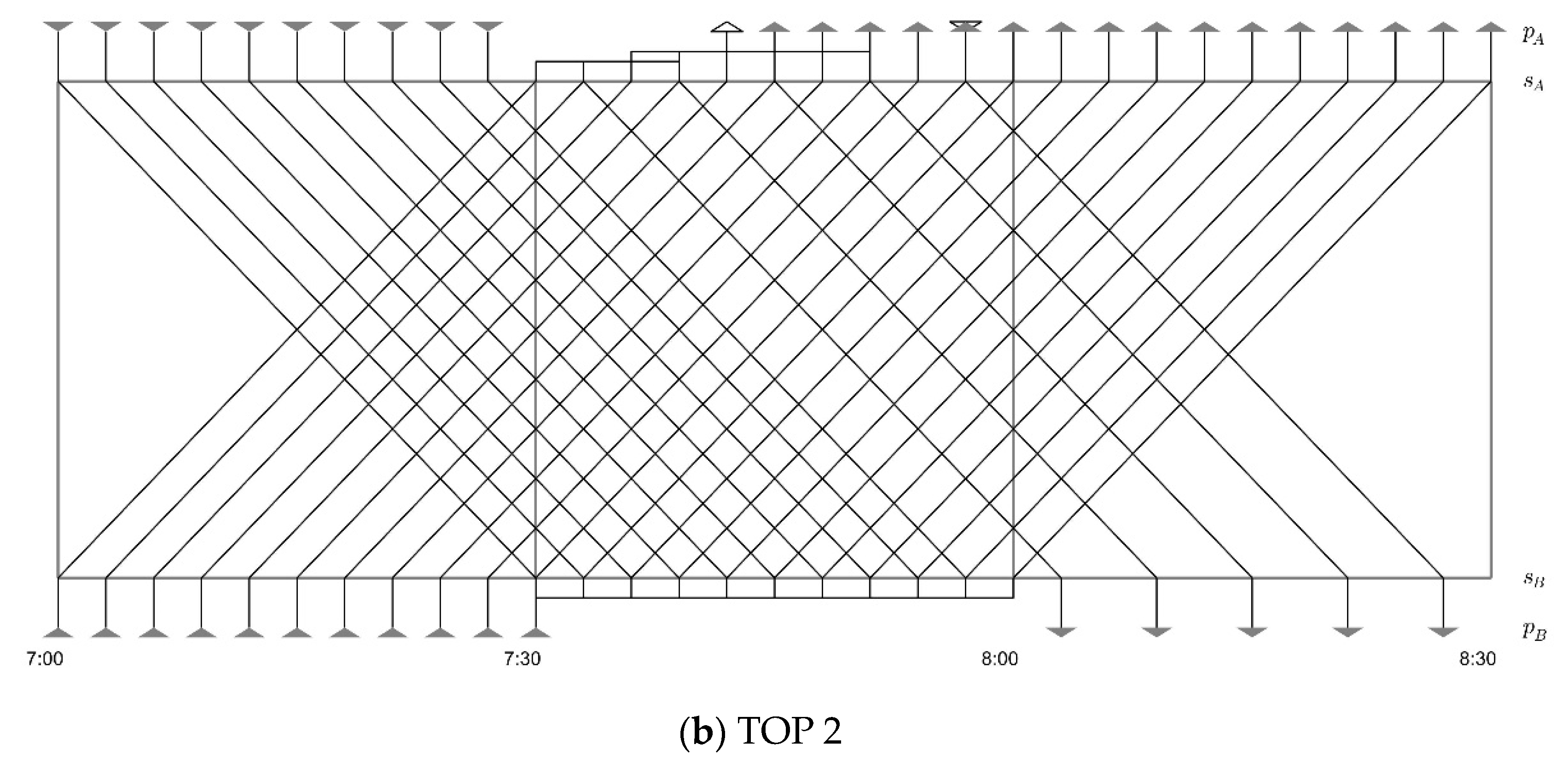




| TOP | TTN | NRS | DRS | CDS |
|---|---|---|---|---|
| TOP 1 | 28 | 22 | 14 | |
| TOP 2 | 36 | 21 | 1 |
| Rolling Stock | Connection Sequence |
|---|---|
| 1 | 1-7′-22->71′-70-93′88-113′-120-136′-147->165′ (returning ) |
| 2 | 2-8′-23-47′-53-68′-67-88′-83-108′-110-128′ (returning ) |
| 3 * | 3-9′-24-74′-72-95′-90-115′-123-138′-148-152′-164 (returning ) |
| 4 | 4-10′-25-48′->115-132′ (returning ) |
| 5 | 5-12′-27-49′-54-69′-68-90′-85-110′-114-131′-144-164′ (returning ) |
| 6 * | 6-13′-28-50′-55-70′-69-92′-87-112′-118-134′-146-151′-162 (returning ) |
| 7 * | 7-14′-29-80′-77-102′-98 (returning ) |
| 8 * | 8-16′-31-83′-79-104′-102 (returning ) |
| 9 | 9-17′-32-52′-56-72′-131-143′-152-155′ (returning ) |
| 10 * | 10-18′-33->86′-81-106′-106 (returning ) |
| 11 * | 11-19′-34-53′-57-73′-71-94′-89-114′-121 (returning ) |
| 12 * | 12-21′-36->89′-84-109′-112 (returning ) |
| 13 * | 13-22′->97-121′-134 (returning ) |
| 14 | 14-25′->99-122′-135-145′-154-158′ (returning ) |
| 15 | 21-46′->113-130′ (returning ) |
| Rolling Stock | Connection Sequence |
|---|---|
| 1 | 1′-15-29′-41->96′-91-116′-125 (returning ) |
| 2 | 2′-16-33′-44->100′-95 (returning ) |
| 3 * | 3′-17-37′->107-126′-140-147′-157-160′ (returning ) |
| 4 * | 4′-18-41′-49-64′-64-84′->141-163′ (returning ) |
| 5 | 5′-19-44′-51-66′-128 (returning ) |
| 6 | 6′-20-45′-52-67′-66-87′-82-107′-108 (returning ) |
| 7 * | 11′-26-77′-74-98′-93-118′-129-142′-151-166′ (returning ) |
| 8 | 15′-30-51′-117-133′-145-150′-161 (returning ) |
| 9 * | 20′-35-54′->119-135′-155-157′ (returning ) |
| 10 | 23′-37-55′-58-75′-73-97′-92-117′-127-141′-150-154′-166 (returning ) |
| 11* | 24′-38-56′-59-76′->133-144′-153-156′ (returning ) |
| 12 | 26′-39->91′-86-111′-116 (returning ) |
| 13 * | 27′-40-57′->122-137′->158-162′ (returning ) |
| 14 * | 28′->101-123′-137-146′-156-159′ (returning ) |
| 15 | 30′-42-58′-60-78′-75-99′-94-119′-130 (returning ) |
| 16 | 31′->103-124′-138 (returning ) |
| 17 | 32′-43-59′-61-79′-76-101′-96-120′-132 (returning ) |
| 18 * | 34′->105-125′-139->161′ (returning ) |
| 19 | 35′-45-60′->124-139′->163 (returning ) |
| 20 | 36′-46-61′-62-81′->136 (returning ) |
| 21 | 38′-47-62′-63-82′-78-103′-100 (returning ) |
| 22 | 39′-48-63′->126-140′-149-153′-165 (returning ) |
| 23 | 40′->109-127′-142-148′-159 (returning ) |
| 24 | 42′-50-65′-65-85′-80-105′-104 (returning ) |
| 25 | 43′-111-129′-143-149′-160 (returning ) |
| TOP | TTN | NRS (Total//) | NDO (Total//) | DRS |
|---|---|---|---|---|
| Practical TOP | 328 | 47/8/39 | 146/64/82 | 31 |
| Solved TOP | 332 | 40/15/25 | 156/76/80 | 10 |
| TOP | TTN | NRS (Total//) | NDO (Total//) | DRS |
|---|---|---|---|---|
| Existing approach | 292 | 76/5/71 | 250/108/142 | 66 |
| Proposed approach | 332 | 40/15/25 | 156/76/80 | 10 |
| TTN | NRS (Total//) | NDO (Total//) | DRS | |
|---|---|---|---|---|
| 0 | 342 | 40/20/20 | 174/86/88 | 0 |
| 0.25 | 332 | 40/15/25 | 156/76/80 | 10 |
| 0.50 | 326 | 40/12/28 | 160/78/82 | 16 |
| 0.75 | 318 | 40/8/32 | 160/70/90 | 24 |
| 1 | 318 | 40/8/32 | 156/66/90 | 24 |
| - | 318 | 40/8/32 | 156/68/88 | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Wu, J.; Li, Z.; Meng, G. Train Operational Plan Optimization for Urban Rail Transit Lines Considering Circulation Balance. Sustainability 2022, 14, 5226. https://doi.org/10.3390/su14095226
Zhao S, Wu J, Li Z, Meng G. Train Operational Plan Optimization for Urban Rail Transit Lines Considering Circulation Balance. Sustainability. 2022; 14(9):5226. https://doi.org/10.3390/su14095226
Chicago/Turabian StyleZhao, Shuo, Jinfei Wu, Zhenyi Li, and Ge Meng. 2022. "Train Operational Plan Optimization for Urban Rail Transit Lines Considering Circulation Balance" Sustainability 14, no. 9: 5226. https://doi.org/10.3390/su14095226
APA StyleZhao, S., Wu, J., Li, Z., & Meng, G. (2022). Train Operational Plan Optimization for Urban Rail Transit Lines Considering Circulation Balance. Sustainability, 14(9), 5226. https://doi.org/10.3390/su14095226






